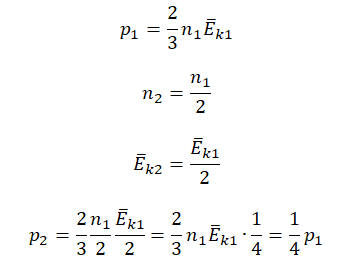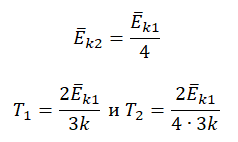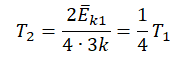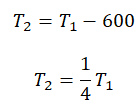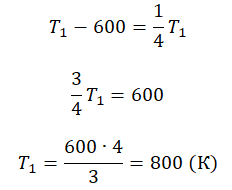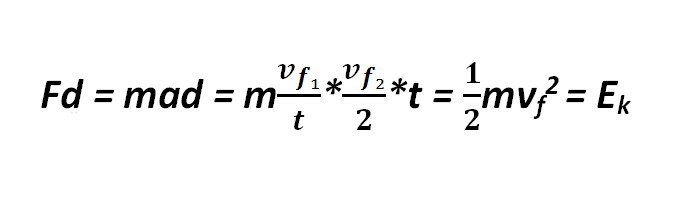Как найти изменение кинетической энергии молекул - Autoru.top

Средняя кинетическая энергия теплового движения молекул газа.

Уравнение состояния
идеального газа в форме pV
= nRT
или p
= nkT может
быть обосновано и методами кинетической
теории газов. На основе кинетического
подхода сравнительно просто выводится
выражение для давления идеального газа
в сосуде, которое получается как результат
усреднения импульсов молекул, передаваемых
стенке сосуда при многочисленных
соударениях молекул со стенкой. Величина
получаемого при этом давления определяется
как

Где бv²с – среднее
значение квадрата скорости молекул, m
– масса молекулы.

Средняя кинетическая
энергия молекул газа (в расчете на одну
молекулу) определяется выражением

Кинетическая
энергия поступательного движения атомов
и молекул, усредненная по огромному
числу беспорядочно движущихся частиц,
является мерилом того, что называется
температурой. Если температура T
измеряется в градусах Кельвина (К), то
связь ее с E_k
дается соотношением

Это соотношение
позволяет, в частности, придать более
отчетливый физический смысл постоянной
Больцмана

Внутренняя
энергия идеального газа.

В теории идеального газа потенциальная
энергия взаимодействия молекул считается
равной нулю. Поэтому внутренняя энергия
идеального газа определяется кинетической
энергией движения всех его молекул.
Средняя энергия движения одной молекулы
равна

Так как в одном киломоле содержится
молекул,
то внутренняя энергия одного киломоля
газа будет

Учитывая,
что,
получим

Для любой массы m газа, т.е. для любого
числа киломолей
внутренняя
энергия

(10.12)

Из этого выражения следует, что внутренняя
энергия является однозначной функцией
состояния и, следовательно, при совершении
системой любого процесса, в результате
которого система возвращается в исходное
состояние, полное изменение внутренней
энергии равно нулю. Математически это
записывается в виде тождества

Распределение
Максвелла

Распределение
Ма́ксвелла—распределение
вероятности, встречающееся вфизикеихимии.
Оно лежит в основаниикинетической
теории газов, которая объясняет
многие фундаментальные свойства газов,
включаядавлениеидиффузию.
Распределение Максвелла также применимо
для электронных процессов переноса и
других явлений. Распределение Максвелла
применимо к множеству свойств
индивидуальных молекул в газе. О нём
обычно думают как о распределении
энергий молекул в газе, но оно может
также применяться к распределению
скоростей, импульсов, и модуля импульсов
молекул. Также оно может быть выражено
как дискретное распределение по множеству
дискретных уровней энергии, или как
непрерывное распределение по некоторому
континууму энергии.

Распределение Максвелла может и должно
быть получено при помощи статистической
механики(см. происхождениестатсуммы).
Как распределение энергии, оно
соответствует самому вероятному
распределению энергии, в
столкновительно-доминируемой системе,
состоящей из большого количества
невзаимодействующих частиц, в которой
квантовые эффекты являются незначительными.
Так как взаимодействие между молекулами
в газе является обычно весьма небольшим,
распределение Максвелла даёт довольно
хорошее приближение ситуации, существующей
в газе.

Во многих других случаях, однако, даже
приблизительно не выполнено условие
доминирования упругих
соударенийнад всеми другими
процессами. Это верно, например, в физикеионосферыи космическойплазмы,
где процессы рекомбинации и столкновительного
возбуждения (то есть излучательные
процессы) имеют большое значение, в
особенности для электронов. Предположение
о применимости распределения Максвелла
дало бы в этом случае не только
количественно неверные результаты, но
даже предотвратило бы правильное
понимание физики процессов на качественном
уровне. Также, в том случае где квантоваяде
Бройлева длина волнычастиц
газа не является малой по сравнению с
расстоянием между частицами, будут
наблюдаться отклонения от распределения
Максвелла из-за квантовых эффектов.

Распределение энергии Максвелла может
быть выражено как дискретное распределение
энергии:

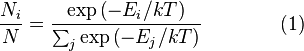
где
является
числом молекул имеющих энергиюпри
температуре системы,является
общим числом молекул в системе и—постоянная
Больцмана. (Отметьте, что иногда
вышеупомянутое уравнение записывается
с множителем,
обозначающим степень вырождения
энергетических уровней. В этом случае
сумма будет по всем энергиям, а не всем
состояниям системы). Поскольку скорость
связана с энергией, уравнение (1) может
использоваться для получения связи
между температурой и скоростями молекул
в газе. Знаменатель в уравнении (1)
известен как каноническаястатистическая
сумма.

Распределение
Больцмана.

Распределение Больцмана—
распределение вероятностей различных
энергетических состоянийидеальной
термодинамической системы (идеальный
газ атомов или молекул)в условияхтермодинамического
равновесия; открытоЛ.
Больцманомв1868—1871.

Согласно распределению Больцманасреднее число частиц с полной энергиейравно

где
—
кратность состояния частицы с энергией—
число возможных состояний частицы с
энергией.
Постояннаянаходится
из условия, что суммапо
всем возможным значениямравна
заданному полному числу частицв
системе (условие нормировки):

В случае, когда движение частиц подчиняется
классической механике, энергию
можно
считать состоящей из

кинетической энергии
(кин)
частицы (молекулы или атома),
внутренней энергии
(вн)
(например, энергии возбуждения электронов)
и
потенциальной энергии
(пот)
во внешнем поле, зависящей от положения
частицы в пространстве:

Явление переноса.
Диффузия

В термодинамически
неравновесных системах происходят
особые необратимые процессы, называемые
явлениями
переноса, в
результате которых осуществляется
пространственный перенос массы, импульса,
энергии. К явлениям переноса относятся
теплопроводность
(перенос энергии), диффузия
(перенос массы) и внутреннее
трение
(перенос импульса). Ограничимся одномерными
явлениями переноса. Систему отсчета
будем выберать так, чтобы ось х была
направлена в сторону в направления пер

Диффузия.
При происходит самопроизвольное
проникновение и перемешивание частиц
двух соприкасающихся газов, жидкостей
и даже твердых тел; диффузия есть обмен
масс частиц этих тел, при этом явление
возникает и продолжается, пока существует
градиент плотности. Во времена становления
молекулярно-кинетической теории по
вопросу явления диффузии возникли
противоречия. Поскольку молекулы
перемещаются в пространстве с огромными
скоростями, то диффузия должна происходить
очень быстро. Если же открыть в комнате
крышку сосуда с пахучим веществом, то
запах распространяется довольно
медленно. Но здесь нет противоречия.
При атмосферном давлении молекулы
обладают малой длиной свободного пробега
и, при столкновениях с другими молекулами,
приемущественно «стоят» на месте.

Явление диффузии для химически
однородного газа подчиняется закону
Фика:

(3)

где j_m
— плотность
потока массы
— величина, определяемая массой вещества,
диффундирующего в единицу времени через
единичную площадку, перпендикулярную
оси х, D — диффузия
(коэффициент
диффузии),
dρ/dx — градиент плотности, который равен
скорости изменения плотности на единицу
длины х в направлении нормали к этой
площадке. Знак минус говорит о том, что
перенос массы происходит в направлении
убывания плотности (поэтому знаки j_mи dρ/dx противоположны). Диффузия D численно
равна плотности потока массы при
градиенте плотности, равном единице.
Согласно кинетической теории газов,(4)

Явление переноса.
Теплопроводность

Теплопроводность.
Если в первой области газа средняя
кинетическая энергия молекул больше,
чем во второй, то вследствие постоянных
столкновений молекул с течением времени
происходит процесс выравнивания средних
кинетических энергий молекул, т. е.,
выравнивание температур. Перенос энергии
в форме теплоты подчиняется закону
Фурье:

(1)

где j_E
— плотность
теплового потока
— величина, которая определяется
энергией, переносимой в форме теплоты
в единицу времени через единичную
площадку, перпендикулярную оси х, λ —
теплопроводность,
— градиент температуры, равный скорости
изменения температуры на единицу длины
х в направлении нормали к этой площадке.
Знак минус говорит о том, что во время
теплопроводности энергия перемещается
в направлении убывания температуры
(поэтому знаки j_E
и – противоположны). Теплопроводность
λ равна плотности теплового потока при
градиенте температуры, равном единице.

Можно показать, что

(2)

где с_V
— удельная
теплоемкость
газа при постоянном объеме (количество
теплоты, которое необходимо для нагревания
1 кг газа на 1 К при постоянном объеме),
ρ — плотность газа, <ν>
— средняя скорость теплового движения
молекул, <l>
— средняя длина свободного пробега.

Явление переноса.
Вязкость

Внутреннее
трение
(вязкость).
Суть механизма возникновения внутреннего
трения между параллельными слоями газа
(жидкости), которые движущутся с различными
скоростями, есть в том, что из-за
хаотического теплового движения
осуществляется обмен молекулами между
слоями, в результате чего импульс слоя,
который движется быстрее, уменьшается,
который движется медленнее — увеличивается,
что приводит к торможению слоя, который
движется быстрее, и ускорению слоя,
который движется медленнее.

Как
известно, сила внутреннего трения между
двумя слоями газа (жидкости) подчиняется
закону
Ньютона:

(5)

где η — динамическая вязкость
(вязкость), dν/dx
— градиент скорости, который показывает
быстроту изменения скорости в направлении
х, перпендикулярном направлению движения
слоев, S — площадь, на которую действует
сила F.

Согласно второму закону
Ньютона взаимодействие двух слоев можно
рассматривать как процесс, при котором
в единицу времени от одного слоя к
другому передается импульс, который по
модулю равен действующей силе. Тогда
выражение (5) можно записать в виде

(6)

где j_p
— плотность
потока импульса
— величина, которая определяется
определяемая полным импульсом, переносимым
в единицу времени в положительном
направлении оси х через единичную
площадку, перпендикулярную оси х, dν/dx
— градиент скорости. Знак минус говорит
о том, что импульс переносится в
направлении убывания скорости (поэтому
знаки j_p
и dν/dx
противоположны).

Динамическая
вязкость η
численно равна плотности потока импульса
при градиенте скорости, равном единице;
она вычисляется по формуле

(7)

Из сопосавления формул (1), (3) и (6),
которые описывают явления переноса,
следует, что закономерности всех явлений
переноса сходны между собой. Эти законы
были известны еще задолго до того, как
они были обоснованы и получены из
молекулярно-кинетической теории, которая
позволила установить, что внешнее
сходство их математических выражений
является следствием общностью лежащего
в основе явлений теплопроводности,
диффузии и внутреннего трения молекулярного
механизма перемешивания молекул в
процессе их хаотического движения и
столкновений друг с другом.

Рассмотренные
законы Фурье, Фика и Ньютона не вскрывают
молекулярно-кинетической сути
коэффициентов λ, D и η. Выражения для
коэффициентов переноса получаются из
кинетической теории. Они записаны без
вывода, поскольку строгое и формальное
рассмотрение явлений переноса довольно
громоздко, а качественное — не имеет
смысла. Формулы (2), (4) и (7) дают связь
коэффициентов переноса и характеристики
теплового движения молекул. Из этих
формул следуют простые зависимости
между λ, D и η:и

Реальный газы.
Уравнение Ван-дер-Ваальса. Изотермы
реального газа.

Реальный газ—газ,
который не описывается уравнением
состояния идеального газа Клапейрона —
Менделеева.

Зависимости между
его параметрами показывают, что молекулы
в реальном газе взаимодействуют между
собой и занимают определенный объём.
Состояние реального газа часто на
практике описывается обобщённым
уравнением Менделеева — Клапейрона:

где p — давление;
V — объем; T — температура; Z_r
= Z_r
(p,T) — коэффициент
сжимаемости
газа; m — масса; М — молярная
масса;
R — газовая
постоянная.

Уравнение
состояния газа Ван-дер-Ваальса—уравнение,
связывающее основные термодинамические
величины
в модели газа Ван-дер-Ваальса.

Хотя модель
идеального
газа
хорошо описывает поведение реальных
газов
при низких давлениях
и высоких температурах,
в других условиях её соответствие с
опытом
гораздо хуже. В частности, это проявляется
в том, что реальные
газы
могут быть переведены в жидкое
и даже в твёрдое
состояние,
а идеальные — не могут.

Для более точного
описания поведения реальных газов при
низких температурах была создана модель
газа Ван-дер-Ваальса, учитывающая силы
межмолекулярного взаимодействия. В
этой модели внутренняя
энергия
становится
функцией не толькотемпературы,
но и объёма.

Уравнение
Ван-дер-Ваальса — это одно из широко
известных приближённых уравнений
состояния, имеющее компактную форму и
учитывающее основные характеристики
газа с межмолекулярным взаимодействием^[1].

-Поскольку весь
процесс происходит при постоянной
температуре T,
кривую, что изображает зависимость
давления р от объёма V,
называют изотермой.
При объёме V₁
начинается конденсация
газа, а при объёме V₂
она заканчивается. Если V > V₁
то вещество будет в газообразном
состоянии, а при V < V₂ —
в жидком.

Твёрдое тело.
Закон Дюлонга и Пти. Тепловое расширение
твердых тел. Плавление.

Твёрдое тело —
это одно из четырёх агрегатных
состояний вещества,
отличающееся от других агрегатных
состояний (жидкости,
газов,
плазмы)
стабильностью формы и характером
теплового
движения
атомов,
совершающих малые колебания
около положений равновесия^[1].

Различают
кристаллические
и аморфные
твёрдые тела. Раздел физики,
изучающий состав и внутреннюю структуру
твёрдых тел, называется физикой
твёрдого тела.
То, как твёрдое тело меняет форму при
воздействиях и движении, изучается
отдельной дисциплиной — механикой
твёрдого (деформируемого) тела.
Движением абсолютно твёрдого тела
занимается третья наука — кинематика
твёрдого тела.

Технические
приспособления, созданные человеком,
используют различные свойства твёрдого
тела. В прошлом твёрдое тело применялось
как конструкционный материал и в основе
употребления лежали непосредственно
ощутимые механические свойства как то
твёрдость,
масса,
пластичность,
упругость,
хрупкость.
В современном мире применение твёрдого
тела основывается на физических
свойствах, которые зачастую обнаруживаются
только при лабораторных исследованиях.

Закон Дюлонга —
Пти
(Закон
постоянства теплоёмкости) —
эмпирический
закон,
согласно которому молярная
теплоёмкость
твёрдых тел при комнатной температуре
близка к 3R^[1]:

где R —
универсальная
газовая постоянная.

Закон выводится
в предположении, что кристаллическая
решетка тела состоит из атомов, каждый
из которых совершает гармонические
колебания
в трех направлениях, определяемыми
структурой решетки, причем колебания
по различным направлениям абсолютно
независимы друг от друга. При этом
получается, что каждый атом представляет
три
осциллятора
с энергией E,
определяемой следующей формулой:

Формула вытекает
из теоремы о равнораспределении энергии
по степеням свободы. Так как каждый
осциллятор имеет одну степень
свободы,
то его средняя кинетическая
энергия
равна
,
а так как колебания происходят
гармонически, то средняяпотенциальная
энергия
равна средней кинетической, а полная
энергия — соответственно их сумме.
Число осцилляторов в одном моле вещества
составляет
,
их суммарная энергия численно равна
теплоемкости тела — отсюда и вытекает
закон Дюлонга-Пти.

Приведем таблицу
экспериментальных значений теплоемкости
ряда химических элементов для нормальных
температур:

Элемент	, кал/(К·моль)	Элемент	, кал/(К·моль)
C	1,44	Pt	6,11
B	2,44	Au	5,99
Al	5,51	Pb	5,94
Ca	5,60	U	6,47
Ag	6,11	—	—

Тепловое
расширение—изменение
линейных размеров и формы тела при
изменении его температуры.
Количественно тепловое расширение
жидкостей и газов при постоянном давлении
характеризуется изобарным
коэффициентом
расширения
(объёмным коэффициентом теплового
расширения). Для характеристики теплового
расширения твёрдых тел дополнительно
вводят коэффициент линейного теплового
расширения.

Раздел физики
изучающий данное свойство называется
дилатометрией.

Тепловое расширение
тел учитывается при конструировании
всех установок, приборов и машин,
работающих в переменных температурных
условиях.

Основной закон
теплового расширения
гласит, что тело с линейным размером
в
соответствующем измерении при увеличении
его температуры нарасширяется
на величину,
равную:

где
—
так называемыйкоэффициент
линейного теплового расширения.
Аналогичные формулы имеются для расчета
изменения площади и объема тела. В
приведенном простейшем случае, когда
коэффициент теплового расширения не
зависит ни от температуры, ни от
направления расширения, вещество будет
равномерно расширяться по всем
направлениям в строгом соответствии с
вышеприведенной формулой.

Плавле́ние—это процесс перехода
тела из кристаллического
твёрдого состояния в жидкое, то есть
переход вещества из одного агрегатного
состояния
в другое. Плавление происходит с
поглощением удельной
теплоты плавления
и является фазовым
переходом
первого рода, которое сопровождается
скачкообразным
изменением теплоёмкости
в конкретной для каждого вещества
температурной точке превращения —
температура
плавления.

Способность
плавиться
относится к физическим
свойствам
вещества^[1]

При нормальном
давлении, наибольшей температурой
плавления
среди металлов
обладает вольфрам
(3422 °C), среди простых
веществ —
углерод
(по разным данным 3500 — 4500 °C^[2])
а среди произвольных веществ — карбид
тантала-гафния
Ta₄HfC₅
(4216 °C). Можно считать, что самой низкой
температурой плавления обладает гелий:
при нормальном давлении он остаётся
жидким при сколь угодно низких
температурах.

Многие вещества
при нормальном давлении не имеют жидкой
фазы. При нагревании они путем сублимации
сразу переходят в газообразное состояние.

Жидкости.
Поверхностное плавление. Смачивание.

Жи́дкость—
вещество, находящееся в жидком агрегатном
состоянии,
занимающем промежуточное положение
между твёрдым и газообразным состояниями^[1].
Основным свойством жидкости, отличающим
её от веществ, находящихся в других
агрегатных состояниях, является
способность неограниченно менять форму
под действием касательных механических
напряжений, даже сколь угодно малых,
практически сохраняя при этом объём.

Поверхностные
явления,физико-химические
явления, которые обусловлены особыми
(по сравнению с объемными) свойствами
поверхностных слоев жидкостей
и твердых тел. Наиболее общее и важное
свойство этих слоев — избыточная свободная
энергия F = sS,
где s-поверхностное (межфазное) натяжение,
для твердых тел — удельная свободная
поверхностная
энергия.
S-площадь
поверхности раздела фаз. Поверхностные
явления протекают наиболее выраженно
в гетерогенных системах с сильно развитой
поверхностью раздела фаз, т. е. в дисперсных
системах. Изучение
закономерностей поверхностных явлений
является составной частью коллоидной
химии
и чрезвычайно важно для всех ее
практических приложений.

Самопроизвольные
поверхностные явления происходят
вследствие уменьшения поверхностной
энергии системы.
Они могут быть обусловлены уменьшением
общей поверхности системы либо уменьшением
поверхностного натяжения на границе
раздела фаз. К поверхностным явлениям,
связанным с уменьшением общей поверхности,
относят: 1) капиллярные
явления.
в частности приобретение каплями (в
туманах) и газовыми пузырьками (в жидкой
среде) сферич. формы, при которой
поверхность капли (пузырька) минимальна.
2) Коалесценция
— слияние капель в эмульсиях
(или газовых пузырьков в пенах)при
их непосредств. контакте. 3) Спекание
мелких твердых частиц в порошках
при достаточно высоких температурах.
4) Собирательная рекристаллизация —
укрупнение зерен поликристаллического
материала при повышении температуры.
5) Изотермическая перегонка
— увеличение объема крупных капель за
счет уменьшения мелких. При этом
вследствие повышенного давления
паров
жидкости с более высокой кривизной
поверхности происходит испарение
мелких капель и последующая их конденсация
на более крупных каплях. Для жидкости,
находящейся на твердой подложке,
существенная роль в переносе вещества
от мелких капель к крупным играет
поверхностная диффузия.
Изотермическая перегонка
твердых частиц может происходить через
жидкую фазу вследствие повышенной
растворимости более мелких частиц.

При определенных
условиях в системе могут происходить
самопроизвольные поверхностные явления,
сопровождающиеся увеличением общей
поверхности раздела фаз. Так,
самопроизвольное диспергирование и
образование устойчивых лиофильных
коллоидных
систем
(например, критических эмульсий)
происходит в условиях, когда увеличение
поверхностной энергии, вызываемое
измельчением
частиц, компенсируется их вовлечением
в тепловое движение и соответствующим
возрастанием энтропии
(см. Микроэмульсии).
При гомогенном
образовании зародышей новой фазы при
конденсации паров, кипении.
кристаллизации
из растворов и расплавов
увеличение энергии системы вследствие
образования новой поверхности
компенсируется уменьшением хим.
потенциала вещества при фазовом
переходе.
Критические размеры зародышей, при
превышении которых выделение новой
фазы идет самопроизвольно, зависят от
поверхностного натяжения, а также от
величины перегрева (переохлаждения,
пересыщения). Связь между этими параметрами
определяется уравнением Гиббса (см.
Зарождение
новой фазы).

Сма́чивание—физическое
взаимодействие жидкости
с поверхностью твёрдого
тела
или другой жидкости. Смачивание бывает
двух видов:

Иммерсионное
(вся поверхность твёрдого тела
контактирует с жидкостью)
Контактное
(состоит из трёх фаз — твердая,
жидкая, газообразная)

Смачивание зависит
от соотношения между силами сцепления
молекул
жидкости с молекулами (или атомами)
смачиваемого тела (адгезия)
и силами взаимного сцепления молекул
жидкости (когезия).

Если жидкость
контактирует с твёрдым телом, то
существуют две возможности:

молекулы жидкости
притягиваются друг к другу сильнее,
чем к молекулам твёрдого тела. В
результате силы притяжения между
молекулами жидкости собирают её в
капельку. Так ведёт себя ртуть
на стекле,
вода
на парафине
или «жирной» поверхности. В этом случае
говорят, что жидкость не
смачивает
поверхность;
молекулы жидкости
притягиваются друг к другу слабее, чем
к молекулам твёрдого тела. В результате
жидкость стремится прижаться к
поверхности, расплывается по ней. Так
ведёт себя ртуть на цинковой
пластине, вода на чистом стекле или
дереве. В этом случае говорят, что
жидкость смачивает
поверхность.

Степень смачивания
характеризуется углом смачивания. Угол
смачивания (или краевой угол смачивания)
— это угол, образованный касательными
плоскостями к межфазным поверхностям,
ограничивающим смачивающую жидкость,
а вершина угла лежит на линии раздела
трёх фаз. Измеряется методом лежащей
капли^[1].
В случае порошков надёжных методов,
дающих высокую степень воспроизводимости,
пока (по состоянию на 2008 год) не разработано.
Предложен весовой метод определения
степени смачивания, но он пока не
стандартизован.

Измерение степени
смачивания весьма важно во многих
отраслях промышленности (лакокрасочная,
фармацевтическая, косметическая
и т. д.). К примеру, на лобовые стёкла
автомобилей наносят особые покрытия,
которые должны быть устойчивы против
разных видов загрязнений. Состав и
физические свойства покрытия стёкол и
контактных линз можно сделать оптимальным
по результатам измерения контактного
угла^[2].

К примеру, популярный
метод увеличения добычи нефти при помощи
закачки воды в пласт исходит из того,
что вода заполняет поры и выдавливает
нефть.
В случае мелких пор и чистой воды это
далеко не так, поэтому приходится
добавлять специальные ПАВ.
Оценку смачиваемости горных пород при
добавлении различных по составу растворов
можно измерить различными приборами.

Источник

Определение

Идеальный газ — газ, удовлетворяющий трем условиям:

Молекулы — материальные точки.
Потенциальная энергия взаимодействия молекул пренебрежительно мала.
Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 ^oC).
По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

∆t = ∆T

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

T = t + 273

Если особо важна точность, следует использовать более точную формулу:

T = t + 273,15

Пример №1. Температура воды равна ^oC. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p=23n−Ek

p — давление идеального газа, n — концентрация молекул газа, −Ek — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p=13m0n−v2

m0— масса одной молекулы газа;

n — концентрация молекул газа;

−v2 — среднее значение квадрата скорости молекул газа.

Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости:

v=√−v2

p=13ρ−v2

ρ — плотность газа

p=nkT

k — постоянная Больцмана (k = 1,38∙10^–3 Дж/кг)

T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v=√3kTm0=√3RTM

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R=NAk=8,31 Дж/К·моль

Температура — мера кинетической энергии молекул идеального газа:

−Ek=32kT

T=2−Ek3k

Полная энергия поступательного движения молекул газа определяется формулой:

E=N−Ek

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Следовательно:

Составим систему уравнений:

Отсюда:

Задание EF19012

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

1.Указать, в каких координатах построен график.

2.На основании основного уравнения МКТ идеального газа и уравнения Менделеева — Клапейрона выяснить, как меняются указанные физические величины во время процессов 1–2 и 2–3.

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

T=2−Ek3

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

pV=νRT

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

νR=p1V1T1=p2V2T2

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

Ответ:

• Участок 1–2 — изобарный процесс. Температура увеличивается, давление постоянно.

• Участок 2–3 — изотермический процесс. Температура постоянно, давление увеличивается.

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17560

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Ответ:

а) 13p1

б) 2p1

в) 23p1

г) 43p1

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для состояний 1 и 2.

4.Выразить искомую величину.

Решение

Исходные данные:

• Начальное давление: p₀.

• Начальная концентрация молекул: n₁ = 3n.

• Конечная концентрация молекул: n₂ = n.

• Начальная средняя энергия хаотичного движения молекул: E_k1 = E_k.

• Конечная средняя энергия хаотичного движения молекул: E_k2 = 2E_k.

Основное уравнение МКТ:

p=23n−Ek

Составим уравнения для начального и конечного состояний:

p1=23n1−Ek1=233n−Ek=2n−Ek

p2=23n2−Ek2=23n2−Ek=43n−Ek

Отсюда:

n−Ek=p12=3p24

p2=4p16=23p1

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18416

Цилиндрический сосуд разделён неподвижной теплоизолирующей перегородкой. В одной части сосуда находится кислород, в другой – водород, концентрации газов одинаковы. Давление кислорода в 2 раза больше давления водорода. Чему равно отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода?

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение средней кинетической энергии молекул кислорода к средней кинетической энергии молекул водорода.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Концентрации кислорода и водорода в сосуде равны. Следовательно, n₁ = n₂ = n.

• Давление кислорода вдвое выше давления водорода. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n−Ek1

p2=23n2−Ek2 или p=23n−Ek2

Выразим среднюю кинетическую энергию молекул газа из каждого уравнения:

−Ek1=3pn

−Ek2=3p2n

Поделим уравнения друг на друга и получим:

−Ek1−Ek2=3pn·2n3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18824

В одном сосуде находится аргон, а в другом – неон. Средние кинетические энергии теплового движения молекул газов одинаковы. Давление аргона в 2 раза больше давления неона. Чему равно отношение концентрации молекул аргона к концентрации молекул неона?

Алгоритм решения

1.Записать исходные данные.

2.Записать основное уравнение МКТ идеального газа.

3.Составить уравнения для обоих газов.

4.Найти отношение концентрации молекул аргона к концентрации молекул неона.

Решение

Анализируя условия задачи, можно выделить следующие данные:

• Средние кинетические энергии теплового движения молекул газов одинаковы. Следовательно, −Ek1=−Ek2=−Ek.

• Давление аргона в 2 раза больше давления неона. Следовательно, p₁ = 2p, а p₂ = p.

Запишем основное уравнение идеального газа:

p=23n−Ek

Применим его для обоих газов и получим:

p1=23n1−Ek1 или 2p=23n1−Ek

p2=23n2−Ek2 или p=23n2−Ek

Выразим концентрации молекул газа из каждого уравнения:

n1=3p−Ek

n2=3p2−Ek

Поделим уравнения друг на друга и получим:

n1n2=3p−Ek·2−Ek3p=2

Ответ: 2

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 10.8k

Источник

Повседневный опыт показывает, что недвижимые тела можно привести в движение, а движимые остановить. Мы с вами постоянно что-то делаем, мир вокруг суетится, светит солнце… Но откуда у человека, животных, да и у природы в целом берутся силы для выполнения этой работы? Исчезает ли механическое движение бесследно? Начнет ли двигаться одно тело без изменения движения другого? Обо всем этом мы расскажем в нашей статье.

Понятие энергии

Для работы двигателей, которые придают движение автомобилям, тракторам, тепловозам, самолетам, нужно топливо, которое является источником энергии. Электродвигатели придают движение станкам при помощи электроэнергии. За счет энергии воды, падающей с высоты, оборачиваются гидротурбины, соединенные с электрическими машинами, производящими электрический ток. Человеку для того, чтобы существовать и работать, также нужна энергия. Говорят, что для того, дабы выполнять какую-нибудь работу, необходима энергия. Что же такое энергия?

Наблюдение 1. Поднимем над землей мяч. Пока он пребывает в состоянии спокойствия, механическая работа не выполняется. Отпустим его. Под действием силы тяжести мяч падает на землю с определенной высоты. Во время падения мяча выполняется механическая работа.
Наблюдение 2. Сомкнем пружину, зафиксируем ее нитью и поставим на пружину гирьку. Подожжем нить, пружина распрямится и поднимет гирьку на некую высоту. Пружина выполнила механическую работу.
Наблюдение 3. На тележку закрепим стержень с блоком в конце. Через блок перекинем нить, один конец которой намотан на ось тележки, а на другом висит грузик. Отпустим грузик. Под действием силы тяжести он будет опускаться книзу и придаст тележке движение. Грузик выполнил механическую работу.

После анализа всех вышеперечисленных наблюдений можно сделать вывод, что если тело или несколько тел во время взаимодействия выполняют механическую работу, то говорят, что они имеют механическую энергию, либо энергию.

Понятие энергии

Энергия (от греч. слова энергия — деятельность) — это физическая величина, которая характеризирует способность тел выполнять работу. Единицей энергии, а также и работы в системе СИ является один Джоуль (1 Дж). На письме энергия обозначается буквой Е. Из вышеуказанных экспериментов видно, что тело выполняет работу тогда, когда переходит из одного состояния в другое. Энергия тела при этом меняется (уменьшается), а выполненная телом механическая работа равна результату изменения ее механической энергии.

Виды механической энергии. Понятие потенциальной энергии

Различают 2 вида механической энергии: потенциальную и кинетическую. Сейчас подробнее рассмотрим потенциальную энергию.

Потенциальная энергия (ПЭ) — это энергия, определяющаяся взаимным положением тел, которые взаимодействуют, либо частями того самого тела. Поскольку любое тело и земля притягивают друг друга, то есть взаимодействуют, ПЭ тела, поднятого над землей, будет зависеть от высоты поднятия h. Чем выше поднято тело, тем больше его ПЭ. Экспериментально установлено, что ПЭ зависит не только от высоты, на которую оно поднято, но и от массы тела. Если тела были подняты на одинаковую высоту, то тело, имеющее большую массу, будет иметь и большую ПЭ. Формула данной энергии выглядит следующим образом: E_п = mgh, где E_п — это потенциальна энергия, m — масса тела, g = 9,81 Н/кг, h — высота.

Потенциальная энергия пружины

Потенциальной энергией упруго деформированного тела называют физическую величину E_п,которая при изменении скорости поступательного движения под действием сил упругости уменьшается ровно на столько, на сколько растет кинетическая энергия. Пружины (как и другие упруго деформированные тела) имеют такую ПЭ, которая равна половине произведения их жесткости k на квадрат деформации: x = kx²:2.

Энергия кинетическая: формула и определение

Иногда значение механической работы можно рассматривать без употребления понятий силы и перемещения, акцентировав внимание на том, что работа характеризует изменение энергии тела. Все, что нам может потребоваться, — это масса некоего тела и его начальная и конечная скорости, что приведет нас к кинетической энергии. Кинетическая энергия (КЭ) — это энергия, принадлежащая телу вследствие собственного движения.

Кинетическую энергию имеет ветер, ее используют для придания движения ветряным двигателям. Движимые массы воздуха оказывают давление на наклонные плоскости крыльев ветряных двигателей и заставляют их оборачиваться. Вращательное движение при помощи систем передач передается механизмам, выполняющим определенную работу. Движимая вода, оборачивающая турбины электростанции, теряет часть своей КЭ, выполняя работу. Летящий высоко в небе самолет, помимо ПЭ, имеет КЭ. Если тело пребывает в состоянии покоя, то есть его скорость относительно Земли равна нулю, то и его КЭ относительно Земли равна нулю. Экспериментально установлено, что чем больше масса тела и скорость, с которой оно движется, тем больше его КЭ. Формула кинетической энергии поступательного движения в математическом выражении следующая:

Где К — кинетическая энергия, m — масса тела, v — скорость.

Изменение кинетической энергии

Поскольку скорость движения тела является величиной, зависящей от выбора системы отсчета, значение КЭ тела также зависит от ее выбора. Изменение кинетической энергии (ИКЭ) тела происходит вследствие действия на тело внешней силы F. Физическую величину А, которая равна ИКЭ ΔЕ_ктела вследствие действия на него силы F, называют работой: А = ΔЕ_к. Если на тело, которое движется со скоростью v₁, действует сила F, совпадающая с направлением, то скорость движения тела вырастет за промежуток времени t к некоторому значению v₂. При этом ИКЭ равно:

Где m — масса тела; d — пройденный путь тела; V_f1 = (V₂— V₁); V_f2= (V₂+ V₁); a = F : m. Именно по этой формуле высчитывается, на сколько изменяется энергия кинетическая. Формула также может иметь следующую интерпретацию: ΔЕ_к= Flcosά, где cosά является углом между векторами силы F и скорости V.

Средняя кинетическая энергия

Кинетическая энергия представляет собой энергию, определяемую скоростью движения разных точек, которые принадлежат этой системе. Однако следует помнить, что необходимо различать 2 энергии, характеризующие разные виды движения: поступательное и вращательное. Средняя кинетическая энергия (СКЭ) при этом является средней разностью между совокупностью энергий всей системы и ее энергией спокойствия, то есть, по сути, ее величина — это средняя величина потенциальной энергии. Формула средней кинетической энергии следующая:

где k — это константа Больцмана; Т — температура. Именно это уравнение является основой молекулярно-кинетической теории.

Средняя кинетическая энергия молекул газа

Многочисленными опытами было установлено, что средняя кинетическая энергия молекул газа в поступательном движении при заданной температуре одна и та же, и не зависит от рода газа. Кроме того, было установлено также, что при нагревании газа на 1 ^оС СКЭ увеличивается на одно и то же самое значение. Сказать точнее, это значение равно: ΔЕ_к = 2,07 х 10^-23Дж/^оС. Для того чтобы вычислить, чему равна средняя кинетическая энергия молекул газа в поступательном движении, необходимо, помимо этой относительной величины, знать еще хотя бы одно абсолютное значение энергии поступательного движения. В физике достаточно точно определены эти значения для широкого спектра температур. К примеру, при температуре t = 500 ^оС кинетическая энергия поступательного движения молекулы Ек = 1600 х 10^-23Дж. Зная 2 величины (ΔЕ_к и Е_к), мы можем как вычислить энергию поступательного движения молекул при заданной температуре, так и решить обратную задачу — определить температуру по заданным значениям энергии.

Напоследок можно сделать вывод, что средняя кинетическая энергия молекул, формула которой приведена выше, зависит только от абсолютной температуры (причем для любого агрегатного состояния веществ).

Закон сохранения полной механической энергии

Изучение движения тел под действием силы тяжести и сил упругости показало, что существует некая физическая величина, которую называют потенциальной энергией Е_п; она зависит от координат тела, а ее изменение приравнивается ИКЭ, которая взята с противоположным знаком: ΔЕ_{п =}—ΔЕ_к. Итак, сумма изменений КЭ и ПЭ тела, которые взаимодействуют с гравитационными силами и силами упругости, равна 0: ΔЕ_п+ ΔЕ_к = 0. Силы, которые зависят только от координат тела, называют консервативными. Силы притяжения и упругости являются консервативными силами. Сумма кинетической и потенциальной энергий тела является полной механической энергией: Е_п+ Е_к = Е.

Этот факт, который был доказан наиболее точными экспериментами,
называют законом сохранения механической энергии. Если тела взаимодействуют силами, которые зависят от скорости относительного движения, механическая энергия в системе взаимодействующих тел не сохраняется. Примером сил такого типа, которые называются неконсервативными, являются силы трения. Если на тело действуют силы трения, то для их преодоления необходимо затратить энергию, то есть ее часть используется на выполнение работы против сил трения. Однако нарушение закона сохранения энергии здесь только мнимое, потому что он является отдельным случаем общего закона сохранения и преобразования энергии. Энергия тел никогда не исчезает и не появляется вновь: она лишь преобразуется из одного вида в другой. Этот закон природы очень важен, он выполняется повсюду. Его еще иногда называют общим законом сохранения и преобразования энергии.

Связь между внутренней энергией тела, кинетической и потенциальной энергиями

Внутренняя энергия (U) тела — это его полная энергия тела за вычетом КЭ тела как целого и его ПЭ во внешнем поле сил. Из этого можно сделать вывод, что внутренняя энергия состоит из КЭ хаотического движения молекул, ПЭ взаимодействия между ними и внутремолекулярной энергии. Внутренняя энергия — это однозначная функция состояния системы, что говорит о следующем: если система находится в данном состоянии, ее внутренняя энергия принимает присущие ему значения, независимо от того, что происходило ранее.

Релятивизм

Когда скорость тела близка к скорости света, кинетическую энергию находят по следующей формуле:

Кинетическая энергия тела, формула которой была написана выше, может также рассчитываться по такому принципу:

Примеры задач по нахождению кинетической энергии

1. Сравните кинетическую энергию шарика массой 9 г, летящего со скоростью 300 м/с, и человека массой 60 кг, бегущего со скоростью 18 км/час.

Итак, что нам дано: m₁ = 0,009 кг; V₁ = 300 м/с; m₂ = 60 кг, V₂ = 5 м/с.

Решение:

Энергия кинетическая (формула): Е_к= mv²:2.
Имеем все данные для расчета, а поэтому найдем Е_к и для человека, и для шарика.
Е_к1= (0,009 кг х (300 м/с)²) : 2 = 405 Дж;
Е_к2= (60 кг х (5 м/с)²) : 2= 750 Дж.
Е_к1< Е_к2.

Ответ: кинетическая энергия шарика меньше, чем человека.

2. Тело с массой 10 кг было поднято на высоту 10 м, после чего его отпустили. Какую КЭ оно будет иметь на высоте 5 м? Сопротивлением воздуха разрешается пренебречь.

Итак, что нам дано: m = 10 кг; h = 10 м; h₁= 5 м; g = 9,81 Н/кг. Е_к1— ?

Решение:

Тело определенной массы, поднятое на некую высоту, имеет потенциальную энергию: E_п = mgh. Если тело падает, то оно на некоторой высоте h₁будет иметь пот. энергию E_п = mgh₁ и кин. энергию Е_к1.Чтобы была правильно найдена энергия кинетическая, формула, которая была приведена выше, не поможет, а поэтому решим задачу по нижеследующему алгоритму.
В этом шаге используем закон сохранения энергии и запишем: Е_п1+ Е_к1 = Е_п.
Тогда Е_к1 = Е_п — Е_п1= mgh — mgh₁= mg(h-h₁).
Подставив наши значения в формулу, получим: Е_к1= 10 х 9,81(10-5) = 490,5 Дж.

Ответ: Е_к1 = 490,5 Дж.

3. Маховик, имеющий массу m и радиус R, оборачивается вокруг оси, проходящей через его центр. Угловая скорость оборачивания маховика — ω. Дабы остановить маховик, к его ободу прижимают тормозную колодку, действующей на него с силой F_трения. Сколько оборотов сделает маховик до полной остановки? Учесть, что масса маховика сосредоточена по ободу.

Итак, что нам дано: m; R; ω; F_{трения.}N — ?

Решение:

При решении задачи будем считать обороты маховика подобными оборотам тонкого однородного обруча с радиусом R и массой m, который оборачивается с угловой скоростью ω.
Кинетическая энергия такого тела равна: Е_к= (Jω²) : 2, где J = mR².
Маховик остановится при условии, что вся его КЭ истратится на работу по преодолению силы трения F_{трения,}возникающей между тормозной колодкой и ободом: Е_к= F_трения*s_,гдеs — это тормозной путь, который равен 2πRN.
Следовательно, F_трения*2πRN= (mR²ω²) : 2, откуда N = (mω²R) : (4πF_тр).

Ответ: N = (mω²R) : (4πF_тр).

В заключение

Энергия — это важнейшая составляющая во всех аспектах жизни, ведь без нее никакие тела не смогли бы выполнять работу, в том числе и человек. Думаем, статья вам внятно дала понять, что собой представляет энергия, а развернутое изложение всех аспектов одной из ее составляющих — кинетической энергии — поможет вам осознать многие процессы, происходящих на нашей планете. А уж о том, как найти кинетическую энергию, вы можете узнать из приведенных выше формул и примеров решения задач.

Источник

Уравнение состояния идеального газа

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: модель идеального газа, связь между давлением и средней кинетической энергией теплового движения молекул идеального газа, связь температуры газа со средней кинетической энергией его частиц, уравнение , уравнение Менделеева—Клапейрона.

Из трёх агрегатных состояний вещества наиболее простым для изучения является газообразное. В достаточно разреженных газах расстояния между молекулами намного больше размеров самих молекул (тогда как в жидкостях и твёрдых телах молекулы «упакованы» весьма плотно).Поэтому силы взаимодействия между молекулами таких газов очень малы.

Для описания разреженных газов в физике используется модель идеального газа. В рамках этой модели делаются следующие допущения.

1. Пренебрегаем размерами молекул. Иными словами, молекулы газа считаются материальными точками.
2. Пренебрегаем взаимодействием молекул на расстоянии.
3. Соударения молекул друг с другом и со стенками сосуда считаем абсолютно упругими.

Таким образом, идеальный газ — это газ, частицы которого являются не взаимодействующими на расстоянии материальными точками и испытывают абсолютно упругие соударения друг с другом и со стенками сосуда.

Средняя кинетическая энергия частиц газа

Оказывается, что ключевую роль в описании идеального газа играет средняя кинетическая энергия его частиц.

Частицы газа двигаются с разными скоростями. Пусть в газе содержится частиц, скорости которых равны . Масса каждой частицы равна m_0 . Кинетические энергии частиц:

$E_1=frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}, E_2=frac{displaystyle m_0 v_2^2 }{displaystyle 2 vphantom{1^a}}, ldots,E_N=frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}}.$

Средняя кинетическая энергия частиц газа это среднее арифметическое их кинетических энергий:

$E=frac{displaystyle E_1+E_2+ ldots+E_N}{displaystyle N vphantom{1^a}}= frac{displaystyle 1}{displaystyle N vphantom{1^a}}left ( frac{displaystyle m_0 v_1^2}{displaystyle 2 vphantom{1^a}}+frac{displaystyle m_0 v_2^2}{displaystyle 2 vphantom{1^a}}+ ldots + frac{displaystyle m_0 v_N^2}{displaystyle 2 vphantom{1^a}} right ) =frac{displaystyle m_0}{displaystyle 2 vphantom{1^a}} frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Последний множитель — это средний квадрат скорости, обозначаемый просто v_2 :

$v_2=frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}.$

Тогда формула для средней кинетической энергии приобретает привычный вид:

$E=frac{displaystyle m_0 v^2}{displaystyle 2 vphantom{1^a}}.$ (1)

Корень из среднего квадрата скорости называется средней квадратической скоростью:

$v=sqrt{ frac{displaystyle v_1^2+v_2^2+ ldots v_N^2}{displaystyle N vphantom{1^a}}}.$

Основное уравнение МКТ идеального газа

Cвязь между давлением газа и средней кинетической энергией его частиц называется основным уравнением молекулярно-кинетической теории идеального газа. Эта связь выводится из законов механики и имеет вид:

$p= frac{displaystyle 2}{displaystyle 3 vphantom{1^a}} nE.$ (2)

где — концентрация газа (число частиц в единице объёма). С учётом (1) имеем также:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} m_0 nv^2.$ (3)

Что такое m_0n ? Произведение массы частицы на число частиц в единице объёма даёт массу единицы объёма, то есть плотность: . Получаем третью разновидность основного уравнения:

$p= frac{displaystyle 1}{displaystyle 3 vphantom{1^a}} rho v^2.$ (4)

Энергия частиц и температура газа

Можно показать, что при установлении теплового равновесия между двумя газами выравниваются средние кинетические энергии их частиц. Но мы знаем, что при этом становятся равны и температуры газов. Следовательно, температура газа — это мера средней кинетической энергии его частиц.

Собственно, ничто не мешает попросту отождествить эти величины и сказать, что температура газа — это средняя кинетическая энергия его молекул. В продвинутых курсах теоретической физики так и поступают. Определённая таким образом температура измеряется в энергетических единицах — джоулях.

Но для практических задач удобнее иметь дело с привычными кельвинами. Связь средней кинетической энергии частиц и абсолютной температуры газа даётся формулой:

$E= frac{displaystyle 3}{displaystyle 2 vphantom{1^a}} kT,$ (5)

где $k=1,38 cdot 10^{-23}$ Дж/К — постоянная Больцмана.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Уравнение состояния идеального газа» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

С течением времени в любом теле или системе тел устанавливается тепловое равновесие ― равенство температур. Если два тела с равными температурами находятся в контакте, между ними не будет происходить обмен тепловой энергией. Если в контакте находятся горячее и холодное тело ― то более нагретое тело будет отдавать энергию, остывая, а более холодное ― получать тепловую энергию, нагреваясь. Процесс теплообмена будет проходить до тех пор, температура двух тел не станет одинаковой.

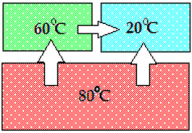
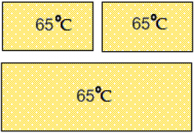
Пример теплообмена для системы из трех тел:

Горячее тело передает тепловую энергию холодному телу:

Тело с температурой 60°С горячее тела с температурой 20°С и передает ему тепло; тело с температурой 80°С передает тепло двум другим телам ― с температурами 60° и 20°С

Спустя некоторое время все три тела придут в состояние теплового равновесия: их температура станет одинаковой, а передача тепла от одного тела к другому прекратится.

Чем выше температура тела, тем выше скорость хаотического движения молекул тела. При нагревании тела кинетическая энергия движения его молекул увеличивается, т. к. кинетическая энергия молекулы прямо пропорциональна квадрату ее скорости.

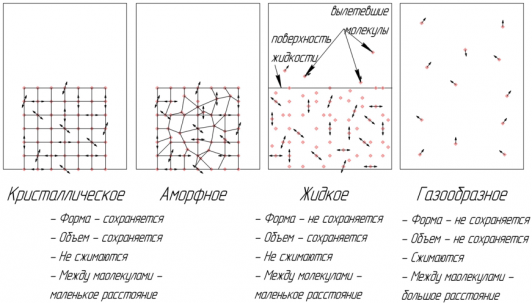
Существуют четыре фазовых (агрегатных) состояния вещества: кристаллическое, аморфное, жидкое и газообразное. Вещество в аморфном состоянии внешне твердое, но его внутренняя структура такая же, как у жидкостей.

Кристаллические и аморфные тела сохраняют свою форму и объем, не сжимаются.

Жидкости сохраняют свой объем, но не сохраняют форму, практически не сжимаются.

Газы занимают весь предоставленный объем. Газы сжимаются за счет того, что расстояние между молекулами газа намного превышает размеры самих молекул.

Структура кристаллических тел обладает дальним порядком ― расположение молекул повторяется практически без изменения на расстояниях, превышающих размеры молекул.

Структура аморфных тел и жидкостей обладает ближним порядком ― расположение повторяется только на расстояниях, соизмеримых с размерами молекулы.

Молекулы газов не связаны друг с другом и порядком расположения молекул не обладают.

Чем выше температура ― тем с большей скоростью колеблются молекулы твердых тел и жидкостей относительно места своего положения. При повышении температуры газов увеличивается скорость свободно перемещающихся в объеме молекул.

Так как у всех молекул скорость движения разная, некоторые молекулы жидкости оказываются достаточно быстрыми, чтобы преодолеть притяжение всех других молекул и вылететь за пределы поверхности жидкости ― из-за вылета молекул происходит постепенно испарение жидкости из открытого сосуда.

Фазовые переходы ― это переходы вещества из одного агрегатного состояния в другое.

Плавление ― переход тела из кристаллического агрегатного состояния в жидкое. При этом вся подводимая тепловая энергия, как только твердое тело нагрето до температуры плавления, тратится на разрыв кристаллической решетки. Потенциальная энергия молекул вещества увеличивается, а кинетическая остается постоянной. Во время плавления не смотря на подвод тепла температура тела остается неизменной.

Кристаллизация ― переход тела из жидкого агрегатного состояния в кристаллическое. Это процесс, обратный процессу плавления, он начинается, когда температура тела опускается до точки кристаллизации (численно она равна точке плавления). Во время кристаллизации тепловая энергия телом выделяется, а потенциальная энергия молекул вещества уменьшается за счет того, что образуется кристаллическая решетка. Температура тела во время кристаллизации постоянна.

Кипение (парообразование) ― переход тела из жидкого агрегатного состояния в газообразное. Кипение начинается, как только температура тела достигла температуры кипения. После этого температура тела не увеличивается, а вся подводимая тепловая энергия расходуется на разрыв связей между молекулами жидкости и увеличение расстояния между ними. Во время кипения переход в газообразное состояние происходит во всем объеме кипящей жидкости.

Конденсация ― переход тела из газообразного агрегатного состояния в жидкое. Это процесс обратный кипению, он начинается, как только температура газа понизилась до точки кипения. Во время конденсации выделяется тепловая энергия, а потенциальная энергия молекул газа уменьшается за счет образования межмолекулярных связей. Температура во время процесса конденсации постоянна.

В некоторых случаях возможна сублимация ― переход сразу из твердого состояния тела в газообразное, и конденсация из газообразного состояния в твердое.

Внутренняя энергия вещества U состоит из кинетической энергии его молекул (или атомов) EK и потенциальной энергии их связей EП.

U = EK + EП.

Кинетическая энергия вещества увеличивается во время нагревания, и уменьшается во время остывания. Потенциальная энергия вещества увеличивается во время плавления и кипения, и уменьшается во время кристаллизации и конденсации. Следовательно, внутренняя энергия вещества увеличивается во время его нагревания, плавления и кипения ― Q ˃ 0, и уменьшается во время остывания, кристаллизации и конденсации ― Q ˂ 0.

Процесс	Количество теплоты Q	Кинетическая энергия молекул EK	Потенциальная энергия связи между молекулами EП
Нагревание	Увеличивается	Увеличивается	Не изменяется
Плавление	Увеличивается	Не изменяется	Увеличивается
Парообразование	Увеличивается	Не изменяется	Увеличивается
Остывание	Уменьшается	Уменьшается	Не изменяется
Кристаллизация	Уменьшается	Не изменяется	Уменьшается
Конденсация	Уменьшается	Не изменяется	Уменьшается

Количество теплоты, затрачиваемое на изменение температуры тела равно:

Q = cm∆T, где

Q ― количество теплоты, которое вещество получило (при нагревании) или отдало (при охлаждении), [Дж],

с ― удельная теплоемкость вещества, [Дж/кг∙К],

m ― масса вещества, [кг],

∆Т ― изменение температуры вещества, [C].

Удельная теплоемкость вещества ― c [Дж/кг∙К] ― показывает, какое количество теплоты нужно затратить на то, чтобы нагреть 1 кг вещества на 1 С или 1 К. Для разных веществ, и для разных агрегатных состояний одного и того же вещества, удельная теплоемкость различна. Такое же количество теплоты выделяется при охлаждении 1 кг вещества на 1 С.

Количество теплоты, которое затрачивается на переход вещества из твердого в жидкое состояние (плавление и кристаллизация):

Q = λm, где

Q ― количество теплоты, которые вещество получило (при плавлении) или отдало (при кристаллизации), [Дж],

λ ― удельная теплота плавления, [Дж/кг],

m ― масса вещества, [кг].

Количество теплоты, которое затрачивается на переход вещества из жидкого в газообразное состояние (парообразование и конденсация):

Q = rm, где

Q ― количество теплоты, которые вещество получило (при кипении) или отдало (при конденсации), [Дж],

r ― удельная теплота парообразования, [Дж/кг],

m ― масса вещества, [кг].

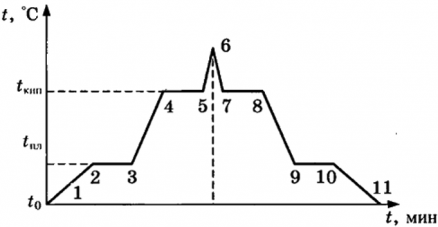
На рисунке показаны тепловые процессы при нагревании и охлаждении тела.

1-2 ― нагревание твердого тела от температуры t0 до температуры плавления tпл;

2-3 ― плавление твердого тела. Тепло к телу подводится, но температура тела остается постоянной и равной tпл;

3-4 ― нагревание жидкости от температуры плавления tпл до температуры кипения tкип;

4-5 ― парообразование. Тепло к телу подводится, но температура остается постоянной и равной tкип;

5-6 ― нагревание газа;

6-7 ― охлаждение газа;

7-8 ― конденсация жидкости из газа. Тело выделяет тепло, температура его остается постоянной и равной tкип;

8-9 ― охлаждение жидкости, от температуры кипения tкип до температуры плавления tпл;

9-10 ― кристаллизация. Тело выделяет тепло, температура его постоянна и равна tпл;

10-11 ― охлаждение твердого тела от tпл до t0.

Испарение ― превращение жидкости в газ при температуре ниже температуры кипения. Испарение происходит из-за того, что скорости теплового движениях всех молекул в жидкости различны, и всегда есть некоторое количество молекул, скорость движения которых достаточно большая, чтобы преодолеть притяжение всех остальных молекул и выскочить за пределы поверхности жидкости.

Испарение происходит только с поверхности жидкости и существует при любой температуре (кипение ― во всем объеме жидкости и только при температуре кипения). При испарении жидкость покидают наиболее быстрые молекулы, следовательно, остаются более медленные ― а значит, общая температура жидкости понижается.

Испарение происходит тем быстрее, чем выше температура жидкости (больше быстрых молекул), чем больше площадь открытой поверхности жидкости и чем ниже влажность воздуха.

Процесс, обратный испарению, когда молекулы из газообразного состояния переходят в жидкое, также называется конденсацией.

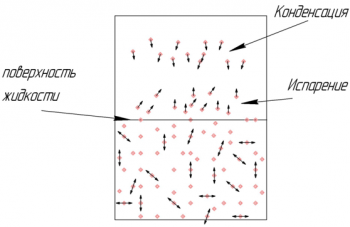
Насыщенный пар ― это пар, находящийся в динамическом равновесии со своей жидкостью: с поверхности жидкости испаряется столько же молекул, переходя в газ, сколько из газа конденсируется молекул, переходя в жидкое состояние.

Давление насыщенного пара не зависит от объема, который он занимает. Давление насыщенного пара увеличивается только за счет повышения его температуры (чем выше температура газа ― тем быстрее скорость молекул).

Относительная влажность воздуха равна:

 $text{Ф} = frac{p_{text{пара}}(Т)}{p_{text{насыщ.пара}}(T)}cdot 100% ;; text{или} ; ; text{Ф} = frac{rho_{text{пара}}(T)}{rho_{text{насыщ.пара}}(T)} cdot 100 %$, где

p пара (Т) ― давление пара при данной температуре Т, [Па],

p насыщ. пара (Т) ― давление насыщенного пара при данной температуре, [Па],

ρ пара (Т) ― плотность пара при данной температуре, [кг/м3]. Плотность пара также называют абсолютной влажностью воздуха,

ρ насыщ. пара( Т) ― плотность насыщенного пара при данной температуре, [кг/м3].

Давление и плотность насыщенного пара обычно определяются по таблицам.

Точка росы ― температура, при которой пар, находящийся в воздухе, становится насыщенным. При этой температуре относительная влажность воздуха равна 100%.

Относительная влажность воздуха не может превышать 100% ― при ϕ = 100% весь пар в воздухе является насыщенным паром ― т. е. сколько молекул испаряется с поверхности жидкости, столько и конденсируется.

Источник

Средняя кинетическая энергия теплового движения молекул газа.

Измерение температуры

Основное уравнение МКТ идеального газа

Следствия из основного уравнения МКТ идеального газа

Понятие энергии

Понятие энергии

Виды механической энергии. Понятие потенциальной энергии

Потенциальная энергия пружины

Энергия кинетическая: формула и определение

Изменение кинетической энергии

Средняя кинетическая энергия

Средняя кинетическая энергия молекул газа

Закон сохранения полной механической энергии

Связь между внутренней энергией тела, кинетической и потенциальной энергиями

Релятивизм

Примеры задач по нахождению кинетической энергии

В заключение

Уравнение состояния идеального газа

Средняя кинетическая энергия частиц газа

Основное уравнение МКТ идеального газа

Энергия частиц и температура газа

Не пропустите также: