Как найти изменение энергии заряженного конденсатора - Autoru.top

Содержание книги

Предыдующая страница

§16. Превращение энергии в электрических и магнитных явлениях

16.7 Изменение энергии конденсатора при изменении его емкости.

Энергия конденсатора зависит от его емкости. Емкость конденсатора можно изменять, когда он заряжен — при этом будет изменяться его энергия. При рассмотрении этих процессов можно выделить два принципиально различных случая: первый — изменение емкости происходит при неизменных зарядах на обкладках; второй – емкость конденсатора изменяется при постоянном напряжении между обкладками (в этом случае конденсатор подключен к источнику постоянной ЭДС).

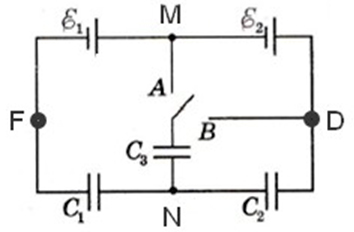
Рассмотрим теперь превращения энергии при изменении емкости плоского конденсатора, образованного двумя параллельными одинаковыми платинами площади S. Размеры пластин будем считать значительно превышающими расстояние между ними, что позволяет пренебречь краевыми эффектами, то есть считать электрическое поле (~vec E) однородным (Рис. 152). Пусть конденсатор заряжен, так что заряды каждой пластины одинаковы по модулю и равны q и противоположны по знаку, поверхностная плотность заряда на каждой пластине равна (~sigma = frac{q}{S}). Напряженность поля между пластинами в этом случае равна

(~E = frac{sigma}{varepsilon_0} = frac{q}{varepsilon_0 S}) , (1)

причем заряды каждой пластины создают поле, напряженность которого в два раза меньше напряженности суммарного поля (1); разность потенциалов между пластинами равна

(~Delta varphi = U = Eh = frac{qh}{varepsilon_0 S}) . (2)

Так заряды пластин разноименные, то пластины будут притягиваться друг к другу с некоторой силой F. Сила, действующая на одну пластину, равна произведению ее заряда на напряженность поля, создаваемого зарядом второй пластины,

(~F = q frac{E}{2} = frac{q^2}{2 varepsilon_0 S}) . (3)

Этой формуле можно придать иной вид, если выразить силу через напряженность электрического поля с помощью формулы (1)

(~F = frac{q^2}{2 varepsilon_0 S} = frac{varepsilon_0 E^2}{2} S) . (4)

Важно отметить, что давление электрического поля на проводящую платину в точности равно объемной плотности энергии поля

(~p = frac{F}{S} = frac{varepsilon_0 E^2}{2} = w) . (5)

Чтобы изменить (для определенности увеличить см. Рис. 152) расстояние между пластинами, к ним необходимо приложить внешнюю силу F₀, превышающую по модулю силе электрического притяжения. При перемещении пластины (увеличении расстояния) на величину Δh эта внешняя сила совершит положительную работу.

Если пластины конденсатора изолированы, то электрический заряд и, как следствие, напряженность поля и сила притяжения не зависят от расстояния между пластинами. Поэтому работа внешней силы по перемещению пластины на расстояние Δh будет минимальна, когда эта сила равна силе притяжения между пластинами, при этом

(~A = F_0 Delta h = frac{varepsilon_0 E^2}{2} S Delta h) . (6)

Благодаря этой работе возрастает энергия электрического поля – при неизменной напряженности и плотности энергии возрастает объем, занятый полем ((Delta V = S Delta h)), что выражается формулой

(~A = Delta W = w Delta V) . (7)

При увеличении расстояния между пластинами емкость конденсатора изменяется (уменьшается). Изменение энергии конденсатора можно также рассчитать, с помощью формулы для его энергии, причем следует выразить энергию через не изменяющийся в данном случае заряд конденсатора, то есть

(~Delta W = W_1 — W_0 = frac{q^2}{2 C_1} — frac{q^2}{2 C_0} = frac{q^2}{2} left(frac{h_1}{varepsilon_0 S} — frac{h_0}{varepsilon_0 S}right) = frac{q^2 Delta h}{2 varepsilon_0 S}) . (8)

Эта формула равносильна полученным выше выражениям для изменения энергии. Таким образом, в рассмотренном процессе превращения энергии понятны: работа внешней силы увеличивает энергию электрического поля конденсатора.

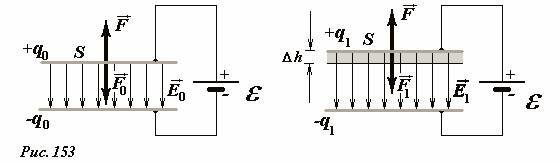
Рассмотрим теперь этот же процесс при условии, что обкладки конденсатора подключены к источнику постоянной ЭДС (Рис. 153). В этом случае при изменении расстояния между пластинами, остается неизменным напряжение U = ε между ними.

В этом случае разноименно заряженные пластины также притягиваются, поэтому для увеличения расстояния между ними внешняя сила также совершает положительную работу, однако при этом энергия конденсатора уменьшается, а не растет! Действительно, при постоянном напряжении между пластинами, изменение энергии конденсатора рассчитывается по формуле

(~Delta W_C = W_1 — W_0 = frac{C_1 U^2}{2} — frac{C_0 U^2}{2} = frac{U^2}{2} left(frac{varepsilon_0 S}{h_1} — frac{varepsilon_0 S}{h_0}right) = frac{varepsilon_0 S U^2}{2} left(frac{1}{h_1} — frac{1}{h_0}right)) . (9)

Так как h₁ > h₀ , то C₁ < C₀ и ΔW_C < 0.

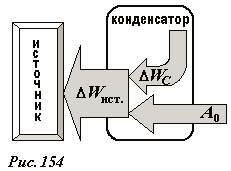
Но и в этом случае нарушения закона сохранения энергии нет, переданная системе энергия (равная совершенной работе) не «теряется» — конденсатор не является замкнутой системой, он же подключен к источнику ЭДС. При увеличении расстояния между пластинами емкость конденсатора уменьшается, поэтому уменьшается заряд на пластинах, которому некуда деться, кроме как вернуться назад, в источник. Их возращению препятствуют сторонние силы (вспомните – сторонние силы источника стремятся «вытолкнуть заряды из источника), поэтому при возвращении зарядов энергия источника повышается. Таким образом, при раздвигании пластин конденсатора происходит подзарядка источника, а энергия, переданная посредством совершенной работы, переходит в энергию источника. Кроме того, энергия поля в конденсаторе также уменьшается, поэтому эта «потеря» энергии также переходит в источник. Иными словами, при перемещении пластины внешняя сила не только совершает работу по подзарядке источника, но и «заставляет» электрическое поле вернуть часть своей энергии. Схематически потоки энергии в этом процессе показаны на Рис. 154.

Подтвердим проведенные рассуждения расчетами энергетического баланса и покажем, что он точно выполняется. Силу притяжения между пластинами (4) выразим через постоянное напряжение между пластинами

(~F = frac{varepsilon_0 E^2}{2} S = frac{varepsilon_0}{2} left(frac{U}{h}right)^2 S = frac{varepsilon_0 U^2 S}{2 h^2}) . (10)

В данном случае эта сила зависит от расстояния между пластинами. Поэтому для расчета работы необходимо разбить процесс движения пластины на малые участки и затем просуммировать работы на этих участках. Чтобы избежать этой громоздкой математической процедуры, будем считать, что смещение Δh мало настолько, что можно пренебречь изменением силы притяжения. В этом приближении работа внешней силы будет равна

(~delta A_0 = F Delta h = frac{varepsilon_0 U^2 S}{2 h^2_0} Delta h) . (11)

Преобразуем также выражение для изменения энергии конденсатора с учетом малости смещения. Запишем (h_1 = h_0 + Delta h) и подставим в формулу (9)

(~Delta W_C = W_1 — W_0 = frac{varepsilon_0 S U^2}{2} left(frac{1}{h_0 + Delta h} — frac{1}{h_0}right) = -frac{varepsilon_0 S U^2}{2} frac{Delta h}{h_0(h_0 + Delta h)} approx -frac{varepsilon_0 S U^2}{2} frac{Delta h}{h^2_0}) . (12)

Наконец, найдем работу по зарядке источника, которая равна произведению «вернувшегося» заряда на ЭДС источника (которая равна напряжению конденсатора):

(~Delta W_{ist} = U(q_0 — q_1) = U(C_0 U — C_1 U) = U^2 left(frac{varepsilon_0 S}{h_0} — frac{varepsilon_0 S}{h_0 + Delta h}right) = varepsilon_0 S U^2 left(frac{1}{h_0} — frac{1}{h_0 + Delta h}right) approx frac{varepsilon_0 S U^2 Delta h}{h^2_0}) .

Итак, проведенный расчет полностью подтверждает сделанные ранее заключения: увеличение энергии источника (что равносильно — работа по его подзарядке) равно сумме работы внешней силы и уменьшения энергии поля конденсатора

(~Delta W_{ist} = delta A_0 + (-Delta W_C)) .

Задание для самостоятельной работы.

Докажите, что в рассмотренном процессе энергетический баланс выполняется при любом (не малом) смещении пластины.

Признавая, что «аналогии ничего не доказывают, но много объясняют», рассмотрим гидростатическую аналогию преобразования энергии при изменении «емкости» сосуда. Как мы указывали, аналогом электрического заряда может служить объем жидкости, налитой в сосуд, аналогом изменения потенциала – изменение уровня жидкости, тогда аналогом электроемкости вертикального сосуда служит площадь его дна. Таким образом, изменению емкости должно соответствовать изменение площади поперечного сечения сосуда. Представим себе сосуд в форме параллелепипеда (аквариума), одна из стенок которого может двигаться – при ее смещении изменяется площадь сосуда, то есть изменяется его «емкость». При уменьшении площади сосуда уменьшается «емкость». В рассмотренных электростатических примерах – уменьшению емкости конденсатора соответствует увеличению расстояния между его пластинами.

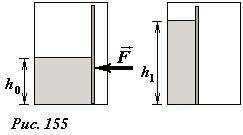
Пусть теперь в нашем сосуде находится некоторый объем жидкости, уровень которой равен h₀ (Рис. 155 ). Чтобы сместить подвижную стенку, к ней необходимо приложить некоторую внешнюю силу F. Если объем жидкости в сосуде сохраняется, то при смещении стенки ее уровень повышается, следовательно, увеличивается ее энергия. Понятно, что увеличение потенциальной энергии жидкости равно работе внешней силы.

Сравните: при неизменном объеме жидкости (электрическом заряде) уменьшение площади сосуда (емкости конденсатора) под действием внешней силы приводит к возрастанию уровня жидкости (разности потенциалов) и гидростатической энергии жидкости (электростатической энергии поля).

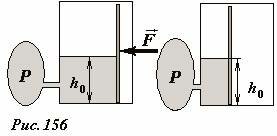
Если конденсатор подключен к источнику постоянной ЭДС, то его напряжение поддерживается постоянным. В гидростатической аналогии необходимо в этом случае говорить о постоянной высоте уровня жидкости в сосуде. В качестве устройства, поддерживающего постоянный уровень можно предложить, например, резиновый сосуд («грушу»), жидкость в которой поддерживается при постоянном давлении. Если теперь наш сосуд «переменной емкости» подключить к источнику постоянного давления (резиновой груше), то получим аналог конденсатора, подключенного к источнику постоянной ЭДС (Рис.156) При смещении подвижной стенки в этом случае внешняя сила также совершает положительную работу, но потенциальная энергия жидкости в сосуде уменьшается, так как уменьшается ее объем при неизменной высоте уровня. Под действием этой внешней силы часть жидкости из сосуда заталкивается в резиновую грушу, при этом энергия последней возрастает. Увеличение ее энергии равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде.

Сравниваем: при постоянном уровне жидкости в сосуде (напряжении конденсатора) уменьшение площади дна (емкости конденсатора) под действием внешней силы приводит к возвращению части жидкости (электрического заряда) в резиновый сосуд, поддерживаемый при постоянном давлении (источник постоянной ЭДС). При этом увеличение энергии жидкости в резиновом сосуде постоянного давления (источника ЭДС) равно сумме работы внешней силы и уменьшения потенциальной энергии жидкости в сосуде (энергии конденсатора).

Задание для самостоятельной работы.

Докажите, что в рассмотренных гидростатических аналогиях энергетический баланс выполняется точно.

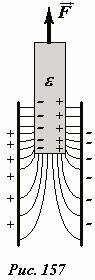
Электроемкость конденсатора зависит также от диэлектрической проницаемости вещества, находящегося между обкладками. Поэтому емкость конденсатора можно изменять, меняя вещество, находящееся между обкладками. Пусть, например, между обкладками плоского конденсатора находится диэлектрическая пластинка. Если конденсатор заряжен, то для извлечения пластинки необходимо приложить к ней внешнюю силу и совершить положительную работу. Механизм возникновения силы, действующей на пластинку со стороны электрического поля, проиллюстрирован на Рис. 157. При ее смещении изначально однородное распределение зарядов на обкладках конденсатора и поляризационных зарядов на пластинке искажается. Как следствие этого перераспределения зарядов искажается и электрическое поле, поэтому возникаю силы, стремящиеся втянуть пластинку внутрь конденсатора.

Расчет этих сил сложен, но энергетические характеристики происходящих процессов могут быть найдены без особого труда. С формальной точки зрения, не важно чем вызваны изменения емкости конденсатора, поэтому можно воспользоваться всеми рассуждениями и выводами предыдущего раздела, как для случая изолированного конденсатора (при сохранении заряда), так для конденсатора подключенного к источнику постоянной ЭДС.

Чрезвычайно интересными и практически важными являются энергетические характеристики процессов поляризации диэлектриков, однако их расчет представляет собой весьма сложную задачу. Для решения возникающих здесь проблем требует привлечения сведения о строении вещества. Некоторые из этих вопросов мы рассмотрим в следующем году после ознакомления с основами теории строения вещества.

Следующая страница

Источник

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.
Ёмкость уединённого проводника
Ёмкость плоского конденсатора
Энергия заряженного конденсатора
Энергия электрического поля

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Предыдущие две статьи были посвящены отдельному рассмотрению того, каким образом ведут себя в электрическом поле проводники и каким образом — диэлектрики. Сейчас нам понадобится объединить эти знания. Дело в том, что большое практическое значение имеет совместное использование проводников и диэлектриков в специальных устройствах — конденсаторах.

Но прежде введём понятие электрической ёмкости.

к оглавлению ▴

Ёмкость уединённого проводника

Предположим, что заряженный проводник расположен настолько далеко от всех остальных тел, что взаимодействие зарядов проводника с окружающими телами можно не принимать во внимание. В таком случае проводник называется уединённым.

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение varphi , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать 1/C , так что

$varphi = frac{displaystyle q}{displaystyle C vphantom{1^a}}.$

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

$C = frac{displaystyle q}{displaystyle varphi }.$ (1)

Например, потенциал уединённого шара в вакууме равен:

$varphi = frac{displaystyle kq}{displaystyle R vphantom{1^a}}=frac{displaystyle q}{displaystyle 4 pi varepsilon_0R vphantom{1^a}},$

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

$varphi = frac{displaystyle q}{displaystyle 4 pi varepsilon_0 varepsilon R vphantom{1^a}}.$

Соответственно, ёмкость шара в раз увеличивается:

(3)

Увеличение ёмкости при наличии диэлектрика — важнейший факт. Мы ещё встретимся с ним при рассмотрении конденсаторов.

Из формул (2) и (3) мы видим, что ёмкость шара зависит только от его радиуса и диэлектрической проницаемости окружающей среды. То же самое будет и в общем случае: ёмкость уединённого проводника не зависит от его заряда; она определяется лишь размерами и формой проводника, а также диэлектрической проницаемостью среды, окружающей проводник. От вещества проводника ёмкость также не зависит.

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным 6400 км.

$C = 4 pi varepsilon_0 R approx 4 cdot 3,14 cdot 8,85 cdot 10^{-12} cdot 6400 cdot 10^3 approx 712$ мкФ.

Как видите, Ф — это очень большая ёмкость.

Единица измерения ёмкости полезна ещё и тем, что позволяет сильно сэкономить на обозначении размерности диэлектрической постоянной . В самом деле, выразим из формулы (2):

$varepsilon_0 = frac{displaystyle C} {displaystyle 4 pi R vphantom{1^a}}.$

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

$varepsilon_0 = 8,85 cdot 10^{-12}$ Ф.

Так легче запомнить, не правда ли?

к оглавлению ▴

Ёмкость плоского конденсатора

Ёмкость уединённого проводника на практике используется редко. В обычных ситуациях проводники не являются уединёнными. Заряженный проводник взаимодействует с окружающими телами и наводит на них заряды, а потенциал поля этих индуцированных зарядов (по принципу суперпозиции!) изменяет потенциал самого проводника. В таком случае уже нельзя утверждать, что потенциал проводника будет прямо пропорционален его заряду, и понятие ёмкости проводника самого по себе фактически утрачивает смысл.

Можно, однако, создать систему заряженных проводников, которая даже при накоплении на них значительного заряда почти не взаимодействует с окружающими телами. Тогда мы сможем снова говорить о ёмкости — но на сей раз о ёмкости этой системы проводников.

Наиболее простым и важным примером такой системы является плоский конденсатор. Он состоит из двух параллельных металлических пластин (называемых обкладками), разделённых слоем диэлектрика. При этом расстояние между пластинами много меньше их собственных размеров.

Для начала рассмотрим воздушный конденсатор, у которого между обкладками находится воздух

Пусть заряды обкладок равны и . Именно так и бывает в реальных электрических схемах: заряды обкладок равны по модулю и противоположны по знаку. Величина — заряд положительной обкладки — называется зарядом конденсатора.

Пусть — площадь каждой обкладки. Найдём поле, создаваемое обкладками в окружающем пространстве.

Поскольку размеры обкладок велики по сравнению с расстоянием между ними, поле каждой обкладки вдали от её краёв можно считать однородным полем бесконечной заряженной плоскости:

$E_+ = E_-=frac{displaystyle sigma }{displaystyle 2 varepsilon_0 vphantom{1^a}}.$

Здесь E_+ — напряжённость поля положительной обкладки, E_- — напряженность поля отрицательной обкладки, sigma — поверхностная плотность зарядов на обкладке:

$sigma =frac{displaystyle q}{displaystyle S vphantom{1^a}}.$

На рис. 1 (слева) изображены векторы напряжённости поля каждой обкладки в трёх областях: слева от конденсатора, внутри конденсатора и справа от конденсатора.

Рис. 1. Электрическое поле плоского конденсатора

Согласно принципу суперпозиции, для результирующего поля vec{E} имеем:

$vec{E} = vec{E}_+ + vec{E}_-$

Нетрудно видеть, что слева и справа от конденсатора поле обращается в нуль (поля обкладок погашают друг друга):

Внутри конденсатора поле удваивается:

$E = E_+ + E_-= frac{displaystyle sigma }{displaystyle varepsilon_0},$

или

$E = frac{displaystyle q}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (4)

Результирующее поле обкладок плоского конденсатора изображено на рис. 1 справа. Итак:

Внутри плоского конденсатора создаётся однородное электрическое поле, напряжённость которого находится по формуле (4). Снаружи конденсатора поле равно нулю, так что конденсатор не взаимодействует с окружающими телами.

Не будем забывать, однако, что данное утверждение выведено из предположения, будто обкладки являются бесконечными плоскостями. На самом деле их размеры конечны, и вблизи краёв обкладок возникают так называемые краевые эффекты: поле отличается от однородного и проникает в наружное пространство конденсатора. Но в большинстве ситуаций (и уж тем более в задачах ЕГЭ по физике) краевыми эффектами можно пренебречь и действовать так, словно утверждение, выделенное курсивом, является верным без всяких оговорок.

Пусть расстояние между обкладками конденсатора равно . Поскольку поле внутри конденсатора является однородным, разность потенциалов между обкладками равна произведению на (вспомните связь напряжения и напряжённости в однородном поле!):

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 S vphantom{1^a}}.$ (5)

Разность потенциалов между обкладками конденсатора, как видим, прямо пропорциональна заряду конденсатора. Данное утверждение аналогично утверждению «потенциал уединённого проводника прямо пропорционален заряду проводника», с которого и начался весь разговор о ёмкости. Продолжая эту аналогию, определяем ёмкость конденсатора как отношение заряда конденсатора к разности потенциалов между его обкладками:

$C=frac{displaystyle q}{displaystyle U vphantom{1^a}}.$ (6)

Ёмкость конденсатора показывает, какой заряд ему нужно сообщить, чтобы разность потенциалов между его обкладками увеличилась на В. Формула (6), таким образом, является модификацией формулы (1) для случая системы двух проводников — конденсатора.

Из формул (6) и (5) легко находим ёмкость плоского воздушного конденсатора:

$C=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}}.$ (7)

Она зависит только от геометрических характеристик конденсатора: площади обкладок и расстояния между ними.
Предположим теперь, что пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Как изменится ёмкость конденсатора?

Напряжённость поля внутри конденсатора уменьшится в раз, так что вместо формулы (4) теперь имеем:

$E=frac{displaystyle q}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (8)

Соответственно, напряжение на конденсаторе:

$U=Ed=frac{displaystyle qd}{displaystyle varepsilon_0 varepsilon S vphantom{1^a}}.$ (9)

Отсюда ёмкость плоского конденсатора с диэлектриком:

$C=frac{displaystyle varepsilon_0 varepsilon S}{displaystyle d vphantom{1^a}}.$ (10)

Она зависит от геометрических характеристик конденсатора (площади обкладок и расстояния между ними) и от диэлектрической проницаемости диэлектрика, заполняющего конденсатор.

Важное следствие формулы (10): заполнение конденсатора диэлектриком увеличивает его ёмкость.

к оглавлению ▴

Энергия заряженного конденсатора

Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится.

Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке. Нетрудно понять, что этой энергией является потенциальная энергия взаимодействия обкладок конденсатора — ведь обкладки, будучи заряжены разноимённо, притягиваются друг к другу.

Мы сейчас вычислим эту энергию, а затем увидим, что существует и более глубокое понимание происхождения энергии заряженного конденсатора.

Начнём с плоского воздушного конденсатора. Ответим на такой вопрос: какова сила притяжения его обкладок друг к другу? Величины используем те же: заряд конденсатора , площадь обкладок .

Возьмём на второй обкладке настолько маленькую площадку, что заряд q_0 этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой

где E_1 — напряжённость поля первой обкладки:

$E_1=frac{displaystyle sigma }{displaystyle 2 varepsilon _0 vphantom{1^a}}=frac{displaystyle q}{displaystyle 2varepsilon_0 S vphantom{1^a}}.$

Следовательно,

$F_0=frac{displaystyle q_0q}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$

Направлена эта сила параллельно линиям поля (т. е. перпендикулярно пластинам).

Результирующая сила притяжения второй обкладки к первой складывается из всех этих сил F_0 , с которыми притягиваются к первой обкладке всевозможные маленькие заряды q_0 второй обкладки. При этом суммировании постоянный множитель вынесется за скобку, а в скобке просуммируются все q_0 и дадут . В результате получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}.$ (11)

Предположим теперь, что расстояние между обкладками изменилось от начальной величины d_1 до конечной величины d_2 . Сила притяжения пластин совершает при этом работу:

Знак правильный: если пластины сближаются , то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины , то работа силы притяжения получается отрицательной, как и должно быть.

С учётом формул (11) и (7) имеем:

$A=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 S vphantom{1^a}}left ( d_1-d_2 right )=frac{displaystyle q^2d_1}{displaystyle 2varepsilon_0 S vphantom{1^a}}-frac{displaystyle q^2d_2}{displaystyle 2varepsilon_0 S vphantom{1^a}}=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}}-frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}=W_1-W_2,$

где
$W_1=frac{displaystyle q^2}{displaystyle 2C_1 vphantom{1^a}},$
$W_2=frac{displaystyle q^2}{displaystyle 2C_2 vphantom{1^a}}$

Это можно переписать следующим образом:

где

$W=frac{displaystyle q^2}{displaystyle 2C vphantom{1^a}}.$ (12)

Работа потенциальной силы притяжения обкладок оказалась равна изменению со знаком минус величины . Это как раз и означает, что — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора.

Используя соотношение q = CU , из формулы (12) можно получить ещё две формулы для энергии конденсатора (убедитесь в этом самостоятельно!):

$W=frac{displaystyle qU}{displaystyle 2 vphantom{1^a}},$ (13)

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}.$ (14)

Особенно полезными являются формулы (12) и (14).

Допустим теперь, что конденсатор заполнен диэлектриком с диэлектрической проницаемостью . Сила притяжения обкладок уменьшится в раз, и вместо (11) получим:

$F=frac{displaystyle q^2}{displaystyle 2 varepsilon_0 varepsilon S vphantom{1^a}}.$

При вычислении работы силы , как нетрудно видеть, величина войдёт в ёмкость , и формулы (12) — (14) останутся неизменными. Ёмкость конденсатора в них теперь будет выражаться по формуле (10).

Итак, формулы (12) — (14) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.

к оглавлению ▴

Энергия электрического поля

Мы обещали, что после вычисления энергии конденсатора дадим более глубокое истолкование происхождения этой энергии. Что ж, приступим.

Рассмотрим воздушный конденсатор и преобразуем формулу (14) для его энергии:

$W=frac{displaystyle CU^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 S}{displaystyle d vphantom{1^a}} cdot frac{displaystyle (Ed)^2}{displaystyle 2 vphantom{1^a}}=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}Sd.$

Но Sd = V — объём конденсатора. Получаем:

$W=frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}V.$ (15)

Посмотрите внимательно на эту формулу. Она уже не содержит ничего, что являлось бы специфическим для конденсатора! Мы видим энергию электрического поля , сосредоточенного в некотором объёме .

Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.

Итак, электрическое поле само по себе обладает энергией. Ничего удивительного для нас тут нет. Радиоволны, солнечный свет — это примеры распространения энергии, переносимой в пространстве электромагнитными волнами.

Величина — энергия единицы объёма поля — называется объёмной плотностью энергии. Из формулы (15) получим:

$omega =frac{displaystyle varepsilon_0 E^2}{displaystyle 2 vphantom{1^a}}.$ (16)

В этой формуле не осталось вообще никаких геометрических величин. Она даёт максимально чистую связь энергии электрического поля и его напряжённости.

Если конденсатор заполнен диэлектриком, то его ёмкость увеличивается в раз, и вместо формул (15) и (16) будем иметь:

$W =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}V.$ (17)

$omega =frac{displaystyle varepsilon_0 varepsilon E^2}{displaystyle 2 vphantom{1^a}}.$ (18)

Как видим, энергия электрического поля зависит ещё и от диэлектрической проницаемости среды, в которой поле находится.
Замечательно, что полученные формулы для энергии и плотности энергии выходят далеко за пределы электростатики: они справедливы не только для электростатического поля, но и для электрических полей, меняющихся во времени.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Конденсатор. Энергия электрического поля» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Вывод формулы для энергии заряженного конденсатора

Раздвигая разноименно заряженные пластины конденсатора, мы совершаем положительную работу, так как пластины притягиваются друг к другу. При этом энергия конденсатора 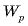увеличивается на величину, равную совершенной нами работе то есть

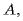
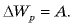
Если увеличить расстояние между пластинами на 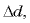то совершенная работа где — сила притяжения пластин, равная заряду одной из пластин, умноженному на напряженность поля, создаваемого другой пластиной. Обе пластины дают равный вклад в напряженность поля внутри конденсатора, поэтому напряженность поля, создаваемого одной пластиной, равна Таким образом, откуда

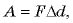
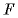
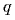
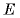
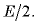
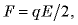
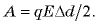
Если начальное расстояние между пластинами равно нулю, а конечное равно 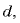то совершенная при раздвигании пластин работа Это и есть энергия заряженного конденсатора. Так как где — разность потенциалов между обкладками конденсатора, получаем

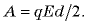
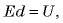
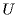
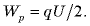
Поскольку 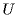и связаны соотношением получаем три эквивалентные формулы для энергии заряженного конденсатора:

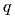
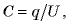
Электродинамика.
2014

Источник

При подготовке к ЕГЭ по физике и решении задач повышенной сложности очень часто обучающиеся сталкиваются с трудностями анализа физических процессов в конденсаторах. Целью данной работы является некоторая систематизация и выделение ключевых позиций при решении задач повышенной сложности по теме «Конденсаторы и их соединение». Реализовывая системно-деятельностный подход к изучению физики, возможно рассмотрение следующих ситуаций анализа решаемых задач, а также вариативных вопросов к ним.

I. Рассмотрим известную задачу, которая раскрывает взаимосвязь физических характеристик конденсатора и последовательность их изменений [2]:

Плоский конденсатор, между пластинами которого находится воздух, заряжен от источника питания. Как меняются заряд конденсатора, напряженность электрического поля, разность потенциалов между пластинами, энергия и плотность энергии электрического поля, если увеличить в n раз расстояние между пластинами в ситуациях, если а) конденсатор отключить от источника питания и б) с включенным источником питания.

Рассмотрим первую ситуацию: изменяем расстояние между пластинами при отключенном источнике.

В ключевых позициях устанавливаем два опорных положения, которые позволяют анализировать изменения физических характеристик

— Что остается неизменным в данном процессе. (q = const, заряд на пластинах конденсатора при отключении источника тока)

— Что происходит с емкостью конденсатора (Конденсатор плоский: d
увеличивается, C уменьшается)

Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:

1) Напряженность электрического поля конденсатора E = ϭ/(2ε₀) (не изменяется)

2) Разность потенциалов между пластинами C = q/U (С уменьшается, U
увеличивается в n раз)

3) Энергия электрического поля W = qU/2 (U увеличивается в n раз, W
увеличивается в n раз)

4) Плотность энергии ω = ε₀E²/2 (не изменяется)

Рассмотрим вторую ситуацию: изменяем расстояние между пластинами при включенном источнике питания.

— Что остается неизменным в данном процессе. (U = const, напряжение на пластинах конденсатора при включении источнике тока)

— Что происходит с емкостью конденсатора (Конденсатор плоский: d
увеличивается, C уменьшается)

Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:

1) При неизменном напряжении и уменьшении емкости, заряд конденсатора должен уменьшиться в n раз (анализ C = q/U)

2) Напряженность электрического поля конденсатора E = ϭ/(2ε₀) (E
уменьшается в n раз при уменьшении заряда в n раз)

3) Энергия электрического поля W = qU/2 (q уменьшается в n раз, W
уменьшается в n раз)

4) Плотность энергии ω = ε₀E²/2 уменьшается в n² раз (при уменьшении напряженности)

Особое внимание следует обратить на энергетические превращения в конденсаторе. При увеличении расстояния между пластинами совершается положительная механическая работа, но энергия конденсатора уменьшается. Согласно закону сохранения энергии источник должен забирать энергию, равную убыли энергии конденсатора и механической работы внешних сил. Иначе, если источник является аккумулятором, то он будет заряжаться от конденсатора. Если источником является гальванический элемент, то на нем будет выделяться тепло.

Поставленную задачу можно не ограничивать данными изменениями, а можно выполнить анализ при изменении площади пластин конденсатора или замене диэлектрика между пластинами. В результате поможет сформировать у обучающихся целостное и устойчивое представление физических процессов и их характеристик в конденсаторе, варьируя ситуации.

II. Рассмотрим две возможные ситуации при параллельном подключении одного конденсатора к другому, если обкладки конденсаторов соединены одноименными зарядами и разноименными зарядами [2]:

Конденсатор емкостью C₁ заряжен до разности потенциалов U₁. Какой заряд и каково напряжение будет на обкладках конденсатора, если к нему подключить параллельно другой конденсатор емкостью C₂, заряженный до разности потенциалов U₂.

Если обкладки конденсаторов соединены одноименными зарядами, то решение задачи сводится к составлению уравнения закона сохранения заряда до соединения и после соединения конденсаторов. Закон сохранения заряда будет ключевым моментом анализа задачи. Второй момент — равенство напряжений на конденсаторах при параллельном подключении, дает возможность упростить и решить данную задачу.

Иначе дело обстоит, если обкладки конденсаторов соединены разноименными зарядами. При соединении двух конденсаторов возникает ситуация, когда при распределении зарядов после подключения происходит перезарядка одного из конденсаторов и смена знаков зарядов на его обкладках. В этом случае при составлении уравнения закона сохранения заряда как ключевого момента следует не забыть изменить знак заряда на противоположный. Положим, в данном примере U₂ > U₁, то при соединении конденсаторов, первый конденсатор перезарядится, и знаки зарядов на его пластинах сменятся. Поэтому удобно при составлении закона сохранения заряда, принять заряд первого конденсатора, до соединения к нему второго, за отрицательный заряд.

Закон сохранения заряда для данного примера будет выглядеть: -q₁+ q₂
= q₁‘+ q₂‘. Последующее равенство напряжений на конденсаторах при параллельном подключении дает возможность упростить и решить данную задачу.

III. Рассмотрим анализ схемы соединения конденсаторов, где их соединения не сводятся к совокупности параллельных и последовательных соединений.

Например, в разветвленной схеме требуется найти напряжения на конденсаторах. Данный пример подробно описан [1]. Из данного примера выделим следующие ключевые моменты:

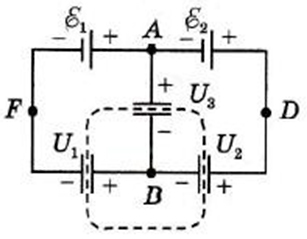
1) Составляем независимые уравнения, связывающие напряжения на конденсаторах с электродвижущими силами, выбрав точки разности потенциалов.

А) Между точками F и D: Ɛ₁+ Ɛ₂= U₁+ U₂

Б) Между точками F и A: Ɛ₁= U₁+ U₃

2) Составляем уравнение алгебраической суммы зарядов в узле точки B:

q₁— q₂— q₃= 0 или C₁U₁— C₂U₂ — C₃U₃= 0

Система трех независимых уравнений с тремя неизвестными дает их решение. Если схема симметрична (Ɛ₁ = Ɛ₂, C₁ = C₂), то U₃ (Напряжение между точками A и B) равно нулю, а напряжение U₁= U₂.

В связи с данным примером, возникает упрощенный анализ схем при переключении в цепи с конденсаторами, например [1]:

Для положения ключа в состоянии A и B между точками F и D выражение Ɛ₁ + Ɛ₂ = U₁ + U₂ справедливо в обоих случаях. Следовательно, U₂не изменяется при переключении.

Для узла N сумма зарядов в узле равна нулю: q₁— q₂± q₃= 0. Следовательно, не изменится заряд третьего конденсатора, а вместе с ним и не изменится напряжение U₃.

После переключения U₂= U₃, конденсаторы соединены параллельно.

В данном примере интересен вывод: точки A и B имеют одинаковый потенциал, следовательно Ɛ₂= 0.

IV. Рассмотрим некоторые варианты изменения энергии конденсатора с точки зрения закона сохранения энергии, подробные объяснения которых обсуждаются в источнике [3].

Изменение энергии конденсатора можно произвести от источника питания или путем совершения механической работы внешними силами.

Увеличение энергии конденсатора при зарядке конденсатора в общем виде можно определить из уравнения закона сохранения:

Aист. = ΔWк + A + Q,

где Aист. – работа источника при зарядке конденсатора, ΔWк – изменение энергии конденсатора, A – механическая работа сил электрического поля, Q – выделяющееся тепло. В идеальном случае, при отсутствии потерь энергии от источника: Aист. = ΔWк

Однако наиболее часто встречаются задания, где изменение энергии заряженного конденсатора происходит путем совершения работы внешней силы в ситуациях с отключенным и подключенным источником тока.

Рассмотрим первую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при отключенном источнике питания.

— обращаем внимание на то, что в данной ситуации остается неизменным заряд q конденсатора.

— обращаем внимание на то, что емкость при выемке диэлектрика или раздвижении пластин уменьшается емкость конденсатора (C = εε₀S/d)

Формируем вывод исходя из формулы энергии при неизменном заряде: W = q₂/2C – энергия конденсатора увеличивается. Увеличение энергии произошло за счет работы внешней силы. ΔWк = Aвнеш.

Рассмотрим вторую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при включенном источнике питания.

— обращаем внимание на то, что в данной ситуации остается неизменным напряжение U на обкладках конденсатора.

Формируем вывод исходя из формулы энергии при неизменном напряжении: W = CU²/2 – энергия конденсатора уменьшается. Уменьшение энергии произошло за счет того, что источник совершает отрицательную работу, забирая часть заряда с обкладок конденсатора при положительной работе внешних сил:. ΔWк = Aист. + Aвнеш.

Возможны и другие очевидные вариации изменения энергии конденсатора с помощью работы внешних сил.

В данной работе рассмотрена лишь небольшая часть анализа ключевых ситуаций по данной теме. Но все рассмотренные ситуации являются опорными для формирования разбора задач и их решения.

Литература

1. Е.И.Бутиков, А.А.Быков, А.С.Кондратьев. Физика в примерах и задачах, МЦНМО, Пероглиф, 2019, стр. 297-301.

2. А.С.Кондратьев, В.М.Уздин. Физика. Сборник задач, М., ФИЗМАТЛИТ, 2020, стр.67-69.

3. А.С.Кондратьев, Л.А.Ларченкова, В.А.Ляпцев. Методы решения задач по физике. М., ФИЗМАТЛИТ, 2019, стр.149-154.

Источник

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Но прежде введём понятие электрической ёмкости.

Характеристики конденсатора

Основной характеристикой данного элемента является емкость, или С. Она определяет способность устройства собирать электрический заряд, зависит от геометрической конфигурации крышек и от электрической проницаемости диэлектрика между крышками.

Важно! Емкость зависит от типа используемого диэлектрика, а также от геометрических размеров элемента.

Для того, чтобы описать принцип работы устройства формулой, необходимо понять, что это постоянная пропорциональность в уравнении, представляющая собой взаимную зависимость накопленного заряда q от площади пластинок и от разности потенциалов V между ними.

Мощность выражается в единицах, называемых фарадами F. Но на практике используются и более мелкие единицы, такие как микрофарады и пикофарады.

Таким образом, если напряжение U приложено к конденсатору, электрический заряд накапливается на крышках детали. Значение накопленного заряда на каждой пластинке одинаково, они отличаются только знаком. Этот процесс накопления электрического показателя на называется зарядкой.

Другим параметром детали является номинальное напряжение, а именно, его максимальное значение, которое может подаваться на конденсатор. При подключении более высокого напряжения возникает пробой диэлектрика. Это приводит к короткому замыканию элемента. Каким будет номинальное значение напряжения, зависит от типа диэлектрика и его толщины.

Важно! Чем толще диэлектрик, тем выше номинальное напряжение, которое он выдерживает.

Ещё одним параметром является ток утечки -значение проводящего показателя, возникающее при подаче постоянного напряжения на концы элемента.

Идея суперконденсатора

Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.

Энергия конденсатора

У конденсатора, как и у любой системы заряженных тел, есть энергия. Чтобы зарядить конденсатор, необходимо совершить работу по разделению отрицательных и положительных зарядов. По закону сохранения энергии эта работа будет как раз равна энергии конденсатора.

Доказать, что заряженный конденсатор обладает энергией, несложно. Для этого понадобится электрическая цепь, содержащая в себе лампу накаливания и конденсатор. При разрядке конденсатора вспыхнет лампа — это будет означать, что энергия конденсатора превратилась в тепло и энергию света.

Чтобы вывести формулу энергии плоского конденсатора, нам понадобится формула энергии электростатического поля.

В случае с конденсатором d будет представлять собой расстояние между пластинами.

Заряд на пластинах конденсатора равен по модулю, поэтому можно рассматривать напряженность поля, создаваемую только одной из пластин.

Напряженность поля одной пластины равна Е/2, где Е — напряженность поля в конденсаторе.

В однородном поле одной пластины находится заряд q, распределенный по поверхности другой пластины.

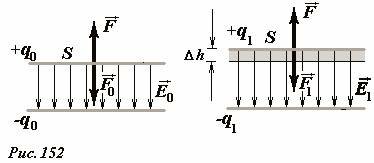
Тогда энергия конденсатора равна:

Wp = qEd/2

Разность потенциалов между обкладками конденсатора можно представить, как произведение напряженности на расстояние:

U = Ed

Поэтому:

Wp = qU/2

Эта энергия равна работе, которую совершит электрическое поле при сближении пластин.

Заменив в формуле разность потенциалов или заряд с помощью выражения для электроемкости конденсатора C = q/U, получим три различных формулы энергии конденсатора:

Энергия конденсатора
Wp = qU/2

Wp — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

U — напряжение на конденсаторе [В]

Энергия конденсатора
Wp = q2/2C

Wp — энергия электростатического поля [Дж]

q — электрический заряд [Кл]

C — электроемкость конденсатора [Ф]

Энергия конденсатора
Wp = CU2/2

Wp — энергия электростатического поля [Дж]

C — электроемкость конденсатора [Ф]

U — напряжение на конденсаторе [В]

Эти формулы справедливы для любого конденсатора.

Единица и формулы расчёта

Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.

Математическое выражение фарада

Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.

Энергия заряженного конденсатора

Существует еще одна эквивалентная запись заряженного конденсатора при использовании соотношения Q=CU:

We=Q22C=CU22=QU2.

Электрическая энергия We рассматривается как потенциальная. Формулы для We аналогичны формулам потенциальной энергии Ep деформированной пружины, а именно:

Ep=kx22=F22k=Fx2, где k является жесткостью пружины, х – деформацией, F=kx – внешней силой.

Современные представления электрической энергии говорят о том, что она сосредоточена между пластинами конденсатора. В связи с этим и получила название энергии электрического поля. Это объяснимо с помощью иллюстрирования заряженного плоского конденсатора.

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

Такое устройство называется плоским конденсатором, а пластины — обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

Каждая из обкладок конденсатора в отдельности создает электрическое поле:

положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E = frac{sigma}{2varepsilon_0thinspacevarepsilon}

Здесь sigma— это поверхностная плотность заряда: sigma = frac{q}{S}, а varepsilon — диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}

Но направления векторов разные — внутри конденсатора вектора направлены в одну сторону, а вне — в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}

А какая же будет величина напряженности вне конденсатора? А все просто — слева и справа от обкладок поля пластин компенсируют друг друга и результирующая напряженность равна 0

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.

Основы электроники. Часть 2. Как работают конденсаторы. Параметры конденсаторов

Часть 1. Заряды, потенциалы, напряжение, ток, сопротивление…
Часть 2. Как работают конденсаторы. Основные параметры конденсаторов.

Итак, конденсатор — это элемент электрической цепи, предназначенный для накопления зарядов. Сразу возникает вопрос: а зачем вообще накапливать заряды? Если вы внимательно читали первую часть, то знаете ответ на этот вопрос: потому что заряды как раз являются источником электрического поля и если в каких-то точках соотношения положительных и отрицательных зарядов разные, то между этими точками будет существовать разность потенциалов. То есть заряженный конденсатор (когда он накопил некоторый заряд) — это как бы мини источник ЭДС, который может отдавать накопленные заряды, поддерживая в цепи электрический ток (при этом сам он, естественно, будет разряжаться). Его принципиальное отличие от источника ЭДС (в котором сторонние силы, обусловленные химической реакцией, переменным магнитным полем или ещё чем-то, разделяют заряды и поддерживают разность потенциалов на его выводах) в том, что в конденсаторе нет сторонних сил (т.е. он сам внутри себя заряды не разделяет) и разность потенциалов между его выводами обеспечивается только теми зарядами, которые он накопил в процессе зарядки (то есть теми зарядами, которые пришли к нему извне).
И ещё одно. Что значит «накапливает заряд»? На самом деле выражение «накапливает» в данном случае означает перераспределение зарядов между обкладками конденсатора и внешней цепью. То есть если заряды на обкладках перераспределятся таким образом, что суммарный заряд на положительной обкладке будет на величину Q больше, чем на отрицательной, то говорят, что конденсатор накопил заряд Q. Куда заряды будут втекать и откуда утекать зависит от того, какая в начальный момент была разность потенциалов между соответствующим выводом конденсатора и той точкой внешней цепи, к которой этот вывод подключили. Короче говоря, главное, что в результате вот этого «накопления» разность зарядов между положительной и отрицательной обкладками станет равна Q.

Важнейшие характеристики конденсатора — это ёмкость и номинальное напряжение.

Итак, сначала ёмкость. Ёмкость — это параметр, который устанавливает связь между изменением заряда на обкладках и изменением напряжения между выводами конденсатора. Ёмкость показывает насколько сильно будет изменяться заряд на обкладках конденсатора при изменении напряжения между его выводами. Ну и, соответственно, от неё же зависит насколько сильно будет изменяться напряжение между выводами при изменении заряда на обкладках. Математически эта связь описывается такой формулой: C=dQ/dU, где dQ — изменение заряда, dU — изменение напряжения между выводами конденсатора. То есть численное значение ёмкости (то, что написано на вашем кондёре) показывает: на сколько Кулон нужно изменить заряд конденсатора, чтобы напряжение между его выводами изменилось на 1 В.

Чтобы было понятнее, можно привести такую аналогию:

Будем считать, что давление воздуха аналогично потенциалу, а количество воздуха (не важно, количество вещества или масса) аналогично заряду. Вполне законное сравнение, если учесть, что давление воздуха в каком-то замкнутом пространстве стремится выровняться по всему объёму и при этом воздух перемещается из областей с высоким давлением в области с низким давлением, причём чем больше разность давлений, тем, при прочих равных условиях, он это делает быстрее (помните, чем больше разность потенциалов — тем больше сила тока, при одинаковом сопротивлении?).

Далее, представьте, что у нас есть закрытая крышкой банка (это будет аналог конденсатора), в которую через дырку в крышке вставлена трубка. Если давление снаружи и внутри банки равно атмосферному, то разности давлений нет, то есть напряжение равно нулю и воздух не будет выходить из банки наружу и не будет заходить снаружи в банку. Теперь представьте, что мы подключили трубку к компрессору, который создаёт на выходе некоторое избыточное давление Pк (избыточное, — то есть на величину Pк больше атмосферного). Компрессор в данном случае будет аналогичен источнику ЭДС. При этом все я думаю прекрасно понимают, что если открыть вентиль, то воздух по трубке начнёт закачиваться в банку, то есть количество воздуха в банке начнёт увеличиваться. Или можно сказать, что наш конденсатор начнёт заряжаться (банка же у нас — это конденсатор). Но по мере увеличения в банке количества воздуха — у нас будет расти и давление в банке, соответственно будет расти разность между давлением в банке и атмосферным давлением (в нашем примере эта разность — аналог напряжения). Давление в банке будет расти до тех пор, пока не сравняется с давлением, создаваемым компрессором. После того, как это произойдёт — ток воздуха по трубке прекратится.

Так вот, величиной, аналогичной электрической ёмкости, в данном случае будет не объём банки (первая ассоциация с ёмкостью, которая приходит на ум, да?), а величина, показывающая на сколько нужно изменить массу воздуха в банке, чтобы давление в ней изменилось на 1 Паскаль. То есть ёмкость в данном случае будет связывать изменение количества воздуха в банке (изменение массы, а не объёма, он у нас постоянный, банка стеклянная и не растягивается) с изменением давления в ней. Математически это выглядело бы вот так C=dM/dP.

Надеюсь с ёмкостью всё понятно, поэтому перейдём ко второй важнейшей характеристике конденсатора — номинальному напряжению. Тут вообще всё просто. Рассмотрим опять аналогию с банкой. Понятно, что если накачивать и накачивать в неё воздух, то давление в ней будет расти, расти и в конце концов банка не выдержит и лопнет. То есть при превышении определённой разницы давлений внутри и снаружи (или можно сказать при превышении напряжения) нашу банку-конденсатор просто разорвёт на части. Точно также обстоят дела и с электрическим конденсатором. Если зарядить его выше некоторого напряжения, то произойдёт пробой, конденсатор разрушится и перестанет функционировать. Обычно в маркировке для конденсатора указывают номинальное напряжение — такое, при котором он может в течение всего срока службы эксплуатироваться без опасений, что произойдёт пробой, разрушение или ещё какие-то его повреждения. В принципе, конденсаторы могут выдерживать некоторые перенапряжения (величина зависит от типа конденсатора, материала диэлектрика и т.д), но тем не менее заряжать конденсатор до напряжения выше номинального крайне не рекомендуется, потому что в этом случае производитель уже не даст гарантии, что параметры конденсатора не ухудшатся и он не разрушится.

Давайте рассуждать дальше. Итак, мы знаем, что напряжение между выводами конденсатора увеличивается вследствие перераспределения зарядов между обкладками и внешней цепью и напрямую связано с количеством накопленного конденсатором заряда. Но заряды у нас не перемещаются мгновенно, следовательно, для того, чтобы конденсатор зарядился и напряжение между его выводами выросло — требуется некоторое время. Точно так же и давление воздуха в банке не вырастает мгновенно при подключении к ней компрессора, а постепенно растёт по мере увеличения количества закачанного воздуха. От чего же зависит скорость заряда конденсатора? Очевидно, что она зависит от того, насколько быстро перераспределяются заряды (то есть от силы тока).

Теперь давайте эти логические рассуждения подкрепим математикой. Возьмём формулу, связывающую ёмкость, заряд и напряжение и перепишем её в таком виде: dQ=C*dU, а затем обе части продифференцируем по времени, получится: dQ/dt=C*dU/dt. В левой части я думаю все узнали выражение для силы тока, поэтому заменив dQ/dt на I, окончательно получим: I=C*dU/dt — выражение, связывающее ёмкость и мгновенные значения силы тока и напряжения на конденсаторе.

«Ну и зачем нам эта формула?», — спросят некоторые товарищи, и будут очень сильно неправы, потому что это вообще-то основная формула, которая используется в расчётах цепей с конденсаторами.

Что нам ещё интересно? Интересно, например, сколько энергии накоплено в конденсаторе и где эта энергия сосредоточена. Как это узнать? Всё так же просто, как и с источником ЭДС, о котором мы говорили в первой части. Раз на обкладках накапливаются заряды и обкладки разделены диэлектриком, значит между обкладками существует электрическое поле. В этом-то электрическом поле и сосредоточена энергия конденсатора. Как её оценить? Очевидно так же, по величине работы, которую это поле может совершить по перемещению зарядов.

Представим, что у нас есть полностью заряженный конденсатор (при этом напряжение на его выводах равно U1) и мы замкнули его выводы между собой (не важно через какое сопротивление). Какая мгновенная мощность будет при этом выделяться в нашей цепи? Как мы знаем мгновенная мощность определяется выражением P=U*dQ/dt. Работа за какой-то промежуток времени — это определённый интеграл от мгновенной мощности на этом промежутке времени. Очевидно, что для того, чтобы посчитать всю запасённую конденсатором энергию, надо измерять работу за промежуток времени от момента, когда мы замкнули полностью заряженный конденсатор до момента его полного разряда, то есть от момента, когда напряжение на конденсаторе было равно U1 до момента, когда напряжение на нём станет равным нулю. Это мы запомним. Изменение напряжения и изменение заряда связаны соотношением dU=dQ/C, отсюда dQ=dU*C. Подставив это выражение в формулу для мощности, получим: P=C*U*dU/dt. Перенесём dt в левую часть и проинтегрируем. В левой части получим работу, а в правой определённый интеграл от напряжения. Какие пределы напряжения брать для вычисления этого определённого интеграла? А вот теперь вспоминайте то, что чуть выше запомнили: «от момента, когда напряжение на конденсаторе было равно U1 до момента, когда напряжение на нём станет равным нулю». Значит в правой части интеграл надо брать от U1 до нуля. В итоге получится A=C*U12/2. Эта работа как раз и равна энергии, запасённой конденсатором. Ровно столько энергии он забирает из внешней цепи, когда заряжается, и ровно столько же энергии отдаёт во внешнюю цепь при разряде.

Ладно, с основными параметрами мы разобрались, где сосредоточена энергия и какова её величина — нашли, теперь переходим к неосновным параметрам, которые характеризуют различные потери на конденсаторе и при определённых условиях бывают очень важны, но значения которых бывает не так просто отыскать.

Первый такой важный параметр — это эквивалентное последовательное сопротивление (обычно употребляют английскую аббревиатуру от equivalent serial resistance — ESR). Что это вообще такое? Дело в том, что при движении по обкладкам и по металлическим выводам конденсаторов электроны испытывают точно такое же сопротивление, как и при движении по любому другому проводнику. Поэтому если мы хотим учесть ESR, то наш конденсатор следует рассматривать как элемент, который обладает не только ёмкостью (обычно именно так представляют идеальный конденсатор), но и последовательно соединённым с ней сопротивлением. Куда девается энергия, отнимаемая у упорядоченно движущихся зарядов в результате наличия сопротивления? Она точно так же, как и в обычном резисторе идёт на нагрев, только в данном случае нагреваются выводы и обкладки конденсатора. Итак, первое, почему важно учитывать ESR — потому, что это основной параметр, определяющий потери энергии в конденсаторе (следовательно от него зависит нагрев конденсатора, если токи заряда/разряда достаточно большие, то нагрев может быть значительным), кроме того, ESR влияет на сглаживающие способности конденсатора.

Именно из-за увеличения ESR при старении обычно вздуваются конденсаторы в блоках питания (ну и ещё из-за уменьшения сопротивления изоляции, но об этом ниже). Можно ли как-то уменьшить это негативное влияние ESR? Да легко, для этого надо подключить параллельно несколько конденсаторов, при этом сопротивления тоже окажутся включенными параллельно. В мощных блоках питания так и делают — ставят целые ряды параллельно включенных конденсаторов, хотя в принципе их можно было бы заменить всего одним или двумя, но большей ёмкости. На рисунке показано как уменьшается ESR при параллельном подключении двух одинаковых конденсаторов. Так что, как видите, включить два конденсатора по 470 мкФ может быть более выгодно, чем один на 1000 мкФ.

Второй важный параметр — это сопротивление изоляции. Этот параметр важен потому, что он позволяет оценить так называемые токи утечки. Что это такое? В принципе у нас обкладки конденсатора разделены диэлектриком, который не пропускает электрический ток, но это в идеале. Реально же сопротивление изоляции не бесконечно велико и, соответственно, когда между обкладками конденсатора есть напряжение, то через изоляцию текут так называемые токи утечки (пусть и очень очень маленькие). С учётом сопротивления изоляции конденсатор можно представить как ёмкость, шунтированную резистором. Каков эффект протекания этих токов? Они естественно тоже влияют на нагрев и сглаживающие свойства конденсатора. Обычно сопротивление изоляции всё таки огромно и токи утечки настолько мизерные, что их вообще не учитывают, но по мере старения конденсатора сопротивление изоляции может ослабнуть и токи утечки могут многократно возрасти. Иногда даже можно услышать: «появились токи утечки», как бы подчёркивая, что раньше они были настолько малы, что их вообще не брали в расчёт. Токи утечки, в свою очередь тоже ведут к повышенному нагреву конденсатора. В этом случае конденсатор просто выкидывают и ставят новый.

Ещё одним важным параметром является эквивалентная последовательная индуктивность — ESI. Она так же как и ESR обусловлена собственной индуктивностью выводов и обкладок конденсатора. Этот параметр начинает оказывать заметное влияние с ростом частоты. Помните, реактивное сопротивление ёмкости с ростом частоты уменьшается, а индуктивности, наоборот, увеличивается. Соответственно, при определённой частоте паразитная индуктивность может начать оказывать большее влияние, чем собственно, ёмкость. Именно поэтому, например, большие толстые электролиты, имеющие большую ESI, крайне плохо справляются с фильтрацией высокочастотных помех, а мелкая керамика, у которой ESI маленькая, — отлично. Хотя по логике, чем больше ёмкость — тем меньше реактивное сопротивление на одной и той же частоте, но в том-то и дело, что на высоких частотах главную роль играет уже не ёмкость, а паразитная индуктивность и ESR. Эквивалентная схема реального конденсатора с учётом ESI приведена на рисунке. Из этой схемы вытекает ещё одно интересное наблюдение. Если мы для борьбы с ESR включили несколько конденсаторов параллельно, то ESR мы конечно уменьшим, но при этом ESI такой сборки — увеличится. Это тоже может быть важным. Ну и хотелось бы добавить, что на нормальных платах ряды электролитов обычно шунтированы такими же рядами керамики (имеющей низкие ESI и ESR), как раз для фильтрации ВЧ помех, которые остаются незамеченными электролитами (с их высокими ESI и ESR).

Идём дальше. Ещё один такой параметр, который очень трудно найти, но тем не менее он существует и иногда его надо учитывать — это максимально допустимый пульсирующий ток через конденсатор, или сокращённо RCR (ripple current ratio, что можно перевести как «величина пульсирующего тока» или «размер токовых пульсаций»).

Ну и наконец последнее, на чём хочется остановиться — это тангенс угла потерь (tgd). Этот параметр равен отношению активной мощности, выделяемой на конденсаторе к реактивной мощности. Активная мощность — это понятное дело в основном мощность обусловленная ESR и сопротивлением изоляции. Реактивная мощность обусловлена ёмкостью и паразитной индуктивностью. Я думаю вполне понятно, что tgd также очень сильно зависит от частоты (потому что компоненты, которые определяют этот параметр зависят от частоты), поэтому сравнивать tgd у разных конденсаторов имеет смысл только когда они измерены для одной и той же частоты. Обычно есть стандартные частоты, на которых измеряют tgd. Буржуины иногда выражают этот параметр в % и называют DF (dissipation factor — фактор рассеяния или фактор потерь) или просто D. А поскольку они очень дотошные товарищи, то у них иногда можно найти даже график зависимости DF от частоты (один раз такой видел).

Обычно если у производителей конденсаторов и можно что-то найти, то это ESR или tgd (DF), но тем не менее надо помнить и про паразитную индуктивность, и про возможность появления токов утечки, и про максимальный ток.

Cпособы маркировки конденсаторов.

Часть 1. Заряды, потенциалы, напряжение, ток, сопротивление…
Часть 2. Как работают конденсаторы. Основные параметры конденсаторов.

Из истории

Первым конденсатором считается лейденская банка. Её разработали независимо сразу двое учёных:

Эвальд Георг фон Клейст (11 октября 1745 года).
Питер ван Мушенбрук (1745 – 1746 годы).

Двумя десятилетиями позже на свет появился электрофорус (1762 год), рассматриваемый как первый плоский конденсатор. Тогда не существовало терминов, вопросы накопления заряда мало интересовали. Учёные пока что развлекались получением статического заряда. К примеру, ван Мушенбрук испытывал лейденскую банку на слишком смелых студентах, когда сам оказался однажды полупарализован электрическим зарядом.

Наука не шла вперёд, хотя светила, включая Бенджамина Франклина, вовсю толкали паровоз. Современный этап развития физики начался с Алессандро Вольта. Учёный оказался привлечён конструкцией электрофоруса и заинтригован. Натёртая резина могла сколь угодно долго заряжать металлическую пластину. В то время предполагалось, что электричество переносится флюидами атмосферы, и Вольта считал аналогично. Узрев, что электрофорус способен запасать заряд, учёный решил посчитать и количество.

Концепция Вольты

Как свидетельствуют записки учёного, уже в 1778 году он получил представление о разнице потенциалов, которые называл tension – напряжение. С 1775 года Вольта придерживается концепции электрической ёмкости – capacita, выдвинутой его учителем Беккарией. Вольта уже знает, что электрофорус способен накопить заряд, называет прибор конденсатором, и решает подтвердить теорию практикой. Иначе – найти взаимосвязь напряжения, ёмкости и объёмом (quantita) заряда.

Вольта начал с лейденской банки. Он заряжал её от статического генератора и пробовал определить энергию конденсатора тремя путями:

Наблюдал получаемую искру электрической дуги от различной конструкции лейденских банок, заряженных одинаковым напряжением.
Измерял количество произведённой электростатическими генераторами трения работу, пока показания электрометра не росли до определённого уровня.
Разряжал лейденские банки на открытом воздухе и пытался сравнить производимый ими электрический шок по истечении времени.

Все перечисленное привело исследователя к странным выводам, что высокие лейденские банки более вместительные (при одинаковых площадях обкладок и прочих равных условиях). Вероятно, это связано со скоростью разряда их дуги на воздухе вследствие различий в кривизне поверхностей. Силу разряда Вольта увязывал с электрическим током: чем быстрее течёт флюид, тем более жаркий (по ощущениям) эффект. В результате, Вольта счёл, что разница потенциалов единственная определяет процесс возникновения удара. Он решил, что напряжение допустимо измерить двумя путями:

Через количество оборотов генератора статического заряда.
Сравнивая силу электрического удара при разряде лейденской банки.

Вольта нашёл, что заряжая пустую лейденскую банку от полной, шок получается вдвое слабее. Постепенно (1782 год) Вольта пришёл к выводу, что вышеуказанные величины соотносятся между собой: tension x capacity ~ load, в современном мире выглядит как U C = q или C = q / U.

Вольта заключил, что ёмкость больше там, где при меньшем напряжении вмещается больше заряда. Последовало заключение, что количество накопленного флюида прямо пропорционально площади обкладок плоского конденсатора. Что согласуется с современными формулами. Вольта обобщил знания на случай произвольного проводника (экспериментировал со стержнями лейденских банок). Изменяя расстояние между обкладками, установил:

С ~ S / d.

Что фактически стало выражением ёмкости плоского конденсатора. Вольта объяснил зависимость наличием некоего сопротивления (resistance) между обкладками, подразумевая воздух. Изменяя дистанцию, удаётся варьировать этот параметр в обе стороны. Это слегка не согласуется с современными концепциями, но Вольта помог Георгу Ому 40 лет спустя вывести зависимость между током и напряжением.

Фактически измерения проделывались на основе работы поля, проявлявшейся лишь вследствие заряда конденсатора. Очевидно, что указанная величина равна энергии – одной из первых физических характеристики, использованных для вывода аналитических выражений.

Мера энергии заряженного конденсатора

При расчёте фильтров цепей питания и прочих электрических фильтров встаёт задача определения номиналов. Кажется, достаточно взять формулу частоты резонансного контура, но простота обманчива. Легко убедиться, что одинаковому ответу соответствует множество значений. Которое выбрать?

Чем больше мощность источника, питания прибора, тем большая энергия здесь проходит в единицу времени. Для конденсатора она зависит от квадрата напряжения и ёмкости, для дросселя – от величины электрического тока и индуктивности. Узнав период единственного колебания, эту цифру легко привязать к мощности, как выполняемой работе в единицу времени.

В результате инженер сумеет сказать приблизительно, какого размера ёмкость требуется в конкретном случае. Расчёт ведётся изначально по энергии заряженного конденсатора.

Аналогичное происходит в любой цепи. Конденсаторы служат для фильтрации и гальванической развязки, обязаны легко пропускать нужную частоту и оставаться ёмкими, чтобы не стать бутылочным горлышком в системе.

Ёмкость уединённого проводника

Потенциал всех точек нашего проводника, как мы знаем, имеет одно и то же значение , которое называется потенциалом проводника. Оказывается, что потенциал уединённого проводника прямо пропорционален его заряду. Коэффициент пропорциональности принято обозначать , так что

Величина называется электрической ёмкостью проводника и равна отношению заряда проводника к его потенциалу:

(1)

Например, потенциал уединённого шара в вакууме равен:

где — заряд шара, — его радиус. Отсюда ёмкость шара:

(2)

Если шар окружён средой-диэлектриком с диэлектрической проницаемостью , то его потенциал уменьшается в раз:

Соответственно, ёмкость шара в раз увеличивается:

(3)

В чём смысл понятия ёмкости? Ёмкость показывает, какой заряд нужно сообщить проводнику, чтобы увеличить его потенциал на В. Чем больше ёмкость — тем, соответственно, больший заряд требуется поместить для этого на проводник.

Единицей измерения ёмкости служит фарад (Ф). Из определения ёмкости (1) видно, что Ф = Кл/В.

Давайте ради интереса вычислим ёмкость земного шара (он является проводником!). Радиус считаем приближённо равным км.

мкФ.

Как видите, Ф — это очень большая ёмкость.

Следовательно, диэлектрическая постоянная может измеряться в Ф/м:

Ф.

Так легче запомнить, не правда ли?

Величина энергии

Как будет вычисляться накопленный энергетический потенциал, разобраться можно с помощью показанного на снимке блока фотовспышки. Следует напомнить о том, что для увеличения емкости применяют параллельное соединение (Cобщ = C1 + C2 +…+ Cn). При последовательном варианте пропорциональная зависимость обратная (1/Cобщ = 1/C1 + 1/C2 +…+ 1/Cn).

Расчет:

2 емкости по 400 мкФ (Cобщ = C1 + C2 = 400 + 400 = 800 мкФ);
источник питания будет заряжать элемент напряжением 300 В;
энергия конденсатора W = ½ *C * U2 = ½ * 800 * 10-6 * 300 = 0,12 джоуля.

Использование конденсаторов

Подученное соотношение величин характерно для всех типов конденсаторов. Его используют для того, чтобы определить накопленную энергию при подключении к источнику питания. Измерить напряжение на выводах можно с помощью мультиметра. Кроме емкости, на корпусе конденсатора указывают другие важные параметры:

рабочий ток;
номинальное напряжение;
диэлектрический материал;
тип элемента.

К сведению. На миниатюрных деталях места для размещения всех данных недостаточно. Применяют систему сокращенных кодировок. Необходимые сведения уточняют в сопроводительной документации либо на официальном сайте производителя.

В следующем перечне приведены примеры электротехнических схем и устройств, которые создают с применением конденсаторов:

частотный (сглаживающий) фильтр;
колебательный контур;
накопитель энергии для формирования мощного импульса (лазер, фотовспышка);
ограничитель силы тока (компенсатор подключаемой реактивной нагрузки);
измерение перемещений (изменение емкости при сближении/ отдалении обкладок).

Для автоматизированного расчета типовой схемы можно использовать специализированный калькулятор онлайн. Следующий пример демонстрирует расчет корректного подключения электродвигателя:

соединение обмоток – треугольник;
мощность потребления – 1 200 Вт;
напряжения сети – 220 В;
cos ϕ – 0,9;
КПД – 85%;
емкость рабочего (пускового) конденсатора – 52 (130) мкФ.

Практические измерения

Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.

Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.

Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.

Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.

Источник

§16. Превращение энергии в электрических и магнитных явлениях

16.7 Изменение энергии конденсатора при изменении его емкости.

Конденсатор. Энергия электрического поля

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Ёмкость уединённого проводника

Ёмкость плоского конденсатора

Энергия заряженного конденсатора

Энергия электрического поля

Вывод формулы для энергии заряженного конденсатора

Темы кодификатора ЕГЭ: электрическая ёмкость, конденсатор, энергия электрического поля конденсатора.

Характеристики конденсатора

Идея суперконденсатора

Энергия конденсатора

Единица и формулы расчёта

Математическое выражение фарада

Энергия заряженного конденсатора

Плоский конденсатор.

Процессы зарядки и разрядки конденсаторов.

Основы электроники. Часть 2. Как работают конденсаторы. Параметры конденсаторов

Из истории

Концепция Вольты

Мера энергии заряженного конденсатора

Ёмкость уединённого проводника

Величина энергии

Использование конденсаторов

Практические измерения

Не пропустите также: