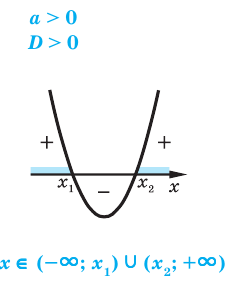
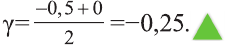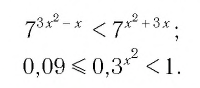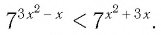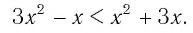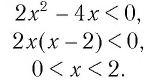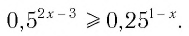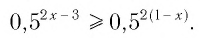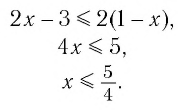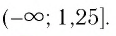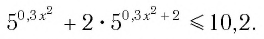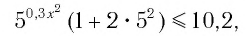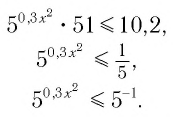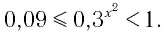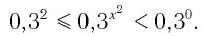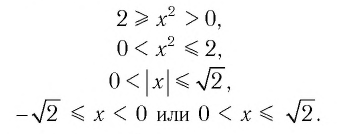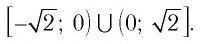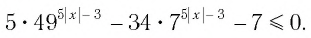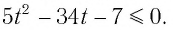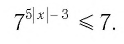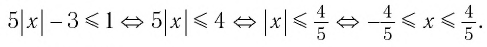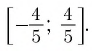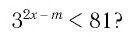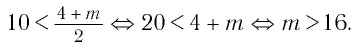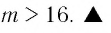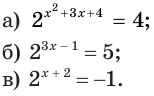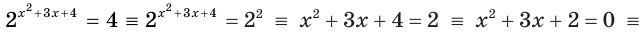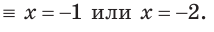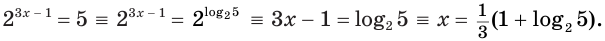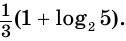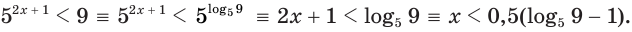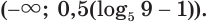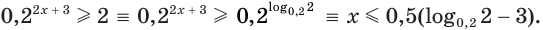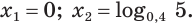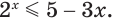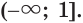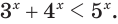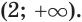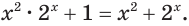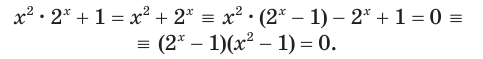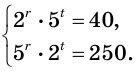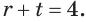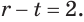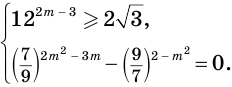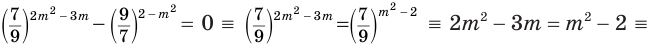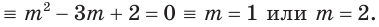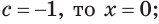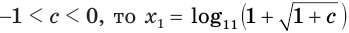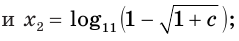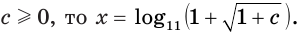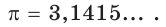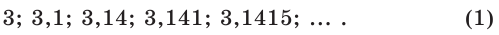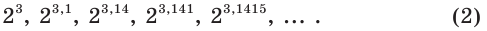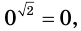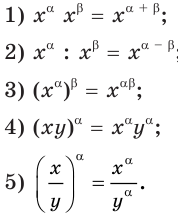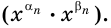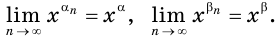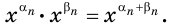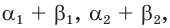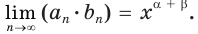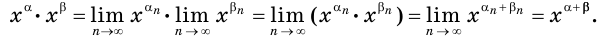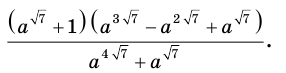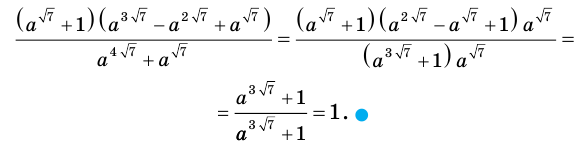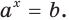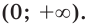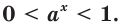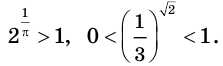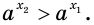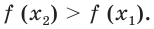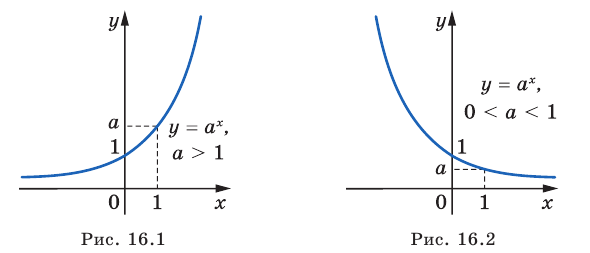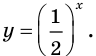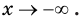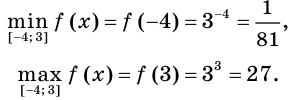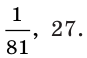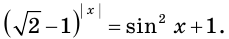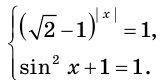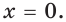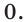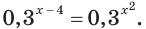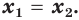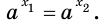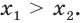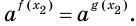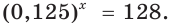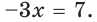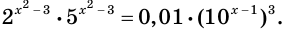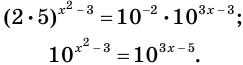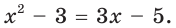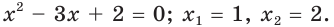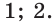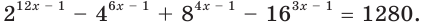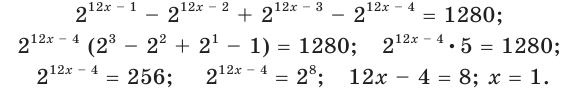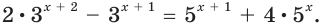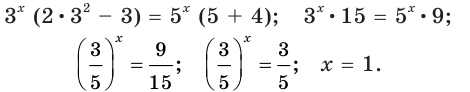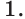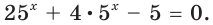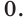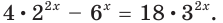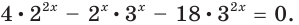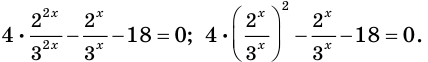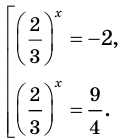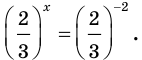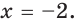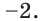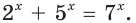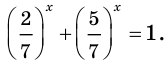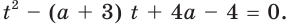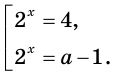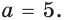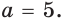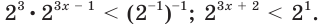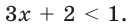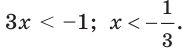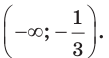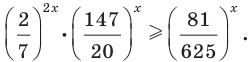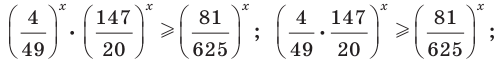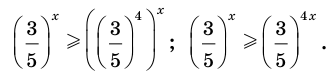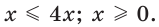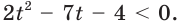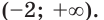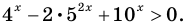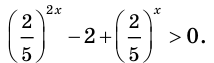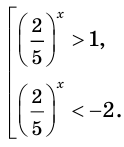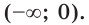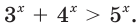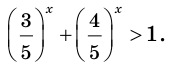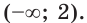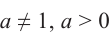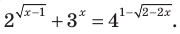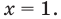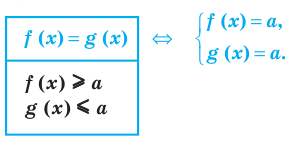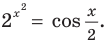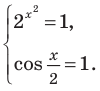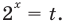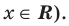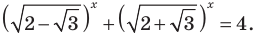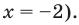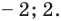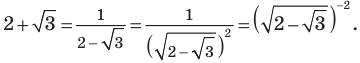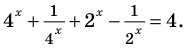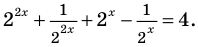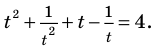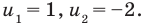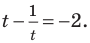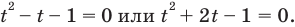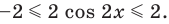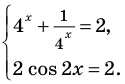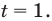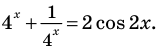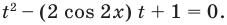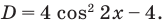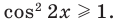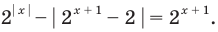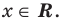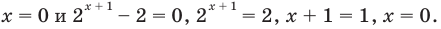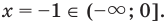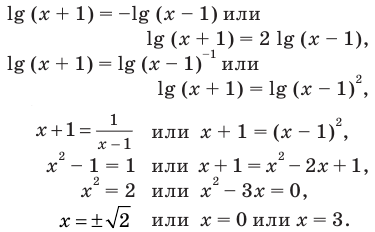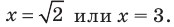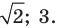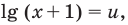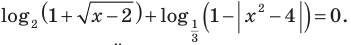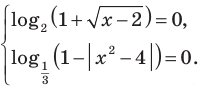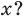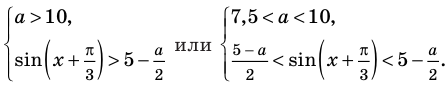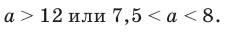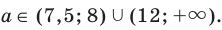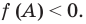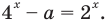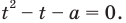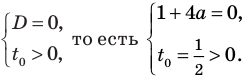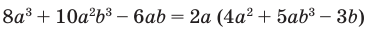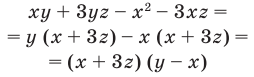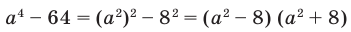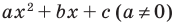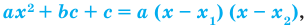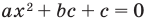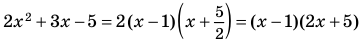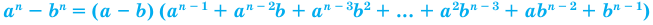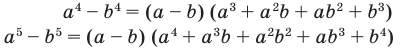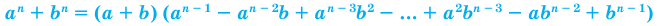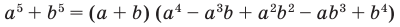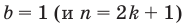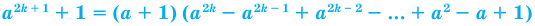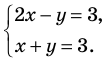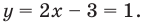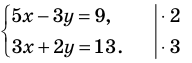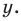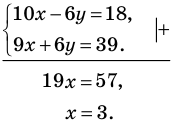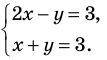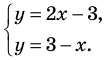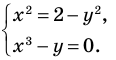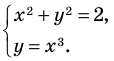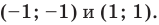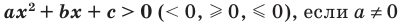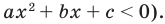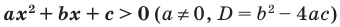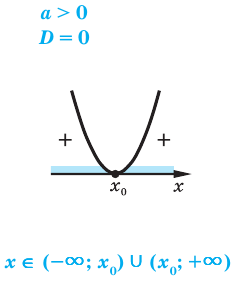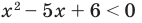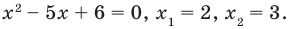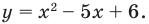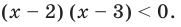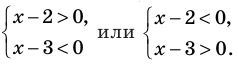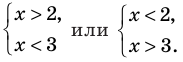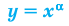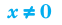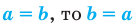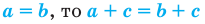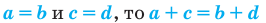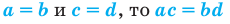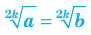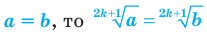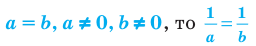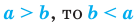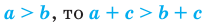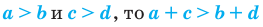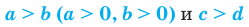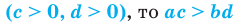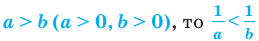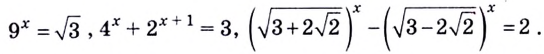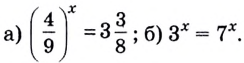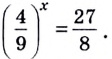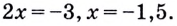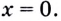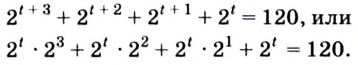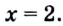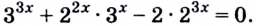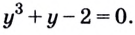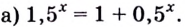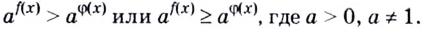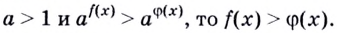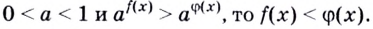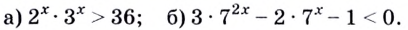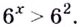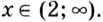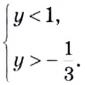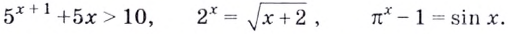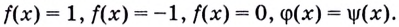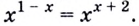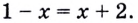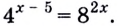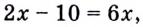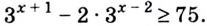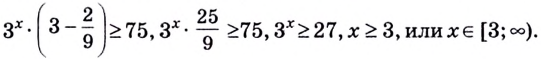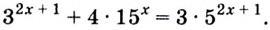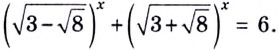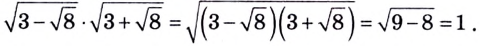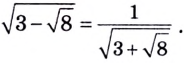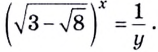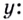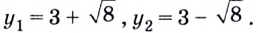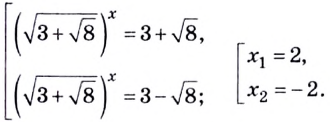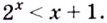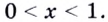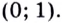3.1. Отделение корней нелинейного уравнения
Отделение корней – это определение их наличия, количества и нахождение для каждого их них достаточно малого отрезка [a, b], которому он принадлежит.
На первом этапе определяется число корней, их тип. Определяется интервал, в котором находятся эти корни, или определяются приближенные значения корней.
В инженерных расчетах, как правило, необходимо определять только вещественные корни. Задача отделения вещественных корней решается Аналитическими и Графическими методами.
Аналитические методы основаны на функциональном анализе.
Для алгебраического многочлена n-ой степени (полинома) с действительными коэффициентами вида
Pn(x) = an x n + an-1xn-1 +. +a1x+ a0 = 0, (an >0) (3.2)
Верхняя граница положительных действительных корней определяется по формуле Лагранжа (Маклорена):
, (3.3)
Где: k ³ 1 – номер первого из отрицательных коэффициентов полинома;
B – максимальный по модулю отрицательный коэффициент.
Нижнюю границу положительных действительных корней можно определить из вспомогательного уравнения
(3.4)
Если для этого уравнения по формуле Лагранжа верхняя граница равна R1, то
= (3.5)
Тогда все положительные корни многочлена лежат в интервале
≤x+≤.
Интервал отрицательных действительных корней многочлена определяется с использованием следующих вспомогательных функций.
и .
≤x–≤ = =.
Рассмотрим пример отделения корней с использованием этого аналитического метода.
Методом Лагранжа определим границы положительных и отрицательных корней многочлена.
3×8 – 5×7 – 6×3 – x – 9 = 0
K = 1 B = |– 9| an = 3
= 4
9×8 + x7 + 6×5 + 5x – 3 = 0
k = 8 B = 3 an = 9
Отсюда границы положительных корней 0,5 ≤ x+ ≤ 4
3×8 + 5×7 + 6×3 + x – 9 = 0
=
9×8 – x7 – 6×5 – 5x – 3 = 0
K = 1 B = 6 an = 9
Следовательно, границы отрицательных корней –2 ≤ x– ≤ –0,6
Формула Лагранжа позволяет оценить интервал, в котором находятся все действительные корни, положительные или отрицательные. Поэтому, для определения расположения каждого корня необходимо проводить дополнительные исследования.
Для трансцендентных уравнений не существует общего метода оценки интервала, в котором находятся корни. Для этих уравнений оцениваются значения функции в особых точках: разрыва, экстремума, перегиба и других.
На практике получил большее распространение Графический метод приближённой оценки вещественных корней. Для этих целей строится график функции по вычисленным её значениям.
Графически корни можно отделить 2-мя способами:
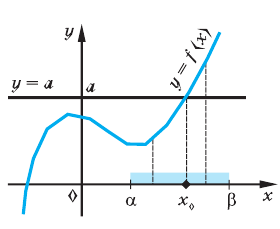
1. Построить график функции y = f(x) и определить координаты пересечений с осью абсцисс− это приближенные значения корней уравнения.На графике 3 корня.
Рис. 3.1 Отделение корней на графике f(x).
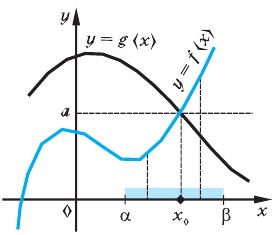
2. Преобразовать f(x)=0 к виду j(x) = y(x), где j(x) и y(x) – элементарные функции, и определить абсциссу пересечений графиков этих функций.
На графике 2 корня.
Рис. 3.2 Отделение корней по графикам функций j(x) и y(x).
Графический метод решения нелинейных уравнений широко применяется в технических расчётах, где не требуется высокая точность.
Для отделения вещественных корней можно использовать ЭВМ. Алгоритм отделения корней основан на факте Изменения знака функции в окрестности корня. Действительно, если корень вещественный, то график функции пересекает ось абсцисс, а знак функции изменяется на противоположный.
Рассмотрим Схему алгоритма отделения корней нелинейного уравнения на заданном отрезке в области определения функции.
Алгоритм позволяет определить приближённые значения всех действительных корней на отрезке [a, b]. Введя незначительные изменения в алгоритм, его можно использовать для определения приближённого значения максимального или минимального корня.
Приращение неизвестного Δx не следует выбирать слишком большим, чтобы не «проскочить» два корня.
Недостаток метода – использование большого количества машинного времени.
Метод интервалов, решение неравенств
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
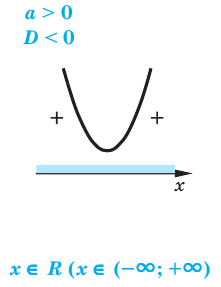
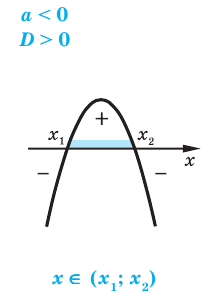
- D 2 + bx + c.
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, 2 + bx + c из левой части квадратного неравенства.
Изобразить координатную прямую и при наличии корней отметить их на ней.
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
Если неравенство со знаком 2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x 2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
- 2 2 + 4 * 2 — 5 = 4 + 8 — 5 = 7.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
- 0 2 + 4 * 0 — 5 = 0 + 0 — 5 = -5.
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
- (-6) 2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
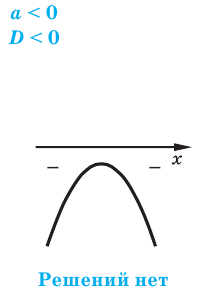
если a 2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
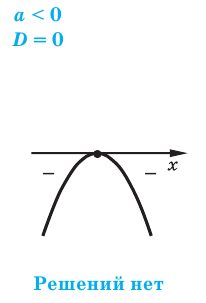
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.
Разложим квадратный трехчлен на множители.
Неравенство примет вид:
Проанализируем два сомножителя:
Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.
Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.
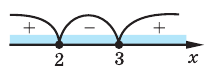
Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
Отобразим эти данные на чертеже:
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.
Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Приближенное нахождение корней уравнения
Задание 2 . 1) Выбрав стартовую точку с координатами x01=0.5 и xo2=0.4, примените метод Ньютона–Рафсона, и с точностью e=0.000001 найдите минимум целевой функции:
Скачать решение
2) Выбрав ту же стартовую точку, примените метод наискорейшего спуска, и вновь найдите минимум целевой функции с точностью e=0.0001.
Пример №1 . Отделить корни аналитически и уточнить один из них методом половинного деления с точностью до 0,01.
Решение.
sin(x+3.14/3)-x/2=0. Скачать
Пример №2 . Определить и найти действительные корни с точностью до 0,001: а) x 4 – 2x – 1 = 0 — методами: 1) деления отрезка пополам; 2) касательных. б) 2log(x) — (x-2) 2 = 0 — методами: 1) хорд; 2) итераций.
Решение.
Найдем корни уравнения:
x 4 -2•x-1 = 0
Используем для этого Метод половинного деления (метод дихотомии).
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Уточним интервалы, в которых будут находиться корни уравнения. Для этого исходный интервал [-1;2] разобьем на 10 подынтервалов.
h1 = -1 + 1*(2-(-1))/10 = -0.7
h2 = -1 + (1+1)*(2-(-1))/10 = -0.4
Поскольку F(-0.7)*F(-0.4) 0, то a=-0.55
Итерация 2.
Находим середину отрезка: c = (-0.55 -0.4)/2 = -0.48
F(c) = 0.000907
F(x) = 0.19
Поскольку F(c)•F(x) > 0, то a=-0.48
Итерация 3.
Находим середину отрезка: c = (-0.48 -0.4)/2 = -0.44
F(c) = -0.0884
F(x) = 0.000907
Поскольку F(c)•F(x) 0, то a=1.25
Итерация 2.
Находим середину отрезка: c = (1.25 + 1.4)/2 = 1.33
F(c) = -0.57
F(x) = -1.06
Поскольку F(c)•F(x) > 0, то a=1.33
Итерация 3.
Находим середину отрезка: c = (1.33 + 1.4)/2 = 1.36
F(c) = -0.28
F(x) = -0.57
Поскольку F(c)•F(x) > 0, то a=1.36
Итерация 4.
Находим середину отрезка: c = (1.36 + 1.4)/2 = 1.38
F(c) = -0.12
F(x) = -0.28
Поскольку F(c)•F(x) > 0, то a=1.38
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 1.25 | 1.1 | 1.4 | -1.06 | -1.06 |
| 2 | 1.33 | 1.25 | 1.4 | -0.57 | -0.57 |
| 3 | 1.36 | 1.33 | 1.4 | -0.28 | -0.28 |
| 4 | 1.38 | 1.36 | 1.4 | -0.12 | -0.12 |
| 5 | 1.39 | 1.38 | 1.4 | -0.0415 | -0.0415 |
| 6 | 1.4 | 1.39 | 1.4 | -0.000217 | -0.000217 |
| 7 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0206 |
| 8 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.0102 |
| 9 | 1.4 | 1.4 | 1.4 | -0.000217 | 0.00498 |
Ответ:
x = 1.4; F(x) = 0.00498
Количество итераций, N = 9
Параметр сходимости.
α = (1.4 — 1.4)/9 = 6.5E-5
Посмотрите как можно быстро решить задачу.
http://skysmart.ru/articles/mathematic/metod-intervalov-reshenie-neravenstv
http://math.semestr.ru/optim/examples_korni.php

Шаговый метод
Дано уравнение F(x)=0. Задан интервал поиска [x0,x1]. Требуется найти интервал [a,b] длиной h, содержащий первый корень уравнения, начиная с левой границы интервала поиска.
Алгоритм метода:
•Установить интервал [a,b] на начало интервала поиска (a=x0).
•Определить координату точки b (b=a+h), а также значения функции в точках a и b: F(a) и F(b).
•Проверить условие F(a)*F(b)<0. Если условие не выполнено — передвинуть интервал [a,b] на один шаг (a=b) и перейти к пункту 2. Если условие
выполнено — закончить алгоритм.
Решением являются координаты точек a и b. Отрезок [a,b] содержит корень уравнения, поскольку функция F(x) на его концах имеет разные знаки (рис
2).
F(x)
Рис. 2. Иллюстрация шагового метода
Найдя первый корень, можно продолжить поиск корней по тому же алгоритму. В этом случае определяются отрезки, содержащие все корни уравнения на интервале поиска [x0,x1]. Если на всем интервале поиска ни разу не было выполнено условие F(a)*F(b)<0, то данный интервал вообще не содержит корней.
Рассмотрим пример ручной реализации метода.
12

Дано уравнение x2 – 4x + 3 = 0 и интервал поиска корня [0;2]. Требуется отделить первый корень уравнения шаговым методом с шагом h=0,3. Построим таблицу в соответствии с алгоритмом метода.
Таблица 1
|
a |
b |
F(a) |
F(b) |
F(a)*F(b)<0 |
|||
|
0 |
0,3 |
3 |
1,89 |
нет |
|||
|
0,3 |
0,6 |
1,89 |
0,96 |
нет |
|||
|
0,6 |
0,9 |
0,96 |
0,21 |
нет |
|||
|
0,9 |
1,2 |
0,21 |
-0,36 |
да |
Ответ: корень расположен на интервале [0,9;1,2].
Достоинство метода: простота алгоритма. Недостаток: для достижения большой точности требуется уменьшать шаг, а это может существенно увеличить время расчета.
Метод половинного деления
Метод основан на последовательном сужении интервала, содержащего единственный корень уравнения F(x)=0 до тех пор, пока не будет достигнута заданная точность ε. Пусть задан отрезок [a,b], содержащий один корень уравнения. Этот отрезок может быть предварительно найден с помощью шагового метода.
Алгоритм метода (рис. 3):
•Определить новое приближение корня x в середине отрезка [a,b]: x=(a+b)/2.
•Найти значения функции в точках a и x: F(a) и F(x).
•Проверить условие F(a)*F(x)<0. Если условие выполнено, то корень расположен на отрезке [a,x]. В этом случае необходимо точку b переместить в точку x (b=x). Если условие не выполнено, то корень расположен на отрезке [x,b]. В этом случае необходимо точку a переместить в точку x (a=x).
•Перейти к пункту 1 и вновь поделить отрезок пополам. Алгоритм про-
должить до тех пор, пока не будет выполнено условие F(x) <ε.
13

F(x)
Рис. 3. Иллюстрация метода половинного деления
Рассмотрим пример ручной реализации метода. Дано уравнение
x2 – 4x + 3 = 0. Известно, что единственный корень уравнения расположен на отрезке [0,9;1,2]. Требуется уточнить значение корня методом половинного деления с точностью ε = 0,01. Построим таблицу в соответствии с алгоритмом метода.
|
a |
x |
b |
F(a) |
F(x) |
F(a)*F(x)<0 |
|
0,9 |
1,05 |
1,2 |
0,21 |
-0,0975 |
да |
|
0,9 |
0,975 |
1,05 |
0,21 |
0,050625 |
нет |
|
0,975 |
1,0125 |
1,05 |
0,050625 |
-0,02484 |
да |
|
0,975 |
0,99375 |
1,0125 |
0,050625 |
0,012539 |
нет |
|
0,99375 |
1,003125 |
1,0125 |
0,012539 |
-0,00624 |
стоп |
Алгоритм остановлен, поскольку -0,00624 <0,01.
Ответ: уточненное значение корня x ≈ 1,0031.
Достоинство метода: более быстрая сходимость к заданной точности, чем у шагового. Недостаток: если на отрезке [a,b] содержится более одного корня, то метод не работает.
Метод Ньютона
Задан отрезок [a,b], содержащий корень уравнения F(x)=0. Уточнение значения корня производится путем использования уравнения касательной. В качестве начального приближения задается тот из концов отрезка [a,b], где значение функции и ее второй производной имеют одинаковые знаки (т.е. выпол-
няется условие F(x0)*F′′(x0)>0). В точке F(x0) строится касательная к кривой
14

y= F(x) и ищется ее пересечение с осью x. Точка пересечения принимается за новую итерацию. Итерационная формула имеет вид:
|
xi +1 |
= xi |
− |
F ( xi ) |
|
|
F ′( xi |
) |
|||
Итерационный процесс продолжается до тех пор, пока не будет выполне-
но условие F(x)<ε , где ε — заданная точность.
x2 x1
Рис. 4. Иллюстрация метода Ньютона
Рис. 4. иллюстрирует работу метода Ньютона. В данном случае вторая производная функции положительна, поэтому в качестве начального приближения выбрана точка x0 = b. Как видно из рисунка, метод имеет очень быструю сходимость: обычно заданная точность достигается за 2-3 итерации.
Рассмотрим пример ручной реализации метода.
Дано уравнение x2 – 4x + 3 = 0. Известно, что корень уравнения расположен на отрезке [0,9;1,2]. Требуется уточнить значение корня методом Ньютона с точностью ε = 0,001.
Найдем первую и вторую производную функции F(x). F’(x)= 2x – 4; F”(x) = 2. F(0,9) = 0,21; F(1,2) = -0,36. Следовательно, в качестве началь-
ного приближения выбираем точку x0 = a = 0,9. Построим таблицу в соответствии с алгоритмом метода.
|
i |
xi |
F(xi) |
F'(xi) |
F(xi)<0,001 |
||||
|
0 |
0,9 |
0,21 |
-2,2 |
нет |
||||
|
1 |
0,99545 |
0,00911 |
-2,0090909 |
нет |
||||
|
2 |
0,99999 |
0,000021 |
-1,00002 |
да |
||||
|
15 |
||||||||
Содержание:
Рассмотрим уравнения, в которых переменная (неизвестное) находится в показателе степени. Например:
Уравнения такого вида принято называть показательными.
Решении показательных уравнений
При решении показательных уравнений нам будет полезно следствие из теоремы о свойствах показательной функции.
Следствие:
Пусть
Каждому значению показательной функции 
Пример:
Решить уравнение
Решение:
Согласно следствию из равенства двух степеней с одинаковым основанием 3 следует равенство их показателей. Таким образом, данное уравнение равносильно уравнению
откуда
Ответ: 2; 3.
Пример:
Решить уравнение:
Решение:
а) Данное уравнение равносильно (поясните почему) уравнению
Если степени с основанием 3 равны, то равны и их показатели:
Решив это уравнение, получим
Ответ:
При решении каждого уравнения из примера 2 сначала обе части уравнения представили в виде степени с одним и тем же основанием, а затем записали равенство показателей этих степеней.
Пример:
Решить уравнение:
Решение:
а) Данное уравнение равносильно уравнению
Решая его, получаем:
Так как две степени с одинаковым основанием 2 равны, то равны и их показатели, т. е. 
б) Разделив обе части уравнения на 

Ответ:
При решении примера 3 а) левую часть уравнения разложили на множители. Причем за скобку вынесли такой множитель, что в скобках осталось числовое выражение, не содержащее переменной.
Пример:
Решить уравнение
Решение:
Обозначим 
Таким образом, из данного уравнения получаем
откуда находим:
Итак, с учетом обозначения имеем:
Ответ: 1; 2.
При решении примера 4 был использован метод введения новой переменной, который позволил свести данное уравнение к квадратному относительно этой переменной.
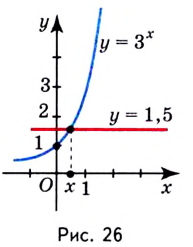
Пример:
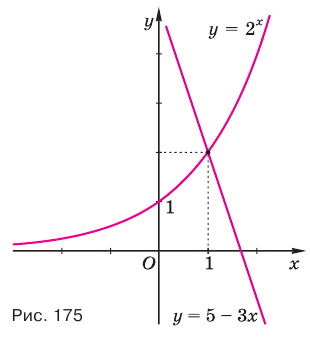
Решить уравнение
Решение:
Можно заметить, что 2 — корень данного уравнения. Других корней уравнение не имеет, так как функция, стоящая в левой части уравнения, возрастающая, а функция, стоящая в правой части уравнения, убывающая. Поэтому уравнение имеет не более одного корня (см. теорему из п. 1.14).
Ответ: 2.
Пример:
Решить уравнение
Решение:
Ответ: 3; 4.
Пример:
При каком значении а корнем уравнения 
Решение:
Поскольку х = 2 — корень, то верно равенство
Решив это уравнение, найдем
Ответ: при
Показательные уравнения и их системы
Показательным уравнением называется уравнение, в ко тором неизвестное входит в показатель степени. При решении показательных уравнений полезно использовать следующие тождества:
Приведем методы решения некоторых типов показательных уравнений.
1 Приведение к одному основанию.
Метод основан на следующем свойстве степеней: если две степени равны и равны их основания, то равны и их показатели, т.е. уравнения надо попытаться привести к виду 
Пример №1
Решите уравнение
Решение:
Заметим, что 
Применив тождество (1), получим Зх — 7 = -7х + 3, х = 1.
Ответ: 1.
Пример №2
Решить уравнение
Решение:
Переходя к основанию степени 2, получим:
Согласно тождеству (2), имеем
Последнее уравнение равносильно уравнению 4х-19 = 2,5х.
2 Введение новой переменной.
Пример №3
Решить уравнение
Решение:
Применив тождество 2, перепишем уравнение как
Введем новую переменную: 
которое имеет корни 


Ответ: х=2.
Пример №4
Решить уравнение
Решение:
Разделив обе части уравнения на 
последнее уравнение запишется так:
Решая уравнение, найдем
Значение 

Пример №5
Решить уравнение
Решение:
Заметим что 
Перепишем уравнение в виде
Обозначим 
Получим
Корнями данного уравнения будут
Следовательно,
III Вынесение общего множителя за скобку.
Пример №6
Решить уравнение
Решение:
После вынесения за скобку в левой части 



Системы простейших показательных уравнений
Пример №7
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей
системе :
Очевидно, что последняя система имеет решение
Пример №8
Решите систему уравнений:
Решение:
По свойству степеней система уравнений равносильна следующей системе: 
Умножив второе уравнение этой системы на (-2) и сложив с первым, получим уравнение —9х=-4. Отсюда, найдем 
Пример №9
Решите систему уравнений:
Решение:
Сделаем замену: 
Очевидно, что эта система уравнений имеет решение
Тогда получим уравнения
Приближенное решение уравнений
Пусть многочлен f(х) на концах отрезка [a,b] принимает значения разных знаков, то есть 

Это утверждение проиллюстрировано на следующем чертеже.
Рассмотрим отрезок 
Метод последовательного деления отрезка пополам заключается в последовательном разделении отрезка [a, b] пополам до тех пор, пока длина полученного отрезка не будет меньше заданной точности
Для этого:
- вычисляется значение f(х) выражения
- отрезок делится пополам, то есть вычисляется значение
- вычисляется значение
выражения f(х) в точке
- проверяется условие
- если это условие выполняется, то в качестве левого конца нового отрезка выбирается середина предыдущего отрезка, то есть полагается, что
(левый конец отрезка переходит в середину);
- если это условие не выполняется, то правый конец нового отрезка переходит в середину, то есть полагается, что b=x;
- для нового отрезка проверяется условие
- если это условие выполняется , то вычисления заканчиваются. При этом в качестве приближенного решения выбирается последнее вычисленное значение х. Если это условие не выполняется, то, переходя к пункту 2 этого алгоритма, вычисления продолжаются.
Метод последовательного деления пополам проиллюстрирован на этом чертеже:
Для нахождения интервала, содержащего корень уравнения 
Оказывается, что для корня 


Пример №10
Найдите интервал, содержащий корень уравнения
Решение:
Поделив обе части уравнения на 2 , получим,
Так как, для нового уравнения
Значит, в интервале, 




Значит, уравнение имеет корень, принадлежащий интервалу (-1; 0).
Нахождение приближенного корня с заданной точностью
Исходя из вышесказанного, заключаем, что если выполнено неравенство 



корень уравнения с точностью 




Пример №11
Найдите приближенное значение корня уравнения 
Решение:
Из предыдущего примера нам известно, что корень лежит в интервале
(-1; 0). Из того, что 
Так как, |(-0,25)41,5(-0,25)2+2,5(-0,25)+0,5| = |-0,046| < 0,1, то х=-0,25 — приближенное значение корня с точностью
Решение показательных неравенств
Рассмотрим неравенства, в которых переменная (неизвестное) находится в показателе степени. Например,
Неравенства такого вида принято называть показательными.
Из теоремы о свойствах показательной функции (п. 2.2, свойство 
Следствие:
Пусть а > 1. Если
Пусть
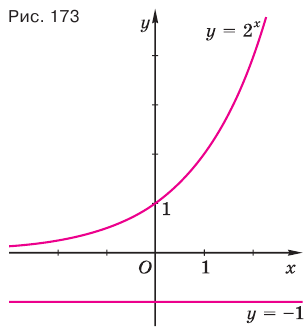
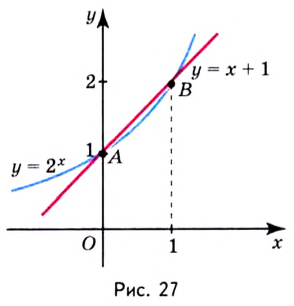
Изображения графиков показательной функции подсказывают это свойство. На рисунке 27 видно, что при а > 1 большему значению функции соответствует большее значение аргумента. А на рисунке 30 видно, что при 0 < а < 1 большему значению функции соответствует меньшее значение аргумента.
При решении показательных неравенств, так же как и при решении показательных уравнений, приходится использовать представление обеих частей неравенства в виде степеней с одним и тем же основанием, разложение одной из частей неравенства на множители, введение новой переменной.
Пример:
Решить неравенство
Решение:
Поскольку из двух степеней с основанием 7 больше та, показатель которой больше, то данное неравенство равносильно неравенству
Решим его:
Ответ: (0; 2).
Пример:
Решить неравенство
Решение:
Данное неравенство равносильно неравенству
Поскольку из двух степеней с одинаковым основанием 0,5 больше та, показатель которой меньше, то имеем
Ответ:
Пример:
Решить неравенство
Решение:
Данное неравенство равносильно неравенству
откуда
Поскольку из двух степеней с основанием 5 больше та, показатель которой больше, то данное неравенство равносильно неравенству
Решений нет, так как 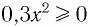
Ответ: нет решений.
Пример:
Решить неравенство
Решение:
Ответ:
Пример:
Решить неравенство
Решение:
Данное неравенство перепишем в виде
Поскольку из двух степеней с основанием 0,3 больше та, показатель которой меньше, то имеем:
Ответ:
Пример:
Решить неравенство
Решение:
Пусть 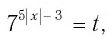
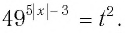
Решив это неравенство, получим: 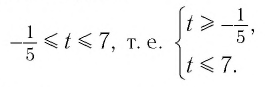
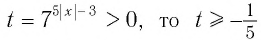
Остается решить второе неравенство системы:
Получим:
Ответ:
Пример:
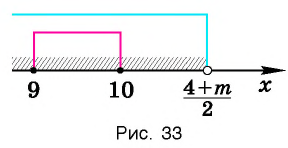
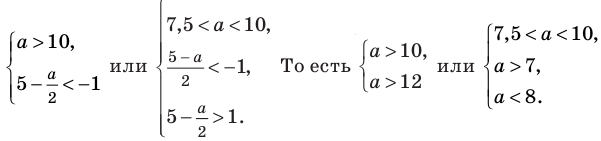
При каких значениях m любое значение х из промежутка [9; 10] является решением неравенства
Решение:
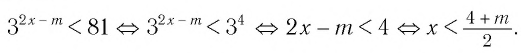
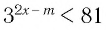
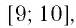
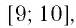
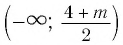
Итак, имеем:
Ответ: при
Показательные уравнения, неравенства и их системы
При решении показательных уравнений и неравенств, т. е. уравнений и неравенств, в которых переменная содержится в показателе степени, используются свойства показательной функции:
Пример №12
Решим уравнение:
а)
Ответ. -1; -2.
б)
Ответ.
в) Поскольку число -1 не принадлежит области значений показательной функции 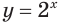
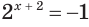
Ответ. Корней нет.
Пример №13
Решим неравенство:
а)
Ответ.
Здесь при переходе от неравенства 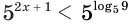
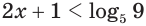
б) Поскольку значениями показательной функции 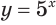
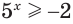
Ответ.
в)
Ответ.
Здесь при переходе от неравенства 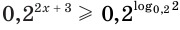
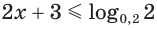
г) Поскольку при любом значении показателя 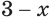
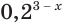
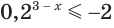
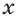
Для сведения показательного уравнения или неравенства к простейшим применяют общие приемы решения уравнений и неравенств: введение вспомогательной переменной, использование графических представлений, использование свойств функций, разложение на множители.
Пример №14
Решим уравнение:
а) Пусть 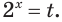
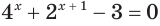
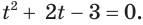
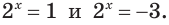
Ответ. 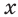
б) Перед введением вспомогательной переменной разделим обе части уравнения 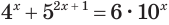
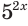
Пусть 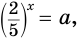
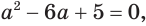
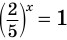
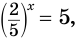
Ответ.
Пример №15
Решим неравенство
Построим графики функций 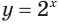
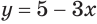
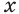
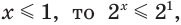
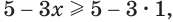
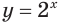
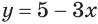
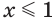
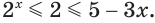
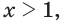
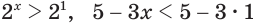
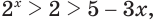
Ответ.
Пример №16
Решим неравенство
Функции, определяемые выражениями, записанными в левой и правой частях уравнения, возрастающие, но возрастают они с разной скоростью. Используем это. Разделим обе части неравенства на выражение 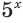
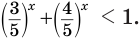
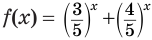
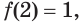
Ответ.
Пример №17
Решим уравнение
Остается решить уравнения 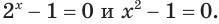
Ответ. 0; -1; 1.
Пример №18
Решим систему уравнений
Перемножив уравнения системы, получим уравнение 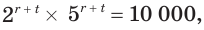
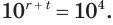
Разделив первое уравнение системы на второе, придем к уравнению 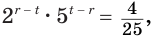
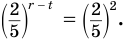
Таким образом, данная система равносильна системе 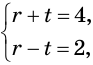
Ответ. (3; 1).
Пример №19
Решим систему
Решим уравнение системы:
Из найденных чисел неравенству удовлетворяет только число 2.
Ответ. 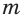
Пример №20
Решим уравнение 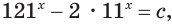
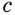
Данное уравнение равносильно уравнению 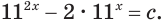
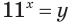
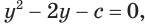
Пусть 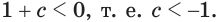
Пусть 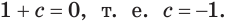
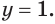
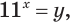
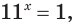
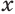
Пусть 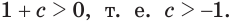
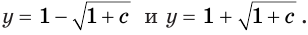
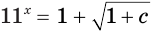
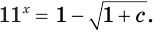
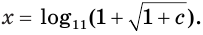
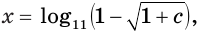
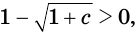
Ответ. Если 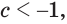
если
если
если
Степень с произвольным действительным показателем
Теперь мы выясним, что представляет собой степень положительного числа с действительным показателем.
Строгое определение степени с действительным показателем и доказательство ее свойств выходит за пределы школьного курса. Текст этого пункта содержит лишь общие пояснения того, как можно провести необходимые обоснования.
Начнем с частного случая. Выясним, что понимают под степенью числа 2 с показателем 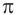
Иррациональное число 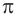
Рассмотрим последовательность рациональных чисел
Понятно, что эта последовательность сходится к числу 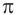
В соответствии с последовательностью 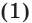
Можно показать, что члены последовательности 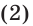
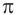

Аналогично можно действовать в общем случае, определяя смысл выражения 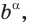
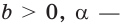
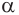
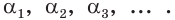
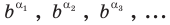
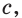
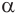
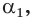
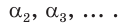
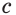
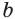
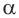
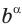
Если основание 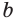
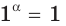
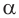
Если основание 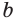
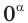
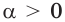
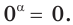
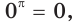
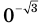
При 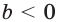
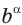
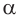
Степень с действительным показателем обладает теми же свойствами, что и степень с рациональным показателем.
В частности, для 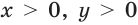
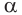
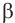
Докажем, например, свойство 1.
Пусть 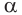
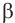
где 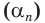
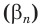
Для положительного числа 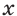
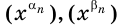
Имеем:
Так как для рациональных показателей 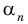
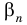
Последовательность рациональных чисел 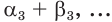
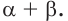
Пример №21
Упростите выражение
Решение:
Имеем:
Выберем некоторое положительное число 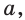
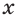
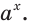
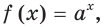
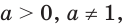
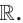
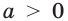
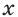
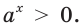
Можно показать, что для данного числа 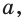
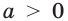
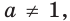
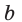
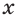
Сказанное означает, что областью значений показательной функции является множество
Показательная функция не имеет нулей, и промежуток 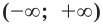
Показательная функция непрерывна.
Покажем, что при 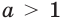
Лемма. Если 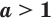
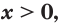
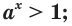
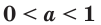
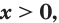
Например,
Рассмотрим произвольные числа 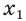
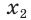
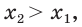
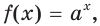
Поскольку 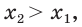
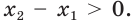
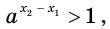
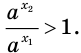
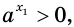
Отсюда
Мы показали, что из неравенства 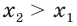
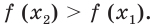
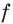
Аналогично можно показать, что при 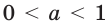
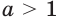
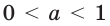
Показательная функция является дифференцируемой. Подробнее о производной показательной функции вы узнаете в п. 23.
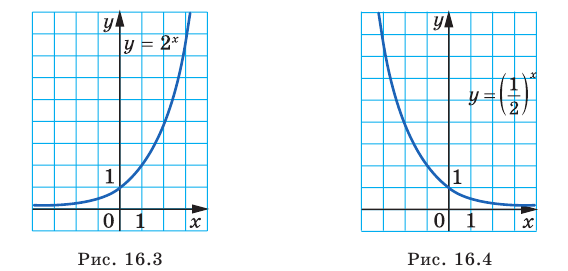
На рисунках 16.1 и 16.2 схематически изображен график показательной функции для случаев 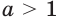
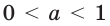
В частности, на рисунках 16.3 и 16.4 изображены графики функций 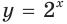
Заметим, что при 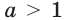
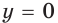
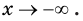
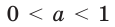
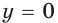
Показательная функция является математической моделью целого ряда процессов, происходящих в природе и в деятельности человека.
Например, биологам известно, что колония бактерий в определенных условиях за равные промежутки времени увеличивает свою массу в одно и то же количество раз.
Это означает, что если, например, в момент времени 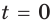
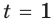
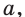

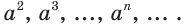
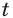
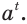
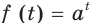
Таким образом, рассмотренный процесс описывают с помощью показательной функции 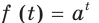
Из физики известно, что при радиоактивном распаде масса радиоактивного вещества за равные промежутки времени уменьшается в одно и то же количество раз.
Если поместить деньги в банк под определенный процент, то каждый год количество денег на счете будет увеличиваться в одно и то же количество раз.
Поэтому показательная функция описывает и эти процессы.
В таблице приведены свойства функции 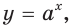
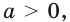
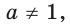
| Область определения | 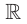 |
| Область значений | 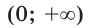 |
| Нули функции |  |
| Промежутки знакопостоянства | 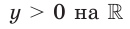 |
| Возрастание / убывание | Если 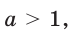 то функция возрастающая; если то функция возрастающая; если 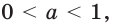 то функция убывающая то функция убывающая |
| Непрерывность | Непрерывная |
| Дифференцируемость | Дифференцируемая |
| Асимптоты | Если 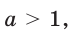 то график функции имеет горизонтальную асимптоту то график функции имеет горизонтальную асимптоту 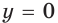 при при 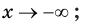 если если 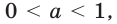 то график функции имеет горизонтальную асимптоту то график функции имеет горизонтальную асимптоту 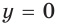 при при 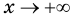 |
Пример №22
Найдите наименьшее и наибольшее значения функции 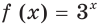
Решение:
Так как функция 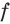
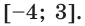
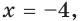
Следовательно,
Ответ:
Пример №23
Решите уравнение
Решение:
Так как 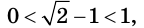
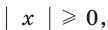
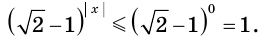
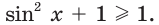
Отсюда
Ответ:
Вычисление показательных уравнений
Рассмотрим уравнения 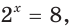
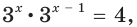
Во всех этих уравнениях переменная содержится только в показателе степени. Данные уравнения — примеры показательных уравнений.
Теорема 17.1. При 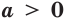
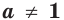
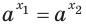
Доказательство. Очевидно, что если 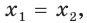
Докажем, что из равенства 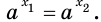
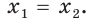
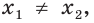
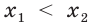
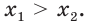
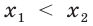
Рассмотрим показательную функцию 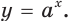
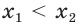
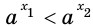
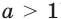
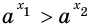
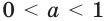
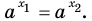
Аналогично рассматривают случай, когда
Следствие. Если 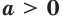
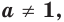
равносильно уравнению
Доказательство. Пусть 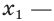
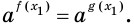
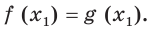
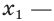
Пусть 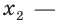
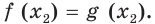
Мы показали, что каждый корень уравнения (1) является корнем уравнения (2) и наоборот, каждый корень уравнения (2) является корнем уравнения (1). Следовательно, уравнения (1) и (2) равносильны. А
Рассмотрим примеры решения показательных уравнений.
Пример №24
Решите уравнение
Решение:
Представим каждую из частей уравнения в виде степени с основанием 2. Имеем: 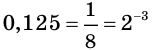
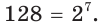
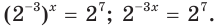
Отсюда 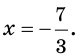
Пример №25
Решите уравнение
Решение:
Воспользовавшись свойствами степени, представим каждую из частей уравнения в виде степени с основанием 10. Имеем:
Переходим к равносильному уравнению:
Отсюда
Ответ:
Пример №26
Решите уравнение
Решение:
Имеем:
Ответ:
Пример №27
Решите уравнение
Решение:
Имеем:
Ответ:
Пример №28
Решите уравнение
Решение:
Так как 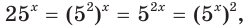
Пусть 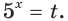
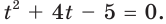
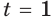
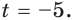
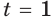
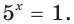
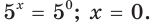
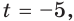
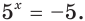
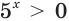
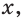
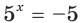
Пример №29
Решите уравнение
Решение:
Имеем:
Так как 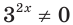
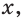
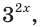
Пусть 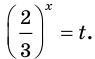
Отсюда 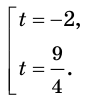
Так как 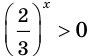
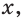
Отсюда
Ответ:
Пример №30
Решите уравнение
Решение:
Очевидно, что 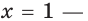
Разделив обе части исходного уравнения на 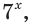
Рассмотрим функцию 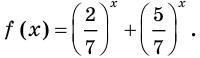
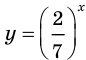
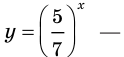
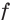
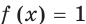
Ответ:
Пример №31
При каких значениях параметра 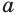
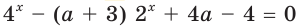
Решение:
Пусть 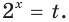
Отсюда 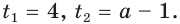
Первое уравнение совокупности имеет единственный корень 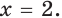
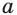
Для выполнения условия задачи второе уравнение совокупности либо должно не иметь корней, либо должно иметь единственный корень, равный 2.
Если 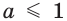
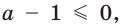
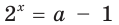
Число 2 является корнем второго уравнения совокупности, если 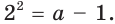
Ответ: 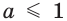
Вычисление показательных неравенств
Неравенства 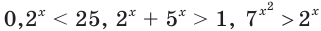
При решении многих показательных неравенств используют следующую теорему.
Теорема 18.1. При 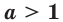
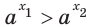
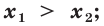
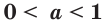
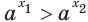
Справедливость этой теоремы следует из того, что при 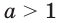
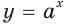
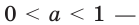
Следствие. Если 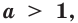
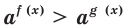
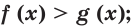
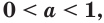
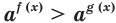
Воспользовавшись идеей доказательства следствия из теоремы 17.1, докажите это следствие самостоятельно.
Рассмотрим примеры решения показательных неравенств.
Пример №32
Решите неравенство
Решение:
Имеем:
Так как основание степеней 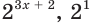
Отсюда
Ответ:
Пример №33
Решите неравенство
Решение:
Имеем:
Так как 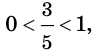
Ответ:
Пример №34
Решите неравенство
Решение:
Перепишем данное неравенство так:
Отсюда
Ответ:
Пример №35
Решите неравенство
Решение.
Имеем:
Пусть 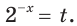
Решив это неравенство, получим 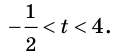
Так как 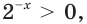
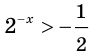
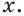
Имеем:
Ответ:
Пример №36
Решите неравенство
Решение:
Имеем: 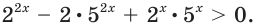
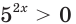
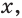
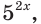
Пусть 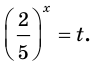
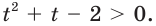
Отсюда:
Из неравенства 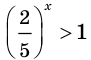
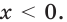
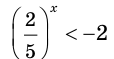
Ответ:
Пример №37
Решите неравенство
Решение:
Имеем:
Рассмотрим функцию 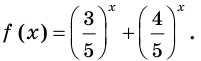
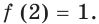

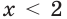
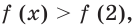
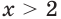
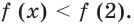

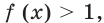
Свойство показательной функции
При условии, что
равенство 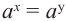
1)показательное уравнение 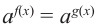
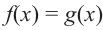
2)если в уравнении 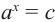
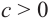
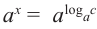
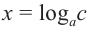
Применение свойств степени
Пример №38
Проверка.
Пример №39
Уравнения с разными основаниями можно решить разделив обе стороны на одну из степеней или логарифмированием обеих частей:
Примеры:
Введение новой переменной:
Пример:
Ответ: х = 2
Если уравнение состоит из членов, которые имеют одинаковую степень, а основания являются последовательными членами геометрической прогрессии, то обе части уравнения делится на один из крайних членов и вводится новая переменная.
Пример:
Зависимость между температурой и временем при охлаждении задаётся формулой Ньютона 
t — время.
Решение показательных и логарифмических уравнений и неравенств
1. Конечная ОДЗ:
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Пример №40
ОДЗ:
Итак, ОДЗ:
Проверка. 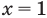
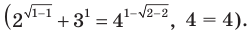
Ответ: 1.
2. Оценка значений левой и правой частей уравнения:
Если требуется решить уравнение вида 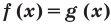
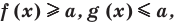
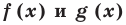
Пример №41
Оценим значения левой и правой частей данного уравнения: 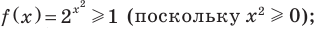
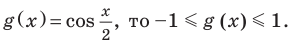
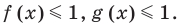
Из первого уравнения получаем 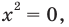
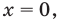
Ответ: 0.
3. Использование монотонности функций
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку значений левой и правой частей уравнения).
Теоремы о корнях уравнения:
1. Если в уравнении 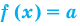
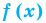
Пример №42
Уравнение 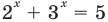
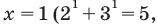
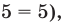
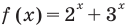
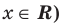
2. Если в уравнении 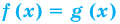
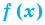

Пример:
Уравнение 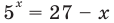
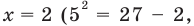
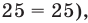
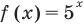
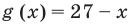
4. «Ищи квадратный трехчлен»
Попытайтесь рассмотреть заданное уравнение как квадратное относи# тельно некоторой переменной (или относительно некоторой функции).
Пример:
Запишем 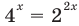
Получаем 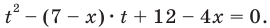
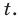
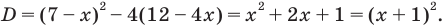
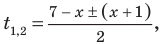
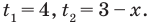
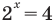
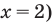
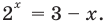
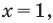
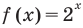
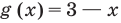
Ответ: 1; 2.
Пример №43
Решите уравнение
Решение:
Если 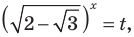
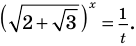
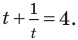
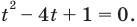
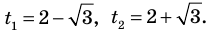
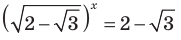
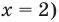
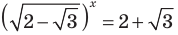
Ответ:
Комментарий:
Замечаем, что 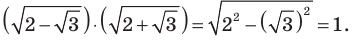
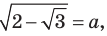
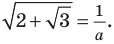
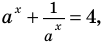
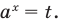
Пример №44
Решите уравнение
Комментарий:
Если привести все степени к одному основанию 2 и обозначить 
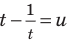
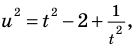
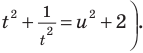

Решение:
Замена 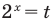
Обозначим 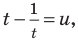
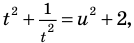
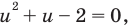
Обратная замена дает 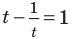
Тогда
Получаем 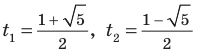
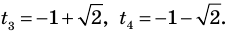
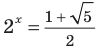
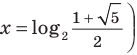
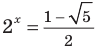
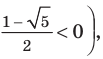
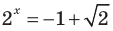
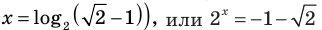
Ответ:
- Заказать решение задач по высшей математике
Пример №45
Решите уравнение
I способ
Комментарий:
Учитывая, что 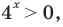
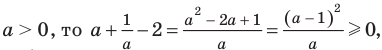
Для оценки значений правой части достаточно вспомнить, что областью значений функции 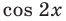
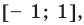
Решение:
Оценим значения левой и правой частей уравнения, 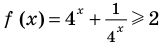
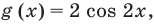
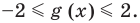
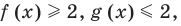
Из первого уравнения, используя замену 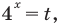
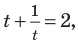
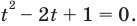
Тогда 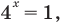
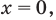
Ответ: 0.
II способ решения уравнения
Комментарий:
Если обозначить 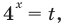
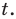
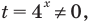
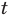
Решение:
После замены 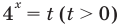
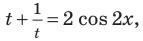
Рассмотрим уравнение (2) как квадратное относительно переменной 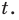
Уравнение (2) может иметь корни только тогда, когда 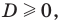
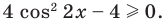
У этого неравенства знак «больше» не может выполняться 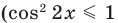
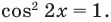
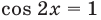
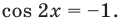
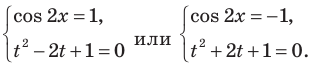
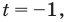
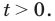
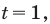
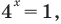
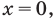
Ответ: 0.
Пример №46
Решите уравнение
Комментарий:
Для решения уравнения с несколькими модулями можем применить общую схему (с. 240):
- найти ОДЗ;
- найти нули всех подмодульных функций;
- отметить нули на ОДЗ и разбить ОДЗ на промежутки;
- найти решения уравнения в каждом из промежутков.
Решение:
ОДЗ:
Нули подмодульных функций:
Этот нуль 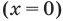
Промежуток I. При 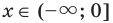
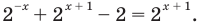
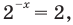
Промежуток II. При 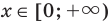
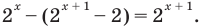
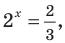
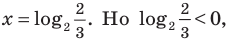
Ответ: -1.
Пример №47
Решите уравнение
Решение:
ОДЗ 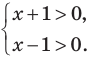
Поскольку 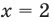
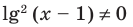
После замены 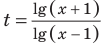
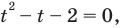
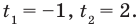
Тогда на ОДЗ имеем равносильные уравнения:
Учитывая ОДЗ, получаем
Ответ:
Комментарий:
Если выполнить замену 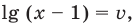
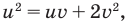
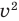
Чтобы не потерять корни уравнения при делении на выражение с переменной, необходимо те значения переменной, при которых это выражение равно нулю, рассмотреть отдельно. Значение 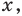
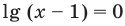
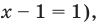
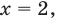
Для реализации полученного плана решения не обязательно вводить переменные 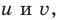
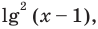
В конце учитываем, что все преобразования были равносильными на ОДЗ, следовательно, необходимо выбирать только те из найденных корней, которые входят в ОДЗ.
Пример №48
Решите уравнение
Комментарий:
Логарифмические функции, стоящие в левой части данного уравнения, принимают только неотрицательные значения.
Действительно, на всей области определения 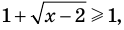
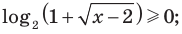
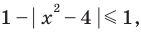
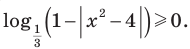
Заметим, что при переходе от данного уравнения к системе уравнений ОДЗ не изменяется, таким образом, ее можно не записывать в явном виде. При решении полученных простейших логарифмических уравнений ОДЗ также учитывается автоматически, поэтому ее можно вообще не записывать в решение.
Решение:
Поскольку на всей области определения 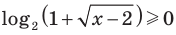
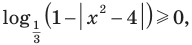
Из первого уравнения системы получаем 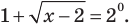
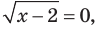
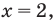
Ответ: 2.
Пример №49
При каких значениях параметра 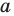
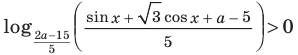
Комментарий:
Сначала воспользуемся формулой 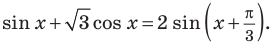
При дальнейшем анализе полученных неравенств учитываем, что неравенство 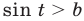
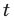
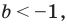
Решение:
Данное неравенство равносильно неравенству
Эта неравенство равносильно совокупности систем
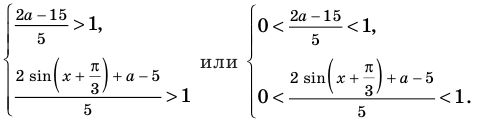
Неравенство с переменной 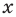
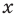
Тогда
Ответ: при
Пример №50
При каких значениях параметра а уравнение log2 (4′ имеет единственный корень?
Комментарий:
Выполняя равносильные преобразования данного уравнения, учитываем, что при использовании определения логарифма для решения этого простейшего логарифмического уравнения его ОДЗ учитывается автоматически.
При выполнении замены переменной в задании с параметром учитываем, что после замены требование задачи может измениться.
Исследуя расположение корней квадратного трехчлена 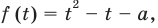
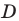
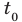
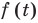
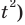
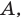
Решение:
Данное уравнение равносильно уравнению
То есть 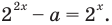
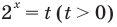
Требование задачи будет выполняться тогда и только тогда, когда уравнение (2) будет иметь единственный положительный корень. Это будет в одном из двух случаев:
- уравнение (2) имеет единственный корень, и он положительный;
- уравнение (2) имеет два корня, из которых только один положительный, а второй — отрицательный или нуль.
Для первого случая получаем
Таким образом,
Для второго случая значение 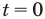
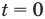
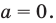
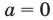
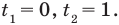
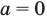
Остается еще один случай — корни уравнения (2) имеют разные знаки (расположены по разные стороны от нуля). Это будет тогда и только тогда, когда будет выполняться условие 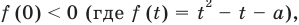
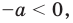
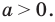
Ответ: при 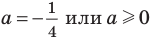
Справочный материал
Формулы сокращенного умножения. Разложение алгебраических выражений на множители
Основные приемы разложения многочлена на множители
Вынесение общего множителя за скобки
Способ группировки
Применение формул сокращенного умножения
Разложение на множители квадратного трехчлена
где 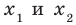
Поскольку 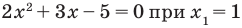
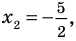
Обобщение некоторых формул сокращенного умножения
Примеры:
При 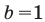
Примеры:
При
Системы уравнений
Если ставится задача найти все общие решения двух (или больше) уравнений с одной или несколькими переменными, то говорят, что требуется решить систему уравнений. Записывают систему уравнений, объединяя их фигурной скобкой. Решением системы называется такое значение переменной или такой упорядоченный набор значений переменных (если переменных несколько), которые удовлетворяют всем уравнениям системы. Решить систему уравнений — значит найти все ее решения или доказать, что решений нет. Если система не имеет решения, то ее называют несовместной.
Примеры:
1)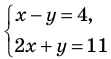
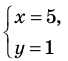
2) 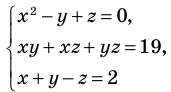
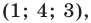
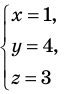
Равносильность систем уравнений:
Две системы уравнений называются равносильными на некотором множестве, если на этом множестве они имеют одинаковые решения (то есть каждое решение первой системы на этом множестве является решением второй и, наоборот, каждое решение второй системы является решением первой). Если изменить порядок уравнений заданной системы, то получим систему, равносильную заданной. Если одно из уравнений системы заменить на равносильное ему уравнение, то получим систему, равносильную заданной.
Областью допустимых значений (ОДЗ) системы называется общая область определения всех функций, входящих в запись этой системы. Все равносильные преобразования систем выполняются на ОДЗ исходной системы.
Основные способы решения систем уравнений
Способ подстановки:
Выражаем из одного уравнения системы одну переменную через другую (или через другие) и подставляем полученное выражение вместо соответствующей переменной во все другие уравнения системы (затем решаем полученное уравнение или систему и подставляем результат в выражение для первой переменной).
Пример №51
Решить систему
Решение:
Из первого уравнения системы 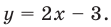
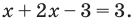
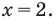
Ответ: (2; 1).
Способ сложения:
Если первое уравнение системы заменить суммой первого уравнения, умноженного на число 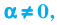

Пример №52
Решить систему
Решение:
Умножим обе части первого уравнения системы на 2, а второго — на 3 (чтобы получить как коэффициенты при переменной 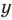
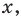
Тогда
Ответ: (3; 2).
Основные способы решения систем уравнений
Способ подстановки:
Выполняем равносильные преобразования заданной системы так, чтобы удобно было строить графики всех уравнений, входящих в систему. Затем строим соответствующие графики и находим координаты точек пересечения построенных линий — эти координаты и являются решениями системы.
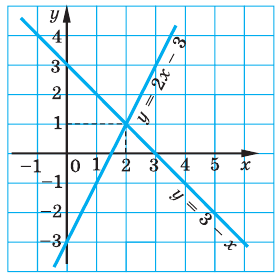
Пример №53
Решить графически систему
Решение:
Заданная система равносильна системе
Графиком каждого из уравнений системы является прямая. Для построения прямой достаточно построить две ее точки. Например, для
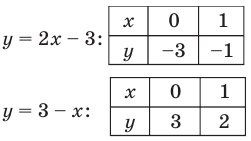
Графики пересекаются в единственной точке 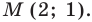
Ответ: (2; 1).
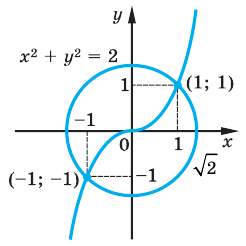
Пример №54
Решить графически систему
Решение:
Заданная система равносильна системе
График первого уравнения — окружность радиуса 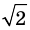
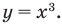
Ответ: 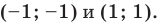
Квадратные неравенства
Квадратным неравенством называется неравенство вида
Для решения квадратного неравенства достаточно найти корни квадратного трехчлена 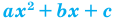
Как ответ записывают промежутки оси 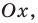
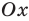
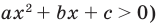
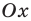
Если квадратный трехчлен имеет два разных корня 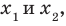
Разные случаи решения неравенства
Пример №55
Решите неравенство
І способ
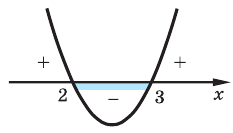
1.
2. Строим эскиз графика функции
Ответ: (2 ; 3)
ІІ способ (метод интервалов)
Обозначим
1. Область определения:
2. Нули функции:
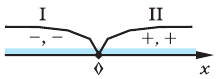
3. Отмечаем нули на области определения (на всей числовой прямой) и находим знак в каждом промежутке, на которые разбивается область определения (см. рисунок).
Для нахождения знаков функции 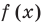
Ответ: (2; 3).
ІІІ способ (равносильные преобразования)
Поскольку 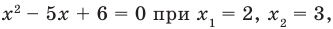
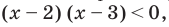
Тогда
Из первой системы получаем 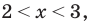
Ответ: (2; 3).
Нахождение области определения функции
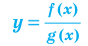
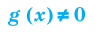
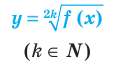
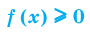
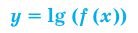
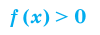
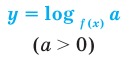
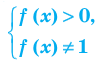
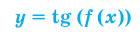
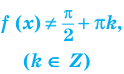
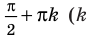
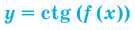
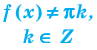
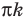
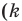

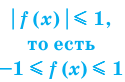
а) 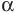

б) 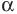
в) 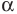
г) 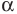
Основные свойства числовых равенств и неравенств
Свойства числовых равенств:
1 Если
2. Если 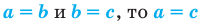
3. Если
4. Если
5. Если
6. Если
7. Если
8. а) Если 
б) Если
9. Если
10. 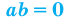
11. 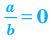
Свойства числовых неравенств
1. Если
2. Если 
3. Если
4. Если
5. а) Если
б) Если
6. Если
7. а) Если 
б) Если
8. а) Если 
б) Если
9. Если
10. 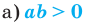

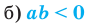

11. а) 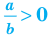

б) 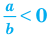

Определение показательных уравнений и неравенств
Уравнение называется показательным, если его переменные входят только в показатели степеней.
Примеры:
Существует много видов показательных уравнений и различных подходов к их решению. Основными методами решения показательных уравнений являются:
- Метод приведения обеих частей уравнения к степеням с одинаковыми основаниями.
- Метод введения новой переменной.
- Функционально-графический метод. Рассмотрим каждый из этих методов подробнее.
Метод приведения обеих частей уравнения к степеням с одинаковыми основаниями
Метод приведения обеих частей уравнения к степеням с одинаковыми основаниями применяется в двучленных уравнениях, которые можно свести к виду 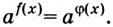
Если 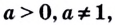
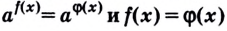
Пример №56
Решите уравнение:
Решение:
а) Представим правую часть уравнения в виде неправильной дроби:
Запишем правую и левую части уравнения в виде степени с основанием 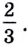
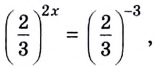
б) Поскольку 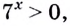
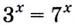
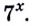
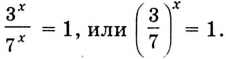
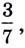
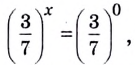
Существуют двучленные уравнения, члены которых вы пока не можете свести к степеням с одинаковыми основаниями. В общем виде их можно записать так:
Если 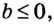
Если 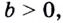
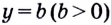
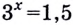
Методом введения новой переменной решаются многие виды уравнений
Рассмотрим решение некоторых из них на конкретных примерах.
Пример №57
Решите уравнение:
Решение:
В показателе каждой степени этого уравнения содержится одно и то же выражение 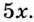
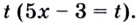
Вынесем общий множитель 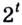
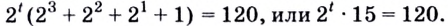
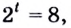
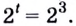
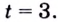
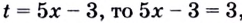
Решая такие уравнения, не обязательно вводить новую переменную, а можно сразу выносить общий множитель за скобки 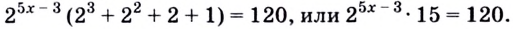
Именно поэтому этот способ называют способом вынесения общего множителя за скобки.
б) Пусть 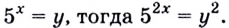
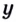
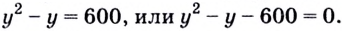
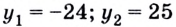
Поскольку 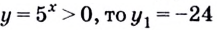
Следовательно,
в) Запишем данное уравнение в виде
Разделим каждый член уравнения на 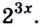
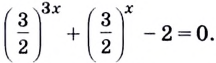
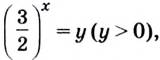
Поскольку 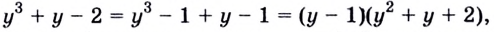
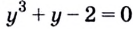
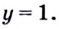
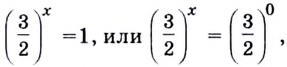
Функционально-графический метод
Функционально-графический метод состоит в следующем:
- с помощью построения графиков (или путём подбора) находят один корень уравнения;
- доказывают, что других корней уравнение не имеет.
Пример №58
Решите уравнение:
Решение:
Графически или методом проб убеждаемся, что 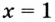
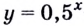
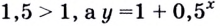
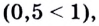
Если в показательном уравнении знак равенства изменить на знак неравенства, то получим показательное неравенство.
Неравенство называется показательным, если его переменные входят только в показатели степеней.
Для решения показательных неравенств используют те же методы, что и для решения показательных уравнений. А также правила решения простейших показательных неравенств, т.е. неравенств вида
Решая простейшие показательные неравенства, используют монотонность (возрастание или убывание) показательной функции. А именно:
1. Если
2. Если
Пример №59
Решите неравенство:
Решение:
а) Представим правую и левую части неравенства в виде степени с основанием 6:
Поскольку 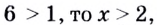
б) Пусть 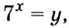
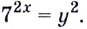
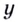
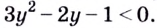
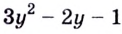
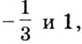
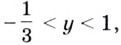
Поскольку 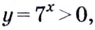
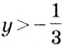
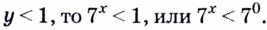
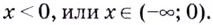
Только для некоторых из подобных уравнений можно указать точные решения. Их приближённые корни находят в основном графическим способом.
Уравнения вида 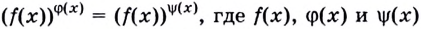
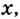
Их решают, проверяя, не будут ли решениями данного уравнения корни уравнений:
Полученные таким образом корни подлежат проверке.
Пример №60
Решите уравнение
Решение:
1) Подставим 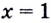
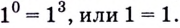
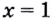
2) Если 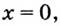
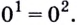
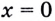
3) Если 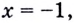
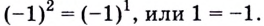
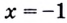
4) Решим уравнение
Его корень 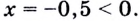
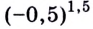
Ответ. 0; 1.
Пример №61
Решите уравнение
Решение:
Запишем правую и левую части как степени числа 2: 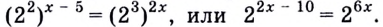
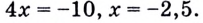
Пример №62
Решите неравенство
Решение:
Запишем неравенство в виде 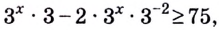
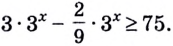
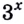
Пример №63
Решите уравнение
Решение:
Запишем уравнение в виде
Разделим левую и правую части уравнения на 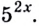
Если 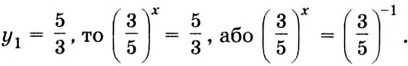
Пример №64
Решите уравнение
Решение:
Найдём произведение оснований степеней:
То есть
Обозначим 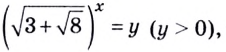
Перейдём к уравнению с переменной
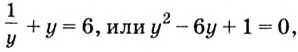
Получим:
Пример №65
Решите графически неравенство
Решение:
Построим в одной системе координат графики функций 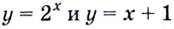
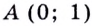
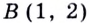
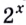
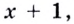
Ответ.
- Логарифмические уравнения и неравенства
- Степенная функция — определение и вычисление
- Степень с целым показателем
- Корень n-й степени
- Логарифмические выражения
- Показательная функция, её график и свойства
- Производные показательной и логарифмической функций
- Показательно-степенные уравнения и неравенства
На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
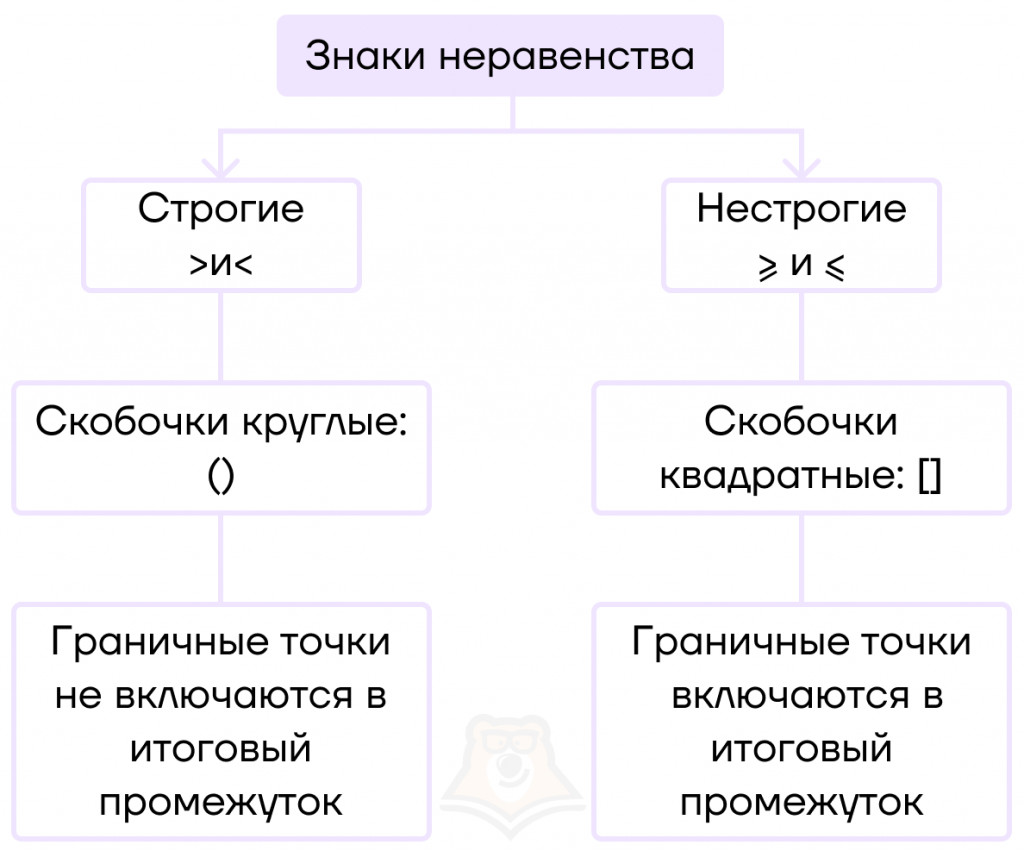
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
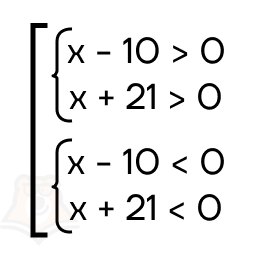
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
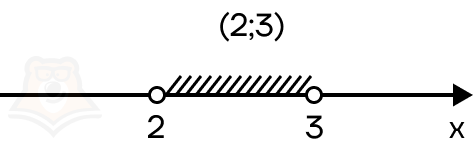
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
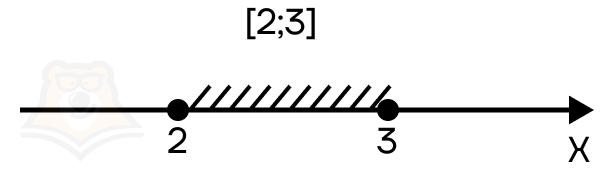
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
В случае сомнений мы всегда можем проверить себя по простой схеме.
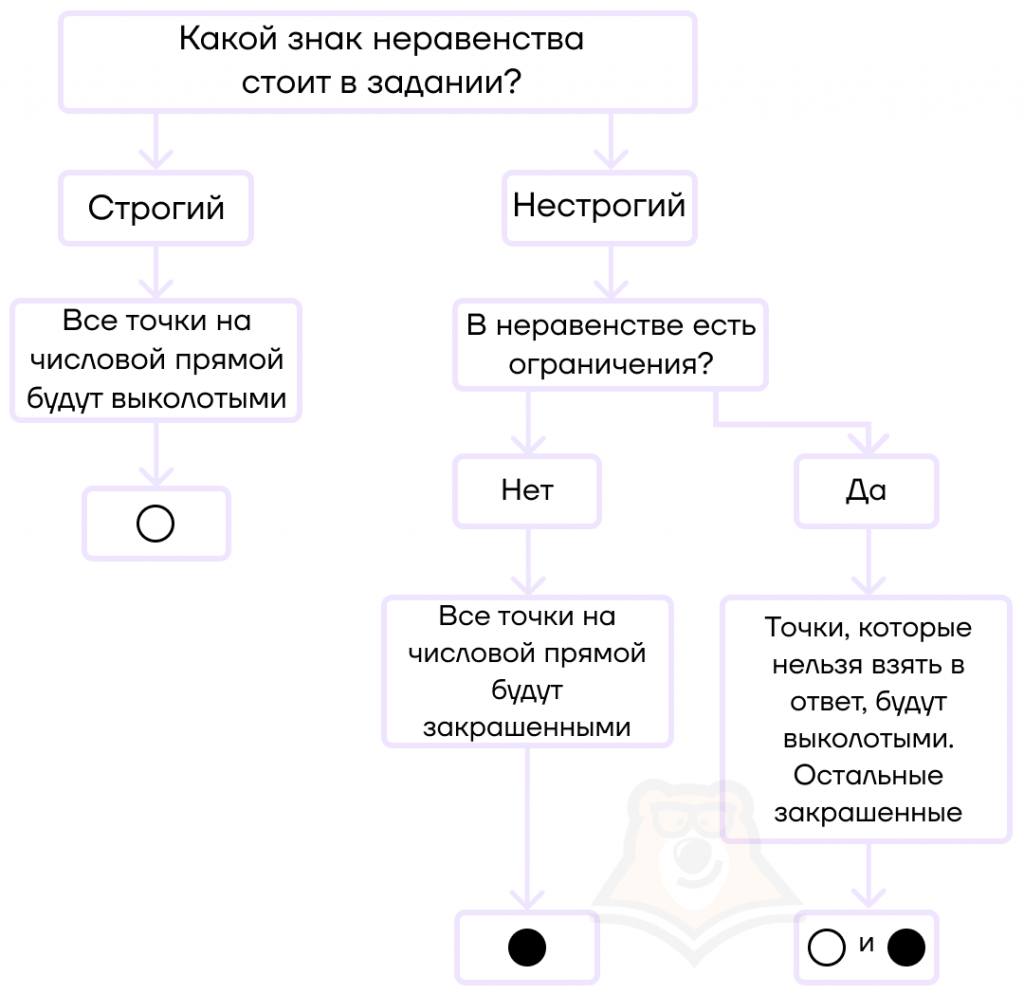
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
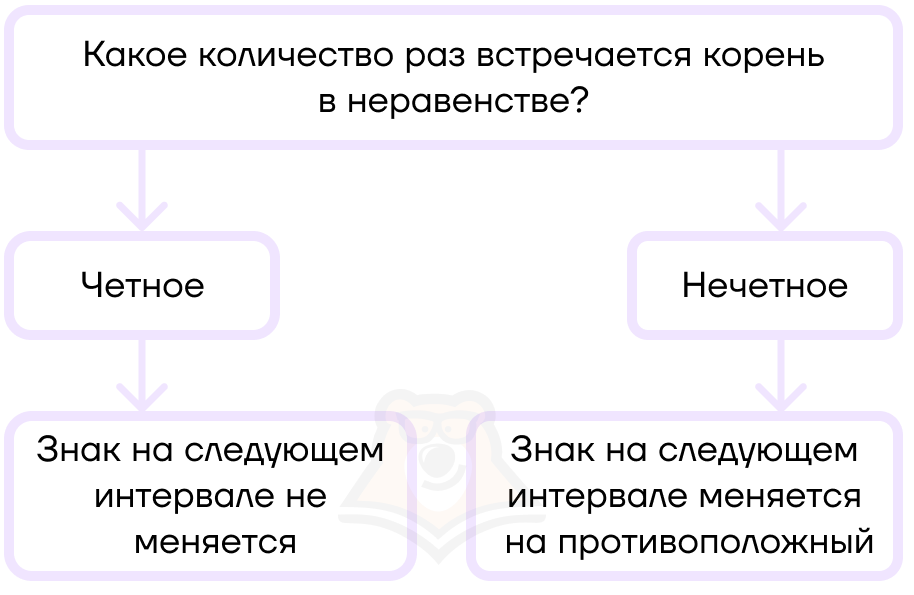
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
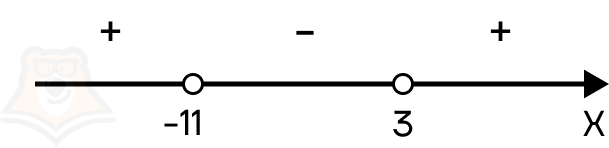
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
Сообщения без ответов | Активные темы
| Автор | Сообщение | ||
|---|---|---|---|
|
Заголовок сообщения: Интервал на котором искать корни
|
|||
|
Всем привет, подскажите как изначально находят интервал [a ; b ] на котором в дальнейшем ищут корни ?
|
||
| Вернуться к началу |
|
||
|
HappyRomio |
Заголовок сообщения: Re: Интервал на котором искать корни
|
|
А без графопостроителя ?
|
|
| Вернуться к началу |
|
|
HappyRomio |
Заголовок сообщения: Re: Интервал на котором искать корни
|
|
Хороший вопрос. Я наверное сам не знаю что мне нужно. вот задание которое у меня есть: Отделить корни графически и уточнить один из них с точностью до 0,001 с помощью методов: и уравнение на подобии первого. Вот ресурс которым я руководствуюсь при решении. http://cismet.blogspot.com/p/blog-page_28.html Написано всё понятно, и я даже понимаю что мне нужно делать, только я не понимаю где мне брать этот отрезок [a;b] на котором я буду искать корень.
|
|
| Вернуться к началу |
|
|
mad_math |
Заголовок сообщения: Re: Интервал на котором искать корни
|
|
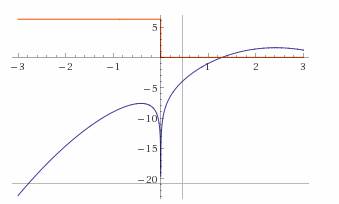
HappyRomio писал(а): Отделить корни графически Это и значит построить график функции [math]y=x^3-2x+1[/math] и определить на каких интервалах находятся точки пересечения с осью Ох. Раз написано «уточнить один из них», то берёте любую из 3 точек. Обычно берут для уточнения наибольший положительный корень, но тут он, очевидно, равен 1, так что попробуйте уточнить тот, который находится на интервале [0,5;0,7]
|
|
| Вернуться к началу |
|
|
Avgust |
Заголовок сообщения: Re: Интервал на котором искать корни
|
|
Я корни всегда ищу методом Ньютона. Вот как это делается в Мапл: NI := proc (expr, x) local iter; iter := x-expr/(diff(expr, x)); unapply(iter, x) end proc; получаются результаты: -1.640414508 (количество циклов 5 принял исходя из того, чтобы два последних числа совпали) x0:=0.5; 0.6000000000 x0:=0.9; 1.065116279
|
|
| Вернуться к началу |
|
|
Avgust |
Заголовок сообщения: Re: Интервал на котором искать корни
|
|
Формула Кордано дает точные решения: [math]x_1=-frac{sqrt{5}+1}{2}[/math] [math]x_2=frac{sqrt{5}-1}{2}[/math] [math]x_3=1[/math]
|
|
| Вернуться к началу |
|
| Похожие темы | Автор | Ответы | Просмотры | Последнее сообщение |
|---|---|---|---|---|
|
Найти интервал, на котором функция простая
в форуме Пределы числовых последовательностей и функций, Исследования функций |
Korama01 |
4 |
129 |
25 окт 2019, 11:52 |
|
Для любителей искать математические ошибки
в форуме Литература и Онлайн-ресурсы по математике |
WithLoveIn |
5 |
410 |
26 окт 2020, 12:51 |
|
Буду искать другой форум
в форуме Палата №6 |
Korvet |
131 |
7162 |
27 апр 2015, 03:58 |
|
Когда искать ОДЗ(x) при решении логарифмических уравнений
в форуме Алгебра |
alekscooper |
3 |
322 |
21 янв 2019, 20:54 |
|
Не получается решить задание, где искать решение уже не знаю
в форуме Теория вероятностей |
p985850 |
1 |
265 |
18 авг 2017, 20:55 |
|
Источник в котором описаны все математические закорючки
в форуме Литература и Онлайн-ресурсы по математике |
izhadapter |
2 |
458 |
08 апр 2017, 07:21 |
|
Найти p, при котором выполняется заданное соотношение
в форуме Теория вероятностей |
blueberry10 |
1 |
564 |
20 апр 2016, 14:44 |
|
Как инициализировать массив в котором не все значения даны
в форуме Maple |
SVD102 |
0 |
271 |
12 май 2016, 07:04 |
|
Найти значение х, при котором матрица является вырожденной
в форуме Линейная и Абстрактная алгебра |
Ryslannn |
2 |
2032 |
12 окт 2014, 15:53 |
|
Задание, в котором я не понимю что от меня хотят. ЦСУТП
в форуме Начала анализа и Другие разделы школьной математики |
Baguvix |
0 |
247 |
17 янв 2020, 19:35 |
Кто сейчас на конференции |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 1 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |












































































 выражения f(х) в точке
выражения f(х) в точке 

 (левый конец отрезка переходит в середину);
(левый конец отрезка переходит в середину);