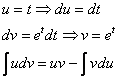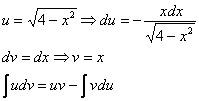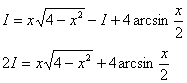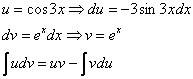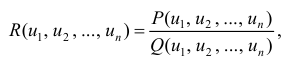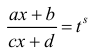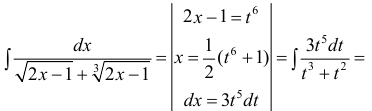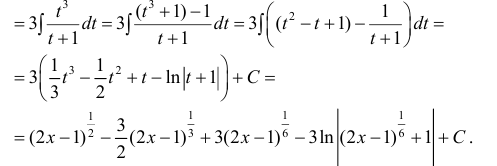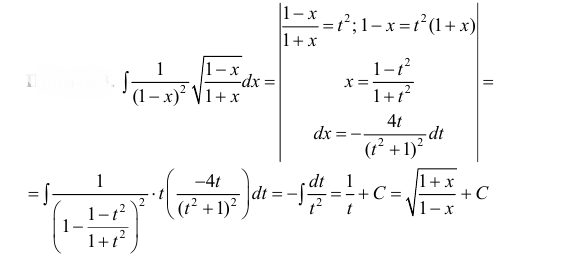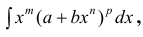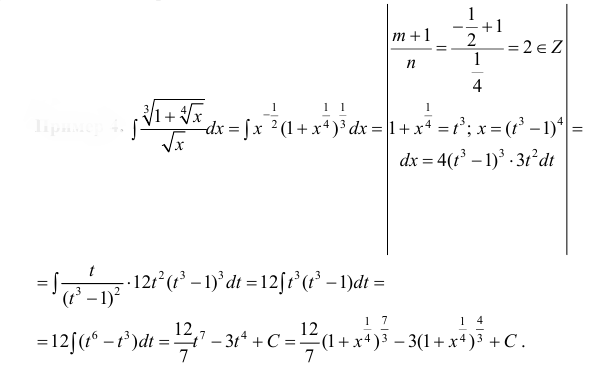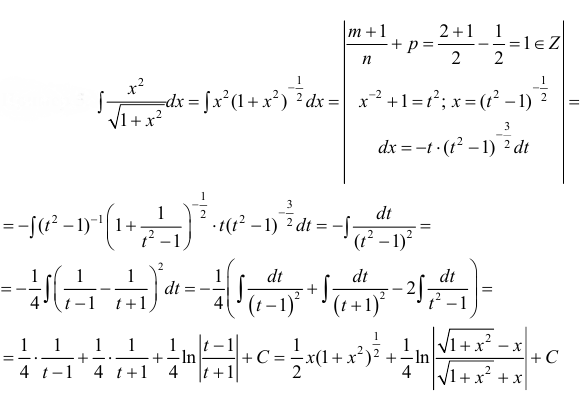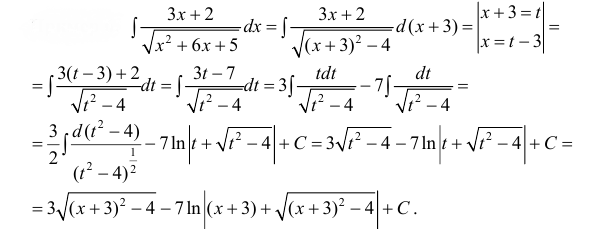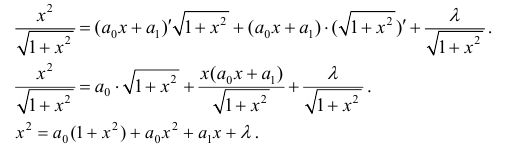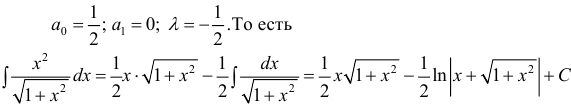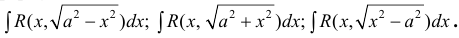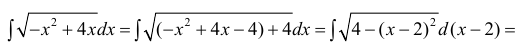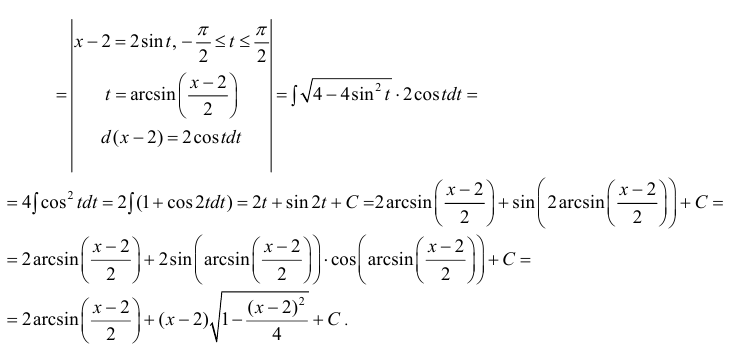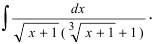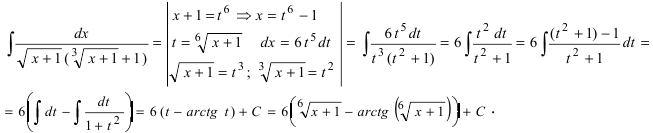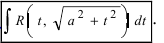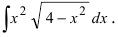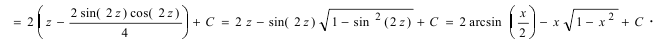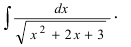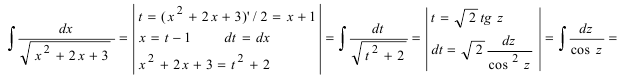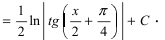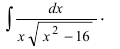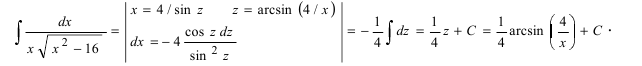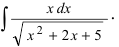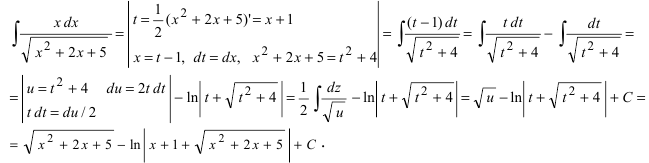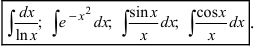Как найти интеграл дроби с корнем - Autoru.top - решение различных проблем

Интеграл от корня из дроби

Интеграл,
который мы рассмотрим, встречается
достаточно редко, но я буду очень рад,
если единственный пример данного
параграфа вам поможет.

Корнями
всё начиналось, корнями и закончится.
Рассмотрим неопределенный интеграл:

,
где
–
числа. Руководствуясь законом подлости,
считаем, что все эти числа коэффициенты
не равны нулю. Это уже не смешно, так
обычно и бывает.

В
подынтегральной функции у нас находится
корень, а под корнем – дробь, в числителе
и знаменателе которой располагаются
линейные функции.

Метод
стар – необходимо избавиться от корня.
Стар и уныл, но сейчас станет веселее,
поскольку придется проводить непростую
замену.

Замена,
с помощью которой мы гарантированно
избавимся от корня, такова:

Теперь
нужно выразить «икс» и найти, чему равен
дифференциал
.

Выражаем
«икс»:

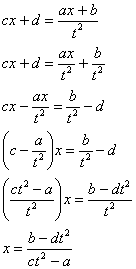
Теперь
найдем дифференциал:

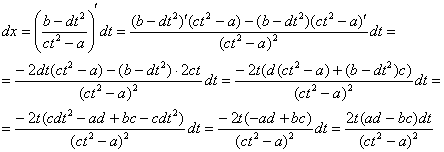
Зачем
были эти нелепые скучные телодвижения?

Я
вывел готовые формулы, которыми можно
пользовать при решении интеграла вида
!

Формулы
замены таковы:

Это
было ни в коем случае не хвастовство,
просто я не смог быстро найти эти формулы
в близлежащей литературе и Сети –
оказалось проще вывести. Да и может быть
кто-нибудь для реферата возьмет.

Опять
– двадцать пять, заключительный пример:

Пример
25

Найти
неопределенный интеграл

Проведем
замену:

В
данном примере:

Таким
образом:

Еще
куда ни шло, могло всё оказаться
значительно хуже. Такой интеграл, кстати,
уже фигурировал в Примере 13. Интегрируем
по частям:

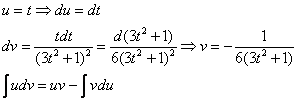
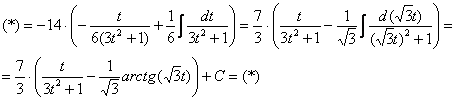
Проведем
обратную замену. Если изначально
,
то обратно:

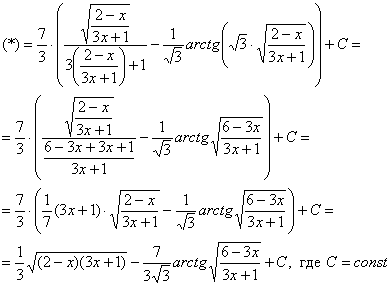
Некоторым
страшно, а я это продифференцировал,
ответ верный!

Иногда
встречаются интегралы вида
,
,
но это нужно быть либо слишком умным
либо попасть под раздачу. Идея та же –
избавиться от корня, причем во втором
случае, как все догадались, следует
проводить подстановку
и
самостоятельно выводить, чему будет
равняться дифференциал
.

Теперь
вам практически любой интеграл по силам,
успехов!

Решения
и ответы:

Пример
2: Решение:

Проведем
замену:

Интегрируем
по частям:

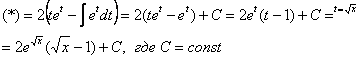
Пример
3: Ответ:

Пример
4: Ответ:

Пример
6: Решение:

Интегрируем
по частям:

Таким
образом:

В
результате:

Пример
8: Решение:

Дважды
интегрируем по частям и сводим интеграл
к себе:

Таким
образом:

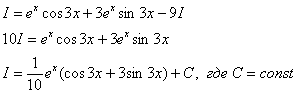
Пример
10: Решение:

Проведем
замену:

Пример
11: Решение:

Замена:

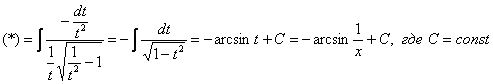
Пример
12: Решение:

Замена:

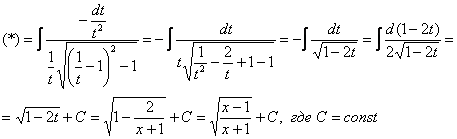
Пример
14: Решение:

Дважды
используем рекуррентную формулу

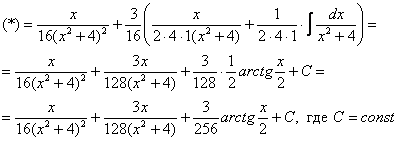
Пример
16: Решение:

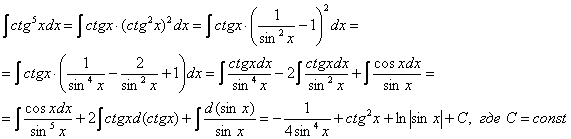
Пример
18: Решение:

Используем
формулу приведения:
и
формулу двойного угла:
.

Пример
19: Решение:

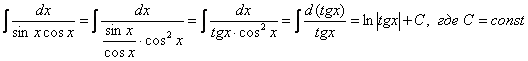
Пример
21: Решение:

–3
– 3 = –6 – целое отрицательное число

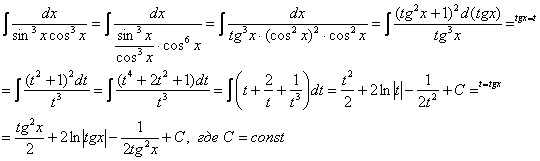
Пример
23: Решение:

Пример
24: Решение:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Преподаватель который помогает студентам и школьникам в учёбе.

Интегрирование иррациональных функций с примерами решения

Содержание:

Интегрирование иррациональных функций.

Определение 1. Функция вида

Пример 1.
— рациональная функция переменных u и v, при этом:

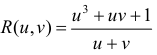
п.1. Интегралы вида:

Пусть s – общий знаменатель дробей 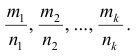Тогда подстановка
делает подинтегральную функцию рациональной.

Пример 2.

Пример 3

п.2. Интегралы вида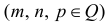— интегралы от дифференциального бинома.
Интегралы вида (1) выражаются через элементарные функции в следующих случаях:
а) p∈Z — интегралы рассмотрены в п.1.
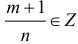
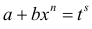
б) , тогда подстановка , где s – знаменатель р приводит интегральную функцию к рациональной.
в) , тогда подстановка , где s – знаменатель р приводит интегральную функцию к рациональной.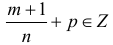
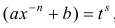
Во всех других случаях интегралы (1) выразить через элементарные функции нельзя (теорема Чебышева).

Пример 4.

Пример 5.

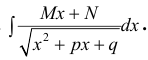
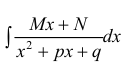
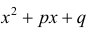
п.3. Интегралы вида Вычисление интегралов проводится аналогично интегралам выделением полного квадрата в трехчлене
(см. § 21, примеры 1, 2).

Пример 6.

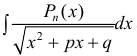
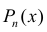
п 4. Интегралы вида , где — многочлен степени n.
Для вычисления интегралов используют равенство:
многочлен степени n−1 . Коэффициенты многочлена а также число λ находятся, если продифференцировать правую и левую часть равенства (2).

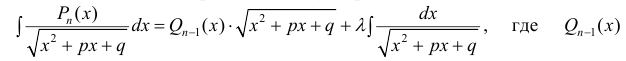
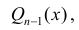
Заказать решение задач по высшей математике

Пример 7.
После взятия производной:

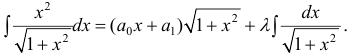
Приравниваем друг к другу коэффициенты при одинаковых степенях х в правой и левой частях.

Решив систему (3), получим :

(сравни с примером 5).

п.5. Интегралы вида
В данных интегралах можно избавиться от иррациональности, если применить подходящую тригонометрическую или гиперболическую подстановку.
— для первого интеграла,
— для второго,
— для третьего (см. § 23).

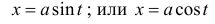
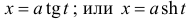
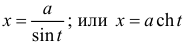
Пример 8.

Пример 9.

Интегрирование некоторых иррациональных функций

1. Интегралы вида .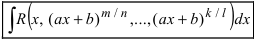

Интегралы такого типа вычисляются по следующей схеме:

В результате приведенных действий данный интеграл переходит в неопределенный интеграл от рациональной функции.

Пример:

Вычислить

Решение:

В данном примере 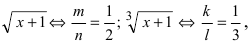следовательно, наименьший общий знаменатель этих дробей равен 6. Таким образом.

2. Интегралы вида .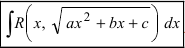

Такие интегралы путем замены 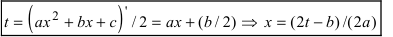приводятся к одному из интегралов вида:

1. 2. 3.

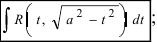
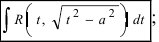
Для вычисления этих интегралов применяют следующие тригонометрические замены

1. 2. 3. — которые позволяют избавиться от квадратного корня.

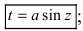
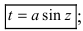
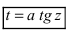
Пример:

Вычислить

Решение:

Данный интеграл соответствует интегралам типа 1., поэтому

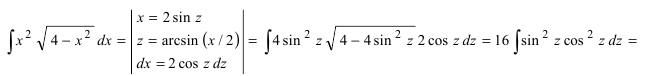
Пример:

Вычислить

Решение:

Воспользуемся указанной выше заменой

(интеграл вычислен в п. 2а)

Пример:

Вычислить

Решение:

Пример:

Вычислить

Решение:

Воспользуемся указанной выше заменой

Понятие о неберущихся интегралах

Определение: Интегралы, первообразные которых не выражаются через элементарные функции, называются неберущимися:

Прямоугольная система координат на плоскости и ее применение
Линии второго порядка
Полярные координаты
Непрерывность функции
Формула Тейлора и ее применение
Интегрирование рациональных дробей
Интегрирование тригонометрических функций
Интегрирование тригонометрических выражений

Источник

Универсального способа решения иррациональных уравнений нет, так как их класс отличается количеством. В статье будут выделены характерные виды уравнений с подстановкой при помощи метода интегрирования.

Для использования метода непосредственного интегрирования необходимо вычислять неопределенные интегралы типа ∫kx+bp dx, где p является рациональной дробью, k и b являются действительными коэффициентами.

Пример 1

Найти и вычислить первообразные функции y=13x-13.

Решение

По правилу интегрирования необходимо применить формулу ∫f(k·x+b)dx=1k·F(k·x+b)+C, а таблица первообразных говорит о том, что имеется готовое решение данной функции. Получаем, что

∫dx3x-13=∫(3x-1)-13dx=13·1-13+1·(3x-1)-13+1+C==12(3x-1)23+C

Ответ: ∫dx3x-13=12(3x-1)23+C.

Имеют место быть случаи, когда можно использовать метод подведения под знак дифференциала. Это решается по принципу нахождения неопределенных интегралов вида ∫f'(x)·(f(x))pdx, когда значение p считается рациональной дробью.

Пример 2

Найти неопределенный интеграл ∫3×2+5×3+5x-776dx.

Решение

Отметим, что dx3+5x-7=x3+5x-7’dx=(3×2+5)dx. Тогда необходимо произвести подведение под знак дифференциала с использованием таблиц первообразных. Получаем, что

∫3×2+5×3+5x-776dx=∫(x3+5x-7)-76·(3×2+5)dx==∫(x3+5x-7)-76d(x3+5x-7)=x3+5x-7=z==∫z-76dz=1-76+1z-76+1+C=-6z-16+C=z=x3+5x-7=-6(x3+5x-7)6+C

Ответ: ∫3×2+5×3+5x-776dx=-6(x3+5x-7)6+C.

Решение неопределенных интегралов предусматривает формулу вида ∫dxx2+px+q, где p и q являются действительными коэффициентами. Тогда необходимо выделить полный квадрат из-под корня. Получаем, что

x2+px+q=x2+px+p22-p22+q=x+p22+4q-p24

Применив формулу, расположенную в таблице неопределенных интегралов, получаем:

∫dxx2±α=lnx+x2±α+C

Тогда вычисление интеграла производится:

∫dxx2+px+q=∫dxx+p22+4q-p24==lnx+p2+x+p22+4q-p24+C==lnx+p2+x2+px+q+C

Пример 3

Найти неопределенный интеграл вида ∫dx2x2+3x-1.

Решение

Для вычисления необходимо вынести число 2 и расположить его перед радикалом:

∫dx2x2+3x-1=∫dx2x2+32x-12=12∫dxx2+32x-12

Произвести выделение полного квадрата в подкоренном выражении. Получим, что

x2+32x-12=x2+32x+342-342-12=x+342-1716

Тогда получаем неопределенный интеграл вида 12∫dxx2+32x-12=12∫dxx+342-1716==12lnx+34+x2+32x-12+C

Ответ: dxx2+3x-1=12lnx+34+x2+32x-12+C

Интегрирование иррациональных функций производится аналогичным способом. Применимо для функций вида y=1-x2+px+q.

Пример 4

Найти неопределенный интеграл ∫dx-x2+4x+5.

Решение

Для начала необходимо вывести квадрат знаменателя выражения из-под корня.

∫dx-x2+4x+5=∫dx-x2-4x-5==∫dx-x2-4x+4-4-5=∫dx-x-22-9=∫dx-(x-2)2+9

Табличный интеграл имеет вид ∫dxa2-x2=arcsinxa+C, тогда получаем, что ∫dx-x2+4x+5=∫dx-(x-2)2+9=arcsinx-23+C

Ответ: ∫dx-x2+4x+5=arcsinx-23+C.

Процесс нахождения первообразных иррациональных функций вида y=Mx+Nx2+px+q, где имеющиеся M, N, p, q являются действительными коэффициентами, причем имеют схожесть с интегрированием простейших дробей третьего типа. Это преобразование имеет несколько этапов:

подведение дифференциала под корень, выделение полного квадрата выражения под корнем, применение табличных формул.

Пример 5

Найти первообразные функции y=x+2×2-3x+1.

Решение

Из условия имеем, что d(x2-3x+1)=(2x-3)dx и x+2=12(2x-3)+72, тогда (x+2)dx=12(2x-3)+72dx=12d(x2-3x+1)+72dx.

Рассчитаем интеграл: ∫x+2×2-3x+1dx=12∫d(x2-3x+1)x2-3x+1+72∫dxx2-3x+1==12∫(x2-3x+1)-12d(x2-3x+1)+72∫dxx-322-54==12·1-12+1·x2-3x+1-12+1+72lnx-32+x-32-54+C==x2-3x+1+72lnx-32+x2-3x+1+C

Ответ: ∫x+2×2-3x+1dx=x2-3x+1+72lnx-32+x2-3x+1+C.

Поиск неопределенных интегралов функции ∫xm(a+bxn)pdx осуществляется при помощи метода подстановки.

Для решения необходимо ввести новые переменные:

Когда число p является целым, тогда считают, что x=zN, а N является общим знаменателем для m, n.
Когда m+1n является целым числом, тогда a+bxn=zN, а N является знаменателем числа p.
Когда m+1n+p является целым числом, то необходим ввод переменной ax-n+b=zN, а N является знаменателем числа p.

Пример 6

Найти определенный интеграл ∫1x2x-9dx.

Решение

Получаем, что ∫1x2x-9dx=∫x-1·(-9+2×1)-12dx. Отсюда следует, что m=-1, n=1,p=-12, тогда m+1n=-1+11=0 является целым числом. Можно ввести новую переменную вида -9+2x=z2. Необходимо выразить x через z. На выходы получим, что

-9+2x=z2⇒x=z2+92⇒dx=z2+92’dz=zdz-9+2x=z

Необходимо произвести подстановку в заданный интеграл. Имеем, что

∫dxx2x-9=∫zdzz2+92·z=2∫dzz2+9==23arctgz3+C=23arcctg2x-93+C

Ответ: ∫dxx2x-9=23arcctg2x-93+C.

Для упрощения решения иррациональных уравнений применяются основные методы интегрирования.