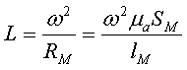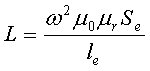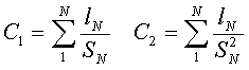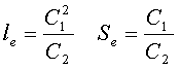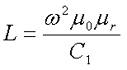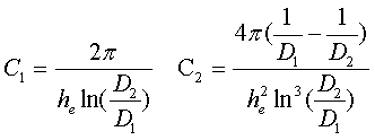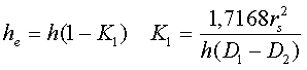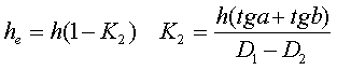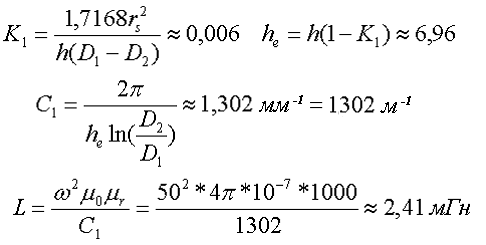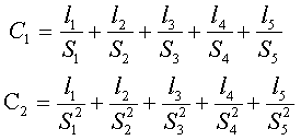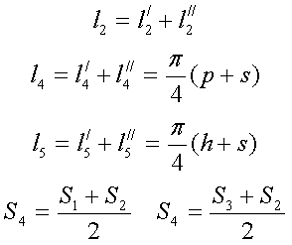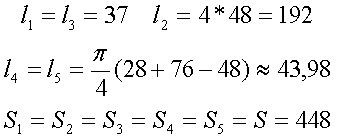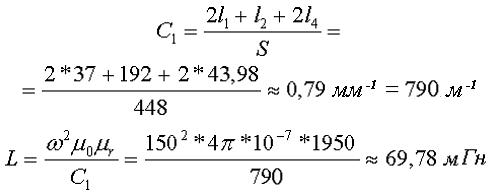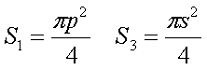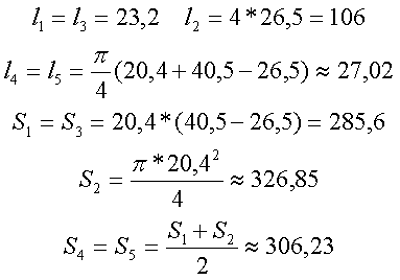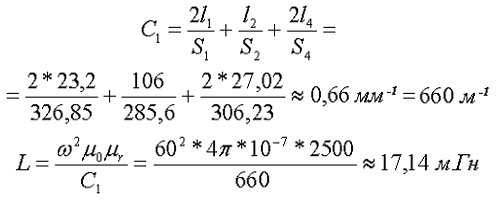Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Особенности расчёта индуктивных элементов с сердечниками
В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.
Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения
где ω – количество витков катушки,
RM – сопротивление магнитной цепи,
μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,
SM – площадь поперечного сечения сердечника,
lM – длина средней магнитной силовой линии,
Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.
Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника.
Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1;
С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;
где N – количество разнородных участков сердечника,
lN – длина N – го участка сердечника,
SN – площадь N – го участка сердечника.
Тогда величины Se и le определятся из следующих выражений
Кроме индуктивности с помощью постоянных С1 и С2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.
Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.
Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.
Расчёт катушки с тороидальным сердечником
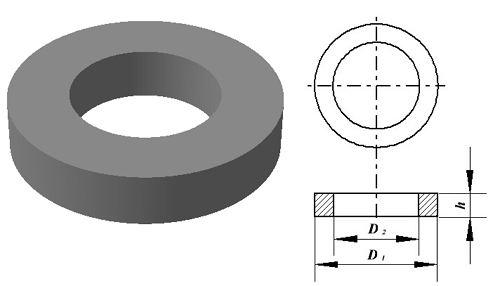
Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.
Тороидальный сердечник.
Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D1 – внешний диаметр, D2 – внутренний диаметр, h – высота сердечника.
Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют
где he – эффективная высота сердечника,
D1 – внешний диаметр сердечника,
D2 – внутренний диаметр сердечника.
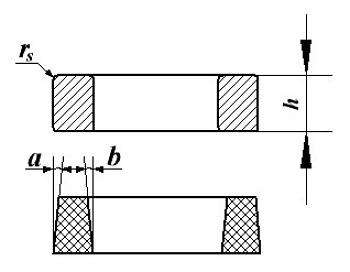
Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей.
Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).
Рассмотрим несколько случаев:
а) прямоугольное поперечное сечение с острыми кромками
б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления rs
в) трапецеидальное поперечное сечение с острыми кромками
г) трапецеидальное поперечное сечение со скруглёнными кромками
Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000.
Так как рассчитываем только индуктивность, то в расчёте коэффициента С2 нет необходимости
Расчёт катушки с П–образным сердечником прямоугольного сечения
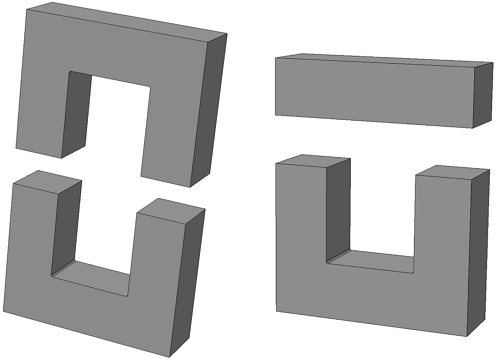
В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.
Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.
П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).
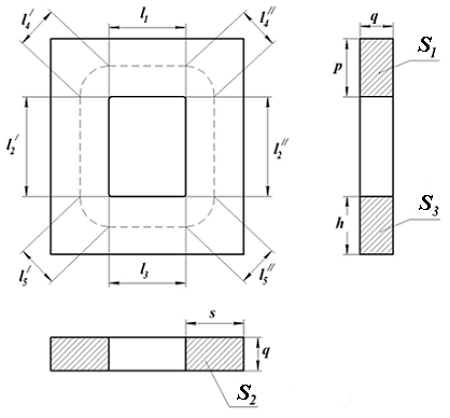
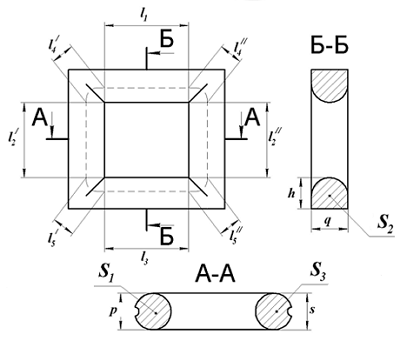
Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника
Сечение П-образного прямоугольного сердечника.
Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят
Неизвестные величины можно найти следующим образом
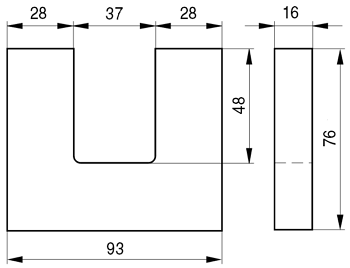
Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.
Сердечник Epcos U93/76/16.
Таким образом, расчётные параметры сердечника составят
Таким образом коэффициент С1 и индуктивность L составят
Расчёт катушки с П-образным сердечником круглого сечения
Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей
П-образный сердечник с круговым сечением.
Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.
Сечение П-образного сердечника с круговым сечением.
Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь
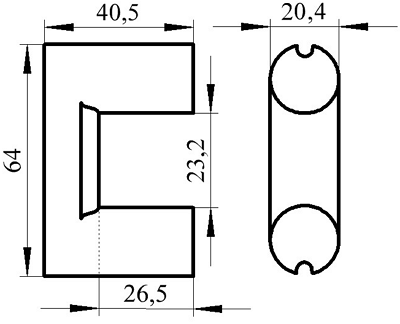
Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μr = 2500), количество витков ω = 60.
Сердечник типа SDMR 40 UY20.
Параметры сердечника для расчёта составят
Таким образом коэффициент С1 и индуктивность L составят
На сегодня всё. Продолжение смотри в следующей статье.
-
Методики расчета индуктивности катушек
Основным
элементом катушек индуктивности является
токовод. Величина индуктивности
определяется конструкцией токовода и
его размерами.
Полная
индуктивность медного провода круглого
сечения длиной lПРи диаметромd0равна
(3.1)
Из
(3.1) следует, что индуктивность провода
уменьшается с ростом его диаметра. Это
свойство широко используют в УКВ
аппаратуре для уменьшения индуктивности
соединительных проводов за счет
увеличения их диаметра.
Если
одиночный проводник согнуть, например,
в кольцо, то его индуктивность уменьшится
из-за встречного направления токов в
соседних частях кольца. Однако, для
круглого кольца индуктивность будет
наибольшей по сравнению с индуктивностью
витка любой другой конфигурации,
поскольку круглый виток охватывает
наибольшую площадь, обеспечивая
наибольшее потокосцепление.
Индуктивность
круглого плоского витка диаметром Dиз провода круглого сечения длинойlПРи диаметромdПРравна
(3.2)
При
сворачивании проводника в несколько
витков wодинакового
диаметра образуется катушка, индуктивность
которой можно определить как суммарную
индуктивность всех витков с учетом
взаимоиндукцииMмежду
ними:
(3.3)
Индексы при Муказывают на взаимную индуктивность
между первым и вторым, вторым и третьим,
первым и третьим витками и т.д. Если
известен коэффициент связи, который
определяется равенством
,
(3.4)
то индуктивность
катушки с произвольным числом витков
определяется из
. (3.5)
Коэффициент связи
между витками, расположенными на
расстоянии τ, в однослойной катушке
определяется выражением

Для сплошной намотки
τ=d0.
Индуктивность
многослойной катушки незначительно
зависит от диаметра провода, так как
определяется в основном взаимоиндукцией
между витками.
Из-за трудности
определения коэффициента связи выражение
(3.5) обычно применяют для расчета катушек
индуктивности с небольшим числом витков
(обычно не более шести).
Для катушек с однородным
замкнутым магнитопроводом (с тороидальным
сердечником) выражение для определения
индуктивности принимает вид
, (3.7)
где μ– начальная магнитная
проницаемость сердечника (μ=1 для
диэлектрического каркаса или воздуха);
μ0=4π·10-7Гн/м – магнитная постоянная;
w– число витков обмотки;
S
— площадь поперечного сечения катушки;
— длина намотки катушки;
Таким
образом, увеличение индуктивности
катушки может быть достигнуто за счет
увеличения числа витков, магнитной
проницаемости сердечника, площади
поперечного сечения магнитопровода, а
также уменьшения длины намотки.
В
высокочастотных катушках замкнутый
магнитопровод как правило отсутствует,
поэтому индуктивность катушки будет
меньше, рассчитанной по (3.7). Для учета
рассеивания магнитного потока на краях
катушки вводится поправочный коэффициент
k, который зависит от
отношения диаметра катушки к длине
намотки

Для
практических расчетов однослойных
цилиндрических катушек, намотанных
виток к витку (рис.3.2 а),используют
выражение

где

краевые эффекты;
μ– начальная магнитная
проницаемость сердечника (μ=1 для
катушек без магнитного сердечника);
μ0=4π·10-7Гн/м –
магнитная постоянная;
w– число витков обмотки;
— площадь поперечного сечения круглой
катушки;
D– диаметр катушки;
— длина намотки.
Для
практических расчетов однослойных
цилиндрических катушек без сердечника,
намотанных с принудительным шагом τ(рис.3.2 б),индуктивн
рассчитывают по (3.9), но полученный
результат уменьшают на поправкуΔL
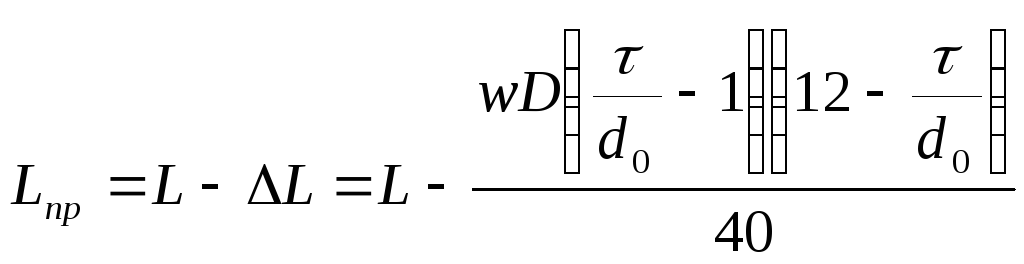
где τ– шаг намотки;
L–
индуктивность катушки, определенная
по (3.9) приμ=1.
Для
практических расчетов индуктивности
тороидальной однослойной катушки,
намотанной сплошным слоем на круглом
магнитном сердечнике прямоугольного
сечения (рис.3.2 в), используют
выражение
, (3.11)
где
— площадь поперечного сечения сердечника
тороида;
— средняя длина сердечника тороида;
D– внешний диаметр сердечника тороида;
d– внутренний диаметр сердечника тороида;
h– высота сердечника тороида.
Для практических
расчетов многослойных катушек без
сердечника(рис.3.2 г) используют
выражение

г
– средний диаметр катушки;
t— толщина катушки;
l— длина катушки.
Для
практических расчетов многослойных
секционированных катушек без сердечника
(рис.3.2 д) используют выражение
, (3.13)
где LC
– индуктивность одной секции катушки;
n– число секций;
kCB– коэффициент связи между смежными
секциями, зависящий от отношения(рис.3.3);
b
– расстояние между секциями.
Для
практических расчетов плоских круглых
спиральных катушек (рис.3.2 е) используют
выражение
, (3.14)
где DBH,DH –внутренний и наружный диаметры
катушки, соответственно.
Для
практических расчетов плоских
квадратных спиральных катушек (рис.3.2
ж) используют выражение
, (3.15)
где АBH,АH
–внутренняя и наружная стороны
катушки, соответственно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
10.02.20165.15 Mб192.doc
- #
- #
- #
- #
- #
- #
Если у вас имеется катушка индуктивности с воздушным сердечником и необходимо рассчитать её индуктивность, то вам поможет онлайн калькулятор. Достаточно ввести основные параметры катушки и вы сразу получите результат.
Найти индуктивность катушки с воздушным сердечником проще простого. Введите в калькулятор диаметр и длину катушки, а также количество витков. Останется только нажать кнопку «расчет» и вы узнаете индуктивность такой катушки.
Формула индуктивности катушки с воздушным сердечником
Расчет однослойной катушки индуктивности без сердечника производится по формуле:
L = (D2 * n2) / (45 * D + 100 * l) , где
L — индуктивность катушки в мкГн,
D — диаметр катушки в см,
n — число витков в шт,
l — длина намотки в см.
Формула конечно не сложная, но лучше всего индуктивность катушки с воздушным сердечником рассчитывать на нашем онлайн калькуляторе. Это как минимум убережёт вас от ошибок и сэкономит максимум времени.
Единицы измерения индуктивности
Единицей измерения индуктивности является Генри (Гн). В таблице ниже приводим зависимости между разными величинами.
| Название | Обозначение | Международное | Перевод единиц |
|---|---|---|---|
| Генри | Гн | H | — |
| Килогенри | кГн | kH | 1 кГн = 103 Гн |
| Миллигенри | мГн | mH | 1 мГн = 10-3 Гн |
| Микрогенри | мкГн | µH | 1 мкГн = 10-6 Гн |
| Наногенри | нГн | nH | 1 нГн = 10-9 Гн |
| Пикогенри | пГн | pH | 1 пГн = 10-12 Гн |
Пример расчета индуктивности однослойной катушки с воздушным сердечником
Давайте рассмотрим пример расчета индуктивности однослойной катушки на 1/4 волны с воздушным сердечником. Допустим у нас катушка диаметром 10 мм, длиной 50 мм и с количеством витков 200 штук. Подставим имеющиеся значения в формулу:
L = (12 * 2002) / (45 * 1 + 100 * 5) = 73,394 мкГн.
Надо помнить что эта формула эмпирическая и подходит для простого частного случая. Она не учитывает ни диаметр проволоки ни рабочую частоту на которой будет работать катушка. Для более сложных расчетов нужен будет другой калькулятор индуктивности.
Вот мы и рассмотрели как считается катушка индуктивности с воздушным сердечником. Эти знания вам обязательно пригодятся.
Было полезно? Поделитесь с друзьями!
На рисунке выше показана однослойная катушка индуктивности: Dc — диаметр катушки, D — диаметр оправки или каркаса катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и di — диаметр провода с изоляцией
Для расчета индуктивности LS применяется приведенная ниже формула из статьи Р. Уивера (R. Weaver) Численные методы расчета индуктивности:
Здесь
D — диаметр оправки или каркаса катушки в см,
l — длина катушки в см,
N — число витков и
L — индуктивность в мкГн.
Эта формула справедлива только для соленоида, намотанного плоским проводом. Это означает, что катушка намотана очень тонкой лентой без зазора между соседними витками. Она является хорошим приближением для катушек с большим количеством витков, намотанных проводом круглого сечения с минимальным зазором между витками. Американский физик Эдвард Беннетт Роса (Edward Bennett Rosa, 1873–1921) работавший в Национального бюро стандартов США (NBS, сейчас называется Национальное бюро стандартов и технологий (NIST) разработал так называемые корректирующие коэффициенты для приведенной выше формулы в форме (см. формула 10.1 в статье Дэвида Найта, David W. Knight):
Здесь LS — индуктивность плоской спирали, описанная выше, и
где ks — безразмерный корректирующий коэффициент, учитывающий разницу между самоиндукцией витка из круглого провода и витка из плоской ленты; km — безразмерный корректирующий коэффициент, учитывающий разницу в полной взаимоиндукции витков из круглого провода по сравнению с витками из плоской ленты; Dc — диаметр катушки в см, измеренный между центрами проводов и N — число витков.
Величина коэффициента Роса km определяется по формуле 10.18 в упомянутой выше статье Дэвида Найта:
Коэффициент Роса ks, учитывающий различие в самоиндукции, определяется по формуле 10.4 в статье Д. Найта:
Здесь p — шаг намотки (расстояние между витками, измеренное по центрам проводов) и d — диаметр провода. Отметим, что отношение p/d всегда больше единицы, так как толщина изоляции провода конечна, а минимально возможное расстояние между двумя соседними витками с очень тонкой изоляцией, расположенными без зазора, равна диаметру провода d.
Факторы, влияющие на индуктивность катушки
На индуктивность катушки влияют несколько факторов.
- Количество витков. Катушка с большим количеством витков имеет бóльшую индуктивность по сравнению с катушкой с меньшим количеством витков.
- Длина намотки. Две катушки с одинаковым количеством витков, но разной длиной намотки имеют разную индуктивность. Более длинная катушка имеет меньшую индуктивность. Это связано с тем, что магнитное поле менее компактной катушки более слабое и оно не может хорошо концентрироваться в растянутой катушке.
- Диаметр катушки. Две плотно намотанные катушки с одинаковым количеством витков и разными диаметрами имеют разную индуктивность. Катушка с бóльшим диаметром имеет бóльшую индуктивность.
- Сердечник. Для увеличения индуктивности в катушку часто вставляется сердечник из материала с высокой магнитной проницаемостью. Сердечники с более высокой магнитной проницаемостью позволяют получить более высокую индуктивность. Сердечники, изготовленные из магнитной керамики — феррита, часто используются в катушках и трансформаторах различных электронных устройств, так как у них очень низкие потери на вихревые токи.
Упрощенная эквивалентная схема реальной катушки индуктивности: Rw — сопротивление обмотки и ее выводов; L — индуктивность идеальной катушки; Rl — сопротивление вследствие потерь в сердечнике; и Cw — паразитная емкость катушки и ее выводов.
Эквивалентная схема реальной катушки индуктивности
В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.
Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.
Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками
Если индуктивность большая, то сопротивление обмотки (Rw на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.
Катушки индуктивности и обмотки в различных устройствах
Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр – индуктивность. Для того чтобы рассчитать индуктивность катушки без сердечника можно воспользоваться универсальной формулой:
где μ0 – магнитная проницаемость вакуума, μ – магнитная проницаемость сердечника (можно взять из таблицы 1), N – число витков, S – площадь сечения катушки, l – длина намотки. Такой способ является универсальным и может использоваться, как для полых катушек, так и для имеющих сердечник.
Таблица 1
| Материал | — µ — (Гн/м) |
| Воздух | 1.25663753*10−6 |
| Алюминий | 1.256665*10−6 |
| Аустенитная нержавеющая сталь | 1.260*10−6 — 8.8*10−6 |
| Вакуум (µ0) | 4π*10−7 |
| Вода | 1.256627*10−6 |
| Водород | 1.2566371*10−6 |
| Висмут | 1.25643*10−6 |
| Дерево | 1.25663760*10−6 |
| Железо (чистота 99.8%) | 6.3*10−3 |
| Железо (99.95% чистое Fe отожженное в водороде) | 2.5*10−1 |
| Железо-кобальтовые сплавы | 2.3*10−2 |
| Медь | 1.256629*10−6 |
| Никель-цинковый феррит — магнит | 2.0*10−5 – 8.0*10−4 |
| Мартенситная нержавеющая сталь (отожженная) | 9.42*10−4 — 1.19*10−3 |
| Мартенситная нержавеющая сталь (закаленная) | 5.0*10−5 — 1.2*10−4 |
| NANOPERM® — магнитомягкий нанокристаллический сплав | 1.0*10−1 |
| Неодимовый магнит | 1.32*10−6 |
| Никель | 1.26*10−4 — 7.54*10−4 |
| Пермаллой (сплав 80% никеля и 20% железа) | 1.0*10−2 |
| Платина | 1.256970*10−6 |
| Сарфир | 1.2566368*10−6 |
| Сверхпроводники | 0 |
| Углеродистая сталь | 1.26*10−4 |
| Ферритная нержавеющая сталь (отожженная) | 1.26*10−3 — 2.26*10−3 |
| Фторопласт 4, Ф-4, Teflon | 1.2567*10−6 |
Если рассматривать частный вариант – катушку с воздушным сердечником, то для расчета ее индуктивности можно использовать формулу:
Где D – диаметр катушки, n – количество витков, а l – длина ее намотки.
Такой способ расчета будет справедливым для катушек, имеющих однослойную структуру, набираемых в один уровень. В случае если катушка наматывается в несколько слоев, то их толщина вносит дополнительные изменения в расчет. При этом формула расчета преобразится к виду:
Где D – диаметр катушки, n – количество витков, h – высота самой катушки, g – толщина слоя намотки.
Для упрощения процесса расчета индуктивности катушки без сердечника можно воспользоваться онлайн калькулятором. Здесь вы указываете ее основные параметры – диаметр, длину и количество витков, после чего нажать кнопку «Рассчитать» и вы получите значение индуктивности без лишних вычислений и затрат времени.