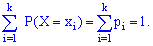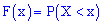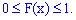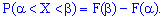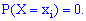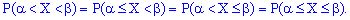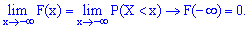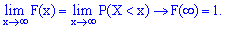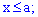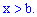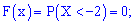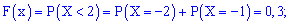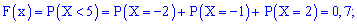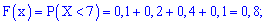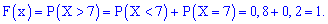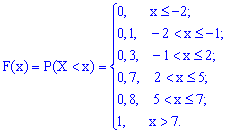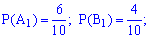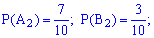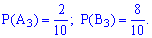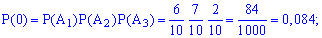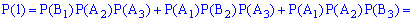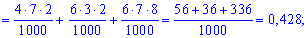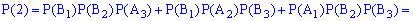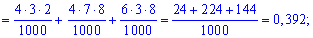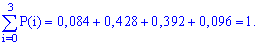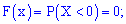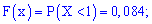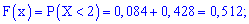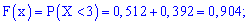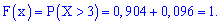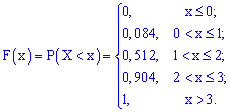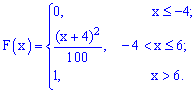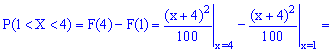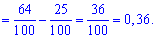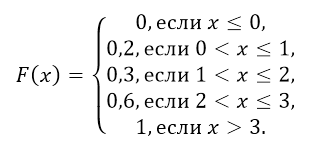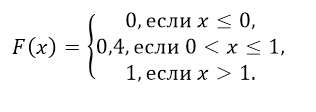Функция распределения случайной величины
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
Краткая теория
Пусть
– действительное число. Вероятность события,
состоящего в том, что
примет значение, меньшее
, то есть вероятность
события
обозначим через
. Разумеется, если
изменяется, то, вообще говоря, изменяется и
, то есть
– функция от
.
Функцией распределения называют функцию
, определяющую вероятность
того, что случайная величина
в результате испытания примет значение,
меньшее
, то есть:
Геометрически
это равенство можно истолковать так:
есть вероятность того, что случайная величина примет
значение, которое изображается на числовой оси точкой, лежащей левее точки
.
Иногда
вместо термина «функция распределения» используют термин «интегральная
функция».
Функцию
распределения дискретной случайной величины
можно представить следующим соотношением:
Это
соотношение можно переписать в развернутом виде:
Функция
распределения дискретной случайной величины есть разрывная ступенчатая функция,
скачки которой происходят в точках, соответствующих возможным значениям
случайной величины и равны вероятностям этих значений. Сумма всех скачков
функции
равна 1.
Свойства функции распределения
Свойство 1.
Значения
функции распределения принадлежат отрезку
:
Свойство 2.
– неубывающая функция, то есть:
,
если
Свойство 3.
Если возможные значения случайной величины
принадлежат интервалу
,
то:
1)
при
;
2)
при
Свойство 4.
Справедливо равенство:
Свойство 5.
Вероятность того, что непрерывная случайная
величина
примет одно определенное значение, равна нулю.
Таким образом, не представляет интереса говорить о
вероятности того, что непрерывная случайная величина примет одно определенное
значение, но имеет смысл рассматривать вероятность попадания ее в интервал,
пусть даже сколь угодно малый.
Заметим, что было бы неправильным думать, что
равенство нулю вероятности
означает, что событие
невозможно (если, конечно, не ограничиваться
классическим определением вероятности). Действительно, в результате испытания
случайная величина обязательно примет одно из возможных значений; в частности,
это значение может оказаться равным
.
Свойство 6.
Если возможные значения непрерывной случайной величины
расположены на всей оси
,
то справедливы следующие предельные соотношения:
Свойство 7.
Функция распределения непрерывная слева, то есть:
Смежные темы решебника:
- Дискретная случайная величина
- Непрерывная случайная величина
- Математическое ожидание
- Дисперсия и среднее квадратическое отклонение
Примеры решения задач
Пример 1
Дан ряд
распределения случайной величины
:
|
|
1 | 2 | 6 | 8 |
|
|
0,2 | 0,3 | 0,1 | 0,4 |
Найти и изобразить ее функцию распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Будем задавать различные значения
и находить для них
1. Если
,
то, очевидно,
в том числе и при
2. Пусть
(например
)
Очевидно, что и
3. Пусть
(например
);
Очевидно, что и
4. Пусть
Очевидно, что и
5. Пусть
Итак:
График функции распределения
Пример 2
Случайная
величина
задана функцией распределения:
Найти
вероятность того, что в результате испытания
примет значение:
а) меньше
0,2;
б) меньше
трех;
в) не
меньше трех;
г) не
меньше пяти.
Решение
а) Так
как при
функция
, то
то есть
при
б)
в)
События
и
противоположны, поэтому
Отсюда:
г) сумма
вероятностей противоположных событий равна единице, поэтому
Отсюда, в
силу того что при
функция
, получим:
Пример 3
Задана
непрерывная случайная величина X своей плотностью
распределения вероятностей f(x). Требуется:
1)
определить коэффициент A;
2) найти
функцию распределения F(x);
3)
схематично построить графики функций f(x) и F(x);
4)
вычислить математическое ожидание и дисперсию X;
5)
определить вероятность того, что X примет значение из
интервала (a,b).
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
1)
Постоянный параметр
найдем из
свойства плотности вероятности:
В
нашем случае эта формула имеет вид:
Получаем:
2)
Функцию распределения
найдем из
формулы:
Учитывая
свойства
, сразу можем отметить,
что:
и
Остается
найти выражение для
, когда х принадлежит интервалу
:
Получаем:
3) Построим графики функций:
График плотности распределения
График функции распределения
4) Вычислим
математическое ожидание:
В нашем случае:
Вычислим дисперсию:
Искомая дисперсия:
5) Вероятность того, что
примет значение из интервала
:
Задачи контрольных и самостоятельных работ
Задача 1
Закон
распределения случайной величины X задан таблицей.
Найти ее
математическое ожидание, дисперсию и значение функции распределения в заданной
точке.
F(1)=
M[X]=
D[X]=
Задача 2
Случайная
величины X задана функцией распределения
Найти
плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить графики дифференциальной и интегральной функций.
Найти вероятность попадания случайной величины X в интервалы (1,2; 1,8),
(1,8; 2,3)
Задача 3
Дискретная
случайная величина X задана рядом распределения. Найти:
1)
функцию распределения F(x) и ее график;
2)
математическое ожидание M(X);
3)
дисперсию D(X).
|
|
-5 | 5 | 25 | 45 | 65 |
|
|
0.2 | 0.15 | 0.3 | 0.25 | 0.1 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
В задаче
дискретная случайная величина задана рядом распределения.
Найти
; M(X), D(X), P(0≤X≤2); F(x).
Начертить график F(x)
Задача 5
В задаче
непрерывная случайная величина X задана функцией
распределения F(x).
Найти a; f(x); M(X); D(X); P(X<0.2)
Начертить
графики функций f(x);F(x).
Задача 6
Функция
распределения непрерывной случайной величины X (времени безотказной работы
некоторого устройства) равна
(
). Найти вероятность безотказной
работы устройства за время x больше либо равно T.
Задача 7
Функция
распределения непрерывной случайной величины задана выражением:
Найдите:
1)
параметр a;
2)
плотность вероятностей;
4) P(0<x<1)
Постройте
графики интегральной и дифференциальной функции распределения.
Задача 8
Дана
интегральная функция распределения. Найти: дифференциальную функцию f(x),M(X),σ(X),D(X).
Задача 9
Дана
функция распределения F(х) случайной величины Х.
Найти плотность
распределения вероятностей f(x), математическое ожидание M(X),
дисперсию D(X) и вероятность попадания X на
отрезок [a,b]. Построить графики
функций F(x) и f(x).
Задача 10
НСВ X имеет
плотность вероятности (закон Коши)
Найти:
а)
постоянную C=const;
б)
функцию распределения F(x);
в)
вероятность попадания в интервал -1<x<1
г)
построить графики f(x), F(x).
- Краткая теория
- Примеры решения задач
- Задачи контрольных и самостоятельных работ
2.2.7. Функция распределения случайной величины
Стандартное обозначение: 
И для дискретной, и для непрерывной случайной величины она определяется одинаково:
, где 
– вероятность того, что случайная величина
примет значение,
МЕНЬШЕЕ, чем переменная 
, которая«пробегает» все действительные значения от «минус» до
«плюс» бесконечности.
Построим функцию распределения для нашей подопытной игры:
Начинаем разбираться. Чему, например, равно значение 
? Это вероятность того, что выигрыш будет меньше, чем –20. И это невозможное событие: 
. Совершенно понятно, что 
и для всех «икс» из интервала 
, а также для 
. Почему? По определению функции распределения:
– вы согласны? Функция
возвращает вероятность того,
что в точке 
выигрыш
будет СТРОГО МЕНЬШЕ «минус» пяти.
Таким образом: 
, если 
.
На интервале 
функция 
, поскольку левее
любой точки этого интервала есть только одно значение 
случайной величины, которое появляется с вероятностью 0,5. Кроме того,
сюда же следует отнести точку 
,
так как:
– очень хорошо осознайте этот
момент!
Таким образом, если 
, то 
Далее рассматриваем промежуток 
. СТРОГО ЛЕВЕЕ любой точки этого промежутка находятся два выигрыша 
, поэтому:
И, наконец, если 
, то 
, ибо все значения
случайной величины 
лежат СТРОГО левее
любой точки интервала 
Заметим, кстати, важную особенность: коль скоро функция 
характеризует вероятность, то
она может принимать значения лишь из промежутка 
– и никакие другие!
Итак, функция распределения вероятностей ДСВ является кусочной и, как многие знают, в таких случаях принято использовать
фигурные скобки:
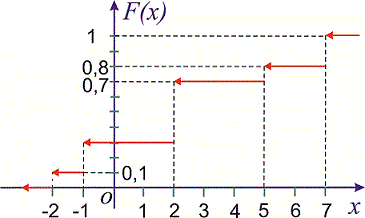
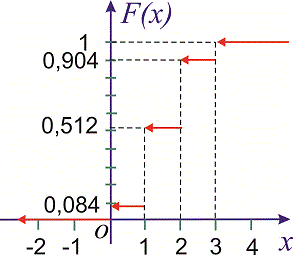
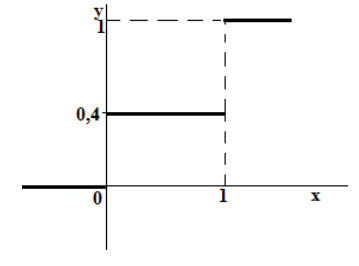
График данной функции имеет разрывный «ступенчатый» вид:
Причём, функция 
или её
график однозначно определяют сам закон распределения: в точке 
высота «ступеньки» (разрыв) составляет 
(следим по графику), в точке 
«скачок» разрыва равен 
и, наконец, в точке 
он равен в точности 
.
Таким образом, функция распределения вероятностей – это ещё один способ ЗАДАТЬ случайную величину. И этот способ
особо важен для непрерывной случайной величины – по той причине, что её невозможно описать таблицей (ввиду бесконечного и
несчётного количества принимаемых значений). Однако, всему своё время, и НСВ – тоже.
Освоим технические моменты решения типовой задачи:
Задача 93
Построить функцию распределения случайной величины 
Найти вероятности того, что случайная величина примет значение из следующих промежутков:
…, пожалуй, достаточно.
Решение: На практике удобно использовать формальный алгоритм построения функции распределения:
Сначала берём первое значение 
и составляем нестрогое неравенство 
. На этом промежутке 
.
На промежутке 
(между
и 
):
На промежутке 
(между
и 
):
На промежутке 
(между
и 
):
И, наконец, если 
строго
больше самого последнего значения 
, то:
Легко заметить, что с увеличением «икс» идёт накопление (суммирование) вероятностей, и поэтому функцию 
иногда называют интегральной функцией распределения. В
практических задачах проведённые выше действия обычно выполняют устно, а результат сразу записывают под единую скобку:
Выполним чертёж:
и проконтролируем правильность решения с помощью «скачков» графика: в точке 
«скачок» равен 
, в точке 
составляет 
, в точке 
равен 
, и, наконец, в точке 
– 
.
При выполнении чертежа от руки оптимален следующий масштаб:
горизонтальная ось: 1 ед. = 2 или 1 тетрадная клетка;
вертикальная ось: 0,1 = 1 тетрадная клетка.
На левых концах ступенек (кроме нижнего луча) можно ставить выколотые точки – дело вкуса. Левый нижний луч следует прочертить жирно
(чтобы он не сливался с координатной осью) и до конца оси! Правая верхняя линия не должна заканчиваться раньше
острия оси! Такие оплошности могут говорить о непонимании функции распределения, а это, как вы понимаете, скверно. То было ручное
построение. Ну а о том, как строить такие красивые графики в Экселе можно узнать в этом ролике на Ютубе, к слову, полигон (многоугольник) распределения строится ещё проще.
Переходим ко второй части задания, её коротко можно сформулировать так:
2.2.8. Вероятность попадания в промежуток
2.2.6. Многоугольник распределения
Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Эмпирическая функция распределения
Содержание:
- Что называют эмпирической функции распределения
- Свойства функции
- Как найти
- Как построить график
- Примеры задач
Что называют эмпирической функции распределения
Допустим, известно статистическое распределение частот количественного признака Х. Обозначим nх – количество наблюдений со значением меньше x1, n – всего наблюдений. Очевидно, что относительная частота события Х<x будет равна nх/n.
Определение
Эмпирическая функция распределения – это функция F*(x), которая определяет для каждого значения x относительную частоту события X
Данное понятие можно записать в виде формулы:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(Fast(x)=frac{n_x}n)
В этой записи nx – количество вариантов, меньших x; n – объем выборочной совокупности.
Существует также теоретическая функция распределения (функция распределения генеральной совокупности). Ее отличие от выборочной функции распределения состоит в определении объективной возможности или вероятности события X<x.
Свойства функции
Функция распределения выборки обладает рядом свойств, которые следуют из определения понятия.
- Значения рассматриваемой функции F*(x) располагаются на отрезке [0; 1].
- Функция имеет неубывающий характер.
- При минимальной варианте x1 верно равенство F*(x)=0 при условии, что х<х1. При максимальной варианте хk верно равенство F*(x)=1 при условии х>xk.
Таким образом, функция распределения выборки помогает оценить теоретическую функцию распределения.
Как найти
Выборочная функция распределения для случайной величины рассчитывается по формуле:
(F(x)=P(xi<x))
Данное равенство читается так: функция распределения равна вероятности события, при котором случайная величина будем меньше x.
Поскольку при условии, что x меньше или равно 1, событие ξ20<1 невозможно (ξ20 не принимает значение менее 1, вероятность невозможного события равна 0), верно следующее выражение:
(F(x)=P(xi20<1)=0)
При принадлежности x отрезку (1; 2] событие ξ20<2 представляет собой равенство ξ20=1, значит, вероятность этого события равно 0,1. В записи это выглядит так:
(F(x)=P(xi20<2)=0,1)
Когда x принадлежит отрезку (2; 4], событие ξ20<4 состоит в равенстве ξ20 значению 1 или 2, то есть вероятность рассматриваемого события равна 0,1+0,2=0,3 или:
(F(x)=P(xi20<4)=0,3)
Если 4 < x ≤ 5, то событие ξ20<5 означает, что ξ20 принимает значение либо 1, либо 2, либо 4. Следовательно, вероятность данного события вычисляется так: 0,1+0,2+0,35=0,65, то есть:
(F(x)=P(xi20<5)=0,65)
При 5 < x ≤ 6 событие ξ20<6 заключается в том, что ξ20 принимает значение 1, 2, 4 или 5. Значит его вероятность равно 0,1+0,2+0,35+0,1=0,75 или:
(F(x)=P(xi20<6)=0,75)
И так далее.
Итак, эмпирическая функция распределения имеет следующий вид:
Как построить график
Построение графика эмпирической функции распределения возможно после вычисления ее значений на всей числовой оси. Для рассмотренного примера схематическое изображение будет выглядеть так:
График ступенчатого вида, построенный на отрезках. Совпадение графика с горизонтальной осью означает, что левее минимального значения x=1 функция приобретает значение нуля. Увеличение в каждой следующей точке xi происходит на величину вероятности νi. Правее максимального значения х8=13 функция равна 1. Стрелки и точки на концах отрезков указывают на определение функции на полуинтервалах.
Примеры задач
Задача
В таблице даны значения эмпирического распределения:
Необходимо найти объем выборочной совокупности, составить выборочную функцию распределения, построить ее график.
Решение
- Вычислим объем выборки: n=5+10+15+20=50.
- Из свойства эмпирической функции распределения: Fn(x)=0 при x≤1, Fn(x)=1 при x>4.
Выходит, что:
По полученным значениям построим график:
Рассмотрим пространство элементарных событий, в котором каждому элементарному событию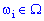 
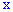
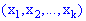
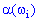
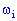
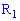
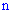
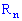
в соответствие ставится число 
или вектор 
, т.е. на множестве 
есть определенная функция 
, которая для каждого элементарного события 
находит элемент одномерного пространства 
или 
— мерного пространства 
.
Эту функцию называют случайной величиной. В случае, когда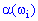 
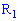
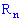
отражает множество 
на одномерное пространство 
случайную величину называют одномерной. Если отображение осуществляется на 
, то случайную величину называют n— мерной (системой n случайных величин или n — мерным случайным вектором).
Величина называется случайной, если в результате проведения опыта под влиянием случайных факторов она приобретает то или другое возможное числовое значение с определенной вероятностью.
Если множество возможных значений случайной величины является счетно, то ее называют дискретной. В противном случае ее называют непрерывной.
Случайные величины для удобства обозначают прописными буквами латинского алфавита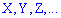 
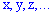
, а их возможные значения — строчными 
.
Для установления случайной величины необходимо знать не только множество возможных ее значений, но и указать, с какими вероятностями она приобретает то или иное возможное значение.
С этой целью вводят понятие закона распределения вероятностей – зависимость, которая устанавливает связь между возможными значениями случайной величины и соответствующими им вероятностями.
Закон распределения дискретной случайной величины 
часто задают в табличной форме, функцией, или графически с помощью вероятностного многоугольника.
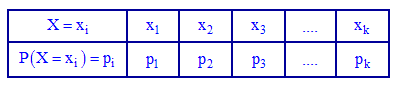
При табличной формы записи закона указывается множество возможных значений случайной величины находится в порядке их возрастания в первой строке, и соответствующих им вероятностей в следующей:
Случайные события должны быть попарно несовместимы и образовывать полную группу, то есть удовлетворять условие:
Приведенную зависимость называют условием нормировки для дискретной случайной величины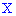 
, а таблицу распределения – рядом распределения.
Функция распределения вероятностей и ее свойства
Закон распределения вероятностей можно представить в виде функции распределения вероятностей случайной величины 
, которая может использоваться как для дискретных, так и для непрерывных случайных величин.
Функцию аргумента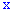 
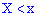
, устанавливающую вероятность случайного события 
называют функцией распределения вероятностей:
Ее следует понимать как функцию, которая устанавливает вероятность случайной величины, которая может принимать значения, меньше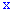 
.
Функция распределения обладает следующими свойствами:
1. Она всегда положительная со значениями в пределах от нуля до единицы 
2. Функция является монотонно возрастающей, а именно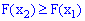 
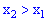
, если 
.
С этого свойства получают приведенные выводы:
a) Вероятность вступления случайной величиной возможных значений из промежутка 
равна прироста ее интегральной функции на этом промежутке:
б) Вероятность, что непрерывная случайная величина примет конкретное возможное значение, всегда равна нулю
Для непрерывной случайной величины выполняются такие равенства:
3. На крайних точках непрерывная случайная величина принимает значение 0 и 1.
Из этих границ следует, что для дискретной случайной величины с возможными значениями из ограниченного промежутка 
имеем
для 
для 
—————————-
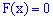
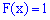
Приведем решения задач на отыскание функции распределения.
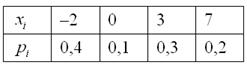
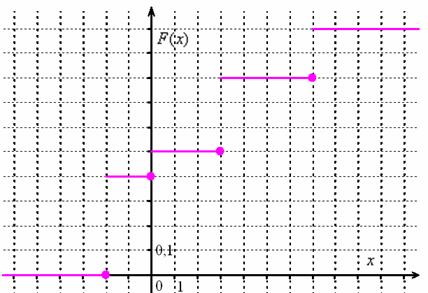
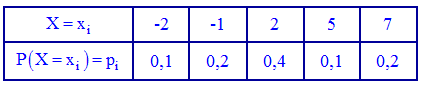
Пример 1. Закон распределения дискретной случайной величины задан таблицей:
Построить функцию распределения и ее график.
Решение. Согласно свойствами функции получим приведенные дальше значение.
1) 
2) 
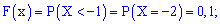
3) 
4) 
5) 
6) 
Компактно функция распределения иметь запись
График функции распределения изображен на рисунке ниже
—————————-
Пример 2. Есть три коробки с шарами. В первой содержится 6 желтых и 4 синие шарики, во втором — 7 желтых и 3 синие, а в третьем — 2 желтых и 8 синих. Из каждой коробки наугад берут по одному шарику. Построить закон распределения вероятностей дискретной случайной величины – появления числа синих шариков среди трех наугад взятых, определить закон распределения и построить график этой функции.
Решение. Среди трех наугад взятых шариков число синих может быть 0, 1, 2, 3.
В табличной форме закон распределения дискретной случайной величины имеет вид:
Вычислим вероятности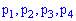 
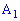
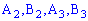
. С этой целью обозначим 
— случайное событие, заключающееся соответственно в появлении желтого шарики и 
– появление синего с первой коробки. Подобным образом для остальных коробок 
. Вероятности этих событий такие:
Поскольку случайные события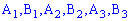 
независимы, то вероятности находим по формулам:
Вычисление достаточно просты и сделаны обозначения полностью все объясняют. Проверим выполнение условия нормировки
Всегда выполняйте проверку данного условия: это достаточно просто сделать и позволяет быстро проверить правильность вычислений вероятности. В случаях, когда условие нормировки не выполняется нужно отыскать ошибку и исправить ее.
У нас же все вычисления правильны, потому записываем закон распределения вероятностей в табличной форме:
Вычисляем значение интегральной функции
1) 
2) 
3) 
4) 
5) 
В случае ошибок при нахождении вероятностей последнее соотношение дает отличный от единицы результат, поэтому можете проверять и по этому значению. Упрощенно функция распределения будет иметь вид
а ее график следующий
—————————-
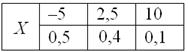
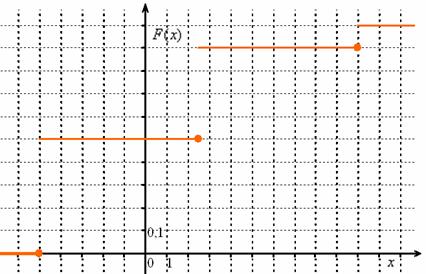
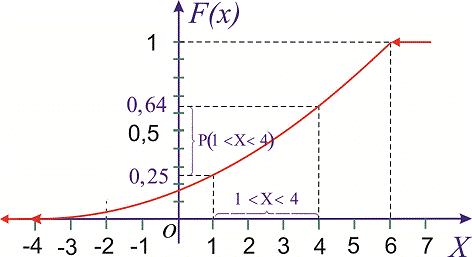
Пример 3. Закон распределения случайной величины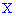 
задан функцией распределения вероятностей
Построить график функции распределения и вычислить вероятность, что случайная величина принадлежит промежутку 
.
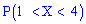
Решение. Функция распределения будет иметь вид.
Используя определение, вычислим
Таким образом вероятность, что случайная величина принадлежит промежутку [1,4] равна 0,36.
—————————-
Внимательно разберитесь с приведенными примерами нахождения функции распределения, это Вам пригодится на практических занятиях. Старайтесь проверять условие нормирования, чтобы избежать дальнейших ошибок и правильно определяйте вероятности.
———————————————-
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение функции распределения
Пусть $X$ – случайная величина, а $x$ – вероятность распределения этой случайной величины.
Определение 1
Функцией распределения называется функция $F(x)$ удовлетворяющая условию $Fleft(xright)=P(X
Также иначе функцию распределения иногда называются интегральной функцией распределения или интегральным законом распределения.
В общем виде график функции распределения представляет собой график неубывающей функции с областью значений, принадлежащей отрезку $left[0,1right]$ (причем 0 и 1 обязательно входят в область значений). При этом функция может, как иметь, так и не иметь скачков функции (рис. 1)
Рисунок 1. Пример графика функции распределения
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
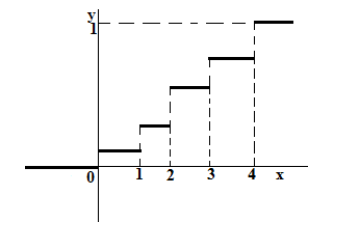
Функция распределения дискретной случайной величины
Пусть случайная величина $X$ является дискретной. И пусть для нее дан ряд её распределения. Для такой величины функцию распределения вероятностей можно записать в следующем виде:
ступенчатую функцию
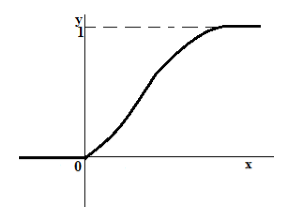
Функция распределения непрерывной случайной величины
Пусть случайная величина $X$ теперь является непрерывной.
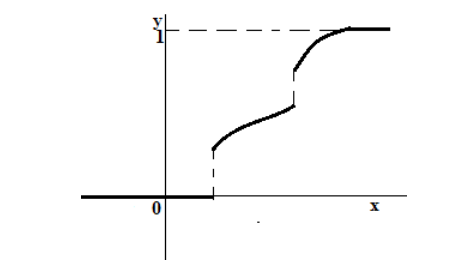
График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 3).
«Определение функции распределения» 👇
Функция распределения смешанной случайной величины
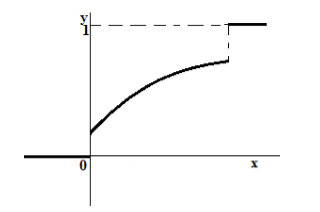
Рассмотрим теперь случай, где случайная величина $X$ является смешанной.
График функции распределения такой случайной величины всегда представляет собой неубывающую функцию, которая имеет минимальное значение в 0, максимальное значение в 1, но которая не на всей области определения является непрерывной функцией (то есть имеет скачки в отдельных точках) (рис. 4).
Рисунок 4. Функция распределения смешанной случайной величины
Примеры задач на нахождение функции распределения
Пример 1
Приведен ряд распределений появления события $A$ в трех опытах
Рисунок 5.
Найти функцию распределения вероятностей и построить её график.
Решение.
Так как случайная величина является дискретной, то мы можем пользоваться формулой $ Fleft(xright)=sumlimits_{x_i
При $xle 0$, $Fleft(xright)=0$;
При $0
При $1
При $2
При $x>3$, $Fleft(xright)=0,2+0,1+0,3+0,4=1$;
Отсюда получаем следующую функцию распределения вероятностей:
Рисунок 6.
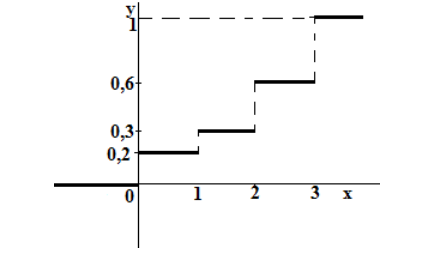
Построим ее график:
Рисунок 7.
Пример 2
Проводится один опыт, в котором событие $A$ может, как произойти, так и не произойти. Вероятность того, что данное событие произойдет равно $0,6$. Найти и построить функцию распределения случайной величины.
Решение.
Так как вероятность того, что событие $A$ произойдет равно $0,6$, то вероятность того, что данное событие не произойдет равно $1-0,6=0,4$.
Построим для начала ряд распределения данной случайной величины:
Рисунок 8.
Так как случайная величина является дискретной, найдем функцию распределения по аналогии с задачей 1:
При $xle 0$, $Fleft(xright)=0$;
При $0
При $x>1$, $Fleft(xright)=0,4+0,6=1$;
Таким образом, получаем следующую функцию распределения:
Рисунок 9.
Построим ее график:
Рисунок 10.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме