Содержание:
Системы случайных величин или случайные векторы:
При изучении случайных явлений в зависимости от их сложности приходится использовать два, три и большее число случайных величин.
Например, 1) попадание снаряда в цель определяется не одной, а двумя случайными величинами: абсциссой и ординатой точки попадания, 2) случайное отклонение точки разрыва снаряда при дистанционной стрельбе определяется комплексом трех случайных величин: тремя координатами этой точки.
Определение 57. Совместное рассмотрение двух или нескольких случайных величин приводит к системе случайных величин или к случайному вектору.
(X, Y) — двумерный случайный вектор или система двух СВ.
Изучать систему — значит изучать сами случайные величины, ее составляющие; связи и зависимости между ними.
Геометрическая интерпретация системы: 1) систему двух случайных величин (X, У) рассматривают как случайную точку на плоскости (Охх) или как случайный вектор с составляющими X, У; 2) систему трех случайных величин (X, У, Z) рассматривают как случайную точку на плоскости (Оxyz) или как случайный вектор с составляющими X, У; Z и т.д.
В зависимости от типа случайных величин, образующих систему, могут быть дискретные, непрерывные и смешанные системы.
Определение 58. Двумерный случайный вектор (X, У) называется вектором дискретного типа (СВДТ), если множество его возможных значений не более, чем счетно.
Определение 59. (первое определение) Двумерный случайный вектор (X, У) называется вектором непрерывного типа (СВНТ), если множество его возможных значений непрерывно заполняет некоторую область плоскости (Оху)-
Определение 60. Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.
Законы распределения СВДТ и СВНТ
Таблица распределения — закон распределения СВДТ:
Рассмотрим двумерный случайный вектор (X, У), где X и У — дискретные случайные величины с возможными значениями
Пример:
Из цифр 1, 2, 3, 4, 6, 8, 9 наудачу отбирают две цифры. Х — число четных цифр в выборке, Y — число нечетных. Описать закон распределения.
Решение.
X (четные) — 2, 4, 6, 8; Y ( нечетные) — 1, 3, 9. Следовательно, возможные значения X 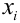
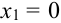
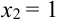
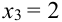
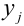
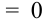
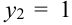
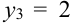
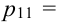
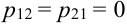
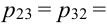
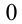
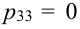
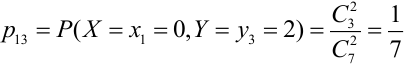
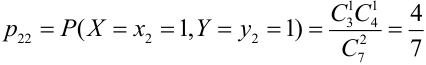
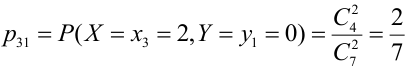
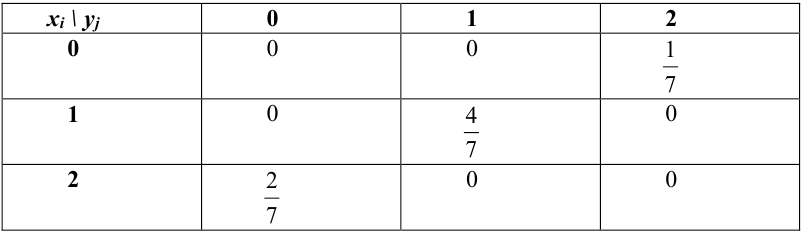
Таблица распределения имеет вид:
Проверка:
Пример:
Дана таблица распределения случайного вектора (X, Y). Получить ряды распределения для Х и Y отдельно.
Решение.
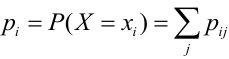
Проверка:
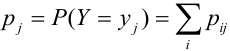
Проверка:
Функция распределения — закон распределения СВДТ и СВНТ
Функция распределения — универсальный закон распределения случайных векторов как дискретного, так и непрерывного типа.
Определение 61. Функцией распределения системы двух случайных величин называется функция двух аргументов F(x,y), равная вероятности совместного выполнения двух неравенств: X < х, Y < у, т.е.
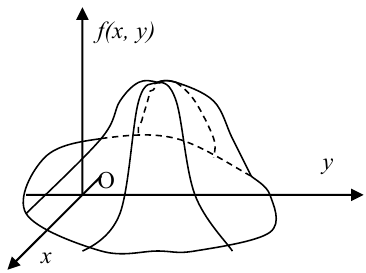
Геометрически F(x,y) представляет вероятность попадания случайной точки (X,Y) в левый нижний бесконечный квадрант плоскости с вершиной в точке (х,у).
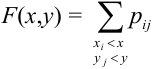
Свойства F(x;y).
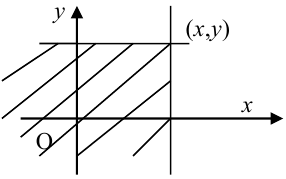
1. Условие согласованности:
Пояснение. Отодвигая одну из границ квадранта в бесконечность, получаем полуплоскость, вероятность попадания в которую есть функция распределения одной случайной величины.
2.
Пояснение. Квадрант обращается во всю координатную плоскость, попадание случайной точки в которую есть достоверное событие.
3.
Пояснение. Отодвигая ту или иную границу квадранта в (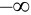
4. F(x, у) — неубывающая функция по каждому аргументу.
5. Вероятность попадания случайной точки (X, У) в произвольный прямоугольник со сторонами, параллельными координатным осям, вычисляется по формуле:
Определение 62. (второе определение) Двумерный случайный вектор называется случайным вектором непрерывного типа (СВНТ), если его функция распределения непрерывна на всей плоскости и существует неотрицательная и интегрируемая по Риману в бесконечных пределах по х, у функция 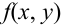
Пример №1
Найти функцию распределения, если случайный вектор задан таблицей распределения:
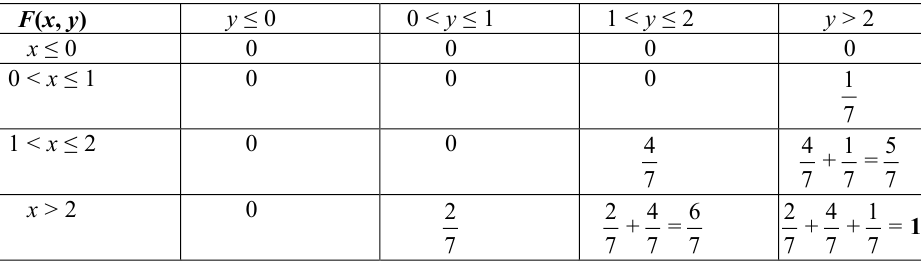
Решение.
Случайный вектор дискретного типа, следовательно,
Плотность распределения (Для СВНТ)
Определение 63. (первое определение) Плотностью распределения системы двух непрерывных случайных величин называется предел отношения вероятности попадания случайной точки (X, Y) в элементарный прямоугольник к площади прямоугольника, когда оба его размера стремятся к нулю:
Распишем интервальную вероятность с помощью функции распределения:
Правая часть равенства — определение смешанной производной функции двух переменных F(x, у), отсюда следует
Определение 64. (второе определение) Плотностью распределения системы двух непрерывных случайных величин называется смешанная частная производная от функции распределения системы:
Отсюда,
Геометрически 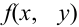
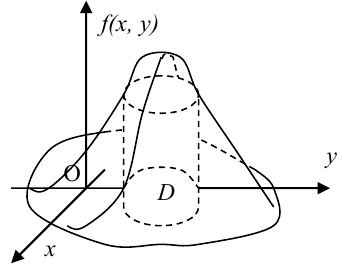
Вероятность попадания случайной точки в некоторую область D плоскости (Oxy) находится по формуле:
Геометрически вероятность попадания случайной точки в область D плоскости (Oxy) изображается объемом цилиндрического тела, ограниченного поверхностью распределения и опирающегося на эту область.
Свойства плотности
1. 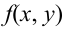
2. Условие нормировки:
Пример №2
Дана плотность распределения непрерывного вектора
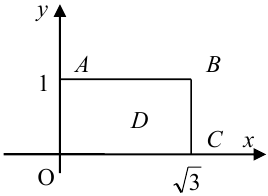
Найти: 1) коэффициент а, 2) функцию распределения F(x, у), 3) вероятность попадания случайной точки в прямоугольник с вершинами в точках O(0,0), A(0,1),
Решение.
1) Для вычисления коэффициента а применим условие нормировки:
2) По определению
3) Вероятность попадания в прямоугольник.
1 способ:
2 способ (по 5 свойству):
Пример №3
Дана плотность распределения непрерывного вектора 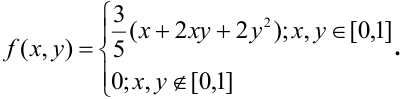
Решение.
Плотность распределения задана в квадрате. Область пересечения квадрата с заданным треугольником заштрихованный треугольник, ограниченный снизу прямой 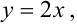
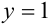
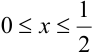
Плотности распределения отдельных величин, входящих в систему
Пусть известна плотность распределения 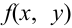
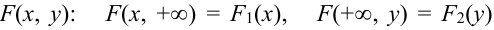
Отсюда, дифференцированием первого равенства по х, а второго по у, получим, что плотности распределения одной из величин равны интегралу от плотности распределения системы в бесконечных пределах по аргументу, соответствующему другой случайной величине:
Ставится вопрос, как по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. В общем случае эта задача не разрешима, но, с другой стороны, закон распределения системы должен содержать все сведения о величинах, входящих в систему, в том числе и сведения о том, как они связаны между собой.
Определение 65. Случайные величины X и Y, входящие в систему, называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае, они называются зависимыми.
Теорема. Для того, чтобы дискретные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
Для того, чтобы непрерывные случайные величины X и Y , входящие в систему, были независимыми, необходимо и достаточно, чтобы выполнялось равенство:
Пример №4
Дана плотность распределения непрерывного вектора:
Зависимы или независимы случайные величины, входящие в систему?
Решение.
Представим плотность в виде произведения:
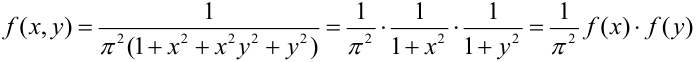
Пример №5
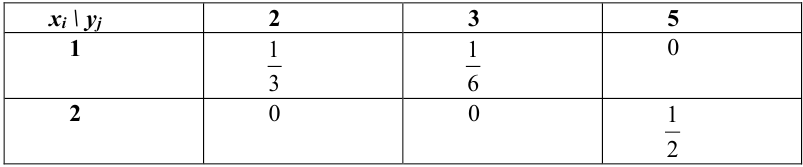
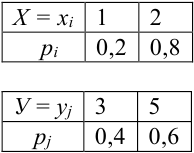
Дано распределение дискретных независимых случайных величин Х и Y:
Записать закон распределения случайного вектора (Х + Y).
Решение.
Найдем возможные значения случайного вектора (Х+ Y): 1 + 3 = 4, 2 + 3 =5, 1+5 = 6, 2 + 5 = 7.
Найдем их вероятности, пользуясь условием независимости:
Следовательно, ряд распределения случайного вектора (Х + Y) имеет вид:
Замечание. Одним из наиболее простых распределений системы двух непрерывных величин является равномерное распределение.
Определение 66. Система двух непрерывных случайных величин имеет равномерное распределение в области D плоскости (Оху), если плотность распределения в точках области D постоянна и равна нулю в остальных точках плоскости:
В силу свойства 2 плотности имеем, что 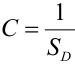
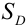
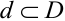
Определение 67. Пусть Х и Y независимые величины, распределенные по нормальному закону, их плотности распределения имеет вид:
Следовательно, плотность распределения системы (Х,Y) на основании теоремы умножения плотностей распределения для случая независимых величин получим в виде
Если X и Y зависимы между собой, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему, что привело к введению условных законов распределения.
Определение 68. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.
Обозначим G (х,у) — множество возможных значений случайного вектора (X, Y).
Рассмотрим СВДТ.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у называется совокупность возможных значений 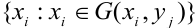
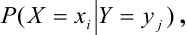
Рассмотрим CBHT.
Условный закон распределения случайной компоненты X при условии, что Y приняла определенное значение у :
Теорема (умножения законов распределения):
Условие нормировки:
Условие независимости Х от Y:
Числовые характеристики системы
Определение 69. Начальным моментом 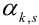
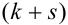
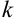
Математическое ожидание дискретных случайных величин Х и Y, входящих в систему:
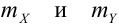
Определение 70. Центральным моментом 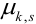
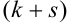
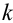
Дисперсия случайных величин X и Y, входящих в систему — характеристика рассеивания случайной точки в направлении осей (ох) и (оу):
Дисперсия дискретных случайных величин Х и Y, входящих в систему:
Дисперсия непрерывных случайных величин Х и Y, входящих в систему:
Замечание. Для краткого описания условных законов распределения используются различные характеристики, наиболее важной из которых является математическое ожидание:
Определение 71. Условным математическим ожиданием дискретной случайной величины X при условии, что Y принимает одно из своих возможных значений 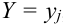
Для непрерывной случайной величины X:
Аналогично, вводится понятие условного мат. ожидания для СВ Y.
Пример №6
По некоторой цели производится два выстрела. Вероятность попадания при одном выстреле равна р. Рассмотрим две случайные величины: X — число попаданий в цель, Y — число промахов. Составить таблицу распределения, записать функцию распределения системы F(x,y) и найти числовые характеристики
Решение.
Случайный вектор дискретного типа, следовательно,
Пояснение:
Ковариация, корреляция и линии регрессии
Особую роль при исследовании системы играет второй смешанный центральный момент.
Определение 72. Второй смешанный центральный момент 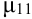
Теория корреляции решает две задачи: 1) установление формы связи между случайными величинами, 2) определение тесноты и силы этой связи.
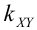
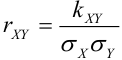
(Иногда его обозначают как 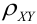
Средние квадратические отклонения случайных величин X и Y равны
Определение 17. X и Y называются некоррелированными случайными величинами, если их коэффициент корреляции 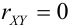
Свойства коэффициента корреляции
Свойства коэффициента корреляции 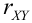
1. Если X и Y — независимые СВ, то 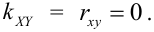
2.
3. В случае 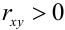
4. В случае 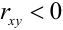
Взаимная связь двух случайных величин, помимо 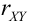
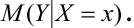
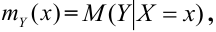
Аналогично, зависимость Х от Y описывает функция
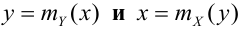
Линии, определенные этими уравнениями, называются кривыми или линиями регрессии. (Вводятся лишь для непрерывных СВ, для ДСВ линии будут состоять из точек.)
Если обе линии регрессии — прямые, то корреляционную зависимость называют линейной (линейная корреляция). Для нормально распределенного случайного вектора (X,Y) уравнения регрессии линейные:
Связь коэффициента корреляции и линий регрессии
1) Если 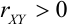
2) Если 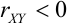
3) Если 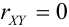
4) Если, 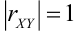
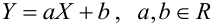
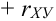
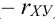
Часто пишут уравнение в виде: 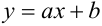
Определение 73. Ковариационной матрицей случайного вектора называется симметрическая действительная матрица, элемент которой представляет собой ковариации соответствующих пар компонент:
Определение 74. Корреляционной матрицей случайного вектора называется нормированная ковариационная матрица
Пример №7
Дано уравнение парной регрессии 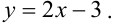
Решение.
Из рассмотрения исключаем 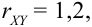
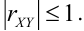
Замечание. Можно было знак 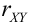
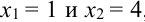
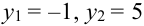
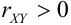
Пример №8
Дано уравнение парной регрессии 
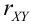
Решение.
Из формулы 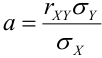
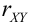
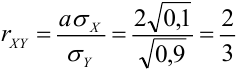
Свойства математического ожидания и дисперсии
1. X, Y как зависимые, так и независимые случайные величины, тогда
2.
Если X, Y — некоррелированные, то
Если X, Y- независимые, то
3.
Если X, Y- некоррелированные, то
4. Если X, Y-независимые, то
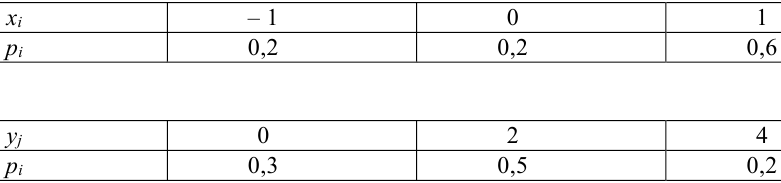
Пример №9
Даны законы распределения случайных величин X, Y:
Найти
Решение.
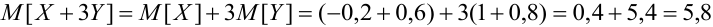
- Вероятность и риск
- Определения вероятности событий
- Предельные теоремы теории вероятностей
- Точечные оценки, свойства оценок
- Алгебра событий — определение и вычисление
- Свойства вероятности
- Многомерные случайные величины
- Случайные события — определение и вычисление
Закон распределения вероятностей двумерной случайной величины
Законом
распределениядискретной двумерной
случайной величиныназывают перечень возможных значений
этой величины, т.е. пар чисел,
гдеи
–
возможные значения величини
,
соответственно, и вероятностейих совместного появления
.
Двумерная дискретная
случайная величина
задается в видетаблицы распределения
вида:
где первая строка
таблицы указывает возможные значения
составляющей
,
а первый столбец – все возможные значения
составляющей.
Так как события
(
;
)
образуют полную группу, то.
Зная закон
распределения двумерной дискретной
случайной величины, можно найти законы
распределения каждой из ее составляющих.
Так, например, вероятность того, что
примет значение
,
равна.
Совместная
функция распределения двух случайных
величин
Функция
,
определяющая для каждой пары чиселвероятность того, что
примет значение меньшее
,
и при этомпримет значение меньшее
,
называетсясовместной функцией
распределениядвух случайных
величин=
.
Геометрически это
равенство можно истолковать так:
– это вероятность того, что случайная
точка ()
попадет в бесконечный квадрант с вершиной
(),
расположенный левее и ниже этой вершины.
Свойства совместной функции распределения двух случайных величин
-
Значения
совместной функции распределения
удовлетворяют неравенству:
.
-
–неубывающая
функция по каждому аргументу, т.е.
,
если
;
,
если
.
Совместная функция
распределения имеет следующие предельные
значения:
;
;
;
.
-
При
или
совместная функция распределения
системы становится функцией распределения
одной из составляющих:;
Плотность совместного распределения вероятностей непрерывной двумерной случайной величины
Непрерывную
двумерную случайную величину можно
задать с помощью плотности распределения.
Плотность совместного распределения
вероятностейдвумерной непрерывной случайной величины
(,
)
– это вторая смешанная частная производная
от функции распределения:
.
Зная плотность
совместного распределения
,
можно найти совместную функцию
распределенияпо формуле
следующей из
определения плотности распределения
двумерной непрерывной случайной величины
(,
).
Смысл плотности
совместного распределения вероятностей:
вероятность попадания случайной точки
в прямоугольник (с вершиной в точке
и сторонами
и
равна произведению
,
когда стороны этого прямоугольника
стремятся к нулю.
В связи с этим,
вероятность попадания случайной точки
в произвольную область D
равна двойному интегралу по областиDот функции:
Свойства двумерной плотности вероятности
-
Двумерная плотность
вероятности неотрицательна:
.
-
Двойной несобственный
интеграл с бесконечными пределами от
двумерной плотности вероятности равен
единице:.
Независимые случайные величины
Две случайные
величины называются независимыми,
если закон распределения одной из них
не зависит от того, какие возможные
значения приняла другая величина.
Теорема.
Для того чтобы случайные величиныи
были
независимыми, необходимо и достаточно,
чтобы функция распределения системы
(,
)
была равна произведению функций
распределения составляющих:.
Следствие.Для того чтобы случайные величиныи
были
независимыми, необходимо и достаточно,
чтобы плотность совместного распределения
системы (,
)
была равна произведению плотностей
распределения составляющих:.
Содержание:
- Функции от случайной величины
- Закон распределения суммы двух случайных величин
Функции случайных величин
В приложениях часто приходится рассматривать случайные величины, которые являются некоторыми функциями случайных величин. Например, необходимо рассмотреть квадрат случайной величины или произведение двух случайных величин. При этом часто необходимо выяснить закон распределения получающейся случайной величины. В данной главе мы рассматриваем задачи, связанные с решением такого типа проблем.
Функции от случайной величины
Понятие функции случайной величины уже рассматривалось. Там же мы установили, что для непрерывной функции
будет снова случайной величиной.
В данном параграфе мы будем рассматривать задачу нахождения функции плотности 



По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Примеры с решением
Пример 8.1.
Пусть 


Решение:
Пусть 




Подставляя выражение (8.1) в (8.2), получим
Возможны два случая. Если 





Если 


откуда формула для плотности:
Возможно вам будут полезны данные страницы:
Формулы (8.5), (8.6) можно записать единообразно с использованием абсолютной величины. Это легко запомнить, если сообразить, что так как левая часть принимает только положительные значения, то и числовой множитель в правой части должен быть положительным. Итак, заключительная формула для искомой плотности имеет вид:
В качестве следствия получим следующее утверждение.
Теорема 8.1. Если 


Тогда согласно (8.8) имеем 


Пример 8.2.
Пусть 


Решение:
Найдем сначала функцию распределения 
где 

Рассмотренные примеры служат двум целям: во-первых, дать подход к нахождению функции плотности в типичных случаях и, во-вторых, использовать полученные формулы в дальнейших приложениях.
Закон распределения суммы двух случайных величин
Пусть дана система двух случайных величин 

Заметим, что для любой непрерывной функции 


Теорема 8.2. Если система случайных величин 



Доказательство. Найдем функцию распределения случайной величины 




Тогда функцию распределения для случайной величины 
Дифференцируя no 
Поскольку выражение для плотности симметрично относительно переменных 
Тем самым мы получили искомое выражение (8.11) и доказательство теоремы закончено полностью.
Особого внимания заслуживает случай, когда случайные величины 
где 


Отвлекаясь от существа решаемой задачи, можно заметить, что полученная нами формула (8.14) определяет весьма интересную операцию над функциями: каждой паре функций 



Пример 8.3.
Даны две независимые случайные величины 

Решение:
Поскольку 



При 




При 

И наконец, при 

Итак,
На рис. 8.2 изображен график соответствующей функции плотности, который называется законом распределения Сэмпсона.
Если 

Следующий пример связан с нахождением закона распределения величины
где все 
Формула (8.10) 
поскольку
Заметим, что свойство нормированности плотности (8.17) следует из определения 
Свойство 1.
Свойство 2.
Свойство 3.
Свойство 1 выводится с помощью формулы (8.14) и замены переменной 
К последнему интегралу применим формулу интегрирования по частям. Положим
Тогда получим
Первое выражение в скобках равно нулю, поскольку 
Интеграл от функции плотности равен единице по свойству нормированности, и мы получаем искомую формулу.
Свойство 3 доказывается совершенно аналогично, только интегрировать по частям придется дважды. Вывод предлагаем провести читателю.
Пример 8.4.
Найти закон распределения случайной величины 
Решение:
Случайная величина 


По свойству 2 

Теорема 8.3. Функция плотности случайной величины 
Математическое ожидание и дисперсия равны соответственно


Из рисунка видно, что графики плотности не являются симметричными относительно математического ожидания, однако с ростом числа степеней свободы они становятся все более симметричными.
Наряду с суммой случайных величин в приложениях часто приходится иметь дело с частным непрерывных случайных величин. Для нахождения функции плотности частного сделаем сначала предварительное замечание.
Пусть 

Отметим следующие свойства
Свойство 1. 
Действительно, производная 
где 


Очевидно, что 

по свойству функции плотности.
Свойство 3. Если функция 


Для проверки этого свойства достаточно доказать свойство нормированности. Иными словами, надо проверить, что
Имеем
Доказанные свойства позволяют рассматривать функцию 
Теорема 8.4. Пусть даны непрерывные случайные величины 








Рассматривая параметр 




Следующая теорема использует формулу (8.23), чтобы найти функцию плотности, которая будет использована для описания распределения Фишера.
Теорема 8.5. Если случайные величины 


Доказательство. Подставляя в формулу (8.23) выражения для плотностей (8.17), получим
В последнем интеграле произведем замену 

П0ЛУЧИМ ИСКОМУЮ Формулу для плотности.
Определение. Распределением Фишера называется распределение случайной величины


Применяя теорему 8.5, получим выражение для плотности величины, распределенной по закону Фишера.
Теорема 8.6. Случайная величина 
Графики функций плотности для трех случаев: а) 




Определение. Случайная величина подчинена закону распределения Стьюдента с 
где 
Плотность распределения Стьюдента с 

В частности, 





Лекции:
- Случайный вектор распределения
- Системы случайных величин
- Условное нормальное распределение
- Нормальное распределение на плоскости
- Многомерный нормальный закон
- Математическое ожидание: пример решения
- Законы распределения случайных величин
- Моменты случайной величины
- Моменты высших порядков
- Метод моментов
Двумерная непрерывная случайная величина
- Краткая теория
- Примеры решения задач
Краткая теория
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Непрерывной называют двумерную величину, составляющие которой непрерывны.
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Функция распределения двумерной случайной величины и ее свойства
Функцией распределения двумерной случайной величины
называют функцию
, определяющую для каждой
пары чисел
вероятность того, что
примет значение, меньшее
, и при этом
примет значение, меньшее
.
Свойство 1.
Значения
функции распределения удовлетворяют двойному неравенству:
Свойство 2.
есть неубывающая функция по каждому аргументу,
то есть:
если
если
Свойство 3.
Имеют место предельные соотношения:
1)
2)
3)
4)
Свойство 4.
При
функция распределения системы становится
функцией распределения составляющей
:
При
функция распределения системы становится
функцией распределения составляющей
:
Плотность распределения двумерной случайной величины и ее свойства
Плотностью совместного распределения вероятностей
двумерной непрерывной случайной величины
называют вторую смешанную частную производную
от функции распределения:
Зная
плотность совместного распределения
можно найти функцию распределения
по формуле:
Свойство 1.
Двумерная
плотность вероятности неотрицательна:
Свойство 2.
Двойной
несобственный интеграл с бесконечными пределами от двумерной плотности равен единице:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Безусловные и условные законы распределения составляющих
Пусть
известна плотность совместного распределения вероятностей системы двух
случайных величин. Найдем плотности распределения каждой из составляющих.
Аналогично
находится плотность распределения составляющей
:
Итак,
плотность распределения одной из составляющих равна несобственному интегралу с
бесконечными пределами от плотности совместного распределения системы, причем
переменная интегрирования соответствует другой составляющей.
Пусть
— непрерывная двумерная случайная величина.
Условной
вероятностью
распределения составляющих
при данном значении
называют отношение плотности совместного
распределения
системы
к плотности распределения
составляющей
:
Аналогично
определяется условная плотность составляющей
при данном значении
:
Если
известна плотность совместного распределения
, то условные плотности
составляющих могут быть найдены по формулам:
Эти
формулы можно записать в виде:
Аналогично
определяется условная плотность составляющей
при данном значении
:
То есть
умножая закон распределения одной из составляющих на условный закон
распределения другой составляющей, найдем закон распределения системы случайных
величин.
Смежные темы решебника:
- Двумерная дискретная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Примеры решения задач
Пример 1
Найти
плотность совместного распределения f(x,y) системы случайных величин (X,Y) по
известной функции распределения:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
По определению плотности совместно
распределения:
Искомая плотность совместного распределения:
Пример 2
Найти
функцию распределения системы случайных величин F(x,y) по известной плотности
совместного распределения f(x,y):
Решение
Воспользуемся
формулой:
В нашем
случае:
Ответ:
Пример 3
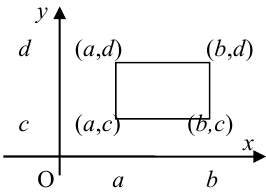
Двумерная
случайная величина (X,Y) имеет равномерное распределение вероятностей в
треугольнике ABC. Определить функции плотности распределения
компонент этой случайной величины f(x), f(y), их математические
ожидания M(X), M(Y), дисперсии D(X), D(Y),
коэффициент корреляции rxy. Выяснить, являются ли
случайные величины X и Y независимыми?
A(0;0),B(-1;1),C(1;1)
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Решение
где
– площадь треугольника
Разделим
область
на две равные части вдоль оси
, тогда из условия:
или
Тогда
плотность двумерной случайной величины
:
Вычислим
плотность составляющей
:
при
:
Откуда
плотность составляющей
:
Вычислим
плотность составляющей
:
при
Плотность
составляющей
:
Найдем
условную плотность составляющей
:
при
Следовательно,
случайные величины
и
зависимы
Найдем
математическое ожидание случайной величины
:
Найдем
дисперсию случайной величины
:
Найдем
математическое ожидание случайной величины
:
Найдем
дисперсию случайной величины
:
Найдем
математическое ожидание двумерной случайной величины
:
Тогда
ковариация:
Значит
коэффициент корреляции:
Следовательно,
случайные величины
и
– зависимые, но некоррелированные
Пример 4
Двумерная
случайная величина (X,Y) имеет плотность
распределения:
Найти
вероятность попадания значения (X,Y) в область x1≤x≤x2,
y1≤y≤y2, вероятность попадания значения X в
интервал x1≤x≤x2, математическое ожидание M[X] и
условное математическое ожидание M[Y⁄X=x].
a=8, b=2, x1=6, x2=9, y1=0, y2=4
Решение
Найдем
вероятность попадания в область
по формуле:
При
вычислении интеграла учитывается та часть области
, где
, т.е.
Плотность
вероятности для составляющей
имеет вид:
Если
или
, то
и
. При
находим:
Таким
образом, плотность имеет вид:
Тогда:
Условное математическое ожидание
определяется с
помощью условной плотности распределения
составляющей
Получаем:
Искомое
математическое ожидание:
- Краткая теория
- Примеры решения задач

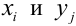

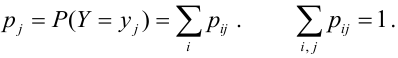
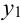

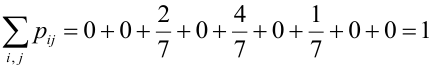
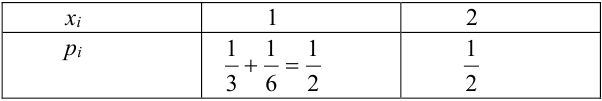
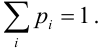

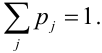
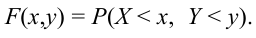
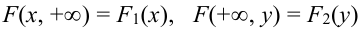
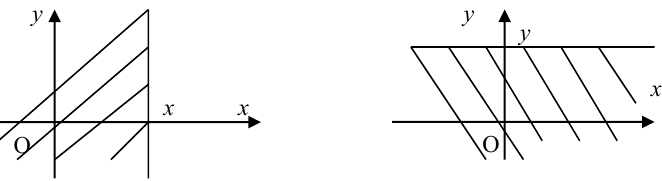
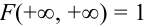
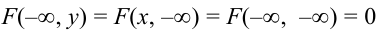
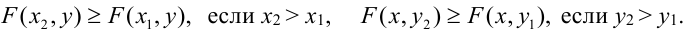
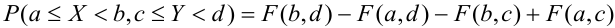
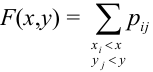
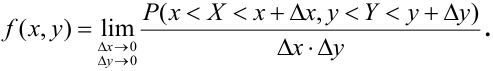
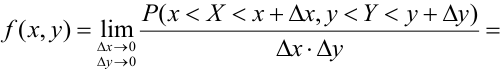
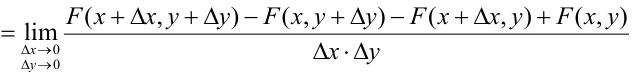
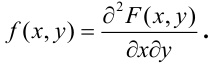
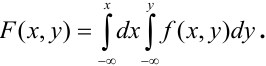
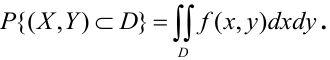
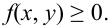
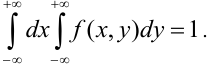
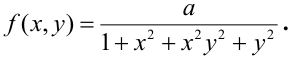
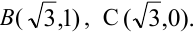
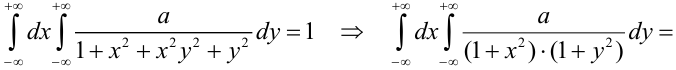
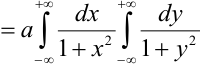
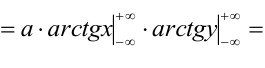
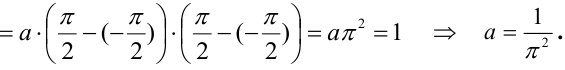
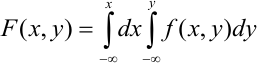
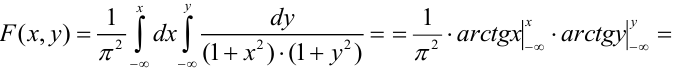
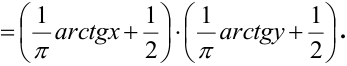
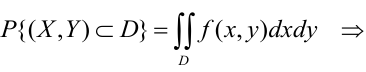
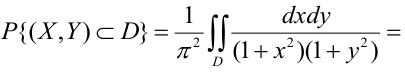
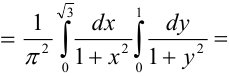
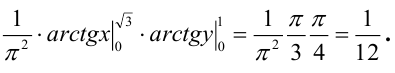
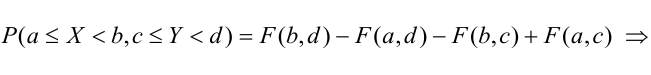
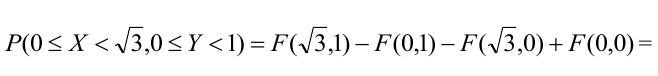
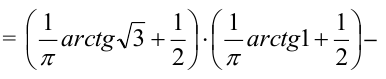
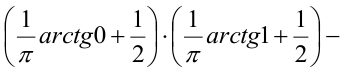
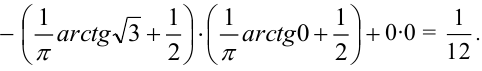
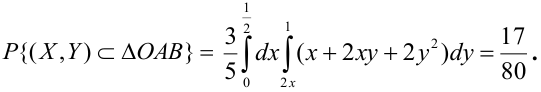
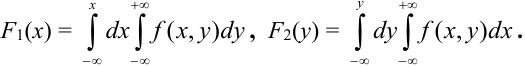
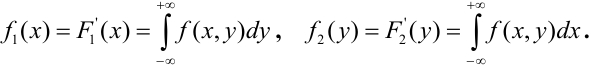
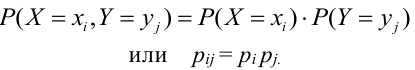
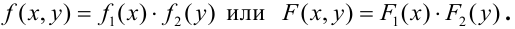
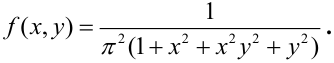
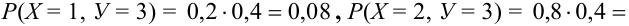
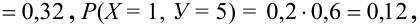
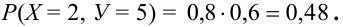

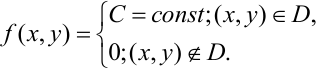
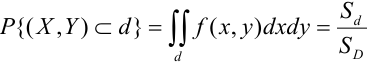
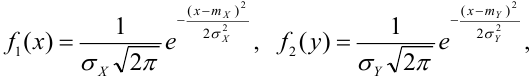
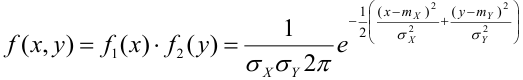
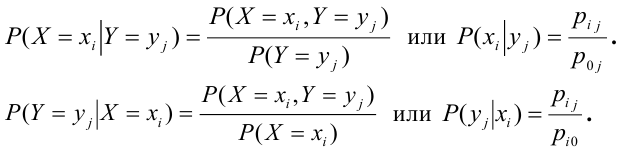
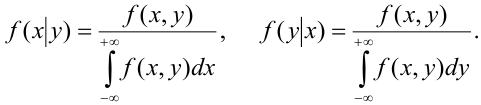
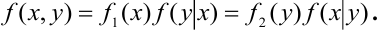
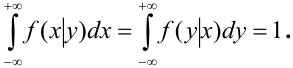
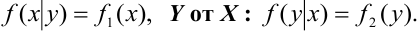
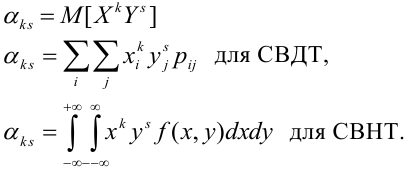
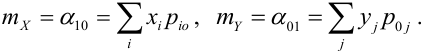
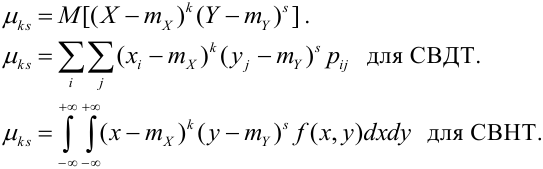

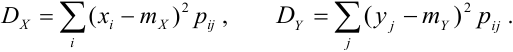
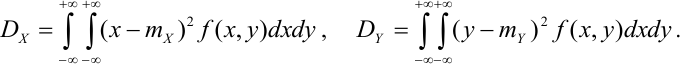
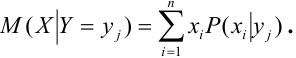
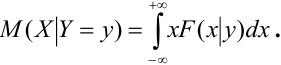

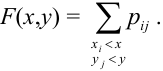


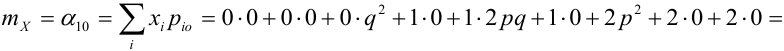
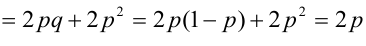
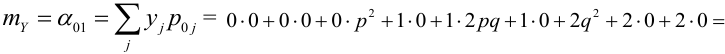
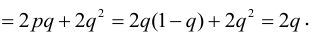
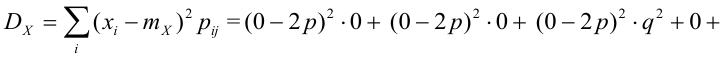
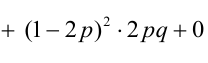
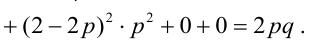
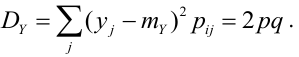
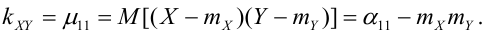
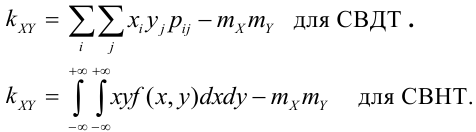
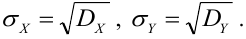
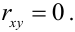
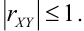
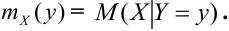
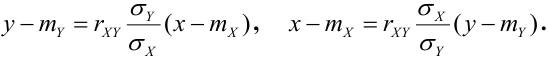
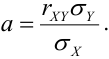
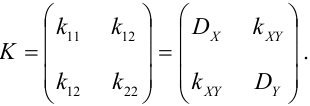
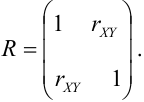
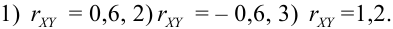
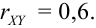
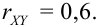
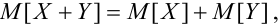
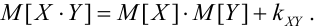
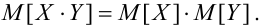
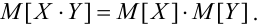
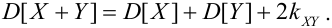
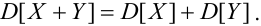
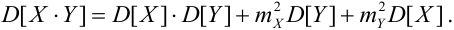
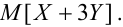
 будет снова случайной величиной.
будет снова случайной величиной.



























































