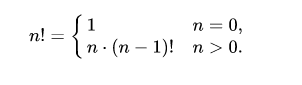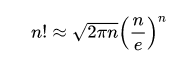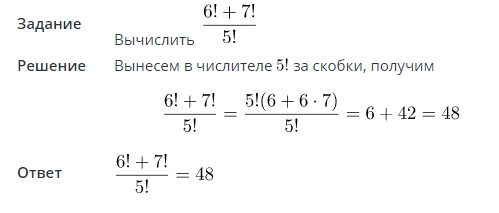Факториал дробного числа — факториал вычисляемый от аргумента — ….
Вычисляется по формуле:
где ![[x]](https://www.wikiznanie.ru/wikipedia/images/math/3/e/5/3e5314e9fd31509fdeb83faa0f729ba2.png)



Например, для 

Вычисляемое таким способом значение факториала дробного числа является приближенным. Для точных расчетов необходимо использовать гамма-функцию.
Факториалы нецелых (дробных) чисел появляются при статистическом описании нейросетевых преобразователей биометрия/код ключа доступа биномиальным законом распределения зависмимых биометрических данных.
См. также[править]
- факториал
- гамма-функция
I derived a form of the gamma function (see here) using some calculus and neat little tricks.
Anyways, define the factorial with two conditions:
-
$n!=n(n-1)!$
-
$1!=1$
From this, you can get the factorial for any integer value, but it does nothing to show you fractional values, at least not yet.
Define a function $f(x):=ln(x!)$ and manipulate as follows:
$$f(x)=ln(x!)=ln(x(x-1)!)=ln((x-1)!)+ln(x)=f(x-1)+ln(x)$$
$$f(x)=f(x-1)+ln(x)tag1$$
Differentiate both sides (since the equation holds true for all $x$)
$$f'(x)=f'(x-1)+frac1xtag2$$
If you put $x-1$ into $(2)$, we get $f'(x-1)=f'(x-2)+frac1{x-1}$, and repeat this process over and over…
$$f'(x)=f'(x-2)+frac1{x-1}+frac1x$$
$$f'(x)=f'(x-3)+frac1{x-2}+frac1{x-1}+frac1x\vdots\f'(x)=f'(0)+frac11+frac12+dots+frac1{x-1}+frac1xtag3$$
Note that $(3)$ only holds true for integer $x$, just like the factorial, but it is much easier to generalize.
Recall the geometric sum:
$$frac{1-r^n}{1-r}=1+r+r^2+dots+r^{n-1}$$
Integrate both sides with respect to $r$ from $0$ to $1$,
$$begin{align}
int_0^1frac{1-r^n}{1-r}dr & =int_0^11+r+r^2+dots+r^{n-1}dr\
& =left.frac11r+frac12r^2+frac13r^3+dots+frac1nr^nright|_0^1\
& =frac11+frac12+dots+frac1{x-1}+frac1xtag4\
end{align}$$
This is exactly what we need to extend $(3)$ to arbitrary $x$:
$$f'(x)=f'(0)+int_0^1frac{1-r^x}{1-r}drtag{3.1}$$
We then integrate this and apply the FTOC:
$$f(x)-require{cancel}cancelto0{f(0)}=int_0^xleft(f'(0)+int_0^1frac{1-r^phi}{1-r}drright)dphi$$
$$f(x)=f'(0)x+int_0^xint_0^1frac{1-r^phi}{1-r}dr dphi$$
Recall what $f(x)$ was:
$$ln(x!)=f'(0)x+int_0^xint_0^1frac{1-r^phi}{1-r}dr dphi$$
Use the second condition of the factorial and $x=1$
$$ln(1!)=f'(0)+int_0^1int_0^1frac{1-r^phi}{1-r}dr dphi$$
$$f'(0)=-int_0^1int_0^1frac{1-r^phi}{1-r}dr dphitag5$$
So then,
$$x!=expleft[-xint_0^1int_0^1frac{1-r^phi}{1-r}dr dphi+int_0^xint_0^1frac{1-r^phi}{1-r}dr dphiright]$$
which is equivalent to the gamma function.
Математическая формула представлена восклицательным знаком «!». Термин был введен в 1800 году, а обозначение появилось только в 1808. В формуле нужно умножить все целые числа от 1 до значения самого числа, стоящего под знаком факториала.
Это очень просто, вот пример:
7! = 1 * … * 7 = 5040.
Факторизация — разложение функции на множители.
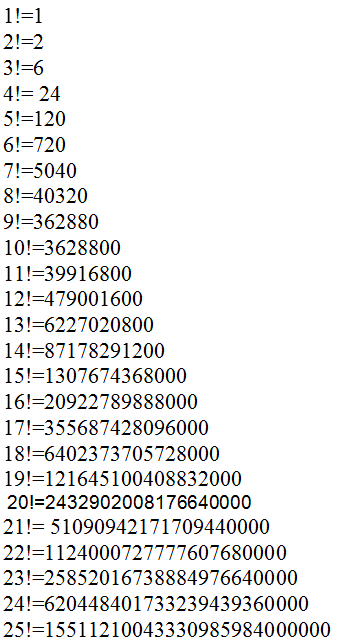
Таблица факториалов
Свойства факториалов
Рекуррентная формула
Комбинаторная интерпретация
Функция n может интерпретироваться как количество перестановок. К примеру, для 3-х элементов есть 3! = 6 перестановки.
Формула Стирлинга
Позволяет не перемножать большие числа. Обычно необходим только главный член:
Можно ли вычислить 0,5 или -3,217? Нет, нельзя. Но можно использовать нечто под названием «Гамма-функция», что намного сложнее.
Расчет по предыдущему значению
Функцию легко вычислить из предыдущего значения:
-
3! = 3 × 2! = 6;
-
41160 = 5! +8! + 6!
А как вычислить факториал нуля? Если вернуться к определению, то видно, что применять его в случае «0» нет смысла. Положительных чисел до 0 нет, поэтому 0 x 0 = 0.
Однако было решено, что в случае 0 результат будет равен 1.
Некоторые очень большие значения
Онлайн калькулятор поможет сделать вычисление – всего лишь надо найти знак, похожий на «x!» или «n!». Нужно обратить внимание, что браузеры могут испытывать затруднения при попытке отобразить более крупные числа и может произойти сбой.
Некоторые браузеры могут не позволять копировать, поэтому необходимо будет загрузить большие результаты в виде текстового файла.
Примеры вычисления факториалов больших чисел:
-
70! приблизительно 1 19785716669969869891796072783721 x 10100, что немного больше, чем «гуголь» (1 и 100 нулей);
-
100! это примерно 9 33262154444944152681699238856 x 101576 x 10157;
-
200! это примерно 7 88657867867364479050355236321393 x 103743.
Как найти функцию в Паскаль? Вычисление легко реализуется на разных языках программирования. Можно выбрать два метода: итеративный, то есть он создает цикл, в котором временная переменная умножается на каждое натуральное число от 1 до n, или рекурсивный, в котором функция вызывает себя до достижения базового варианта 0! = 1.
Программа на языке Паскаль:
На языке Си вычисления делаются с помощью рекурсивной функции. Следует заметить, что если начать вычислять факториал отрицательного числа в неаккуратно написанной функции, то это приведет к зацикливанию.
Факториал дроби (½) — это половина квадратного корня pi = (½)√π.
Примеры задач с решениями
Задание 1
Задание 2
Использование факториалов
Математика и многие ее области используют функцию. В комбинаторике функция была введена именно для расчета перестановки. Также понятие тесно связано с биномом ньютона (формула бинома Ньютона необходима для разложения степени (x + y) n в многочлен).
Часто нужно с использованием закона умножения вычислить произведения натуральных чисел по порядку, начиная с (1).
Например,
1⋅2⋅3⋅4⋅5⋅6⋅7
и т. д. Не всегда важно вычислить числовое произведение. Чтобы можно было короче записать выражения такого вида, в математике используется знак «(!)».
Произведение всех натуральных чисел от 1 до (n) включительно называется факториалом числа n и записывается
n!
(читается как «эн факториал»).
Принято, что (0! = 1).
Пример:
1 задание.
Вычисли значение выражения.
a)
5!+4!=5⋅4⋅3⋅2⋅1+4⋅3⋅2⋅1=120+24=144
.
b)
7!−5!4!=7⋅6⋅5⋅4!−5⋅4!4!=5⋅4!(42−1)4!=5⋅41=205
((4!) выносится за скобки. В дроби равные факториалы можно сокращать).
c)
80!79!+59!58!=80⋅79!79!+59⋅58!58!=80+59=139
.
Каждый больший факториал можно выразить меньшим факториалом, т. е.
(n! = n(n-1)! = n(n-1)(n-2)! = n(n-1)(n-2)(n-3)!) и т. д.
Пример:
2 задание.
Сократи дробь:
.
3 задание.
Упрости выражение:
.
При увеличении значения (n) значение (n!) стремительно возрастает. Знак факториала удобно использовать, если нужно записывать большие числа.
Пример:
сколькими различными способами можно составить список учеников, если в нём должно быть (25) различных учеников?
1⋅2⋅3⋅…⋅24⋅25=25!
Ответ: список можно составить (25!) различными способами.
- Факториал
- Таблица факториалов
- Примеры решения факториалов
- Калькулятор факториалов
Факториал
ЧТО ТАКОЕ ФАКТОРИАЛ
Для нахождения факториала нужно умножить все целые числа от выбранного нами числа до 1.
Факториал обозначается символом «!»
Пример факториалов:
4! = 4 · 3 · 2 · 1 = 24
5! = 5 · 4 · 3 · 2 · 1 = 120
Обычно говорят 4! как «факториал четырех».
ВЫЧИСЛЕНИЕ ФАКТОРИАЛА
Можно легко рассчитать факториал, зная значение факториала предыдущего числа:
Можно это записать в виде таблицы:
| n | n! | ||
| 1 | 1 | 1 | 1 |
| 2 | 2 x 1 | = 2 x 1! | = 2 |
| 3 | 3 x 2 x 1 | = 3 x 2! | = 6 |
| 4 | 4 x 3 x 2 x 1 | = 4 x 3! | = 24 |
| 5 | 5 x 4 x 3 x 2 x 1 | = 5 x 4! | = 120 |
| 6 | и так далее | и так далее |
Для точного определения факториала любого числа следует воспользоваться таблицей факториалов
- Чтобы вычислить 6!, нужно 5!=120 умножить на 6, получается 720
- Чтобы вычислить 8!, нужно 7!=5040 умножить на 8, получается 40.320
Пример:
9! равно 362.880. Попробуйте посчитать 10!
10! = 9!х10
10! = 362.880 х 10 = 3.628.800
ФОРМУЛА ФАКТОРИАЛА
Существует правило как найти n факториал:
n! = n × (n — 1)!
Которое означает:
«факториал любого числа — это число, умноженное на факториал предыдущего целого числа»
Итак, 12! = 12 × 11!, … и 100! = 100 × 99!, и т. д.
ФАКТОРИАЛ 0
Это очень интересная тема. Принято, что 0! = 1. А почему?
Никакое умножение чисел не приводит к 1, но давайте проследим факториалы в обратном порядке, скажем, от 4!:
И во многих задачах 0! = 1 просто имеет смысл.
ФАКТОРИАЛ ОТРИЦАТЕЛЬНОГО ЧИСЛА
Можем ли мы найти факториалы для чисел меньших нуля?
Нет. Факториалы для таких чисел не определены.
Почему? Легко объяснить на примере.
Пример
Начнем с 3! = 3 × 2 × 1 = 6 и спускаемся вниз:
2! = 3! / 3 = 6 / 3 = 2
1! = 2! / 2 = 2 / 2 = 1
0! = 1! / 1 = 1 / 1 = 1
(поэтому 0! = 1)
(−1)! = 0! / 0 = 1 / 0 = ой, деление на ноль не определено
И с этого момента все целочисленные факториалы не определены.
ФАКТОРИАЛ ДРОБНОГО ЧИСЛА
Можем ли мы найти факториалы для таких чисел, как 0,4 или −8,116?
Да мы можем! Но нам нужно углубиться в тему под названием Гамма-функция, которая выходит за рамки этой страницы.
И они могут быть отрицательными (кроме целых чисел).
Вот несколько значений дробных факториалов:
| (-1/2)! | √π |
| (1/2)! | (1/2)√π |
| (3/2)! | (3/4)√π |
| (5/2)! | (15/8)√π |
ПРИМЕНЕНИЕ ФАКТОРИАЛА
Факториалы незаменимы для вычисления количества перестановок, сочетаний и размещений.
Пример:
Сколько существует разных способов, с помощью которых 7 человек могут прийти первым, вторым и третьим ?
Список довольно длинный, если 7 человек обозначим как a, b, c, d, e, f и g, то список включает:
abc, abd, abe, abf, abg, acb, acd, ace, acf, … и т. д.
Формула для расчета: 7!/(7−3)! = 7!/4!
Выпишем умножение полностью:
(7 × 6 × 5 × 4 × 3 × 2 × 1)/(4 × 3 × 2 × 1) = 7 × 6 × 5
Пояснение: 4 × 3 × 2 × 1 сокращено, т.к. они встречаются в числителе и знаменателе, и осталось только 7 × 6 × 5 . получаем:
7 × 6 × 5 = 210
Итак, есть 210 различных способов, которыми 7 человек могут прийти первым, вторым и третьим.
Решено!
Пример:
Что такое 100! / 98!
Используя наши знания из предыдущего примера, мы можем сразу перейти к следующему:
100!/98! = 100 × 99 = 9900
Другие примеры задач с факториалом и их решение на странице решение факториалов.
ИНТЕРЕСНЫЕ ФАКТЫ
70! приблизительно 1,197857 … x 10100 , что чуть больше, чем в Googol (цифра 1, за которой следует сотня нулей).
100 факториал: 100! приблизительно 9,3326215443944152681699238856 x 10157
200 факториал: 200! приблизительно 7,8865786736479050355236321393 x 10374
Полезные материалы по теме
- Таблица факториалов
- Примеры решения факториалов
- Калькулятор факториалов

![log(x!)=log([x]!)+{x}cdot log([x]+1).](https://www.wikiznanie.ru/wikipedia/images/math/e/e/d/eed25a9b9d103197653897638f6fc539.png)