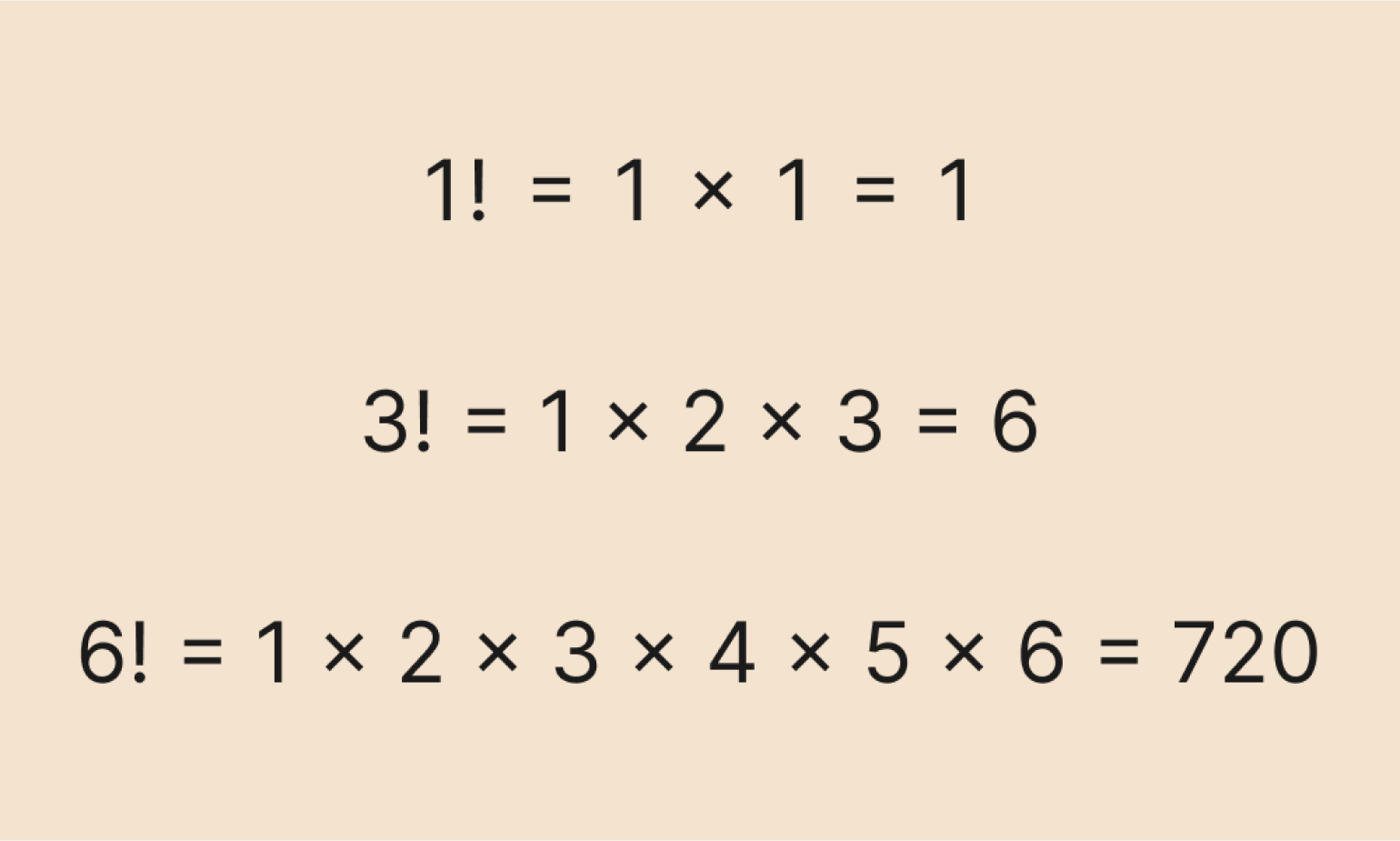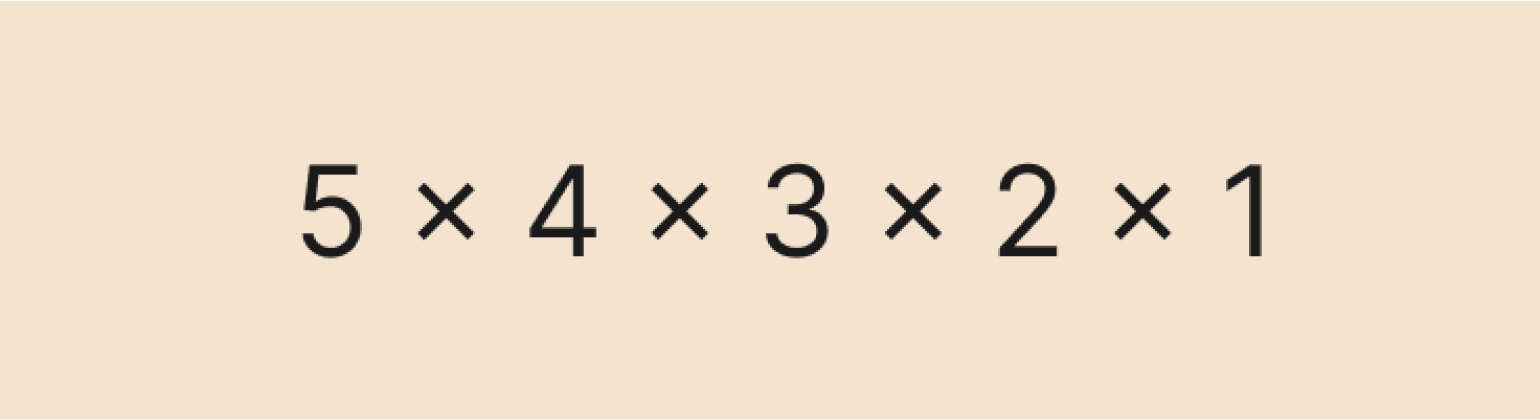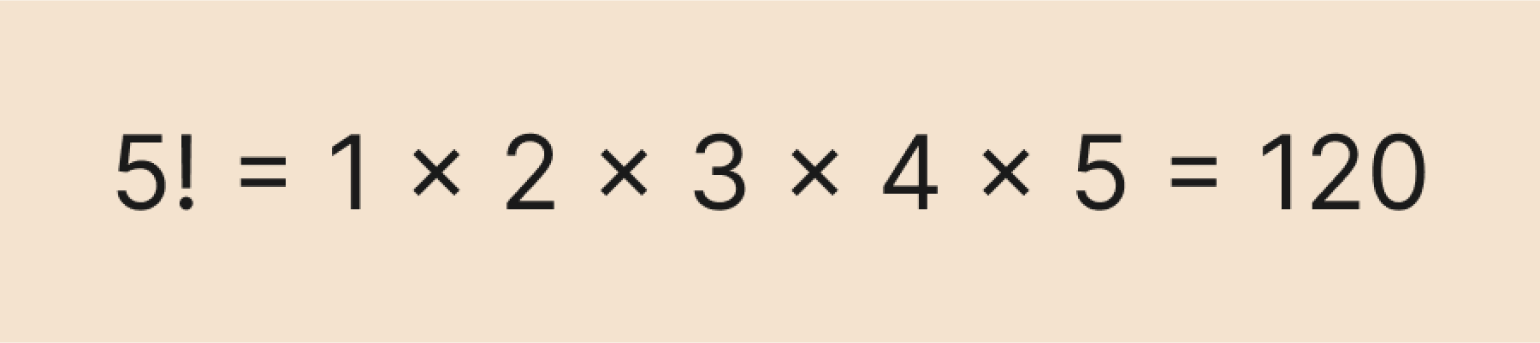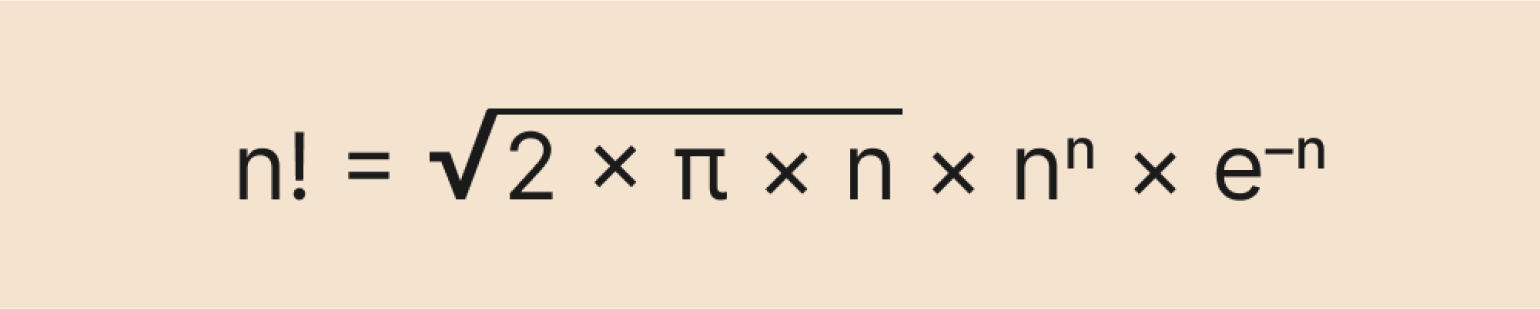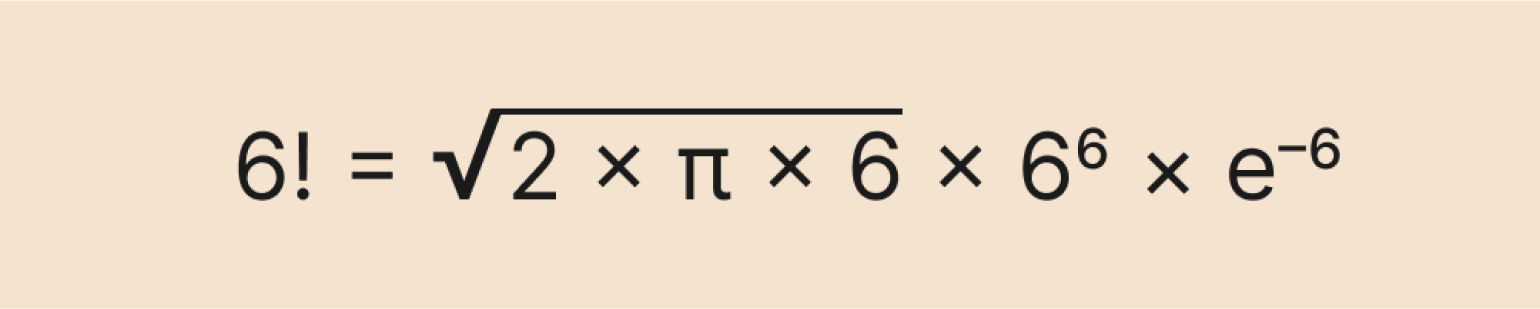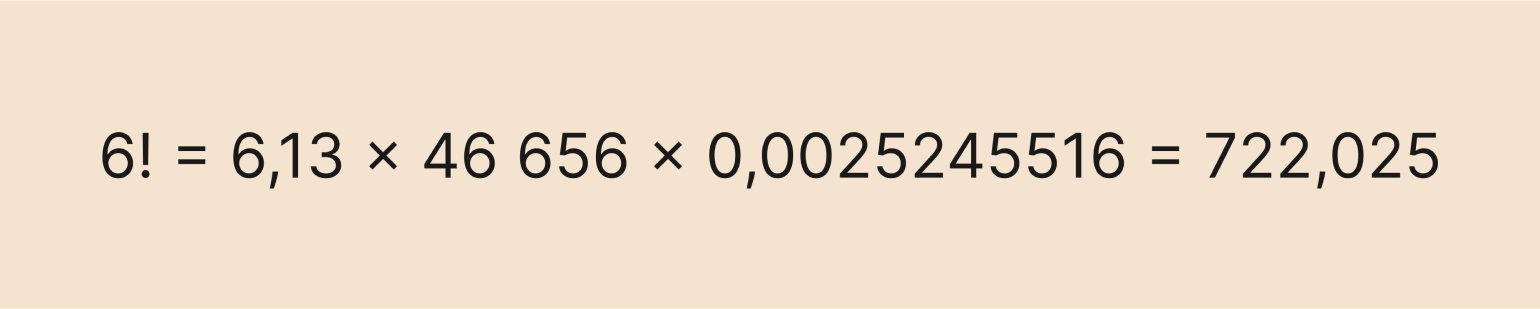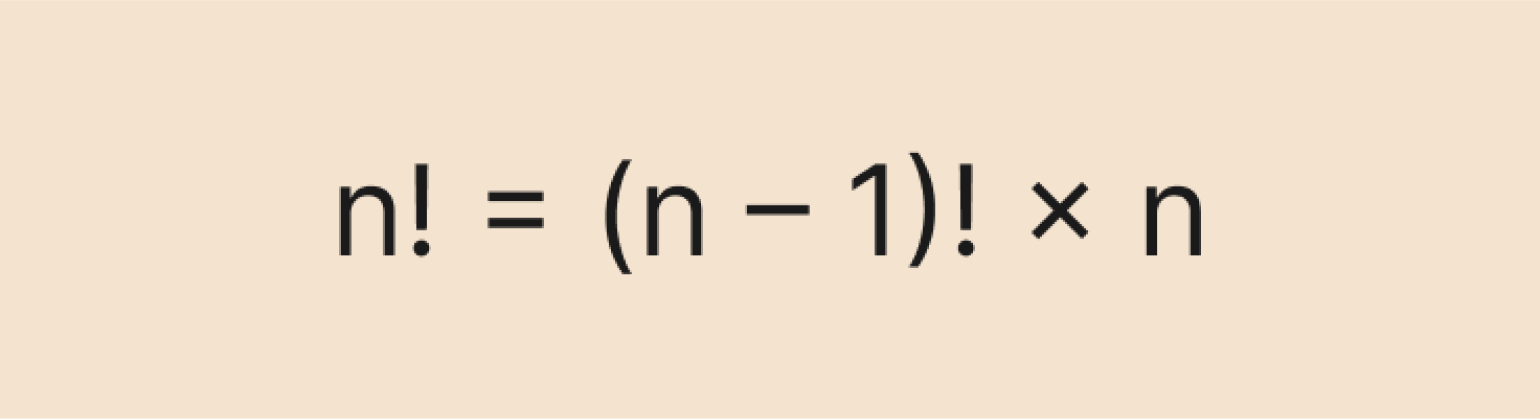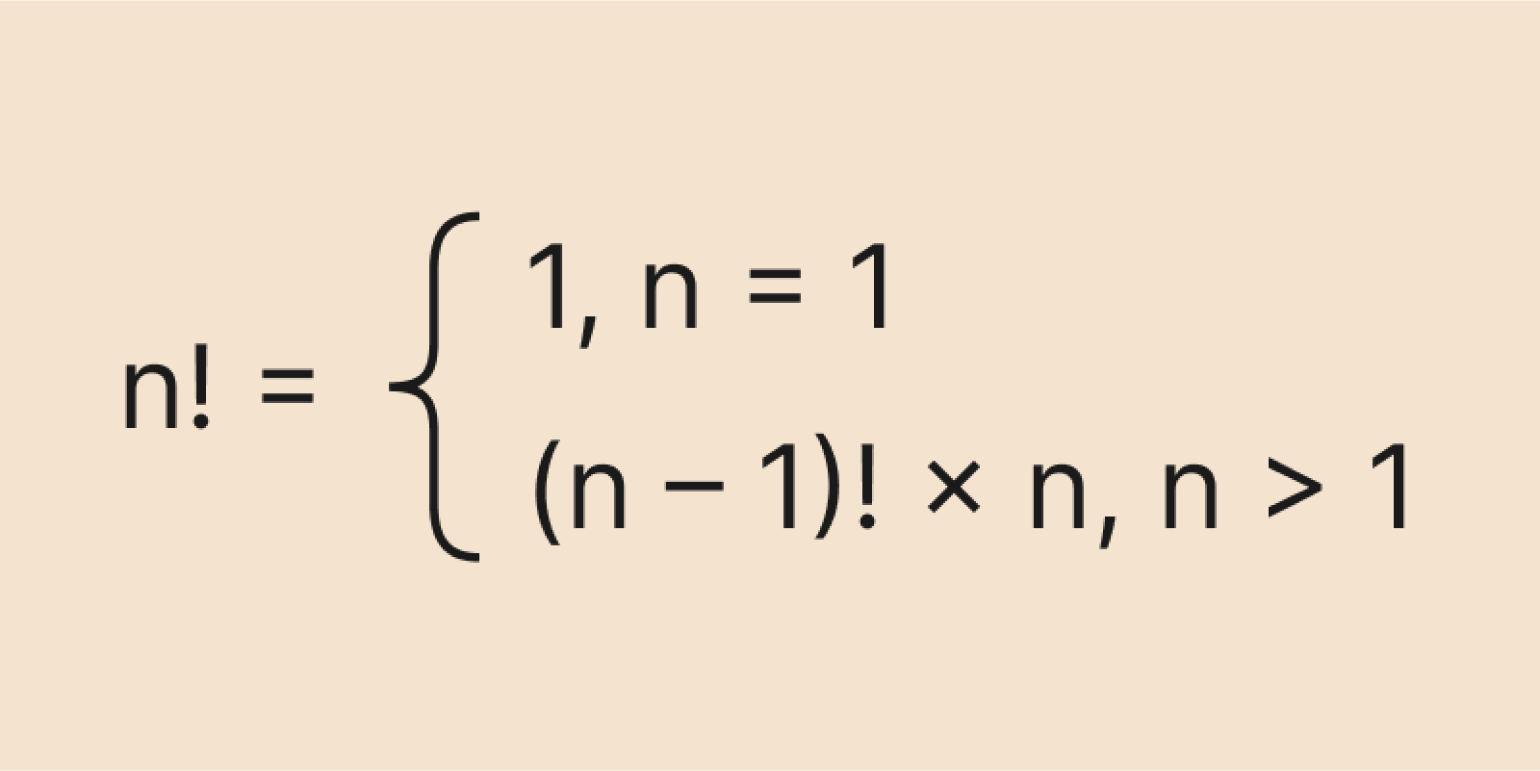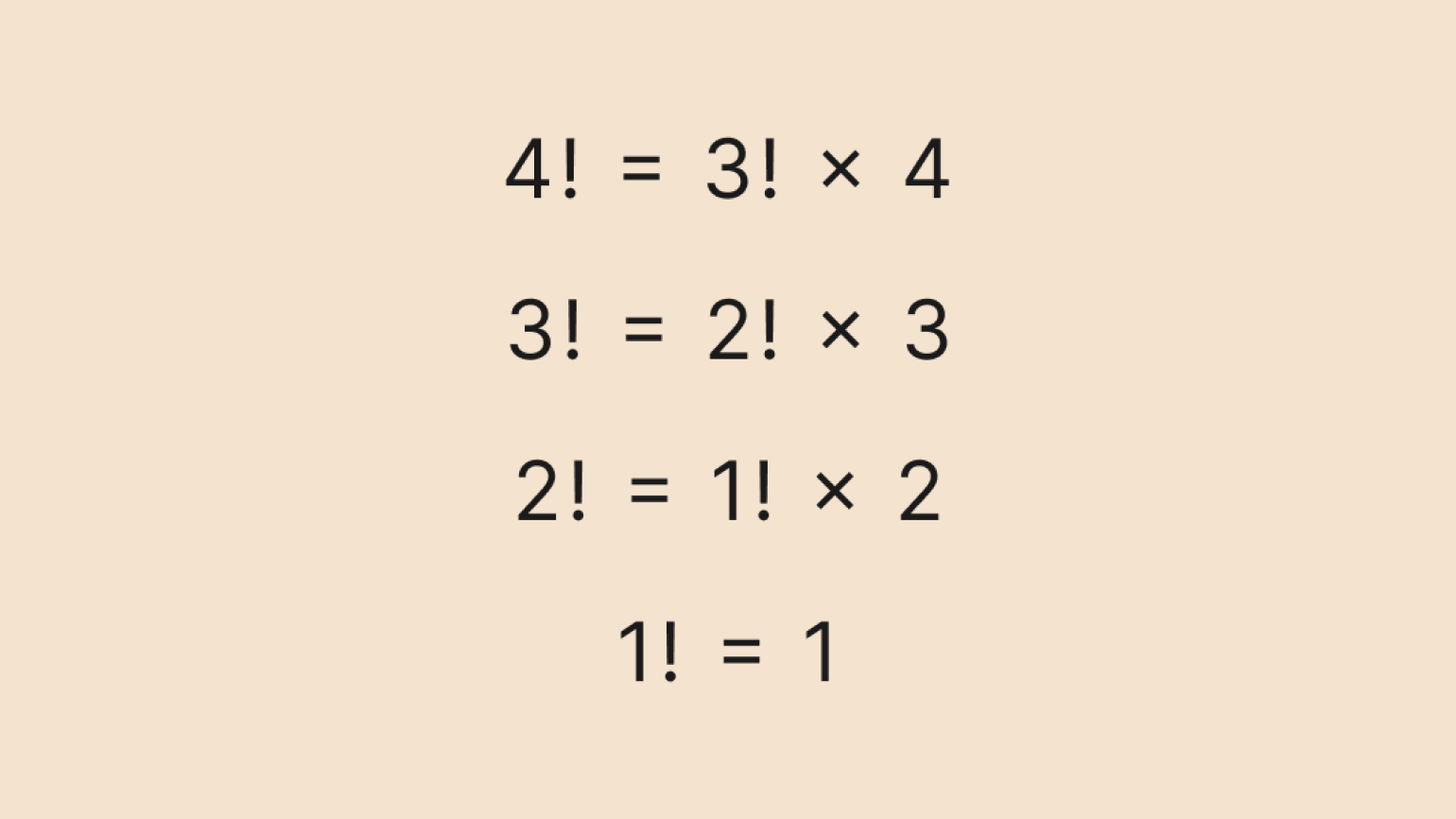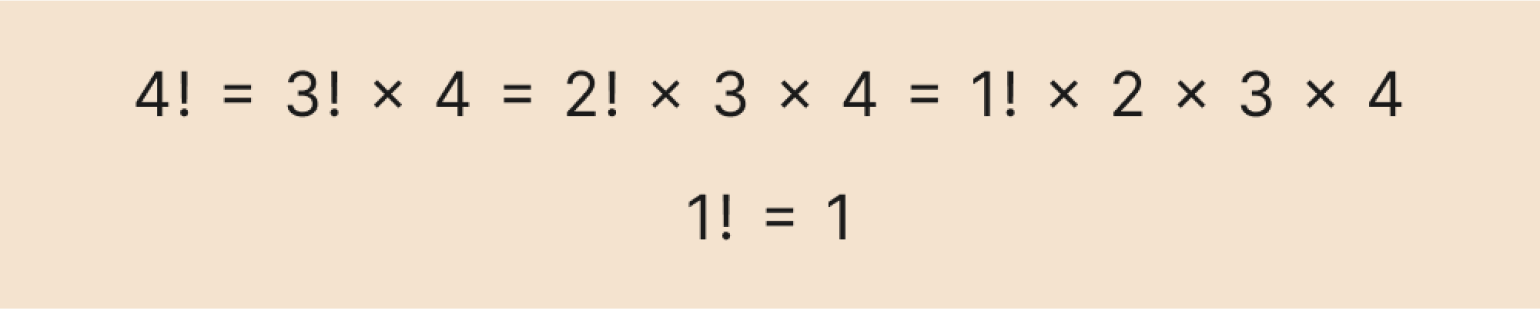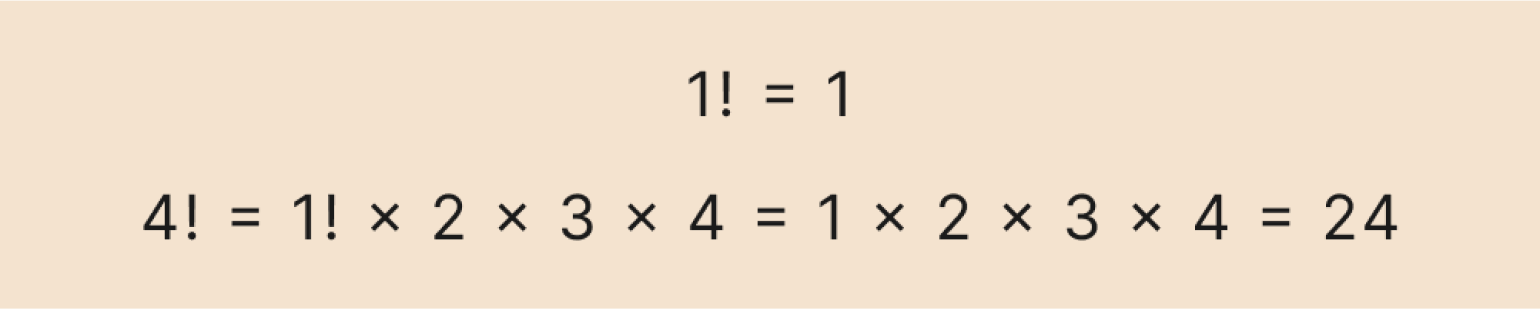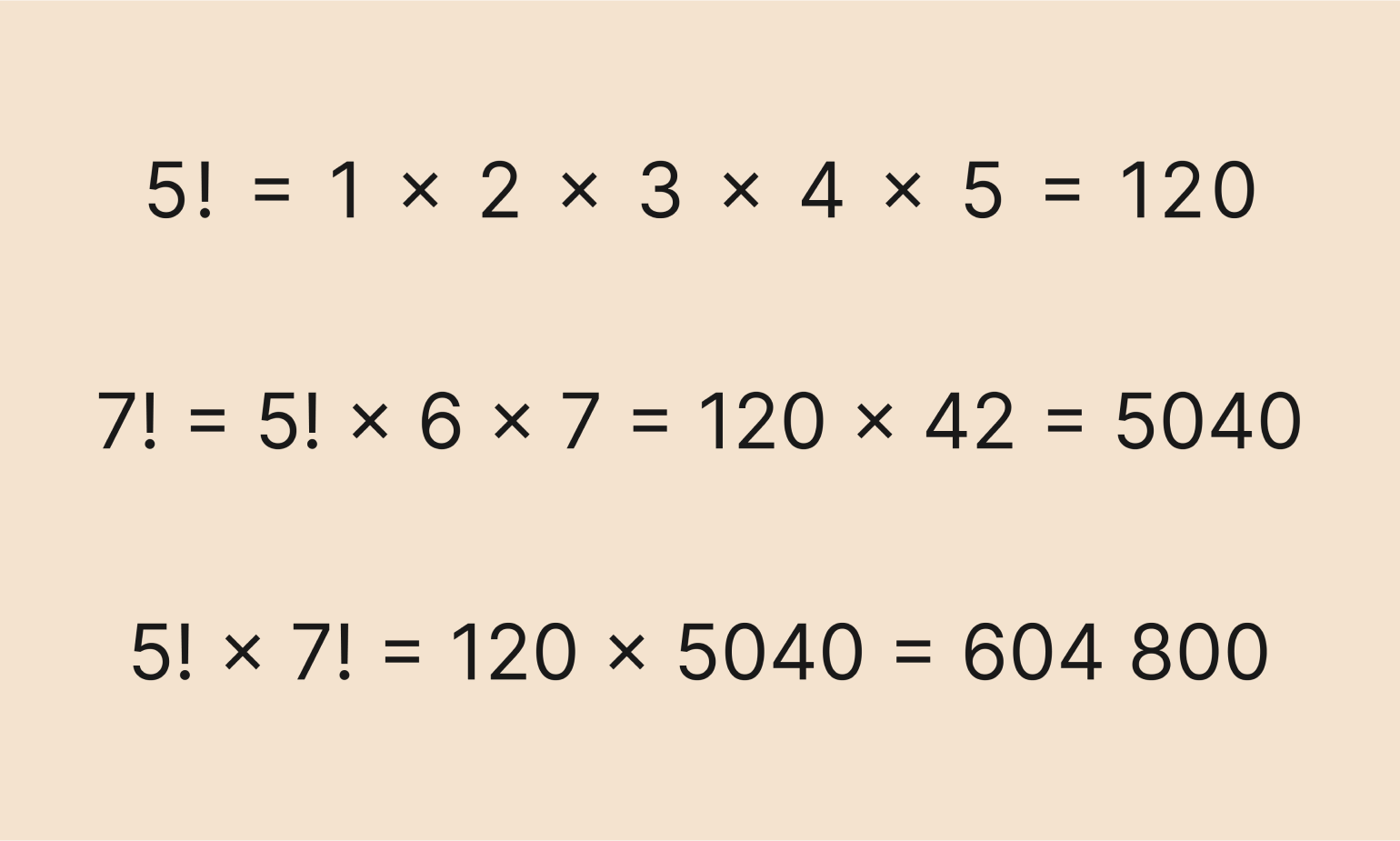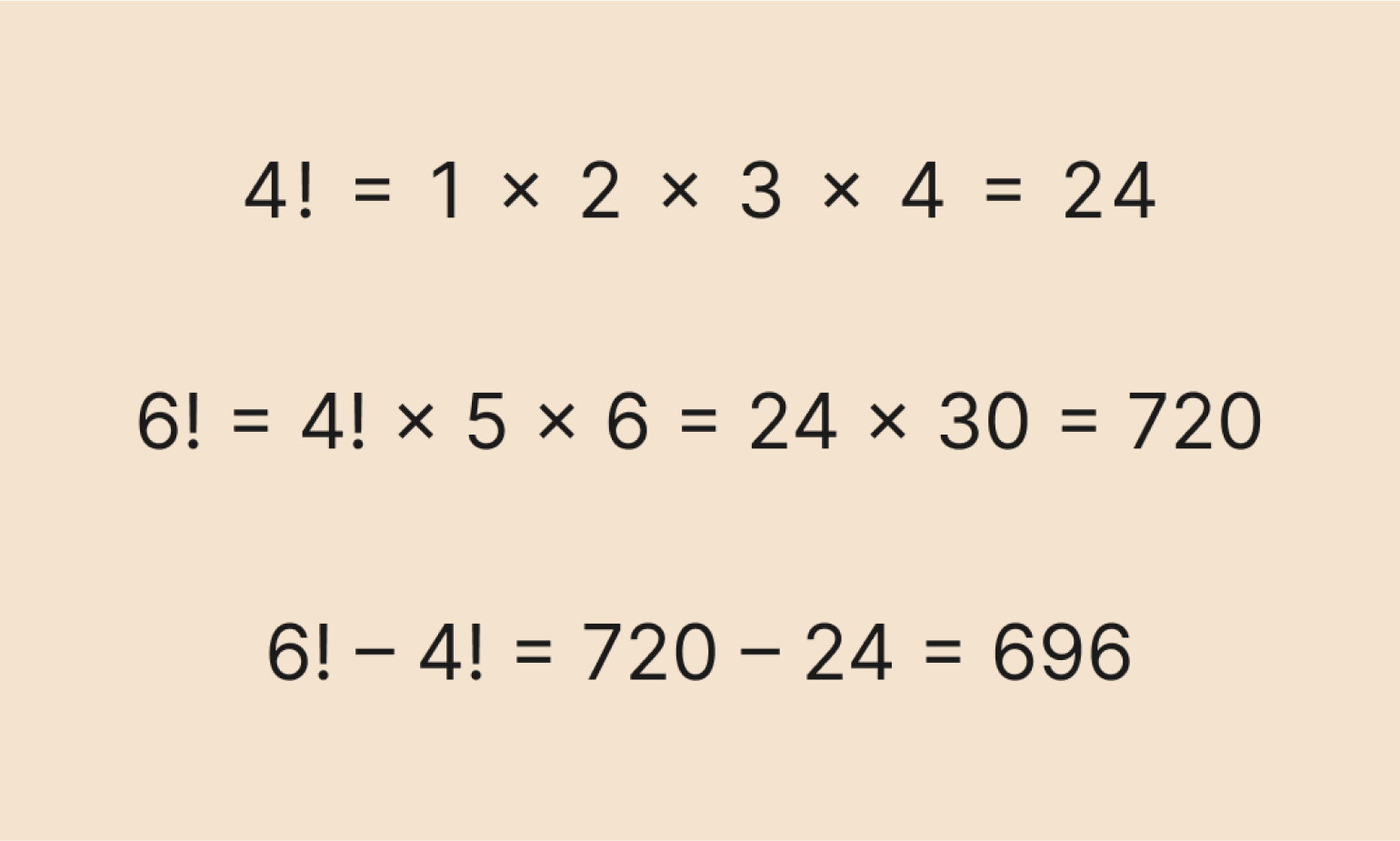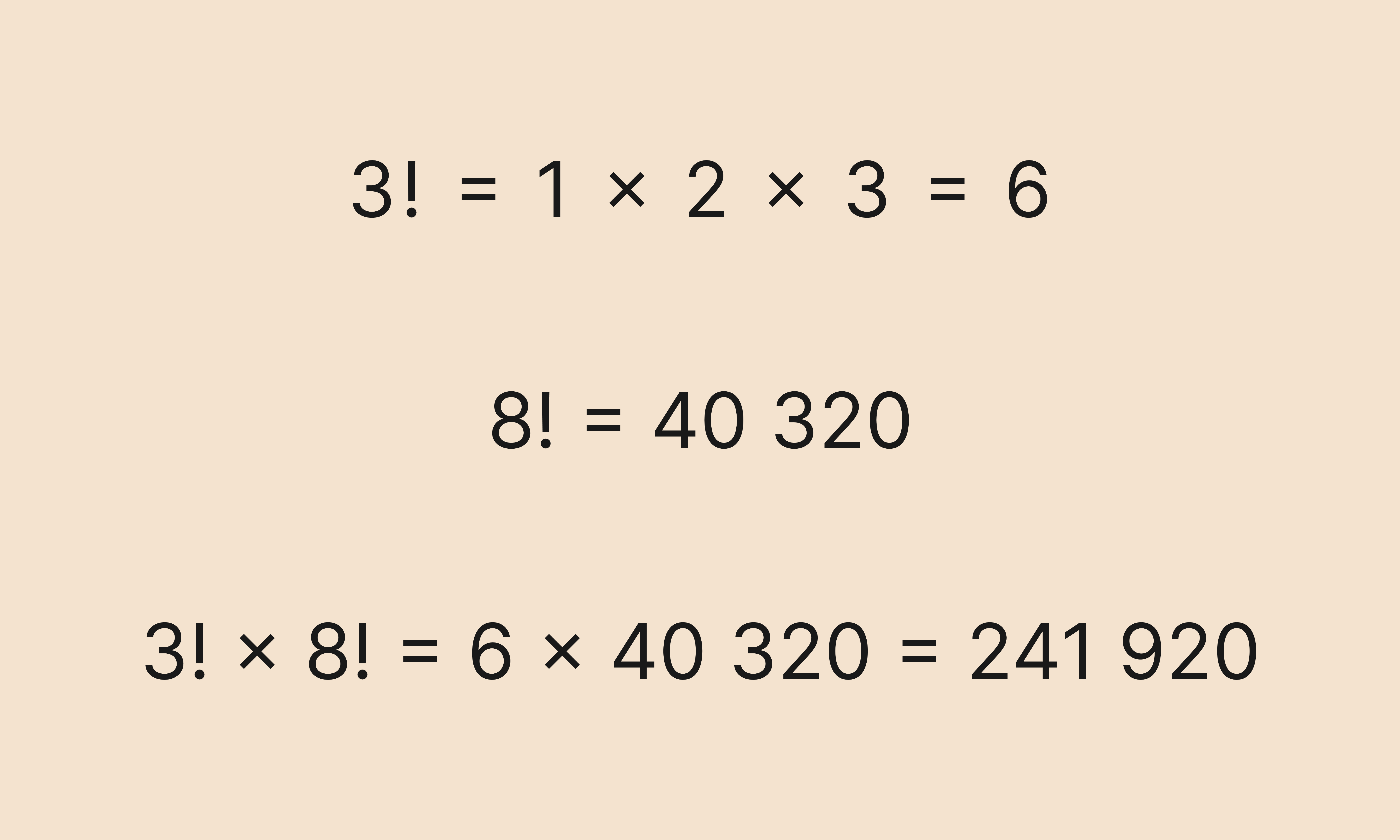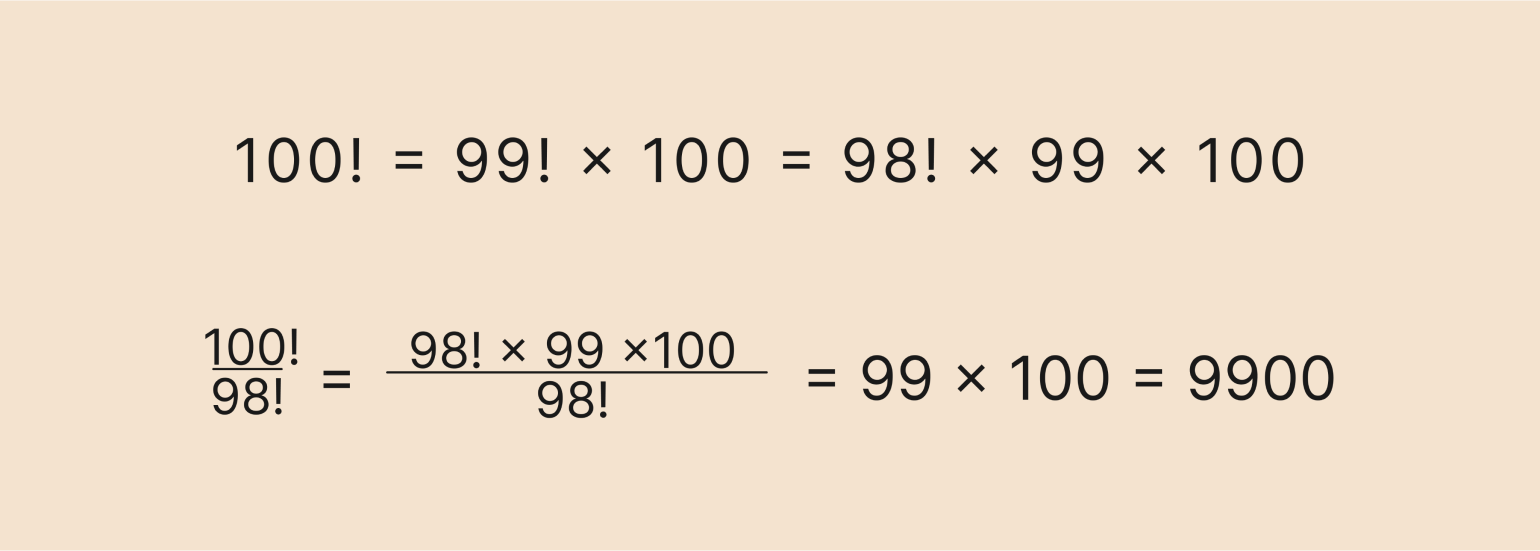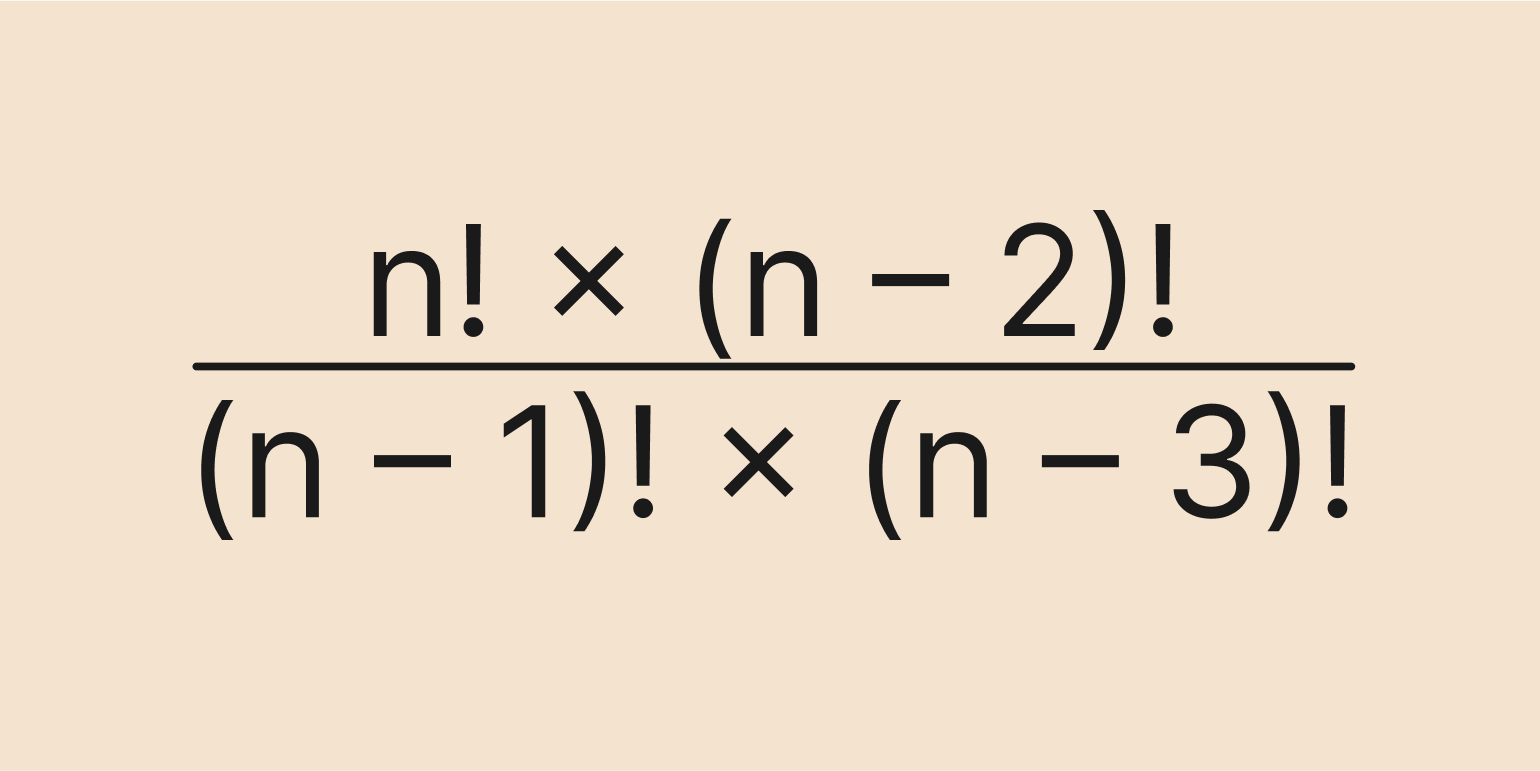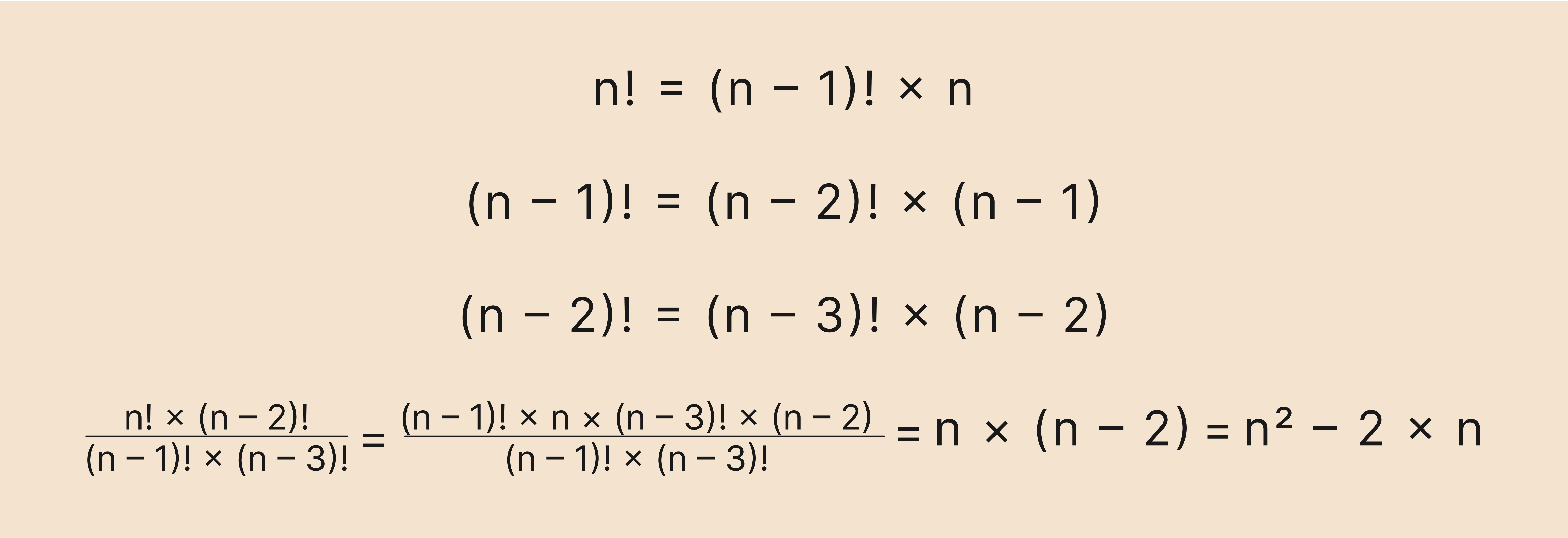- Факториал
- Таблица факториалов
- Примеры решения факториалов
- Калькулятор факториалов
Факториал
ЧТО ТАКОЕ ФАКТОРИАЛ
Для нахождения факториала нужно умножить все целые числа от выбранного нами числа до 1.
Факториал обозначается символом «!»
Пример факториалов:
4! = 4 · 3 · 2 · 1 = 24
5! = 5 · 4 · 3 · 2 · 1 = 120
Обычно говорят 4! как «факториал четырех».
ВЫЧИСЛЕНИЕ ФАКТОРИАЛА
Можно легко рассчитать факториал, зная значение факториала предыдущего числа:
Можно это записать в виде таблицы:
| n | n! | ||
| 1 | 1 | 1 | 1 |
| 2 | 2 x 1 | = 2 x 1! | = 2 |
| 3 | 3 x 2 x 1 | = 3 x 2! | = 6 |
| 4 | 4 x 3 x 2 x 1 | = 4 x 3! | = 24 |
| 5 | 5 x 4 x 3 x 2 x 1 | = 5 x 4! | = 120 |
| 6 | и так далее | и так далее |
Для точного определения факториала любого числа следует воспользоваться таблицей факториалов
- Чтобы вычислить 6!, нужно 5!=120 умножить на 6, получается 720
- Чтобы вычислить 8!, нужно 7!=5040 умножить на 8, получается 40.320
Пример:
9! равно 362.880. Попробуйте посчитать 10!
10! = 9!х10
10! = 362.880 х 10 = 3.628.800
ФОРМУЛА ФАКТОРИАЛА
Существует правило как найти n факториал:
n! = n × (n — 1)!
Которое означает:
«факториал любого числа — это число, умноженное на факториал предыдущего целого числа»
Итак, 12! = 12 × 11!, … и 100! = 100 × 99!, и т. д.
ФАКТОРИАЛ 0
Это очень интересная тема. Принято, что 0! = 1. А почему?
Никакое умножение чисел не приводит к 1, но давайте проследим факториалы в обратном порядке, скажем, от 4!:
И во многих задачах 0! = 1 просто имеет смысл.
ФАКТОРИАЛ ОТРИЦАТЕЛЬНОГО ЧИСЛА
Можем ли мы найти факториалы для чисел меньших нуля?
Нет. Факториалы для таких чисел не определены.
Почему? Легко объяснить на примере.
Пример
Начнем с 3! = 3 × 2 × 1 = 6 и спускаемся вниз:
2! = 3! / 3 = 6 / 3 = 2
1! = 2! / 2 = 2 / 2 = 1
0! = 1! / 1 = 1 / 1 = 1
(поэтому 0! = 1)
(−1)! = 0! / 0 = 1 / 0 = ой, деление на ноль не определено
И с этого момента все целочисленные факториалы не определены.
ФАКТОРИАЛ ДРОБНОГО ЧИСЛА
Можем ли мы найти факториалы для таких чисел, как 0,4 или −8,116?
Да мы можем! Но нам нужно углубиться в тему под названием Гамма-функция, которая выходит за рамки этой страницы.
И они могут быть отрицательными (кроме целых чисел).
Вот несколько значений дробных факториалов:
| (-1/2)! | √π |
| (1/2)! | (1/2)√π |
| (3/2)! | (3/4)√π |
| (5/2)! | (15/8)√π |
ПРИМЕНЕНИЕ ФАКТОРИАЛА
Факториалы незаменимы для вычисления количества перестановок, сочетаний и размещений.
Пример:
Сколько существует разных способов, с помощью которых 7 человек могут прийти первым, вторым и третьим ?
Список довольно длинный, если 7 человек обозначим как a, b, c, d, e, f и g, то список включает:
abc, abd, abe, abf, abg, acb, acd, ace, acf, … и т. д.
Формула для расчета: 7!/(7−3)! = 7!/4!
Выпишем умножение полностью:
(7 × 6 × 5 × 4 × 3 × 2 × 1)/(4 × 3 × 2 × 1) = 7 × 6 × 5
Пояснение: 4 × 3 × 2 × 1 сокращено, т.к. они встречаются в числителе и знаменателе, и осталось только 7 × 6 × 5 . получаем:
7 × 6 × 5 = 210
Итак, есть 210 различных способов, которыми 7 человек могут прийти первым, вторым и третьим.
Решено!
Пример:
Что такое 100! / 98!
Используя наши знания из предыдущего примера, мы можем сразу перейти к следующему:
100!/98! = 100 × 99 = 9900
Другие примеры задач с факториалом и их решение на странице решение факториалов.
ИНТЕРЕСНЫЕ ФАКТЫ
70! приблизительно 1,197857 … x 10100 , что чуть больше, чем в Googol (цифра 1, за которой следует сотня нулей).
100 факториал: 100! приблизительно 9,3326215443944152681699238856 x 10157
200 факториал: 200! приблизительно 7,8865786736479050355236321393 x 10374
Полезные материалы по теме
- Таблица факториалов
- Примеры решения факториалов
- Калькулятор факториалов
I derived a form of the gamma function (see here) using some calculus and neat little tricks.
Anyways, define the factorial with two conditions:
-
$n!=n(n-1)!$
-
$1!=1$
From this, you can get the factorial for any integer value, but it does nothing to show you fractional values, at least not yet.
Define a function $f(x):=ln(x!)$ and manipulate as follows:
$$f(x)=ln(x!)=ln(x(x-1)!)=ln((x-1)!)+ln(x)=f(x-1)+ln(x)$$
$$f(x)=f(x-1)+ln(x)tag1$$
Differentiate both sides (since the equation holds true for all $x$)
$$f'(x)=f'(x-1)+frac1xtag2$$
If you put $x-1$ into $(2)$, we get $f'(x-1)=f'(x-2)+frac1{x-1}$, and repeat this process over and over…
$$f'(x)=f'(x-2)+frac1{x-1}+frac1x$$
$$f'(x)=f'(x-3)+frac1{x-2}+frac1{x-1}+frac1x\vdots\f'(x)=f'(0)+frac11+frac12+dots+frac1{x-1}+frac1xtag3$$
Note that $(3)$ only holds true for integer $x$, just like the factorial, but it is much easier to generalize.
Recall the geometric sum:
$$frac{1-r^n}{1-r}=1+r+r^2+dots+r^{n-1}$$
Integrate both sides with respect to $r$ from $0$ to $1$,
$$begin{align}
int_0^1frac{1-r^n}{1-r}dr & =int_0^11+r+r^2+dots+r^{n-1}dr\
& =left.frac11r+frac12r^2+frac13r^3+dots+frac1nr^nright|_0^1\
& =frac11+frac12+dots+frac1{x-1}+frac1xtag4\
end{align}$$
This is exactly what we need to extend $(3)$ to arbitrary $x$:
$$f'(x)=f'(0)+int_0^1frac{1-r^x}{1-r}drtag{3.1}$$
We then integrate this and apply the FTOC:
$$f(x)-require{cancel}cancelto0{f(0)}=int_0^xleft(f'(0)+int_0^1frac{1-r^phi}{1-r}drright)dphi$$
$$f(x)=f'(0)x+int_0^xint_0^1frac{1-r^phi}{1-r}dr dphi$$
Recall what $f(x)$ was:
$$ln(x!)=f'(0)x+int_0^xint_0^1frac{1-r^phi}{1-r}dr dphi$$
Use the second condition of the factorial and $x=1$
$$ln(1!)=f'(0)+int_0^1int_0^1frac{1-r^phi}{1-r}dr dphi$$
$$f'(0)=-int_0^1int_0^1frac{1-r^phi}{1-r}dr dphitag5$$
So then,
$$x!=expleft[-xint_0^1int_0^1frac{1-r^phi}{1-r}dr dphi+int_0^xint_0^1frac{1-r^phi}{1-r}dr dphiright]$$
which is equivalent to the gamma function.
Факториал дробного числа — факториал вычисляемый от аргумента — ….
Вычисляется по формуле:
где ![[x]](https://www.wikiznanie.ru/wikipedia/images/math/3/e/5/3e5314e9fd31509fdeb83faa0f729ba2.png)



Например, для 

Вычисляемое таким способом значение факториала дробного числа является приближенным. Для точных расчетов необходимо использовать гамма-функцию.
Факториалы нецелых (дробных) чисел появляются при статистическом описании нейросетевых преобразователей биометрия/код ключа доступа биномиальным законом распределения зависмимых биометрических данных.
См. также[править]
- факториал
- гамма-функция
#статьи
- 19 май 2023
-
0
Что такое факториал и как его вычислить
Статья, после которой вы начнёте щёлкать факториалы как орешки.
Иллюстрация: Катя Павловская для Skillbox Media
Любитель научной фантастики и технологического прогресса. Хорошо сочетает в себе заумного технаря и утончённого гуманитария. Пишет про IT и радуется этому.
Даже если вы уже давно окончили школу, факториалы всё равно могут доставить немало приятных флешбэков — например, если вы обучаетесь программированию и знакомитесь с задачками на рекурсию или комбинаторику. Поэтому мы решили максимально просто объяснить, что такое факториал, как его вычислять и зачем он вообще нужен.
Эта статья будет полезна как опытным программистам, которые хотят освежить знания, так и тем, кто ещё учится: школьникам, студентам и совсем зелёным джунам.
Содержание:
- Что такое факториал
- Для чего он нужен
- Основные свойства и формулы
- Шпаргалка: таблица факториалов
- Решаем задачи на факториалы
- Что запомнить
Факториал числа n — это произведение всех натуральных чисел от единицы до n. Обозначается факториал символом восклицательного знака: !.
Это определение из учебника, и оно пока звучит сложновато — неясно, зачем эти факториалы вообще нужны и как они могут пригодиться в науке и технике. Но об этом чуть позже — для начала давайте посмотрим на примеры факториалов:
Чтобы вычислить их, нам нужно перемножить все числа от единицы до числа, стоящего под знаком факториала — так гласит определение. Получаем выражения:
Ещё в математическом определении сказано, что факториал не может быть отрицательным или дробным — то есть вот такие факториалы вычислить нельзя:
Факториалы незаменимы там, где нужно быстро посчитать количество комбинаций и сочетаний разных предметов. В математике этому посвящён даже целый раздел — комбинаторика. Её методы используют много где: от лингвистики до криптографии и анализа ДНК. И во всех этих сферах факториал помогает упрощать сложные вычисления.
Разберём на примере, как это работает.
Допустим, у вас есть пять шоколадок и вы решили раздать их пяти друзьям — каждому по одной. Задача — выяснить, сколько существует способов раздать эти шоколадки. Начинаем размышлять:
- первую шоколадку можно отдать одному из пяти друзей;
- вторую — одному из четырёх друзей, потому что один уже получил свою шоколадку;
- третью — одному из трёх, потому что двое уже наслаждаются своими шоколадками;
- четвёртую — одному из двух;
- пятую — последнему другу.
Получается, что способов раздать первую шоколадку — 5, вторую — 4, третью — 3, четвёртую — 2, а пятую — всего 1. По правилам математики, чтобы выяснить общее количество всех вариантов, нужно перемножить их между собой. Ну а кто мы такие, чтобы с этими правилами спорить?
Смотрим на выражение выше и понимаем: ведь оно идеально вписывается в определение факториала — произведение натуральных чисел от одного до n (в нашем случае n равно 5). Следовательно, это выражение можно коротко и изящно записать в виде факториала:
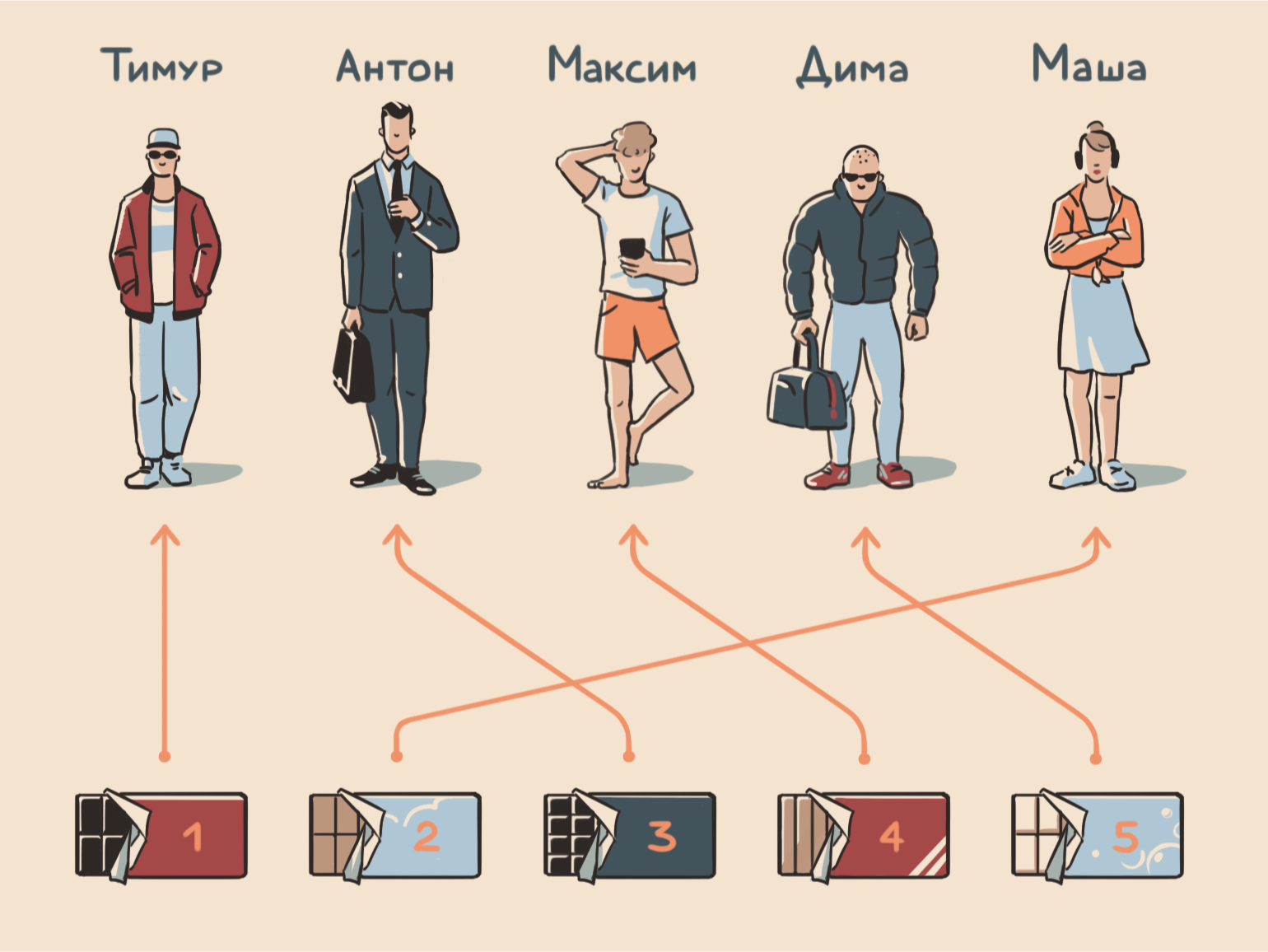
Выходит, что всего способов раздать пять шоколадок пяти друзьям существует 120. Вот как может выглядеть один из них:
Конечно, в жизни вам вряд ли придётся считать количество способов раздать друзьям шоколадки. Но, например, в статистике, теории вероятностей, матанализе и программировании факториалы используют сплошь и рядом. Так что, если видите себя в будущем на матмехе или, на худой конец, в IT, то лучше познакомиться с ними хотя бы бегло.
Так как факториалы используются в разных областях математики, свойств у них довольно много — каждая область привносит какие-то свои методы вычислений. Одно из свойств вы уже знаете: факториал — это всегда целое положительное число. Вот ещё несколько, которые стоит запомнить:
- Факториал нуля равен единице — 0! = 1.
- Факториал единицы тоже равен единице: 1! = 1.
- Рекурсия: n! = (n – 1)! × n. Это основное свойство факториалов, о нём мы чуть подробнее поговорим дальше.
Мы видим, что каждое свойство описывается какой-то формулой — и некоторые из этих формул могут быть весьма полезны. Они позволяют нам находить факториалы проще и быстрее, чем простым перемножением натуральных чисел. Разберём эти формулы тоже.
Чтобы вычислить факториал, не используя так много операций умножения, придумали формулу Стирлинга. Вот как она выглядит:
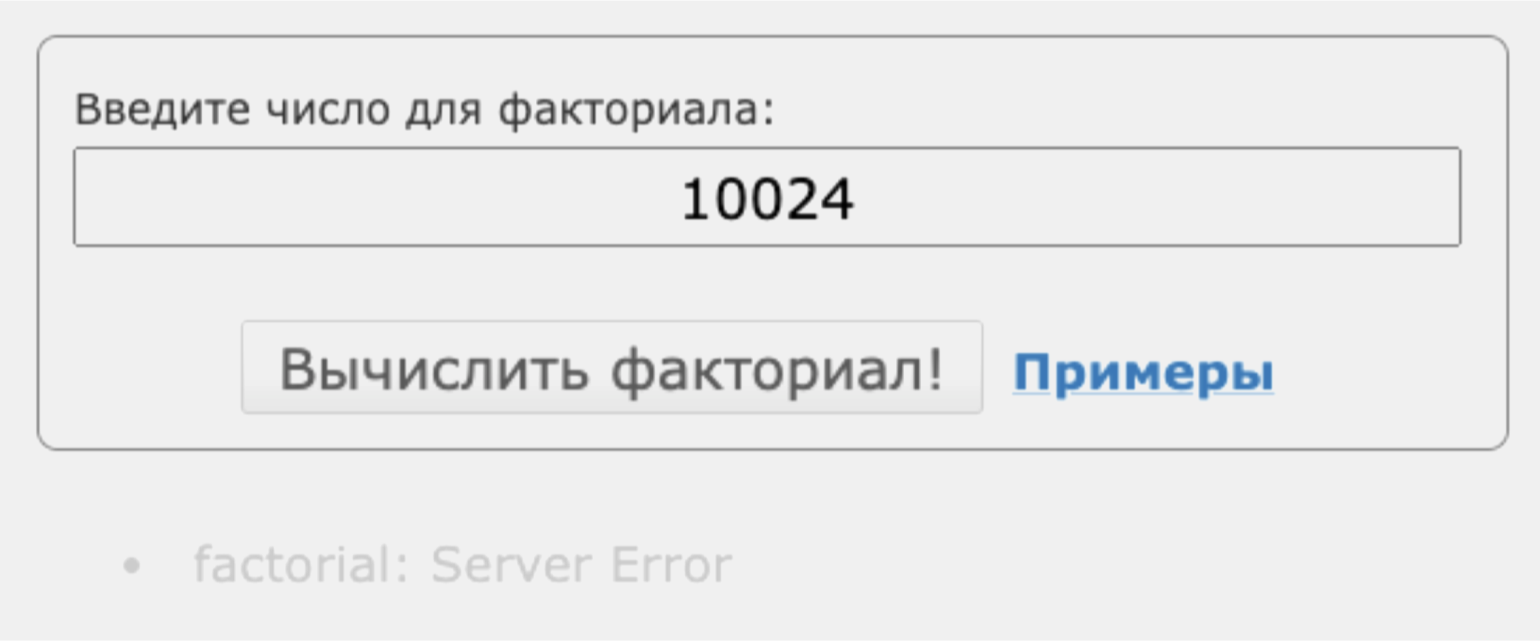
Выглядит страшно, но на самом деле она очень полезная. Её используют, когда хотят приблизительно узнать факториал большого числа. Обычным способом это будет сделать сложно даже мощному компьютеру — например, попробуйте посчитать в онлайн-калькуляторе факториал числа 10 024 (спойлер: это может занять несколько часов и даже дней).
Скришнот: «Контрольная работа РУ — калькуляторы онлайн» / Skillbox Media
Давайте попробуем вычислить факториал числа 6 по этой формуле:
Число e примерно равно 2,71, а π — 3,14. Подставляем их в выражение и получаем ответ:
Получили приближённое значение настоящего факториала, который равен 720. Но можно сделать ответ и более точным. Для этого нужно добавить больше знаков после запятой всем переменным — например, если взять 20 знаков, то ответ будет таким:
Это уже больше похоже на правду. Хотя погрешность всё равно есть.
Рекуррентная формула позволяет вычислить факториал числа n, основываясь на факториале предыдущего числа — (n – 1). Выглядит она так:
В целом рекуррентная формула не приносит нам большой пользы, так как всё равно приходится вычислять факториал предыдущего числа. Если он равен какому-то большому числу (например, 100), то использование формулы теряет смысл — слишком уж много вычислений это потребует.
Рекуррентная формула основана на главном свойстве факториалов — рекурсии: n! = (n – 1)! × n. Это свойство особенно полезно при решении задач по комбинаторике: так мы можем быстро сокращать факториалы и упрощать выражения.
Однако рекуррентная формула хорошо подходит для алгоритмов — в частности, для программирования. Мы можем задать начальное значение: например, что 0! = 1 или 1! = 1, а затем считать следующие факториалы по формуле:
Получим алгоритм для вычисления факториалов. Не очень эффективный, но простой.
Давайте вычислим по этой формуле факториал числа 4. Сначала распишем рекуррентную формулу до базового значения — факториала числа 1:
Можно записать это и в сокращённом виде:
Теперь последовательно подставляем значение факториала, которое мы уже знаем, и вычисляем результат:
Получили ответ — 24. Ничего сложного, просто перемножаем числа.
Кстати, всю эту формулу можно обернуть в реально работающую функцию на языке Python:
def factorial(n): # Определяем функцию if n == 0 or n == 1: # Базовый случай return 1 else: # Рекуррентный случай return factorial(n-1) * n # Вызываем эту же функцию, но с меньшим аргументом print(factorial(4)) # Печатаем факториал 4 # Вывод: # 24
Можете попробовать запустить её в онлайн-интерпретаторе и посмотреть, как работает. Тут есть один нюанс: Python не даст вам посчитать факториал числа больше 998, так как у него есть ограничение на количество вызовов функции — в программировании это называется глубиной рекурсии.
Чтобы быстро находить, чему равен факториал, можно запомнить или сохранить в заметки вот такую табличку. Она рассчитана всего на 12 чисел, но для большинства учебных задач этого хватит.
| 1! | 1 |
| 2! | 2 |
| 3! | 6 |
| 4! | 24 |
| 5! | 120 |
| 6! | 720 |
| 7! | 5040 |
| 8! | 40 320 |
| 9! | 362 880 |
| 10! | 3 628 800 |
| 11! | 39 916 800 |
| 12! | 479 001 600 |
С теорией вроде разобрались — теперь попробуем решить несколько задач с факториалами, чтобы закрепить знания на практике.
Задача: перемножить два факториала.
Решение:
Сперва нужно вычислить значения факториалов, а затем перемножить полученные значения:
Обратите внимание: во второй строке мы применили рекуррентную формулу, чтобы быстрее вычислить факториал числа 7.
Задача: вычесть из одного факториала другой.
Решение:
Используем тот же подход, что и в предыдущей задаче: сначала вычисляем факториалы, а затем получаем ответ на всё выражение.
Вроде бы ничего сложного, главное — не запутаться в умножении.
Задача: умножить один факториал на другой:
Решение:
Вычисляем факториалы, потом перемножаем их значения:
Во второй строке мы воспользовались таблицей выше и быстро нашли значение факториала от числа 8.
Задача: сократить дробь и вычислить её значение.
Решение:
Здесь мы воспользуемся рекуррентной формулой для вычисления факториала и разложим верхний факториал на множители:
В первой строке мы применили рекуррентную формулу два раза, а во второй — просто сократили одинаковые факториалы в числителе и в знаменателе.
Задача: сократить дробь.
Решение:
Хотя здесь нет конкретных чисел, но принцип решения остаётся таким же: используем рекуррентную формулу и сокращаем одинаковые значения в числителе и знаменателе.
Главное — не запутаться и правильно применить рекуррентную формулу.
- Факториал — это произведение всех натуральных чисел от 1 до данного числа. Например, факториал числа 5 будет равен 1 × 2 × 3 × 4 × 5 = 120.
- Его используют во многих областях науки — например, комбинаторике, теории вероятностей и математическом анализе.
- Помимо стандартной формулы для вычисления факториала можно использовать формулы Стирлинга и рекуррентную формулу.
- Формула Стирлинга нужна для того, чтобы посчитать факториал без большого числа операций умножения.
- Рекуррентная формула позволяет вычислить факториал на основе предыдущего факториала.

Научитесь: Профессия Data Scientist
Узнать больше




![log(x!)=log([x]!)+{x}cdot log([x]+1).](https://www.wikiznanie.ru/wikipedia/images/math/e/e/d/eed25a9b9d103197653897638f6fc539.png)