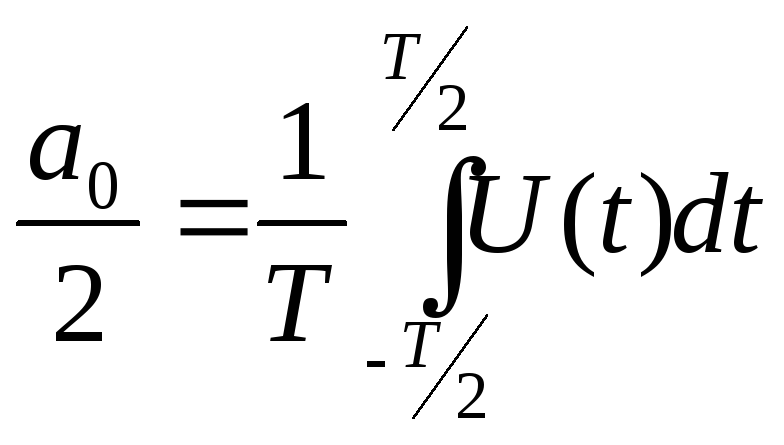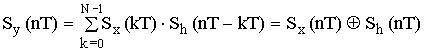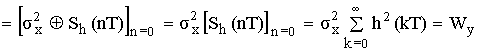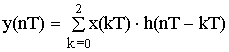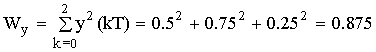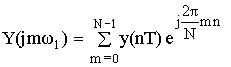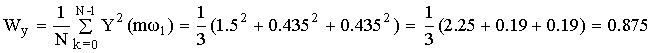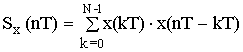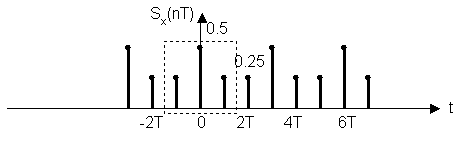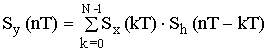Как найти энергию сигнала формула - Autoru.top - решение различных проблем

Расчёт полной энергии сигналов

Показатели энергии и мощности сигналов одни из важнейших характеристик, определяющих коэффициент полезного действия передатчика, качество работы приемника системы связи.

Поскольку существуют временное и спектральное представления сигналов, то данные показатели могут быть вычислены двумя способами.

Энергия одиночного сигнала вычисляется через временную функцию сигнала по формуле

Бесконечные пределы в интеграле записаны для общего случая и будут уточнены для конкретного сигнала.

Спектральное представление сигнала позволило определить эти же энергетические характеристики по спектрам сигналов. Для этого существуют равенства Парсеваля. Для непериодического сигнала, при условии, что сигнал начинается в начале координат:

Если сигнал симметричен относительно начала координат, то формула (1.12) будет выглядеть следующим образом:

Рассчитаем энергию сигнала 1 по формуле (1.11). Так как сигнал конечен, то бесконечные пределы заменяем конечными.

Найдём энергию второго сигнала по формуле (1.11). Для определения пределов интегрирования, оценим скорость убывания функции. Подставим в качестве пределов интегрирования ориентировочные значения t. После расчёта числового значения интеграла увеличим принятые пределы в два раза и снова посчитаем интеграл. Если полученный результат совпадает с предыдущим с точностью до двух значащих цифр, то можно оставить принятые в первом случае пределы в качестве окончательных. После подбора примем, что верхний предел интегрирования t_в = — 0.0016 с, а нижний соответственно t_н= 0.0016 с.

Подставив их в (1.11), получим:

Энергию сигнала 3 определим аналогично, подставив вместо пределов интегрирования верхнюю и нижнюю границы сигнала.

Расчёт неполной энергии сигналов

По заданному проценту определим неполную энергию сигналов. Для первого сигнала:

Для второго сигнала

Для третьего сигнала

Методом итераций рассчитаем граничные частоты спектров сигналов по рассчитанной выше неполной мощности. Для расчёта граничных частот используем формулы (1.12) и (1.13). Граничные частоты: ₁ = 109000 рад/с; ₂ = 139500 рад/с; ₃ = 259000 рад/с.

Построим графики полной энергии сигналов и отметим на них процент от полной энергии. Графики сигналов 1 3 изображены соответственно на рисунках 1.8 1.10.

Энергия сигнала

На практике часто используются такие характеристики, как энергия и мощность сигнала. Если к резистору с сопротивлением R приложено постоянное напряжение U, то выделяющаяся в резисторе мощность будет

За время Т в этом резисторе выделится тепловая энергия

Если к тому же резистору приложить не постоянное напряжение, а напряжение, описываемое сигналом S(t), то рассеивающаяся в резисторе мощность также будет зависеть от времени. Тогда мгновенную мощность можно описать выражением

Чтобы вычислить выделяющуюся за время Тэнергию, мгновенную мощность необходимо интегрировать в пределах интервала Т.

Можно ввести также понятие средней мощности за заданный промежуток времени, разделив энергию на длительность временного интервала:

Во все формулы входит сопротивление нагрузки R. Однако если энергия и мощность интересуют нас не как физические величины, а как средство сравнения различных сигналов, то этот параметр можно из формул исключить, приняв R = 1 Ом. Тогда можем определить энергию, мгновенную мощность и среднюю мощность сигнала, принятые в теории сигналов:

Фактически сигнал не производит работы и физически энергии нет, так как сигнал — это абстрактное понятие. Однако формально, взяв квадрат от сигнала, мы говорим о мощности или об энергии сигнала, применяя эти характеристики к сигналу.

В теории передачи информации практическое значение имеет равенство Парсеваля, формально описывающее закон сохранения энергии применительно к сигналам при переходе от временного представления сигнала S(t) к частотному спектру Ф(/ю). Для получения равенства Парсеваля выполним следующие действия.

1. Запишем выражение для определения энергии сигнала S(t) в виде

2. Выразим энергию через спектральную плотность амплитуд, т.е. используем обратное преобразование Фурье (3.17):

Поскольку S (/) не зависит от со, то внесем S (t) во второй интеграл:

В результате получим равенство Парсеваля:

в котором проявляется закон сохранения энергии сигнала: энергия сигнала во временной области равна энергии спектра сигнала в частотной области.

Энергия сигнала может быть конечной или бесконечной. Например, любой сигнал конечной длительности будет иметь конечную энергию (если он не содержит 6-функций или ветвей, уходящих в бесконечность). А периодический сигнал имеет бесконечную энергию, так как формально он бесконечен во времени. Если энергия сигнала бесконечна, то можно определить его среднюю мощность на всей временной оси. В результате выполнения предельного перехода интервал усреднения стремится к бесконечности:

Если взять квадратный корень из средней мощности, то это даст среднеквадратичное (действующее) значение или эффективное значение сигнала:

Энергетические характеристики сигналов. Спектральная плотность энергии

Пусть дан некоторый сигнал , который характеризует изменение напряжения или силы тока во времени. Тогда будет определять мгновенную мощность, выделяемую на сопротивлении 1 Ом.

Таким образом, периодические сигналы, повторяющиеся на всей оси времени мы можем характеризовать конечной средней мощностью , поскольку их энергия бесконечна. Непериодические сигналы характеризуются конечной энергией , потому что их средняя мощность на всей оси времени равна нулю.

Выражения (1)–(3) справедливы и для комплексного сигнала . В этом случае, мгновенную мощность можно определить как .

Пусть даны два сигнала и , в общем случае комплексные. Скалярным произведением сигналов называется величина равная:

Заметим, что скалярное произведение сигнала с самим собой возвращает энергию данного сигнала:

Подставим в (4) вместо обратное преобразование Фурье его спектральной плотности . Тогда:

связывающее среднюю мощность периодического сигнала. Для непериодических сигналов мы можем получить аналогичное равенство энергии сигнала во времени и в частотной области. Для этого в обобщенную формулу Рэлея подставим и получим:

Если в выражениях (7)–(9) использовать частоту , выраженную в герц, вместо циклической частоты , измеряемой в единицах рад/c, то и множитель сокращается:

было введено понятие спектральной плотности сигнала и была приведена аналогия поясняющая понятие спектральной плотности, и ее отличие от спектра периодического сигнала.

Из равенства (9) следует, что энергия сигнала может быть представлена как интеграл по всей оси частот:

Сделаем важное замечание. Спектральная плотность энергии игнорирует ФЧХ сигнала. Тогда можно заключить, что одной и той же спектральной плотности энергии могут соответствовать множество различных сигналов, имеющих одинаковую АЧХ и различные ФЧХ.

и на практике анализ поведения убывающей спектральной плотности с ростом частоты имеет важное значение. Однако графический анализ бывает затруднителен ввиду высокой скорости убывания спектральной плотности по частоте, а в случае спектральной плотности энергии затруднителен вдвойне, поскольку возведение АЧХ в квадрат только ускоряет убывание. Поэтому широкое распространение получило представление спектральной плотности энергии в логарифмическом масштабе, выраженной в единицах децибел (дБ):

В качестве примера на рисунке 1 приведены спектральные плотности энергии прямоугольного, треугольного, двустороннего экспоненциального и гауссова импульсов в линейном и логарифмическом масштабе.

Как видно из рисунка 1а, спектральные плотности энергии импульсов в линейном масштабе практически сливаются и очень сложно различимы.

Логарифмическая шкала представления спектральной плотности энергии оказывается удобной при сравнении характеристик сигналов. Если энергии двух сигналов отличаются в 100 раз, то в логарифмической шкале отношение их энергий составляет 20 дБ. Если же энергии отличаются в 1000000 раз, то в логарифмической шкале это соответствует 60 дБ. Удвоение энергии сигнала, в логарифмической шкале соответствует прибавлению 3 дБ.

В данном разделе мы рассмотрели энергетические характеристики периодических и непериодических сигналов. Мы показали, что периодические сигналы имеют бесконечную энергию, но конечную среднюю мощность. Средняя мощность непериодических сигналов стремится к нулю, а их энергия конечна.

Было введено понятие скалярного произведения сигналов и получена обобщенная формула Релея,связывающая скалярное произведение во временной и частотной областях.

Установлено равенство Парсеваля для непериодических сигналов, как частный случай формулы Релея.

Введено понятие спектральной плотности энергии как квадрата модуля спектральной плотности сигнала. Также рассмотрено представление спектральной плотности энергии в линейном и логарифмическом масштабе для различных сигналов.

Источник

Если к резистору
с сопротивлением R
приложено постоянное напряжение U,
то выделяющаяся в резисторе мощность
будет равна:

За время Т в этом
резисторе выделяется тепловая энергия:

Пусть теперь к
тому же резистору приложено не постоянное
напряжение, а сигнал S(t).
Рассеивающаяся в резисторе мощность
при этом тоже будет зависеть от времени
(речь идет о мгновенной мощности).

Чтобы вычислить
теряющуюся за время T
энергию, мгновенную мощность необходимо
проинтегрировать:

Можно ввести и
понятие средней мощности за заданный
промежуток времени, разделив энергию
на длительность временного интервала:

Во все приведенные
формулы входит сопротивление нагрузки
R.
Если энергия и мощность интересуют нас
не как физические величины, а как средние
сравнения различных сигналов, этот
параметр можно из формул исключить
(принять R=1).
Тогда мы получим определение энергии
мгновенной мощности и средней мощности,
принятой в теории сигналов

— энергия сигнала

— мгновенная
мощность

(1)

Данные параметры
иногда называются удельной мощностью
и энергией, чтобы подчеркнуть, подразумевая
при этом единичное значение сопротивления
нагрузки.

Энергия сигнала
может быть конечной или бесконечной.
Любой сигнал конечной длительности
будет иметь конечную энергию, а любой
периодический – бесконечную. Если
энергия сигнала бесконечна, можно
определить его среднюю мощность на всей
временной оси. Для этого из формулы (1)
путем предельного перехода, устремив
интервал усреднения в бесконечность

(2)

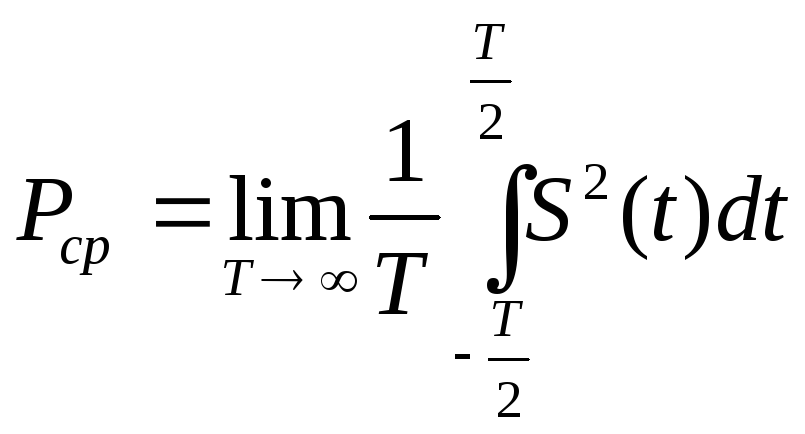
Квадратный корень
из Рср даст среднеквадратичное значение
мощности сигнала

(3)

5 Спектральный анализ периодических сигналов. Условия Дирихле. Ряд Фурье.

Для периодического
сигнала с периодом Т выполняется
соотношение:S(t+nT)
= S(t)
при любом t.

где n
— произвольное целое число; Т – период
сигнала.Величина обратная периоду
называется частотой повторения сигнала
(f
= 1/T).
Используют понятие круговой частоты.
(ω
= 2πf)

Разложению в ряд
Фурье могут подвергаться периодические
сигналы.

Чтобы такое
разложение существовало, фрагмент
сигнала длительностью в один период
должен удовлетворять условиям
Дирихле:

не должно быть
разрывов 2-го рода (с уходящими в
бесконечность ветвями функции)
число разрывов
1-го рода (скачков) должно быть конечным
число экстремумов
должно быть конечным

Различают несколько
форм записи ряда Фурье:

синусно – косинусная
вещественная
комплексная

Синусно-косинусная
форма записи ряда Фурье

Входящие в формулу
кратные основной частоте (ω₁)
частоты называются гармониками. Гармоники
нумеруются в соответствии с индексом
k,
частота ω_k
= k
ω₁ называется
к-ой гармоникой сигнала.

Коэф-ты, входящие
в данный ряд определяются след образом:

; ;

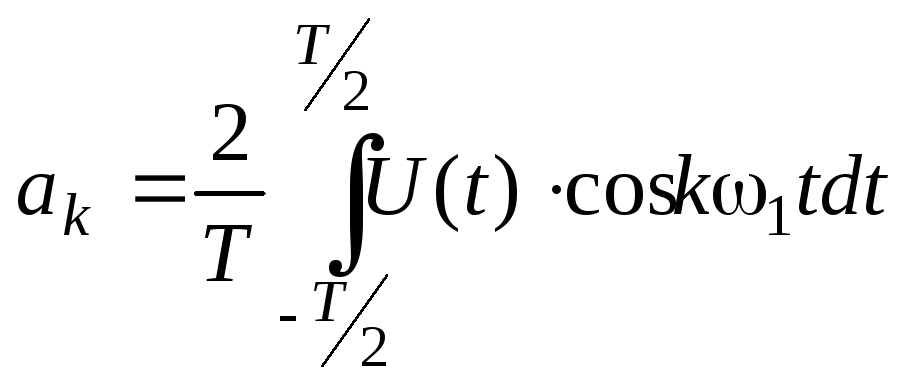
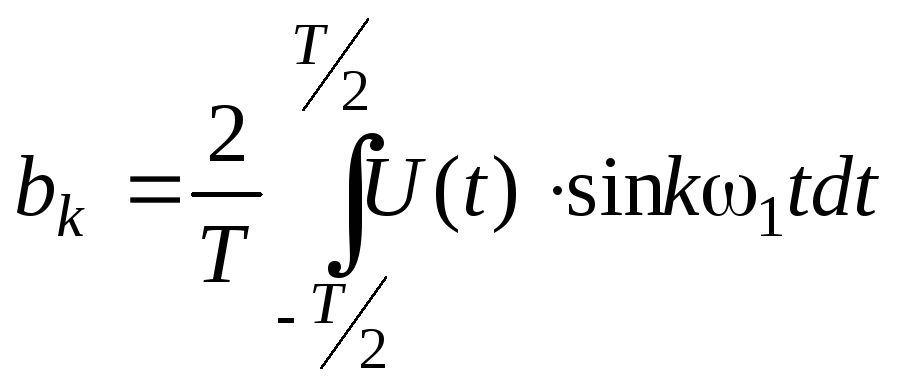
a₀/2
– среднее значение с-ла на периоде.

Если S(t)
— чётная ф-ция, то все b_к
= 0 и в ф-ле
ряда Фурье будут только косинусные
слагаемые. Если S(t)
— нечётная ф-ция, то все а_к
= 0 и в ф-ле
ряда Фурье будут только синусные
слагаемые.

Вещественная
форма записи

Некоторое неудобство
синусно-косинусной формы ряда Фурье
состоит в том, что для каждого значения
индекса суммирования к в формуле
фигурируют два слагаемых синус и косинус.

,
где
;— фазаk—ой
гармоники.

Если S(t)
является чётной функцией фазы φ_кмогут
принимать значения 0 и π, а если S(t)
функция нечётная, то возможны значения
фазы ±π/2.

Комплексная
форма записи

Данная форма
представления является наиболее
употребимой в радиотехнике. Она получается
из вещественной формы представления
косинуса в виде полусуммы комплексных
экспонент. Вытекает из формулы Эйлера:
е^jx
= cos(x)
+ jsin(x),
cos(x)
= ½ ( e^jx
+ e^—^jx
).

Применив данное
преобразование к вещественной форме
ряда Фурье получим:

Учитывая, что

,получим
.
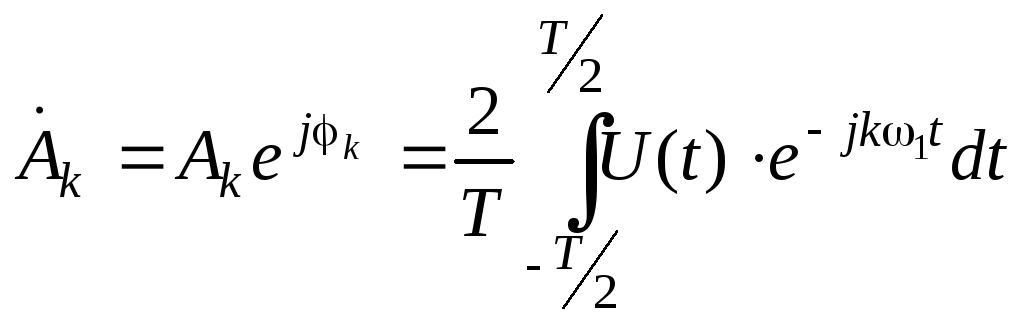
Формулы называются парой преобразований
Фурье. Вторая формула из них позволяет
найти спектр, т.е. совокупность
гармонических составляющих, образующих
в сумме колебание.

Спектр периодической
последовательности импульсов состоит
из постоянной составляющей и множества
гармонических составляющих, частоты
которых образуют дискретный ряд значений
()
кратных основной частоте колебаний.
Амплитуды гармонических составляющих
или сокращенно гармоник равны,
а начальные фазы.
Такой спектр называется дискретным или
линейчатым. Постоянную составляющую
можно рассматривать как гармонику с
нулевой частотой колебания и амплитудой_.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Энергетические характеристики сигналов. Спектральная плотность энергии

Содержание

Обнаружили ошибку?
Выделите ее мышью
и нажмите

Энергия и средняя мощность сигналов

Пусть дан некоторый сигнал s(t) , который характеризует изменение напряжения или силы тока во времени. Тогда будет определять мгновенную мощность, выделяемую на сопротивлении 1 Ом.

Проинтегрируем мгновенную мощность p(t) на некотором интервале времени и получим энергию сигнала на данном интервале:

(1)

Тогда средняя мощность $P_{textrm{ср}}$ сигнала s(t) на данном интервале времени равна:

(2)

Если сигнал s(t) является периодическим, то среднюю мощность можно получить путем усреднения на одном периоде повторения сигнала. В случае абсолютно-интегрируемого непериодического сигнала s(t) , интервал интегрирования может быть расширен на всю ось времени:

(3)

Можно заметить, что средняя мощность абсолютно-интегрируемого непериодического сигнала s(t) равна нулю при усреднении на бесконечном интервале времени. Аналогично, энергия периодического сигнала на всей оси времени равна бесконечности.

Таким образом, периодические сигналы, повторяющиеся на всей оси времени мы можем характеризовать конечной средней мощностью $P_{textrm{ср}}$ , поскольку их энергия бесконечна. Непериодические сигналы характеризуются конечной энергией , потому что их средняя мощность на всей оси времени равна нулю.

Выражения (1)–(3)
справедливы и для комплексного сигнала s(t) . В этом случае, мгновенную мощность можно определить как .

Скалярное произведение сигналов. Обобщенная формула Рэлея

Пусть даны два сигнала a(t) и b(t) , в общем случае комплексные.
Скалярным произведением сигналов называется величина равная:

(4)

Интеграл (4) возвращает одно число (скаляр), в общем случае комплексное.

Заметим, что скалярное произведение сигнала a(t) с самим собой возвращает энергию данного сигнала:

(5)

Тогда скалярное произведение (4) можно трактовать как величину взаимной энергии сигналов a(t) и b(t) , т.е. степень взаимного влияния одного сигнала на другой. Если два сигнала a(t) и b(t) имеют нулевое скалярное произведение, то говорят, что они ортогональны.

Подставим в (4) вместо b(t) обратное преобразование Фурье его спектральной плотности . Тогда:

(6)

Поменяем в (6) порядок интегрирования:

(7)

Можно сделать вывод: скалярное произведение сигналов во временно́й области, с точностью до множителя $frac{1}{2pi}$ , равно скалярному произведению спектральных плотностей данных сигналов. Выражение (7) носит название обобщенной формулы Рэлея [1, стр. 67].

Равенство Парсеваля

Ранее мы уже рассматривали равенство Парсеваля,

(8)

или с учетом (4) равенство Парсеваля [2, стр. 49]:

(9)

Таким образом, энергия сигнала во временно́й и частотной областях равна с точностью до множителя $frac{1}{2pi}$ .

Если в выражениях (7)–(9) использовать частоту $f = frac{omega}{2pi}$ , выраженную в герц, вместо циклической частоты omega , измеряемой в единицах рад/c, то и множитель $frac{1}{2pi}$ сокращается:

(10)

(11)

Спектральная плотность энергии сигнала

При рассмотрении предельного перехода к преобразованию Фурье

Из равенства (9) следует, что энергия сигнала может быть представлена как интеграл по всей оси частот:

(12)

Тогда использую ту же аналогию,
что и в разделе

«Преобразование Фурье непериодических сигналов»

можно заключить, что представляет собой спектральную плотность энергии сигнала. Проинтегрировав по всей оси omega , мы получим полную энергию сигнала, равно как проинтегрировав плотность стержня по длине мы получим полную массу.

Спектральная плотность энергии представляет собой квадрат АЧХ сигнала. Кроме того является вещественной неотрицательной функцией частоты omega . Спектральная плотность энергии сигнала измеряется в единицах джоуль на герц (Дж/Гц) или ватт, умноженный на секунду в квадрате (Вт cdot с).

Спектральные плотности сигналов

имеют убывающий по частоте характер

(13)

Рисунок 1. Спектральная плотность энергии некоторых сигналов
а — в линейном масштабе; б — в логарифмическом масштабе

В логарифмическом масштабе (рисунок 1б), спектральные плотности энергии обнаруживают значительные отличия. Треугольный и экспоненциальный импульсы имеют одинаковую скорость убывания спектральной плотности энергии, а прямоугольный импульс имеет очень медленное затухание спектральной плотности энергии с ростом частоты. Гауссов импульс, напротив, отличается очень быстрым затуханием .

Выводы

В данном разделе мы рассмотрели энергетические характеристики периодических и непериодических сигналов. Мы показали, что периодические сигналы имеют бесконечную энергию, но конечную среднюю мощность.
Средняя мощность непериодических сигналов стремится к нулю, а их энергия конечна.

Установлено равенство Парсеваля для непериодических сигналов, как частный случай формулы Релея.

Смотри также

Преобразования Фурье непериодических сигналов
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов

Список литературы

[1]

Радиотехнические цепи и сигналы.
Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[2]

Гоноровский И.С.
Радиотехнические цепи и сигналы
Москва, Советское радио, 1977, 608 c.

[3]

Bracewell R.
The Fourier Transform and Its Applications
McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

Последнее изменение страницы: 12.05.2022 (19:42:49)

Страница создана Latex to HTML translator ver. 5.20.11.14

Источник

Расчет корреляционной функции на выходе цепи:

корреляционная функция выходного сигнала – S_y(nT), S_x(nT) и S_h(nT).

Где – условное обозначение свертки.

Докажем справедливость этой формулы:

т.к. система линейная и математические операции линейные, то сигнал можно сочетать различными способами

Согласно полученному выражению энергию полученного сигнала можно получить без расчета выходного сигнала.

n = 0

Рассмотрим важный частный случай: пусть x(nT) – случайный сигнал с нулевым средним. Для такого сигнала:

S_x(nT) = S_x(0T) = W_x = σ_x² – дисперсия сигнала x(nT)

Тогда

– формула расчета выходного сигнала (применяется для расчета шумов квантования в цифровых фильтрах).

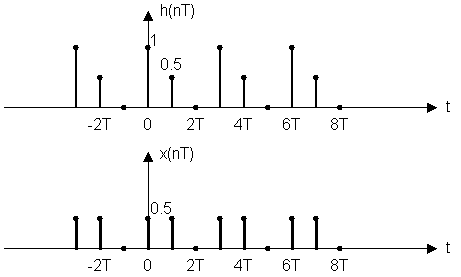
Пример: определить энергию сигнала на выходе цепи с импульсной характеристикой.

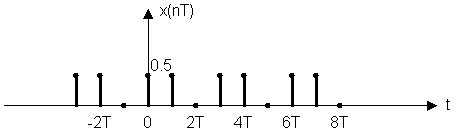
h(nT) = {1.0; 0.5} и x(nT) = {0.5; 0.5}

a) расчет энергии W_y во временной области.

Определяем y(nT) с помощью круговой свертки.

N₁ = 2; N₂= 2; N = N₁ + N₂ –1 = 3

h(nT) = {1; 0.5; 0} x(nT) = {0.5; 0.5; 0}

n = 0 y(0T) = x(0T)·h(0T) + x(1T) ·h(-1T) + x(2T) ·h(-2T) =

= 0.5·1 + 0.5·0 + 0·0 = 0.5

n = 1 y(1T) = x(0T) ·h(1T) + x(1T) ·h(0T) + x(2T) ·h(-1T) = 0.75

n = 2 y(2T) = x(0T) ·h(2T) + x(1T) ·h(1T) + x(2T) ·h(0T) = 0.25

b) расчет энергии W_y в частотной области.

С помощью равенства Парсеваля определяем частотные отсчеты выходного сигнала по формуле прямого ДПФ.

m = 0 Y(j0ω₁) = y(0T) + y(1T) + y(2T) = 1.5

m = 1 Y(j1ω₁) = y(0T)e^{j 0} + y(1T)e^{–j 120} + y(2T)e^{–j 240} = –j0.435

m = 2 Y(j2ω₁) = y(0T)e^{j 0} + y(1T)e^{–j 240} + y(2T)e^{–j 480} = j0.435

Y(j0ω₁) = {1.5; –j0.435; j0.435}

с) расчет энергии сигнала W_y по корреляционным функциям S_x(nT) и S_h(nT).

x(nT) = {0.5; 0.5}; h(nT) = {1.0; 0.5}

N₁ = 2; N₂ = 2; N = N₂ + N₁ – 1 = 3

x(nT) = {0.5; 0.5; 0}

n = 0; S_x(0T) = x(0T)·x(0T) + x(1T) ·x(1T) + x(2T) ·x(2T) =

= 0.5·0.5 + 0.5·0.5 + 0·0 = 0.5

n = 1; S_x(1T) = x(0T)·x(1T) + x(1T) ·x(2T) + x(2T) ·x(3T) = 0.25

n = 2; S_x(2T) = x(0T)·x(2T) + x(1T) ·x(3T) + x(2T) ·x(4T) = 0.25

S_x(nT) = {0.5; 0.25; 0.25}

S_h(nT) = {1.25; 0.5; 0.5}

N₁ = 3; N₂ = 3; N = N₁ + N₂ – 1 = 5

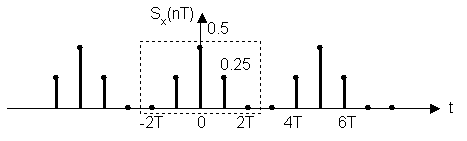
Периоды корреляционных функций, участвующих в свертке, нужно увеличить таким образом, чтобы четный характер корреляционной функции сохранился.

Исходная периодическая последовательность для S_x(nT) (период =3)

Последовательность после увеличения периода (период = 5):

В результате выравнивания периода получаем:

S_x(nT) = {0.5; 0.25; 0; 0; 0.25}

S_h(nT) = {1.25; 0.5; 0; 0; 0.5}

n = 0; S_y(0T) = W_y = S_x(0T)·S_h(0T) + S_x(1T)·S_h(-1T) + S_x(2T)·S_h(-2T) +

+ S_x(3T)·S_h(-3T) + S_x(4T)·S_h(-4T) = 0.5·1.25 + 0.25·0.5 + 0·0 + 0·0 + 0.25·0.5 =

= 0.625 + 0.125 + 0.125 = 0.875

W_y = 0.875

Источник

Общие сведения

Показатели энергии и мощности сигналов важнейшие характеристики, определяющие коэффициент полезного действия передатчика и качество работы приемника системы связи. Поскольку существует два вида представления сигналов временное и спектральное, то данные показатели могут быть вычислены двумя способами.

Полная энергия одиночного сигнала вычисляется через временную функцию сигнала по формуле:

(1.10)

Неполная энергия, необходимая для вычисления граничных частот, определяется как процент от полной, в данной работе процент составляет . Получается, что:

(1.11)

Спектральное представление сигнала позволяет определить эти же энергетические характеристики по спектрам сигнала при помощи равенства Парсеваля для непериодических функций:

(1.12)

Знак «» в выражениях (1.10) и (1.12) означает, что в создании энергии и мощности сигнала участвует бесконечный спектр частот. Если знак «» заменить в формуле (1.12) на конечную величину , то по полученной формуле определяется только часть мощности и энергии сигнала. Этим способом пользуются при ограничении спектров сигналов.

Энергия первого сигнала

Найдем энергию первого сигнала аналитически.

Полную энергию первого сигнала можно вычислить по точной формуле:

Решая с помощью программы Mathcad получаем аналогичный результат.

Вычисление неполной энергии второго сигнала производится при подстановке полной энергии сигнала в формулу (1.11):

, Дж

Вычисление энергии первого сигнала через равенство Парсеваля производится при подстановке аналитического вида из подпункта 1.1.1 в формулу (1.12):

, Дж

Графики зависимости энергии первого сигнала от частоты приведены соответственно на рисунке 1.7.

Рисунок 1.7 — Зависимость энергии первого сигнала от частоты

Энергия второго сигнала

Полную энергию второго сигнала вычислим по точной формуле:

, Дж

Вычисление энергии второго сигнала через равенство Парсеваля производится при подстановке аналитического вида из параграфа 1.1.1 в формулу (1.12):

, Дж

Графики зависимости энергии второго сигнала от частоты приведены соответственно на рисунке 1.8.

Рисунок 1.8 — Зависимость энергии второго сигнала от частоты

Энергия третьего сигнала

Найдем энергию третьего сигнала аналитически:

Решая с помощью программы Mathcad получаем аналогичный результат.

, Дж

Вычисление неполной энергии третьего сигнала производится при подстановке полной энергии сигнала в формулу (1.11):

, Дж

Вычисление энергии третьего сигнала через равенство Парсеваля производится при подстановке аналитического вида из параграфа 1.1.1 в формулу (1.12):

, Дж

Графики зависимости энергии третьего сигнала от частоты приведены соответственно на рисунке 1.9.

Рисунок 1.9 — Зависимость энергии третьего сигнала от частоты

Граничные частоты спектров сигналов

Граничная частота спектра первого сигнала

По графику, изображенному на рисунке 1.7, определяется граничная частота как пересечение графиков неполной энергии и энергии, вычисленной через равенство Парсеваля.

рад/с

Граничная частота спектра второго сигнала

По графику, изображенному на рисунке 1.8, определяется граничная частота как пересечение графиков неполной энергии и энергии, вычисленной через равенство Парсеваля.

рад/с

Граничная частота спектра третьего сигнала

По графику, изображенному на рисунке 1.9, определяется граничная частота как пересечение графиков неполной энергии и энергии, вычисленной через равенство Парсеваля.

рад/с

Так как для дальнейших расчетов курсового проекта требуется только один сигнал из рассмотренных выше, то делается выбор в пользу сигнала с наименьшей граничной частотой. То есть во всех следующих расчетах будет фигурировать третий сигнал (№4 по заданию).

Источник

Расчёт полной энергии сигналов

Расчёт неполной энергии сигналов

Энергия сигнала

Энергетические характеристики сигналов. Спектральная плотность энергии

5 Спектральный анализ периодических сигналов. Условия Дирихле. Ряд Фурье.

Энергетические характеристики сигналов. Спектральная плотность энергии

Общие сведения

Энергия первого сигнала

Энергия второго сигнала

Энергия третьего сигнала

Граничные частоты спектров сигналов

Граничная частота спектра первого сигнала

Граничная частота спектра второго сигнала

Граничная частота спектра третьего сигнала

Не пропустите также: