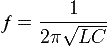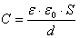Как найти емкость конденсатора формула через частоту

Конденсатор – пассивный электронный компонент, главной характеристикой которого является емкость. Предназначен в основном для накопления энергии, разделения цепей постоянного тока, фильтрации помех, создания резонансных цепей и т.п. Чтобы применение конденсаторов на практике было осознанным, следует ознакомиться с их основными параметрами, методами измерения и изменения емкости.

От чего зависит и в чем измеряется емкость конденсатора

Конденсатор в общем случае состоит из двух проводящих обкладок, разделенных диэлектриком. Если к обкладкам приложить напряжение, такое устройство запасает электрическую энергию путем накопления заряда. (говорят, что конденсатор заряжается). Количественно запасенная конденсатором электрическая энергия выражается формулой , где W – величина энергии, U – напряжение между обкладками, а С – емкость, то есть, величина, характеризующая способность конденсатора запасать энергию. В целом ёмкость зависит от площади обкладок, расстояния между ними и свойствами разделяющего диэлектрика.

Единицей измерения емкости в СИ является фарад (1 Ф) (устаревшее название – фарада). Для практических целей это слишком большая единица. Так, земной шар имеет ёмкость менее 1 Ф, поэтому в технике используют, в основном, дольные единицы:

• пикофарады – 1 пФ (1 pF) =10^-12 Ф;
• нанофарады – 1 нФ (1 nF) =10^-9 Ф;
• микрофарады – 1мкФ (1 µF) = 10^-6 Ф.

Более крупные единицы до недавнего времени не использовались, так как емкости порядка больших дольных единиц были труднодостижимыми. Лишь с появлением ионисторов появилась возможность оперировать величинами порядка единиц и даже десятков фарад.

Как узнать емкость конденсатора

Чтобы использовать конденсатор для практических целей, надо знать его емкость. Выяснить эту величину можно различными способами.

По маркировке

В первую очередь, надо попробовать определить параметры конденсатора по его маркировке. На оксидные конденсаторы, имеющие емкость которых составляет от долей до нескольких тысяч микрофарад, эта характеристика наносится на корпус в виде цифры, обозначающей емкость в микрофарадах, с индексом uF (для отечественных изделий предыдущих годов выпуска после цифры стоит индекс мкФ).

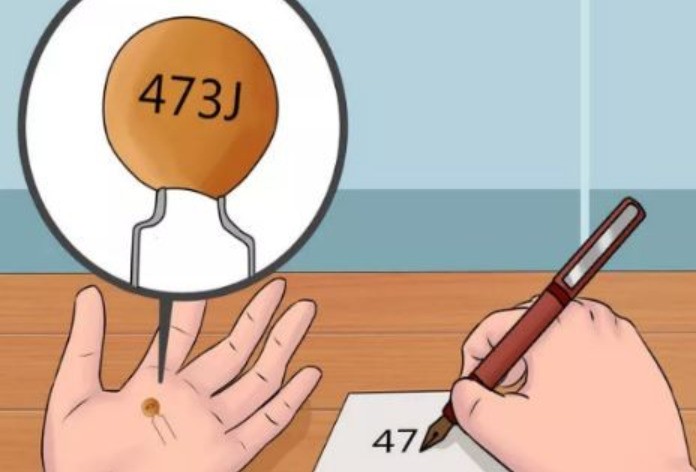
Конденсаторы, обладающие емкостью от единиц пикофарад до единиц микрофарад маркируют тремя цифрами:

• первые два символа — мантисса;
• третья цифра – множитель.

Попросту говоря, к первым двум цифрам надо приписать количество нулей, обозначаемое третьей цифрой.

Например, на конденсатор на рисунке нанесено обозначение 473. К цифрам 47 надо приписать три нуля, тогда получится 47000 пФ. Удобнее представить это значение в виде 47нФ или 0,047 мкФ.

Такое обозначение применяется не всегда (особенно, на старых типах отечественных изделий). Иногда на корпусе наносят явное значение ёмкости с единицей измерения.

Но и единицу измерения указывают не всегда. Принцип таков:

• если нет множителя или не указана единица, считается, что ёмкость в пикофарадах;
• если есть множитель, он указывается одной буквой (n – нанофарады, µ — микрофарады и т.п.).

На зарубежных конденсаторах выпуска до 70-х годов можно встретить обозначение µµF. Так маркировалась ёмкость в пикофарадах («микро-микрофарады»).

Если емкость неизвестна, надпись но корпусе отсутствует или есть сомнения, лучше провести измерения одним из известных способов.

Мультиметром

Сделать это можно, например, с помощью цифрового тестера. Многие современные мультиметры имеют функцию измерения емкости конденсаторов. Надо всего лишь выбрать соответствующий режим, обычно обозначаемый символом конденсатора или буквами Cx, и подключить конденсатор к щупам или специально выделенным гнездам. При измерении надо иметь в виду, что:

1. Нижний предел измеряемой величины довольно большой, и для большинства распространенных приборов составляет не менее 1000 пФ.
2. Измерительные провода со щупами имеют собственную ёмкость (до 100 пФ), и ее надо учитывать при измерениях.

Поэтому тестеры, у которых для измерения ёмкости предназначен отдельный выход, измеряют параметры более точно.

Чтобы обмерить конденсатор с меньшей ёмкостью, лучше воспользоваться специализированным тестером (можно приобрести на интернет-площадках, расположенных в Юго-Восточной Азии). Они позволяют измерять ёмкость от десятков или даже единиц пикофарад.

Осциллографом

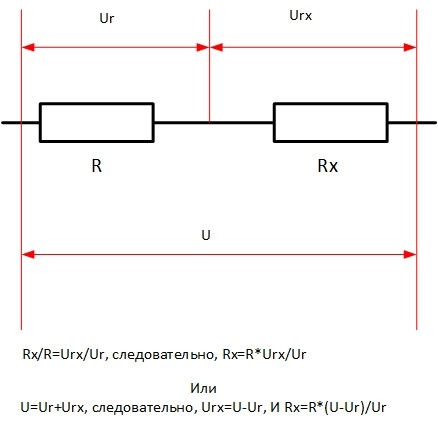
Если есть два резистора – один с известным сопротивлением R, а другой с неизвестным Rx, их можно соединить последовательно (сделать делитель напряжения), подать на него напряжение, и измерить падение на каждом элементе или на общей цепи. Измерения можно провести тестером в режиме вольтметра. Тогда Rx можно вычислить по одной из формул, указанных на рисунке.

Известно, что конденсатор обладает сопротивлением переменному току, которое зависит от частоты по формуле Xc=1/(2*π*f*C), где:

• f – частота тока в Герцах;
• С – ёмкость конденсатора в Фарадах.

Можно сделать подобный делитель из конденсаторов, и сравнить сопротивление неизвестного прибора Xcx с сопротивлением эталонного конденсатора Xc, откуда легко вычислить неизвестную ёмкость:

откуда

Далее несложно найти С.

При этом возникают две проблемы:

1. Измерения нельзя проводить на постоянном токе – сопротивление реального конденсатора при f=0 близко к бесконечности.
2. При измерении переменного напряжения достаточно высокой частоты тестер будет давать значительную погрешность.

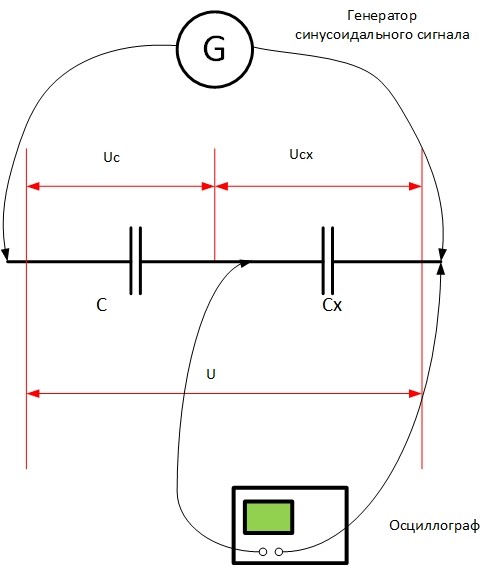
Поэтому в качестве источника тока надо использовать генератор сигнала высокой частоты (чем меньше предполагаемая ёмкость, тем выше должна быть частота, в противном случае точность замеров будет невысокой), а в качестве измерительного прибора – осциллограф.

В качестве эталонного элемента для делителя можно взять резистор с известным сопротивлением (вместо Xc в формулу надо подставить R) или катушку (дроссель) с известной индуктивностью. В этом случае вместо Xc в формулу надо подставить X_L (вычисляется, как X_L=2* π*f*L).

Если имеется эталонная индуктивность, можно найти емкость, составив колебательный контур. Его надо подключить по указанной схеме, а затем, перестраивая генератор, найти резонансную частоту (при ней амплитуда сигнала на осциллографе будет максимальной). Ёмкость можно рассчитать по известной формуле Томсона .

Формулы для расчета емкости

Хотя общая зависимость ёмкости от геометрических размеров и свойств диэлектрика определена выше, для конкретных типов конденсаторов удобнее пользоваться приведенными формулами.

Электроемкость плоского конденсатора

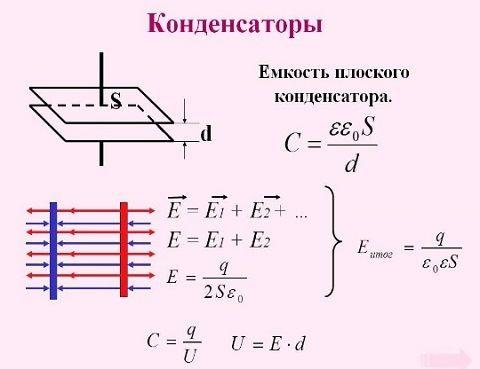
Самый распространённый тип конденсатора, применяемый в технике – плоский. Его обкладки состоят из двух параллельных пластин, между которыми находится диэлектрик. Чтобы уменьшить габариты такого прибора, обкладки с диэлектриком между ними сворачивают в рулон или складывают в прямоугольный пакет. Емкость такого конденсатора рассчитывается по формуле , где:

• С – ёмкость, Ф;
• S – площадь обкладок, кв.м;
• d – расстояние между обкладками;
• ε – диэлектрическая проницаемость диэлектрика;
• ε_{0 –} электрическая постоянная, равная 8.85*10^-12 Кл²/Н*м².

Очевидно, что емкость тем больше, чем больше площадь обкладок и меньше расстояние между ними. Кроме того, можно выбрать диэлектрик с высоким ε и пропорционально увеличить ёмкость в тех же габаритах.

Электроемкость сферического конденсатора

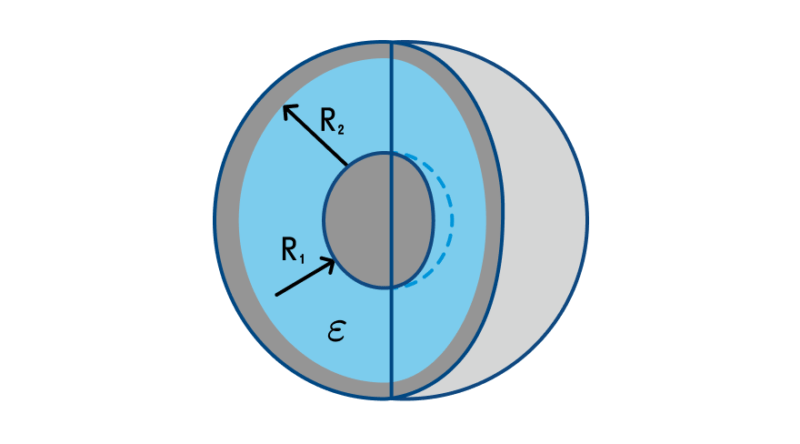
Сферическим конденсатором называется устройство, состоящее из двух проводящих сфер – большой радиусом R1 и малой радиусом R2. Малая сфера вложена в большую. Поверхности сфер служат обкладками. Пространство между сферами может заполняться твердым, жидким диэлектриком или воздухом (воздушный сферический конденсатор). Такие приборы используются для лабораторных исследований (например, для изучения фотоэлектрических явлений).

Формула емкости для такого прибора выглядит, как , где:

• С – ёмкость, Ф;
• R1 – радиус внутренней сферы;
• R2 – радиус внешней сферы;
• ε – диэлектрическая проницаемость диэлектрика;
• ε_{0 –} электрическая постоянная, равная 8.85*10^-12 Кл²/Н*м².

Очевидно, что зависимость емкости от геометрии подобна плоскому конденсатору. Емкость увеличивается при увеличении площади поверхностей сфер (которые зависят от квадрата радиусов) и уменьшается при увеличении расстояния между обкладками (R2-R1).

Электроемкость цилиндрического конденсатора

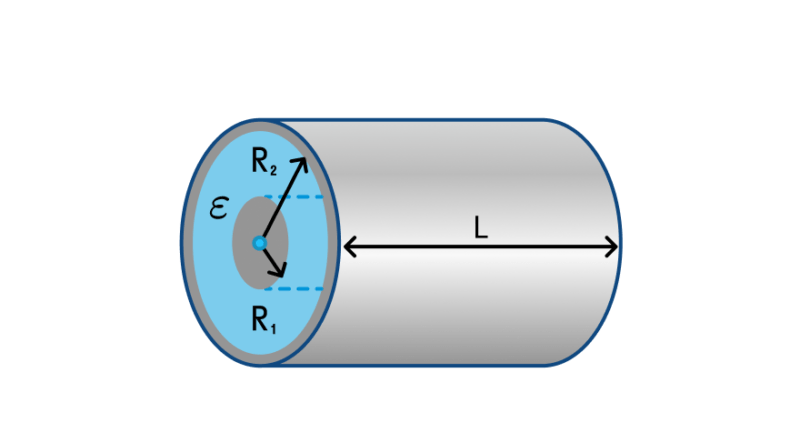
У цилиндрического конденсатора обкладки представляют собой два коаксиальных (расположенных на общей оси) цилиндра длиной l каждый с радиусами R1 (меньший) и R2 (больший). Пространство между ними также может быть заполнено либо воздухом, либо другим диэлектриком. Такие приборы используют в масс-спектрометрии и в некоторых типах счетчиков заряженных частиц. Формула для емкости будет выглядеть, как .

Здесь также прослеживается зависимость от площади (при росте длины увеличивается площадь обкладок, следовательно, растет емкость) и расстояния между обкладками. При росте отношения R2/R1 расстояние увеличивается, а ёмкость падает.

Как изменится емкость при параллельном и последовательном соединении

В реальных схемах конденсаторы могут быть включены последовательно или параллельно. При этом суммарная емкость будет разной.

Если включить n конденсаторов параллельно, то в этом случае:

• к каждой ячейке прикладывается одно и то же напряжение (U₁=U₂=..=U_n=U);
• запасенные в каждом конденсаторе заряды складываются.

Тогда общая емкость равна С=U*q=U*(q₁+q₂+..+q_n)=U*q₁+U*q_2+..+ U*q_n=C1+C2+..+Cn. То есть, при параллельном включении ёмкость батареи равна сумме ёмкостей всех элементов. Это эквивалентно сложению площадей всех пластин.

Батарею можно собрать и последовательно, при этом одна обкладка каждого элемента подключается к выводу соседнего конденсатора, а другая – к выводу другой ячейки. Напряжение подается на свободные выводы крайних элементов.

При этом действуют следующие соотношения (в качестве примера рассмотрена батарея из трех элементов):

• заряды –q1 и q2, -q2 и q3 равны, так как обкладки с этими зарядами соединены между собой;
• заряды q1 и –q1, q2 и –q2, q3 и –q3 равны между собой по модулю, но их знак противоположен.

Заряды каждого конденсатора одинаковы и равны q, но при различной емкости разности потенциалов между обкладками каждого элемента определяются из соотношений:

• U₁=q/ C₁;
• U₂=q/ C₂;
• U₃= q/ C₃.

Следовательно, напряжения на ячейках батареи распределяются пропорционально емкостям. Суммарная емкость равна С=q/(U₁+U₂+U₃), следовательно 1/С=(U₁+U₂+U₃)/q=1/С₁+1/С₂+1/С₃.

Для n элементов, включенных последовательно, выполняется равенcтво:

1/С=1/С₁+1/С₂+..+1/С_n.

Формула достаточно громоздка, но если последовательная цепь состоит из двух элементов, соотношение приводится к виду С= С₁* С₂/( С₁+ С₂).

Последовательное соединение на практике обычно применяется не для снижения общей ёмкости, а для уменьшения напряжения на каждом элементе при использовании конденсаторов в высоковольтных цепях.

Разобравшись с факторами, влияющими на ёмкость конденсатора и способами изменения этого параметра, можно научиться анализировать не только пассивные, но и активные (содержащие полупроводниковые приборы) цепи. Это позволит сделать шаг на пути к развитию навыков и повышению квалификации специалиста.

Конденсаторы часто встречающийся элемент в электрических схемах.
Они нужны для накопления заряда, сглаживания пульсаций электрического тока, фильтрация отдельных видов частот,
создание фазовых сдвигов обеспечивающих работу электрических двигателей и для других технических решений.

Что такое конденсатор

Конденсаторы — это компоненты в электронике, которые могут накапливать электрические заряды.

Эти детали используются в любом электронном устройстве.

Свойство конденсатора – это накопление заряда и последующая его отдача.

От чего зависит емкость и заряд конденсатора

Емкость конденсатора это физическая величина по которой производится оценка его возможностей выполнять свои функциональные задачи.

Практическое значение емкости выражается в способности электрического устройства к накоплению заряда.

Величина напряжения на пластинах в прямой пропорции влияет на количественные характеристики заряда на обкладках.
Формула определения емкости выглядит как

C = q/U,

где С — емкость конденсатора,

q — означает количество заряда на одной из пластин,

U — разница потенциалов на обкладках.
Приведенная формула расчета имеет в большей степени теоретический характер.

Существует иное определение емкости, которое полезнее в практическом смысле.

В формуле C = єS/d обозначена ее связь с площадью S обкладок, расстоянием между пластинами d и свойствами диэлектрика є.

Из формулы следует, что чем больше площадь обкладок, тем больший заряд может на них разместиться и чем больше расстояние между пластинами,
тем слабее заряженные частицы будут притягиваться друг к другу, увеличивая их шансы покинуть обкладку.

Максимальная диэлектрическая проницаемость материала, расположенного между пластинами, увеличивает емкость конденсатора без изменения габаритных характеристик.

Как устроен конденсатор

Конденсатор состоит из двух или нескольких металлических пластин, между которыми располагается диэлектрический материал.
Электроны начинают двигаться, но не в состоянии преодолеть диэлектрик, из-за этого между пластинами накапливается электрический заряд.

Хорошими диэлектрическими свойствами обладают бумага покрытая оксидом алюминия, слюда, электролит, керамика и подобные материалы.

Заряды на разных обкладках одинаковые по величине, но противоположные по знаку.

Виды конденсаторов

Конденсаторы различаются по целому ряду параметров: по конфигурации, по типу диэлектрика,
по материалу обкладок, по виду изменения емкости (постоянные, переменные, подстрочные),
по рабочему напряжению.
Ниже на рисунке рассмотрим основные виды электрических устройств различной конфигурации.

Плоский

Плоский вид устройства, – это две пластины, которые располагаются параллельно друг против друга.
Они отличаются компактностью, сохраняя при этом большую емкость.

Емкость плоского конденсатора возрастает по мере увеличения площади пластин и при уменьшении расстояния между ними.

Для расчета емкости плоского конденсатора следует пользоваться формулой C = ε₀ εS / d

Сферический

Сферический конденсатор это две концентрично расположенные сферы с находящимся между ними тонким диэлектриком.
Наружную поверхность внешней обкладки заземляют для создания электрического поля непосредственно между обкладками.
С учетом геометрии обкладок расчет емкости сферического конденсатора производится по формуле

C = 4πεε₀ Rr/ R — r, где R — радиус наружной обкладки, r — радиус внутренней.

Цилиндрический

Цилиндрический конденсатор выполнен из двух полых цилиндров с разными радиусами образующих их окружностей с общей осью.
Между наружной поверхностью малого цилиндра и внутренней поверхностью большого находится диэлектрик.
Для расчета емкости цилиндрического конденсатора можно воспользоваться формулой
C = 2πєє0L/ ln (R2/R1),

где L — длина цилиндрических обкладок,

R2 — радиус наружного цилиндра,

R1 — радиус внутреннего цилиндра,

ln — обозначение логарифмического действия.

Полярные

Полярные конденсаторы – это приборы, имеющие полярность, а именно плюс и минус.
Важно чтобы плюсовой контакт был соединен с «плюсом» источника питания, а минусовой с его «минусом».
Нарушение полярности может привести даже к взрыву конденсатора.
К полярным принадлежат танталовые, ионисторы, конденсаторы с электролитическим диэлектриком.

Танталовые

В танталовых конденсаторах, относящихся к электролитическому типу, в качестве диэлектрика используется спеченный танталовый порошок оксид тантала, отсюда происходит их название.
Такой диэлектрик сводит практически к нулю ток утечки.

Недостаток заключается в невозможности работать в электрических цепях с высоким напряжением.

Танталовый конденсатор включает в себя 4 элемента – анод, диэлектрик, электролит и катод.

В отличие от электролитических танталовые имеют меньшую собственную индуктивность, благодаря чему их можно применять на высоких частотах.

Компактность танталовых устройств позволяет их использовать в качестве составляющих монтажных схем.

Ионисторы

Ионисторы принадлежат к разряду электрохимических конденсаторов.
Особенность конструкции заключается в сочетании свойств обычного конденсатора и аккумуляторной батареи.
Пространство между электродами заполняется твердым электролитом на основе рубидия и аналогичных материалов.
Такая конструкция исключает самопроизвольный разряд ионистора.

Быстрая разрядка и зарядка делают возможным его использование в некоторых видах электрических схем вместо аккумулятора.

Аккумулятор, в отличие от ионистора, потребует значительное время для своей зарядки.
Емкость ионистора отличается повышенным значением среди всех электролитических устройств.

Работает ионистор только с источником постоянного напряжения.

Электролитические

Большое распространение получили электролитические конденсаторы, у которых одна из обкладок выполнена в виде алюминиевой фольги.
Другой обкладкой служит твердый или жидкий электролит обеспечивающий движение заряженных частиц для сохранения оксидной пленки.

Емкость электролитического конденсатора на сегодняшний день является наибольшей при соотношении емкости и объема элемента.

Электролитические элементы устанавливаются в фильтрах, но важно соблюдение полярности.

По сравнению с танталовыми конденсаторами в электролитических  идут значительный ток утечки.

Процессы переноса заряженных частиц происходят медленно, что увеличивает количество выделяемого тепла.
Отсюда перегрев и низкий срок службы.

Неполярные

Неполярные конденсаторы корректно работают при любых вариантах подключения их в электрическую схему.

Это связано с похожей структурой материалов образующих границу между обкладкой и диэлектриком.
Стороны одинаковы. Все это приводит к тому, что во время установки конденсатора нет необходимости соблюдать полярность.
В качестве неполярных электрических устройств в основном используются сухие, реже электролитические, изготовленные по измененной технологии.

Керамические

Керамические конденсаторы имеют высокие электрические показатели, маленькие габариты и приемлемую стоимость.

Устанавливаются элементы в контурах радиоаппаратуры.
Керамические конденсаторы подразделяются на

• с постоянной емкостью
• подстроечные.

Элементы с постоянной емкостью – устанавливают в контурах генераторов и гетеродинов.
Подстроечные – используются для подгонки параметров колебательных контуров.
Широкое распространение получили благодаря разнообразию емкостей, широкому диапазону рабочих напряжений,
стандартными типоразмерами аналогичными керамическим устройствам разных производителей.

Пленочные

Особенностью таких устройств будет диэлектрик в виде пленки.
Пленка изготавливается из фторопласта, металлизированной бумаги, полипропилена, поликарбоната и подобных материалов.
Металлическая пленка или фольга напыляются или напрессовываются на диэлектрик.

Благодаря большому количества слоев – получается увеличение площади, соответственно, существенно увеличивается емкость.

Из достоинств пленочного конденсатора следует отметить сравнительно высокую надежность, стабильность теплового состояния при действии нагрузок вызванных переменным током.

К недостаткам можно отнести невысокое значение диэлектрической проходимости.

Пленочные конденсаторы используются в цепях постоянного тока, всевозможных фильтрах и резонансных схемах.

Smd

В цепях управления некоторых видов плат используются небольшие по размерам Smd конденсаторы, имеющие форму маленьких кирпичиков.
На плату радиоэлемент устанавливается посредством правила поверхностного монтажа.
Smd устройства бывают следующих видов:

• электролитические
• керамические;
• танталовые.

Керамические SMD конденсаторы, имеющие диэлектрик с высокой проницаемостью, маркируются тремя буквами.
Первыми двумя буквами обозначается нижняя и верхняя предельно допустимая граница рабочего диапазона температур,
третья буква используется при обозначении отклонений изменения емкости для измеряемых диапазонов.

Маленькие размеры Smd конденсаторов не всегда позволяют нанести маркировку на корпус или она будет очень мелкая.

В таких случаях без специального измерительного прибора, например, мультиметра не обойтись.

Переменные

Конденсаторы переменной емкости (КПЕ) состоят из части секций металлических пластин.
Одна из них двигается плавно по отношению ко второй.
Во время передвижения получается, что подвижные пластины (ротора), попадают в зазоры неподвижной пластины (статора).
Благодаря процессу площадь перекрытия одних пластин другими изменяется, в результате чего изменяется у конденсатора емкость.
Слоем диэлектрика в этом случае является воздух.

В конденсаторах, установленных в небольших устройствах, используется твердый диэлектрик, например, фторопласт или полиэтилен.

В старых радиоприемниках устройство применялось для настройки на определенную частоту колебательного контура работающей радиостанции.

Максимальное рабочее напряжение на конденсаторе

Напряжение, подаваемое на конденсатор, не должно превышать максимальное, так как может произойти пробой диэлектрика и выход элемента из строя.

Для анализа работы конденсатора в цепи переменного тока, критерием для сравнения следует брать максимальную амплитудную величину напряжения.

Это значит, что если на нем обозначено какое то максимальное напряжение DC WV , то в действительности при включении в сеть оно должно быть на 1,4 меньше.

Величина и значение потери у конденсатора

Ток утечки конденсатора – критический фактор для использования, особенно если его применяют для силовой электроники.
Потеря напрямую завязана со свойствами диэлектрика.

Никакой диэлектрик не способен гарантировать на 100% изоляцию металлических обкладок.

Через изолятор всегда будет проходить ток, меньший или больший в зависимости от свойств диэлектрика и теряться энергия.
Кроме изолирующих способностей диэлектрика на ток утечки влияют факторы:

• температура окружающего пространства;
• срок годности конденсатора без напряжения, температура;
• величина тока утечки прямо пропорциональна приложенному к обкладкам напряжению.

Восстановить работоспособность конденсатора после длительного хранения можно, приложив к нему рабочее напряжение с выдержкой в течение нескольких минут.

При этом этапе окислительный слой заново накапливается и восстанавливает работоспособность конденсатора.

Конденсатор в цепи электрического тока

Принцип работы конденсатора простой – подается напряжение и накапливается заряд.
Накопитель по-разному ведет себя в двух вариантах электрической цепи.

Постоянного

Если в цепь с присоединенным к ней конденсатором подать ток, то стрелка на амперметре придет в движение и быстро вернется в предыдущее положение.
Это связано с тем, что прибор быстро заряжается и ток исчез.
Через обкладки разделенные диэлектриком постоянный ток проходить не может.
Практическое применение конденсатора в такой цепи вызывает много вопросов.
В условиях постоянного тока конденсатор функционирует, но непродолжительное время.
Переходные процессы в виде зарядки и разрядки снимают все сомнения.
В электронных схемах на постоянном токе конденсаторы один из самых распространенных компонентов.

Переменного

При подключении переменного напряжения полюса конденсатора меняют плюс на минус с частотой подачи напряжения.
В данном случае электроны передвигаются сначала в одну, а потом в другую.
На обкладках при такой смене остаются излишки заряда, которые собственно и создают ток во внешней цепи.

Конденсатор в цепи переменного тога выступает в качестве резистора.

Сопротивления конденсатора в зависимости от

Сопротивление конденсатора зависит от частоты подаваемого на него напряжения и показателя емкости.

Частоты и сдвига фаз

Устройство накопления зарядов одинаковой емкости на разных частотах оказывает различный уровень сопротивления.
Оно растет или уменьшается.

При повышении частоты входного напряжения сопротивление, называемое емкостным уменьшается.

На низких частотах имеется сдвиг по фазе входного напряжения и напряжения на нагрузке.

С увеличением частоты сдвиг по фазе уменьшается.

При достижении частоты определенного уровня фазовый сдвиг стремиться к нулю.

Хс = 1/ωС,

где ω — круговая частота, равная произведению 2πf,

С—емкость цепи в фарадах.

Номинала конденсатора

Емкость конденсатора влияет на процесс зарядки и разрядки при прохождении через него переменного тока.

Устройство с меньшей емкостью будет быстрее отдавать заряд и вновь заряжаться.

Сопротивление переменному току будет выше, чем при медленной зарядке и разрядке.

Отсюда вывод: емкостное сопротивление находится в обратной зависимости от номинала конденсатора.

Последовательное и параллельное соединение конденсаторов

Наиболее популярным типом соединения конденсаторов является параллельное.
При этом подключении электроемкость повышается, а напряжение остается исходным.

К одной точке может подключаться несколько конденсаторов.

Так как электрическая емкость конденсаторов равна площади обкладок, общая емкость при таком виде соединения пропорциональна сумме емкостей всех конденсаторов в цепи.

Собщ.= C1+C2.

При последовательном соединении конденсаторов общая емкость снижается, а напряжение работы конденсатора возрастает.

Конденсаторы подключены так, что только первый и последний имеют доступ к источнику ЭДС/тока одной из своих пластин.
Заряд одинаковый на всех пластинах, но наружные получают заряд от источника, а внутренние образуются благодаря разделению зарядов ранее нейтрализовавших друг друга.
Емкость последовательного соединения двух конденсаторов мы можем вычислить по формуле

Собщ.= С1*С2/ C1+C2.

Формулы для вычисления

Измерения емкости осуществляется по специально выведенной формуле.
Электрическая емкость (С) — это отношение сообщенного заряда (Q) к образующему в результате этого потенциалу (U).
Формулу, которую используют, чтобы измерить емкость, выглядит следующим образом:
C=Q/V .
Единицей измерения служит фарада, которая обозначается буквой Ф.
Емкость величиной 1 фарада будет хранить заряд q = 1 кулон при напряжении на обкладках U =1 Вольт.
Так как конденсаторы имеют разные виды, формулы также используются разные.

Посредством математических выражений

Математическое выражение для определения емкости конденсатора С = q*U в единицах измерения в системе СИ каждой из входящих в формулу
физических величин определяет значение 1 фарады.

Как зависит емкость от среды диэлектрика

Влияние изолятора на емкость конденсатора зависит от проводящих свойств вещества внутри этой прокладки.
Способность межпластинного проводника на изоляцию называют диэлектрической проницаемостью.
С учетом характеристик диэлектрика формула емкости плоского устройства станет:
С = є0є S/d,
где под буквой є стоит значение диэлектрической проницаемости изолятора,
а є0 — постоянная величина равная диэлектрической проницаемости вакуума (воздуха).

На практике применяется коэффициент, обозначающий во сколько раз применяемый диэлектрик уменьшает электрическое поле по сравнению с воздухом.

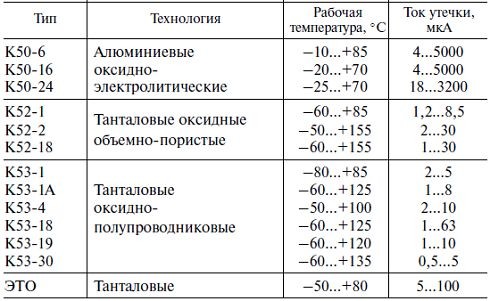
Таблица:

Как измерить емкость

Существует некоторое количество способов измерения емкости конденсатора с помощью приборов и различных методик.
В статье описывается использование мультиметра, осциллографа, тестера и мостовых измерителей.

Мультиметром

В начале, прежде чем начать измерение емкости конденсатора, его необходимо разрядить до полного исчезновения тока.

Как пример: сделать это с путем замыкания выводов отверткой.

Если пренебречь этим нюансом, то мультиметр может поломаться.

Измерить емкость с помощью мультиметра можно следующим образом:
активируйте режим «Сх» и установите предел замера 2000 пФ, если он есть.
На стандартном устройстве он равный 20 мкФ;
Установите конденсатор в соответствующие гнезда в мультиметре или используйте щупы для подключения конденсатора.
На экране прибора будет отображено значение емкости.

Осциллографом

Для измерения понадобиться кроме осциллографа собрать схему из тестируемого конденсатора, резистора и генератора синусоидальных колебаний.

Точки подключения осциллографа к схеме находятся до резистора и после конденсатора.

Частота колебаний генератора изменяется до получения на экране осциллографа одинаковых по амплитуде синусоидальных кривых.
Это делается для точности измерений.
Представьте как рассчитать емкость конденсатора с помощью амплитудных значений напряжений?
Для этого  требуется воспользоваться формулой UR/UC*2πfR подставив в нее измеренные значения.
С его помощью также рассчитывается ток утечки конденсатора косвенным способом – через снижение напряжения на предварительно известном сопротивлении.
Осциллограф способен вычислить емкость конденсаторов от 20 pF до 200 mkF.

Тестером не имеющим прямой функции

Для нахождения варианта определения емкости с помощью тестера, но без функции замера емкости,
обратите внимание на формулу мгновенного значения тока во время его зарядки или разрядки i = С dU/dt.

Здесь дело в том, что кроме тестера, секундомера следует собрать схему с источником питания,

конденсатором и резистором с большим сопротивлением для увеличения времени процесса зарядки или разрядки.
После снятия всех показаний с тестера и секундомера можно, достаточно приближенно вычислить и узнать емкость.
Зная, как определить емкость конденсатора современными приборами, будет несложно разобраться и с устройством со времен СССР.
На экране происходит вывод не цифр, а отклонения стрелки, за которой важно внимательно следить.
Измерение емкости осуществляется только на разряженном конденсаторе.
Щупы выведите к контактам конденсатора, если он рабочий, то стрелка изначально отклонится и по мере заряда займет исходную позицию.
Скорость передвижения стрелки зависит от объема емкости.
Если стрелка тестера не сдвинулась с места, либо эта величина минимальная или отклонилась и зависла в одном положении – это показатель неисправности конденсатора.

Мостовыми измерителями

Емкость конденсатора измеряется методом сравнения с эталонной емкостью.
Для чего выполняется мостовая схема, где одно плечо работает с образцовым электрическим устройством, другое с тестируемым.
Показания моста могут быть реализованы на цифровых носителях.

Единицы расчета

Математическое выражение фарада

C=Q/V, где С – электрическая емкость, Q – сообщенный заряд, V – приложенное напряжение.

Диэлектрическая проницаемость

D = εF, где D – электрическая индукция в среде, ε — диэлектрическая проницаемость среды, F — сила взаимодействия между зарядами в вакууме.

Маркировка конденсаторов

На корпусе каждого конденсатора имеется специальная маркировка – буква и цифра.
По сравнению с резисторами, маркировка конденсатора, обозначающая емкость и код отклонения емкости, довольно-таки сложная и разнообразная.
Иногда обозначения наносятся прописными буквами – MF (микрофарады), fd – фарады.
Также на корпусе указаны положительные и отрицательные символы, помогающие определить полярность конденсатора.

Способы обозначения конденсатора

Единицей измерения емкости конденсатора является фарад, поэтому на корпусе элемента обязательно присутствует буква Ф или F:

• 1 миллифарад = 10-3 фарад = 1мФ;
• 1 микрофарад = 10-6 фарад = 1 мкФ;
• 1 нанофарад = 10-9 фарад = 1 нФ;
• 1 пикофарад = 10-12 фарад = 1 пФ.

Если на элементе не обозначен номинал, то целое значение свидетельствует о том, что емкость указана в пикофарадах.
На корпусе емкость указывается с отклонением, если указана буква J – то диапазон отклонения менее 5%, буква М – 20%.

Код конденсаторов импортных

Устройства зарубежного производства, так же как и российские, имеют маркировку согласно международных стандартов.
Данный нормативный документ предполагает нанесение кода из трех цифр. Первые две цифры обозначают емкость в пикофарадах.
Третья цифра говорит о количестве нулей, например, если емкость будет меньше 1 пикофарады, цифра будет выглядеть как «0».

Кодовая для конденсаторов поверхностного монтажа

Маркировка электролитических SMD конденсаторов состоит из емкости и рабочего напряжения.
Например,108V, где закодирована электроемкость 10 пф и рабочее напряжение 8 Вольт.
Знак плюс находится рядом с полоской.
Есть три основных способа кодировки:
код из двух или трех знаков (буквы или цифры), которые указывают на рабочее напряжение и номинальную емкость.
Показатели указываются буквой, а цифра является множителем;
четыре знака, обозначающие напряжение и номинальную емкость.
Первая буква – это рабочее напряжение, следующие символы – емкость в пикофарадах, последняя цифра – количество нулей;

если площадь корпуса большая, кода располагают на две строки.
Верхняя строка – номинал емкости, нижняя – рабочее напряжение.

Емкость конденсаторов, проводов и других элементов электрической цепи измеряется в фарадах (Ф); индуктивность проводов, катушек и других элементов цепей измеряется в генри (Гн).

Емкость плоского конденсатора, состоящего из п пластин площадью пластины

где d — расстояние между пластинами, м.

Емкость цилиндрического конденсатора (коаксиального кабеля) длиной / (м), Ф:

где R1 — радиус внутренней обкладки (жилы), м;

R2 — радиус внешней обкладки, м.

Емкость прямолинейного провода длиной / и радиусом по­перечного сечения г (м) (второй провод — в бесконечности), Ф:

Индуктивность уединенного прямолинейного провода круглого сечения радиусом г и длиной / (м), Гн:

Индуктивность кольца со средним радиусом R и радиусом сечения кольца г (м), Гн:

Индуктивность многослойной катушки толщиной обмот­ки d, радиусом обмотки R (от оси до среднего слоя обмотки), длиной / (м) и числом витков w (рис. 1.2, а), Гн

Индуктивность тороидальной катушки кругового сече­ния (рис. 1.2, б), Гн:

где w — число витков катушки,

D — средний диаметр тора, м;

d — диаметр среднего витка, м.

Взаимная индуктивность двух тороидальных катушек с числами витков w^ и w2, Гн:

Рис. 1.3. Концентрически расположенные катушки индуктивности

Взаимная индуктивность концентрических катушек прямоугольного сечения, имеющих одинаковую длину и примы­кающих друг к другу (рис. 1.3), Гн:

где L12 — индуктивность катушки, состоящей из первой и второй катушек;

L1, L2 — собственные индуктивности катушек.

После несложной процедуры регистрации Вы сможете пользоваться всеми сервисами и создать свой веб-сайт.

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

— Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
— Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Свободные электрические колебания в параллельном контуре.

Основные свойства индуктивности:

— Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
— Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток его разряда, создавая магнитное поле в катушке.

Магнитный поток, увеличиваясь от нуля, создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в цепи, поэтому конденсатор разрядится не мгновенно, а через время t₁, которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L. Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Изменение (уменьшение) магнитного потока накопленной энергии катушки создаст в ней ЭДС, которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t₂ = t₁, он перезарядит конденсатор от нуля до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление. Магнитная энергия вновь будет накапливаться в катушке в течении времени t₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄), накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U (в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников, фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура, на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Расчёт ёмкости:

Расчёт индуктивности:

Похожие страницы с расчётами:

Замечания и предложения принимаются и приветствуются!

По формуле циклической частоты свободных электромагнитных колебаний , где L — индуктивность катушки (Гн), C — ёмкость конденсатора (Ф). Циклическую частоту расписываем как: , где V — «ню» частота колебаний (Гц). Данную формулу подставляем в формулу циклической частоты свободных электромагнитных колебаний: . Поизводим преобразования и выражаем искомую ёмкость конденсатора:

В системе СИ: 10 МГц = 10*10⁶ Гц; 5,1 мкГн = 5,1*10⁻⁶ Гн. Подставляеи вычисляем:

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме.

Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10^-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W_эл = CU²/2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U_c = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I_зар = Е/R_i, поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I_ут = U/R_d, где I_ут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а R_d – сопротивление изоляции.