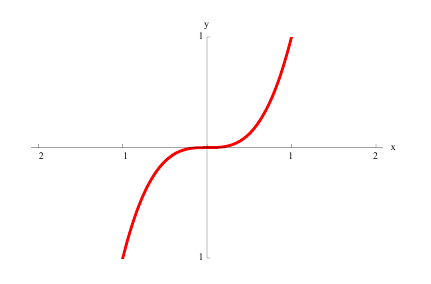
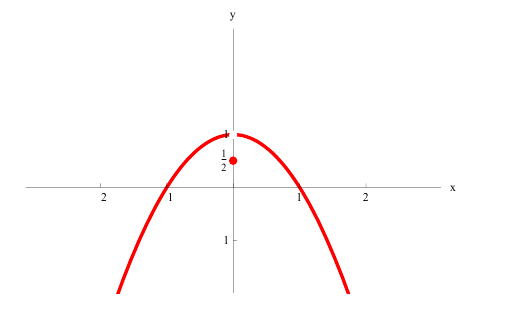
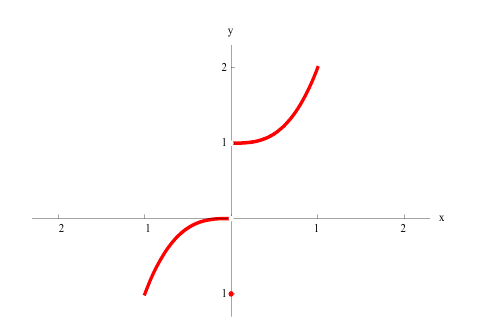
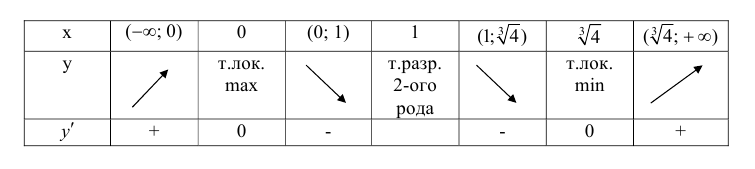
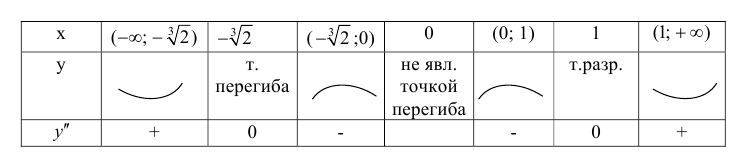
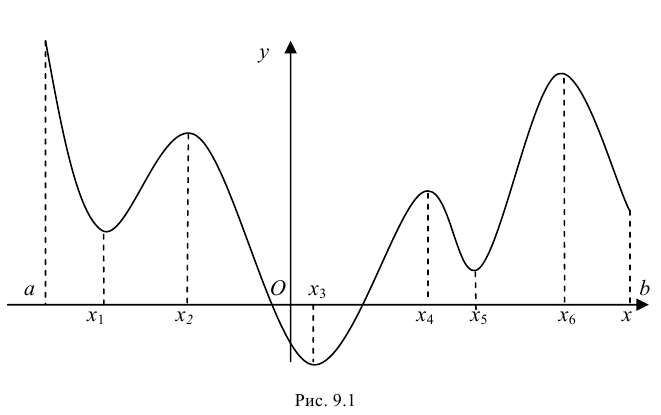
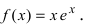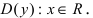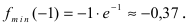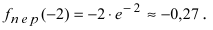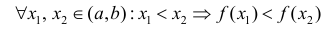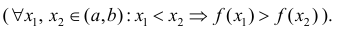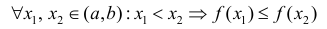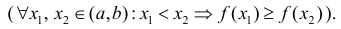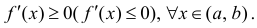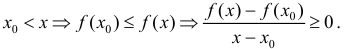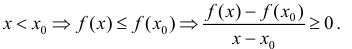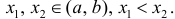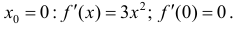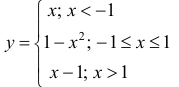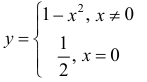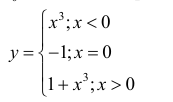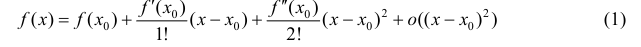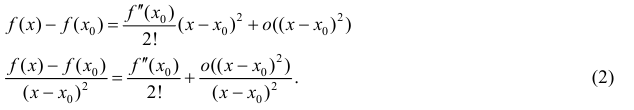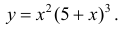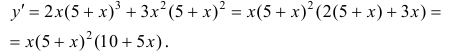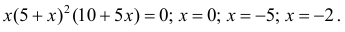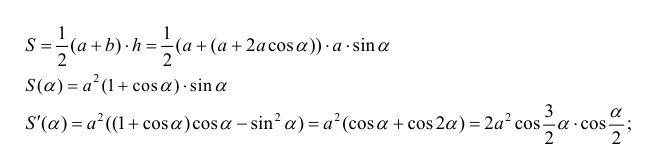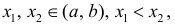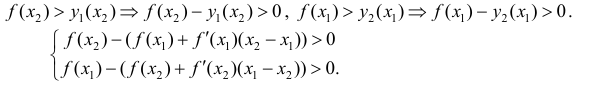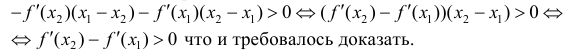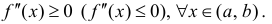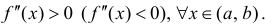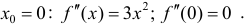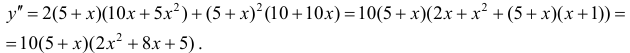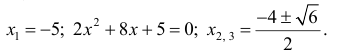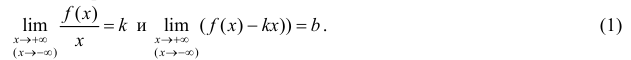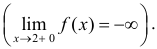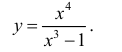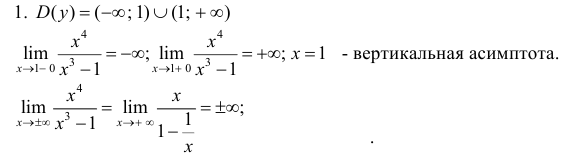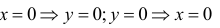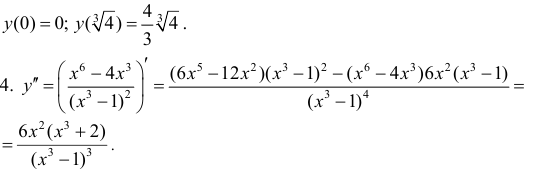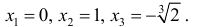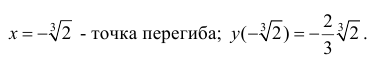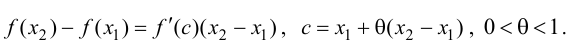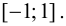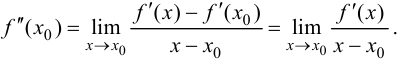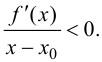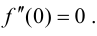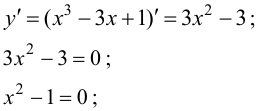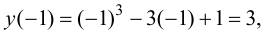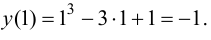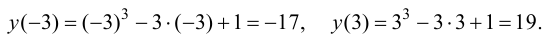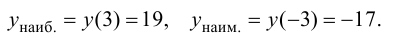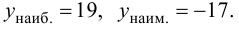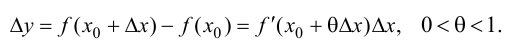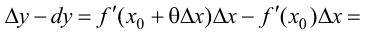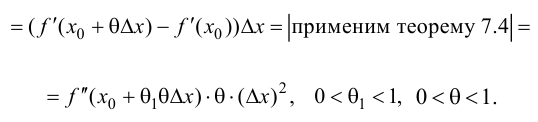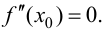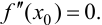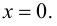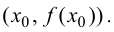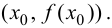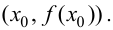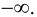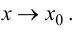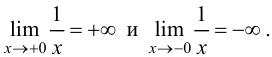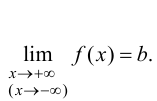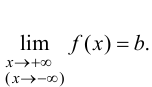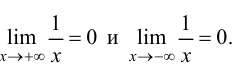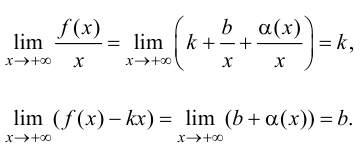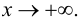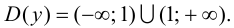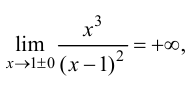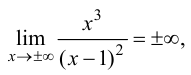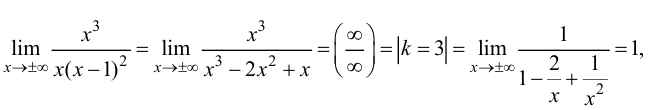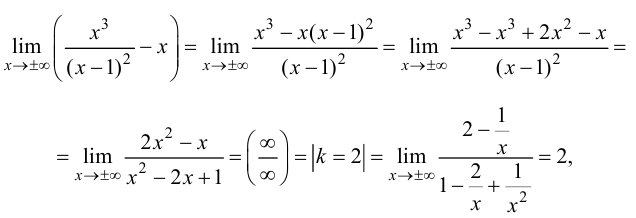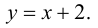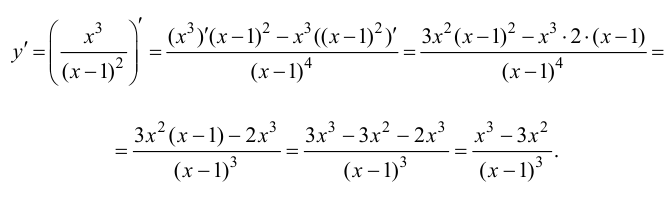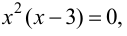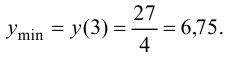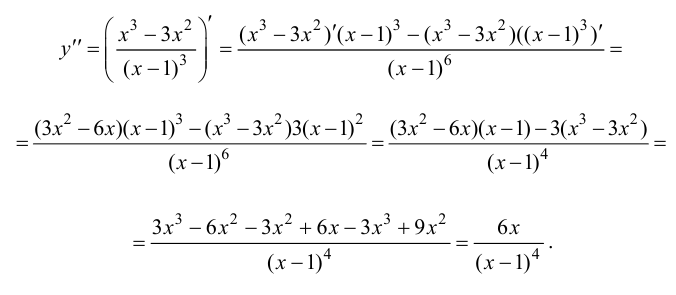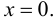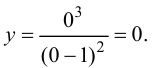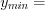Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.
Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.
Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.
Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.
В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.
Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.
Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).
Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).
Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).


Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:
— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.
С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).
Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.
(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.
(- 9): функция возрастает, а потом убывает – максимум.
(-7): минимум.
(3): максимум.
Все вышесказанное можно обобщить следующими выводами:
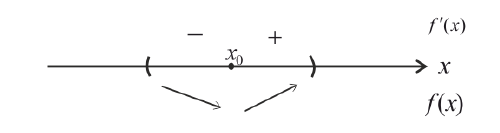
— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
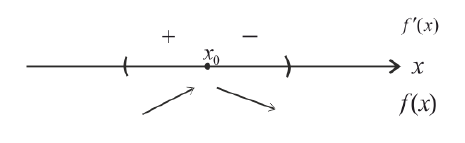
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.
Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?
Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:
- Найдите производную функции (f'(x)).
- Найдите корни уравнения (f'(x)=0).
- Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
- Определите знак производной в каждом промежутке (методом интервалов).
- Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
- Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.
Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

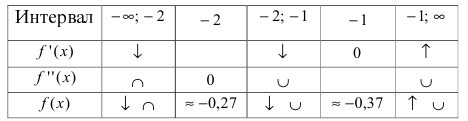
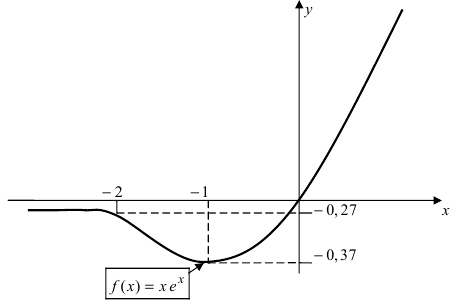
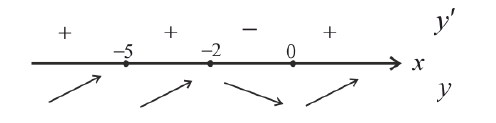
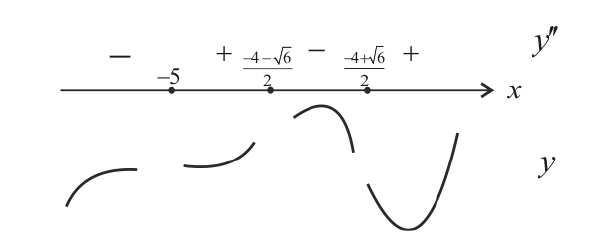
Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:
(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)
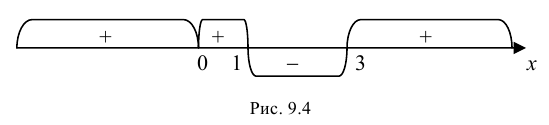
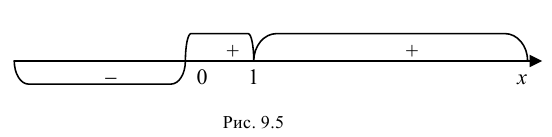
3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:
Теперь очевидно, что точкой максимума является (-2).
Ответ. (-2).
Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов
Скачать статью
Содержание:
Исследование функций с помощью производных
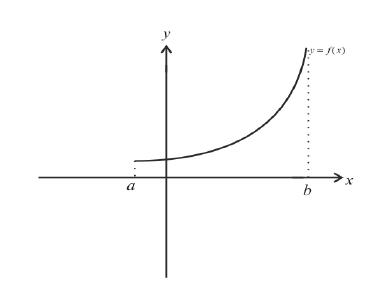
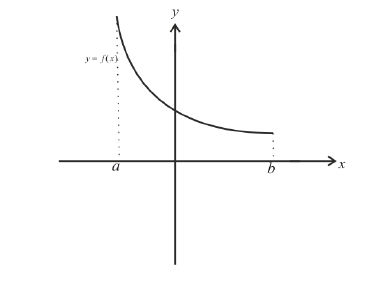
Необходимое условие возрастания и убывания функции
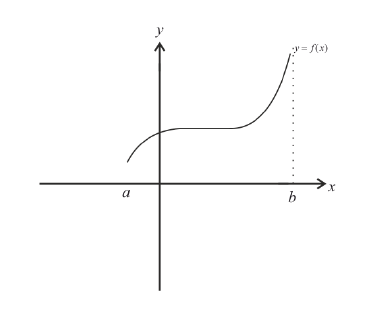
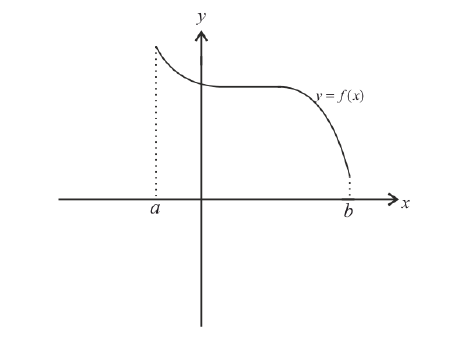
Из определений возрастающей и убывающей функций следует необходимое условие возрастания и убывания функции.
Теорема: Если дифференцируемая функция
Доказательство: Пусть дифференцируемая функция 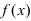
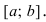
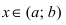
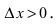
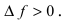
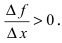
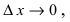
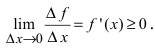
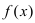
Замечание: С геометрической точки зрения возрастающая на сегменте 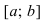
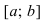
Пример:
Найти интервалы возрастания и убывания функции
Решение:
Из графика этой функции видно, что 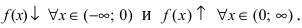
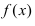
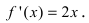
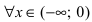
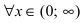
Достаточное условие возрастания и убывания функции
Теорема: Пусть функция 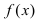
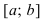
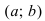
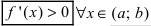
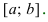
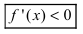
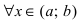
Доказательство: Пусть первая производная функции 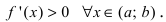
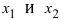
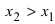
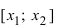
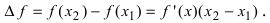
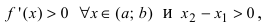
Таким образом, функция 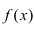
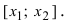
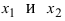
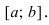
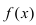
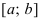
Условия постоянства функции на сегменте (a; b)
Условия постоянства функции на сегменте 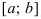
ТЗ. Пусть функция 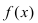
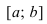
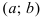
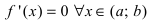
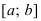
Доказательство: Пусть первая производная функции 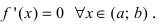
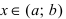
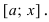
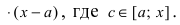
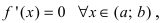
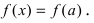
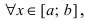
Минимум и максимум (экстремумы) функции
Пусть функция 
Определение: Функция 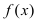
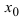
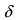
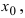
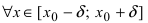
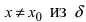

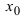
Обозначение
Определение: Функция 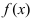
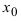
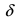
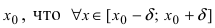
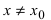
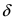
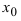
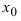
Обозначение
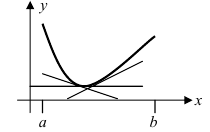
Пример:
Найти на заданном графике точки максимума и минимума (Рис. 77).
Рис. 77. Максимумы и минимумы заданной функции.
Решение:
Определение: Точки минимума и максимума объединяются под общим названием точки экстремума.
Замечание: Точки экстремума всегда являются внутренними точками области определения функции.
Замечание: Не следует путать минимальное значение функции 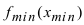
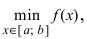
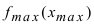
Замечание: Из определения экстремума следует, что в точке минимума выполняется неравенство 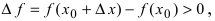
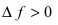
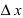
Необходимое условие существования экстремума функции
Теорема: Если дифференцируемая функция 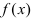
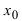
Доказательство: Пусть в точке 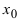
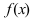
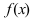
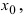
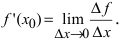
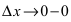
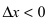
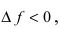
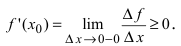
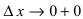
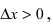
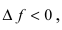
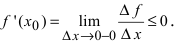
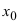
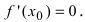
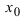
Замечание: Обращение в нуль первой производной функции в точке х0 я взлетел необходимым, но не достаточным условием существования экстремума в этой точке. Непрерывная функция может иметь экстремум в точке х0 даже в том случае, когда ее первая производная в этой точке не существует. В этом случае говорят об “острых” экстремумах.
Пример:
Доказать, что функция 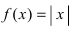
Решение:
Из Рис. 72 видно, что в точке 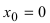
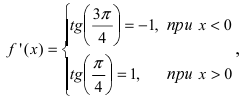
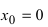
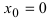
Определение: Точки, в которых первая производная функции обращается в нуль или не существует, называются критическими (стационарными или подозрительными на экстремум).
Замечание: Всякая точка экстремума является критической точкой, однако не любая критическая точка будет экстремумом.
Пример:
Доказать, что функция 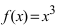
Решение:
В точке 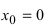
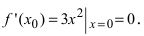
Исследование функций с помощью производных
Первый и второй достаточные признаки существования экстремума
Первый достаточный признак существования экстремума:
Теорема: Если функция 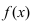
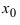
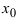
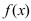
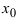
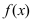
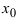
Второй достаточный признак существования экстремума:
Теорема: Если в точке 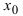
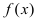
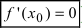
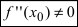
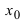
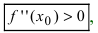
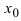
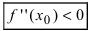
Пример:
Найти и определить тип экстремумов функции
Решение:
Вычислим первую производную функции и приравняем ее к нулю с целью отыскания критических точек: 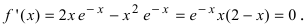
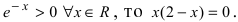
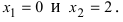
При переходе слева направо через точку 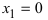
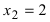
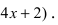
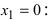
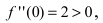
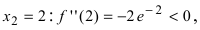
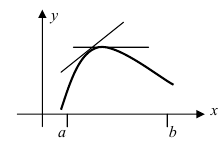
Наименьшее и наибольшее значения функции на сегменте (a; b)
Наименьшее и наибольшее значения функции на сегменте
Пусть функция 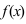
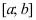
- Находят область определения функции и убеждаются в том, что заданный сегмент входит в эту область.
- Находят критические точки, для чего решают уравнение
и точки, в которых первая производная функции не существует.
- Вычисляют значения функции в критических точках, принадлежащих заданному сегменту, в точках, в которых первая производная функции не существует и на концах заданного сегмента.
- Из полученных чисел выбирают наименьшее
и наибольшее
.
Пример:
Найти наименьшее и наибольшее значения функции 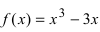
Решение:
Действуя согласно вышеприведенной схеме, находим:
1. 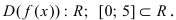
2. Вычислим первую производную 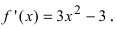
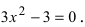
3. Вычислим значение функции в критических точках и на концах заданного сегмента:
4. Из полученных чисел выбираем наименьшее 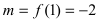
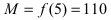
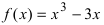
Выпуклость и вогнутость графика функции. Точки перегиба
Определение: График функции 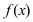
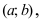
Рис. 78. Выпуклый график функции
Определение: График функции 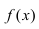
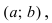
Рис. 79. Вогнутый график функции
Достаточные условия выпуклости и вогнутости графика функции на том или ином интервале определяются теоремой:
ТЗ. Если вторая производная функции 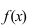
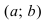
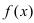
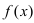
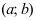
Пример:
Определить интервалы вогнутости и выпуклости графика функции
Решение:
Найдем вторую производную от заданной функции 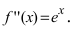
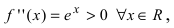
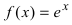
Пример:
Определить интервалы вогнутости и выпуклости графика функции
Решение:
Найдем вторую производную от заданной функции 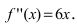
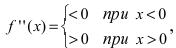
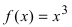
Определение: Точка, отделяющая вогнутую часть графика функции от выпуклой (или выпуклую часть графика функции от вогнутой), называется точкой перегиба.
Необходимое и достаточное условия существования точки перегиба
Рассмотрим необходимое условие существования точки перегиба.
Теорема: Если функция 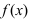
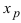
Замечание: Обращение в нуль второй производной функции в точке перегиба является необходимым, но не достаточным условием существования такой точки на графике функции.
Пример:
Доказать, что точка 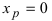
Решение:
Если вычислить вторую производную от заданной функции, то она будет равна 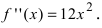
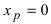
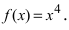
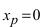
Теорема: Пусть функция 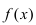
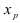
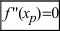
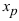
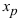
Пример:
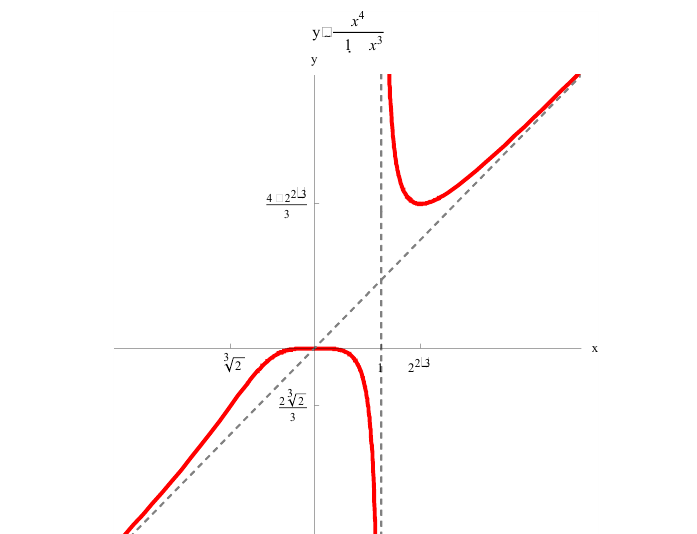
Найти точки перегиба и интервалы выпуклости и вогнутости графика функции
Решение:
Найдем вторую производную заданной функции 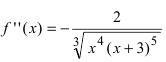
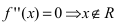

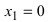
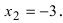
Из рисунка видно, что точка 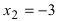
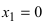
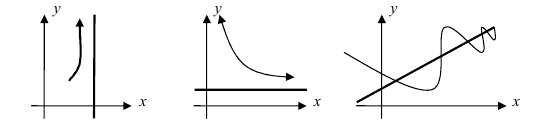
Асимптоты графика функции f (x)
Асимптоты графика функции
В большинстве практических случаев необходимо знать поведение функции при неограниченном росте (убыли) аргумента. Одним из наиболее интересных случаев, которые возникают при таком исследовании, является случай, когда график функции неограниченно приближается к некоторой прямой.
Определение: Прямая (l): 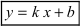
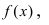
Замечание: График функции может приближаться к асимптоте сверху, снизу, слева, справа или колеблясь возле этой прямой (Рис. 80).
Рис. 80. Различные случаи приближения графика функции к асимптотам.
Различают вертикальные, горизонтальные и наклонные асимптоты.
Определение: Вертикальная прямая 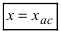
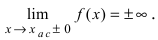
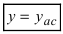
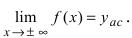
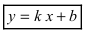
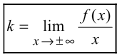
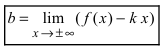
Горизонтальная асимптота является частным случаем наклонной асимптоты: если 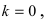
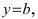
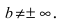
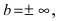
Полная схема исследования функции с помощью производных
Из изложенного в Лекциях № 20 и №21 материала следует следующая схема исследования функции с помощью производных:
- Находят область определения функции. При наличии точек разрыва II рода изучают поведение функции в их малой окрестности, т.е. вычисляют лево- и правосторонние пределы. При задании функции словесным образом также вычисляют лево- и правосторонние пределы для граничных точек интервалов, на которых функция описывается разными формулами.
- Находят точки пересечения с координатными осями.
- Определяют четная, нечетная или общего вида заданная функция.
- Определяют периодическая или непериодическая заданная функция.
- Находят критические точки, решая уравнение
и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (
) и убывания(
) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.
- Находят точки подозрительные на перегиб, решая уравнение
и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (
) и выпуклости (
) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.
- Находят асимптоты графика функции.
- Результаты исследования заносят в сводную таблицу
- Поданным таблицы строят схематичный график функции.
Замечание: При нахождении области определения функции надо помнить о действиях, запрещенных в области действительного переменного:
- нельзя делить на нуль, поэтому выражение, стоящее в знаменателе дроби, не должно равняться нулю;
- нельзя извлекать корень четной степени из отрицательного числа, поэтому выражение, стоящее под корнем четной степени, должно быть неотрицательным (
);
- основание логарифмической функции должно быть строго положительным и не равным единице;
- выражение, стоящее под логарифмом, должно быть строго положительным;
- выражение, стоящее под знаком arcsin или arccos, по модулю не должно превышать единицу (
).
Пример:
Исследовать и построить схематичный график функции
Решение:
Используя схему исследования графика функции с помощью производных, найдем:
1.
2. Найдем точки пересечения графика функции с координатными осями
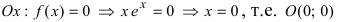
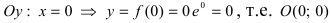
3. Вычислим 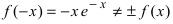
4. Функция непериодическая (периодическими среди элементарных функций являются функции: sinx, cosx, tgx и ctgx).
5. Найдем первую производную функции 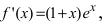
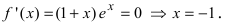

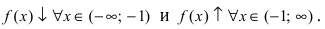
6. Найдем вторую производную функции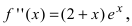
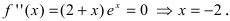

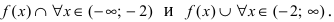
7. Найдем асимптоты графика функции, для чего вычислим угловой коэффициент прямой 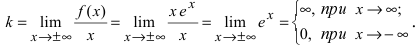
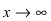
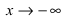
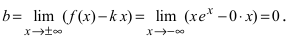
8. Построим сводную таблицу
О(0; 0) — точка пересечения с координатными осями.
у = 0 — горизонтальная асимптота.
9. Построим схематичный график функции, выбрав по координатным осям разные масштабы измерения:
———
Исследование функций с помощью производных
Определение 1. Функция y=f(x) называется возрастающей (убывающей) на интервале ( a,b ), если
Функция y=f(x) называется неубывающей (невозрастающей) на
интервале ( a,b ), если
Возрастает:
Убывает:
Неубывает:
Невозрастает:
Функции из определения 1 называются монотонными.
Теорема 1. Для того, чтобы дифференцируемая на интервале ( a,b ) функция
y=f(x) не убывала (не возрастала) на этом интервале необходимо и достаточно,
чтобы
Доказательство. Необходимость. Рассмотрим случай, когда f(x) не
убывает и докажем, что производная 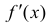
Пусть
Пусть
Таким образом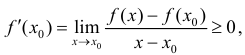
Достаточность. Рассмотрим случай, когда 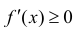
Тогда по теореме Лагранжа (теорема 4 § 12) ∃ точка 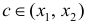
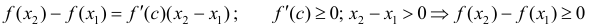
Теорема 2. Для того, чтобы дифференцируемая на интервале ( a,b ) функция
y=f(x) возрастала (убывала) на этом интервале достаточно, чтобы
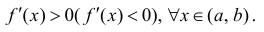
Доказательство теоремы аналогично доказательству достаточности в теореме 1. Нужно заметить, что условие 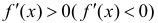
Пример 1.
Рассмотрим функцию 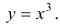
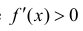
Теорема 3. (необходимое условие экстремума).
Пусть функция y=f(x) определена в некоторой окрестности точки 
Доказательство.
Если производная 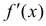

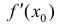
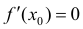
Определение 2. Пусть функция y=f(x) непрерывна в точке 

Замечание. Для непрерывной функции любая точка локального экстремума
будет критической. Наоборот – не верно.
Пример 2.
Для функции 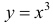
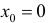
Для функции
(см. пример 9 §5) 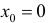

Для функции
точка 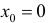



Для функции
точка 


Теорема 4. (достаточное условие экстремума функции). Пусть функция y=f(x)
дифференцируема в некоторой окрестности 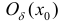


а) Пусть при переходе через точку 
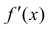
на «+» :
Тогда 
Пусть при переходе через точку 
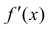
Тогда 
б) Пусть при переходе через точку 
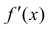
Тогда 
Доказательство следует из теоремы 2. При этом важно, чтобы функция y=f(x) была непрерывна в точке 

Теорема 5. (второе достаточное условие экстремума функции).
Пусть 
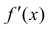
Пусть 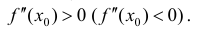

максимума).
Доказательство. Запишем формулу Тейлора 2-ого порядка для функции y=f(x) в окрестности точки 
(см. теорему 1 §14).
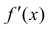
Из (2) следует, что ∃ окрестность точки 
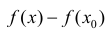
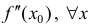
Теорема 6. Пусть функция y=f(x) имеет в точке 
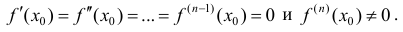
1) если n – четное и 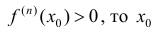
2) если n – четное и 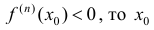
3) если n – нечетное, то в точке 
Доказательство аналогично доказательству теоремы 5.
Пример 3.
Исследовать на экстремум функцию
Решение. Функция непрерывна ∀x∈R .
Найдем критические точки:
x=-2 — точка локального максимума: y(-2) = 108 y;
x = 0 — точка локального минимума; y(0) = 0.
x = −5 — не является точкой экстремума.
При исследовании функции на экстремум точки разрыва(если они есть)
также наносят на числовую прямую. При переходе через эти точки может
изменятся направление возрастания (убывания) функции.
Замечание. При решении ряда технических и экономических задач приходится находить не локальные, а глобальные экстремумы (наибольшие и наименьшие значения функций на некотором множестве). Из теоремы Вейерштрасса (см. теорему 1 §11) следует, что для непрерывной функции y=f(x) заданной на отрезке [ a,b] глобальные min и max существуют. При этом точки с 1 и с 2 – глобального min и max лежат либо на концах отрезка [ a,b], либо являются критическими для функции f(x).
Пример 4.
Найти наибольшее и наименьшее значение функции 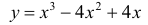
Решение. Функция непрерывна ∀x∈R. Найдем критические точки:
Пример 5.
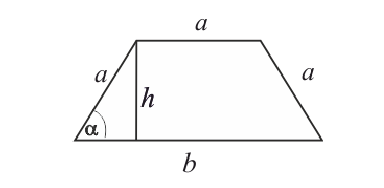
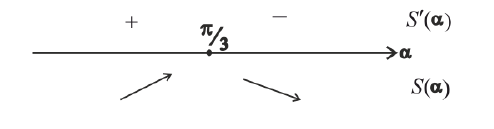
Боковые стороны и меньшее основание трапеции = а . Найти
длину большего основания, при котором площадь трапеции – наибольшая.
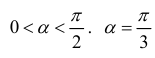
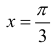
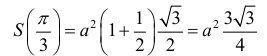
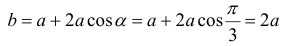
——-
Исследование функций с помощью производных(часть вторая)
Определение 1. Пусть функция y=f(x) дифференцируема на интервале ( a,b) . И пусть 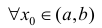
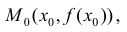
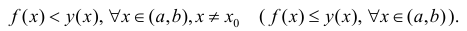
Пусть 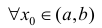
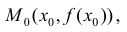
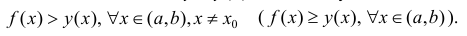
Пример 1.
а) 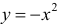
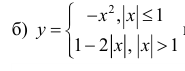
в) 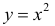
г) 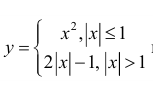
Теорема 1. Для того, чтобы дифференцируемая функция y=f(x) была вогнутой (выпуклой) на интервале ( a,b ) необходимо и достаточно, чтобы ее производная 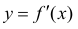
Докажем для случая, когда y=f(x) — вогнута.
Необходимость. Пусть
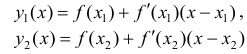
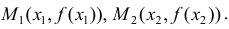
Сложим эти неравенства:
Достаточность. Пусть 
Пусть 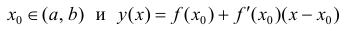
Пусть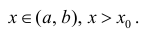
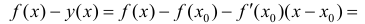
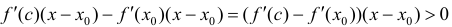
Теорема 2. Для того, чтобы дифференцируемая функция y=f(x) была нестрого вогнутой (нестрого выпуклой) на интервале ( a,b ) необходимо и достаточно, чтобы производная 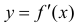
Доказательство аналогично доказательству теоремы 1.
Теорема 3. Для того, чтобы дважды дифференцируемая на интервале (a,b) функция y=f(x) была не строго вогнутой (не строго выпуклой) необходимо и
достаточно, чтобы
Доказательство следует из теоремы 2 и теоремы 1 §15.
Теорема 4. Для того, чтобы дважды дифференцируемая на интервале (a,b)
функция y=f(x) была вогнутой (выпуклой) на этом интервале достаточно, чтобы
Доказательство следует из теоремы 1 и теоремы 2 §15. Нужно заметить, что
условие 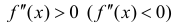
Пример 2.
Рассмотрим функцию 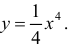
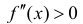
Теорема 6 (достаточное условие перегиба функции). Рассмотрим функцию
y=f(x) дважды дифференцируемую в некоторой окрестности 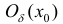
возможного перегиба 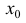
Предположим также, что вторая производная 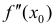
через точку 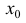
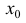
Доказательство следует из теоремы 4.
Пример 3.
Найдем точки перегиба и интервалы выпуклости-вогнутости функции
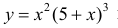
Решение.
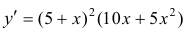
Найдем точки возможного перегиба(точки, где y′′ равна 0 или не существует).
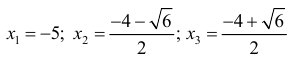
При нахождении интервалов выпуклости-вогнутости точки, где функции
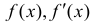
через эти точки может меняться направление выпуклости-вогнутости.
Определение 4. Прямая y= kx +b называется наклонной асимптотой функции y=f(x) при x →+∞ (x→−∞), если 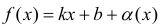
Теорема 7. Для того, чтобы прямая y =kx +b была наклонной асимптотой для функции y=f(x) при x →+∞ (x→−∞) необходимо и достаточно, чтобы существовали пределы
Доказательство. Рассмотрим, например, случай x → +∞ .
Необходимость. Пусть 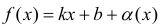
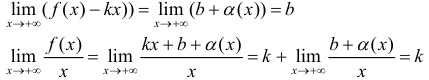
Достаточность. Пусть выполняется (1). Докажем, что y =kx +b — асимптота для y=f(x).
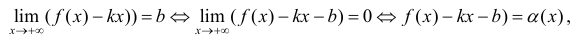
Замечание. Наличие наклонной асимптоты значит, что при x →+∞ (x→−∞) график функции очень близок к прямой линии y =kx +b.
Пример 4.
Для функции 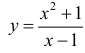
Для функции 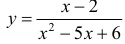
Для функции 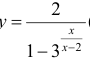
Для функции , 1(0 1) 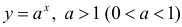
асимптота при x →+∞ (x→−∞).
Определение 5. Прямая 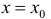
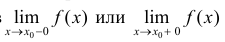
Пример 5.
Для функции 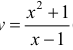
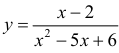
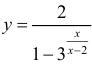
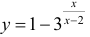
При построении графиков функции используют результаты §15, 16. Это можно проводить по следующей схеме:
1. Найти область определения D(f) функции и исследовать поведение функции в граничных точках D(f) . Определить точки разрыва, вертикальные асимптоты, нули функции, исследовать функцию на периодичность, четность, нечетность.
2. Найти наклонные асимптоты.
3. Найти интервалы монотонности, точки локального экстремума.
4. Найти интервалы выпуклости, вогнутости, точки перегиба.
5. Построить график.
Пример 6.
Провести полное исследование и построить график функции
Нули функции
Таким образом график пересекает оси координат в точке О(0; 0). Функция
ни четная, ни нечетная, не периодическая.
2. Наклонные асимптоты. По формулам (1);
x = 0 — точка локального максимума; 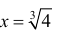
Точки где y′′ равна 0 или не существует:
5. График функции.
———
Исследование функции с помощью производных
Монотонность функции
Теорема 9.1. Пусть функция 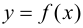
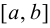
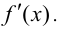
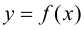
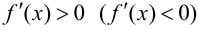
Доказательство.
Возьмем отрезок 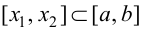
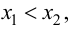
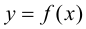
Тогда, если 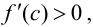
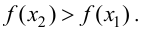
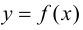
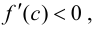
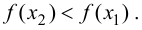
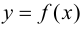
Замечание 9.1. Утверждение теоремы сохраняет силу и в том случае, если 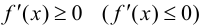
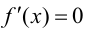
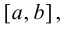
Пример 9.1. Рассмотрим функцию 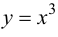
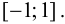
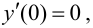
- Заказать решение задач по высшей математике
Достаточные условия экстремума
Теорема 9.2 (первое достаточное условие экстремума). Пусть функция 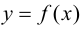
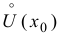
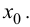
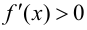
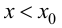
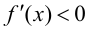
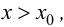
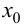
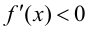
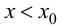
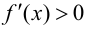
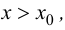
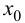
Доказательство следует из теоремы 9.1.
Теорема 9.3 (второе достаточное условие экстремума). Если в критической точке 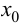
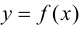
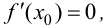
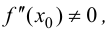
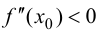
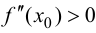
Доказательство.
Если в точке 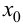
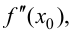
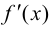
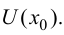
Пусть 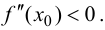
При 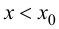
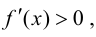
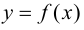
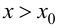
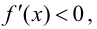
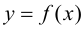
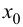
Случай 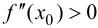
Замечание 9.2. Так как теорема формулирует только достаточное условие, то при 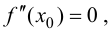
Пример 9.2. Функция 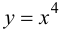
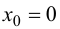
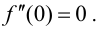
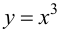
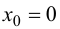
Наибольшее и наименьшее значения функции на отрезке
Пусть функция 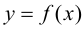
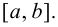
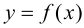
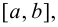
Таким образом, непрерывная функция 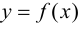
Исходя из вышесказанного, можно предложить следующий алгоритм поиска наибольшего и наименьшего значений непрерывной функции 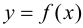
1. Найти все критические точки. Если критическая точка 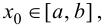
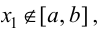
2. Вычислить значения функции на концах отрезка, т. е. найти 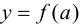
3. Из всех полученных выше значений функции выбрать наибольшее и наименьшее, они и будут представлять собой наибольшее и наименьшее значения функции 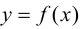
Пример 9.3. Найти наибольшее и наименьшее значения функции 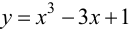
Решение.
Так как функция 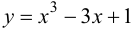
1. Найдем критические точки функции.
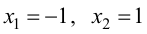
Так как 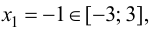
так как 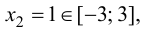
2. Определим значения функции на концах отрезка:
3. Сравним вычисленные значения функции и выберем наибольшее и наименьшее:
Ответ:
Выпуклость и вогнутость графика функции, точки перегиба
Пусть функция 
Определение 9.1. График функции 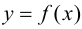
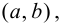
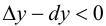
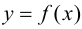
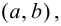
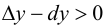
Определение 9.2. Точки графика функции, в которых выпуклость сменяется вогнутостью или наоборот, называются точками перегиба графика.
Теорема 9.4. Пусть функция 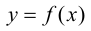
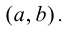
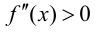
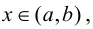
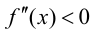
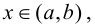
Доказательство.
Рассмотрим разность 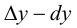
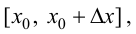
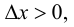
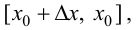
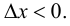
Поэтому
Тогда, при 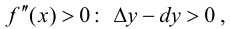
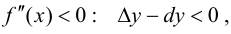
Теорема 9.5 (необходимое условие точки перегиба). Пусть график функции 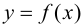
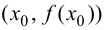
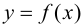
Доказательство.
Пусть 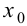
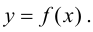
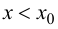
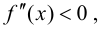
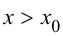
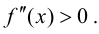

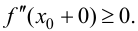
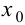
Определение 9.3. Точка 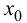
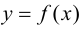
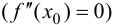
Замечание 9.3. Не всякая точка 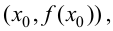
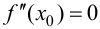
Пример 9.4. График функции 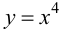
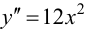
Теорема 9.6 (достаточное условие точки перегиба). Пусть функция 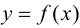
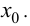
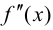
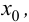
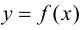
Доказательство.
Из того, что 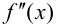
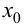
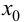
Замечание 9.4. Теорема остается верной, если функция 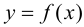
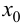
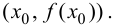
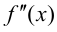
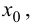
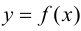
Пример 9.5. Точка (0; 0) является точкой перегиба графика функции 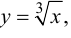
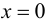
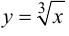
Асимптоты графика функции
При исследовании поведения функции на бесконечности, т. е. при 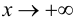
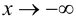
Определение 9.4. Прямая 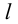
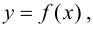
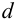
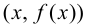
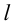
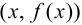
Существуют три вида асимптот: вертикальные, горизонтальные и наклонные.
Определение 9.5. Прямая 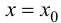
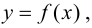
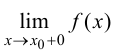
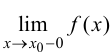
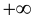
В этом случае расстояние от точки графика функции 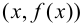
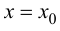
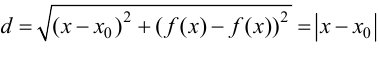
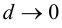
Пример 9.6. График функции 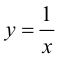
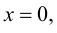
Определение 9.6. Прямая 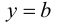
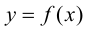
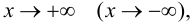
В этом случае расстояние от точки графика функции 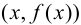
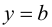
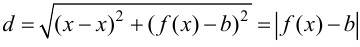
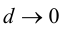
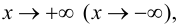
Пример 9.6 (продолжение). График функции 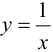
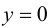
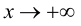
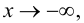
Определение 9.7. Прямая 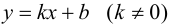
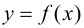
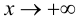
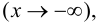
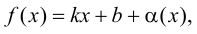
где 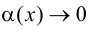
Теорема 9.7. Для того чтобы прямая 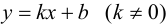
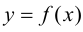
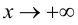
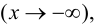
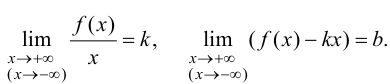
Доказательство. Рассмотрим случай
Необходимость.
Если 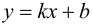
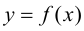
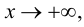
Достаточность.
Пусть существуют пределы (9.2). Тогда из второго равенства следует, что
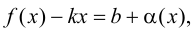
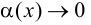
Полученное равенство легко преобразовать к виду (9.1), т. е. прямая 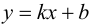

Схема исследования функции и построения ее графика
Рассмотрим примерный план, по которому целесообразно исследовать поведение функции и строить ее график:
1. Найти область определения функции.
2. Проверить выполнение свойств четности или нечетности, периодичности.
3. Указать промежутки непрерывности, точки разрыва и их тип, проверить наличие асимптот.
4. Найти промежутки монотонности и точки экстремума.
5. Найти промежутки выпуклости и вогнутости, точки перегиба.
6. Найти точки пересечения графика функции с осями координат.
7. Построить график функции.
Замечание 9.5. Если исследуемая функция 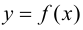
Замечание 9.6. Если исследуемая функция 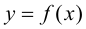
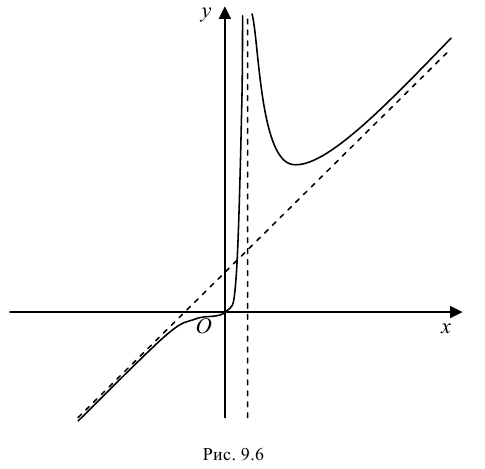
Пример 9.7. Исследовать функцию 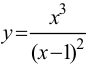
Решение.
1.
2. Так как область определения функции несимметрична относительно начала координат, то эта функция общего вида, т. е. функция ни четная, ни нечетная, непериодическая.
3. Функция непрерывна на области определения как элементарная. Точкой разрыва является 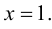
то 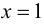
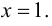
Проверим наличие горизонтальных асимптот. Так как
то данная функция не имеет горизонтальных асимптот. Проверим наличие наклонных асимптот. Так как
то график функции имеет наклонную асимптоту с угловым коэффициентом 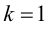
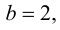
4. Определим промежутки возрастания и убывания функции, точки экстремума. Для этого найдем критические точки первого рода:
Решим уравнение 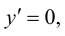
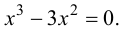
откуда 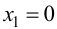
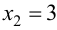
Так как 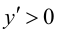
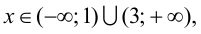
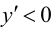
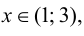
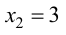
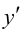
5. Определим промежутки выпуклости и вогнутости графика функции, точки перегиба. Для этого найдем критические точки второго рода:
Решим уравнение 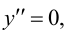
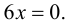
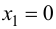
Так как 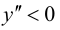
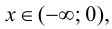
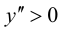
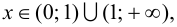
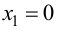
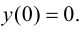
6. Найдем точки пересечения графика функции с осями координат.
Для точек оси 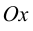
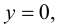
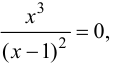
Для точек оси 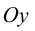
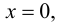
Таким образом, единственной точкой пересечения графика функции с осями координат является начало системы координат
7. Построим график функции на рис. 9.6.
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
- Замечательные пределы
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
7. Взаимосвязь функции и ее производной
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Связь производной с точками экстремума функции
В данных задачах речь идет о непрерывных функциях (простым языком, функция будет непрерывна на интервале, если ее график можно нарисовать на этом интервале, не отрывая ручку от листа).
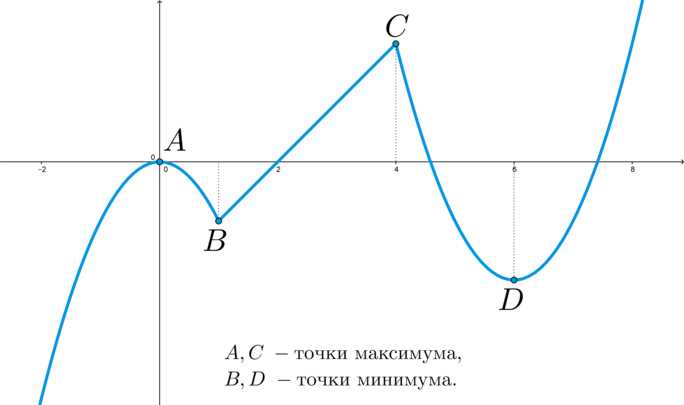
(blacktriangleright) (color{royalblue}{text{Точки}}) (локального) (color{royalblue}{text{экстремума}}) функции – это точки (локального) максимума и минимума.
Окрестность – это интервал вокруг точки некоторого радиуса. Например, окрестностью точки (x=0) можно назвать интервал ((-1;1)), или ((-0,1;0,1)), или ((-0,0000001;0,0000001)) и т.д.
(blacktriangleright) (color{royalblue}{text{Точка}}) (color{royalblue}{text{максимума}}) (x_{max}) – такая внутренняя точка области определения функции, для которой выполнено: (f(x)leqslant
f(x_{max})) для любого (x) из некоторой окрестности точки (x_{max}).
То есть можно найти такую окрестность, что для любой точки из этой окрестности будет выполнено данное неравенство.
Заметим, что, например, если функция определена на отрезке ([0;2]), то все точки интервала ((0;2)) будут внутренними, а вот точки (0) и (2) – граничными (то есть не внутренними).
(blacktriangleright) (color{royalblue}{text{Точка}}) (color{royalblue}{text{минимума}}) (x_{min}) – такая внутренняя точка области определения функции, для которой выполнено: (f(x)geqslant
f(x_{min})) для любого (x) из некоторой окрестности точки (x_{min}).
Например, для точки (C) за окрестность можно взять интервал ((3;5)) или даже ((2;6)), а можно совсем маленький — ((4-0,01;4+0,01)).
Следующие факты помогают искать точки экстремума функции.
(blacktriangleright) Если производная (f’) в точке (x) равна нулю и меняет свой знак слева направо с “(+)” на “(-)” , то эта точка является точкой максимума.
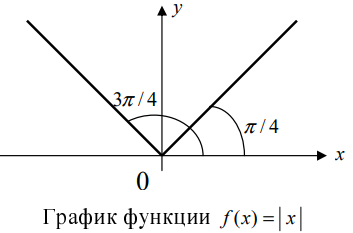
Заметим также, что если производная (f’) в точке (x) не существует и меняет свой знак слева направо с “(+)” на “(-)” (но (x) – внутренняя точка области определения функции (f,)!), то эта точка является точкой максимума.
Пример: в точке (A) производная равна нулю и эта точка является точкой максимума; в точке (C) производная не “равна нулю”, а не существует, при этом точка (C) также является точкой максимума.
(blacktriangleright) Если производная в точке (x) равна нулю и меняет свой знак слева направо с “(-)” на “(+)” , то эта точка является точкой минимума.
Также, если производная (f’) в точке (x) не существует и меняет свой знак слева направо с “(-)” на “(+)” (но (x) – внутренняя точка области определения функции (f,)!), то эта точка является точкой минимума.
(blacktriangleright) Заметим, что точки экстремума – это значение абсциссы (x).
(blacktriangleright) Заметим, что существует такое понятие, как критические точки — это все точки, в которых производная функции либо равна нулю, либо не существует.
Таким образом, только часть критических точек является точками экстремума.
Задание
1
#3107
Уровень задания: Равен ЕГЭ
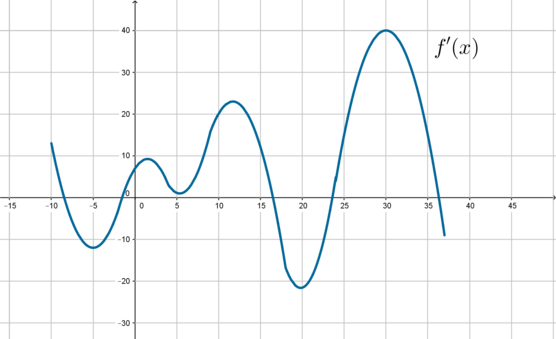
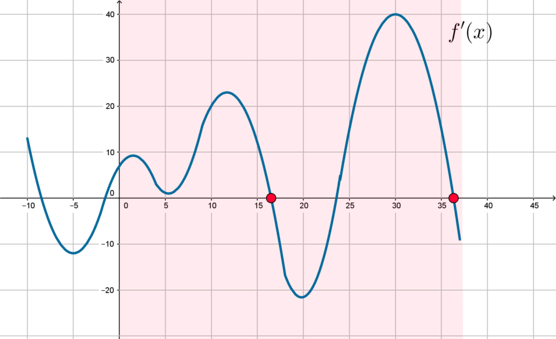
На рисунке изображен график производной функции (f(x)), определенной на отрезке ([-10;37]). Найдите количество точек максимума функции (f(x)) на отрезке ([0;37]).
Точка максимума – значение (x), в котором производная меняет свой знак с “(+)” на “(-)”. Следовательно, в этой точке ее график пересекает ось абсцисс “сверху вниз” (если двигаться по рисунку слева направо). Отметим отрезок ([0;37]) и увидим, что таких точек 2:
Ответ: 2
Задание
2
#2962
Уровень задания: Равен ЕГЭ
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2,4; 8,7)). Найдите сумму точек экстремума этой функции на отрезке ([1;6]).
Так как на рисунке изображен график функции, то точки экстремума – это точки на графике, в которых функция меняется с возрастания на убывание или наоборот. Эти точки: (x=-1; 0; 2; 4; 5; 8.) Из них на отрезке ([1;6]) лежат только точки (2; 4; 5), следовательно, их сумма равна (2+4+5=11.)
Ответ: 11
Задание
3
#730
Уровень задания: Равен ЕГЭ
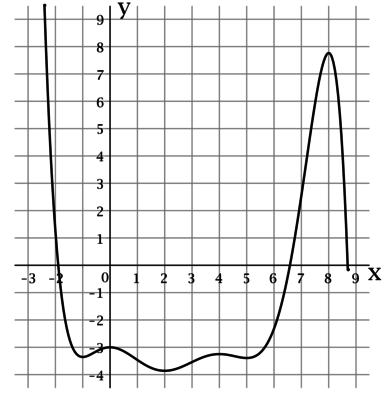
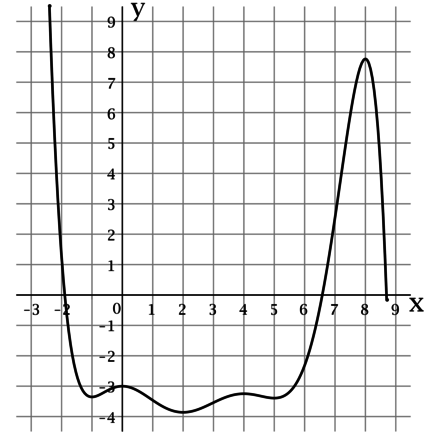
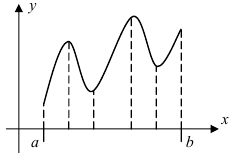
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-3; 8,5)). Найдите сумму точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (0), (4) и (8), а локально максимальные значения в точках (-2), (1) и (6). Таким образом, сумма точек экстремума этой функции равна (0 + 4 + 8 + (-2) + 1 + 6 = 17).
Ответ: 17
Задание
4
#731
Уровень задания: Равен ЕГЭ
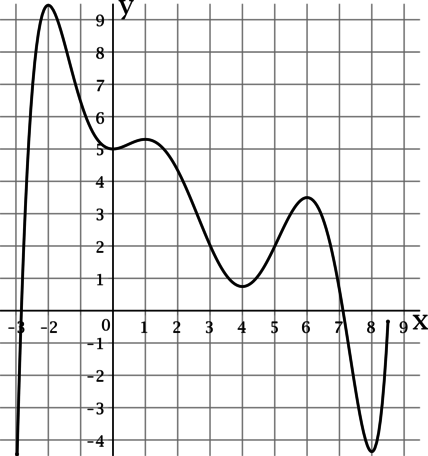
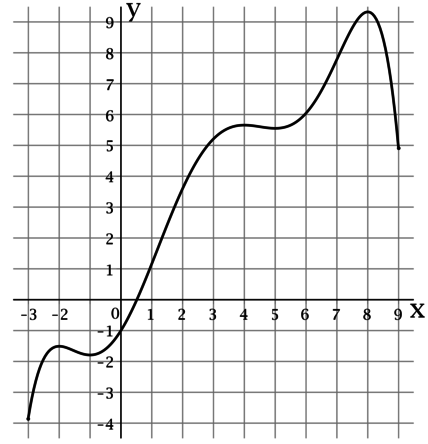
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2,4; 8,7)). Найдите сумму точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (-1), (2) и (5), а локально максимальные значения в точках (0), (4) и (8). Таким образом, сумма точек экстремума этой функции равна (-1 + 2 + 5 + 0 + 4 + 8 = 18).
Ответ: 18
Задание
5
#732
Уровень задания: Равен ЕГЭ
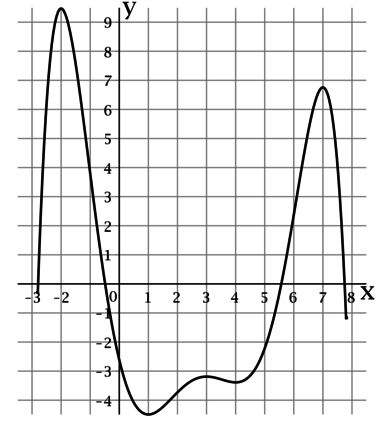
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-3; 9)). Найдите произведение точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (-1) и (5), а локально максимальные значения в точках (-2), (4) и (8). Таким образом, произведение точек экстремума этой функции равно ((-1)cdot 5cdot (-2)cdot 4cdot 8 = 320).
Ответ: 320
Задание
6
#733
Уровень задания: Равен ЕГЭ
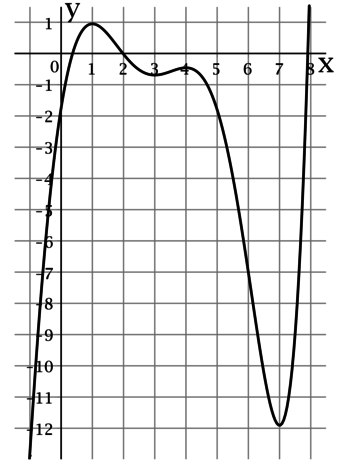
На рисунке изображен график функции (y = f(x)), определенной на интервале ((-2.8; 7.8)). Найдите произведение точек экстремума этой функции.
Точкой экстремума функции называется точка, в которой функция достигает локально минимальное или локально максимальное значение.
По рисунку можно определить, что функция (f(x)) достигает локально минимальные значения в точках (1) и (4), а локально максимальные значения в точках (-2), (3) и (7). Таким образом, произведение точек экстремума этой функции равно (1cdot 4cdot (-2)cdot 3cdot 7 = -168).
Ответ: -168
Задание
7
#734
Уровень задания: Равен ЕГЭ
На рисунке изображен график (y = f'(x)) – производной функции (y = f(x)), определенной на интервале ((-1; 8)). В какой точке отрезка ([2; 5]) функция (y = f(x)) принимает наибольшее значение?
По рисунку можно определить, что функция (y = f'(x)) на отрезке ([2; 5]) принимает неположительные значения, при этом (f'(2) = 0). Так как на полуинтервале ((2; 5]) производная функции (f(x)) отрицательна, то сама функция (f(x)) на ((2; 5]) убывает, тогда (y = f(x)) на отрезке ([2; 5]) принимает наибольшее значение при (x = 2).
Ответ: 2
Итоговый экзамен по математике для выпускников 11-х классов обязательно включает задания на поиск точек максимума и минимума функциональных зависимостей. Их решение проводится аналитически – методом дифференцирования. Применение производной для исследования функции на экстремум сокращает время анализа и позволяет представить общий вид графика зависимости еще до выполнения построений.
Обучающий ресурс «Школково» позволит учащимся освежить в памяти главные моменты темы – уточнить теоретические знания и отработать их в решении ряда задач. Наш подход к обучению в отношении поиска точек экстремума функции через производную в типовых заданиях ЕГЭ основан на принципе глубокой взаимосвязи теории и практики. Сначала ученик читает правила «Теоретической справки», потом смотрит видео с объяснениями учителя, а затем работает с реальным педагогом. В процессе просмотра предлагаемых на сайте вебинаров можно задать интересующие вопросы и получить помощь в решении конкретных задач.
В разделе «Каталог» имеются подборки тематических заданий на нахождение точек экстремума функции с помощью производной, а также нахождения производной угла наклона касательной. Каждый пример содержит готовое решение и правильный ответ, с которыми можно ознакомиться после окончания самостоятельной работы. «Конструктор» примерных вариантов ЕГЭ позволит провести исследование экстремумов функций с помощью производных в ходе пробного выполнения экзаменационной работы.

Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Как готовиться к сочинению за 2 дня до ЕГЭ? Четко и без воды
Теоремы о дифференцируемых функциях
Рассмотрим функции 

![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png)

Теорема Ферма
: если функция 

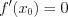
Геометрический смысл теоремы: касательная к графику функции в точке 
Теорема Лагранжа: 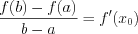

Геометрический смысл теоремы: касательная к графику функции в точке 
Теорема Ролля: если 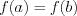

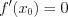
Геометрический смысл теоремы: у графика функции существует точка, в которой касательная параллельна оси абсцисс.
Теорема Коши: если 
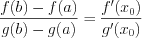
Исследование функции с помощью первой производной
С помощью производной функции можно определить характер монотонности функции, точки экстремума, а также ее наибольшее и наименьшее значение на заданном промежутке.
Достаточное условие возрастания (убывания) функции:
а) если на заданном промежутке 
б) если 
Экстремум
функции
Максимумом (минимумом)
функции 
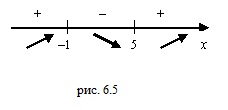
Максимум и минимум функции имеют локальный характер, поскольку отдельные минимумы некоторой функции могут оказаться больше максимумов той же функции (рис. 6.4).
Максимум и минимум функции называются
экстремумом функции
. Значение аргумента, при котором достигается экстремум, называется
точкой экстремума
. На рисунке 6.4 значения 

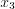
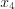
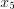

Критическими точками
функции называют те значения аргумента, при которых производная функции равна нулю или не существует. Критические точки функции находят, решая уравнение: 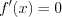
Алгоритм нахождения точек экстремума функции:
1) находим область определения функции 
2) находим 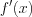
3) находим критические точки функции, решая уравнение 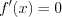
4) наносим критические точки на область определения функции;
5) определяем знак производной функции на полученных промежутках;
6) определяем точки экстремума функции по правилу:
если при переходе через критическую точку производная меняет знак c «+» на «–», то имеем точку максимума, а если с «–» на «+», то имеем точку минимума.
Рассмотрим функцию 
![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png)
Алгоритм нахождения наибольшего и наименьшего
значений
функции 
1) находим 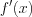
2) находим критические точки функции, решая уравнение 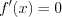
3) находим значение функции на концах отрезка и в критических точках, принадлежащих данному отрезку;
4) определяем наибольшее и наименьшее значение из полученных.
Исследование
функции с помощью второй производной
Критическими точками второго рода
функции 
Критические точки второго рода функции 
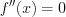
Если при переходе через критическую точку второго рода вторая производная функции меняет знак, то имеем точку перегиба
графика функции.
Если на некотором промежутке выполняется неравенство 

на этом промежутке, а если 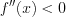
выпукла
на этом промежутке.
Пример 1.
Найдите промежутки монотонности и точки экстремума функции 
Решение . Используя таблицу производных найдем производную функции: 
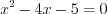
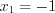
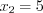


Ответ
: На промежутках 

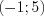


Пример 2.
Найдите точки перегиба и промежутки выпуклости и вогнутости графика функции
Решение
. 1. Используя таблицу производных найдем первую производную функции: 
2. Используя таблицу производных найдем вторую производную функции: 
3. Найдем критические точки второго рода: 
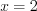
4. Нанесем точку 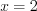
Ответ
: На промежутке 

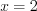
Пример 3.
Найдите наибольшее и наименьшее значение функции 
![[1;e] LaTeX formula: [1;e]](https://helpy.quali.me/uploads/formulas/eb6e890201c9d8770f7e173603dbc77ae36dc386.1.1.png)
Решение
. 1. По формуле 

2. Найдем критические точки функции, решая уравнение 


3. Найдем значение функции на концах отрезка ![[1;e] LaTeX formula: [1;e]](https://helpy.quali.me/uploads/formulas/eb6e890201c9d8770f7e173603dbc77ae36dc386.1.1.png)




Ответ
: 

Приведем схему полного исследования функции 
1. Находим область определения функции.
2. Определяем, является ли функция четной или нечетной.
3. Выясняем, является ли функция периодической.
4. Находим точки пересечения графика функции с осью ординат.
5. Находим нули функции (точки пересечения графика функции с осью абсцисс).
6. Проводим исследование функции с помощью первой производной:
а) находим критические точки первого рода;
б) находим промежутки возрастания и убывания функции;
в) находим точки экстремума функции и значение функции в точках экстремума.
7. Проводим исследование функции с помощью второй производной:
а) находим критические точки второго рода;
б) находим промежутки выпуклости и вогнутости функции;
в) находим точки перегиба графика функции.
8. Находим асимптоты графика функции.
9. Строим график функции.
10. Находим промежутки знакопостоянства функции: промежутки, на которых функция положительна и промежутки, на которых функция отрицательна.
11. Находим область значений функции.

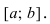
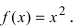
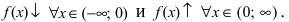
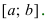
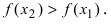
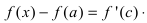
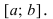
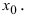
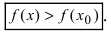
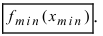
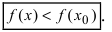
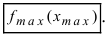
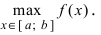
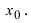
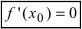
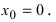
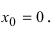
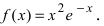

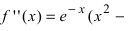
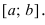
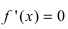 и точки, в которых первая производная функции не существует.
и точки, в которых первая производная функции не существует.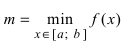 и наибольшее
и наибольшее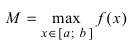 .
.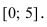
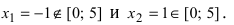
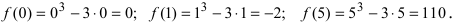
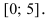
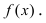
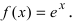
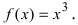
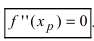
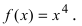
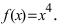
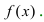
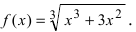

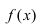
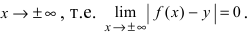
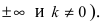
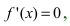 и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (
и определяют точки, в которых первая производная функции не существует. Точки откладывают на числовой оси и определяют знак первой производной на каждом интервале, определяя тем самым интервалы возрастания (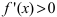 ) и убывания(
) и убывания( 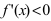 ) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.
) функции. Используя первый достаточный признак существования экстремума, находят точки экстремума и вычисляют значение функции в этих точках.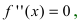 и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (
и определяют точки, в которых вторая производная функции не существует. Точки откладывают на числовой оси и определяют знак второй производной на каждом интервале, определяя тем самым интервалы вогнутости (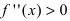 ) и выпуклости (
) и выпуклости (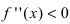 ) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.
) функции. Используя достаточный признак существования точки перегиба, находят точки перегиба и вычисляют значение функции в этих точках.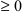 );
);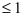 ).
).