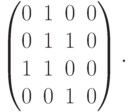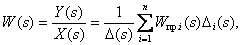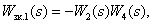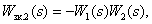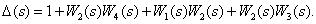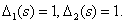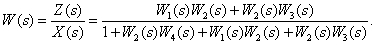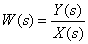-
Основные
определения
Ребро
в графеG
может быть
ориентированным и иметь начало и конец.
Такое ребро называется дугой,
а граф, содержащий дуги, называется
ориентированным, или орграфом.
На рисунке дуга изображается стрелкой.
Многие понятия,
введенные для неографов, для орграфов
приобретают другое определение. Матрица
расстояний для орграфа несимметрична,
и эксцентриситет вершины зависит от
того, как выбирается максимум. Если
максимум ищется в строке, то эксцентриситет
вершины называется числом
внешнего разделения,
а если в столбце – числом
внутреннего разделения.
Соответственно определяются внешний
и внутренний центры.
Основание
орграфа
– неограф с теми же вершинами, но ребрами
вместо соответствующих дуг.
Маршрут в орграфе
– последовательность вершин, соединенных
дугами, направленными в одну сторону.
Маршрут, в котором
все дуги разные, есть путь.
Путь, в котором
начало и конец совпадают, есть контур.
Длина пути измеряется числом входящих
в него дуг, а для взвешенного орграфа –
это сумма весов дуг.
В орграфе две
локальные степени вершины v:
– число дуг, входящих вv,
и
– число дуг, выходящих изv.
Лемма о рукопожатиях для орграфа имеет
вид
, (13.1)
где суммирование
производится по всем вершинам графа.
Множество
вершинv,
образующих дугу [v,
u]
с вершиной u,
называется множеством предшественников
вершины u,
а множество
вершинu,
образующих дугу [v,
u]
с вершиной v,
называется множеством преемников
вершины v.
Мощности этих множеств соответственно
равны:
,
.
В дальнейшем под
графом будем понимать как неограф, так
и орграф.
-
Маршруты в
орграфе
Задачи, связанные
с маршрутами в орграфе, имеют большое
практическое значение, что и дает стимул
к развитию и совершенствованию методов
их решения. Наиболее часто встает вопрос
о минимальных и максимальных расстояниях,
о числе маршрутов определенной длины.
Пример 13.1.
Дан орграф (рис. 13.1). Сколько в нем
маршрутов длиной 3?
Рис. 13.1
Решение.
Используем алгебраический метод решения
задачи на основании теоремы 12.4. Запишем
матрицу смежности. Матрица смежности
орграфа – несимметричная.


Возведем эту
матрицу в степень 3. Суммируя все элементы
полученной матрицы, находим, что число
маршрутов длиной 3 равно восьми. Три
единицы, стоящие по диагонали, показывают,
что сюда входит 3 помеченных контура.
Очевидно, что это контуры: 1–4–3, 4–3–1,
3–1–4.
-
Транзитивное
замыкание
Прямым
(декартовым) произведением множеств A
и B
называется множество
.Бинарное
отношение
на X
– любое подмножество прямого произведения:
.
Отношение
наX
рефлексивно,
если для любого
пара
.
Отношение
наX
антирефлексивно,
если для любого
пара
.
Отношение
наX
симметрично,
если для любой пары
из условия
следует
.
Отношение
наX
антисимметрично,
если из условий
и
следуетx
= y.
Отношение
наX
асимметрично,
если для любой пары
из условия
следует
.
Отношение
наX
транзитивно,
если для любых двух пар
и
из условий
и
следует
.
Отношение
называется замыканием отношения
на свойствоA,
если
обладает свойствомA,
и для любого отношения
со свойствомA
справедливо вложение
.
Композицией
бинарных отношений
и
называют отношение
,
состоящее из пар,
таких, чтои
.
Транзитивное
замыкание
отношения
имеет вид
,
где,
.
Теорема 13.1.
Отношение
транзитивно
тогда и только тогда, когда
.
Граф есть отношение
на множестве вершин. Элементами этого
отношения являются дуги (или ребра, если
отношение симметрично).
Орграф называется
транзитивным,
если для любых его дуг
и
существует замыкающая дуга
.
Пример 13.2.
Дано отношение, заданное матрицей

Исследовать
отношение на симметрию, антисимметрию,
асимметрию, рефлексивность,
антирефлексивность. Найти транзитивное
замыкание отношения. Построить граф
отношения
и его транзитивного замыкания.
Решение.
-
Данное отношение
не является симметричным, так как
матрица несимметрична. Например, пара
(2, 1) принадлежит
,
а пара (1, 2) ему не принадлежит. -
Отношение
антисимметрично, так как нет ни одной
пары
,
.
-
Отношение
антисимметрично, но не асимметрично,
так как на диагонали матрицы имеются
элементы, равные 1. -
Все диагональные
элементы матрицы рефлексивного отношения
равны 1. Данное отношение не является
рефлексивным. -
Отношение не
обладает свойством антирефлексивности,
так как диагональ матрицы ненулевая. -
Данное отношение
не является транзитивным, так как,
например, пары (1, 4) и (4, 3) принадлежат
,
а пара (1, 3) ему не принадлежит.
Найдем транзитивное
замыкание графа, заданного отношением
.
Процедура транзитивного замыкания
сводится к добавлению в матрицу смежности
минимального числа единиц, так, чтобы
соответствующее отношение обладало
свойством транзитивности. Для этого
выполняем следующие операции.
-
Вычисляем матрицу
композиции
.
Для этого умножаем (с использованием
операции логического умножения) матрицуA
саму на себя:
.
Такое произведение называетсяпроизведением
булевых матриц.
Результат произведения получают
следующим образом. Элемент результирующей
матрицы
,
если хотя бы в одном случаеk-й
элемент i-й
строки первого сомножителя и k-й
элемент j-го
столбца второго сомножителя одновременно
равны единице. В противном случае
.

-
Находим логическую
сумму (дизъюнкцию) матриц. Поэлементная
дизъюнкция матриц дает:

-
Сравним
сA.
Если
=A,
то
– искомая матрица. Если
,
то полагаем,
возвращаемся к п. 1 и повторяем всю
процедуру для новой матрицы. В данном
случае.
Поэтому принимаем:

Умножаем матрицу
саму на себя:

Находим логическую
сумму:

Сравниваем:
.
Полагаеми повторяем процедуру еще раз.


Сравниваем:
.
Следовательно,– матрица транзитивного замыкания
заданного отношения.
На рис. 13.2 (а и б)
представлены графы отношения
и его транзитивного замыкания. Диагональные
элементы матрицы соответствуют петлям
на графе. Матрица несимметрична, поэтому
граф отношения – ориентированный.
Рис. 13.2
-
Компоненты
сильной связности графа
Понятие сильной
связности относится только к орграфам.
Основание
орграфа – неограф с теми же вершинами,
но ребрами вместо соответствующих дуг.
Орграф называется
связным,
если связно его основание.
Вершина u
достижима
из вершины v,
если существует маршрут из v
в u.
Орграф называется
сильно
связным,
если любая его вершина достижима из
любой вершины.
Граф называется
ориентируемым,
если он является основанием сильно
связного графа.
Пример 13.3.
Найти компоненты сильной связности
графа, изображенного на рис. 13.3.
Рис. 13.3
Решение.
Матрица смежности графа имеет вид

В графе 7 дуг,
поэтому наибольший путь будет не длиннее
семи. Построим матрицу достижимости:

Выделим из этой
матрицы главные миноры максимального
порядка, не содержащие нули. Если граф
связен, то в матрице будут строки, не
содержащие нулей. Это строки 2, 4, 6:

Минор со строками
и столбцами с этими номерами соответствует
одной компоненте связности:

Удалим из матрицы
строки и столбцы с этими номерами,
Получим минор, соответствующий второй
компоненте связности:

Итак, в графе две
компоненты сильной связности: подграф
с вершинами 1, 3, 5 и подграф с вершинами
2, 4, 6.
Рис. 13.4
На рис. 13.4 (а, б)
показаны обе компоненты сильной связности
в виде отдельных графов. Общее число
ребер в компонентах меньше размера
исходного графа. Дуга [2, 3] не вошла ни в
одну компоненту.
Соседние файлы в предмете Дискретная математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
Аннотация: Определения. Эйлеровы и гамильтоновы орграфы. Турниры.
Определения
Сначала напомним некоторые определения из
«Основные понятия теории графов»
.
Орграфом 
пара 

конечное множество элементов, называемых вершинами, а 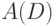
конечное семейство упорядоченных пар элементов из 
называемых дугами (или ориентированными ребрами ). Дуга, у которой
вершина 
— вторым, называется дугой
из 

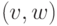
дуги 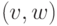

— различные объекты, в определенных случаях графы можно рассматривать как орграфы, в
которых каждому ребру соответствуют две противоположно ориентированные
дуги. 
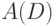
множеством вершин и семейством дуг орграфа 
Рис.
9.1.
На (рис. 9.1) представлен орграф, дугами которого являются 
на дуге указан стрелкой. Граф, полученный из орграфа 
стрелок, то есть заменой каждой дуги вида 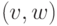


определения, данные для графов, можно перенести на орграфы. К примеру, две вершины 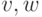

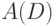
дуга вида 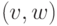

вершины 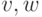
вершинам ). Два орграфа называются изоморфными, если
существует изоморфизм между их основаниями, сохраняющий порядок вершин на
каждой дуге. Матрицей смежности орграфа с множеством вершин 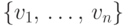

вида 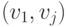
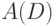
смежности для начерченного графа
Орграфы, не
содержащие петель и кратных ребер, называются простыми. Ориентированный маршрут
в орграфе 
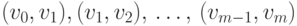
последовательность можно записывать в виде
и говорить об ориентированном маршруте из 
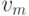
Аналогичным образом можно определить ориентированные цепи, ориентированные простые цепи и
ориентированные циклы — орцепи, простые орцепи и орциклы.
Заметим, что хотя орцепь не может содержать данную дугу
более одного раза, она может содержать одновременно
и 
Например, на (рис. 9.1) 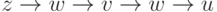
Теория графов. Термины и определения в картинках
Время на прочтение
5 мин
Количество просмотров 95K

В этой статье мы познакомимся с основными терминами и определениями Теории графов. Каждый термин схематично показан на картинках.
Самый объёмный модуль на курсе «Алгоритмы и структуры данных» посвящён теории графов.
Граф — это топологичекая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена.
Например, граф на рисунке состоит из 8 вершин и 8 рёбер.
Очень многие задачи могут быть решены используя богатую библиотеку алгоритмов теории графов. Для этого достаточно лишь принять объекты за вершины, а связь между ними — за рёбра, после чего весь арсенал алгоритмов теории графов к вашим услугам: нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.
В этой статье мы познакомимся с основными терминами и определениями теории графов. На курсе “Алгоритмы и Структуры данных” в компании Отус “Теория графов” изучается в самом объёмном модуле из 6 вебинаров, где мы изучаем десяток самых популярных алгоритмов.
Вершина — точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины, её расположение, цвет, вкус, размер; однако при решении некоторых задачах вершины могут раскрашиваться в разные цвета или сохранять числовые значения.
Ребро — неупорядоченная пара двух вершин, которые связаны друг с другом. Эти вершины называются концевыми точками или концами ребра. При этом важен сам факт наличия связи, каким именно образом осуществляется эта связь и по какой дороге — не имеет значения; однако рёбра может быть присвоен “вес”, что позволит говорить о “нагруженном графе” и решать задачи оптимизации.
Инцидентность — вершина и ребро называются инцидентными, если вершина является для этого ребра концевой. Обратите внимание, что термин “инцидентность” применим только к вершине и ребру.
Смежность вершин — две вершины называются смежными, если они инцидентны одному ребру.
Смежность рёбер — два ребра называются смежными, если они инцедентны одной вершине.
Говоря проще — две вершины смежные, если они соединены ребром, два ребра смежные — если они соединены вершиной.
Петля — ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине.
Псевдограф — граф с петлями. С такими графами не очень удобно работать, потому что переходя по петле мы остаёмся в той же самой вершине, поэтому у него есть своё название.
Кратные рёбра — рёбра, имеющие одинаковые концевые вершины, по другому их называют ещё параллельными.
Мультиграф — граф с кратными рёбрами.
Псевдомультиграф — граф с петлями и кратными рёбрами.
Степень вершины — это количество рёбер, инцидентных указанной вершине. По-другому — количество рёбер, исходящих из вершины. Петля увеливает степень вершины на 2.
Изолированная вершина — вершина с нулевой степенью.
Висячая вершина — вершина со степенью 1.
Подграф. Если в исходном графе выделить несколько вершин и несколько рёбер (между выбранными вершинами), то мы получим подграф исходного графа.
Идея подграфов используется во многих алгоритмах, например, сначала создаётся подграф их всех вершин без рёбер, а потом дополняется выбранными рёбрами.
Полный граф — это граф, в котором каждые две вершины соединены одним ребром.
Сколько рёбер в полном графе? Это известная задача о рукопожатиях: собралось N человек (вершин) и каждый с каждым обменялся рукопожатием (ребро), сколько всего было рукопожатий? Вычисляется как сумма чисел от 1 до N — каждый новый участник должен пожать руку всем присутствующим, вычисляется по формуле: N * (N — 1) / 2.
Регулярный граф — граф, в котором степени всех вершин одинаковые.
Двудольный граф — если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным. Например, клиент-серверное приложение содержит множество запросов (рёбер) между клиентом и сервером, но нет запросов внутри клиента или внутри сервера.
Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он называется “планарным графом” или “плоским графом”.
Если это невозможно сделать, то граф называется “непланарным”.
Минимальные непланарные графы — это полный граф К5 из 5 вершин и полный двудольный граф К3,3 из 3+3 вершин (известная задача о 3 соседях и 3 колодцах). Если какой-либо граф в качестве подграфа содержит К5 или К3,3, то он является непланарным.
Путь или Маршрут — это последовательность смежных рёбер. Обычно путь задаётся перечислением вершин, по которым он пролегает.
Длина пути — количество рёбер в пути.
Цепь — маршрут без повторяющихся рёбер.
Простая цепь — цепь без повторяющихся вершин.
Цикл или Контур — цепь, в котором последняя вершина совпадает с первой.
Длина цикла — количество рёбер в цикле.
Самый короткий цикл — это петля.
Цикл Эйлера — цикл, проходящий по каждому ребру ровно один раз. Эйлер доказал, что такой цикл существует тогда, и только тогда, когда все вершины в связанном графе имеют чётную степень.
Цикл Гамильтона — цикл, проходящий через все вершины графа по одному разу. Другими словами — это простой цикл, в который входят все вершины графа.
Взвешенный граф — граф, в котором у каждого ребра и/или каждой вершины есть “вес” — некоторое число, которое может обозначать длину пути, его стоимость и т. п. Для взвешенного графа составляются различные алгоритмы оптимизации, например поиск кратчайшего пути.
Пока ещё не придуман алгоритм, который за полиномиальное время нашёл бы кратчайший цикл Гамильтона в полном нагруженном графе, однако есть несколько приближённых алгоритмов, которые за приемлимое время находят если не кратчайший, то очень короткий цикл, эти алгоритмы мы также рассматриваем на курсе Отуса — “Алгоритмы и структуры данных”.
Связный граф — граф, в котором существует путь между любыми двумия вершинами.
Дерево — связный граф без циклов.
Между любыми двумя вершинами дерева существует единственный путь.
Деревья часто используются для организации иерархической структуры данных, например, при создании двоичных деревьев поиска или кучи, в этом случае одну вершину дерева называют корнем.
Лес — граф, в котором несколько деревьев.
Ориентированный граф или Орграф — граф, в котором рёбра имеют направления.
Дуга — направленные рёбра в ориентированном графе.
Полустепень захода вершины — количество дуг, заходящих в эту вершину.
Исток — вершина с нулевой полустепенью захода.
Полустепень исхода вершины — количество дуг, исходящих из этой вершины
Сток — вершина с нулевой полустепенью исхода.
Компонента связности — множество таких вершин графа, что между любыми двумя вершинами существует маршрут.
Компонента сильной связности — максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам.
Компонента слабой связности — максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам без учёта направления (по дугам можно двигаться в любом направлении).
Мост — ребро, при удалении которого, количество связанных компонент графа увеличивается.
Это только основные термины и определения теории графов, которые мы рассматриваем на первом вебинаре модуля “Теория графов”. Цель статьи — дать наглядное и понятное представление об этих терминах, для чего и были нарисованы эти картинки.
-
Узнать о курсе подробнее
-
Записаться на интенсив: «Алгоритм сжатия данных — код Хаффмана. Создание Архиватора.». День 1
-
Записаться на интенсив: «Алгоритм сжатия данных — код Хаффмана. Создание Архиватора.». День 2
Привет, Вы узнаете про ориентированные графы систем автоматического управления, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
ориентированные графы систем автоматического управления , настоятельно рекомендую прочитать все из категории Математические основы теории автоматического управления.
Математическую модель САУ можно наглядно представить с помощью ориентированных графов (орграфов).
Орграфы используются в сложных САУ, особенно при управлении и автоматизации технологических процессов в промышленности, когда описание в виде структурных схем становится громоздким и сложным для восприятия. Рассмотрим простейший орграф динамического звена САУ.
Рис. 1
Орграфом САУ является графическое представление САУ в виде совокупности вершин, соответствующих переменным, и дуг, соединяющих вершины.
Рассмотрим основные свойства орграфа:
-
Каждая дуга со стрелкой, указывающей направление распространения сигнала, изображает звено и характеризуется оператором изображаемого звена (передаточной функцией);
-
Каждой вершине, отмеченной кружком, ставится в соответствие одна из переменных САУ (изображение переменной по Лапласу);
-
Входная величина дуги равна переменной вершины, из которой эта дуга исходит;
-
Выходная величина дуги получается как результат преобразования оператором входной величины;
-
Если к вершине подходят несколько дуг, то соответствующая вершине переменная равна сумме выходных величин этих дуг (аналог суммирующего звена структурных схем);
-
Если из вершины исходит несколько дуг, то входные величины всех этих дуг одинаковы (аналог точки ветвления в структурных схемах).
Ориентированный граф (орграф) можно построить по структурной схеме и наоборот. При построении орграфа по структурной схеме необходимо придерживаться следующих правил:
-
Модифицируют структурную схему так, чтобы в сумматорах все переменные складывались с положительным знаком, отрицательные знаки вносятся в передаточные функции соответствующих звеньев;
-
Каждый сумматор структурной схемы заменяется вершиной, которой ставится в соответствие выходная переменная сумматора;
-
Каждое динамическое звено заменяется дугой с оператором, равным передаточной функции звена;
-
Каждой переменной, включая и входные воздействия, соответствует своя вершина.
Рассмотрим пример. На рис. 2 показана структурная исходная схема, на рис. 3 показан полученный орграф САУ.
Рис. 2
Рис. 3
Преобразовать орграф САУ можно, как и структурную схему, используя правила эквивалентных преобразований для орграфов, которые легко могут быть получены по аналогичным правилам для структурных схем.
-
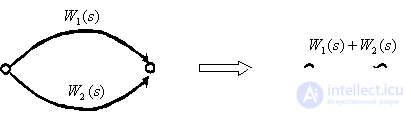
Последовательное соединение динамических звеньев.
-
Параллельное соединение динамических звеньев.
-
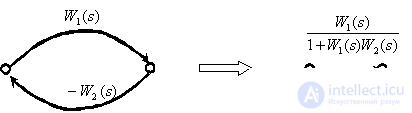
Замкнутый контур с отрицательной обратной связью.
-
Замкнутый контур с положительной обратной связью.
-
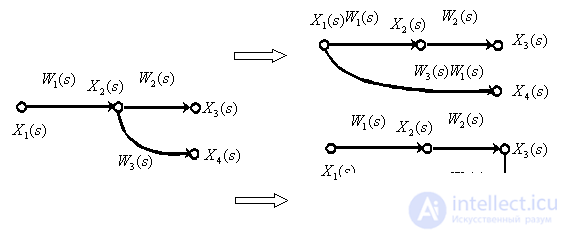
Перенос точки ветвления через динамическое звено.
-
Перенос суммирующего звена через динамическое звено.
Использование формулы Мейсона для преобразования структурных схем и ориентированных графов
Когда структурная схема преобразована в орграф, для нахождения необходимой передаточной функции можно использовать формулу Мейсона (правило некасающихся контуров), которая позволяет получить передаточную функцию, связывающую переменные в сложных, многоконтурных САУ.
Рассмотрим общий вид формулы и поясним ее компоненты:
|
|
(1) |
где 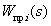
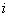

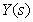

|
|
(2) |
где 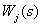






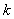

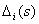
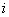
Поясним использование формулы Мейсона.
В начале выявляются все отдельные прямые пути между входной и выходной переменными, для которых необходимо определить передаточную функцию . Об этом говорит сайт https://intellect.icu . Отдельным прямым путем считается такая последовательность дуг и вершин, которая соединяет вершины, соответствующие входному и выходному сигналам. При этом отдельный прямой путь не должен пересекать в вершинах сам себя.
Далее выявляются все замкнутые контуры в орграфе САУ. Замкнутым считается такой контур, когда между двумя вершинами имеется как прямая, так и обратная связь. Передаточная функция замкнутого контура определяется как произведение передаточных функций всех дуг, входящих в контур с учетом знаков.
После того как выявлены все замкнутые контуры орграфа, необходимо проанализировать – есть ли контуры, которые не касаются ни дугами, ни вершинами, есть ли пары, тройки и т. д. таких контуров.
На основании полученного формируется определитель орграфа по формуле (2).
Определители орграфов, полученных после изъятия 
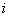
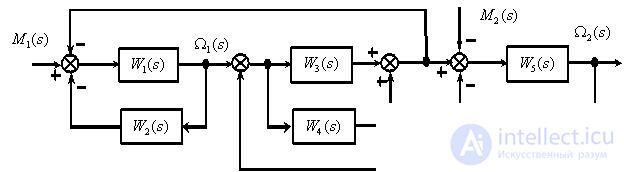
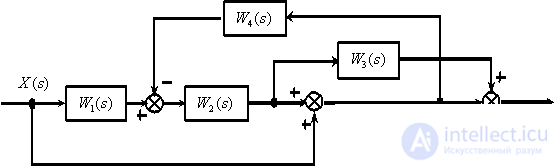
В качестве примера определим передаточную функцию между 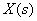
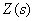

Рис. 4
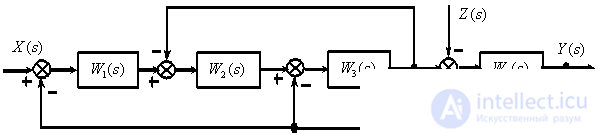
Преобразуем структурную схему в ориентированный граф (рис. 5).
Рис. 5
Определим прямые пути:
Определим замкнутые контуры:
Все контуры имеют общую дугу 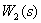
При изъятии 1-го или 2-го прямых путей в орграфе не сохраняется ни одного замкнутого контура, поэтому
Передаточная функция имеет вид
Контрольные вопросы и задачи
-
Дайте определение орграфа динамического звена.
-
Поясните процедуру преобразования структурной схемы САУ в ориентированный граф.
-
Что называется отдельным прямым путем при использовании правила некасающихся контуров?
-
Какие замкнутые контуры называют некасающимися?
-
Определите передаточную функцию
по следующей структурной схеме
Ответ:

-
Определите передаточную функцию
по следующей структурной схеме
Ответ:
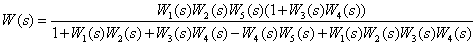
-
Определите передаточную функцию
по следующей структурной схеме
Ответ:

-
Определите передаточную функцию
по следующей структурной схеме
Ответ:
На этом все! Теперь вы знаете все про ориентированные графы систем автоматического управления, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое ориентированные графы систем автоматического управления
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Математические основы теории автоматического управления
Ответы на вопросы для самопроверки пишите в комментариях,
мы проверим, или же задавайте свой вопрос по данной теме.
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§17. Графы.
Что такое граф?
Ключевые слова:
• граф • вершина • ребро • матрица смежности • степень вершины • связный граф • взвешенный граф • весовая матрица • ориентированный граф • оптимальный путь • количество путей
Давайте подумаем, как можно наглядно представить такую информацию:
От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.
Можно, например, нарисовать такую схему (рис. 3.17, а).

Рис. 3.17
В информатике для исследования таких схем используют графы.
Граф — это набор вершин (узлов) и связей между ними — рёбер.
Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.
Матрица смежности графа
Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).

Рис. 3.18
Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).
Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?
В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.
Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).
Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?
Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).

Рис. 3.19
Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.

Рис. 3.20
Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?
Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?
Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?
Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?
Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?
Связный граф
В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.
Связный граф — это граф, между любыми вершинами которого существует путь.
Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).

Рис. 3.21
Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.
Постройте матрицу смежности графа, изображённого на рис. 3.21.
Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.
Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.
Найдите все циклы в графе на рис. 3.17.
Дерево — это связный граф, в котором нет циклов.
Взвешенный граф
Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Рис. 3.22
Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.
Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Как хранить информацию о таком графе? Ответ напрашивается сам собой — нужно в таблицу записывать не 1 или 0, а вес ребра. Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например, число -1 или очень большое число. Такая таблица называется весовой матрицей, потому что содержит веса рёбер. В данном случае она выглядит так (рис. 3.23).

Рис. 3.23
Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.
Что означают пустые ячейки в весовой матрице?
Как по весовой матрице сразу определить, сколько рёбер в графе?
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Рис. 3.24
Оптимальный путь в графе
Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.
Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?
Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).

Рис. 3.25
Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.
Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую

Рис. 3.26
Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).

Рис. 3.27
Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?
Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.
Почему нельзя на этом остановиться, ведь путь из А в В найден?
Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)

Рис. 3.28
Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.
Аналогично строим вторую часть схемы (рис. 3.29).

Рис. 3.29
Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.
Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?
Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.
Ориентированный граф
Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.
Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.
Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.
На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.

Рис. 3.30
Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.
Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.

Рис. 3.31
Количество путей
Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.

Рис. 3.32
Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.
В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.
По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?
Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).

Рис. 3.33
Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).

Рис. 3.34
В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).

Рис. 3.35
Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).

Рис. 3.36
Выводы
• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.
Подготовьте сообщение
а) «Задача о Кёнигсбергских мостах»
б) «Решение логических задач с помощью графов»
Оглавление
§16. Списки и деревья.
§17. Графы.
§18. Игровые стратегии.