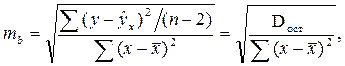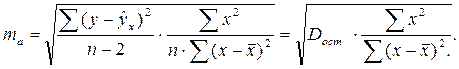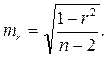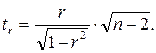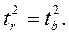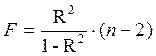2.1.
Значимость коэффициента корреляции.
Для
того чтобы при уровне значимости α
проверить нулевую гипотезу о равенстве
нулю генерального коэффициента корреляции
нормальной двумерной случайной величины
при конкурирующей гипотезе H1
≠ 0, надо вычислить наблюдаемое значение
критерия
и
по таблице критических точек распределения
Стьюдента, по заданному уровню значимости
α
и числу степеней свободы k = n — 2 найти
критическую точку tкрит
двусторонней критической области. Если
tнабл
< tкрит
оснований отвергнуть нулевую гипотезу.
Если |tнабл|
> tкрит
— нулевую гипотезу отвергают.
По
таблице Стьюдента с уровнем значимости
α=0.05
и степенями свободы k=13 находим tкрит:
tкрит
(n-m-1;α/2)
= (13;0.025) = 2.16
где
m = 1 — количество объясняющих переменных.
Если
tнабл
> tкритич,
то полученное значение коэффициента
корреляции признается значимым (нулевая
гипотеза, утверждающая равенство нулю
коэффициента корреляции, отвергается).
Поскольку
tнабл
> tкрит,
то отклоняем гипотезу о равенстве 0
коэффициента корреляции. Другими
словами, коэффициент корреляции
статистически — значим
В
парной линейной регрессии t2r
= t2b
и тогда проверка гипотез о значимости
коэффициентов регрессии и корреляции
равносильна проверке гипотезы о
существенности линейного уравнения
регрессии.
2.2. Интервальная оценка для коэффициента корреляции (доверительный интервал).
Доверительный
интервал для коэффициента корреляции
r(-1;-0.64)
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной
оценкой дисперсии возмущений является
величина:
S2y
= 0.00817 — необъясненная дисперсия (мера
разброса зависимой переменной вокруг
линии регрессии).
Sy
= 0.0904 — стандартная ошибка оценки
(стандартная ошибка регрессии).
Sa
— стандартное отклонение случайной
величины a.
Sb
— стандартное отклонение случайной
величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое
прогнозирование на основе построенной
модели предполагает, что сохраняются
ранее существовавшие взаимосвязи
переменных и на период упреждения. Для
прогнозирования зависимой переменной
результативного признака необходимо
знать прогнозные значения всех входящих
в модель факторов.
Прогнозные
значения факторов подставляют в модель
и получают точечные прогнозные оценки
изучаемого показателя.
(a
+ bxp
± ε)
где
Рассчитаем
границы интервала, в котором будет
сосредоточено 95% возможных значений Y
при неограниченно большом числе
наблюдений и Xp
= 14
(2.01
-0.0702*14 ± 0.0683)
(0.96;1.09)
С
вероятностью 95% можно гарантировать,
что значения Y при неограниченно большом
числе наблюдений не выйдет за пределы
найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1)
t-статистика. Критерий Стьюдента.
С
помощью МНК мы получили лишь оценки
параметров уравнения регрессии, которые
характерны для конкретного статистического
наблюдения (конкретного набора значений
x и y).
Для
оценки статистической значимости
коэффициентов регрессии и корреляции
рассчитываются t-критерий Стьюдента и
доверительные интервалы каждого из
показателей. Выдвигается гипотеза Н0
о случайной природе показателей, т.е. о
незначимом их отличии от нуля.
Чтобы
проверить, значимы ли параметры, т.е.
значимо ли они отличаются от нуля для
генеральной совокупности используют
статистические методы проверки гипотез.
В
качестве основной (нулевой) гипотезы
выдвигают гипотезу о незначимом отличии
от нуля параметра или статистической
характеристики в генеральной совокупности.
Наряду с основной (проверяемой) гипотезой
выдвигают альтернативную (конкурирующую)
гипотезу о неравенстве нулю параметра
или статистической характеристики в
генеральной совокупности.
Проверим
гипотезу H0
о равенстве отдельных коэффициентов
регрессии нулю (при альтернативе H1
не равно) на уровне значимости α=0.05.
В
случае если основная гипотеза окажется
неверной, мы принимаем альтернативную.
Для проверки этой гипотезы используется
t-критерий
Стьюдента.
Найденное
по данным наблюдений значение t-критерия
(его еще называют наблюдаемым или
фактическим) сравнивается с табличным
(критическим) значением, определяемым
по таблицам распределения Стьюдента
(которые обычно приводятся в конце
учебников и практикумов по статистике
или эконометрике).
Табличное
значение определяется в зависимости
от уровня значимости (α)
и числа степеней свободы, которое в
случае линейной парной регрессии равно
(n-2), n-число наблюдений.
Если
фактическое значение t-критерия больше
табличного (по модулю), то основную
гипотезу отвергают и считают, что с
вероятностью (1-α)
параметр или статистическая характеристика
в генеральной совокупности значимо
отличается от нуля.
Если
фактическое значение t-критерия меньше
табличного (по модулю), то нет оснований
отвергать основную гипотезу, т.е. параметр
или статистическая характеристика в
генеральной совокупности незначимо
отличается от нуля при уровне значимости
α.
tкрит
(n-m-1;α/2)
= (13;0.025) = 2.16
Поскольку
5.19 > 2.16, то статистическая значимость
коэффициента регрессии b подтверждается
(отвергаем гипотезу о равенстве нулю
этого коэффициента).
Поскольку
11.81 > 2.16, то статистическая значимость
коэффициента регрессии a подтверждается
(отвергаем гипотезу о равенстве нулю
этого коэффициента).
Доверительный
интервал для коэффициентов уравнения
регрессии.
Определим
доверительные интервалы коэффициентов
регрессии, которые с надежность 95% будут
следующими:
(b
— tкрит
Sb;
b + tкрит
Sb)
(-0.0702
— 2.16 • 0.0135; -0.0702 + 2.16 • 0.0135)
(-0.0995;-0.041)
С
вероятностью 95% можно утверждать, что
значение данного параметра будут лежать
в найденном интервале.
(a
— tкрит
Sa;
a + tкрит
Sa)
(2.01
— 2.16 • 0.17; 2.01 + 2.16 • 0.17)
(1.64;2.37)
С
вероятностью 95% можно утверждать, что
значение данного параметра будут лежать
в найденном интервале.
2)
F-статистика. Критерий Фишера.
Коэффициент
детерминации R2
используется для проверки существенности
уравнения линейной регрессии в целом.
Проверка
значимости модели регрессии проводится
с использованием F-критерия Фишера,
расчетное значение которого находится
как отношение дисперсии исходного ряда
наблюдений изучаемого показателя и
несмещенной оценки дисперсии остаточной
последовательности для данной модели.
Если
расчетное значение с k1=(m)
и k2=(n-m-1)
степенями свободы больше табличного
при заданном уровне значимости, то
модель считается значимой.
где
m – число факторов в модели.
Оценка
статистической значимости парной
линейной регрессии производится по
следующему алгоритму:
1.
Выдвигается нулевая гипотеза о том, что
уравнение в целом статистически
незначимо: H0:
R2=0
на уровне значимости α.
2.
Далее определяют фактическое значение
F-критерия:
где
m=1 для парной регрессии.
3.
Табличное значение определяется по
таблицам распределения Фишера для
заданного уровня значимости, принимая
во внимание, что число степеней свободы
для общей суммы квадратов (большей
дисперсии) равно 1 и число степеней
свободы остаточной суммы квадратов
(меньшей дисперсии) при линейной регрессии
равно n-2.
Fтабл
— это максимально возможное значение
критерия под влиянием случайных факторов
при данных степенях свободы и уровне
значимости α.
Уровень значимости α
— вероятность отвергнуть правильную
гипотезу при условии, что она верна.
Обычно α
принимается равной 0,05 или 0,01.
4.
Если фактическое значение F-критерия
меньше табличного, то говорят, что нет
основания отклонять нулевую гипотезу.
В
противном случае, нулевая гипотеза
отклоняется и с вероятностью (1-α)
принимается альтернативная гипотеза
о статистической значимости уравнения
в целом.
Табличное
значение критерия со степенями свободы
k1=1
и k2=13,
Fтабл
= 4.67
Поскольку
фактическое значение F > Fтабл,
то коэффициент детерминации статистически
значим (найденная оценка уравнения
регрессии статистически надежна).
Связь
между F-критерием Фишера и t-статистикой
Стьюдента выражается равенством:
Дисперсионный
анализ.
При
анализе качества модели регрессии
используется теорема о разложении
дисперсии, согласно которой общая
дисперсия результативного признака
может быть разложена на две составляющие
– объясненную и необъясненную уравнением
регрессии дисперсии.
Задача
дисперсионного анализа состоит в анализе
дисперсии зависимой переменной:
∑(yi
— ycp)2
= ∑(y(x) — ycp)2
+ ∑(y — y(x))2
где
∑(yi
— ycp)2
— общая сумма квадратов отклонений;
∑(y(x)
— ycp)2
— сумма квадратов отклонений, обусловленная
регрессией («объясненная» или «факторная»);
∑(y
— y(x))2
— остаточная сумма квадратов отклонений.
|
Источник |
Сумма |
Число |
Дисперсия |
F-критерий |
|
Модель |
0.22 |
1 |
0.22 |
26.9 |
|
Остаточная |
0.11 |
13 |
0.00846 |
1 |
|
Общая |
0.33 |
15-1 |
Показатели
качества уравнения регрессии.
|
Показатель |
Значение |
|
Коэффициент |
0.67 |
|
Средний |
-0.77 |
|
Средняя |
6.65 |
Проверка
на наличие автокорреляции остатков.
Важной
предпосылкой построения качественной
регрессионной модели по МНК является
независимость значений случайных
отклонений от значений отклонений во
всех других наблюдениях. Это гарантирует
отсутствие коррелированности между
любыми отклонениями и, в частности,
между соседними отклонениями.
Автокорреляция
(последовательная корреляция)
определяется как корреляция между
наблюдаемыми показателями, упорядоченными
во времени (временные ряды) или в
пространстве (перекрестные ряды).
Автокорреляция остатков (отклонений)
обычно встречается в регрессионном
анализе при использовании данных
временных рядов и очень редко при
использовании перекрестных данных.
В
экономических задачах значительно чаще
встречается положительная
автокорреляция,
нежели отрицательная
автокорреляция.
В большинстве случаев положительная
автокорреляция вызывается направленным
постоянным воздействием некоторых
неучтенных в модели факторов.
Отрицательная
автокорреляция
фактически означает, что за положительным
отклонением следует отрицательное и
наоборот. Такая ситуация может иметь
место, если ту же зависимость между
спросом на прохладительные напитки и
доходами рассматривать по сезонным
данным (зима-лето).
Среди
основных
причин, вызывающих автокорреляцию,
можно выделить следующие:
1.
Ошибки спецификации. Неучет в модели
какой-либо важной объясняющей переменной
либо неправильный выбор формы зависимости
обычно приводят к системным отклонениям
точек наблюдения от линии регрессии,
что может обусловить автокорреляцию.
2.
Инерция. Многие экономические показатели
(инфляция, безработица, ВНП и т.д.) обладают
определенной цикличностью, связанной
с волнообразностью деловой активности.
Поэтому изменение показателей происходит
не мгновенно, а обладает определенной
инертностью.
3.
Эффект паутины. Во многих производственных
и других сферах экономические показатели
реагируют на изменение экономических
условий с запаздыванием (временным
лагом).
4.
Сглаживание данных. Зачастую данные по
некоторому продолжительному временному
периоду получают усреднением данных
по составляющим его интервалам. Это
может привести к определенному
сглаживанию колебаний, которые имелись
внутри рассматриваемого периода, что
в свою очередь может служить причиной
автокорреляции.
Последствия
автокорреляции схожи с последствиями
гетероскедастичности:
выводы по t- и F-статистикам, определяющие
значимость коэффициента регрессии и
коэффициента детерминации, возможно,
будут неверными.
Обнаружение
автокорреляции
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет доверительных интервалов и прогнозов для линейного уравнения регрессии
Как правило, в линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров.Показатели корреляционной связи, вычисленные по ограниченной совокупности (по выборке), являются лишь оценками той или иной статистической закономерности, поскольку в любом параметре сохраняется элемент не полностью погасившейся случайности, присущей индивидуальным значениям признаков. Поэтому необходима статистическая оценка степени точности и надежности параметров корреляции. Под надежностью здесь понимается вероятность того, что значение проверяемого параметра не равно нулю, не включает в себя величины противоположных знаков.
Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцениваемой величины со средней случайной ошибкой оценки. Для коэффициента парной регрессии b средняя ошибка оценки вычисляется как:
где Dост – остаточная дисперсия на одну степень свободы.
Для нашего примера величина стандартной ошибки коэффициента регрессии составила:
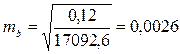
Для оценки того, насколько точные значения показателей могут отличаться от рассчитанных, осуществляется построение доверительных интервалов. Они определяют пределы, в которых лежат точные значения определяемых показателей с заданной степенью точности, соответствующей заданному уровню значимости α (α – вероятность отвергнуть правильную гипотезу при условии, что она верна, обычно принимается равной 0,05 или 0,01).
Для оценки статистической значимости коэффициента линейной регрессии и линейного коэффициента парной корреляции, а также для расчета доверительных интервалов b, применяется t – критерий Стьюдента.
Для оценки существенности коэффициента регрессии его величина сравнивается с его стандартной ошибкой, т.е. определяется фактическое значение t-критерия Стьюдента: 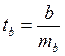
В рассматриваемом примере фактическое значение t-критерия для коэффициента регрессии составило:
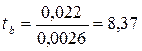
Этот же результат получим, извлекая квадратный корень из найденного F-критерия, т.е.
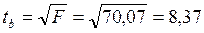
Действительно, справедливо равенство 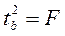
При 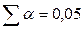
Для расчета доверительных интервалов для параметров a и b уравнения линейной регрессии определяем предельную ошибку ∆ для каждого показателя:
Формулы для расчета доверительных интервалов имеют вид:
Если границы интервала имеют разные знаки, т.е. в эти границы попадает ноль, то оцениваемый параметр принимается нулевым.
Доверительный интервал для коэффициента регрессии определяется как 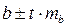
0,022 ± 2,16·0,0026 = 0,022 ± 0,0057, т.е.
Поскольку коэффициент регрессии в эконометрических исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, -10 ≤ b ≤ 40. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть.
Стандартная ошибка параметра а определяется по формуле:
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии; вычисляется t-критерий: 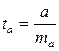
Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции mr:
Фактическое значение t-критерия Стьюдента определяется как
Данная формула свидетельствует, что в парной линейной регрессии 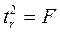
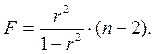
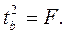
Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
В рассматриваемом примере tr совпало с tb. Величина tr =8,37 значительно превышает табличное значение 2,16 при а=0,05. Следовательно, коэффициент корреляции существенно отличен от нуля и зависимость является достоверной.
Прогноз, полученный подстановкой в уравнение регрессии ожидаемого значения фактора, называют точечным прогнозом. Вероятность точной реализации такого прогноза крайне мала. Необходимо сопроводить его значением средней ошибки прогноза или доверительным интервалом прогноза с достаточно большой вероятностью.
Точечный прогноз заключается в получении прогнозного значения yp, которое определяется путем подстановки в уравнение регрессии
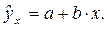
Интервальный прогноз заключается в построении доверительного интервала прогноза, т.е. верхней и нижней границы ypmin, ypmax интервала, содержащего точную величину для прогнозного значения
(ypmin 2 – индекс детерминации;
n – число наблюдений;
m – число параметров при переменных х.
Величина m характеризует число степеней свободы для факторной суммы квадратов, а (n – m — 1) – число степеней свободы для остаточной суммы квадратов.
Для степенной функции 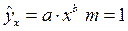
Для параболы второй степени y=a + b·x + c·x 2 + ε m=2 и 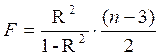
Для оценки качества построенной модели используется также средняя ошибка аппроксимации. Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т.е. у и . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у— ) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует объему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Для сравнения берутся величины отклонений, выраженные в процентах к фактическим значениям. Так, если для первого наблюдения у=20, а для второго у=50, ошибка аппроксимации составит 25% для первого наблюдения и 20% — для второго.
Поскольку (у— ) может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:
.
Для нашего примера представим расчет средней ошибки аппроксимации в таблице 4.
Пример нахождения доверительных интервалов коэффициентов регрессии
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Постройте уравнение зависимости экспорта нефти от цены на нефть.
3. Рассчитайте среднюю ошибку аппроксимации и коэффициент детерминации. Оценить статистическую значимость параметров регрессии и уравнения в целом.
4. Оцените полученные результаты, выводы оформите в аналитической записке.
Таблица 5
Цена нефти марки Urals (Россия), долл/барр.
Экспорт нефти и нефтепродуктов, млн.т.
Решение:
Уравнение имеет вид y = ax + b
1. Параметры уравнения регрессии.
Средние значения
Связь между признаком Y фактором X сильная и прямая
Уравнение регрессии
| x | y | x 2 | y 2 | x ∙ y | y(x) | (y- y ) 2 | (y-y(x)) 2 | (x-x p ) 2 |
| 119 | 298.12 | 14161 | 88875.53 | 35476.28 | 219.63 | 232120.8 | 6160.56 | 24362.01 |
| 203 | 481.03 | 41209 | 231389.86 | 97649.09 | 521.16 | 89328.76 | 1610.26 | 5196.01 |
| 281 | 539.12 | 78961 | 290650.37 | 151492.72 | 801.15 | 57979.42 | 68658.51 | 35.01 |
| 305 | 653.57 | 93025 | 427153.74 | 199338.85 | 887.3 | 15961.59 | 54628.94 | 895.01 |
| 381 | 987.66 | 145161 | 975472.28 | 376298.46 | 1160.11 | 43160.41 | 29738.57 | 11218.34 |
| 363 | 1252.85 | 131769 | 1569633.12 | 454784.55 | 1095.5 | 223673.03 | 24760.35 | 7729.34 |
| 389 | 1276.88 | 151321 | 1630422.53 | 496706.32 | 1188.83 | 246980.01 | 7753.57 | 12977.01 |
| 387 | 1396.70 | 149769 | 1950770.89 | 540522.9 | 1181.65 | 380430.93 | 46248.04 | 12525.34 |
| 315 | 952.03 | 99225 | 906361.12 | 299889.45 | 923.19 | 29625.58 | 831.49 | 1593.34 |
| 217 | 619.96 | 47089 | 384350.4 | 134531.32 | 571.41 | 25583.74 | 2356.85 | 3373.67 |
| 149 | 384.40 | 22201 | 147763.36 | 57275.6 | 327.32 | 156427.5 | 3258.23 | 15897.01 |
| 192 | 516.59 | 36864 | 266865.23 | 99185.28 | 481.67 | 69336.98 | 1219.24 | 6902.84 |
| 3301 | 9358.91 | 1010755 | 8869708.45 | 2943150.82 | 9358.91 | 1570608.75 | 247224.62 | 102704.92 |
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (10;0.05) = 1.812
Поскольку Tнабл > Tтабл , то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициента корреляции статистически — значим.
Анализ точности определения оценок коэффициентов регрессии
S a = 0.4906
Доверительные интервалы для зависимой переменной
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X = 1
(-587.75;179.86)
Проверка гипотез относительно коэффициентов линейного уравнения регрессии
1) t-статистика
Статистическая значимость коэффициента регрессии a подтверждается (7.32>1.812)
Статистическая значимость коэффициента регрессии b не подтверждается (1.46 Fkp, то коэффициент детерминации статистически значим.
Доверительные интервалы для зависимой переменной
Уравнение тренда имеет вид y = at 2 + bt + c
1. Находим параметры уравнения методом наименьших квадратов.
Система уравнений
Для наших данных система уравнений имеет вид (см. таблицу).
Получаем a0 = -11.37, a1 = 88.47, a2 = 2151.09
Уравнение тренда: y = -11.37t 2 +88.47t+2151.09
Оценим качество уравнения тренда с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве тренда
Средние значения
т.е. в 87.35 % случаев влияет на изменение данных. Другими словами — точность подбора уравнения тренда — высокая
| t | y | t 2 | y 2 | x ∙ y | y(t) | (y-y cp ) 2 | (y-y(t)) 2 | (t-t p ) 2 | (y-y(t)) : y | t 3 | t 4 | t 2 y |
| 1 | 2225.3 | 1 | 4951960.09 | 2225.3 | 2228.19 | 65.6099 | 8.352 | 16 | 6431.117 | 1 | 1 | 2225.3 |
| 2 | 2254.9 | 4 | 5084574.01 | 4509.8 | 2282.55 | 462.25 | 764.5225 | 9 | 62347.985 | 8 | 16 | 9019.6 |
| 3 | 2332.3 | 9 | 5439623.29 | 6996.9 | 2314.17 | 9781.21 | 328.6969 | 4 | 42284.599 | 27 | 81 | 20990.7 |
| 4 | 2365.8 | 16 | 5597009.64 | 9463.2 | 2323.05 | 17529.76 | 1827.5625 | 1 | 101137.95 | 64 | 256 | 37852.8 |
| 5 | 2295.4 | 25 | 5268861.16 | 11477 | 2309.19 | 3844 | 190.1641 | 0 | 31653.566 | 125 | 625 | 57385 |
| 6 | 2303.9 | 36 | 5307955.21 | 13823.4 | 2272.59 | 4970.25 | 980.3161 | 1 | 72135.109 | 216 | 1296 | 82940.4 |
| 7 | 2166.7 | 49 | 4694588.89 | 15166.9 | 2213.25 | 4448.89 | 2166.9025 | 4 | 100859.885 | 343 | 2401 | 106168.3 |
| 8 | 2080.4 | 64 | 4328064.16 | 16643.2 | 2131.17 | 23409 | 2577.5929 | 9 | 105621.908 | 512 | 4096 | 133145.6 |
| 9 | 2075.9 | 81 | 4309360.81 | 18683.1 | 2026.35 | 24806.25 | 2455.2025 | 16 | 102860.845 | 729 | 6561 | 168147.9 |
| 45 | 20100.6 | 285 | 44981997.26 | 98988.8 | 20100.51 | 89317.2199 | 11299.312 | 60 | 625332.964 | 4050 | 30666 | 1235751.2 |
2. Анализ точности определения оценок параметров уравнения тренда.
Анализ точности определения оценок параметров уравнения тренда
S a = 4.8518
Доверительные интервалы для зависимой переменной
По таблице Стьюдента находим Tтабл
Tтабл (n-m-1;a) = (7;0.05) = 1.895
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и t = 6
2151.09 + 88.47*6 + -11.37*62 — 1.895*39.911 ; 2151.09 + 88.47*6 + -11.37*62 — 1.895*39.911
(-55.3814;95.8814)
Интервальный прогноз.
Определим среднеквадратическую ошибку прогнозируемого показателя.
где L — период упреждения; уn+L — точечный прогноз по модели на (n + L)-й момент времени; n — количество наблюдений во временном ряду; Sy — стандартная ошибка прогнозируемого показателя; Tтабл — табличное значение критерия Стьюдента для уровня значимости а и для числа степеней свободы, равного n — 2.
Точечный прогноз, t = 10: y(10) = -11.37*10 2 + 88.47* + 2151.09 = 1898.79
K1 = 247.4924
1898.79 — 247.4924 = 1651.2976 ; 1898.79 + 247.4924 = 2146.2824
t = 10: (1651.2976;2146.2824)
Точечный прогноз, t = 11: y(11) = -11.37*11 2 + 88.47* + 2151.09 = 1748.49
K2 = 261.9213
1748.49 — 261.9213 = 1486.5687 ; 1748.49 + 261.9213 = 2010.4113
t = 11: (1486.5687;2010.4113)
Точечный прогноз, t = 12: y(12) = -11.37*12 2 + 88.47* + 2151.09 = 1575.45
K3 = 278.0099
1575.45 — 278.0099 = 1297.4401 ; 1575.45 + 278.0099 = 1853.4599
t = 12: (1297.4401;1853.4599)
Точечный прогноз, t = 13: y(13) = -11.37*13 2 + 88.47* + 2151.09 = 1379.67
K4 = 295.4871
1379.67 — 295.4871 = 1084.1829 ; 1379.67 + 295.4871 = 1675.1571
t = 13: (1084.1829;1675.1571)
Точечный прогноз, t = 14: y(14) = -11.37*14 2 + 88.47* + 2151.09 = 1161.15
K5 = 314.1213
1161.15 — 314.1213 = 847.0287 ; 1161.15 + 314.1213 = 1475.2713
t = 14: (847.0287;1475.2713)
3. Проверка гипотез относительно коэффициентов линейного уравнения тренда.
1) t-статистика. Критерий Стьюдента.
Статистическая значимость коэффициента уравнения подтверждается
Статистическая значимость коэффициента тренда подтверждается
Доверительный интервал для коэффициентов уравнения тренда
Определим доверительные интервалы коэффициентов тренда, которые с надежность 95% будут следующими (tтабл=1.895):
(a — tтабл·Sa; a + tтабл·Sa)
(-20.5642;-2.1758)
(b — t табл·Sb; b + tтаблS·b)
(36.7313;140.2087)
2) F-статистика. Критерий Фишера.
Fkp = 5.32
Поскольку F > Fkp, то коэффициент детерминации статистически значим
4. Тест Дарбина-Уотсона на наличие автокорреляции остатков для временного ряда.
| y | y(x) | e i = y-y(x) | e 2 | (e i — e i-1 ) 2 |
| 2225.3 | 2228.19 | -2.89 | 8.3521 | 0 |
| 2254.9 | 2282.55 | -27.65 | 764.5225 | 613.0576 |
| 2332.3 | 2314.17 | 18.13 | 328.6969 | 2095.8084 |
| 2365.8 | 2323.05 | 42.75 | 1827.5625 | 606.1444 |
| 2295.4 | 2309.19 | -13.79 | 190.1641 | 3196.7716 |
| 2303.9 | 2272.59 | 31.31 | 980.3161 | 2034.01 |
| 2166.7 | 2213.25 | -46.55 | 2166.9025 | 6062.1796 |
| 2080.4 | 2131.17 | -50.77 | 2577.5929 | 17.8084 |
| 2075.9 | 2026.35 | 49.55 | 2455.2025 | 10064.1024 |
| 11299.3121 | 24689.8824 |
Критические значения d1 и d2 определяются на основе специальных таблиц для требуемого уровня значимости a, числа наблюдений n и количества объясняющих переменных m.
Не обращаясь к таблицам, можно пользоваться приблизительным правилом и считать, что автокорреляция остатков отсутствует, если 1.5
Задача №3. Расчёт параметров регрессии и корреляции с помощью Excel
По территориям региона приводятся данные за 200Х г.
| Номер региона | Среднедушевой прожиточный минимум в день одного трудоспособного, руб., х | Среднедневная заработная плата, руб., у |
|---|---|---|
| 1 | 78 | 133 |
| 2 | 82 | 148 |
| 3 | 87 | 134 |
| 4 | 79 | 154 |
| 5 | 89 | 162 |
| 6 | 106 | 195 |
| 7 | 67 | 139 |
| 8 | 88 | 158 |
| 9 | 73 | 152 |
| 10 | 87 | 162 |
| 11 | 76 | 159 |
| 12 | 115 | 173 |
Задание:
1. Постройте поле корреляции и сформулируйте гипотезу о форме связи.
2. Рассчитайте параметры уравнения линейной регрессии
.
3. Оцените тесноту связи с помощью показателей корреляции и детерминации.
4. Дайте с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
5. Оцените с помощью средней ошибки аппроксимации качество уравнений.
6. Оцените с помощью F-критерия Фишера статистическую надёжность результатов регрессионного моделирования.
7. Рассчитайте прогнозное значение результата, если прогнозное значение фактора увеличится на 10% от его среднего уровня. Определите доверительный интервал прогноза для уровня значимости .
8. Оцените полученные результаты, выводы оформите в аналитической записке.
Решение:
Решим данную задачу с помощью Excel.
1. Сопоставив имеющиеся данные х и у, например, ранжировав их в порядке возрастания фактора х, можно наблюдать наличие прямой зависимости между признаками, когда увеличение среднедушевого прожиточного минимума увеличивает среднедневную заработную плату. Исходя из этого, можно сделать предположение, что связь между признаками прямая и её можно описать уравнением прямой. Этот же вывод подтверждается и на основе графического анализа.
Чтобы построить поле корреляции можно воспользоваться ППП Excel. Введите исходные данные в последовательности: сначала х, затем у.
Выделите область ячеек, содержащую данные.
Затем выберете: Вставка / Точечная диаграмма / Точечная с маркерами как показано на рисунке 1.
Рисунок 1 Построение поля корреляции
Анализ поля корреляции показывает наличие близкой к прямолинейной зависимости, так как точки расположены практически по прямой линии.
2. Для расчёта параметров уравнения линейной регрессии
воспользуемся встроенной статистической функцией ЛИНЕЙН.
1) Откройте существующий файл, содержащий анализируемые данные;
2) Выделите область пустых ячеек 5×2 (5 строк, 2 столбца) для вывода результатов регрессионной статистики.
3) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
4) В окне Категория выберете Статистические, в окне функция – ЛИНЕЙН. Щёлкните по кнопке ОК как показано на Рисунке 2;
Рисунок 2 Диалоговое окно «Мастер функций»
5) Заполните аргументы функции:
Известные значения у – диапазон, содержащий данные результативного признака;
Известные значения х – диапазон, содержащий данные факторного признака;
Константа – логическое значение, которое указывает на наличие или на отсутствие свободного члена в уравнении; если Константа = 1, то свободный член рассчитывается обычным образом, если Константа = 0, то свободный член равен 0;
Статистика – логическое значение, которое указывает, выводить дополнительную информацию по регрессионному анализу или нет. Если Статистика = 1, то дополнительная информация выводится, если Статистика = 0, то выводятся только оценки параметров уравнения.
Щёлкните по кнопке ОК;
Рисунок 3 Диалоговое окно аргументов функции ЛИНЕЙН
6) В левой верхней ячейке выделенной области появится первый элемент итоговой таблицы. Чтобы раскрыть всю таблицу, нажмите на клавишу , а затем на комбинацию клавиш + + .
Дополнительная регрессионная статистика будет выводиться в порядке, указанном в следующей схеме:
| Значение коэффициента b | Значение коэффициента a |
| Стандартная ошибка b | Стандартная ошибка a |
| Коэффициент детерминации R 2 | Стандартная ошибка y |
| F-статистика | Число степеней свободы df |
| Регрессионная сумма квадратов |
Остаточная сумма квадратов
Рисунок 4 Результат вычисления функции ЛИНЕЙН
Получили уровнение регрессии:
Делаем вывод: С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата возрастает в среднем на 0,92 руб.
3. Коэффициент детерминации означает, что 52% вариации заработной платы (у) объясняется вариацией фактора х – среднедушевого прожиточного минимума, а 48% — действием других факторов, не включённых в модель.
По вычисленному коэффициенту детерминации можно рассчитать коэффициент корреляции: .
Связь оценивается как тесная.
4. С помощью среднего (общего) коэффициента эластичности определим силу влияния фактора на результат.
Для уравнения прямой средний (общий) коэффициент эластичности определим по формуле:
Средние значения найдём, выделив область ячеек со значениями х, и выберем Формулы / Автосумма / Среднее, и то же самое произведём со значениями у.
Рисунок 5 Расчёт средних значений функции и аргумент
Таким образом, при изменении среднедушевого прожиточного минимума на 1% от своего среднего значения среднедневная заработная плата изменится в среднем на 0,51%.
С помощью инструмента анализа данных Регрессия можно получить:
— результаты регрессионной статистики,
— результаты дисперсионного анализа,
— результаты доверительных интервалов,
— остатки и графики подбора линии регрессии,
— остатки и нормальную вероятность.
Порядок действий следующий:
1) проверьте доступ к Пакету анализа. В главном меню последовательно выберите: Файл/Параметры/Надстройки.
2) В раскрывающемся списке Управление выберите пункт Надстройки Excel и нажмите кнопку Перейти.
3) В окне Надстройки установите флажок Пакет анализа, а затем нажмите кнопку ОК.
• Если Пакет анализа отсутствует в списке поля Доступные надстройки, нажмите кнопку Обзор, чтобы выполнить поиск.
• Если выводится сообщение о том, что пакет анализа не установлен на компьютере, нажмите кнопку Да, чтобы установить его.
4) В главном меню последовательно выберите: Данные / Анализ данных / Инструменты анализа / Регрессия, а затем нажмите кнопку ОК.
5) Заполните диалоговое окно ввода данных и параметров вывода:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные факторного признака;
Метки – флажок, который указывает, содержит ли первая строка названия столбцов или нет;
Константа – ноль – флажок, указывающий на наличие или отсутствие свободного члена в уравнении;
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
6) Новый рабочий лист – можно задать произвольное имя нового листа.
Затем нажмите кнопку ОК.
Рисунок 6 Диалоговое окно ввода параметров инструмента Регрессия
Результаты регрессионного анализа для данных задачи представлены на рисунке 7.
Рисунок 7 Результат применения инструмента регрессия
5. Оценим с помощью средней ошибки аппроксимации качество уравнений. Воспользуемся результатами регрессионного анализа представленного на Рисунке 8.
Рисунок 8 Результат применения инструмента регрессия «Вывод остатка»
Составим новую таблицу как показано на рисунке 9. В графе С рассчитаем относительную ошибку аппроксимации по формуле:
Рисунок 9 Расчёт средней ошибки аппроксимации
Средняя ошибка аппроксимации рассчитывается по формуле:
Качество построенной модели оценивается как хорошее, так как не превышает 8 – 10%.
6. Из таблицы с регрессионной статистикой (Рисунок 4) выпишем фактическое значение F-критерия Фишера:
Поскольку при 5%-ном уровне значимости, то можно сделать вывод о значимости уравнения регрессии (связь доказана).
8. Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительного интервала каждого из показателей.
Выдвигаем гипотезу Н0 о статистически незначимом отличии показателей от нуля:
.
для числа степеней свободы
На рисунке 7 имеются фактические значения t-статистики:
t-критерий для коэффициента корреляции можно рассчитать двумя способами:
I способ:
где – случайная ошибка коэффициента корреляции.
Данные для расчёта возьмём из таблицы на Рисунке 7.
II способ:
Фактические значения t-статистики превосходят табличные значения:
Поэтому гипотеза Н0 отклоняется, то есть параметры регрессии и коэффициент корреляции не случайно отличаются от нуля, а статистически значимы.
Доверительный интервал для параметра a определяется как
Для параметра a 95%-ные границы как показано на рисунке 7 составили:
Доверительный интервал для коэффициента регрессии определяется как
Для коэффициента регрессии b 95%-ные границы как показано на рисунке 7 составили:
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью параметры a и b, находясь в указанных границах, не принимают нулевых значений, т.е. не являются статистически незначимыми и существенно отличны от нуля.
7. Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит:
Тогда прогнозное значение прожиточного минимума составит:
Ошибку прогноза рассчитаем по формуле:
где
Дисперсию посчитаем также с помощью ППП Excel. Для этого:
1) Активизируйте Мастер функций: в главном меню выберете Формулы / Вставить функцию.
2) В окне Категория выберете Статистические, в окне функция – ДИСП.Г. Щёлкните по кнопке ОК.
3) Заполните диапазон, содержащий числовые данные факторного признака. Нажмите ОК.
Рисунок 10 Расчёт дисперсии
Получили значение дисперсии
Для подсчёта остаточной дисперсии на одну степень свободы воспользуемся результатами дисперсионного анализа как показано на Рисунке 7.
Доверительные интервалы прогноза индивидуальных значений у при с вероятностью 0,95 определяются выражением:
Интервал достаточно широк, прежде всего, за счёт малого объёма наблюдений. В целом выполненный прогноз среднемесячной заработной платы оказался надёжным.
Условие задачи взято из: Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2003. – 192 с.: ил.
http://math.semestr.ru/corel/prim1.php
http://ecson.ru/economics/econometrics/zadacha-3.raschyot-parametrov-regressii-i-korrelyatsii-s-pomoschju-excel.html
§ 8. Построение доверительных интервалов для коэффициентов регрессии
Найденные по МНК из нормальной системы значения коэффициентов регрессии, само уравнение регрессии – это не истинные значения, а приближенные, как и все, что мы находим по статистическим данным.
Те же самые формулы для другой серии наблюдений дадут и другие результаты, немного отличающиеся.
Для истинных значений мы можем построить доверительные интервалы:

Истинные значения коэффициентов с заданной вероятностью g будут лежать в построенных интервалах.
Размах доверительных интервалов определяется формулами:


Рекомендуемые материалы
В результате проработки технического задания на модернизацию части системы управления бортовой РЛС (система обзора) возникло три варианта модернизации. Для их оценки предлагается использовать показатели качества, приведенные в табл. 8.1.1.
Доклад Конвенции N 132 № 138 Международной организации труда
Используя запланированное снижение себестоимости изделий в ре-зультате ФСА, установить очередность ФСА для выпускаемых предприяти-ем изделий. Изделие №3 будет снято с производства через один год, осталь-ные – через большее число лет. Исходные данные
Предположим, что каждый доллар, предназначенный для сделок, обращается в среднем 4 раза в год и направляется на покупку конечных товаров и услуг. Номинальный ВНП составляет 2000 млрд. долл. В таблице представлена величина спроса на деньги со стороны
FREE
Черная масса вала руля – 8,5 кг. Чистая масса – 7 кг. Цена заготовки – 1,15 д.е. Цена отходов – 7,01 д.е. за тонну. Заработная плата на всех опера-циях вала составила 0,28 д.е. Расходы по цеху составляют 250%, общеза-водские расходы – 130% от заработ
Здесь коэффициент 


Чем меньше разброс статистических данных относительно построенной линии регрессии, тем меньше дисперсия и стандартное отклонение остатков, тем уже доверительные интервалы.
С другой стороны размах доверительных интервалов можно уменьшить, увеличивая объем выборки n, т.е. количество наблюдений.
Доверительная зона для линии регрессии
Уравнения регрессии – это тоже не истинные уравнения, это приблизительное знание о них. И подсчитанные по ним теоретические значения фактора Y, т.е. 

Размах доверительных интервалов определяется формулой:
Если подсчитать эти значения 
IV. Прогноз и его доверительный интервал
Прогноз — научное предвидение вероятностных путей развития экономических процессов в более-менее удаленном будущем.
Период упреждения — промежуток времени от момента, для которого есть последние статистические данные до момента, которому принадлежит прогноз.
yp = a + bxp
Для прогнозируемого значения доверительный интервал определяется:
Коэффициент эластичности — в экономических задачах применяется для оценки влияния некоторого фактора (х) на соответствующий показатель (y).
В общем случае, статистический коэффициент эластичности, как правило, определяется на основе статистического ряда:
Точные значения коэффициента эластичности получают на основании операции предельного перехода, при 
kx будет определяться для парной регрессии:
6. Построение доверительных интервалов
для коэффициентов регрессии
Найденные значения коэффициентов ( a, b, c, d ) в уравнениях регрессии – это не истинные значения, это только оценка для них. (Как и любая другая информация, которую мы получаем по выборочным, статистическим данным
7. Построение доверительной зоны для линии регрессии
Уравнения регрессии – это тоже не истинные уравнения, это приблизительное знание о них. И подсчитанные по ним теоретические значения фактора Y, т.е. 

Размах доверительных интервалов определяется формулой:
Если подсчитать эти значения 
· В столбце BL ( ΔYi ) вычислить доверительные интервалы для 
Выделяя весь столбец, программируем формулу
Для чисел ( Sост , n ,


· В столбцах BM «нижн грань » и BN «верхн грань » вычислить границы
доверительной зоны.: 
Выделять весь столбец, программировать формулу с именами. Закончить ввод сочетанием Ctrl + Enter.
· Построить график доверительной зоны. Для этого выделить пять столб-
цов данных (вместе с заголовками):
¨ столбец N, в котором находятся статистические данные для фактора X.
¨ нажав клавишу Ctrl:
§ столбец O для фактора Y,
§ столбец AG для линии регрессии Y на X,
§ столбцы BM и BN для границ доверительной зоны.
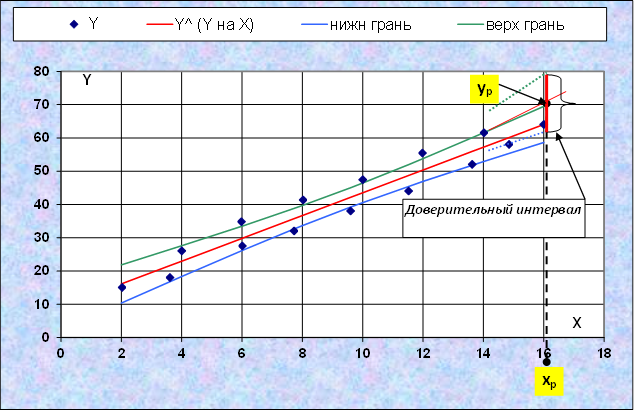
Затем вызвать Мастер Диаграмм и построить Точечную Диаграмму. Отредактировать ее, так чтобы точки, указывающие линию регрессии и линии границы доверительной зоны на графике были линиями без маркеров ( желательно линию регрессии и границы – разным цветом). График должен выглядеть так же, как приведенный выше.
8. Определение прогноза и доверительного интервала для прогноза
Построенное уравнение регрессии можно теперь использовать для прогнозирования. Задавая любое значение фактора X можно подсчитать соответствующее среднее значение фактора Y.
Найденное таким образом значение, во–первых среднее, а во–вторых, опять таки, приблизительное. Истинное прогнозное значение с заданной вероятностью γ следует ожидать в доверительном интервале 
Размах доверительного интеграла для прогноза определяется формулой, почти такой же, как и при построении доверительной зоны:

· В ячейку BS29 скопировать из N23 заданное для прогноза значение Xp.
· В ячейке BV29 вычислить по найденной формуле регрессии прогнозное значение Yp :
· Размах доверительного интервала для прогноза найти в ячейке BS32 по приведенной формуле
· В ячейках BU32 и BW32 подсчитать границы доверительного интервала для прогноза:
§ 9. Прогноз и доверительные интервал для прогноза
Построенное уравнение регрессии можно теперь использовать для прогнозирования. Задавая любое значение фактора X можно подсчитать соответствующее среднее значение фактора Y.
Найденное таким образом значение, во–первых среднее, а во–вторых, опять таки, приблизительное. Истинное прогнозное значение с заданной вероятностью γ следует ожидать в доверительном интервале 
Размах доверительного интеграла для прогноза определяется формулой, почти такой же, как и при построении доверительной зоны:
Люди также интересуются этой лекцией: Правовые основы лизинговых операций.

 |