Страница 5 из 13
Ответы есть в атласе на страницах 10 и 11.
Задания
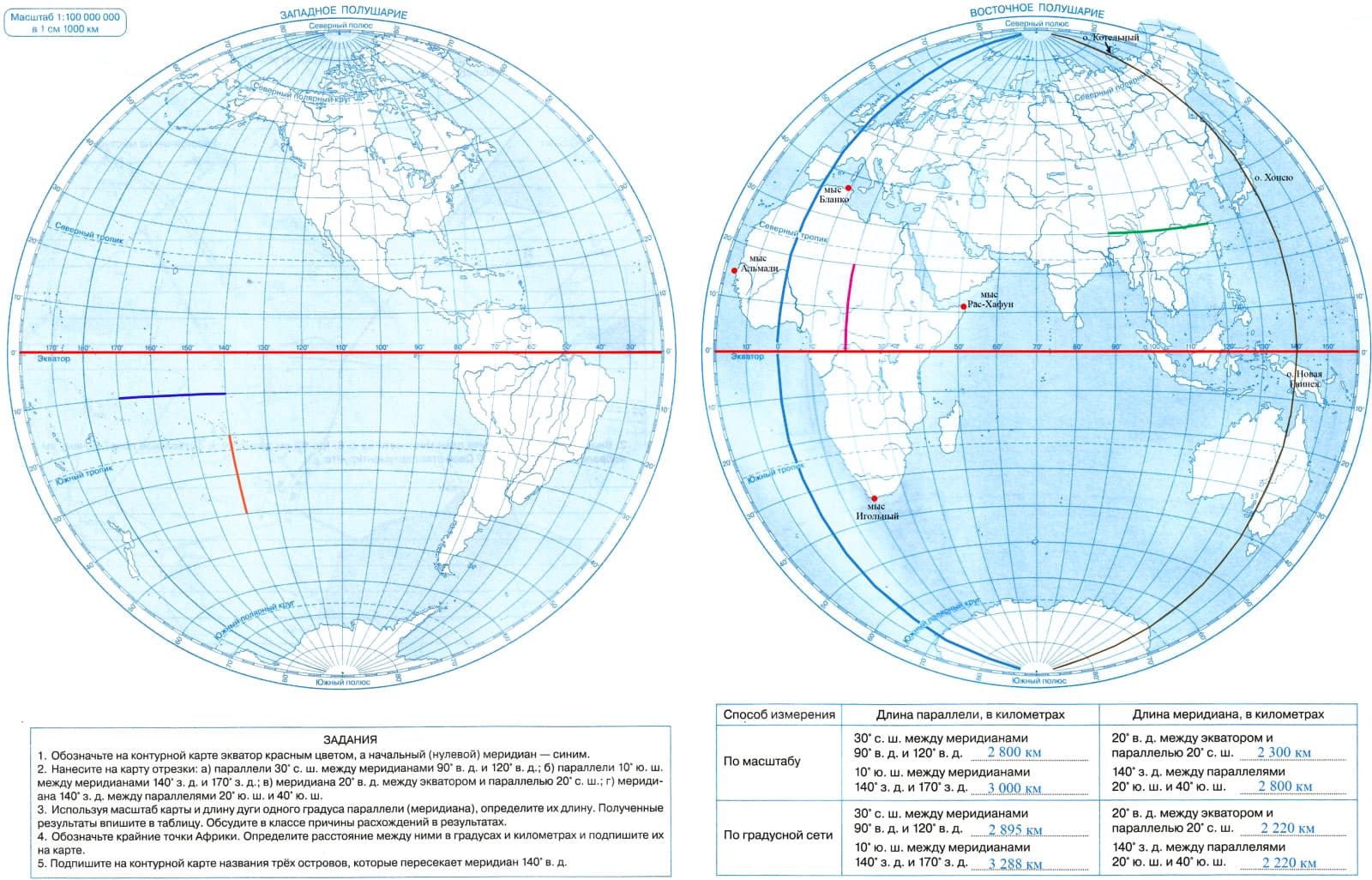
1. Обозначьте на контурной карте экватор красным цветом, а начальный (нулевой) меридиан — синим.
Экватор — красная линия.
Нулевой меридиан — синяя линия.
2. Нанесите на карту отрезки:
а) параллели 30° с. ш. между меридианами 90° в. д. и 120° в. д. — зелёная линия;
б) параллели 10° ю. ш. между меридианами 140° з. д. и 170° з. д. — фиолетовая линия;
в) меридиана 20° в. д. между экватором и параллелью 20° с. ш. — розовая линия;
г) меридиана 140° з. д. между параллелями 20° ю. ш. и 40° ю. ш. — оранжевая линия.
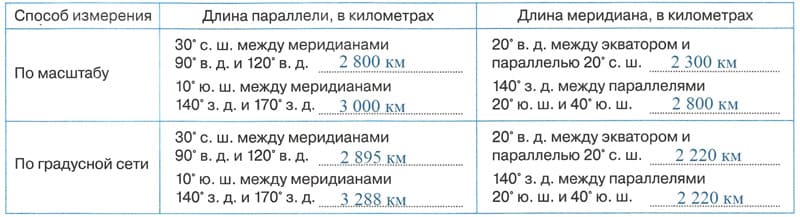
3. Используя масштаб карты и длину дуги одного градуса параллели (меридиана), определите их длину. Полученные результаты впишите в таблицу. Обсудите в классе причины расхождений в результатах.
Сначала измерим длины параллелей и меридианов по масштабу. Для этого надо линейкой измерить расстояние между точками и перевести расстояние на карте в реальный масштаб (масштаб карты 1:100 000 000, в 1 см 1 000 км):
дуга параллели 30° с. ш. между меридианами 90° в. д. и 120° в. д. (зелёная линия) = 2,8 см, то есть в реальности это будет 2 800 км;
дуга параллели 10° ю. ш. между меридианами 140° з. д. и 170° з. д. (фиолетовая линия) = 3 см, то есть в реальности это будет 3 000 км;
дуга меридиана 20° в. д. между экватором и параллелью 20° с. ш. (розовая линия) = 2,3 см, то есть в реальности это будет 2 300 км;
дуга меридиана 140° з. д. между параллелями 20° ю. ш. и 40° ю. ш. (оранжевая линия) = 2,8 см, то есть в реальности это будет 2 800 км.Теперь определим расстояния по градусной сети:
дуга параллели 30° с. ш. между меридианами 90° в. д. и 120° в. д. (зелёная линия) — длина 1° параллели 30° равна 96,5 км, 120° — 90° = 30°, считаем 30 • 96,5 = 2 895 км;
дуга параллели 10° ю. ш. между меридианами 140° з. д. и 170° з. д. (фиолетовая линия) — длина 1° параллели 10° равна 109,6 км, 170° — 140° = 30°, считаем 30 • 109,6 = 3 288 км;
дуга меридиана 20° в. д. между экватором и параллелью 20° с. ш. (розовая линия) — длина 1° меридиана равна 111 км, 20° — 0° = 20°, считаем 20 • 111= 2 220 км;
дуга меридиана 140° з. д. между параллелями 20° ю. ш. и 40° ю. ш. (оранжевая линия) — длина 1° меридиана равна 111 км, 140° — 20° = 20°, считаем 20 • 111= 2 220 км.Занесём результаты в таблицу.
Вычислим расхождения в результатах:
дуга параллели 30° с. ш. между меридианами 90° в. д. и 120° в. д. (зелёная линия) — расхождение между измерением по масштабу и измерением по градусной сети 2 895 — 2 800 = 95 км;
дуга параллели 10° ю. ш. между меридианами 140° з. д. и 170° з. д. (фиолетовая линия) — расхождение между измерением по масштабу и измерением по градусной сети 3 288 — 3 000 = 288 км;
дуга меридиана 20° в. д. между экватором и параллелью 20° с. ш. (розовая линия) — расхождение между измерением по масштабу и измерением по градусной сети 2 300 — 2 220 = 80 км;
дуга меридиана 140° з. д. между параллелями 20° ю. ш. и 40° ю. ш. (оранжевая линия) — расхождение между измерением по масштабу и измерением по градусной сети 2 800 — 2 220 = 580 км.Земля — это объемное трёхмерное тело сферической формы. Карта же представляет собой двухмерное изображение на плоскости. Именно поэтому любое изображение объемной Земли на плоской бумаге неизменно приводит к искажению расстояний между точками на земной поверхности и к искажению самой формы географических объектов.
Мы видим, что более точным способом определения расстояния между двумя географическими точками является метод вычисления при помощи длины дуги меридиана и длины дуги параллели. При измерении же по карте при помощи масштаба данные могут отличаться от реальных расстояний на сотни и даже на тысячи километров. Причем, чем дальше измеряемые дуги находятся от экватора, тем более заметно проявляются искажения карты.
Это хорошо видно на примере измерения меридианов, которые мы провели: расхождение длины дуги меридиана между экватором и 20-й параллелью составляет всего 80 км, а между 20-й и 40-й параллелями уже 580 км.
4. Обозначьте крайние точки Африки. Определите расстояние между ними в градусах и километрах и подпишите их на карте.
Крайние точки Африки (обозначены красными крупными точками)
Северная — мыс Бланко 37° северной широты 10° восточной долготы.
Южная — мыс Игольный 36° южной широты 20° восточной долготы.
Западная — мыс Альмади 15° северной широты 16° западной долготы.
Восточная — мыс Рас-Хафун 10° северной широты 52° восточной долготы.
Измерим расстояния между крайними северной и южной точками на карте и в градусах:
расстояние между крайней северной и крайней южной точкой Африки на карте 8,8 см, то есть в масштабе это будет 8 800 км;
крайняя северная точка находится на 37° северной широты, а крайняя южная — на 36° южной широты, значит между ними 37 + 36 = 73°. Это соответствует расстоянию в 73 • 111 = 8 103 км.
Измерим расстояния между крайними западной и восточной точками на карте и в градусах:
расстояние между крайней западной и крайней восточной точкой Африки на карте 6,7 см, то есть в масштабе это будет 6 700 км.
крайняя западная точка находится на 16° западной долготы, а крайняя восточная — на 52° восточной долготы, значит между ними 16 + 52 = 68°. Длина дуги 1° 10-й параллели (на ней находится восточная точка) равна 109,6 км, а длина дуги 1° 15-й параллели (на ней находится западная точка) равна 107,6 км. Для расчётов возьмём среднее значение — 108,6 км = длина 1° дуги. Значит 68° будет соответствовать 68 • 108,6 = 7 385 км.
Как видим, при расчётах расстояния между крайними точками получаются значительные расхождения. В реальности расстояние между крайней северной и крайней южной точкой примерно равно 8000 км, а расстояние между крайней западной и крайней восточной точкой — 7 500 км.
Выше даны приблизительные координаты крайних точек Африки. Точные координаты следующие:
Северная — мыс Бланко 37°20′28″ с. ш. 9°44′48″ в. д.
Южная — мыс Игольный 34°49′43″ ю. ш. 20°00′09″ в. д.
Западная — мыс Альмади 14°44′27″ с. ш. 17°31′48″ з. д.
Восточная — мыс Рас-Хафун 10°27′00″ с. ш. 51°24′00″ в. д.
5. Подпишите на контурной карте названия трёх островов, которые пересекает меридиан 140° в. д.
140-й меридиан восточной долготы (обозначен на карте коричневой линией) пересекает острова:
Котельный (в Северном Ледовитом океане);
Хонсю (один из островов Японии);
Новая Гвинея (рядом с Австралией).
Для этого с помощью измерителя или
линейки определяют по карте (с точностью
до 0,5 мм) ..длины дуг меридиана и -параллели,
на которых лежит данная точка, причем
измерения производятся по меридиану
к северу и югу, по параллели -к востоку
и западу от точки А (рис. 4). Соответствующие
им величины на эллипсоиде берут из
табл. 5. Частные масштабы выражают в
долях главного, вычисляют с точностью
до 0,01 по следующим формулам:
m
= l1
/h1*
M n = l2
/L2*
M
где т —
частныймасштаб по меридиану в долях
главного масштаба,
п — частный
масштаб по параллели в долях главного
масштаба,
l1
— длина дуги меридиана на карте, —
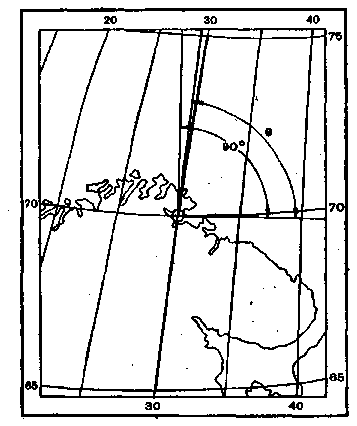
Рис. 4. Часть карты СССР в масштабе
1:6 000 000 (уменьшена в четыре раза)
L1—
длина соответствующей дуги меридиана
на эллипсоиде,
l2
— длина дуги параллели на карте,
L2
— длина соответствующей дуги параллели
на эллипсоиде,
M
— знаменатель главного масштаба карты.
2. Измерить угол между
меридианом и параллелью и вычислить
его отклонение от прямого; величина
угла определяется с точностью до 0,50
. Для этого проводят касательные к
меридиану и параллели в заданной
точке и угол между касательными (в)
измеряют транспортиром,
где E
— отклонение угла О
от 90°; 0
— величина угла на
карте между меридианом и параллелью.
3.Вычислить величины p,
а ,
b
, w
, k
по
указанным формулам. Вычисления можно
вести с помощью логарифмической линейки
или
по таблицам натуральных значений
тригонометрических функций, с
использованием микрокалькуляторов с
точностью до 0,01.
4. Определить величины p
и k , пользуясь
картографической cеткой
поликонической проекции Т.Д.Салмановой
с изоколами площадей
р (прил.
19 ) и изоколами форм -к
( прил.20). По
картографическим сеткам с изоколами
-р и
4, в
видоизмененной поликоничес-кой проекции
Т.Д.Салмановой найти точку с заданными
координатами (например, (φ-
70° с.ш., λ,
= 30° в.д.). В таблице с
изоколами p
эта точка расположена на изоколе 1,20,
следовательно, р =
1,20. Аналогично определяется искажение
форм к
= 1,15. В случае, если точка находится
между изоколами, искажение p
и k
определяется путем интерполирования.
Расхождения в значениях величин,
определяемых различными способами,
могут возникать за счет неточностей
измерений или интерполирования.
Результаты работы представить в виде
таблицы
Указания
к выполнению
задания.
-
Изучив
легенду и содержание каждой карты,
выяснить, какиеявления
показаны на карте (явления, локализованные
в пунктах, налиниях,
на отдельных площадях; сплошного или
рассеянного распространения). -
Определить картографические
способы, используемые для каждого
изображенного на карге явления. -
Установить,
какие качественные и количественные
характеристики
передаются каждым картографическим
способом изображения икакие
оформительские приемы использованы
для них на карге.
Пример
выполнения работы.
Название
атласа,
карта,
страница
Явления,
показанные
на карте
Способ
изображения
явлений
Характеристика
(качественная,
количественная)
явлений
Оформительские
приемы
Атлас
Ростовской области.
М., 1973.
Почвенная
карта.
С.12
Генетические
типы,
подтипы и виды почв
Качественный
фон
Генезис
почв —
качественная
характеристика
Цветной
Атлас
Астраханской
области.
М., 1968.
Карта
животноводства.
С24
Вкрапления
почв
иных
ТИПОВ
внутри
основного
почвенного
массива
Размещение
поголовья
лошадей
и верблюдов
Ареалы
Точечный
способ
Поголовье
лошадей и верблюдов
в
количественном выражении-«вес
точки»-50
голов скота
Геометрические
значки
Точки различного
цвета
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
показать содержание
Условие(я):
Условие(я) задания(й):
1. Обозначьте на контурной карте экватор красным цветом, а начальный (нулевой) меридиан — синим. 2. Нанесите на карту отрезки. 3. Используя масштаб карты и длину дуги одного градуса параллели (меридиана), определите их длину. Полученные результаты впишите в таблицу. Обсудите в классе причины расхождений в результатах. 4. Обозначьте крайние точки Африки. Определите расстояние между ними в градусах и километрах и подпишите их на карте. 5. Подпишите на контурной карте названия трёх островов, которые пересекает меридиан 140° в. д.
Нажми по картинке c решением и она увеличится
Оцени решение:
ГДЗ: Правильный(е) ответ(ы) или решения(е) 1-5
из
Градусная сеть стр. 8-9
,
География. 6 класс. Контурные карты. Курбский
Длина дуги параллелей и меридианов, с учётом полярного сжатия Земли
Для определения расстояния по туристической карте, в километрах между пунктами, число градусов умножают на длину дуги 1° параллели и меридиана (по долготе и широте, в системе географических координат), точные расчётные значения которых берутся из таблиц. Приблизительно, с определённой погрешностью, их можно посчитать по формуле, на калькуляторе.
Пример из школьного урока географии (по старому учебнику и из учебного пособия для факультативного курса)
Определить частный масштаб мелкомасштабной (1:1 000 000, 1:6000000, 1:20 000 000 и мельче) карты земной поверхности (атлас для VI класса) в районе Казани и Свердловска (ныне - Екатеринбург, смотреть список переименованных городов). Оба эти города располагаются, приблизительно, на широте 56° СШ.
Долгота Казани - 49° ВД, Екатеринбурга - 60°ВД.
Расстояние между ними на карте - 1,1 см (определяется с помощью измерительного циркуля и линейки с миллиметровыми делениями).
Длина дуги параллели в 1° для широты 56°СШ - равна 62394 метров.
Решение
60 - 49 = 11° (разница в долготах).
L = 62394 * 11 = 686 334 метров = 68 633 400 см (расстояние между пунктами в сантиметрах).
m = 1 / (68 633 400 / 1,1) ~ 1 / 62 400 000
Ответ: частный масштаб (m) - в 1 см 624 км.
Главный масштаб (подписанный в зарамочном
оформлении этой карты) - 1 / 75 000 000 (1 см 750км).
Частный м-б может быть и больше и меньше главного, в зависимости от расположения выбранного участка на карте.
Пример перевода числовых значений географических координат из десятых долей в градусы и минуты.
Приближенная долгота города Свердловска - 60.8° (шестьдесят целых и восемь десятых градуса) восточной долготы.
8 / 10 = X / 60
X = (8 * 60) / 10 = 48 (из пропорции находим числитель правой дроби).
Итог: 60.8° = 60° 48' (шестьдесят градусов и сорок восемь минут).
Чтобы добавить символ градуса ( ° ) – нажмите Альт+248 (цифрами в правой цифровой панели клавиатуры; в ноутбуке — с нажатой спец.кнопкой Fn или включив NumLk)). Так делается в операционных системах Windows и Linux, а в ОС Mac — с помощью клавиш Shift+Option+8
Координаты широты всегда указываются перед координатами долготы (и печатая на компьютере, и записывая на бумаге).
В сервисе maps.google.ru, поддерживаемые форматы определяются правилами.
Примеры, как будет правильно:
Полная форма записи угла (градусы, минуты, секунды с долями):
41° 24' 12.1674", 2° 10' 26.508"
Сокращённые формы записи угла:
Градусы и минуты с десятичными долями – 41 24.2028, 2 10.4418
Десятичные градусы (DDD) – 41.40338, 2.17403
Сервис Гугл-мап имеет онлайн-конвертер для преобразований координат и перевода их в нужный формат.
В качестве десятичного разделителя числовых величин, на сайтах в Интернет и в компьютерных программах — рекомендуется использовать точку.
Таблицы
Длина дуги параллели в 1°, 1′ и 1″ по долготе, метров
| Широта, градус |
Длина дуги параллели в 1° по долготе, м |
Длина дуги паралл в 1′,м |
Длина дуги пар. в 1″,м |
|---|---|---|---|
| 0 | 111321 | 1855 | 31 |
| 1 | 111305 | 1855 | 31 |
| 2 | 111254 | 1854 | 31 |
| 3 | 111170 | 1853 | 31 |
| 4 | 111052 | 1851 | 31 |
| 5 | 110901 | 1848 | 31 |
| 6 | 110716 | 1845 | 31 |
| 7 | 110497 | 1842 | 31 |
| 8 | 110245 | 1837 | 31 |
| 9 | 109960 | 1833 | 31 |
| 10 | 109641 | 1827 | 30 |
| 11 | 109289 | 1821 | 30 |
| 12 | 108904 | 1815 | 30 |
| 13 | 108487 | 1808 | 30 |
| 14 | 108036 | 1801 | 30 |
| 15 | 107552 | 1793 | 30 |
| 16 | 107036 | 1784 | 30 |
| 17 | 106488 | 1775 | 30 |
| 18 | 105907 | 1765 | 29 |
| 19 | 105294 | 1755 | 29 |
| 20 | 104649 | 1744 | 29 |
| 21 | 103972 | 1733 | 29 |
| 22 | 103264 | 1721 | 29 |
| 23 | 102524 | 1709 | 28 |
| 24 | 101753 | 1696 | 28 |
| 25 | 100952 | 1683 | 28 |
| 26 | 100119 | 1669 | 28 |
| 27 | 99257 | 1654 | 28 |
| 28 | 98364 | 1639 | 27 |
| 29 | 97441 | 1624 | 27 |
| 30 | 96488 | 1608 | 27 |
| 31 | 95506 | 1592 | 27 |
| 32 | 94495 | 1575 | 26 |
| 33 | 93455 | 1558 | 26 |
| 34 | 92386 | 1540 | 26 |
| 35 | 91290 | 1522 | 25 |
| 36 | 90165 | 1503 | 25 |
| 37 | 89013 | 1484 | 25 |
| 38 | 87834 | 1464 | 24 |
| 39 | 86628 | 1444 | 24 |
| 40 | 85395 | 1423 | 24 |
| 41 | 84137 | 1402 | 23 |
| 42 | 82852 | 1381 | 23 |
| 43 | 81542 | 1359 | 23 |
| 44 | 80208 | 1337 | 22 |
| 45 | 78848 | 1314 | 22 |
| 46 | 77465 | 1291 | 22 |
| 47 | 76057 | 1268 | 21 |
| 48 | 74627 | 1244 | 21 |
| 49 | 73173 | 1220 | 20 |
| 50 | 71697 | 1195 | 20 |
| 51 | 70199 | 1170 | 19 |
| 52 | 68679 | 1145 | 19 |
| 53 | 67138 | 1119 | 19 |
| 54 | 65577 | 1093 | 18 |
| 55 | 63995 | 1067 | 18 |
| 56 | 62394 | 1040 | 17 |
| 57 | 60773 | 1013 | 17 |
| 58 | 59134 | 986 | 16 |
| 59 | 57476 | 958 | 16 |
| 60 | 55801 | 930 | 16 |
| 61 | 54108 | 902 | 15 |
| 62 | 52399 | 873 | 15 |
| 63 | 50674 | 845 | 14 |
| 64 | 48933 | 816 | 14 |
| 65 | 47176 | 786 | 13 |
| 66 | 45405 | 757 | 13 |
| 67 | 43621 | 727 | 12 |
| 68 | 41822 | 697 | 12 |
| 69 | 40011 | 667 | 11 |
| 70 | 38187 | 636 | 11 |
| 71 | 36352 | 606 | 10 |
| 72 | 34505 | 575 | 10 |
| 73 | 32647 | 544 | 9 |
| 74 | 30780 | 513 | 9 |
| 75 | 28902 | 482 | 8 |
| 76 | 27016 | 450 | 8 |
| 77 | 25122 | 419 | 7 |
| 78 | 23219 | 387 | 6 |
| 79 | 21310 | 355 | 6 |
| 80 | 19394 | 323 | 5 |
| 81 | 17472 | 291 | 5 |
| 82 | 15544 | 259 | 4 |
| 83 | 13612 | 227 | 4 |
| 84 | 11675 | 195 | 3 |
| 85 | 9735 | 162 | 3 |
| 86 | 7791 | 130 | 2 |
| 87 | 5846 | 97 | 2 |
| 88 | 3898 | 65 | 1 |
| 89 | 1949 | 32 | 1 |
| 90 | 0 |
Упрощённая формула расчёта дуг параллелей (без учета искажений от полярного сжатия):
l пар = l экв * cos(Широта).
Длина дуги меридиана в 1°, 1′ и 1″ по широте, метров
| Широта, градус |
Длина дуги меридиана в 1° по широте, м |
в 1′, м | 1″,м |
|---|---|---|---|
| 0 | 110579 | 1843 | 31 |
| 5 | 110596 | 1843 | 31 |
| 10 | 110629 | 1844 | 31 |
| 15 | 110676 | 1845 | 31 |
| 20 | 110739 | 1846 | 31 |
| 25 | 110814 | 1847 | 31 |
| 30 | 110898 | 1848 | 31 |
| 35 | 110989 | 1850 | 31 |
| 40 | 111085 | 1851 | 31 |
| 45 | 111182 | 1853 | 31 |
| 50 | 111278 | 1855 | 31 |
| 55 | 111370 | 1856 | 31 |
| 60 | 111455 | 1858 | 31 |
| 65 | 111531 | 1859 | 31 |
| 70 | 111594 | 1860 | 31 |
| 75 | 111643 | 1861 | 31 |
| 80 | 111677 | 1861 | 31 |
| 85 | 111694 | 1862 | 31 |
| 90 |
Рисунок. 1-секундные дуги меридианов и параллелей (упрощённая формула).
Андреев Н.В. Топография и картография: Факультативный курс. М., Просвещение, 1985
Учебник по математике.
ru.wikipedia.org/wiki/Географические_координаты
Подробнее читайте на Интернет-странице сайта:
http://www.kakras.ru/mobile/book/dlina-dugi.html
Опубликовано: 10 апреля 2015 года
Масштаб. Определение расстояний
Масштаб — это отношение длины линии на чертеже, плане или карте к длине соответствующей линии в действительности. Он показывает, во сколько раз расстояние на карте уменьшено относительно реального расстояния на местности. Если, например, масштаб географической карты 1 : 1 000 000, это значит, что 1 см на карте соответствует 1 000 000 см на местности, или 10 км.
Различают численный, линейный и именованный масштабы.
Численный масштаб изображается в виде дроби, у которой числитель равен единице, а знаменатель – число, показывающее, во сколько раз уменьшены линии на карте (плане) относительно линий на местности. Например, масштаб 1:100 000 показывает, что все линейные размеры на карте уменьшены в 100 000 раз. Очевидно, чем больше знаменатель масштаба, тем масштаб мельче, при меньшем знаменателе — крупнее. Численный масштаб – это дробь, поэтому числитель и знаменатель даются в одинаковых измерениях (сантиметрах).
Линейный масштаб представляет собой прямую линию, разделенную на равные отрезки. Эти отрезки соответствуют определенному расстоянию на изображаемой местности; деления обозначаются цифрами. Мера длины, по которой нанесены деления на масштабной линейке, называются основанием масштаба. В нашей стране основание масштаба принято равным 1 см. Количество метров или километров, соответствующее основанию масштаба, называют величиной масштаба. При построении линейного масштаба цифру 0, от которой начинается отсчет делений, обычно ставят не у самого конца масштабной линии, а отступив на одно деление (основание) вправо; на первом же отрезке налево от 0 наносят наименьшие деления линейного масштаба – миллиметры. Расстояние на местности, соответствующее одному наименьшему делению линейного масштаба, отвечает точности масштаба, а 0,1 мм – предельной точности масштаба. Линейный масштаб по сравнению с численным имеет то преимущество, что дает возможность без дополнительных вычислений определять действительное расстояние на плане и карте.
Именованный масштаб – масштаб, выраженный словами, например, в 1 см 32 км.
Измерение расстояний на карте и плане.
Измерение расстояний с помощью масштаба. Нужно прочертить прямую линию (если нужно узнать расстояние по прямой) между двумя точками и с помощью линейки измерить это расстояние в сантиметрах, а затем следует умножить полученное число на величину масштаба. Например, на карте масштаба 1 : 100 000 (в 1 см 1 км) расстояние равно 5 см, т. е. на местности это расстояние составляет 1 * 5 = 5 (км). Измерять расстояние по карте можно и с помощью циркуля-измерителя. В этом случае удобно пользоваться линейным масштабом.
Измерение расстояний с помощью градусной сети. Для расчета расстояний по карте или глобусу можно использовать следующие величины: длина дуги 1° меридиана и 1° экватора равна приблизительно 111 км. Для меридианов это верно всегда, а длина дуги 1° по параллелям уменьшается к полюсам. На экваторе его можно тоже принять равному 111 км. А на полюсах – 0 (т. к. полюс – это точка). Поэтому необходимо знать число километров, соответствующее длине 1° дуги каждой конкретной параллели. Чтобы определить расстояние в километрах между двумя пунктами, лежащими на одном меридиане, вычисляют расстояние между ними в градусах, а затем число градусов умножают на 111 км. Для определения расстояния между двумя точками на экваторе, также нужно определить расстояние между ними в градусах, а затем умножить на 111 км.
Следующая тема:
Рельеф. Изображение неровностей