Диагональ параллелограмма можно найти, точнее её половину, как сторону треугольника. Значит нужно знать по крайней мере еще две величины (если получается прямоугольный треугольник) или три (2 стороны и угол).
Вот формулы для определения длины меньшей диагонали d:
d = √a^2 + b^2 + 2ab·cosβ, d = √a^2 + b^2 — 2ab·cosα, где a и b — стороны параллелограмма, а β больший угол, α — меньший угол, D — длина большей диагонали.
1
Как найти меньшую диагональ параллелограмма?
Как найти меньшую диагональ параллелограмма?
1 ответ:
0
0
Диагональ параллелограмма можно найти, точнее её половину, как сторону треугольника. Значит нужно знать по крайней мере еще две величины (если получается прямоугольный треугольник) или три (2 стороны и угол).
Вот формулы для определения длины меньшей диагонали d:
d = √a^2 + b^2 + 2ab·cosβ, d = √a^2 + b^2 — 2ab·cosα, где a и b — стороны параллелограмма, а β больший угол, α — меньший угол, D — длина большей диагонали.
Читайте также
- Да, биссектрисы смежных углов параллелограмма перпендикулярны. Объяснение: сумма смежных углов параллелограмма равна 180 градусам, значит сумма их половинок равна 90 градусов. Это значит, что третий угол треугольника,образов<wbr />анного пересечением биссектрис равна тоже 90 градусам, то есть они перпендикулярны.
- Если ВК = 2, и сторона АВ тоже равна 2, так как биссектрисы перпендикулярны и они при пересечении со сторонами ВС м АD образуется ромб. Так как CL=CD+DL, то DL=6-4=2 DL=KC. Значит ВС=6, тогда периметр равен 2*(4+6)=20.
- Да, диагональ АС=7. Объяснение. Высота ВН равна 3V3/2, так как АН равна 1,5 (как сторона лежащая против угла в 30 градусов). Если опустить перпендикуляр СМ=ВН на сторону АД, то получим прямоугольный треугольник АСМ. AM=AC+CM=5+1,5=6,5. АС гипотенуза, по теореме Пифагора АС^2=AM^2+CM^2=169/4 + 27/4 = 196/4=49. Поэтому АС=7.
Так как площадь параллелограмма вычисляется по формуле
<h2>S = |a |*|b | * sin (a)/ (b) </h2>
где в формуле использованы модули векторов a , b и угол между этими векторами.
А эта формула есть не что иное , как векторное произведение двух векторов.
То есть площадь параллелограмма , построенного на двух векторах не что иное , как векторное произведение этих векторов.
Площадь параллелограмма находится через произведение длины основания a на высоту h. S = a * h.
Если это школьная задачка, в которой высота не известна, то должен быть известен какой-то другой параметр, через который можно вычислить высоту.
Если будет более конкретный вопрос, то тогда можно будет дать более конкретный ответ.
При известных длинах двух смежных сторон и угле между ними площадь параллелограмма находится очень просто. Вот формула:
S = a * b * sin (alfa)
где
S — площадь параллелограмма (искомая);
a, b — длины двух смежных, то есть соседних, соприкасающихся сторон. Обычно буквой a обозначают бо́льшую сторону, буквой b — меньшую;
alfa — величина угла между сторонами a и b.
Пример. Стороны параллелограмма равны 7 см и 6 см, а угол между ними равен 30°. Тогда площадь нашей фигуры будет равна: S = 7 см * 6 см * sin 30° = 21 (см^2).
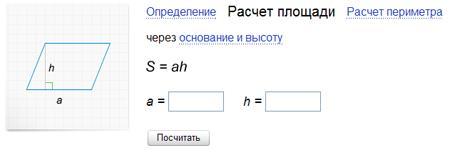
<h2>Площадь параллелограмма</h2>
Простые геометрические расчеты, такие как нахождение площади параллелограмма, можно производить при помощи Яндекса. Наберите в Яндексе:
площадь параллелограмма
Яндекс предложит следующий интерфейс, в который нужно будет подставить значения:
<h2>Формула площади параллелограмма</h2>
S=ah
где «a» — основание, «h» — высота.
- Категория: Задачи по планиметрии
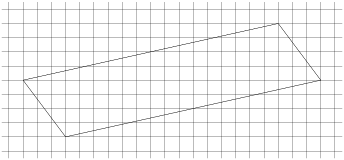
На клетчатой бумаге с размером клетки 1 х 1 изображён параллелограмм. Найдите длину его меньшей диагонали.
Решение:
Ответ: 17.
Найти длину меньшей из диагоналей параллелограмма..
Задание:
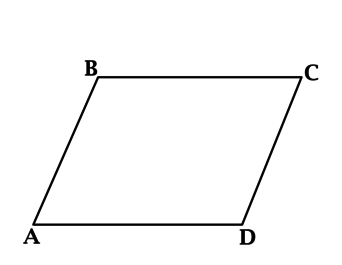
Найти длину меньшей из диагоналей параллелограмма, вершины которого имеют координаты (1;4), (5;4), (6;8), (2;8).
Решение:
Для решения данной задачи, нужно начертить в тетради в клетку ось OX и ось OY, и самое главное, понять правильную расстановку букв, должен получится примерно такой рисунок, что представлен выше.
Нам нужно найти меньшую диагональ — BD, по теореме Пифагора:
BD2 = BH2 + HD2
После того, как вы начертите рисунок, нужно подсчитать длины этих отрезков по клеткам, BH = 4, а HD = 3..
BD2 = BH2 + HD2
BD2 = 42 + 32
BD2 = 16 + 9 = 25
BD = √25
BD = 5
Ответ: 5
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Параллелограмм и его свойства
Сумма внутренних углов любого четырехугольника равна (360^circ).
Свойства параллелограмма:
(blacktriangleright) Противоположные стороны попарно равны;
(blacktriangleright) Диагонали точкой пересечения делятся пополам;
(blacktriangleright) Противоположные углы попарно равны, а сумма соседних равна (180^circ).
Признаки параллелограмма.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – параллелограмм:
(blacktriangleright) если противоположные стороны попарно равны;
(blacktriangleright) если две стороны равны и параллельны;
(blacktriangleright) если диагонали точкой пересечения делятся пополам;
(blacktriangleright) если противоположные углы попарно равны.
Площадь параллелограмма
Площадь параллелограмма равна произведению высоты на основание, к которому проведена эта высота.
Задание
1
#1783
Уровень задания: Легче ЕГЭ
Периметр параллелограмма равен (100), его большая сторона равна (32). Найдите меньшую сторону параллелограмма.
Так как у параллелограмма противоположные стороны равны, то его периметр равен удвоенной сумме его непараллельных сторон, тогда сумма большей и меньшей сторон равна (100 : 2 = 50), значит, меньшая сторона параллелограмма равна (50 — 32 = 18).
Ответ: 18
Задание
2
#1784
Уровень задания: Равен ЕГЭ
Периметр параллелограмма равен (15). При этом одна сторона этого параллелограмма на (5) больше другой. Найдите меньшую сторону параллелограмма.
У параллелограмма противоположные стороны равны. Пусть (BC = AB +
5), тогда периметр параллелограмма (ABCD) равен (AB + BC + CD + AD =
AB + AB + 5 + AB + AB + 5 = 4cdot AB + 10 = 15), откуда находим (AB
= 1,25). Тогда меньшая сторона параллелограмма равна (1,25).
Ответ: 1,25
Задание
3
#273
Уровень задания: Равен ЕГЭ
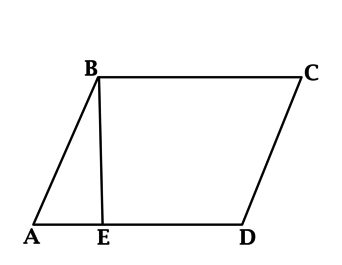
В параллелограмме (ABCD): (BE) – высота, (BE = ED = 5). Площадь параллелограмма (ABCD) равна 35. Найдите длину (AE).
Площадь параллелограмма равна произведению основания на высоту, проведённую к этому основанию, тогда (35 = BE cdot AD = 5cdot(5 + AE)), откуда находим (AE = 2).
Ответ: 2
Задание
4
#1785
Уровень задания: Равен ЕГЭ
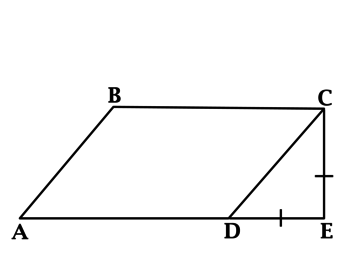
Из точки (C) параллелограмма (ABCD) опустили перпендикуляр на продолжение стороны (AD) за точку (D). Этот перпендикуляр пересёк прямую (AD) в точке (E), причём (CE = DE). Найдите (angle B) параллелограмма (ABCD). Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, тогда (angle EDC = angle DCE). Так как (angle DEC = 90^{circ}), а сумма углов треугольника равна (180^{circ}), то (angle EDC =
45^{circ}), тогда (angle ADC = 180^{circ} — 45^{circ} =
135^{circ}). Так как в параллелограмме противоположные углы равны, то (angle B = angle ADC = 135^{circ}).
Ответ: 135
Задание
5
#1686
Уровень задания: Равен ЕГЭ
Диагональ (BD) параллелограмма (ABCD) перпендикулярна стороне (DC) и равна (4). Найдите площадь параллелограмма (ABCD), если (AD=5).
По теореме Пифагора находим: (AB^2=AD^2 — BD^2 = 25 — 16 = 9) (Rightarrow) (AB = 3). (S_{ABCD} = 4cdot3 = 12).
Ответ: 12
Задание
6
#1685
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (P_{triangle AOB} = 
(P_{triangle AOB} = AO + OB + AB), (P_{triangle AOD} = AO + OD + AD), (BO = OD) (Rightarrow) (P_{triangle AOD} — P_{triangle AOB} = AD — AB = 1), но (AD + AB = 7) (Rightarrow) (AD = 4), (AB = 3) (Rightarrow) (ADcdot AB = 12).
Ответ: 12
Задание
7
#3617
Уровень задания: Равен ЕГЭ
Стороны параллелограмма равны (9) и (15). Высота, опущенная на первую сторону, равна (10). Найдите высоту, опущенную на вторую сторону параллелограмма.
Площадь параллелограмма равна произведению высоты на сторону, к которой высота проведена. Следовательно, с одной стороны, площадь (S=9cdot 10), с другой стороны, (S=15cdot h), где (h) – высота, которую нужно найти.
Следовательно, [9cdot 10=15cdot hquadLeftrightarrowquad h=6]
Ответ: 6
Задачи из раздела «Геометрия на плоскости» являются обязательной частью аттестационного экзамена у выпускников средней школы. Теме «Параллелограмм и его свойства» в ЕГЭ традиционно отводится сразу несколько заданий. Они могут требовать от школьника как краткого, так и развернутого ответа с построением чертежа. Поэтому если одним из ваших слабых мест являются именно задачи на вычисление площадей параллелограмма или его сторон и углов, то вам непременно стоит повторить или вновь разобраться в материале.
Сделать это легко и эффективно вам поможет образовательный портал «Школково». Наши опытные специалисты подготовили необходимый теоретический материал, изложив его таким образом, чтобы школьники с любым уровнем подготовки смогли восполнить пробелы в знаниях и легко решить задачи ЕГЭ на вычисление площадей, сторон, углов или свойства биссектрисы параллелограмма. Найти базовую информацию вы можете в разделе «Теоретическая справка».
Чтобы успешно решить задачи ЕГЭ по теме «Параллелограмм и его свойства», предлагаем попрактиковаться в выполнении соответствующих упражнений. Большая подборка заданий представлена в блоке «Каталог». Специалисты портала «Школково» регулярно дополняют и обновляют данный раздел.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.

УСТАЛ? Просто отдохни