Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Математический маятник
Определения и формулы математического маятника
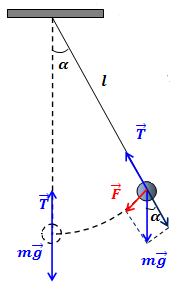
Рис.1. Математический маятник
Математический маятник – это модель системы, совершающей гармонические колебания. Свободные колебания математического маятника при малых углах отклонения описываются уравнением гармонических колебаний.
В положении равновесия сила тяжести и сила упругости нити уравновешивают друг друга, и материальная точка находится в покое. При отклонении материальной точки от положения равновесия на малый угол на тело будет действовать возвращающая сила
, которая является тангенциальной составляющей силы тяжести:
Эта сила сообщает материальной точке тангенциальное ускорение, направленное по касательной к траектории, и материальная точка начинает двигаться к положению равновесия с возрастающей скоростью. По мере приближения к положению равновесия возвращающая сила, а следовательно, и тангенциальное ускорение точки, уменьшаются. В момент прохождения положения равновесия угол отклонения , тангенциальное ускорение также равно нулю, а скорость материальной точки максимальна. Далее материальная точка проходит по инерции положение равновесия и, двигаясь в направлении, противоположном силе
, сбавляет скорость. В крайнем положении материальная точка останавливается, и затем начинает двигаться в обратном направлении.
Период колебаний математического маятника
Период колебаний математического маятника не зависит от массы груза и амплитуды колебаний.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Расчет длины маятника
Маятник — это тело или система тел, подвешенная в поле тяжести и совершающая механические колебания.
Формула расчета длины маятника:
L = (T / 2π) 2 * g, где
L — длина маятника в метрах;
T — период колебаний в секундах;
g — ускорение свободного падения в м/с 2 .
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета длины маятника по простой математической формуле в зависимости от периода колебаний и ускорения свободного падения. С помощью этой программы вы в один клик сможете рассчитать длину маятника.
Расчет длины нити математического маятника
Период колебания математического маятника (в секундах) приближенно можно вычислить по формуле , где — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет секунды.
Решение задачи
В данном уроке показано, как грамотно рассчитать длину нити математического маятника. По условию задана формула , с помощью которой приблизительно вычисляются колебания маятника. — это период колебания маятника, который известен по условию задачи ( секунды), а – это длина нити маятника, которую и необходимо рассчитать. Для решения задачи достаточно преобразовать формулу (представленную в виде алгебраического выражение) и подставить в нее известные данные. Для этого из формулы выражается переменная , в процессе этого выполняются операции упрощения выражения. Далее, для получения окончательного ответа, вместо переменной подставляется его числовое значение. Ответ представлен в виде десятичной дроби
При подготовке к ОГЭ можно успешно воспользоваться решением этой задачи, в частности при решении задач типа ОГЭ 20.
Как найти длину нити
Математическим маятником называют тело небольших размеров, подвешенное на тонкой нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела. В положении равновесия, когда маятник висит по отвесу, сила тяжести уравновешивается силой натяжения нити При отклонении маятника из положения равновесия на некоторый угол появляется касательная составляющая силы тяжести (рис. 2.3.1). Знак «минус» в этой формуле означает, что касательная составляющая направлена в сторону, противоположную отклонению маятника.
Если обозначить через линейное смещение маятника от положения равновесия по дуге окружности радиуса , то его угловое смещение будет равно . Второй закон Ньютона, записанный для проекций векторов ускорения и силы на направление касательной, дает:
Это соотношение показывает, что математический маятник представляет собой сложную нелинейную систему, так как сила, стремящаяся вернуть маятник в положение равновесия, пропорциональна не смещению , а
Только в случае малых колебаний , когда приближенно можно заменить на математический маятник является гармоническим осциллятором , т. е. системой, способной совершать гармонические колебания. Практически такое приближение справедливо для углов порядка ; при этом величина отличается от не более чем на . Колебания маятника при больших амплитудах не являются гармоническими.
Для малых колебаний математического маятника второй закон Ньютона записывается в виде
Таким образом, тангенциальное ускорение маятника пропорционально его смещению , взятому с обратным знаком. Это как раз то условие, при котором система является гармоническим осциллятором. По общему правилу для всех систем, способных совершать свободные гармонические колебания, модуль коэффициента пропорциональности между ускорением и смещением из положения равновесия равен квадрату круговой частоты:
Эта формула выражает собственную частоту малых колебаний математического маятника .
Любое тело, насаженное на горизонтальную ось вращения, способно совершать в поле тяготения свободные колебания и, следовательно, также является маятником. Такой маятник принято называть физическим (рис. 2.3.2). Он отличается от математического только распределением масс. В положении устойчивого равновесия центр масс физического маятника находится ниже оси вращения на вертикали, проходящей через ось. При отклонении маятника на угол возникает момент силы тяжести, стремящийся возвратить маятник в положение равновесия:
Здесь – расстояние между осью вращения и центром масс .
Здесь – собственная частота малых колебаний физического маятника .
Более строгий вывод формул для и можно сделать, если принять во внимание математическую связь между угловым ускорением и угловым смещением: угловое ускорение есть вторая производная углового смещения по времени:
Поэтому уравнение, выражающее второй закон Ньютона для физического маятника, можно записать в виде
Это уравнение свободных гармонических колебаний (см. уравнение (*) §2.2). Коэффициент в этом уравнении имеет смысл квадрата круговой частоты свободных гармонических колебаний физического маятника.
По теореме о параллельном переносе оси вращения (теорема Штейнера) момент инерции можно выразить через момент инерции относительно оси, проходящей через центр масс маятника и параллельной оси вращения:
Окончательно для круговой частоты свободных колебаний физического маятника получается выражение:
Enter the acceleration due to gravity (m/s^2) and the frequency (hz) into the Pendulum Length Calculator. The calculator will evaluate the Pendulum Length.
- All Length Calculators
- Pendulum Calculator (Frequency & Period)
- Pendulum Force Calculator
- Pendulum Velocity Calculator
Pendulum Length Formula
The following two example problems outline the steps and information needed to calculate the Pendulum Length.
PL = g / (4*pi^2*f^2)
- Where PL is the Pendulum Length (m)
- g is the acceleration due to gravity (m/s^2)
- f is the frequency (hz)
How to Calculate Pendulum Length?
The following example problems outline how to calculate Pendulum Length.
Example Problem #1:
- First, determine the acceleration due to gravity (m/s^2).
- The acceleration due to gravity (m/s^2) is given as: 9.81.
- Next, determine the frequency (hz).
- The frequency (hz) is provided as: 2.
- Finally, calculate the Pendulum Length using the equation above:
PL = g / (4*pi^2*f^2)
The values provided above are inserted into the equation below and computed.
PL = 9.81 / (4*pi^2*2^2) = .062 (m)
Example Problem #2:
For this problem, the variables required are provided below:
acceleration due to gravity (m/s^2) = 9.81
frequency (hz) = 3
Test your knowledge using the equation and check your answer with the calculator..
PL = g / (4*pi^2*f^2) = ?
Формулы математического маятника в физике
Формулы математического маятника
Определение и формулы математического маятника
Определение
Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого
сосредоточена в одной точке, центре масс маятника.
Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.
Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.
Уравнение движения математического маятника
Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:
[ddot{varphi }+{omega }^2_0varphi =0 left(1right),]
где $varphi $ — угол отклонения нити (подвеса) от положения равновесия.
Решением уравнения (1) является функция $varphi (t):$
[varphi (t)={varphi }_0{cos left({omega }_0t+alpha right)left(2right), }]
где $alpha $ — начальная фаза колебаний; ${varphi }_0$ — амплитуда колебаний; ${omega }_0$ — циклическая частота.
Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.
Циклическая частота и период колебаний математического маятника
Циклическая частота математического маятника зависит только от длины его подвеса:
[ {omega }_0=sqrt{frac{g}{l}}left(3right).]
Период колебаний математического маятника ($T$) в этом случае равен:
[T=frac{2pi }{{omega }_0}=2pi sqrt{frac{l}{g}}left(4right).]
Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.
Уравнение энергии для математического маятника
При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:
[E=E_k+E_p=frac{mv^2}{2}+mgh=frac{mv^2}{2}+frac{mgx^2}{2l}=constleft(5right),]
где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:
[varphi =frac{x}{l}left(6right).]
Максимальное значение потенциальной энергии математического маятника равно:
[E_{pmax}=mgh_m=frac{mg{x^2}_m}{2l}left(7right);;]
Максимальная величина кинетической энергии:
[E_{kmax}=frac{mv^2_m}{2}=frac{m{omega }^2_0{x^2}_m}{2l}=E_{pmax}left(8right),]
где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m={omega }_0x_m$ — максимальная скорость.
Примеры задач с решением
Пример 1
Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?
Решение. Сделаем рисунок.
Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:
[frac{mv^2}{2}=mgh left(1.1right).]
Из уравнения (1.1) найдем искомую высоту:
[h=frac{v^2}{2g}.]
Ответ. $h=frac{v^2}{2g}$
Пример 2
Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1 м$, совершает колебания с периодом равным $T=2 с$? Считайте колебания математического маятника малыми.textit{}
Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:
[T=2pi sqrt{frac{l}{g}}left(2.1right).]
Выразим из нее ускорение:
[g=frac{4{pi }^2l}{T^2} .]
Проведем вычисления ускорения силы тяжести:
[g=frac{4{pi }^2cdot 1}{2^2}={pi }^2approx 9,87 left(frac{м}{с^2}right).]
Ответ. $g=9,87 frac{м}{с^2}$
Читать дальше: формулы пружинного маятника.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

![Rendered by QuickLaTeX.com [T=2pi sqrt{frac{l}{g}} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-f94e775e57dc29864031f59536d37b71_l3.png)

