Трапеция является фигурой с двумя параллельными основаниями. Зная боковую сторону трапеции и угол при большем основании, можно найти его биссектрису. В этом незаменимым помощником будет параллелограмм, в котором биссектриса вычисляется по аналогичному принципу. Если рассматривать биссектрису, как секущую при параллельных основаниях, то равенство внутренних накрест лежащих углов доказывает, что образованный этим построением треугольник – равнобедренный. Биссектриса, проведенная из смежного угла, является одновременно высотой треугольника, деля его на два прямоугольных конгруэнтных треугольника, катетом которых является половина биссектрисы, гипотенузой – боковая сторона трапеции, а угол между катетом и гипотенузой – половина угла при основании трапеции. Поэтому биссектриса будет равна удвоенному произведению боковой стороны на косинус половины угла α:
Главная » Геометрия » Биссектриса трапеции – свойства биссектрис углов трапеции
Биссектриса трапеции – свойства биссектрис углов трапеции
Опубликовано 21.04.2021
Биссектрисы трапеции обладают рядом интересных свойств, которые часто используются в задачах экзамена по математике. Давайте рассмотрим все замечательные свойства биссектрис трапеции здесь. Сначала дадим определение биссектрисы трапеции.
Биссектриса трапеции
Биссектриса трапеции – это биссектриса угла трапеции, то есть это луч, исходящий из вершины трапеции и делящий угол трапеции пополам. Рассмотрим теперь разные варианты пересечения биссектрис в трапеции и узнаем какими свойствами обладают биссектрисы в трапеции.
Свойства пересечения биссектрис в трапеции
1 Свойство – биссектрисы углов при боковой стороне пересекаются под прямым углом.
Давайте докажем это свойство. Рассмотрим трапецию . Проведем в этой трапеции биссектрисы углов
и
. Получим биссектрисы
и
. Докажем, что угол K – прямой.
Сумма углов при боковой стороне трапеции равна 1800. То есть .
Так как и
биссектрисы углов
и
соответственно, то они делят эти углы пополам. А это значит, что
или
.
Делим левую и правую части этого равенства на 2, получим: . Что и требовалось доказать.
2 Свойство биссектрис трапеции – точка пересечения биссектрис углов трапеции при одной боковой стороне лежит на средней линии трапеции.
Доказательство. Нарисуем трапецию и биссектрисы
и
. Докажем, что точка
пересечения биссектрис трапеции лежит на средней линии MN трапеции.
Продолжим биссектрису до пересечения со стороной
трапеции
. Точку пересечения биссектрисы и основания трапеции обозначим
.
Рассмотрим треугольник . Этот треугольник равнобедренный. Так как
, поскольку
, поскольку
– биссектриса, а
как накрест лежащие углы при параллельных
и
и секущей
.
В равнобедренном треугольнике биссектриса
также является медианой, то есть делит основание
пополам, а значит, точка
лежит на средней линии трапеции MN согласно теореме Фалеса: если прямая отсекает равные отрезки на одной стороне угла, то она отсекает равные отрезки и на другой стороне угла. Таким образом если
, то и
и MN – средняя линия трапеции. Вот мы и доказали второе свойство биссектрис в трапеции.
Из доказательства второго свойства вытекает важное свойство биссектрисы трапеции:
Биссектриса тупого угла трапеции отсекает от нее равнобедренный треугольник.
Эти свойства биссектрис трапеции важно знать, поскольку они помогают в решении задач на трапецию в ОГЭ и в ЕГЭ.
( 3 оценки, среднее 5 из 5 )
Рассмотрим некоторые задачи, в которых биссектрисы углов трапеции пересекаются.
I. Биссектрисы углов при боковой стороне трапеции пересекаются.
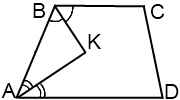
2) ∠ABK+∠KAB=(∠ABC+∠BAD):2=90º(так как биссектрисы делят углы пополам).
3) Так как сумма углов треугольника равна 180º, в треугольнике ABK имеем: ∠ABK+∠KAB+∠AKB=180º, отсюда ∠AKB=180-90=90º.
Вывод:
Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
Это утверждение, в частности, применяется при решении базовой задачи на трапецию, в которую вписана окружность.
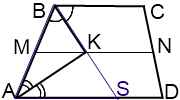
Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN∥AD.
Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK∥AS.
Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
Вывод:
Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
II. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.
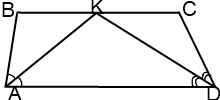
Вывод:
Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции.
В частности, у равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
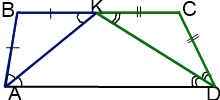
III.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
Вывод:
Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.
У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.
Виды трапеции
- Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
- Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
- Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне
Свойства трапеции
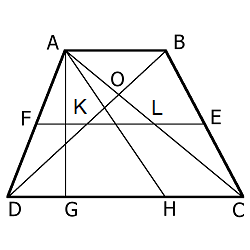
-
Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме
$$
FE = {AB + DC over 2}
$$ -
Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD - Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
- Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
- В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
-
Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е.
$$
KL = {DC — AB over 2}
$$ - Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
- Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности
Свойства и признаки равнобедренной трапеции

- В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
- В равнобедренной трапеции длины диагоналей равны (AC = BD)
- Если трапецию можно вписать в окружность, то трапеция – равнобедренная
- Около равнобедренной трапеции можно описать окружность
- Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований
Формулы площади произвольной трапеции

Площадь трапеции через основания и высоту
$$
S = {AB + DC over 2} * AG
$$
Площадь трапеции через среднюю линию и высоту
$$
S = FE * AG
$$
Площадь трапеции через диагонали и угол между ними
$$
S = {AC * BD over 2} * sin(∠AOD) = {AC * BD over 2} * sin(∠AOB)
$$
Площадь трапеции через четыре стороны
$$
S = {DC + AB over 2} * sqrt{AD^2 — ({(DC — AB)^2 + AD^2 — BC^2 over 2 * (DC — AB)})^2}
$$
Формулы площади равнобедренной трапеции


Площадь трапеции через стороны
$$
S = {DC + AB over 2} * sqrt{AD^2 — {(DC — AB)^2 over 4}}
$$
Площадь трапеции через стороны и угол
$$
S = AD * sin(∠ADC) * (DC — AD * cos(∠ADC))
$$
$$
S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC))
$$
Площадь трапеции через диагонали и угол между ними
$$
S = {AC^2 over 2} * sin(∠AOD) = {AC^2 over 2} * sin(∠BOC)
$$
Площадь трапеции через среднюю линию, боковую сторону и угол при основании
$$
S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB)
$$
Площадь трапеции если в нее вписана окружность
$$
S = {4 * R_В^2 over sin(∠ADC)} = {4 * R_В^2 over sin(∠DAB)}
$$
$$
S = {AB * DC over sin(∠ADC)} = {AB * DC over sin(∠DAB)}
$$
Формулы сторон произвольной трапеции

Основание через другое основание и среднюю линию
$$
AB = 2 * FE — DC
$$
$$
DC = 2 * FE — AB
$$
Основание через другое основание, диагонали и угол между ними
$$
DC = {AC * BD over AG} * sin(∠AOD) — AB
$$
$$
AB = {AC * BD over AG} * sin(∠AOD) — DC
$$
Длины сторон
$$
DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
AB = DC — AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD)
$$
$$
AB = DC — AD * cos(∠ADC) — BC * cos(∠BCD)
$$
$$
AD = {AG over sin(∠ADC)}
$$
$$
BC = {AG over sin(∠BCD)}
$$
Формулы сторон равнобедренной трапеции


Длины сторон
$$
AD = {AG over sin(∠ADC)}
$$
$$
AD = {DC — AB over 2 * cos(∠ADC)}
$$
$$
DC = AB + 2 * AG * ctg(∠ADC)
$$
$$
AB = DC — 2 * AG * ctg(∠ADC)
$$
$$
DC = AB + 2 * AB * cos(∠ADC)
$$
$$
AB = DC — 2 * AB * cos(∠ADC)
$$
Длина основания через диагональ, боковую сторону и другое основание
$$
DC = {AC^2 — DA^2 over AB}
$$
$$
AB = {AC^2 — DA^2 over DC}
$$
Длина боковой стороны через диагональ и основания
$$
AD = sqrt{AC^2 — AB * DC}
$$
Длина основания через высоту, другое основание, диагонали и угол между ними
$$
DC = {AC^2 over AG} * sin(∠AOD) — AB
$$
$$
AB = {AC^2 over AG} * sin(∠AOD) — DC
$$
Длина основания через высоту, другое основание и площадь трапеции
$$
DC = {2 * S over AG} — AB
$$
$$
AB = {2 * S over AG} — DC
$$
Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании
$$
AD = {S over FE * sin(∠ADC)} = {S over FE * sin(∠DAB)}
$$
Длина боковой стороны через площадь трапеции, основания и угол при основании
$$
AD = {2 * S over (AB + DC) * sin(∠ADC)}
$$
$$
AD = {2 * S over (AB + DC) * sin(∠DAB)}
$$
Формулы сторон прямоугольной трапеции

Длины оснований
$$
DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD)
$$
$$
AB = DC — BC * cos(∠BCD) = DC — AD * ctg(∠BCD)
$$
$$
DC = AB + sqrt{BC^2 — AD^2}
$$
$$
AB = DC — sqrt{BC^2 — AD^2}
$$
Длина основания через боковую сторону, другое основание, диагонали и угол между ними
$$
DC = {AC * BD over AD} * sin(∠AOD) — AB
$$
$$
AB = {AC * BD over AD} * sin(∠AOD) — DC
$$
Длина основания через площадь трапеции, другое основание и высоту
Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG)
$$
DC = {2 * S over AD} — AB
$$
$$
AB = {2 * S over AD} — DC
$$
Формулы диагоналей произвольной трапеции

Длина диагоналей через четыре стороны
$$
BD = sqrt{BC^2 + DC * AB — {DC * (BC^2 — AD^2) over DC — AB}}
$$
$$
AC = sqrt{AD^2 + DC * AB — {DC * (AD^2 — BC^2) over DC — AB}}
$$
Длина диагоналей по теореме косинусов
$$
BD = sqrt{DC^2 + BC^2 — 2 * DC * BC * cos(∠BCD)}
$$
$$
AC = sqrt{DC^2 + AD^2 — 2 * DC * AD * cos(∠ADC)}
$$
Длина диагоналей через высоту
$$
BD = sqrt{AG^2 + (DC — AG * ctg(∠BCD))^2}
$$
$$
BD = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$
$$
BD = sqrt{DC^2 + BC^2 — 2 * DC * sqrt{BC^2 — AG^2}}
$$
$$
AC = sqrt{AG^2 + (DC — AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠BCD))^2}
$$
$$
AC = sqrt{DC^2 + AD^2 — 2 * DC * sqrt{AD^2 — AG^2}}
$$
Длина диагоналей через стороны и другую диагональ
$$
BD = sqrt{AD^2 + BC^2 + 2 * DC * AB — AC^2}
$$
$$
AC = sqrt{AD^2 + BC^2 + 2 * DC * AB — BD^2}
$$
Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей
$$
BD = {AG * (DC + AB) over AC * sin(∠AOD)}
$$
$$
AC = {AG * (DC + AB) over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей
$$
BD = {2 * S over AC * sin(∠AOD)}
$$
$$
AC = {2 * S over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей
$$
BD = {2 * FE * AG over AC * sin(∠AOD)}
$$
$$
AC = {2 * FE * AG over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$
Формулы диагоналей равнобедренной трапеции


Длина диагоналей через стороны
$$
AC = sqrt{AD^2 + AB * DC}
$$
Длина диагоналей по теореме косинусов
$$
AC = sqrt{DC^2 + AD^2 — 2 * DC * AD * cos(∠ADC)}
$$
$$
AC = sqrt{DC^2 + AD^2 + 2 * DC * AD * cos(∠DAB)}
$$
$$
AC = sqrt{AB^2 + AD^2 — 2 * AB * AD * cos(∠DAB)}
$$
$$
AC = sqrt{AB^2 + AD^2 + 2 * AB * AD * cos(∠ADC)}
$$
Длина диагоналей
$$
AC = sqrt{AG^2 + FE^2}
$$
$$
AC = sqrt{AG^2 + {(DC + AB)^2 over 4 }}
$$
$$
AC = sqrt{{AG * (AB + DC) over sin(∠AOD)}} = sqrt{{2 * S over sin(∠AOD)}} = sqrt{{2 * FE * AG over sin(∠AOD)}}
$$
Длина диагоналей через высоту основание и угол при основании
$$
AC = sqrt{AG^2 + (DC — AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$
Длина диагоналей через сторону и высоту
$$
AC = sqrt{DC^2 + AD^2 — 2 * DC * sqrt{AD^2 — AG^2}}
$$
Формулы диагоналей прямоугольной трапеции

$$
BD = sqrt{AD^2 + AB^2}
$$
$$
AC = sqrt{AC^2 + DC^2}
$$
Формулы средней линии произвольной трапеции

Длина средней линии через основания
$$
FE = {DC + AB over2}
$$
Длина средней линии через основание, высоту и углы при нижнем основании
$$
FE = DC — AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$
Длина средней линии через площадь и высоту
$$
FE = {S over AG}
$$
Формулы средней линии равнобедренной трапеции


Длина средней линии через основания
$$
FE = {DC + AB over2}
$$
Длина средней линии через основание, высоту и углы при нижнем основании
$$
FE = DC — AG * ctg(∠ADC) = AB + AG * ctg(∠ADC)
$$
Длина средней линии через основания, боковую сторону и высоту
$$
FE = DC — sqrt{AD^2 — AG^2} = AB + sqrt{AD^2 — AG^2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC^2 over 2 * AG} * sin(∠AOD) = {AC^2 over 2 * AG} * sin(∠AOB)
$$
Длина средней линии через площадь и боковую сторону
$$
FE = {S over AD * sin(∠ADC)}
$$
Формулы средней линии прямоугольной трапеции

Длина средней линии через основания, высоту и угол при нижнем основании
$$
FE = DC — AG * {ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠BCD) over 2}
$$
Длина средней линии через основания, боковую сторону и угол при нижнем основании
$$
FE = DC — BC * {cos(∠BCD) over 2}
$$
$$
FE = AB + BC * {cos(∠BCD) over 2}
$$
Длина средней линии через основания и боковые стороны
$$
FE = DC — {sqrt{BC^2 — AD^2} over 2}
$$
$$
FE = AB + {sqrt{BC^2 — AD^2} over 2}
$$
Длина средней линии через диагонали, высоту и угол между диагоналями
$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$
Формулы высоты произвольной трапеции

Длина высоты через четыре стороны
$$
AG = sqrt{AD^2 — ({(DC — AB)^2 + AD^2 — BC^2 over 2 * (DC — AB)})^2}
$$
Длина высоты через боковую сторону и прилегающий угол к основанию
$$
AG = AD * sin(∠ADC) = BC * sin(∠BCD)
$$
Длина высоты через диагонали и углы между ними
$$
AG = {AC * BD over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC * BD over AB + DC} * sin(∠AOB)
$$
Длина высоты через среднюю линию, диагонали и углы между ними
$$
AG = {AC * BD over 2 * FE} * sin(∠AOD)
$$
$$
AG = {AC * BD over 2 * FE} * sin(∠AOB)
$$
Длина высоты через площадь и основания
$$
AG = {2 * S over AB + DC}
$$
Длина высоты через площадь и среднюю линию
$$
AG = {S over FE}
$$
Формулы высоты равнобедренной трапеции


Длина высоты через по сторонам
$$
AG = sqrt{AD^2 — {(DC — AB)^2 over 4}}
$$
Длина высоты через боковую сторону и прилегающий угол к основанию
$$
AG = AD * sin(∠ADC)
$$
Длина высоты через основания и прилегающий угол к основанию
$$
AG = {DC — AB over 2} * tg(∠ADC)
$$
Длина высоты через диагонали и углы между ними
$$
AG = {AC^2 over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC^2 over AB + DC} * sin(∠AOB)
$$
Длина высоты через площадь и основания
$$
AG = {2 * S over AB + DC}
$$
Длина высоты через площадь и среднюю линию
$$
AG = {S over FE}
$$
Формулы боковых сторон прямоугольной трапеции

Сторона AD
Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.
Сторона BC по трём сторонам
$$
BC = sqrt{AD^2 + (DC — AB)^2}
$$
Сторона BC через основания и угол ∠BCD
$$
BC = {DC — AB over cos(∠BCD)}
$$
Сторона BC через Сторону AD
$$
BC = {AD over sin(∠BCD)}
$$
Сторона BC через площадь, среднюю линию и угол ∠BCD
$$
BC = {S over FE * sin(∠BCD)}
$$
Сторона BC через площадь, основания и угол ∠BCD
$$
BC = {2 * S over (AB + DC) * sin(∠BCD)}
$$
Трапеция. Свойства трапеции
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны .
Если боковые стороны равны, трапеция называется равнобедренной .
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной .
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Вписанная в трапецию окружность
Когда в трапецию можно вписать окружность? Какими свойствами обладает вписанная в трапецию окружность? Где находится центр этой окружности? Чему равен ее радиус?
1. В трапецию можно вписать окружность тогда и только тогда когда суммы ее противоположных сторон равны.
1) В трапецию ABCD можно вписать окружность, если AD+BC=AB+CD.
2) Обратно, если AD+BC=AB+CD, то в трапецию ABCD можно вписать окружность.
2. Центр вписанной в трапецию окружности — точка пересечения её биссектрис.
O — точка пересечения
биссектрис трапеции ABCD.
3. По свойству биссектрис трапеции, прилежащие к её боковой стороне,
и точка O лежит на средней линии трапеции.
4. Точки касания, лежащие на сторонах, выходящих из одной вершины, равноудалены от этой вершины:
5.
6. Диаметр вписанной в трапецию окружности равен высоте трапеции, радиус — половине высоты:
Узнать ещё
Знание — сила. Познавательная информация
Биссектрисы трапеции
Рассмотрим некоторые задачи, в которых биссектрисы углов трапеции пересекаются.
I. Биссектрисы углов при боковой стороне трапеции пересекаются.
1)∠ ABC+ ∠ BAD=180 º (как внутренние односторонние при AD ∥ BC и секущей AB).
2) ∠ ABK+ ∠ KAB=( ∠ ABC+ ∠ BAD):2=90 º (так как биссектрисы делят углы пополам).
3) Так как сумма углов треугольника равна 180 º , в треугольнике ABK имеем: ∠ ABK+ ∠ KAB+ ∠ AKB=180 º , отсюда ∠ AKB=180-90=90 º .
Биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
Это утверждение, в частности, применяется при решении базовой задачи на трапецию, в которую вписана окружность.
Пусть биссектриса угла ABC пересекает сторону AD в точке S. Тогда треугольник ABS — равнобедренный с основанием BS (доказательство можно посмотреть здесь). Значит, его биссектриса AK является также медианой, то есть точка K — середина BS.
Если M и N — середины боковых сторон трапеции, то MN — средняя линия трапеции и MN ∥ AD.
Так как M и K — середины AB и BS, то MK — средняя линия треугольника ABS и MK ∥ AS.
Поскольку через точку M можно провести лишь одну прямую, параллельную данной, точка K лежит на средней линии трапеции.
Точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
II. Точка пересечения биссектрис острых углов при основании трапеции принадлежит другому основанию.
В этом случае треугольники ABK и DCK — равнобедренные с основаниями AK и DK соответственно.
Таким образом, BC=BK+KC=AB+CD.
Если биссектрисы острых углов трапеции пересекаются в точке, принадлежащей меньшему основанию, то меньшее основание равно сумме боковых сторон трапеции.
В частности, у равнобедренной трапеции в этом случае меньшее основание в два раза больше боковой стороны.
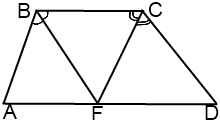
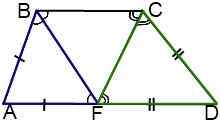
III.Точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
В этом случае треугольники ABF и DCF — равнобедренные с основаниями BF и CF соответственно.
Отсюда AD=AF+FD=AB+CD.
Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.
У равнобедренной трапеции в этом случае большее основание в два раза больше боковой стороны.





