Как найти дисперсию цены - Autoru.top - решение различных проблем

Аудит /

Институциональная экономика /

Информационные технологии в экономике /

История экономики /

Логистика /

Макроэкономика /

Международная экономика /

Микроэкономика /

Мировая экономика /

Операционный анализ /

Оптимизация /

Страхование /

Управленческий учет /

Экономика /

Экономика и управление народным хозяйством (по отраслям) /

Экономическая теория /

Экономический анализ

Главная

Экономика

Микроэкономика

ГАЛЬПЕРИН В. М., ИГНАТЬЕВ С. М., МОРГУНОВ В. И.. МИКРОЭКОНОМИКА. Том 2, 1999

Дисперсией (от лат. dispersus — рассеянный) цен называют множественность рыночных цен на однородный товар на одном рынке. Повседневно наблюдаемая дисперсия цен находится в очевидном противоречии с допущением о совершенной информированности субъектов рынка и ее следствием — законом единой рыночной цены. Но, как заметил еще В. С. Войтинский, лв действительности рыночной цены как особого самостоятельного единства не существует вовсе: рыночная цена представляет собой не что иное, как суммарное обозначение для всех различных цен на данный товар, стоящих в различных магазинах рынка. Магазин, или ллавку с кругом ее покупателей, Войтинский называл жклеточкой рынка, поэтому различия в лавочных ценах объясняются в этом случае отчасти различиями в местоположении лавок (см. раздел 12.7) и в лкруге покупателей. Кроме того, эти различия могут объясняться наличием (оказанием) дополнительных услуг, скажем, симпатичностью или любезностью лавочника или его приказчика (сидельца). Однако едва ли не главной причиной дисперсии конкурентных цен является принципиальная невыполняемость допущения о совершенной информированности субъектов рынка, высокая стоимость информации. Это относится и к продавцам, которые плохо представляют не только функции спроса своих покупателей, но и собственных затрат, и в еще большей степени к покупателям, не знающим уровня цен других продавцов и их местоположения. На это еще в начале века обратил внимание В. С. Войтинский. Полная осведомленность, — так называл он совершенную информированность, — которой экономисты наделяют купцов и покупателей своего современного рынка, не только не является их действительным свойством на реальном рынке, но даже в виде тенденции не наблюдается в типической действительности… исторически Досведомленность относительно всех условий» обнаруживает скорее тенденцию к понижению, чем к повышению, скорее принадлежит прошедшему, чем настоящему. Поэтому, считал Войтинский, лтребование единой цены для каждого товара, с которым обращаются экономисты к своему теоретическому рынку, является просто застарелым суеверием. Покажем это, использовав пример, приведенный признанным основоположником современной экономической теории информации Дж. Стиглером. На всех рынках, — писал Дж. Стиг- лер, — цены меняются более или менее часто, и, если только рынок не централизован полностью, никому не будут известны все цены, устанавливаемые в любой данный момент различными продавцами (или покупателями). Покупатель (или продавец), желающий определить наилучшую цену, должен опросить разных продавцов (или покупателей), и это явление я буду называть Дпоиск».о Чтобы иллюстрировать этот поиск и его результаты, допустим, что продавцы делятся на две равные группы, одна из которых предлагает некий товар за 30 ООО, а другая за 20 ООО руб. Покупатель осуществляет поиск приемлемой цены, пользуясь либо телефоном, либо общественным транспортом. Допустим, что один телефонный звонок, как и одна поездка, обходится ему в 2000 руб. Спрос носит единичный характер, т. е. каждый покупатель намерен приобрести единицу товара. Результаты поиска представлены в табл. 9.1. Таблица 9.1 Поиск приемлемой цены покупателем и его результаты Число опро-шенных продавцов, п Вероятность цены Вероятная цена товара для покупателя, руб. + Р2(1 — Р)) Предельная экономия на цене в результате поиска, руб. Предельные затраты на поиск, руб. ij =30000 руб. (Р = 0.5″) Р2 = 20000 руб. (1-F) 1 0.5 0.5 25000 Ч 2000 2 0.25 0.75 22500 2500 2000 3 0.125 0.875 21250 1250 2000 4 0.0625 0.9375 20625 625 2000 5 0.03125 0.96875 20312 313 2000 Вероятность выхода на наилучшую цену увеличивается с ростом числа опрошенных продавцов с 0.5 до 0.9688, при этом вероятная цена падает с 25 000 до 20 312 руб. Однако опрос пяти продавцов, приводящий к наименьшей вероятной цене покупки, обойдется покупателю, как следует из последней графы, в 10 000 руб., тогда как покупка у первого попавшегося продавца потребует лишь 2000 руб. дополнительных затрат. Ско- рее всего, рациональный покупатель ограничится опросом двух продавцов, поскольку предельные затраты на опрос третьего (2000 руб.) превысят вероятную (в том случае) предельную экономию на цене (1250 руб.). А тот покупатель, для которого приемлемый уровень цены равен (или выше) 27 000 руб., согласится купить товар у первого попавшегося продавца. Таким образом, несовершенная информированность покупателей (и часто продавцов) может быть причиной повседневно наблюдаемой дисперсии цен. Очевидно также, что дисперсия цен относительно дорогостоящих товаров меньше, чем недорогостоящих, поскольку большая вероятная предельная экономия от поиска приемлемой цены в первом случае делает этот поиск более выгодным и, значит, более продолжительным и эффективным, чем в случае дешевых товаров.. Существует еще одна причина наблюдаемой дисперсии цен — наличие и функционирование оптовых и розничных посредников — перепродавцов. Однако в микроэкономике традиционно их роль не рассматривается, предполагается, что предприятие является не только производителем, но и продавцом выпускаемых товаров. Совершенная информированность субъектов рынка и, следовательно, определенность и единственность рыночной цены возможны лишь в гипотетической ситуации нащупывания (фр. tatonnement) равновесия, когда рынок координируется справедливым посредником — аукционистом (см. раздел 15.1.3). На аукционе не только все сделки совершаются по равновесной цене, нащупываемой аукционистом, но и сам процесс нащупывания должен быть открытым для всех, в том числе и для потенциальных участников аукциона (потенциальных продавцов и покупателей). При несовершенной информированности субъектов рынка, когда существует дисперсия цен, соотношение спроса и предложения (даже в условиях, близких к совершенной конкуренции) определяет не единственно возможный уровень рыночной цены, а (как и предполагал В. С. Войтинский) весь спектр рыночных цен, или, иначе, среднюю рыночную цену. Поэтому в ряде специальных работ, особенно по проблемам отраслевой организации, функции спроса, предложения, затрат отображаются иногда не четкими линиями (кривыми), лишенными толщины, а нечеткими множествами точек, имеющими неясные очертания (англ. blurred zones). Иногда такой метод анализа называют квазистатичным, или мягким (англ. soft), в противоположность жесткому, детерминированному анализу, преобладающему в курсах экономической теории. Рис. 9.6. Кривые рыночного спроса и предложения как нечеткие множества. На рис. 9.6 кривые спроса и предложения на совершенно конкурентном рынке, показанные на рис. 9.2, о четкими линиями, представлены как нечеткие множества. Здесь в отличие от рис. 9.2, а Р* и Q* отображают области дисперсии равновесной цены и соответственно объема рынка, границами которых являются координаты границ нечеткого пересечения кривых Sz и Dz — Е. Подобным же образом могут быть показаны и другие отражающие экономические зависимости кривые. Мягкий анализ предпола-гает, таким образом, некоторую неопределенность рыночной цены и/или объема выпуска (подобно принципу неопределенности в современной физике). Определенность, — пишет один из пропагандистов такого анализа, крупный американский специалист в области отраслевой организации У. Шеферд, — требует существования точных функций затрат и спроса, воплощенных в четких кривых и точных уравнениях. Многие десятилетия мы принимали эту точность на веру — и при определении затрат, и принимая технологию жестко определенной в каждом периоде и для всех фирм. В случае спроса потребительский выбор считался специ-фицированным и постоянным в каждом периоде. Лишь если набор условий (затраты, спрос и реакция на них) неизменны и известны, можно получить точные результаты. В противном случае определенность отсутствует. В действительности эти условия никогда не известны в точности, а во многих случаях даже приблизительно. Многие функции существуют как области и полосы (zones), но не как четкие линии. Некоторые последствия несовершенства информированности и обусловленной ею неопределенности рыночной цены мы рассмотрим в следующем разделе.
<< Предыдушая	Следующая >>
= К содержанию =
Похожие документы: «9.2.4. ДИСПЕРСИЯ ЦЕН»
9.2.5.1. ПРЕДЛОЖЕНИЕ ОТРАСЛИ В СЛУЧАЕ НЕЗАВИСИМОСТИ ЗАТРАТ ПРЕДПРИЯТИЙ дисперсии цен (выпуск Q0 может быть продан по ценам несколько ниже, а выпуск Q, — несколько выше Р0). При этом дисперсия цен поддерживается несовершенной информированностью 26.3 Экологический паспорт предприятия дисперс ной — твердые частицы или капельки жидкости. Газовые выбросы делят на организованные и неорганизованные. Организованные поступают в атмосферу через специально сооруженные газоходы, трубы и т.д. Неорганизованные — в результате нарушения герме тичности оборудования, неудовлетворительной работы оборудова ния по отсосу газа. При оценке загрязнения атмосферы важно учитывать суммар ный объем 3.3. Концепции конвергенции и эмпирические свидетельства ее существования. дисперсии распределения доходов в рассматри ваемом обзоре стран охватывают стандартные отклонения дохо дов на душу населения в различные моменты времени. В этой свя зи о-конвергенция имеется в том случае, если дисперсия доходов на душу населения с течением времени сокращается. Из графика 3.3.1 может быть видно, что для представленных 117 стран о-конвергенция не может быть установлена эмпириче з 3. Концепции плюралистической демократии дисперсия (рассеяние) государственного суверенитета: политическая власть рассредоточится по многочисленным объединениям, представляющим различные социальные интересы. Увеличение числа центров власти отразит федеративную природу общества, его дифференцированную социальную структуру. Аргументируя эти положения, Ласки подверг критике предшествующие учения о государственном суверенитете (Ж. Боден, Т. з 5. Теория демократического социализма дисперсия власти над обществом между взаимодействующими ассоциациями и государством и, следовательно, снятие остроты проблемы борьбы за государственную власть. Вместо завоевания власти рабочим классом речь должна идти об исполнении власти его представителями — социалистическими партиями в условиях существующих форм демократии, позволяющих создать благоприятные условия для наступления социализма 6.5. Капитальная цена фактора производства дисперсии): = (щ ~пг) != 1 Не для всех людей гарантированная величина некоторого дохода и равное ей среднеожидаемое значение рискового (вероятностного) до хода равнозначны, так как индивиды по-разному относятся к риску. Одни, например, являются завсегдатаями казино и считают риск бла гом, другие к нему равнодушны, а третьи стремятся не рисковать. Рас пределить людей по трем перечисленным 9.3.4. ПРЕДЛОЖЕНИЕ В ДЛИТЕЛЬНОМ ПЕРИОДЕ. ОТРАСЛИ С НЕИЗМЕННЫМИ, ВОЗРАСТАЮЩИМИ И УБЫВАЮЩИМИ ЗАТРАТАМИ дисперсия, правда, по иной, чем указанной в разделе 9.2.4, причине. Наоборот, в случае, если рыночное предложение окажется выше рыночного спроса по реально действующей цене, отдельное предприятие не сможет продать столько своей продукции, сколько пожелает, по рыночной цене. Чтобы увеличить объем продаж, ему необходимо будет снизить цену, а это значит, что кривая спроса на продукцию такого 12.1. Выбор в условиях неопределенности дисперсию и стандартное (среднеквадратичное) отклонение Дисперсия — средневзвешенная величина квадратов отклонений действительных результатов от ожидаемых: о2 = X к[х — Е(х)]2 га 1=1 В данном случае дисперсия равна: а2 = Дх, — Е(х)]2 + 7t2[x2 — Е(х)]2, (12.2) где а2 — дисперсия; xi — возможный результат, п — вероятность соответствующего результата; Е'(х) — ожидаемое значение. В нашем случае 12.4. Риск инвестиционных решений дисперсию прибыли от вкладов на фондовой бирже через ст, а их стандартное отклонение через ст . Тогда стандартное отклонение средневзвешенной ожидаемой прибыли (ст ) будет равно b х ст : Р m ст=Ьхст и b = ст /ст . (12.6) р m р’ m v f Подставив значение части сбережений, размещенных на фондовой бирже (Ь), в уравнение (12.5), получим: R -R. R = R. + Ч2 хст. (12.7) р 1 ст р ш Данное уравнение Вопросы для повторения дисперсии психологических значений выигрыша. Согласны ли вы со следующими утверждениями: а) производитель продукции не должен скрывать информацию о местах покупки сырья, особенностях технологии, иначе он применяет методы нечестной конкуренции, б) информация — ценный товар и должна предоставляться за плату; в) если информация не может быть куплена, следует применять другие способы ее получения,

Источник

Генеральная и выборочная дисперсия

Для анализа полученных данных в математической статистике используют различные виды показателей вариации, среди которых:

размах вариации;
среднее абсолютное отклонение;
дисперсия.

Разберем понятие дисперсии, ее виды и свойства.

Дисперсия — величина, являющаяся мерой разброса полученных в ходе наблюдений данных относительно истинного значения.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Дисперсия является точечной оценкой параметра, так как имеет одно конкретное числовое значение.

Статистический анализ при исследовании некоторого объекта может быть сплошным или выборочным в зависимости от охватываемого объема данных.

В обоих вариантах результаты анализа распространяют на генеральную совокупность, однако при сплошном анализе наблюдению подвергают абсолютно все имеющиеся данные. Выборочный анализ, напротив, предполагает наблюдение только за некоторой выбранной частью данных. При этом выбранная совокупность должна сохранять структуру и закономерности генеральной.

Дисперсию также делят на два вида в зависимости от используемых данных:

генеральная дисперсия;
выборочная дисперсия.

Как видно из названия, дисперсии отличаются объемом выборки, на основе которой происходит расчет и анализ.

Выборочная дисперсия, определение, формулы для вычисления

Пусть имеется некоторая выборка Y из генеральной совокупности объемом n. Среднее значение выборки обозначим как ({overline y}_в).

Выборочная дисперсия (D_в) — величина, равная среднему арифметическому отклонению квадратов разности признаков выборки (y_1,;y_2,;…y_n) от ее среднего значения ({overline y}_в).

Данные в выборке могут располагаться хаотично, то есть быть несгруппированными, или же сформированы в вариационный ряд.

Выборочную дисперсию для несгруппированной выборки можно посчитать по формуле:

Формула 1

(D_в=frac{{displaystylesum_{i=1}^n}(y_i-{overline y}_в)}n)

В случае вариационного ряда используют кратные значения и частоты для дискретного представления; середины частичных интервалов и частоты для интервального представления.

Формула 2

(D_в=frac{{displaystylesum_{i=1}^k}(y’_i-{overline y}_в)cdot n_i}n)

где (y’_i )— кратное (одинаковое) значение в выборке или значение, соответствующее середине интервала;

(n_i )— частота.

Выборочная дисперсия, рассчитанная по приведенным выше формулам, дает недостоверное (заниженное) значение. Это значит, что при большом количестве экспериментов выборочная дисперсия будет давать смещенное относительно истинного значения генеральной совокупности значение.

Чтобы получить несмещенную выборочную дисперсию, используют следующую формулу:

Формула 3

(D_в=frac{{displaystylesum_{i=1}^n}{(y_i-{overline y}_в)}^2}{n-1})

Примечание 1

Как правило при использовании термина «выборочная дисперсия» имеют в виду именно несмещенную выборочную дисперсию.

Генеральная дисперсия, определение, что является оценкой, формулы для вычисления

Пусть имеется некоторая генеральная совокупность X объемом N и среднее значение признаков совокупности (X — {overline x}_г.)

Генеральная дисперсия (D_г) есть среднее арифметическое отклонение квадратов разности признаков (x_1,;x_2,;…x_n) генеральной совокупности X от их среднего значения ({overline x}_г).

Примечание 2

Иногда генеральную дисперсию называют теоретической.

Аналогично выборочной, генеральная дисперсия может быть рассчитана для несгруппированных данных генеральной совокупности:

Формула 4

(D_г=frac{{displaystylesum_{i=1}^N}{(x_i-{overline x}_г)}^2}N)

и для сформированного вариационного ряда:

Формула 5

(D_г=frac{{displaystylesum_{i=1}^K}{(x’_i-{overline x}_г)}^2cdot n_i}N)

Значение теоретической дисперсии бывает сложно вычислить из-за большого объема данных или их недостатка. Тогда для оценки используют выборочную дисперсию. Но если для оценки генеральной дисперсии применить выборочную, это приведет к возникновению ряда систематических ошибок. В результате оценка будет произведена неверно, а значение генеральной дисперсии занижено.

Чтобы устранить возникающую погрешность в качестве оценки генеральной дисперсии используют исправленную или несмещенную выборочную дисперсию, формула которой представлена выше.

Оценки параметров распределения

Оценкой параметра в статистике считают численное значение какого-либо параметра данной выборки.

Приведем оценки параметров распределения случайной величины, которые связаны с дисперсией.

Среднеквадратическое отклонение (δ) — характеристика рассеивания случайной величины относительно ее математического ожидания. Определяется как корень квадратный из дисперсии.

Формула 6

(delta=sqrt D)

Математическое ожидание случайной величины X — среднее (по весу вероятностей возможных значений) значение случайной величины. Обозначается как M(X).

Математическое ожидание и дисперсия для дискретной случайной величины связаны соотношением:

Формула 7

(D=Mleft[X-M(X)right]^2)

для непрерывной:

Формула 8

(D=int_{-infty}^infty(x-M{(x))}^2cdot f(x)dx)

где f(x) — функция распределения случайной величины.

Отметим, что указанные выше параметры могут быть определены как для генеральной совокупности, так и для некоторой выборки.

Примеры решения задач

Пример 1

Напряжение в цепи измеряют 6 раз с помощью одного и того же вольтметра. Получены следующие значения: 210 В, 200 В, 195 В, 205 В, 190 В, 200 В. Найти выборочную смещенную дисперсию и дать оценку генеральной дисперсии.

Решение.

Сначала вычислим выборочное среднее значение:

({overline x}_в=frac{210+200+195+205+190+200}6=200;B.)

Теперь найдем выборочную дисперсию:

(D_в=frac{{(210-200)}^2+{(200-200)}^2+{(195-200)}^2+{(205-200)}^2+{(190-200)}^2+{(200-200)}^2}6=frac{250}6approx42.)

Оценкой генеральной дисперсии является исправленная или выборочная несмещенная дисперсия. Чтобы вычислить исправленную дисперсию, умножим полученную ранее выборочную дисперсию на множитель (frac n{n-1} (n=6):)

(D_и=frac n{n-1}cdot D_в=frac65cdotfrac{250}6=50.)

Примечание 3

Данный пример показывает, что значение выборочной смещенной дисперсии занижено относительно генеральной.

Пример 2

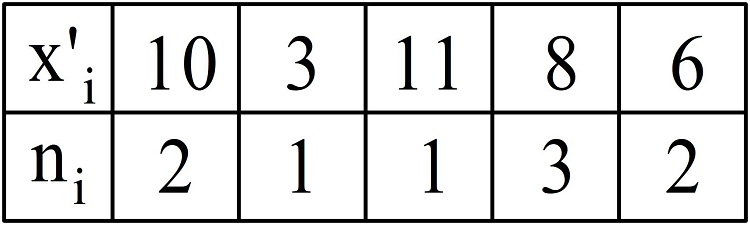
Случайная величина задана следующей таблицей распределения, среднее значение выборки равно 14. Найти выборочную несмещенную дисперсию и среднеквадратическое отклонение.

Решение.

Вычислим выборочную несмещенную дисперсию:

(D_в=frac{2{(10-14)}^2+1{(3-14)}^2+1{(11-14)}^2+3{(8-14)}^2+2{(6-14)}^2}9cdotfrac98=frac{398}8approx50.)

Теперь найдем среднеквадратическое отклонение:

(delta=sqrt{D_в}=sqrt{frac{398}8}=frac{sqrt{199}}2approx7.)

Источник

Онлайн-калькулятор дисперсии поможет вам определить дисперсию, сумму квадратов и коэффициент дисперсии для определенного набора данных. Кроме того, этот калькулятор также отображает среднее значение и стандартное отклонение путем пошагового расчет дисперсии онлайн. Прочтите, чтобы узнать, как найти дисперсию онлайн и стандартное отклонение, используя формулу выборочной дисперсии.

Что такое дисперсия?

Дисперсия группы или набора чисел – это число, которое представляет «разброс» набора. Формально это квадрат отклонения набора от среднего и квадрат стандартного отклонения.

Другими словами, небольшая дисперсия означает, что точки данных имеют тенденцию быть близкими к среднему и очень близко друг к другу. Высокая дисперсия указывает на то, что точки данных далеки от среднего значения и друг от друга. Дисперсия – это среднее значение квадрата расстояния от каждой точки до среднего.

Типы дисперсии:

Вариация выборки: дисперсия выборки не охватывает всю возможную выборку (случайная выборка людей).

Дисперсия населения: дисперсия, которая измеряется для всего населения (например, всех людей).

Однако онлайн-калькулятор стандартного отклонения позволяет определить стандартное отклонение (σ) и другие статистические измерения данного набора данных.

Формулы отклонения:

Формула дисперсии совокупности

дисперсия формула (совокупности):

Дисперсия (обозначается как σ2) выражается как среднеквадратическое отклонение от среднего для всех точек данных. Мы пишем:

$$ σ2 = ∑ (xi – μ) ^ 2 / N $$

где,

σ2 – дисперсия;
μ – среднеквадратическое значение; а также
xᵢ представляет i-ю точку данных среди N общих точек данных.

Вы можете рассчитать его с помощью калькулятора дисперсии генеральной совокупности, в противном случае есть три шага для оценки дисперсии:

Чтобы найти разницу между средним значением точки, используйте формулу: xi – μ
Теперь возьмите в квадрат разницу между средним значением каждой точки: (xi – μ) ^ 2
Затем найдите среднее квадратическое отклонение от среднего: ∑ (xi – μ) ^ 2 / N.

Это дисперсия формула совокупности.

Пример формулы отклонения

Уравнение выборки дисперсии имеет следующий вид:

s2 = ∑ (xi – x̄) 2 / (N – 1)

где,

s2 – оценка дисперсии;

x – выборочное среднее; а также

xi – i-я точка данных среди N общих точек данных.

Как рассчитать дисперсию?

Чтобы найти среднее значение данного набора данных. Подставьте все значения и разделите на размер выборки n.

ni = 1x дюйм x = ∑ i = 1 nx дюйм

Теперь найдите среднюю разницу значений данных, вам нужно вычесть среднее значение данных и возвести результат в квадрат.

(хи – х) ^ 2 (хи – х) ^ 2

Затем вычислите квадратичные разности и сумму квадратов всех квадратичных разностей.

S = ∑ I = 1n (xi – x) ^ 2

Итак, найдите дисперсию, дисперсия формула генеральной совокупности:

Дисперсия = σ ^ 2 = Σ (xi – μ) ^ 2

Уравнение дисперсии набора данных выборки:

Дисперсия = s ^ 2 = Σ (xi – x) ^ {2n − 1}

Эти формулы запоминать не нужно. Чтобы вам было удобно, наш примерный калькулятор дисперсии выполняет все расчет дисперсии онлайн, связанные с дисперсией, автоматически, используя их.

Тем не менее, Калькулятор диапазона среднего среднего значения режима поможет вам рассчитать средний средний режим и диапазон для введенного набора данных.

Пример расчета

Давайте посчитаем дисперсию оценок пяти студентов на экзамене: 50, 75, 89, 93, 93. Выполните следующие действия:

Найдите среднее

Чтобы найти среднее значение (x), разделите сумму всех этих значений на количество точек данных:

х = (50 + 75 + 89 + 93 + 93) / 5

х̄ = 80

Вычислите разницу между средним значением и квадратом отличий от среднего. Следовательно, среднее значение равно 80, мы используем формулу для вычисления разницы от среднего:

xi – x̄

Первая точка – 50, поэтому разница от среднего составляет 50 – 80 = -30.

Квадрат отклонения от среднего – это квадрат предыдущего шага:

(xi – x̄) 2

Итак, квадрат отклонения равен:

(50 – 80) 2 = (-30) 2 = 900

В приведенной ниже таблице квадрат отклонения рассчитан на основе среднего значения всех результатов испытаний. Столбец «Среднее отклонение» – это результат минус 30, а столбец «Стандартное отклонение» – это столбец перед квадратом.

Счет	Отклонение от среднего	Квадратное отклонение
50	-30	900
75	-5	25
89	9	81
93	13	169
93	13	169

Рассчитайте стандартное отклонение и дисперсию

Затем используйте квадраты отклонений от среднего:

σ2 = ∑ (xi – x̄) 2 / N

σ2 = (900 + 25 + 81 + 169 + 169) / 5

σ2 = 268,5

дисперсия случайной величины онлайн результатов экзамена составила 268,8.

Как работает калькулятор дисперсии?

Онлайн-калькулятор дисперсии совокупности вычисляет дисперсию для заданных наборов данных. Вы можете просмотреть работу, проделанную для расчет дисперсии онлайн из набора данных, следуя этим инструкциям:

Вход:

Сначала введите значения набора данных через запятую.
Затем выберите дисперсию для выборки или совокупности.
Нажмите кнопку «Рассчитать», чтобы получить результаты.

Выход:

Калькулятор дисперсии выборки отображает дисперсию, стандартное отклонение, количество, сумму, среднее значение, коэффициент дисперсии и сумму квадратов.
Этот калькулятор также обеспечивает пошаговые вычисления дисперсии, коэффициента дисперсии и стандартного отклонения.

ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ:

В чем разница между стандартным отклонением и дисперсией?

Дисперсия – это квадрат отклонения от среднего, а стандартное отклонение – это квадратный корень из числа. Оба показателя отражают изменчивость распределения, но их единицы разные: стандартное отклонение определяется в той же единице, что и исходное значение (например, минуты или метры).

Значение высокой дисперсии – это плохо или хорошо?

Низкая дисперсия связана с меньшим риском и более низкой доходностью. Акции с высокой дисперсией обычно выгодны для агрессивных инвесторов с меньшим неприятием риска, в то время как акции с низкой дисперсией обычно выгодны для консервативных инвесторов с более низкой толерантностью к риску.

Каков диапазон отклонений?

Диапазон – это разница между высоким и низким значением. Поскольку используются только крайние значения, потому что эти значения будут сильно на него влиять. Чтобы найти диапазон отклонения, возьмите максимальное значение и вычтите минимальное значение.

Заключение:

Воспользуйтесь этим онлайн-калькулятором дисперсии, который работает как с выборкой, так и с наборами данных о генеральной совокупности, используя формулу генеральной и выборочной дисперсии. Это лучший образовательный калькулятор, который расскажет вам, как рассчитать дисперсию заданных наборов данных за доли секунды.

Other Languages: Variance Calculator, Varyans Hesaplama, Calculadora De Variancia, Kalkulator Varians, Kalkulator Wariancji, Výpočet Rozptylu, 分散計算.

Источник

Download Article

What is variance? Variance is a measure of how spread out a data set is, and we calculate it by finding the average of each data point’s squared difference from the mean.^[1] It’s useful when creating statistical models since low variance can be a sign that you are over-fitting your data. Once you get the hang of the formula, you’ll just have to plug in the right numbers to find your answer. Read on for a complete step-by-step tutorial that’ll teach you how to calculate both sample variance and population variance.

1
Use the sample variance formula if you’re working with a partial data set. In most cases, statisticians only have access to a sample, or a subset of the population they’re studying. For example, instead of analyzing the population «cost of every car in Germany,» a statistician could find the cost of a random sample of a few thousand cars. He can use this sample to get a good estimate of German car costs, but it will likely not match the actual numbers exactly.^[2]
- Example: Analyzing the number of muffins sold each day at a cafeteria, you sample six days at random and get these results: 38, 37, 36, 28, 18, 14, 12, 11, 10.7, 9.9. This is a sample, not a population, since you don’t have data on every single day the cafeteria was open.
- If you have every data point in a population, skip down to the method below instead.
2

Write down the sample variance formula. The variance of a data set tells you how spread out the data points are. The closer the variance is to zero, the more closely the data points are clustered together. When working with sample data sets, use the following formula to calculate variance:^[3]

Advertisement
3
Calculate the mean of the sample. The symbol x̅ or «x-bar» refers to the mean of a sample.^[4] Calculate this as you would any mean: add all the data points together, then divide by the number of data points.^[5]
- Example: First, add your data points together: 17 + 15 + 23 + 7 + 9 + 13 = 84
  Next, divide your answer by the number of data points, in this case six: 84 ÷ 6 = 14.
  Sample mean = x̅ = 14.
- You can think of the mean as the «center-point» of the data. If the data clusters around the mean, variance is low. If it is spread out far from the mean, variance is high.^[6]
4

Subtract the mean from each data point. Now it’s time to calculate $x_{i}$ — x̅, where $x_{i}$ is each number in your data set. Each answer tells you that number’s deviation from the mean, or in plain language, how far away it is from the mean.^[7]
5

Square each result. As noted above, your current list of deviations ( $x_{i}$ — x̅) sum up to zero. This means the «average deviation» will always be zero as well, so that doesn’t tell use anything about how spread out the data is. To solve this problem, find the square of each deviation.^[8] This will make them all positive numbers, so the negative and positive values no longer cancel out to zero.^[9]
6
7
Divide by n — 1, where n is the number of data points. A long time ago, statisticians just divided by n when calculating the variance of the sample. This gives you the average value of the squared deviation, which is a perfect match for the variance of that sample. But remember, a sample is just an estimate of a larger population. If you took another random sample and made the same calculation, you would get a different result. As it turns out, dividing by n — 1 instead of n gives you a better estimate of variance of the larger population, which is what you’re really interested in. This correction is so common that it is now the accepted definition of a sample’s variance.^[12]
- Example: There are six data points in the sample, so n = 6.
  Variance of the sample = $s^{2}={frac {166}{6-1}}=$ 33.2
8
Understand variance and standard deviation. Note that, since there was an exponent in the formula, variance is measured in the squared unit of the original data. This can make it difficult to understand intuitively. Instead, it’s often useful to use the standard deviation. You didn’t waste your effort, though, as the standard deviation is defined as the square root of the variance. This is why the variance of a sample is written $s^{2}$ , and the standard deviation of a sample is .
- For example, the standard deviation of the sample above = s = √33.2 = 5.76.

1

Use the population variance formula if you’ve collected data from every point in the population. The term «population» refers to the total set of relevant observations. For example, if you’re studying the age of Texas residents, your population would include the age of every single Texas resident. You would normally create a spreadsheet for a large data set like that, but here’s a smaller example data set:^[13]
2

Write down the population variance formula. Since a population contains all the data you need, this formula gives you the exact variance of the population. In order to distinguish it from sample variance (which is only an estimate), statisticians use different variables:^[14]
3
Find the mean of the population. When analyzing a population, the symbol μ («mu») represents the arithmetic mean. To find the mean, add all the data points together, then divide by the number of data points.^[15]
- You can think of the mean as the «average,» but be careful, as that word has multiple definitions in mathematics.
- Example: mean = μ = ${frac {5+5+8+12+15+18}{6}}$ = 10.5
4

Subtract the mean from each data point. Data points close to the mean will result in a difference closer to zero. Repeat the subtraction problem for each data point, and you might start to get a sense of how spread out the data is.^[16]
5

Square each answer. Right now, some of your numbers from the last step will be negative, and some will be positive. If you picture your data on a number line, these two categories represent numbers to the left of the mean, and numbers to the right of the mean. This is no good for calculating variance, since these two groups will cancel each other out. Square each number so they are all positive instead.^[17]
6
Find the mean of your results. Now you have a value for each data point, related (indirectly) to how far that data point is from the mean. Take the mean of these values by adding them all together, then dividing by the number of values.^[18]
- Example:
  Variance of the population = ${frac {30.25+30.25+6.25+2.25+20.25+56.25}{6}}={frac {145.5}{6}}=$ 24.25
7

Relate this back to the formula. If you’re not sure how this matches the formula at the beginning of this method, try writing out the whole problem in longhand:

Help Calculating Variance

Add New Question

Question

What are deviations?

Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Assistant Professor of Mathematics

Expert Answer
Question

What is the easiest way to find variance?

Mario Banuelos is an Assistant Professor of Mathematics at California State University, Fresno. With over eight years of teaching experience, Mario specializes in mathematical biology, optimization, statistical models for genome evolution, and data science. Mario holds a BA in Mathematics from California State University, Fresno, and a Ph.D. in Applied Mathematics from the University of California, Merced. Mario has taught at both the high school and collegiate levels.

Assistant Professor of Mathematics

Expert Answer

Support wikiHow by
unlocking this expert answer.

First, calculate the mean or average of all of the data points. Then, calculate the difference between each data point and that mean. Square each of those differences, add them all up, then divide them by n (the total number of data points) minus 1.
Question

How do I calculate the variance of four numbers?

Follow these steps: Work out the mean (the simple average of the numbers.) Then, for each number, subtract the mean and square the result (the squared difference). Finally, work out the average of those squared differences.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Using «n-1» instead of «n» in the denominator when analyzing samples is a technique called Bessel’s correction. The sample is only an estimate of the full population, and the mean of the sample is biased to fit that estimate. This correction removes this bias. This is related to the fact that, once you’ve listed n — 1 data points, the final nth point is already constrained, since only certain values will result in the sample mean (x̅) used in the variance formula.^[19]
Since it is difficult to interpret the variance, this value is usually calculated as a starting point for calculating the standard deviation.

References

About This Article

Article SummaryX

To calculate the variance of a sample, or how spread out the sample data is across the distribution, first add all of the data points together and divide by the number of data points to find the mean. For example, if your data points are 3, 4, 5, and 6, you would add 3 + 4 + 5 + 6 and get 18. Then, you would divide 18 by the total number of data points, which is 4, and get 4.5. Therefore, the mean of the data set is 4.5. Next, subtract the mean from each data point in the sample. In this example, you would subtract the mean, or 4.5, from 3, then 4, then 5, and finally 6 and end up with -1.5, -0.5, 0.5, and 1.5. Now, square each of these results by multiplying each result by itself. If you square -1.5, -0.5, 0.5, and 1.5, you would get 2.25, 0.25, 0.25, and 2.25. Then, add up all of the squared values. Here, you would add 2.25 + 0.25 + 0.25 + 2.25 and get 5. Finally, divide the sum by n — 1, where n is the total number of data points. In the example there are 4 data points, so you would divide the sum, which is 5, by 4 — 1, or 3, and get 1.66. Therefore, the variance of the sample is 1.66. To learn how to calculate the variance of a population, scroll down!

Did this summary help you?

Thanks to all authors for creating a page that has been read 2,989,225 times.

Reader Success Stories

«I am currently solving a non-perfect hedge problem between grapefruit and orange juice where I need to calculate…» more

Did this article help you?

Источник

Мишель Мэтьюз, MBA, CPCC

6 октября 2021 г.

Основатель RBG Royalty Enterprises Мишель Мэтьюз — сертифицированный профессиональный карьерный коуч и специалист по работе с кредиторской задолженностью, которая помогает людям вырабатывать стратегические подходы на рабочем месте, используя свою фирменную структуру Boss Up & Hustle.

Что такое дисперсия?

Дисперсия — это статистическое измерение, позволяющее увидеть, насколько далеко каждое число в наборе данных от среднего. Дисперсия часто обозначается этим символом: σ². Этот расчет может быть индикатором для аналитиков и трейдеров того, как часто меняется число, также называемое волатильностью, что также может быть сигналом дальнейших изменений и риска, который они представляют для людей, на которых они влияют. Квадратный корень из дисперсии представляет собой стандартное отклонение (σ), которое помогает определить постоянство доходности инвестиций в течение определенного периода времени.

Прочитайте больше: Меры вариации: определения, примеры и карьера

Понимание дисперсии

Чем выше дисперсия числа, тем больше оно отделено от среднего, рассчитанного на основе чисел набора данных. С другой стороны, небольшая дисперсия оказывает противоположное влияние, делая ее ближе к среднему значению, тогда как нулевая дисперсия показывает, что числа имеют одинаковое значение в наборе данных. Дисперсия не может быть отрицательным значением, так как квадрат числа никогда не может стать отрицательным значением.

Говоря об инвестициях, дисперсия является важным показателем. Волатильность — это показатель риска, который позволяет инвесторам оценить риск, связанный с покупкой конкретного актива, а также его потенциальную прибыльность. Инвесторы могут анализировать дисперсию доходности различных активов в портфеле, чтобы определить наилучшее распределение активов. В финансах дисперсия используется для сравнения эффективности элементов портфеля друг с другом и со средним значением.

Прочитайте больше: Как выполнить анализ рисков

Как рассчитать дисперсию

В статистике дисперсия рассчитывается путем взятия различий между каждым числом в наборе данных и средним значением, затем возведения в квадрат различий, чтобы сделать их положительными, и, наконец, деления суммы квадратов на количество значений в наборе данных.

Дисперсия рассчитывается по следующей формуле:

формула выборочной дисперсии: s2 = ∑ (x - x̄) 2n - 1

Стоимость акций, которые вы инвестируете на открытом рынке, может меняться ежедневно, но вы все равно можете просматривать финансовые отчеты, чтобы отслеживать эффективность ваших инвестиций за определенный период. Мы начнем с определения дисперсии доходности акций, которую можно использовать для помощи в постановке целей в отношении финансового будущего вашей компании. Вот пример и список шагов для расчета дисперсии:

1. Определите доходность акций за определенный период

Для этого примера мы скажем, что вы отслеживаете свои инвестиции в течение трех лет, и они принесли 13% прибыли в первый год, 24% во второй год и -10% в течение третьего года.

2. Рассчитайте среднее значение доходности

Сложите 13, 24 и -10 вместе, и вы получите в общей сложности 27. Вы делите 27 на 3, так как вы вычисляете сумму по числам в наборе данных, и вы получаете 9% как среднюю доходность акций за три года. срок год.

3. Найдите разницу между каждым доходом и средним значением за каждый год.

Затем вам нужно сравнить доход, который вы получали от акций каждый год, и среднее значение, которое вы рассчитали ранее. Для этого вычтите процент доходности акций от среднего, чтобы найти разницу.

Первый год: 13% — 9% = 4%

Второй год: 24% — 9% = 15%

Третий год: -10% — 9% = -19%

4. Возведите в квадрат разницы (отклонения) и сложите их за каждый год.

4² = 16%
15² = 225%
-19²= 361%

16% + 225% + 361% = 602%

5. Разделите сумму отклонений на количество возвратов в вашем наборе данных, чтобы получить дисперсию.

602% / 3 = 206,67%

Это означает, что доходность акций отличается от среднего значения, что означает, что в вашем портфеле находятся акции с высоким риском.

Важно: Волатильность может быть отмечена как стандартное отклонение, а не как дисперсия, потому что ее часто легче интерпретировать.

Чтобы получить стандартное отклонение, вычислите квадратный корень из дисперсии. Используя данный пример, это будет 14,37% для возврата.

Прочитайте больше: Узнайте о том, как стать финансовым консультантом

Дисперсия населения

Далее мы рассмотрим дисперсию с точки зрения населения.

формула дисперсии населения: σ2 = ∑ (xi - x̄) 2N

См. шаги и расчет в примере ниже:

1. Определите население по числам в наборе данных.

Вместо использования процентов числа в наборе данных представляют собой целые числа для каждого человека.

Для этого примера мы скажем, что общее количество каждой совокупности включает 4, 22, 99, 204, 18 и 20.

2. Сложите все числа в наборе данных

4 + 22 + 99 + 204 + 18 + 20 = 367

3. Возведите в квадрат сумму всех чисел

367² = 134 689

4. Разделите сумму на количество чисел, включенных в набор данных.

134 689/6 = 22 448,1667 или 22 448,2

5. Возведите в квадрат числа из исходного набора данных и сложите их.

16 + 484 + 9 801 + 204 + 41 616 + 400 = 52 521

6. Вычтите сумму ваших ответов на пятом шаге из суммы на четвертом шаге.

52 521 — 22 448,2 = 30 072,8

7. Вычтите единицу из количества чисел, включенных в ваш набор данных.

6 — 1 = 5

8. Разделите сумму шестого шага на результат седьмого шага, чтобы получить общую дисперсию населения.

30 072,8 / 5 = 6 014,56

Дисперсия населения составляет 6 014,56 человек.

Источник

Похожие документы: «9.2.4. ДИСПЕРСИЯ ЦЕН»

Генеральная и выборочная дисперсия

Выборочная дисперсия, определение, формулы для вычисления

Генеральная дисперсия, определение, что является оценкой, формулы для вычисления

Оценки параметров распределения

Примеры решения задач

Что такое дисперсия?

Типы дисперсии:

Формулы отклонения:

Формула дисперсии совокупности

Пример формулы отклонения

Как рассчитать дисперсию?

Как работает калькулятор дисперсии?

Вход:

Выход:

ЧАСТО ЗАДАВАЕМЫЕ ВОПРОСЫ:

В чем разница между стандартным отклонением и дисперсией?

Значение высокой дисперсии – это плохо или хорошо?

Каков диапазон отклонений?

Заключение:

Help Calculating Variance

References

About This Article

Reader Success Stories

Did this article help you?

Что такое дисперсия?

Понимание дисперсии

Как рассчитать дисперсию

1. Определите доходность акций за определенный период

2. Рассчитайте среднее значение доходности

3. Найдите разницу между каждым доходом и средним значением за каждый год.

4. Возведите в квадрат разницы (отклонения) и сложите их за каждый год.

5. Разделите сумму отклонений на количество возвратов в вашем наборе данных, чтобы получить дисперсию.

Дисперсия населения

Не пропустите также: