Скачать с Depositfiles
5 Дифференциальные формулы дирекционного угла
Пусть имеется линия с известными координатами
,
и
,
ее концов (рис. 6). Дирекционный угол
этой линии может быть определен из формулы
. (4.18)
|
|
|
Рисунок 6 – К выводу дифференциальной формулы дирекционного угла |
Если точка переместится в положение
, то ее координаты получат приращение
и
. В соответствии с этим изменится и дирекционный угол
линии
на угол
. Если приращения координат
и
будут малыми величинами, то при этих условиях можно считать, что угол
изменится на величину дифференциала
(
).
Для того чтобы найти дифференциал продифференцируем формулу (4.18) по
. В результате получим:
(4.19)
Так как
,
то можно записать:
(4.20)
Введем обозначения

В результате получим
(4.22)
Если конечная точка сохраняет свое положение, а перемещается начальная точка
, то ее координаты изменяются на величину приращений
и
. Тогда проведя аналогичные рассуждения, получим
(4.23)
Формулы (4.22) и (4.23) называются дифференциальными формулами дирекционного угла. В общем случае (рис. 5, в) при одновременном изменении положения обоих концов линии дифференциальная формула принимает вид:
(4.24)
6 Прямая многократная засечка. Составление параметрических уравнений поправок.
Имеется исходных пунктов
,
, …,
с известными координатами
,
,
, с каждого из которых имеется видимость на пункт
, координаты
,
которого неизвестны. С пунктов
выполнены визирования на пункт
и измерены горизонтальные углы
,
, … ,
между линиями с известными дирекционными углами
,
, … ,
и направлениями на пункт
(рис. 7).
|
|
|
Рисунок 7 – Прямая многократная угловая засечка |
Необходимо определить координаты ,
пункта
способом прямой многократной засечки.
Как было отмечено выше, наличие избыточно измеренных величин в многократных засечках приводит к уравнительным вычислениям. Уравнительные вычисления можно производить двумя способами: параметрическим и коррелатным. Оба способа дают равноценные результаты, однако при уравнивании многократных засечек параметрический способ является более предпочтительным.
В параметрическом способе уравнивания каждое неизвестное (параметр) представляют в виде суммы двух слагаемых: приближенного значения и поправки к нему.

Приближенные значения получают из решения однократных засечек, а поправки – из уравнивания результатов измерений по методу наименьших квадратов параметрическим способом с использованием дифференциальной формулы дирекционного угла.
Для начала составим уравнения поправок. Для этого рассмотрим чертеж, показанный на рис. 8. На этом чертеже точка соответствует истинному положению пункта
, координаты которого равны
и
, а точка
— положению, задаваемому приближенными координатами
и
.
|
|
|
Рисунок 8 – К уравниванию прямой многократной засечки |
По координатам точек и
из решения обратной геодезической задачи можно определить приближенные значения длины
и дирекционного угла
стороны
.
Тогда уравненное значение дирекционного угла стороны
можно выразить через приближенное значение
и поправку
к нему
(4.26)
С другой стороны для стороны можно записать значение дирекционного угла
через дирекционный угол
исходной стороны
и измеренный угол
между этой стороной и стороной
(4.27)
Значение угла часто называют «измеренным» дирекционным углом. Определение «измеренный» придано ему не потому что он действительно измерен (дирекционные углы не измеряются), а для того, чтобы отличить данное значение дирекционного угла, которое вычисляется через измеренное значение горизонтального угла
, от значения дирекционного угла
, которое вычисляется чисто расчетным путем..
Уравненное значение дирекционного угла равно «измеренное» значение дирекционного угла плюс поправка
(4.28)
или после перестановки
(4.29)
Уравнений (4.29) будет столько, сколько измерено углов, т.е. в рассматриваемом случае уравнений. Однако эти уравнения пока никак не связаны с поправками к неизвестным величинам.
Подставим (4.26) в (4.29). Получим:
(4.30)
Обозначим
(4.31)
Это свободный член уравнений поправок. Перепишем (4.30) с учетом (4.31)
(4.32)
Перейдем в (4.32) от к
и
, используя дифференциальную формулу дирекционного угла
(4.33)
Введем обозначения

Запишем уравнения (4.32) с учетом (4.33) и (4.34). Получим
(4.35)
Уравнения (4.35) называются параметрическими уравнениями поправок. Это их окончательный вид перед решением. Число параметрических уравнений поправок будет равно числу наблюдаемых направлений на точку .
Решая уравнения (4.35) по методу наименьших квадратов, т.е. под условием
,
придем к системе из двух нормальных уравнений

Полученные уравнения можно решить методом определителей:

Вычислив поправки и
, по формуле (4.25) вычисляются уравненные значения координат пункта
. Далее по формуле (4.35) вычисляются поправки
, после чего по формуле (4.28) вычисляются уравненные значения «измеренных» дирекционных углов.
Для контроля по координатам пункта путем решения обратной геодезической задачи вычисляются дирекционные углы
:
(4.38)
Вычисленные значения должны практически совпадать со значениями, полученными из формулы (4.28).
Совпадение результатов является заключительным контролем уравнивания.
Скачать с Depositfiles
По
известному дирекционному углу n
и по исправленным горизонтальным углам
испр
вычисляются дирекционные углы остальных
сторон теодолитного хода по формулам
для правых горизонтальных углов:
– дирекционный
угол последующей стороны равен
дирекционному углу предыдущей стороны
плюс 180
и минус исправленный горизонтальный
угол правый по ходу.
Величина
дирекционного угла не может превышать
360
и быть меньше 0.
Если величина дирекционного угла больше
360,
то из результата вычислений необходимо
вычесть 360
(см. пример).
Контроль
вычисления дирекционных углов. В
замкнутом теодолитном ходе в результате
вычислений получается дирекционный
угол исходной стороны.
Пример вычисления дирекционных углов: Дирекционный угол исходной стороны 1-2 равен 4545.
;
;
;
;
При
вычислении дирекционного угла получилось
значение 40545.
Из полученного значения вычитается
360.
.
Контроль
вычисления дирекционных углов получился.
Все
результаты вычислений заносятся в
таблицу «Ведомость вычисления координат»
(табл. 6).
3.3 Вычисление приращений координат
Вычисление
приращений координат выполняется по
формулам:
,
где
d
– горизонтальное проложение (длина)
линии;
– дирекционный угол этой линии.
Приращения
координат вычисляются с точностью два
знака после запятой.
Пример вычисления приращений координат:
;
;
;
;
.
;
;
;
;
.
Все
результаты вычисления заносятся
в табл. 6. Пример
вычисления тригонометрических функций
на калькуляторе приведен в
прил. 3.
3.4 Уравнивание линейных измерений
Разность
между суммой вычисленных приращений
координат и теоретической суммой
называется линейной невязкой хода и
обозначается fХ
и fY.
Уравнивание линейных измерений
выполняется по осям Х
и Y.
Линейная невязка
вычисляется по формулам:
.
Теоретическая
сумма приращений координат зависит от
геометрии хода. В замкнутом теодолитном
ходе она равна нулю, тогда невязка равна
.
Прежде,
чем распределять невязки в приращения
координат, необходимо убедиться в их
допустимости. Для чего вычисляется
абсолютная невязка хода fабс
и
относительная
,
где
Р
– периметр хода (сумма длин сторон), м.
Относительная
невязка сравнивается с допустимой
.
В
случае, когда полученная относительная
невязка допустима, т.е.
,
то вычисляются поправки в приращения
координат пропорционально
длинам сторон.
Невязки распределяются с обратным
знаком. Если
,
то проверяются вычисления в п.
3.3 и 3.4.
Поправки
в приращения координат X
и Y
вычисляются
по формулам с округлением до 0,01 м:
,
где
X
и Y
– поправка
в приращение по оси Х
и
Y,
соответственно, м; fX
и fY
–
невязки
по осям, м; Р
–
периметр
(сумма сторон), м; di
–
измеренная
длина (горизонтальное проложение), м.
Знак
у поправки противоположен знаку невязки.
Поправки записываются в «Ведомость
вычисления координат». В примере (табл.
6) поправки показаны красным цветом.
После
вычисления поправок следует сделать
проверку, т.е. сложить все поправки. Если
их сумма будет равна невязке с обратным
знаком, то распределение невязки
выполнено правильно. То есть:
.
Вычисляются
исправленные приращения.
Полученные
поправки алгебраически прибавляются
к соответствующим приращениям и
получаются исправленные приращения:
.
Контроль:
сумма исправленных приращений в замкнутом
теодолитном ходе должна равняться нулю,
т.е. должно выполняться равенство:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как определить дирекционный угол
Дирекционный угол – геодезическое название угла направления ориентирования линии на карте относительно географического или магнитного меридиана. Угол определяется непосредственно по карте местности или по магнитному азимуту.

Вам понадобится
- — карта местности;
- — карандаш и линейка;
- — транспортир, артиллерийский круг или хордоугломер;
- — компас или буссоль.
Инструкция
Существует несколько способов определения дирекционного угла: по карте или аэрофотоснимку с помощью транспортира, хордоугломера или артиллерийского круга, а также по магнитному азимуту с помощью прибора с магнитной стрелкой.
Чтобы определить дирекционный угол с помощью транспортира, найдите на карте исходную точку и предмет на местности (ориентир), отметьте их. С помощью карандаша и линейки соедините их линией. Длина этой линии должна превышать радиус транспортира, начиная от точки пересечения с вертикальной линией координатной сетки.
Наложите транспортир на карту так, чтобы «ноль» на транспортире совпал с вертикальной линией, а центр – с точкой пересечения линий. Отсчитайте дирекционный угол по шкале транспортира по линии, прочерченной между объектами. Измерение артиллерийским кругом схоже с использованием транспортира. Центр круга совмещается с исходной точкой, а нулевая отметка – с северным направлением вертикальной линии координатной сетки или с прямой, параллельной ей.
Для измерения с использованием хордоугломера проведите линию между исходной точкой и ориентиром не меньше 15 см. Из точки пересечения этой линии с вертикальной с помощью циркулеизмерителя сделайте засечки на линиях, образующих острый угол. Для этого проведите дугу окружности радиусом в 10 делений прибора. Затем поставьте циркуль двумя иглами в отмеченные точки, таким образом, сделав раствор циркуля равным длине хорды (расстоянию между точками).
Держа обе иглы циркуля на горизонтальной линии, ведите его левой иглой по крайней левой вертикальной шкале хордоугломера. Продолжайте движение до тех пор, пока правая игла не совпадет с линией пересечения, горизонтальной или наклонной. Снимите измерение.
Для определения дирекционного угла с помощью магнитного азимута используйте компас или другой прибор с магнитной стрелкой, например, буссоль. Для того, чтобы воспользоваться этим методом, необходимо знать поправку направления. Это величина отклонения магнитного меридиана (магнитной стрелки) данной точки от вертикальной линии координатной сетки. Поправка направления обычно указывается на карте в виде рамки.
Определите магнитный азимут, который измеряется по часовой стрелке от северного направления магнитного меридиана (направления магнитной стрелки прибора) до определяемого направления. Дирекционный угол найдите по формуле:α = β + (±dα), где β – магнитный азимут, dα – поправка направления.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Чтобы понять, что такое дирекционный угол, представим на карте линию (отрезок) с начальной точкой А и конечной точкой В.
Теперь проведем из начала отрезка (точки А) луч, параллельный осевому меридиану зоны и направленный на север. И будем поворачивать этот
луч вокруг точки А по часовой стрелке до тех пор, пока он не пересечется с точкой В. Угол, на который мы повернули луч,
и будет называться дирекционным углом линии АВ.
Калькулятор угла по координатам
С помощью этого калькулятора Вы сможете производить расчет дирекционных углов линий на основе заданных координат точки стояния (А) и точки
ориентирования (В), а также рассчитывать расстояние между этими точками.
Калькулятор координат по углу и расстоянию
Этот калькулятор поможет Вам рассчитать координаты конечной точки пути на основе координат начальной точки, дирекционного угла и расстояния между точками.
Угол можно указывать как в десятичных градусах (226,27303°), так и в градусах — минутах — секундах (226° 16′ 22″).
Книга найдена на
http://www.geolink-group.com/tourclub/ — спасибо создателям
Вы можете заказать 2CD
с картами Юга России
Содержание книги
1.14.
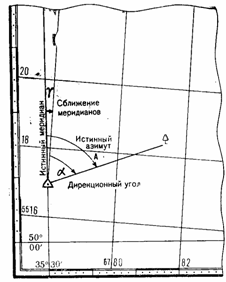
ДИРЕКЦИОННЫЕ УГЛЫ И АЗИМУТЫ
Дирекционный угол — угол а,
измеряемый по ходу часовой стрелки от 0 до 360° между северным направлением
вертикальной линии координатной сетки и направлением на определяемый объект
(рис. 24).
Дирекционные углы направлений
измеряются преимущественно по карте или определяются по магнитным азимутам.
Истинный
азимут—угол А, измеряемый по ходу часовой стрелки от 0 до 360° между
северным направлением истинного (географического) меридиана и направлением
на определяемую точку (рис. 24). Значения истинного азимута и дирекционного
угла отличаются одно от другого на величину сближения меридианов.
Сближение меридианов —
угол f
(рис. 24) между северным направлением истинного меридиана данной точки и
вертикальной линией координатной сетки (или линией,
параллельной ей). Сближение меридианов отсчитывается от северного
направления истинного меридиана до северного направления вертикальной линии.
Для точек, расположенных восточнее среднего меридиана зоны, величина
сближения положительная, а точек, расположенных западнее, — отрицательная.
Рис.
24. Дирекционный угол и сближение меридианов
Величина сближения меридианов на осевом
меридиане зоны равна нулю и возрастает с удалением от среднего меридиана
зоны и от экватора; ее максимальное значение будет вблизи полюсов и не
превышает 3°.
Сближение меридианов, указываемое на
топографических картах, относится к средней (центральной) точке листа; ее
величина в пределах листа карты масштаба 1:100000
в средних широтах может отличаться на 10—15′
от значения, подписанного па карте.
Магнитный азимут—угол, измеряемый по
ходу часовой стрелки от 0 до 360° между северным направлением магнитного меридиана
(направлением установившейся магнитной стрелки компаса или
буссоли) и направлением
на определяемый объект.
Магнитные
азимуты измеряются
на местности компасом или буссолыо, а также
определяются по карте по измеренным дирекционным
углам.
Склонение магнитной
стрелки (магнитное склонение) — угол между
истинным (географическим) и магнитным меридианами.
Величина
склонения магнитной стрелки подвержена
суточным, годовым и вековым колебаниям, а также временным
возмущениям под действием
магнитных бурь. Величина склонения магнитной
стрелки и его годовые изменения показываются на топографических и
специальных картах. В районах магнитных аномалий обычно указывается
амплитуда колебания величины склонения
магнитной стрелки.
Склонение
магнитной стрелки на восток считается восточным (положительным), а на
запад—западным (отрицательным). Переход от
дирекционного угла к магнитному азимуту к обратно производится
различными способами; все необходимые данные для этого имеются на каждом
листе карты масштаба 1:25 000— 1:200
000 в специальной текстовой справке и графической схеме, помещаемых
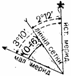
на полях листа в левом нижнем углу (рис. 25).
|
Склонение |
|
Рис. 25. Данные о склонении магнитной
стрелки и сближении меридианов,
помещаемые на картах
Переход через поправку направления. В
текстовой справке, помещаемой на картах, указывается величина (в градусах и
делениях угломера) и знак поправки для перехода
от дирекннонного угла к магнитному азимуту. Например,
в справке, приведенной на рис. 25, указано: «Поправка в дирекционный угол
при переходе к магнитному азимуту плюс (0-16)». Поэтому если дирекционный
угол направления равен 18-00 дел. угл., то магнитный азимут будет равен
18-16 дел. угл.
При обратном переходе, т. е. при
определении дирекционного угла по магнитному азимуту, знак поправки изменяют
на обратный и она вводится в магнитный азимут. Например, если магнитный
азимут равен 10-00, то дирекционный угол этого направления для данной карты
(рис. 25) равен 9-84 (10-00—0-16).
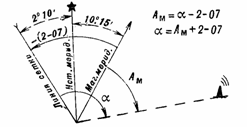
Переходно графической схеме (рис. 26).
На схеме показывают примерное направление на объект и, сообразуясь с положением вертикальной линии
координатной сетки и линии магнитного меридиана, увеличивают или уменьшают
исходный угол на поправку, указанную на схеме в скобках.
Рис. 26. Переход от дирекционного угла
к магнитному азимуту и обратно
Примеры
(см. рис. 26):
1.
Дирекционный угол а= 12-60; магнитный азимут будет равен 10-53 (12-60—2-07).
2.
2 Магнитный азимут Ам = 153°; дирекционный угол будет равен
!65°25′ (153°+2°10^+10°15′).
Переход по формуле. Зависимость между
дирекционным углом
II магнитным азимутом одного и
того же направления выражается формулой
А^=а— Ъ+Ч,
где Ая—магнитный азимут;
а — дирекиионпый угол;
5 — склонение магнитной стрелки;
f
— сближение меридианов.
Это основная исходная формула для
перехода от дирекционного угла к магнитному азимуту и обратно. Она
применяется главным образом, когда приходится учитывать годовое изменение
склонения магнитной стрелки.
Переход от дирекционного угла к
магнитному азимуту с учетом годового изменения склонения магнитной стрелки.
Вначале определяют склонение магнитной стрелки на данное время. Для этого
годовое изменение склонения магнитной стрелки умножают на число лет,
прошедшее после создания карты, и полученную величину алгебраически
суммируют с величиной склонения магнитной стрелки, данной на карте. Затем
производится переход от дирекционного угла к магнитному азимуту по основной
формуле.
Пример перехода от дирекционного угла,
равного 120°30′, к магнитному азимуту этого направления на 1972 г. (исходные
данные взяты с рис. 25).
1. Определение величины изменения
склонения магнитной стрелки за 7 лет (1972—1965 гг.): Д=0°05′,2Х7=0°36′.
2. Вычисление величины склонения
магнитной стрелки на 1972 г.: б =—3°10’+0°36’=—2°34′.
3. Переход от дирекционного угла к
магнитному азимуту по основной формуле (см. выше)
А м =
120°3(У— (—2°34′)+ (—2° 12′) = 120°52′.
Комментарии:
Сообщение от: Алексей
Хотелось бы поподробнее получить информацию о том, как учитывать годовые склонения и сближения. Прям на нескольких примерах. Чтоб чайникам понятно было
Сообщение от: Алексей
Здравствуйте. Под рисунком 26 формула подкосилась неизвестными знаками)
Сообщение от: Павел
Спасибо за статью