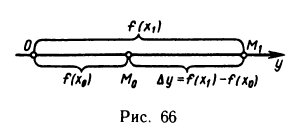
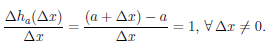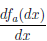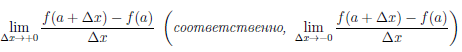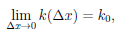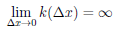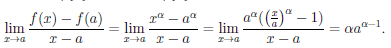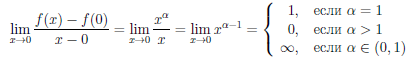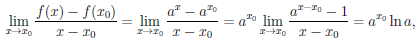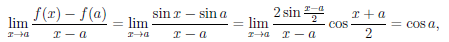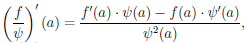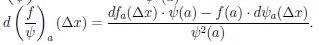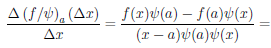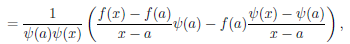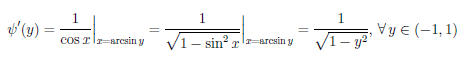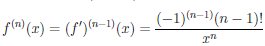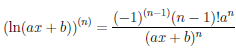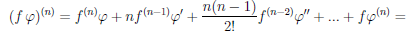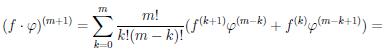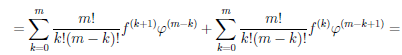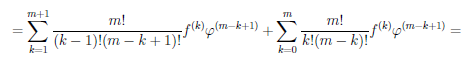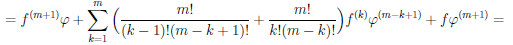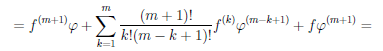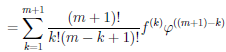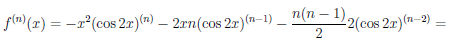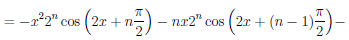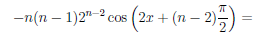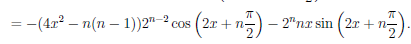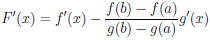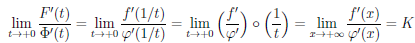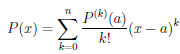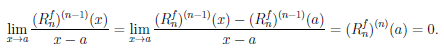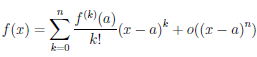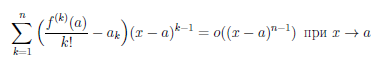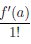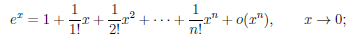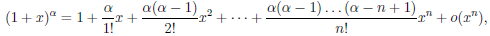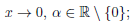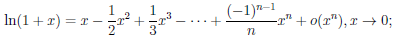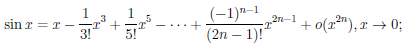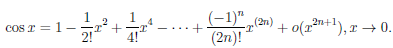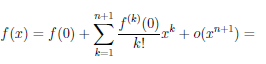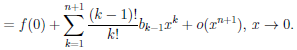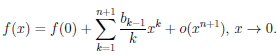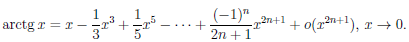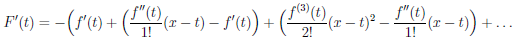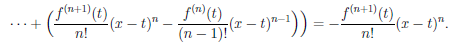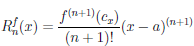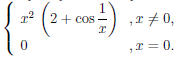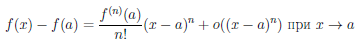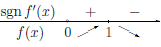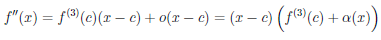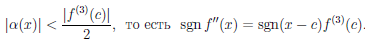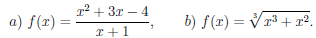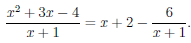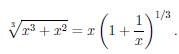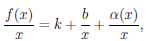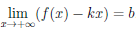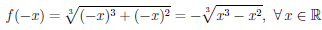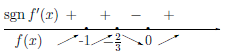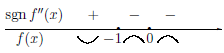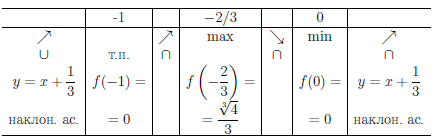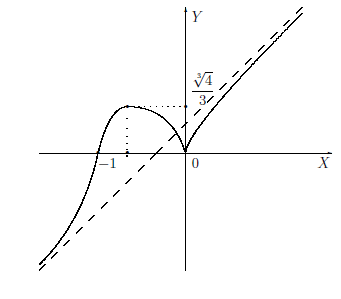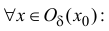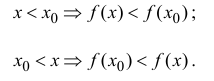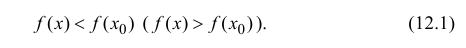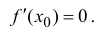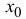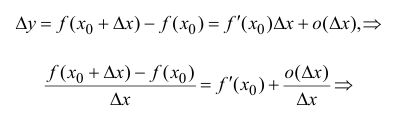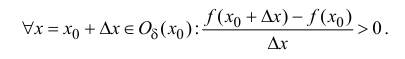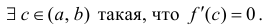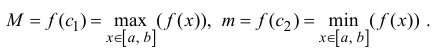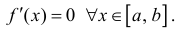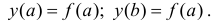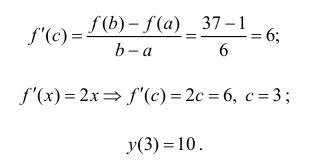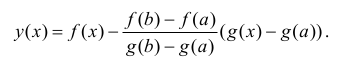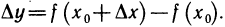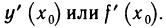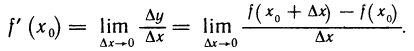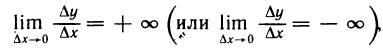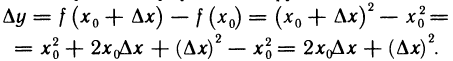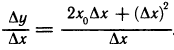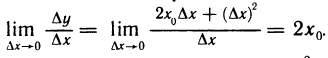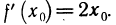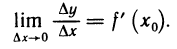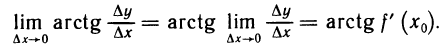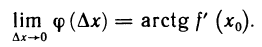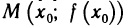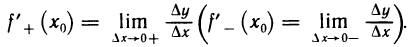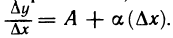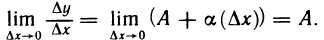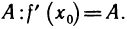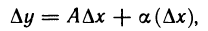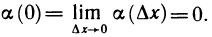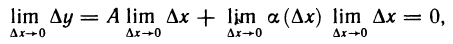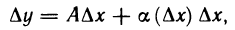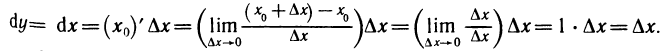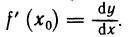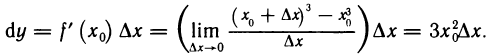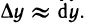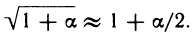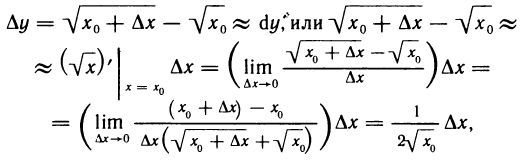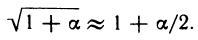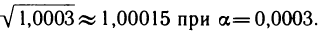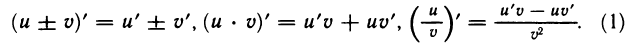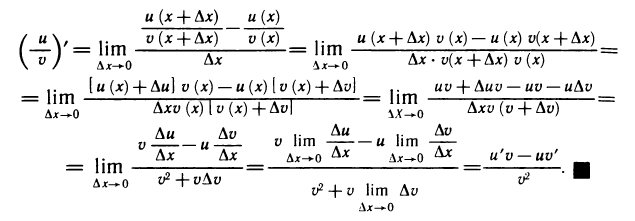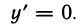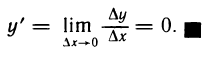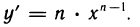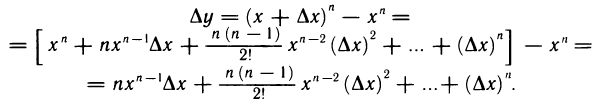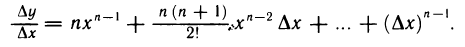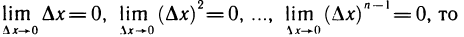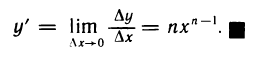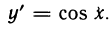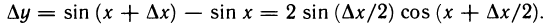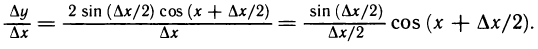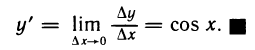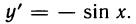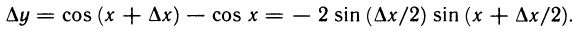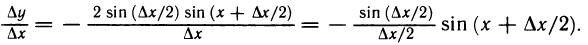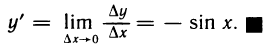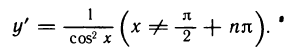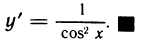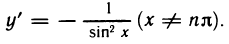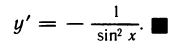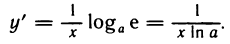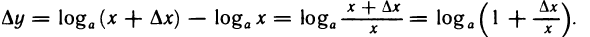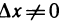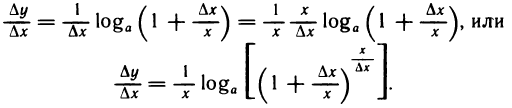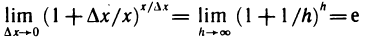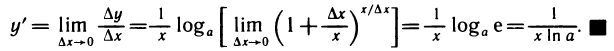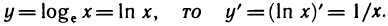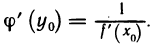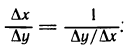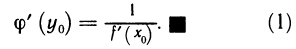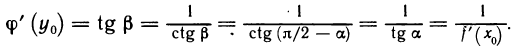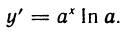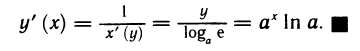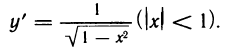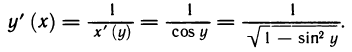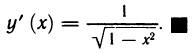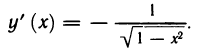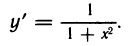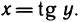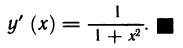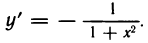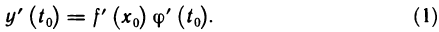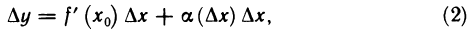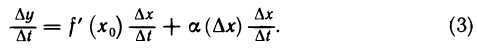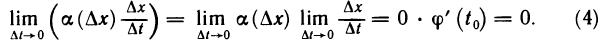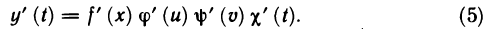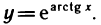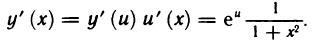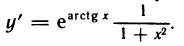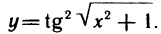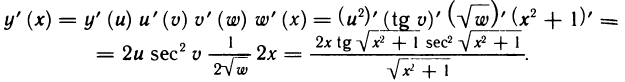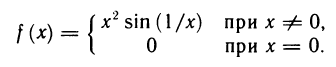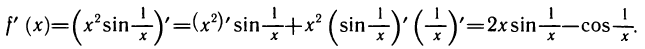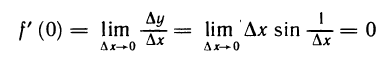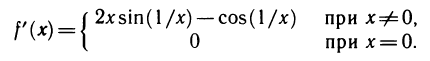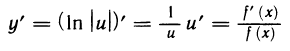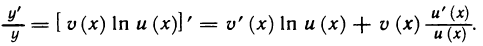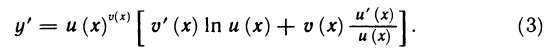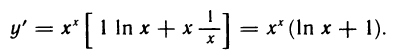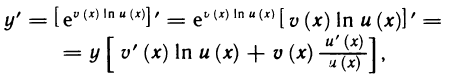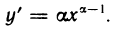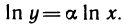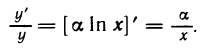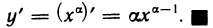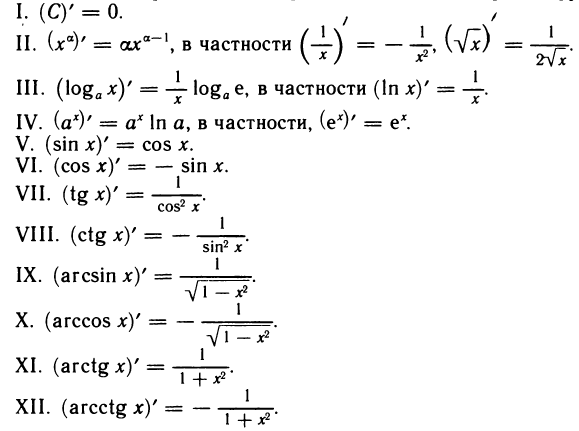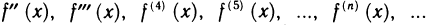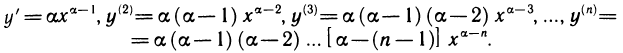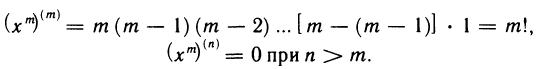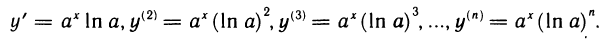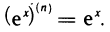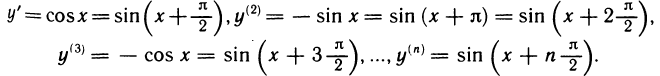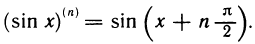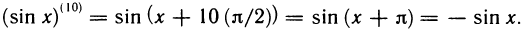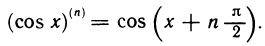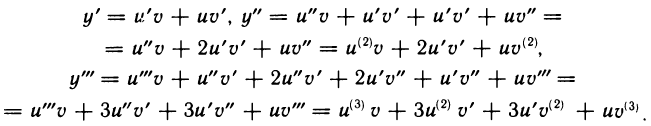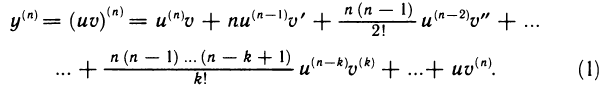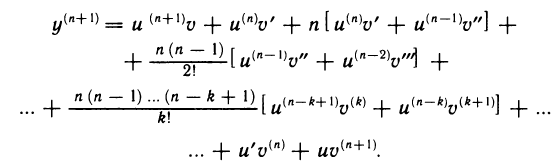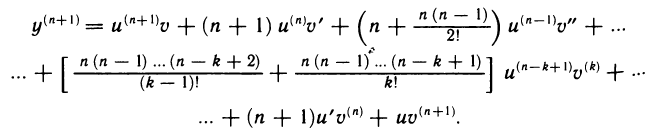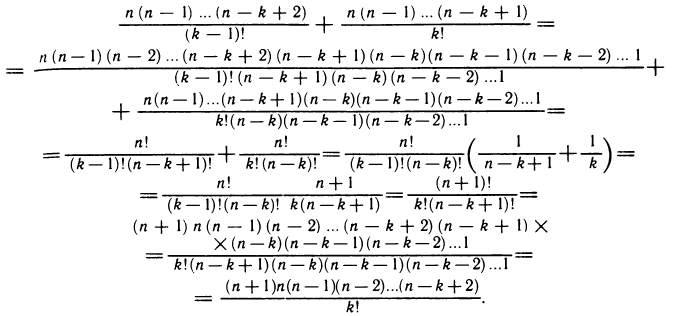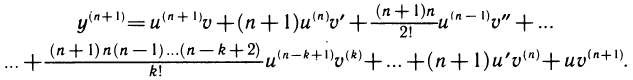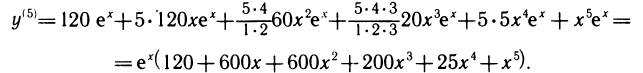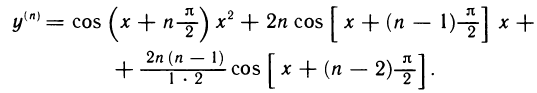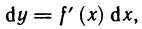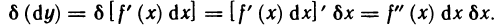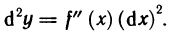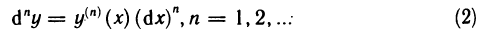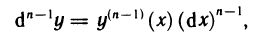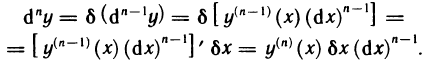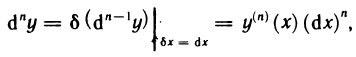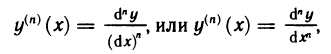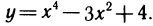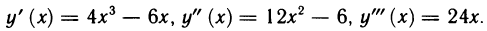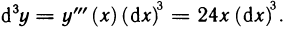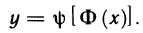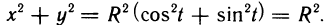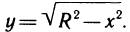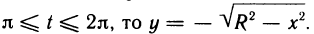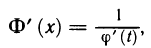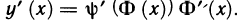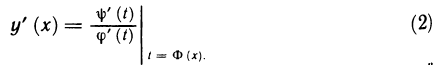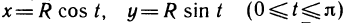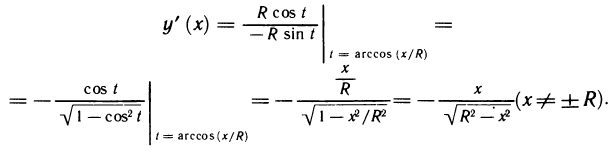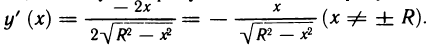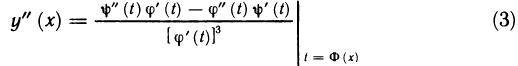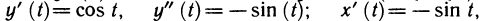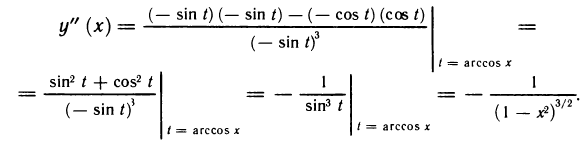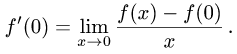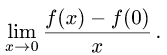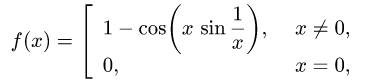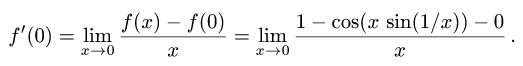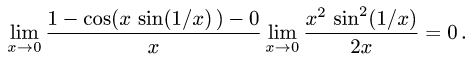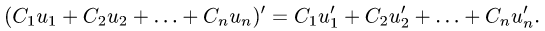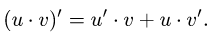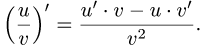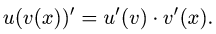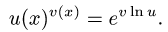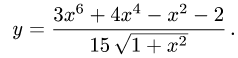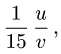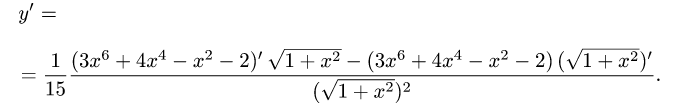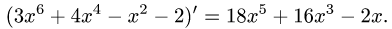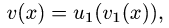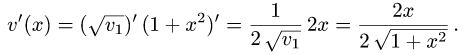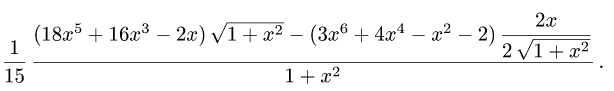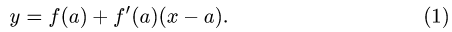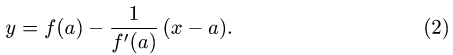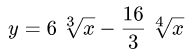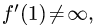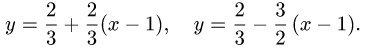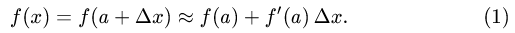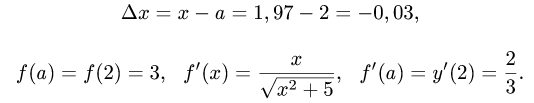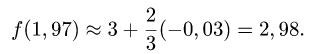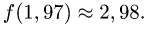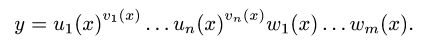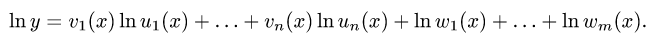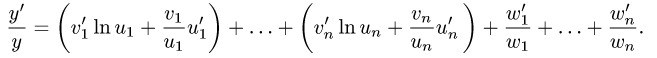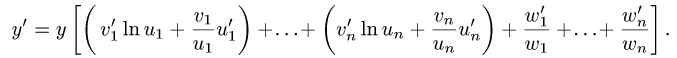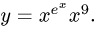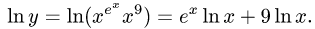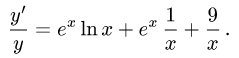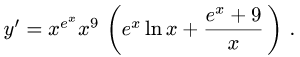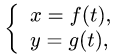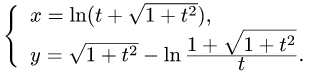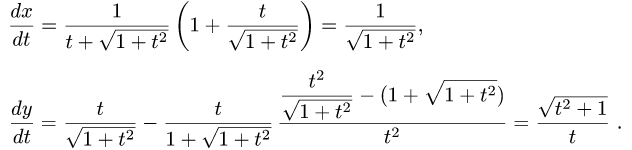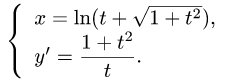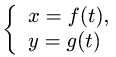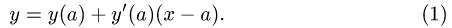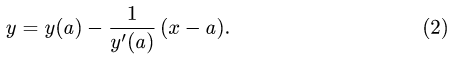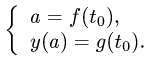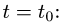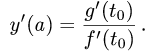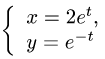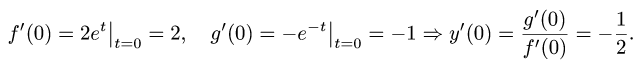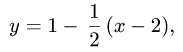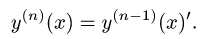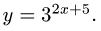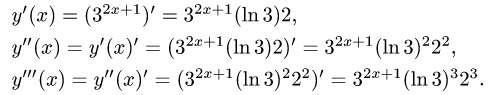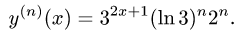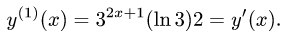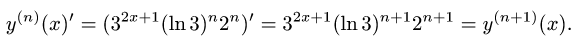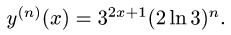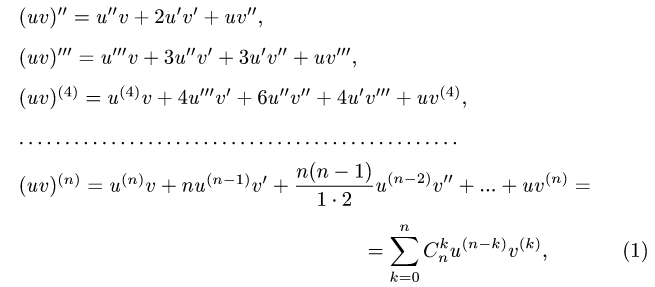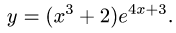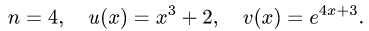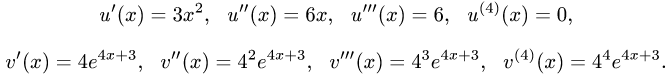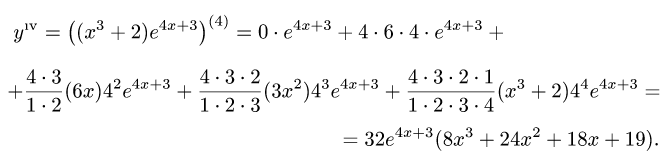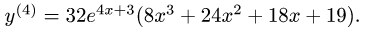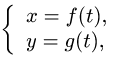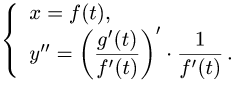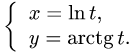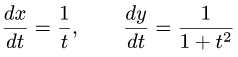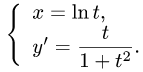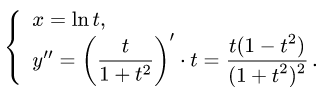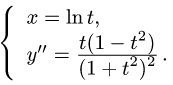Рассмотрим функцию
Известно, что если a ∈ X и является предельной точкой множества X , то функция 



то есть
∆
Выделим класс функций, для которых можно уточнить характеристику приращений ∆fa(∆x) функции f, соответствующих приращению ∆x аргумента.
Определение
Определение 4.1. Пусть функция 

∆
Иными словами, функция 

Учитывая представление функции вида o(∆x) при ∆x → 0, заметим, что дифференцируемая в точке a по множеству X функция имеет вид

где a + ∆x ∈ X и α(∆x) → o при ∆x → o, или


где x ∈ X и α(x — a) → o при x → a.
Определение 4.2. Пусть функция 


Из определения 4.1 следует
Лемма 4.1. Для того чтобы функция 
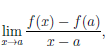
равный числу A из (4.1).
Следствие. Если функция 

Определение 4.3. Пусть функция 
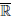


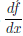
С учетом определения 4.3 лемма 4.1 принимает вид:
Лемма 4.2. Для того чтобы функция 
Таким образом, если функция 
∆



Пример:
Пусть 
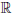



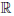
Пусть a — произвольная точка из 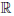
∆
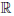
Поэтому 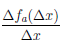
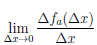


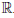
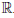
Пример:
Пусть h : 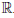
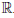
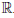
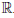
Отсюда следует, что производная функции h в точке a по множеству 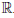
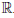
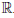
Как видим, для функции h(x) = x приращение функции в точке равно приращению переменной ∆x, а поэтому и дифференциал этой функции в точке так же равен ∆x, то есть, сокращая обозначение, можно написать, что dx = ∆x. Поэтому для произвольной дифференцируемой в точке a функции f равенство dfa(∆x) = 
d


что напоминает символику Лейбница производной функции 
Чтобы объяснить, как на дифференцируемость и значение производной влияет множество X , рассмотрим такой пример.
Пример:
Пусть 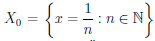
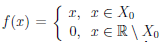
В дальнейшем мы не будем явно указывать, по какому множеству X выполняется дифференцирование, поскольку это будет ясно из контекста определения функции, но забывать о множестве X и его роли в определении дифференцируемости функции не следует.
Теорема 4.1 (необходимое условие дифференцируемости). Если функция 
Доказательство очевидно, поскольку представление (4.2) влечет существование 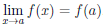
Замечание. Непрерывность функции в точке является необходимым, но не является достаточным условием дифференцируемости функции в точке. Для примера рассмотрим функцию 
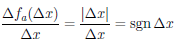
поэтому не существует предел отношения 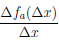

В полной аналогии с понятием левого и правого предела функции в данной точке вводятся понятия левой и правой производной функции 
Определение 4.4. Пусть 
то его называют правой (левой) производной функции 


Правая и левая производные функции 
Теорема 4.2. Пусть функция 







Возвращаясь к 


Геометрический смысл производной и дифференциала
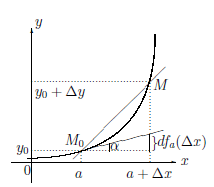
Пусть функция 
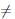




Поскольку точка M0 фиксирована, то угловой коэффициент k секущей MM0 является функцией от ∆x (величина ∆x приращения аргумента вполне определяет точку M графика функции), то есть k = k(∆x). Ясно, что k(∆x) = 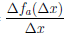
y = k(∆x)(x — a) +y0, где y0 = 
Определение 4.5. Если существует конечный предел
то прямая, соответствующая уравнению y = k0 (x — a) + y0, называется наклонной (невертикальной) касательной к графику Γфункции 
(функция k(∆x) является бесконечно большой в точке 0), то прямая x = a называется вертикальной касательной к Γ
Поскольку угловой коэффициент касательной, в случае ее существования, получен из углового коэффициента секущей с помощью предельного перехода при ∆x → 0, то касательную часто называют предельным положением секущей M0M при M → M0 по Γ



Теорема 4.3. Пусть функция 




y = 

Для того, чтобы график Γ


Так как k(∆x) =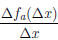


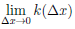

Из определений 4.1 и 4.5 и теоремы 4.3 получаем следующее определение невертикальной касательной к графику функции
Определение 4.6. Пусть функция 



Выясним геометрический смысл дифференциала dfa(∆x). Будем считать, что функция 











Производная и дифференциал функции на множестве
Определение 4.7. Если каждая точка множества X является его предельной точкой и функция 




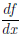
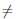



Напомним, что d




Рассмотрим несколько примеров.
Пример:
Пусть 
Заметим, что если α ≥ 0, то 0 ∈ Xα , если α 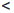
а) Пусть α = 0. Тогда 



б) Пусть α ∈ 
Следовательно, при α ∈ 


в) Пусть α > 0 и a = 0. Тогда
Последнее означает, что функция 



Пример:
Пусть 
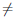

то функция 




Пример:
Пусть 


то функция 




Аналогично доказывается, что функция 


Основные правила вычисления производной
Теорема 4.4. Если функции 


1) (

d(

2) (


d (


3)
Докажем только третью часть утверждения. По условию теоремы функция ψ дифференцируема в точке a и ψ(a)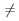

где ∆x = x — a. Учитывая дифференцируемость и непрерывность функций 
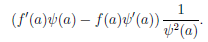
Поэтому существует предел левой части, равный числу (4.5). Значит, функция 
Замечание. Доказательство теоремы 4.4, опирающееся на определение дифференцируемой в точке функции, см. в [4, с.200-202].
Пример №1
Пусть 
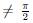

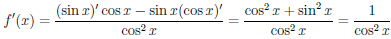
Аналогично доказывается, что функция 
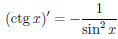
Теорема 4.5 (о дифференцируемости суперпозиции функций). Если X и Y — подмножества в 










По условию теоремы функция ψ дифференцируема в точке y0 , поэтому ∀y ∈ Y {y0}
ψ(y) -ψ(y0) = ψ/(y0)(y-y0) +α(y — y0)(y — y0), (4.6)
где α(y — y0) → 0 при y → y0. Без ограничения общности можно считать, что α(0) = 0. Тогда представление (4.6) функции ψ имеет место на множестве Y . Поскольку 
ψ(


Учитывая, что y0 = 
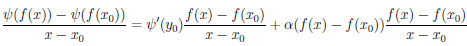
Так как при x → x0 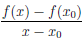
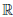




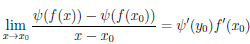
Следовательно, функция ψ ◦ 



Следствие. Пусть функция 
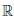

(ψ ◦ 


Теорема 4.6 (о производной обратной функции). Пусть функция 


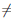



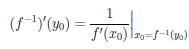
Пусть 


Пусть ∆y 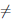

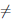
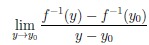
воспользовавшись теоремой Гейне существования предела функции (см. теорему 2.31), и найдем его. Для этого фиксируем произвольную последовательность {yn}: yn ∈ Y , yn 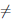



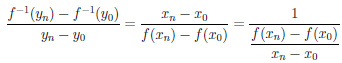
(воспользовались тем, что xn 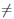

По непрерывности функции 



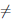
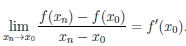
И из (4.7) получаем существование предела
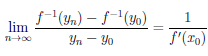
Поскольку {yn} — произвольная последовательность точек множества Y, отличных от y0 , стремящаяся к y0 , то по теореме Гейне
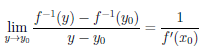
Поэтому функция


Следствие. Пусть функция 




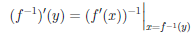
Замечание 1. Если выполняются условия теоремы и функция 


(



Замечание 2. Если функция 


Замечание 3. Если функция 


Пример №2
Покажем, что функция ψ(x) = loga x, a > 0, a 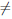
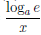
Пусть для определенности a > 1. Функция ψ является обратной к функции 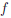
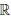
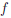

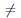
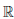
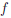
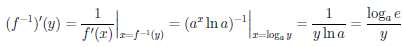
Значит функция ψ(x) = loga x дифференцируема на (0, +∞) и (loga x)/ =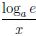

Пример №3
Покажем дифференцируемость на интервале (—1, 1) функции ψ(x) = arcsin x и наличие у нее производной на отрезке [—1, 1].
Известно, что функция ψ : [—1,1] → [—π∕2,π∕2] является непрерывной обратной к функции 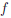
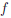
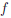
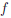
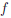
то согласно теореме 4.6 и замечания 2 к ней, функция ψ дифференцируема на (—1, 1),
и ψ/(±1) = ∞.
Пример №4
Пусть функции y = U(x) и y = V (x) дифференцируемы на множестве X ⊂ 
Действительно, так как g(x) = exp(V (x) ln U (x)), то в силу теорем 4.4 — 4.6 и примера 8 функция g дифференцируема на X и
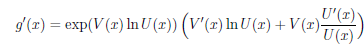
Инвариантность формы первого дифференциала
В начале главы показано, что если функция 
dfx0 (∆x) = f/(x0)dx, где dx = ∆x. (4.8)
Пусть функция x = ψ(t), ψ : T → X, дифференцируема в точке t0 и ψ(t0) = x0 . В силу теоремы о дифференцируемости суперпозиции функций функция 
(


Поскольку t — независимая переменная функции y = 
d(


Кроме того, ψ/(t0)dt = dψt0(∆t). Если обозначить dx = dψt0(∆t), то получим
d(

Сопоставляя полученную формулу с (4.8), замечаем, что форма дифференциала функции y = 
Производные высших порядков
Пусть функция 





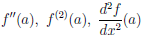
Если функция 







Пример №5
Пусть 

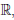
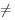

В силу примера 4 функция 
f/(x) = αxα-1, ∀x ∈ (0, +∞).
Поскольку 


Заметим, что если α = 1, то 

Предположим, что n ∈ 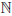


Функция 



В частности, если α = k0 ∈ 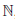


Если α = -1, то 
Из теоремы 4.5 получаем, что функция 
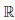
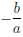
((ax + b)α)(n) = α(α — 1)…(α — n + 1)(ax + b)α-nan.
Наконец, согласно теореме 4.4, многочлен
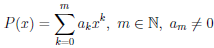
дифференцируем на 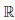
P (n) (x) = 0, ∀n > m, P (m) (x) = m! am, ∀ x ∈ 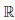
Пример №6
Докажем, что функция 
В примере 8 показано, что рассматриваемая функция 


Замечание. Функция y = ln(ax + b) дифференцируема любое число раз в области её определения и
Можно доказать, что функции abx+c, sin(ax+b), cos(ax+b) дифференцируемы любое число раз на 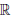
(abx+c)(n) = bnabx+c lnn a, (ebx+c)(n) = ebx+c bn,
(sin(ax + b))(n) = an sin (ax + b + n 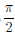
(cos(ax + b))(n) = an cos (ax + b + n 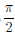
Теорема 4.7. Пусть функции 


(

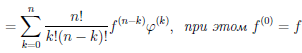
Последняя формула носит имя Лейбница и очень напоминает бином Ньютона. Только её и докажем, используя метод математической индукции. При n = 1 по утверждению 2) теоремы 4.4 имеем: 



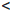

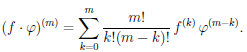
Так как функции 
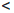




Пример №7
Используя формулу Лейбница, найдем n—ую производную функции f(x) = 2×2 sin2 x.
Так как 
Дифференциалы высших порядков
Пусть функция 
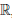
Зафиксируем число ∆x 

d





d2



Для сокращения записи, используются обозначения
(∆x)2 = ∆x2, (dx)2 = dx2.
Следовательно, второй дифференциал функции f в точке x0 вычисляется по формуле
d2



По условию функция 



d2

Индуктивно вводится понятие n-го дифференциала функции 
dk



В этой формуле ∆xk= (∆x)k. Аналогично предыдущему, в ней вместо ∆x можно использовать dx, сокращая в записи (dx)k до dxk.
Лемма 4.3. Дифференциалы второго и высших порядков, вообще говоря, не обладают свойством инвариантности формы.
Доказательство проведем для дифференциалов второго порядка. Пусть функция 
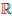






d2(f ◦ φ)(∆t) = d (d(

= d(

= (

Итак, функция 
d2(f ◦ φ)(∆t) = (f// ◦ φ) (dφ(∆t))2 + (
Сравнивая представление второго дифференциала функции 

Замечание. Если φ(t) = at + b, то формы дифференциалов высших порядков функции 

dn

dn(

В заключение приведем определение, которым воспользуемся в дальнейшем.
Определение 4.8. Функция 

Свойства функций, дифференцируемых на промежутках
Теорема 4.8 (Ферма). Пусть функция 


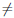
Для определенности будем считать, что функция 







где α(x) → 0 при x → c. По локальному свойству функции, имеющей в точке ◦
конечный, отличный от нуля, предел, найдется окрестность Uc ⊂ X , в которой функция 




Замечание 1. Если функция 

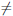

Замечание 2. Если функция 




Замечание 3. Геометрически теорема Ферма означает, что в точке (c, 

Теорема 4.9 (Дарбу). Если функция 


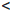


Для определенности будем считать, что 

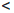

∃p ∈ [a, b] : 

Покажем, что p 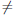

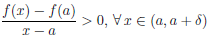
Но x-a > 0,∀x ∈(a, a+δ), поэтому 


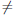

Аналогично доказывается, что p 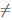

Следствие 1. Пусть функция 




Будем считать, что 
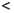




φ/(a) = 
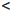

По теореме Дарбу есть такая точка γ ∈ (a, b), что φ,(γ) = 0, то есть
Следствие 2. Если функция 


Замечание 1. Теорема Дарбу имеет сходство с теоремой Больцано-Коши о промежуточном значении непрерывной функции, но не является ее следствием, поскольку функция f/ не обязательно непрерывна на отрезке [a, b].
Замечание 2. Не всякая функция, определенная на отрезке [a, b] может быть производной какой-либо функции. Например, функция sgn x является производной функции y = |x| на промежутках [—1, 0) и (0, 1], но нет функции, для которой она является производной на отрезке [—1, 1].
Теорема 4.10 (Ролля). Пусть функция 



По условию функция 




Если 



Если 
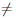


Следствие 1. Пусть функция 


Следствие 2. Если Pn (x) = 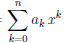
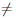
Пусть уравнение Pn(x) = 0 имеет не менее (n+ 1) различных корней 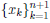
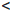
Тогда P/n(x) = 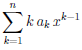
∃ bj ∈ (xj , xj+1), j = 1, . . . , n : P/n (bj) = 0,
то есть уравнение P/n (x) = 0 имеет не менее n различных корней. Продолжая дифференцирование уравнения, и применяя на каждом шаге теорему Ролля, получим, что для каждого m 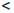
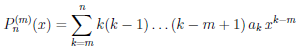
и уравнение Pn(m) (x) = 0 имеет не менее (n — m + 1) различных корней. В частности, при m = n уравнение Pn(n) (x) = 0 имеет не менее 1-го корня. Но, с другой стороны, Pn(n) (x) = n! an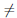
Из результата применения теоремы Ролля в начале доказательства этого
следствия сразу же следует ещё один результат.
Следствие 3. Если Pn(x)= 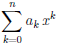
Замечание 1. Если для функции 
Замечание 2. Геометрически теорема Ролля означает следующее: если график непрерывной на отрезке [a, b] функции имеет в точках (x, 



Теорема 4.11 (Лагранжа). Пусть функция 



Для доказательства теоремы рассмотрим вспомогательную функцию
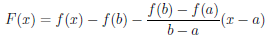
Функция F непрерывна на отрезке [a, b], дифференцируема на интервале (a, b) и F(a) = F (b). Применив к ней теорему Ролля 4.10, найдем точку c ∈ (a, b) такую, что F/ (c) = 0. Поскольку ∀x ∈ (a, b)
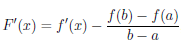
то 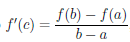
Следствие. Пусть функция 



Последнюю формулу обычно называют формулой Лагранжа конечных приращений. Она имеет место, так как на отрезке [x0,x] ⊂ [x0,x0 + δ) выполнены все условия теоремы Лагранжа и соответствующая точка cx имеет представление сχ = xo + 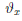
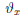
Аналогичные результаты имеют место и на промежутке (x0 — δ, x0].
Замечание 1. Формулу конечных приращений Лагранжа следует отличать от приближенного равенства



которое имеет место при условии дифференцируемости функции 



Замечание 2. Пусть график непрерывной на отрезке [a, b] функции в каждой точке (x, 



Замечание верно, так как 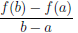



Теорема 4.12 (критерий монотонности функции). Пусть функция 


Пусть функция 
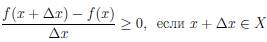
Поэтому 
Пусть 
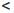



в котором c ∈ (x1, x2). Следовательно, 


Замечание. Аналогично можно доказать, что при выполнении условий теоремы 4.12 функция 

Теорема 4.13 (критерий постоянства функции). Пусть функция 


Если функция 

Пусть теперь 



Следовательно, 

Следствие 1. Пусть функция 




Следствие 2. Если на промежутке X функция 




Теорема 4.14 (Коши). Пусть функции 
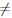
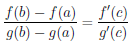
Последнюю формулу называют обобщенной формулой конечных приращений или формулой Коши.
Прежде всего заметим, что g (b) 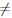
Рассмотрим вспомогательную функцию
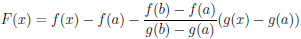
Функция F непрерывна на отрезке [a, b], дифференцируема на интервале (a, b) и F(a) = F (b). Применяя к F теорему Ролля 4.10 и имея в виду, что
делаем вывод, что существует точка c ∈ (a, b) такая, что F/ (c) = 0, то есть
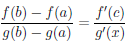
Замечание 1. Теорема Лагранжа 4.11 является частным случаем теоремы
Коши при g(x) = x.
Замечание 2. В формуле Коши конечных приращений не обязательно считать, что a 
Дифференцирование параметрически заданных функций
Пусть заданы две функции φ : T → X, ψ : T → Y. Будем считать, что функция x = φ(t) биективна. Поэтому определена обратная функция t =φ— 1(x), φ-1 : X → T ,а значит и суперпозиция 

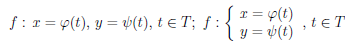
Переменную t называют параметром функции 
Теорема 4.15. Пусть T — промежуток и параметрически заданная функция 

1) функции φ и ψ дифференцируемы на T;
2) φ'(t) 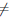
Тогда функция 

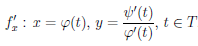
Так как функция φ удовлетворяет условиям 1) — 2), то по следствию 2 теоремы Дарбу (4.9) функция φ’ сохраняет знак на промежутке T. Поэтому, согласно следствию 1 теоремы 4.13, функция φ либо возрастает (если φ'(t) > 0 на T), либо убывает (если φ'(t) > 0 на T). Тогда по теореме 4.6 обратная функция φ-1 : X → T дифференцируема на промежутке X = φ(T) и
(φ- 1)'(x) = 1∕φ'(φ-1 (x)), ∀x ∈ X.
Поскольку функция ψ дифференцируема на X , то по теореме о дифференцируемости суперпозиции функция 
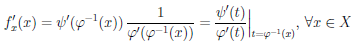
Последнее означает, что функция f/x является параметрически заданной
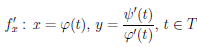
Правила Лопиталя раскрытия неопределенностей
Теорема 4.16. Пусть функции 
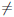
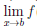
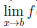
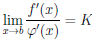
то существует предел
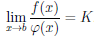
Рассмотрим два случая: b ∈ 
1) Пусть b ∈ 



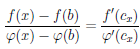
то есть
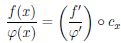
Поскольку 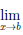
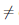
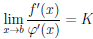
то по теореме 2.37 о пределе суперпозиции функций, условия которой выполнены, правая часть равенства (4.15) имеет предел при x → b и он равен K. Следовательно, существует предел левой части равенства (4.15) при x → b и он равен K .
2) Пусть теперь b = +∞. Без ограничения общности будем считать, что a > 0. По условиям теоремы функции 
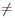
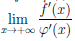

и
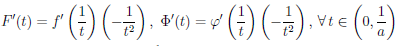
Кроме того, 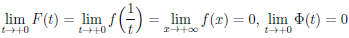
(снова воспользовались теоремой 2.37 о пределе суперпозиции функций).
В силу доказанной первой части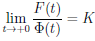
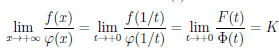
Теорема 4.17. Пусть функции 
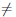
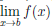
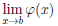
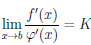
то существует предел
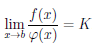
Мы опускаем доказательство этого утверждения, отсылая читателя к книгам [4, с. 318-320], [6, т.1, с. 280-284],[1, т.1, с. 256-260].
Совершенно аналогично формулируются и доказываются теоремы, аналогичные теоремам 4.16 и 4.17, когда 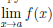
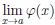
Замечание 1. Предел отношения функций 


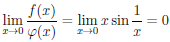
но не существует предела при x → 0 поскольку отношения производных этих функций, поскольку
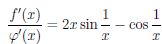
Замечание 2. Если выполнены условия теоремы 4.16 и функции 
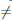
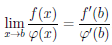
Замечание 3. Пусть функции 
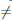
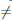
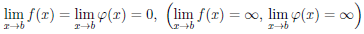
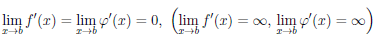
Если существует предел 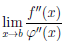
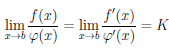
то есть правило Лопиталя можно применить повторно.
Формула Тейлора
Теорема 4.18 (формула Тейлора для многочлена). Пусть a — некоторое число, P — многочлен степени n (n ≥ 1). Тогда
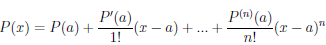
то есть многочлен P степени n однозначно определяется значениями многочлена и его производных P (a), P /(a),…,P (n)(a) в точке a.
Прежде всего заметим, что многочлен 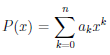
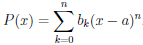
Для этого в многочлене P(x) = 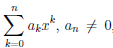
его производных в точке a.
Из равенства (4.16) следует, что P(a) = b0. Последовательно продифференцируем равенство (4.16) k раз (k = 1, . . . , n) и получим, что P(k) (x) =
k!bk + (k + 1)k … 2 bk+1(x — a) + ∙ ∙ ∙ + n(n — 1) … (n — k + 1)bn(x — a)n-k,
поэтому P(k) (a) = k!bk, то есть bk =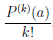
Пусть теперь функция 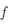
Многочлен 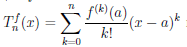
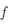
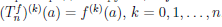
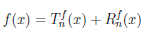
Если функция 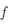
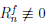
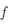
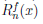
Теорема 4.19 (формула Тейлора с остаточным членом в форме Пеано). Пусть функция 

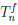
Из равенства (4.17) 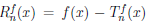
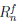
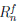
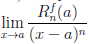
кратном его применении получим, что
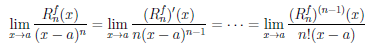
если последний предел существует. Поскольку функция (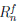
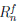
Следовательно, (n — 1)-кратное применение правила Лопиталя законно и при x → a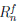
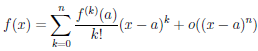
Полученное представление функции 
Замечание. Формула Тейлора с остаточным членом в форме Пеано является обобщением представлений для непрерывной и дифференцируемой в точке a функции.
Следствие. Пусть функции 


Так, например, для функций 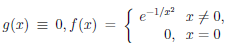
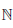

Теорема 4.20. Если выполнены условия теоремы 4.19 и существует многочлен Pn(x) такой, что 
Пусть 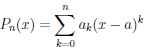
Следовательно,
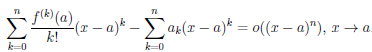
Переходя в этом равенстве к пределу при x → a, получим равенство


Последнее означает, что
Отсюда при x → a получим равенство 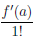
Продолжая этот процесс, по индукции получим, что
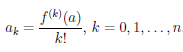
Поэтому многочлен Pn(x) является многочленом Тейлора 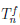

Замечание. Доказанная теорема означает, что никакой многочлен Pn(x) степени n, отличный от многочлена Тейлора 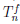

Применяя теорему 4.19 к элементарным функциям при a = 0, получим:
Вывод этих формул читатель может найти в [6, т.1, с. 192-195].
Пример №8
Пусть функция 
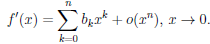
Найти локальную формулу Маклорена функции 
По теореме 4.20 из (4.18) следует, что (


После преобразования получим
В частности, если


Отсюда, учитывая, что arctg 0 = 0, получаем представление
Теорема 4.21. Пусть функция 
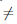
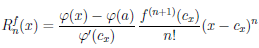
Фиксируем точку x ∈ (a, a + δ). Рассмотрим вспомогательную функцию
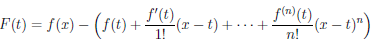
В силу условий теоремы, F ∈ C ([a, a + δ)), дифференцируема на интервале (a, a + δ) и ∀t ∈ (a, a + δ)
Применим к функциям F и φ на отрезке [a, х] теорему Коши 4.14 о конечных приращениях, получим, что существует точка cx ∈ (a, x) такая, что
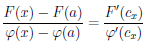
Поскольку F(x) = 0, а
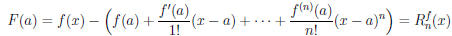
то соотношение (4.20) принимает вид
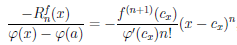
из которого и следует представление (4.19) остаточного члена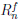
Следствие 1. Если функция 
Замечание. Формулу (4.21) называют формулой Тейлора с остаточным членом в форме Лагранжа. Чтобы её получить, достаточно положить в представлении (4.19) φ(t) = (х — t)n+1. Формула Тейлора с остаточным членом в форме Лагранжа является обобщением теоремы Лагранжа 4.11, которая получается из формулы Тейлора с остаточным членом в форме Лагранжа при n = 0.
Следствие 2. Если функция 
R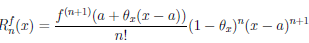
Замечание. Эта форма остаточного члена формулы Тейлора называется формой Коши. Чтобы её получить, достаточно положить в представлении (4.19) φ(t) = (x — t).
Завершая раздел, заметим, что все его результаты остаются в силе, если рассматривать функцию 
Исследование поведения функции на множестве
Экстремум функции
Определение 4.9. Пусть 
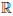

Ua ⊂ X и



Если функция 


Теорема 4.22 (необходимое условие локального экстремума). Если функция 


Утверждение следует непосредственно из теоремы Ферма (теоремы 4.8), примененной к окрестности Ua , указанной в определении экстремума.
Определение 4.10. Стационарными точками функции 

Заметим, что функция 

Теорема 4.23. Если функция 



Определение 4.11. Внутренняя точка множества X, в которой функция непрерывна, а ее производная либо равна нулю, либо бесконечности, либо не существует, называется критической точкой функции 
Например, точка x = 0 является критической точкой функций 









Теорема 4.24 (достаточное условие экстремума в критической точке). Пусть функция 




то a является точкой максимума функции, а если


то a — точка минимума функции. Если же функция 

Пусть 









Аналогично рассматриваются и два других случая.
Замечание. Условие изменения знака производной при переходе через точку a является достаточным условием локального экстремума, но не является необходимым. Для примера можно рассмотреть в окрестности точки x = 0
функцию 
Теорема 4.25 (достаточное условие экстремума в стационарной точке). Пусть a — стационарная точка функции 




Так как a — стационарная точка функции 

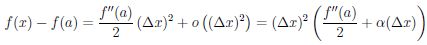
где α(∆x) — бесконечно малая функция при ∆x → 0. Пусть 
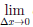
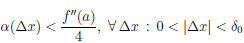
Но тогда для таких ∆x
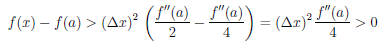
то есть функция 
Аналогично доказывается, что функция 

Замечание. Если 


Теорема 4.26. Пусть функция 




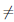
Тогда
a) если n — четное число, то a — точка локального экстремума 

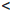

b) если n — нечетное число, то a не является точкой экстремума функции 
Используя формулу Тейлора с остаточным членом в форме Пеано и условие (4.22), получим, что
или
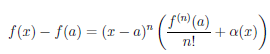
где α(x) → 0 при x → a. Учитывая, что 
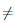
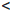
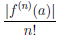
Поэтому в проколотой δ0-окрестности точки a
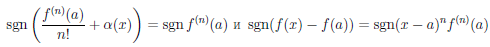
Если n — четное число, то для всех x ∈ (a — δ0, a + δ0) {a}
(x — a)n > 0 и sgn(


Если 





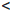





Замечание. Очевидно, что теорема 4.25 является следствием теоремы 4.26.
С задачей локального экстремума тесно связана задача о наибольшем и наименьшем значении непрерывной функции на промежутке. Для функции 



Если 
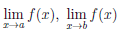
если такие пределы существуют (конечные или бесконечные). Точно также следует поступать и на промежутках [a, b) и (a, b].
В прикладных задачах при нахождении наибольшего (наименьшего) значения функции на промежутке X часто встречается ситуация, когда функция непрерывна на X и имеет на нем единственную критическую точку. Можно доказать, что, если x0 — точка локального максимума, то 



- Заказать решение задач по высшей математике
Пример №9
Исследовать на экстремум 
Функция 


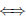
Таким образом, функция 
и теоремы 4.24 следует, что функция 

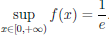
Направление выпуклости графика функции
Будем считать, что функция 


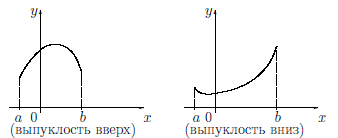
Определение 4.12. Говорят, что график функции 



Определение 4.13. Говорят, что график функции 



Теорема 4.27. Пусть функция 



Пусть f//(x) ≥ 0, ∀ x ∈ (a, b), и c — некоторая точка интервала (a, b). Уравнение касательной, проведенной к Γ




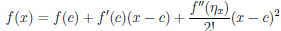
Поэтому 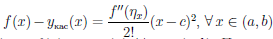



Следствие. Если функция 

Замечание 1. Если на интервале (a, b) 

Замечание 2. Из определений 4.12 и 4.13 следует, что если график Γ



Пример №10
Пусть 

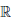

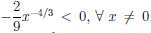
Точки перегиба
Определение 4.14. Пусть функция 


Теорема 4.28 (необходимое условие точки перегиба). Пусть c — точка перегиба функции 


Для простоты доказательства будем считать, что функция 

Предположим, что 
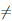







Замечание. Условие 

Как и при рассмотрении необходимых условий экстремума функции, можно показать, что точки перегиба непрерывной на интервале (a, b) функции 


Теорема 4.29 (1-ое достаточное условие перегиба). Пусть функция 




Пусть, например, на интервале (c — δ, c) 



Пример №11
Исследовать на перегиб функцию 
Функция 


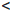




Теорема 4.30 (2-ое достаточное условие перегиба). Пусть функция 



Так как функция 

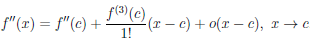
Но 
где α(x) → 0 при x → c, и, значит, найдется δ > 0 такое, что для всех x ∈
Следовательно, в 


Например, x = 0 — точка перегиба функции 


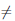
Асимптоты графика функции
Определение 4.15. Пусть функция 


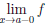
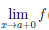
Пример №12
Пусть 



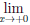


Пример №13
Пусть 

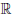



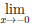


Определение 4.16. Пусть функция 
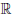


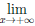

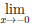

Если k = 0, то асимптоту называют горизонтальной.
Пример №14
Найти асимптоты функций
a) Функция 
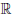
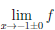
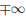

Так как 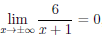
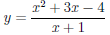
b) Функция непрерывна на 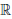
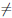
В силу формулы Тейлора с остаточным членом в форме Пеано
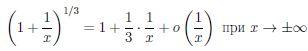
Следовательно, 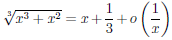
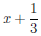
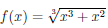
Теорема 4.31. Для того, чтобы прямая y = kx+b была наклонной асимптотой графика функции y = 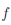
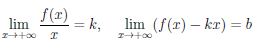
Необходимость. Если y = kx + b — асимптота Γ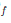

где α(x) → 0 при x → +∞. Разделим обе части полученного равенства на x и получим
откуда следует существование предела 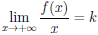

Поэтому
Достаточность. Если существуют конечные пределы, перечисленные в 4.23,
то 

Аналогично формулируется и доказывается критерий существования наклон
ной асимптоты графика Γ
Построение графика функции
Для построения графика функции y = 
- Найти область определения функции
, изучить функцию на четность (нечетность), периодичность.
- Исследовать функцию на непрерывность, указать точки разрыва, найти асимптоты.
- Найти
/(x), исследовать функцию на экстремум, указать промежутки монотонности.
- Найти
//(x), исследовать функцию на перегиб, указать промежутки выпуклости вверх (вниз) графика функции.
- Дать характеристику поведения функции на каждом из полученных промежутков.
- Нарисовать график.
Пример №15
Построить график функции
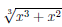
Решение:
1. D(
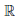
Функция не является периодической, так как обращается в нуль только в двух точках x = 0 и x = —1.
2. 


3. Для всех x ∈ (-∞, —1) S(—1, 0) S(0, +∞)
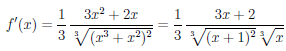
Так как
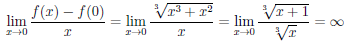
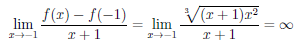
то функция имеет в точках x = —1 и x = 0 бесконечные производные, а значит Γ
Далее, 
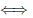
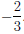
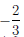

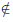
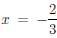
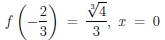
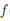
4. Так как




то 
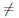


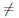
очка x = -1 — точка перегиба заданной функции.
Полученные результаты объединим в таблицу и нарисуем график:
Свойства дифференцируемых функций
Определение 12.1. Функция y=f(x) называется возрастающей в точке 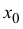
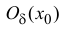
Аналогично определяется убывающая в точке 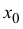
Точка 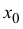
y=f(x), если 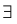
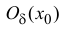
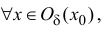
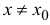
Точки локального максимума и минимума называются точками локального экстремума. Если знаки неравенств в соотношениях (12.1) нестрогие, то говорят о нестрогом локальном максимуме (минимуме).
Теорема 12.1. (теорема Ферма). Пусть функция y=f(x) определена в некоторой окрестности 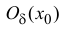
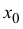
Доказательство
Равенство 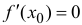
функции y=f(x) в точке 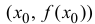
Теорема 12.2. Пусть функция y=f(x) дифференцируема в точке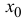
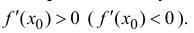
Доказательство
Докажем для случая 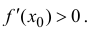
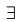
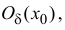
Если 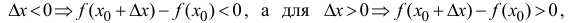
Теорема 12.3 (теорема Ролля). Пусть функция y=f(x):
1) непрерывна на отрезке 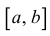
2) дифференцируема на интервале (a ,b );
3) f(a)=f(b).
Тогда
Доказательство
По теореме 11.1 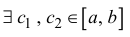
Если M = m, то f( x) – постоянная функция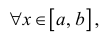
Если 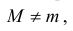
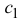
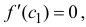
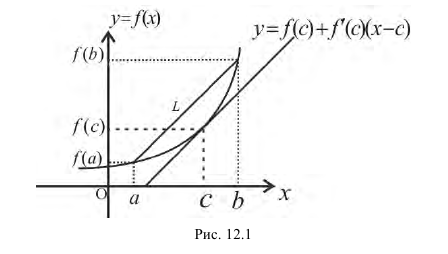
Теорема 12.4 (теорема Лагранжа).
Пусть функция y=f(x):
1) непрерывна на отрезке [a,b];
2) дифференцируема на интервале ( a,b ).
Тогда 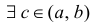
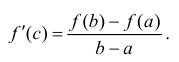
Доказательство
Рассмотрим функцию 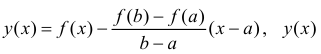
Поэтому y(x) удовлетворяет условиям теоремы 12.3, то есть 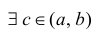
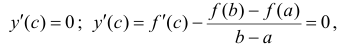
Угловой коэффициент прямой L, проходящей через точки 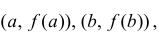
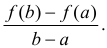
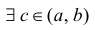
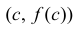
Если х задает время и y=f(x) – путь, пройденный телом при движении по прямой за время х, то 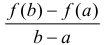
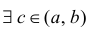
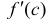
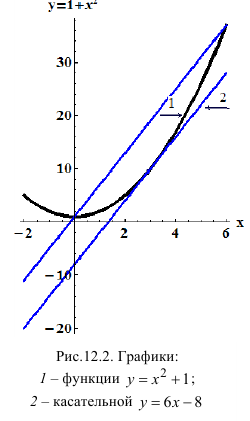
Пример №16
Дана кривая 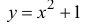
Решение:
Подставив точки А и В в формулу (12.4), получим
Уравнение касательной к кривой 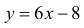
Теорема 12.5. (терема Коши). Пусть функции y=f(x) и y=g(x):
1) непрерывны на отрезке [a b];
2) дифференцируемы на интервале ( a,b ), причем 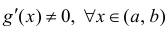
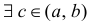
Доказательство
Рассмотрим функцию
y(x) удовлетворяет условиям теоремы 12.3, и далее доказательство аналогично доказательству теоремы 12.4.
- Техника дифференцирования
- Дифференциальная геометрия
- Логарифмическая функция, её свойства и график
- Логарифмические выражения
- Применение производной к исследованию функции
- Приложения производной
- Производные высших порядков
- Дифференциал функции
(схема 30)
При дифференцировании различают функции по способу их задания: явные, неявные и параметрические.
Пусть явно задана функция y=f (x). Функция,
зависящая непосредственно от переменной x, называется
простой.
Рассмотрим для простой функции точку x, принадлежащую ее области определения. Дадим
приращение аргументу ∆x в точке x. Функция
получит при этом соответствующее (3.9) приращение ∆y=f(x+∆x)—f(x).
Производной функции y=f (x) по переменной x в некоторой точке называется предел отношения
приращения функции к приращению аргумента, когда
последнее стремится к нулю, то есть

Функция, имеющая в точке конечную производную,
называется дифференцируемой в этой точке. Процесс нахождения производной называется
дифференцированием и обозначается 
Производная
характеризует скорость изменения функции в достаточно малой окрестности заданной
точки.
Приведем таблицу производных основных элементарных
функций (без доказательства), которые рассматриваются нами как функции простые
и явно заданные.
Теорема 3.9. Если функция
дифференцируема в некоторой точке, то она в этой точке непрерывна
Следствие. В точках разрыва функция производной не имеет
Существуют такие точки, в которых функция непрерывна,
но не дифференцируема. Так, функция y=|x| в точке x=0 непрерывна, но производной не имеет, так как в этой
точке к графику функции можно провести бесконечное множество
касательных (рис. 3.6). Такие точки называются угловыми или точками излома функции. Данный случай показывает, что обратное утверждение к
теореме 3.9 неверно.
Среди явных
функций особое место занимают обратные функции, производная
которых находится с помощью следующей теоремы.
Теорема 3.10. Если
строго монотонная функция y=f (x) дифференцируема на некотором интервале Х, причем ее производная не
обращается в нуль на Х, то обратная к ней функция x=φ(y) также
дифференцируема на этом интервале, при этом:

Доказательство. Дадим функции
y=f (x) в точке x бесконечно малое приращение аргумента ∆x→0, функция при этом получит соответствующее приращение
∆y. Так как по условию теоремы функция
дифференцируема в каждой точке интервала Х, то в каждой точке этого
интервала функция непрерывна (по теореме 3.9). Следовательно, по определению
непрерывности функции выполняется: 
при ∆x→0; ∆y→0.
По
определению производной можно записать:

Среди явных функций выделяют класс сложных функций.
Функция называется
сложной, если она представляет собой композицию нескольких функций: y=f (φ(x)). Функция f называется внешней, а φ — внутренней функцией, выступающей в качестве
независимого переменного.
Теорема 3.11.
Чтобы
продифференцировать сложную
функцию необходимо сначала продифференцировать внешнюю функцию по внутренней,
считая внутреннюю функцию независимой переменной, затем
продифференцировать внутреннюю функцию по независимому переменному и результаты
дифференцирования перемножить, то есть

Пример 3.8. Найти
производную функции .
Решение. Согласно формуле (3.31) и с учетом табли
(3.17), (3.19), (3.29) имеем:

К явным функциям можно отнести функции, заданные
параметрически, вида:
где t –
параметр. Производную такой функции несложно получить:

Пример 3.9. Найти
производную функции 
Решение. Согласно
формуле (3.32) и с учетом табличных формул (3.18), (3.19) имеем:
Примечание. Функция,
заданная в примере 3.9, представляет собой параметрическое уравнение окружности
радиуса a. Действительно, возведем оба уравнения в квадрат и сложим
их почленно, получим:

Помимо таблицы производных
имеют место правила дифференцирования.
Теорема 3.12. Производная суммы двух дифференцируемых функций равна сумме
производных этих функций:

Данная теорема может быть обобщена для произвольного
конечного числа функций-слагаемых.
Пример 3.10.
Найти производную функции
Решение. Согласно
формулам (3.33) и (3.31) и с учетом табличных формул (3.17), (3.20), (3.23) имеем:

Теорема 3.13. Производная произведения двух дифференцируемых функций равна
произведению производной первой функции-сомножителя на вторую функцию плюс
произведение первой функции на производную
второй функции–сомножителя, то есть

Пример 3.11.
Найти производную функции 
Решение. Согласно формуле (3.34) и с учетом табличных формул
(3.22), (3.24) имеем:
Теорема 3.14.
Производная частного двух функций
равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а
числитель есть разность между
произведением знаменателя на производную числителя и произведением
числителя на производную знаменателя, то есть

Пример 3.12.
Найти производную функции
Решение. Согласно формуле (3.35) и с учетом табличных формул
(3.17), (3.29) имеем:

Все рассмотренные выше при дифференцировании функции
были заданы в явном виде, то есть уравнением y=f (x),
разрешенным относительно y.
Функция называется неявно заданной, если она
имеет вид F (x;y)=0.
Неявный способ задания к свойствам функции отношения не имеет. В этом случае
любое выражение, содержащее переменную y, нужно
рассматривать как функцию сложную. Следовательно, при нахождении производной неявных функций следует применять теорему о
дифференцировании сложной функции. В процессе отыскания 
содержащие 

множитель. Слагаемые, не содержащие 
относительно искомой 
Пример 3.13.
Найти производную неявной
функции 
Решение. Согласно формуле (3.31) дифференцирования сложной функции и (3.34) производной
произведения, с учетом табличных формул (3.17) и (3.18)
имеем:
Иногда для упрощения процесса дифференцирования
громоздких функций применяют их предварительное логарифмирование (логарифмическое
дифференцирование). Данный метод целесообразен в тех случаях, когда
функция представляет собой произведение и (или) частное различных функций,
таких как показательные и степенные выражения (особенно иррациональные).
Логарифмическое дифференцирование используется также для нахождения производных
показательно-степенных функций, которые без предварительного логарифмирования
вообще не дифференцируются. При использовании данного метода в левой части получают производную от натурального
логарифма y, которая равна 
условию функцию.
Пример 3.14.
Найти производную функции 
Решение.
Прологарифмируем заданную функцию 
По свойству логарифма степени имеем:
(3.31) дифференцирования сложной функции
и (3.34) производной произведения, с учетом табличных формул (3.19) и (3.29)
можно записать

После умножения обеих частей последнего равенства на y
окончательно получим:
производную заданной функции найти невозможно, так как нельзя обосновать
использование формул дифференцирования (3.17) или (3.22)
Пусть функция y=f (x)
дифференцируема в некоторой текущей точке x и при этом 
записать: 

Дифференциалом функции y=f (x) в точке x называется главная часть приращения этой
функции, равная произведению производной функции на приращение аргумента:

Найдем дифференциал независимой переменной x, то есть
дифференциал функции y=x. Так
как 
функции может быть записана в виде:

Если в формуле
(3.36) отбросить бесконечно малую величину α∙∆x, то
получим приближенное равенство


(3.39)
Формула (3.39) применяется для вычисления приближенных
значений функций.
Пример
3.15. Вычислить приближенно значение 
Решение.
Рассмотрим функцию 
имеем:

Так как x+∆x=0,95, то при x=1 и ∆x=-0,05
получаем:
Процесс дифференцирования может быть многократным. Производная от первой
производной называется второй производной функции или производной 2-го порядка.
Производная от последней, в свою очередь, является производной 3-го порядка и
так далее. Производная функции n-го порядка 
порядка заданной функции, то есть

- Формулы дифференцирования
- Производная суммы двух функций
- Производная функции с постоянным множителем
- Производная произведения двух функций
- Производная частного двух функций
- Производная степенной функции
- Примеры
п.1. Формулы дифференцирования
Нахождение производной называют дифференцированием.
Функция, которая имеет производную в точке (x_0), называется дифференцируемой в этой точке.
Функция, дифференцируемая в каждой точке некоторого промежутка, называется дифференцируемой на этом промежутке.
В примере 2 §42 данного справочника мы получили формулы производных для простейших функций. Обобщим их в таблице:
begin{gather*} C’=0\ x’=1\ (x^2) ‘=2x\ (x^3) ‘=3x^2\ left(frac1xright) ‘=-frac{1}{x^2}\ (kx+b) ‘=k\ (sqrt{x}) ‘=frac{1}{2sqrt{x}} end{gather*}
Теперь не нужно каждый раз использовать определение производной для поиска её уравнения или значения в данной точке. Достаточно помнить таблицу производных.
Например:
Найдем (f'(1)), если (f(x)=x^2)
По таблице производных (f'(x)=(x^2) ‘=2x). Поэтому (f'(1)=2cdot 1=2)
п.2. Производная суммы двух функций
Рассмотрим функцию (h(x)), которую можно представить в виде суммы двух других функций: (h(x)=f(x)+g(x)). Найдем её производную из общего алгоритма.
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции (h(x)): begin{gather*} triangle h=h(x+triangle x)-h(x)=(f(x+triangle x)+g(x+triangle x))-(f(x)+g(x))=\ =(f(x+triangle x)-f(x))+(g(x+triangle x)-g(x))=triangle f+triangle g end{gather*} где (triangle f) и (triangle g) — приращения каждой из функций-слагаемых.
Ищем производную: begin{gather*} h'(x)=lim_{triangle xrightarrow 0}frac{triangle h}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle f+triangle g}{triangle x}= lim_{triangle xrightarrow 0}frac{triangle f}{triangle x}+lim_{triangle xrightarrow 0}frac{triangle g}{triangle x}=f'(x)+g'(x) end{gather*} Или: (left(f(x)+g(x)right)’=f'(x)+g'(x))
Производная суммы двух функций равна сумме производных: $$ left(f(x)+g(x)right)’=f'(x)+g'(x) $$
Например:
(left(x^2+frac1xright)’=(x^2)’+left(frac1xright)’=2x-frac{1}{x^2})
п.3. Производная функции с постоянным множителем
Рассмотрим функцию (h(x)=kcdot f(x)), где k – некоторый действительный постоянный множитель. Найдем её производную из общего алгоритма.
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции (h(x)): begin{gather*} triangle h=h(x+triangle x)-h(x)=kcdot f(x+triangle x)-kcdot f(x)=kcdot (f(x+triangle x)-f(x))=kcdot triangle f end{gather*} где (triangle f) — функции (f(x)).
Ищем производную: begin{gather*} h'(x)=lim_{triangle xrightarrow 0}frac{triangle h}{triangle x}=lim_{triangle xrightarrow 0}frac{kcdot triangle f}{triangle x}=klim_{triangle xrightarrow 0}frac{triangle f}{triangle x}=kf'(x) end{gather*} Или: (left(kcdot f(x)right)’=kcdot f'(x))
Постоянный множитель можно вынести за знак производной: $$ left(kcdot f(x)right)’=kcdot f'(x) $$
Например:
((5x^3)’=5cdot (x^3)’=5cdot 3x^2=15x^2)
п.4. Производная произведения двух функций
Рассмотрим функцию (h(x)), которую можно представить в виде произведения двух других функций: (h(x)=f(x)cdot g(x)). Найдем её производную из общего алгоритма.
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции (h(x)): begin{gather*} triangle h=h(x+triangle x)-h(x)=(f(x+triangle x)cdot g(x+triangle x))-(f(x)cdot g(x)) end{gather*} Приращения каждого из множителей: begin{gather*} triangle f=f(x+triangle x)-f(x)Rightarrow f(x+triangle x)=triangle f+f(x)\ triangle g=g(x+triangle x)-g(x)Rightarrow g(x+triangle x)=triangle g+g(x) end{gather*} Подставим: begin{gather*} triangle h=(triangle f+f(x))cdot (triangle g+g(x))-f(x)cdot g(x)=\ =triangle fcdot triangle g+triangle fcdot g(x)+f(x)cdot triangle g+f(x)cdot g(x)-f(x)cdot g(x)=\ =triangle fcdot triangle g+triangle fcdot g(x)+f(x)cdot triangle g end{gather*} Ищем производную: begin{gather*} h'(x)=lim_{triangle xrightarrow 0}frac{triangle h}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle fcdot triangle g+triangle fcdot g(x)+f(x)cdottriangle g}{triangle x}=\ =lim_{triangle xrightarrow 0}left(frac{triangle f}{triangle x}cdotfrac{triangle g}{triangle x}right)+lim_{triangle xrightarrow 0}frac{triangle f}{triangle x}cdot g(x)+f(x)cdotlim_{triangle xrightarrow 0}frac{triangle g}{triangle x}=\ =f'(x)cdot g'(x)cdot 0+f'(x)cdot g(x)+f(x)cdot g'(x)=f'(x)cdot g(x)+f(x)cdot g'(x) end{gather*} Или: (left(f(x)cdot g(x)right)’=f'(x)cdot g(x)+f(x)cdot g'(x))
Производная произведения двух функций равна сумме двух слагаемых:
производная первой функции на вторую плюс первая функция на производную второй: $$ left(f(x)cdot g(x)right)’=f'(x)cdot g(x)+f(x)cdot g'(x) $$
Например:
( (x^2sqrt{x})’=(x^2)’cdotsqrt{x}+x^2cdot (sqrt{x})’=2xsqrt{x}+frac{x^2}{2sqrt{x}}=xsqrt{x}left(2+frac12right)=frac52xsqrt{x} )
п.5. Производная частного двух функций
Рассмотрим функцию (h(x)), которую можно представить в виде частного двух других функций: (h(x)=frac{f(x)}{g(x)}). Найдем её производную из общего алгоритма.
Пусть (triangle x) — некоторое приращение аргумента. Тогда приращение функции (h(x)): begin{gather*} triangle h=h(x+triangle x)-h(x)=frac{f(x+triangle x)}{g(x+triangle x)}-frac{f(x)}{g(x)} end{gather*} Приращения каждого из множителей: begin{gather*} triangle f=f(x+triangle x)-f(x)Rightarrow f(x+triangle x)=triangle f+f(x)\ triangle g=g(x+triangle x)-g(x)Rightarrow g(x+triangle x)=triangle g+g(x) end{gather*} Подставим: begin{gather*} triangle h=frac{triangle f+f(x)}{triangle g+g(x)}-frac{f(x)}{g(x)}=frac{triangle fcdot g(x)+f(x)cdot g(x)-f(x)cdot triangle g-f(x)cdot g(x)}{left(triangle g+g(x)right)cdot g(x)}=\ =frac{triangle fcdot g(x)-f(x)cdot triangle g}{left(triangle g+g(x)right)cdot g(x)}=frac{triangle fcdot g(x)-f(x)cdot triangle g}{g(x+triangle x)cdot g(x)} end{gather*} Ищем производную: begin{gather*} h'(x)=lim_{triangle xrightarrow 0}frac{triangle h}{triangle x}=lim_{triangle xrightarrow 0}frac{triangle fcdot g(x)-f(x)cdot triangle g}{triangle xcdot g(x+triangle x)cdot g(x)}=\ =frac{lim_{triangle xrightarrow 0}left(frac{triangle f}{triangle x}cdot g(x)right)-lim_{triangle xrightarrow 0}left(f(x)cdotfrac{triangle g}{triangle x}right)}{g(x+0)cdot g(x)}=frac{f'(x)cdot g(x)-f(x)cdot g'(x)}{g^2(x)} end{gather*} Или: ( left(frac{f(x)}{g(x)}right)’=frac{f'(x)cdot g(x)-f(x)cdot g'(x)}{g^2(x)} )
Производная частного двух функций равна дроби:
в числителе производная первой функции на вторую минус первая функция на производную второй, в знаменателе – квадрат второй функции: $$ left(frac{f(x)}{g(x)}right)’=frac{f'(x)cdot g(x)-f(x)cdot g'(x)}{g^2(x)} $$
Например:
begin{gather*} left(frac{3x+2}{x^2}right)’=frac{(3x+2)’cdot x^2-(3x+2)cdot (x^2)’}{(x^2)^2}=frac{3x^2-(3x+2)cdot 2x}{x^4}=\ =frac{3x^2-6x^2-4x}{x^4}=frac{-3x^2-4x}{x^4}=-frac{x(3x+4)}{x^4}=-frac{3x+4}{x^3} end{gather*}
п.6. Производная степенной функции
Из определения производной мы уже получили производные для квадрата и куба от x: $$ (x^2)’=2x, (x^3)’=3x^2 $$ Пользуясь свойством производной произведения, найдем производные для 4-й и 5-й степени от x: begin{gather*} (x^4)’=(xcdot x^3)’=(x)’cdot x^3+xcdot (x^3)’=1cdot x^3+xcdot 3x^2=4x^3\ (x^5)’=(xcdot x^4)’=(x)’cdot x^4+xcdot (x^4)’=1cdot x^4+xcdot 4x^3=5x^4 end{gather*} Мы видим закономерность, на основании которой можем предположить, что для любой целой степени: $$ (x^n)’=nx^{n-1} $$ Докажем это утверждения с помощью математической индукции (см. §25 справочника для 9 класса).
1) для базы индукции (n=1) производная ((x^1 )’=1cdot x^0=1) – верно
2) допустим, что при некотором n производная ((x^n)’=nx^{n-1}). Найдем ((x^{n+1})’): begin{gather*} (x^{n+1})’=(xcdot x^n)’=(x)’cdot x^n+xcdot (x^n)’=1cdot x^n+xcdot nx^{n-1}=\ =x^n(1+n)=(n+1)x^n end{gather*} т.е. для (x^{n+1}) формула также справедлива. Индуктивный переход выполняется.
Следовательно, по принципу математической индукции производная степенной функции ((x^n)’=nx^{n-1}, forall ninmathbb{N}). Что и требовалось доказать.
Производная степенной функции равна произведению показателя степени на основание в степени на 1 меньше: $$ (x^n)’=nx^{n-1} $$
Например:
begin{gather*} (x^{11})’=11x^{10} end{gather*} В §46 данного справочника будет показано, что выведенная формула справедлива также не только для натуральной, но и для любой действительной степени числа x.
п.7. Примеры
Пример 1. Найдите производную функции:
a) ( f(x)=3x^3-11 ) begin{gather*} f'(x)=(3x^3-11)’=3(x^3)’-(11)’=3cdot 3x^2-0=9x^2 end{gather*}
б) ( f(x)=x^2(1-x^5) ) begin{gather*} f'(x)=(x^2-x^7)’=(x^2)’-(x^7)’=2x-7x^6=x(2-7x^5) end{gather*}
в) ( f(x)=3x^2+5sqrt{x} ) begin{gather*} f'(x)=(3x^2+5sqrt{x})’=3(x^2)’+5(sqrt{x})’=3cdot 2x+frac{5}{2sqrt{x}}=6x+frac{5}{2sqrt{x}} end{gather*}
г) ( f(x)=frac{x+11}{x^3} ) begin{gather*} f'(x)=left(frac{x+11}{x^3}right)’=frac{(x+11)’cdot x^3-(x+11)cdot (x^3)’}{(x^3)^2}=frac{1cdot x^3-2x^2(x+11)}{x^6}=\ =frac{x^3-2x^3-22x^2}{x^6}=frac{-x^3-22x^2}{x^6}=-frac{x^2(x+22)}{x^6}=-frac{x+22}{x^4} end{gather*}
Пример 2. Найдите значение производной в точке (x_0), если:
a) ( f(x)=frac2x, x_0=4 ) begin{gather*} f'(x)=2cdotleft(frac1xright)’=2cdotleft(-frac{1}{x^2}right)=-frac{2}{x^2}\ f'(4)=-frac{2}{4^2}=-frac18 end{gather*}
б) ( f(x)=frac{x+2}{x}, x_0=1 ) begin{gather*} f'(x)=frac{(x+2)’x-(x+2)cdot x’}{x^2}=frac{1cdot x-(x+2)cdot 1}{x^2}=frac{x-x-2}{x^2}=-frac{2}{x^2}\ f'(x)=-frac{2}{1^2}=-2 end{gather*}
в) ( f(x)=frac{sqrt{x}}{x+1}, x_0=1 ) begin{gather*} f'(x)=frac{(sqrt{x})’cdot (x+1)-(sqrt{x})cdot(x+1)’}{(x+1)^2}=frac{frac{x+1}{2sqrt{x}}-sqrt{x}cdot 1}{(x+1)^2}=frac{x+1-2sqrt{x}cdotsqrt{x}cdot 1}{2sqrt{x}(x+1)^2}=\ =frac{x+1-2x}{2sqrt{x}(x_1)^2}=frac{1-x}{2sqrt{x}(x+1)^2}\ f'(4)=frac{1-1}{2cdot 1cdot 2^2}=0 end{gather*}
г) ( f(x)=frac{x^3}{5-x}, x_0=7 ) begin{gather*} f'(x)=frac{(x^3)’cdot (5-x)-x^3cdot (5-x)’}{(5-x)^2}=frac{3x^2cdot (5-x)-x^3cdot (-1)}{(5-x)^2}=\ =frac{15x^2-3x^3+x^3}{(5-x)^2}=frac{15x^2-2x^3}{(5-x)^2}=frac{x^2(15-2x)}{(5-x)^2}\ f'(7)=frac{7^2(15-2cdot 7)}{(5-7)^2}=frac{49}{4}=12frac14 end{gather*}
Пример 3. Решите уравнение (f'(x)=0), если:
a) ( f(x)=x-12x^3 ) begin{gather*} f'(x)=x’-12(x^3)’=1-12cdot 3x^2=1-36x^2 end{gather*} Уравнение: begin{gather*} 1-36x^2=0Rightarrow x^2=frac{1}{36}Rightarrow x=pmsqrt{frac{1}{36}}=pmfrac16 end{gather*} Ответ: (left{pmfrac16right})
б) ( f(x)=-frac25x^5+frac13x^3+12 ) begin{gather*} f'(x)=-frac25cdot 5x^4+frac13cdot 3x^2+0=-2x^4+x^2=x^2(1-2x^2) end{gather*} Уравнение: begin{gather*} x^2(1-2x^2)=0Rightarrow left[ begin{array}{l} x=0\ 1-2x^2=0 end{array} right. Rightarrow left[ begin{array}{l} x=0\ x^2=frac12 end{array} right. Rightarrow left[ begin{array}{l} x=0\ x=pmfrac{1}{sqrt{2}} end{array} right. end{gather*} Ответ: (left{0;pmfrac{1}{sqrt{2}}right})
Под термином дифференцирование могут подразумевать различные научные понятия:
- Дифференцирование в математическом анализе — операция взятия полной или частной производной функции.
- Дифференцирование в алгебре — линейное отображение, удовлетворяющее тождеству Лейбница; алгебраическая операция, обобщающая формальные свойства различных определений производных. Изучением дифференцирований и их свойств занимается дифференциальная алгебра.
- Дифференцирование клеток в биологии — формирование специализированного фенотипа при делении клеток в ходе морфогенеза.
Определение производной
Пусть на некотором промежутке X определена функция 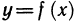
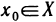
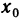
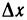
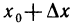
Определение. Производной функции y=f(x) в точке 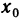
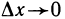
Для обозначения производной функции y=f(x) в точке 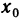
Итак, по определению,
Если для некоторого значения 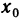
то говорят, что в точке 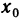
Из определения производной вытекает и способ ее вычисления.
Пример:
Найти производную функции 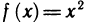
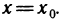
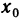
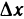
Составим отношение 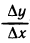
Найдем предел этого отношения при 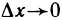
Следовательно, производная функции 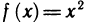
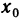
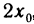
Геометрический смысл производной
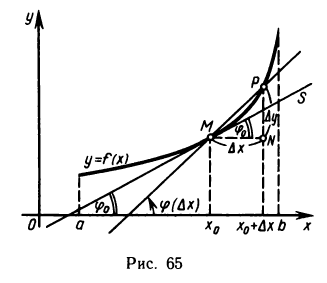
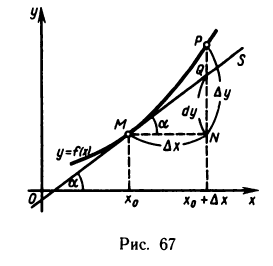
Пусть функция y=f(x) определена на интервале (а, b) и пусть точка М на графике функции соответствует значению аргумента 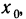
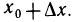
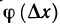
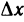
Если существует 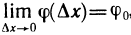
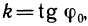
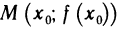
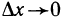
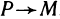
Определение:
Касательной S к графику функции y=f(x) точке М будем называть предельное положение секущей MP, что то же, при 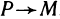
Из определения следует, что для существования касательной, достаточно, чтобы существовал предел 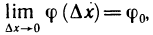
Докажем, что если функция у=f(х) имеет в точке 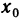
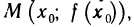
Действительно, из треугольника MNP получаем, что 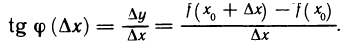
Отсюда
Перейдем в равенстве (1) к пределу при 
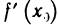
Отсюда и из непрерывности функции 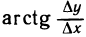
Следовательно, существует предел и левой части равенства (1). Таким образом, получаем
Но это и означает, что существует предельное положение секущей MP, т. e. существует касательная к графику функции y=f(x) в точке 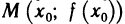
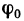
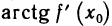
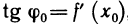
Итак, производная функции y = f(x) в точке 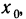
Физический смысл производной
Предположим, что функция y=f(x) описывает закон движения материальной точки М по прямой линии, т. е. y=f(х) — путь, пройденный точкой М от начала отсчета за время х.
Тогда за время 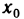
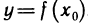
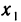
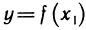
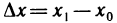
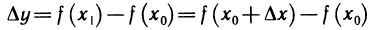
Отношение 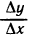
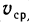
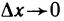
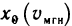
Понятие скорости, заимствованное из физики, удобно при исследовании поведения произвольной функции. Какую бы зависимость ни отражала функция y=f(x), отношение 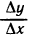
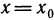
Значение производной состоит в том, что при изучении любых процессов и явлений природы с ее помощью можно оценить скорость изменения связанных между собой величин.
Правая и левая производные
Используя понятие правого и левого предела функции, введем понятия правой и левой произ-в0дных функции у=f(х) в точке 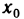
Определение:
Правой (левой) производной функции y=f(x) в точке 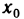
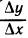
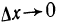
Если функция f(х) имеет в точке 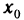
Вместе с тем существуют функции, имеющие в данной точке 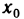
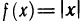
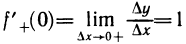
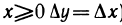
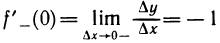
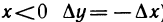
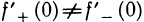
Установим связь между дифференцируемостью функции в точке и существованием производной в той же точке.
Теорема:
Для того чтобы функция y=f(x) была дифференцируема в точке 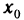
Доказательство:
Необходимость. Пусть функция у=f(х) дифференцируема в точке 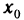
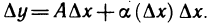
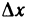
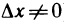
Переходя к пределу при 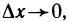
Дх—О Лх Лх-0
Отсюда следует, что производная в точке 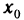
Достаточность. Пусть существует конечная производная 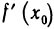
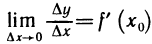
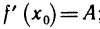
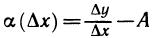
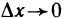
где 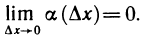
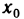
Таким образом, для функций одной переменной дифференци-руемость и существование производной — понятия равносильные. Поэтому операцию нахождения производной часто называют дифференцированием.
Замечание. Введенная при доказательстве достаточности функция 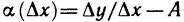
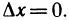
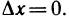
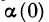
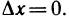
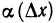
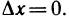
Связь между понятиями дифференцируемости и непрерывности
Теорема:
Если функция у=f(х) дифференцируема в данной точке 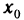
Доказательство. Так как функция у=f(х) дифференцируема в точке 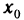
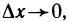
что и означает непрерывность функции y=f(x) в точке 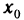
Замечание:
Обратное утверждение неверно. Функция может быть непрерывной в точке, но не быть дифференцируемой, т. е. не иметь производной в этой точке.
Примером такой функции служит функция 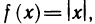
Если функция f(х) имеет производную в каждой точке некоторого промежутка (дифференцируема в каждой точке этого промежутка), то будем говорить, что функция f(х) дифференцируема на указанном промежутке.
Определение и геометрический смысл дифференциала
Пусть функция y=f(x) дифференцируема в точке 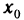
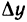
где 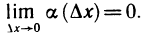
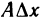
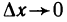
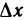
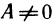
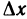
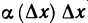
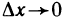
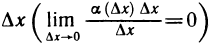
Таким образом, первое слагаемое (при 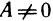
Определение:
Дифференциалом функции y=f(x) в точке 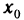
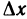
Если 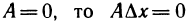
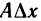
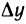
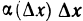
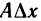
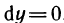
Принимая во внимание теорему 5.1, т. е. учитывая, что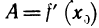
Пусть f(х)=х. Тогда по формуле (2)
Дифференциалом независимой переменной х назовем приращение этой переменной 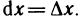
Заметим, что с помощью равенства (3) производную 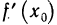
Дифференциал функции имеет геометрический смысл. Пусть точка М на графике функции y=f(x) соответствует значению аргумента 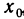
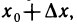
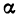
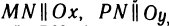
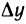
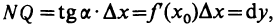
Таким образом, дифференциал dy функции y=f(x) в точке 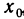
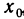
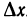
Приближенные вычисления с помощью дифференциала
Из определения дифференциала следует, что он зависит линейно от 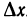
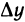
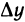
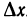
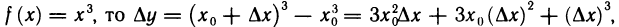
Во многих задачах приращение функции в данной точке приближенно заменяют дифференциалом функции в этой точке:
Абсолютная погрешность при такой замене равна 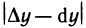
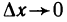
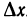
Пример:
Покажем, что если 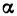
Решение. Рассмотрим функцию 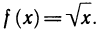
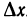
откуда, положив 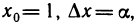
В частности,
Установим теперь правила дифференцирования и вычисления производных простейших элементарных функций. Заметим только, что при выводе формул и практическом вычислении производных обычно пишут не 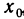
Правила дифференцирования суммы, разности, произведения и частного
Теорема:
Если функции 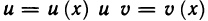
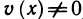
Доказательство:
Для вывода формул (1) воспользуемся определением производной, равенством 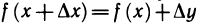
так как 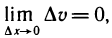
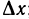
Вычисление производных постоянной, степенной, тригонометрических функций и логарифмической функции
Производная постоянной функции
Производная функции y=f(x)=C, где С — постоянное число, выражается формулой
Доказательство. Для любых 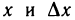
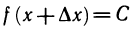
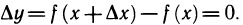
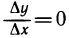
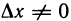
Производная степенной функции
Производная функции 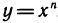
Доказательство:
Используя формулу бинома Ньютона, можно записать:
Таким образом, при 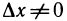
Так как
Замечание:
Случай степенной функции, показатель которой является любым вещественным числом, рассмотрен в п. 2, § 9.
Производные тригонометрических функций
1) Производная функции y = sinx выражается формулой
Доказательство:
Имеем
Таким образом, при
Так как 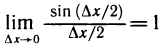
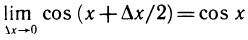
2) Производная функции у=cos х выражается формулой
Доказательство:
Имеем
Таким образом, при 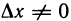
Так как 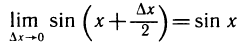
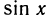
3) Производная функции 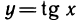
Доказательство:
Так как 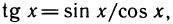
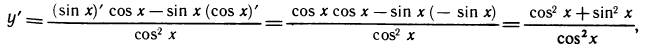
4) Производная функции y=ctgx выражается формулой
Доказательство:
Так как 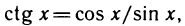
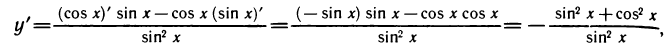
Производная логарифмической функции
Производная функции 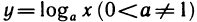
Доказательство:
Имеем
Таким образом, при
Полагая 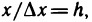
(второй замечательный предел), а так как логарифмическая функция является непрерывной, то
Следствие:
Если
Теорема о производной обратной функции
Пусть функция y=f(х) удовлетворяет условиям теоремы 4.15 об обратной функции и функция 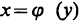
Теорема:
Если функция y=f(x) имеет в точке 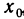
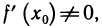
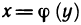
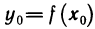
Доказательство:
Дадим аргументу у обратной функции 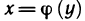
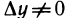
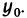
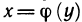
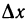
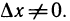
Перейдем в этом равенстве к пределу при 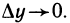
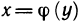
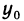
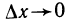
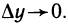
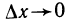
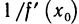
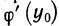
Доказанная теорема имеет простой геометрический смысл. Рассмотрим в некоторой окрестности точки 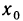
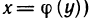
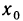
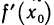
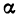
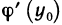
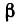
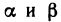
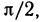
Вычисление производных показательной функции и обратных тригонометрических функций
Используя доказанную выше теорему 5.4, продолжим вычисление производных простейших элементарных функций.
Производная показательной функции
Производная функции 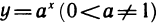
Доказательство:
Показательная функция 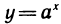
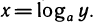
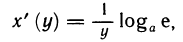
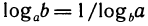
Следствие:
Если 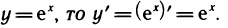
Производные обратных тригонометрических функций
1) Производная функции 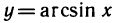
Доказательство:
Функция у=arcsin x является обратной для функции x=sin х. Так как 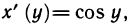
Корень взят со знаком плюс, так как cos у положителен на интервале 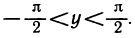
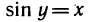
2) Производная функции 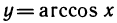
Доказательство аналогично предыдущему.
3) Производная функции 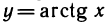
Доказательство. Функция 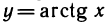
Так как 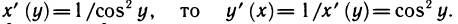
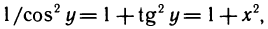
4) Производная функции 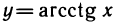
Доказательство аналогично предыдущему.
Правило дифференцирования сложной функции
Теорема:
Если функция 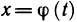
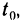
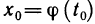
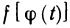
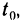
Доказательство:
Так как функция y=f(x) дифференцируема в точке 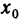
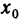
где 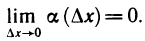
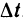
Равенство (3) справедливо при любых достаточно малых 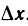
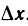
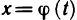
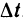
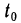
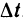
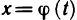
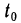
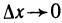
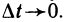
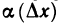
В силу соотношения (4) существует предел правой части равенства (3) при 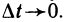
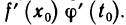
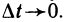
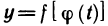
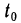
Замечание:
В данной теореме рассмотрена сложная функция, где у зависит от t через промежуточную переменную х. Возможна и более сложная зависимость — с двумя, тремя и большим числом промежуточных переменных, но правило дифференцирования остается таким же.
Так, например, если 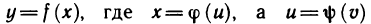
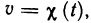
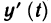
Пример:
Вычислить производную функции
Решение:
Данную функцию можно представить в виде 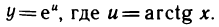
Заменяя 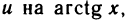
Пример:
Вычислить производную функции
Решение:
Данную функцию можно представить в виде 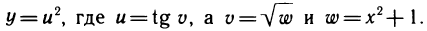
Замечание:
Иногда производную приходится вычислять непосредственно исходя из ее определения. Найдем, например, производную функции
При 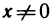
Этим выражением нельзя воспользоваться при х=0. В точке х=0 производную можно вычислить, используя определение производной:
(произведение бесконечно малой функции на ограниченную есть бесконечно малая). Таким образом,
Понятие логарифмической производной функции
Вычислим производную функции 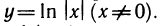
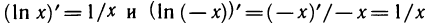
Учитывая формулу (1), вычислим производную сложной функции — дифференцируемая функция. Имеем
или
Производная 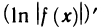
Вычислим с помощью логарифмической производной производную показательно-степенной функции 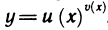
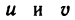
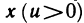
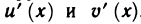
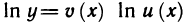
Отсюда, учитывая, что 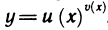
Пример:
Вычислить производную функции 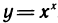
Решение:
Данную функцию можно представить в виде 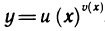
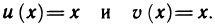
Производную показательно-степенной функции 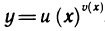
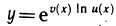
подставляя 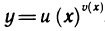
Логарифмическая производная очень удобна при нахождении производной степенной функции с любым вещественным показателем.
Производная степенной функции с любым вещественным показателем
Производная функции 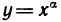
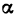
Доказательство:
Так как 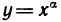
По формуле (2) находим
Отсюда, учитывая, что 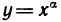
Таким образом, нами вычислены производные всех простейших элементарных функций и мы можем составить следующую таблицу.
Таблица производных простейших элементарных функций
Формулы, приведенные в таблице, а также правила дифференцирования суммы, разности, произведения, частного и правило дифференцирования сложной функции являются основными формулами дифференциального исчисления. На основе правил и формул дифференцирования можно сделать важный вывод: производная любой элементарной функции также элементарная функция. Таким образом, операция дифференцирования не выводит из класса элементарных функций.
Производные и дифференциалы высших порядков
Понятие производной n-го порядка
Как уже отмечалось в § 1 данной главы, производная f'(х) функции y=f(x) сама является некоторой функцией аргумента х. Следовательно, по отношению к ней снова можно ставить вопрос о существовании и нахождении производной.
Назовем f'(х) производной первого порядка функции f(х). Производная от производной некоторой функции называется производной второго порядка (или второй производной) этой функции. Производная от второй производной называется производной третьего порядка (или третьей производной) и т. д. Производные, начиная со второй, называются производными высших порядков и обозначаются 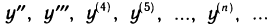
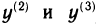
Производная n-го порядка является производной от производной
(n—1)-го порядка, т. е. 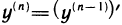
Производные высших порядков имеют широкое применение в физике. Ограничимся физическим истолкованием второй производной f»(х). Если функция y = f(х) описывает закон движения материальной точки по прямой линии, то первая производная f(х) есть мгновенная скорость точки в момент времени х, а вторая производная равна скорости изменения скорости, т. е. ускорению движущейся точки в этот момент.
Формулы для л-х производных некоторых функций
1) Вычислим n-ю производную степенной функции 
(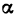
В частном случае, если 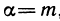
2) Вычислим n-ю производную показательной функции 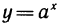
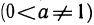
В частности, если 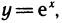
3) Вычислим n-ю производную функции y=sinx. Последовательно дифференцируя, имеем
Таким образом, производную любого порядка от sin х можно вычислять по формуле
Например,
4) Аналогично можно получить формулу n-й производной функции y=cosx:
Формула Лейбница для n-й производной произведения двух функций
Пусть 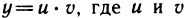
Правые части полученных равенств похожи на разложения различных степеней бинома 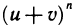
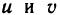
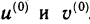
Формула (1) называется формулой Лейбница. Докажем эту формулу методом математической индукции.
При n=1 эта формула принимает вид 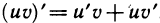
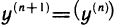
Раскрывая скобки и приводя подобные члены, получаем
По выражение, стоящее в квадратных скобках, можно представить следующим образом:
Поэтому
Формула (1) доказана. ■
Пример:
Вычислить пятую производную функции 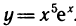
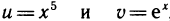
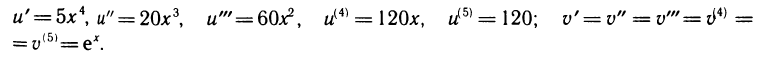
Пример:
Вычислить n-ю производную 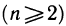
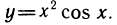
Решение. Полагая 
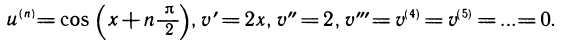
Дифференциалы высших порядков
Рассмотрим дифференциалы высших порядков. Для удобства будем наряду с обозначениями дифференциалов символами dу и dx использовать обозначил
Пусть функция f(х) дифференцируема в каждой точке х некоторого промежутка. Тогда ее дифференциал
который назовем дифференциалом первого порядка, является функцией двух переменных: аргумента х и его дифференциала dx. Пусть функция f'(х), в свою очередь, дифференцируема в некоторой точке х. Будем рассматривать dx в выражении для dy как постоянный множитель. Тогда функция dу представляет собой функцию только аргумента х и ее дифференциал в точке х имеет вид (при рассмотрении дифференциала от dу будем использовать новые обозначения для дифференциалов)
Дифференциал 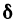
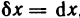
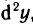
В свою очередь, дифференциал 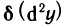
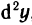
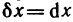
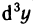
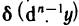
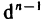
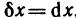
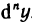
Докажем, что для n-го дифференциала функции справедлива формула
Доказательство проведем по индукции. Для n=1 и n=2 формула (2) доказана. Пусть она верна для дифференциалов порядка n-1:
и функция 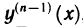
Полагая 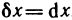
что и требовалось доказать.
Из формулы (2) следует, что для любого справедливо равенство
т е. n-я производная функции y=f(x) в точке х равна отношению n-го дифференциала этой функции в точке х к n-й степени дифференциала аргумента.
Пример:
Вычислить дифференциал 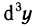
Решение:
Последовательно дифференцируя, получаем
Следовательно,
Параметрическое задание функции
Пусть даны две функции
одной независимой переменной t, определенные и непрерывные в одном и том же промежутке. Если 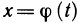
В этом случае говорят, что функция у от х задана параметрически с помощью уравнений (1).
Отметим, что функция 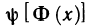
Пример:
Пусть 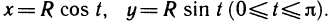
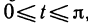
Это еще легче сделать, если заметить, что
Отсюда 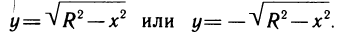
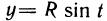
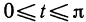
Если
Таким образом, можно сделать вывод, что когда t изменяется 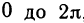
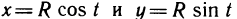
Пример:
Пусть 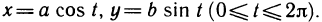
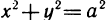
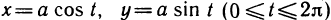
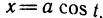
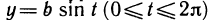
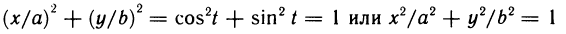
Параметрическое задание функции имеет особо важное значение при изучении движения точки. Если точка движется на плоскости, то ее координаты х, у являются функциями времени t. Задав эти функции 
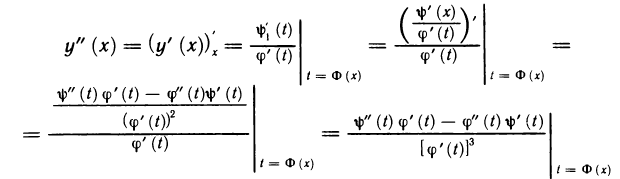
Дифференцирование функции, заданной параметрически
Предположим теперь, что функции 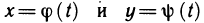
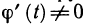
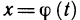
а по теореме 5.5 о производной сложной функции функция 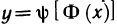
Следовательно,
Таким образом, доказано, что производная функции, заданной параметрически, выражается формулой (2).
Пример:
Найти 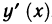
Решение:
По формуле (2) получаем [здесь 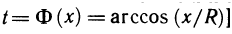
Если воспользоваться явным выражением для функции у от 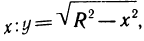
Пусть существуют вторые производные функций 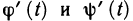
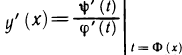
в свою очередь, задана параметрически уравнениями 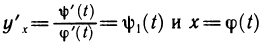
Здесь использовано правило дифференцирования частного. Итак,
Аналогично можно получить производную от у по х любого порядка.
Пример:
Найти 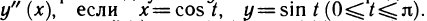
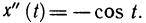
Дифференцирование — решение заданий и задач по всем темам с вычислением
При изучении темы «Дифференцирование» вы познакомитесь
на примерах с понятиями производной и дифференциала функции одной переменной, научитесь вычислять производные, используя правила дифференцирования суммы, произведения, частного и сложной функции, научитесь дифференцировать функции, заданные параметрически, вычислять производные высших порядков, а также применять производные и дифференциалы в приближенных вычислениях и при решении геометрических задач.
Понятие производной
Постановка задачи. Исходя из определения, найти производную функции f(x) в точке х = 0.
План решения.
1.По определению
(Напомним, что при вычислении предела 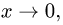
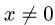
3.Вычисляем предел
3.Если предел существует и равен А, то f'(0) = А, если предел не
существует, то f'(0) не существует.
Пример:
Исходя из определения, найти производную функции
в точке х = 0.
Решение:
1.По определению
2.Так как sin(l/x) — ограниченная, а x — бесконечно малая функции при 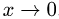
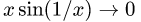
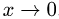
3.Таким образом, предел существует и равен нулю. Следовательно, f'(0) = 0.
Ответ. f'(0) = 0.
Вычисление производных
Постановка задачи. Найти производную функции у = f(x).
План решения. Задача решается в несколько этапов. На каждом
этапе необходимо распознать тип функции и применить соответствующее правило дифференцирования.
Возможны следующие типы функций.
• Функция имеет вид 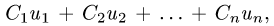
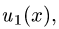

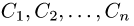
• Функция имеет вид u • v. Используем формулу производной
произведения
• Функция имеет вид 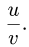
• Функция имеет вид u(v(x)). Используем формулу производной
сложной функции
• Функция имеет вид 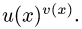
вычисляется с помощью формулы
Переход от этапа к этапу совершается до тех пор, пока под каждым знаком производной не окажется табличная функция.
Пример:
Найти производную функции
Решение:
1.Функция у(х) имеет вид
где 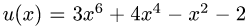
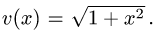
для производной частного, получаем
2.Функция 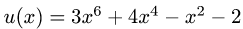
3.Функция 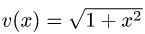
где 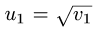
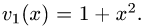
Ответ.
Уравнение касательной и нормали
Постановка задачи. Составить уравнения касательной и нормали к кривой у = f(x) в точке с абсциссой а.
План решения. Если функция f(x) в точке а имеет конечную
производную, то уравнение касательной имеет вид
Если 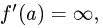
Если 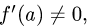
Если 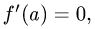
1.Находим значение f(а).
2.Находим производную f'(a).
3.Подставляя найденные значения f(a) и f'(a) в (1) и (2), получаем уравнения касательной и нормали.
Пример:
Составить уравнения касательной и нормали к кривой
в точке с абсциссой а = 1.
Решение:
1.Находим f(1) = 2/3.
2.Находим производную f'(1) = 2/3. Так как 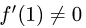
то воспользуемся уравнениями (1) и (2).
3.Подставляя найденные значения f(а) = 2/3 и f'(а) = 2/3 в (1)
и (2), получаем уравнения касательной и нормали:
Ответ. Уравнение касательной: 2х — Зу = 0. Уравнение нормали: 9x+6у — 13 = 0.
Приближенные вычисления с помощью дифференциала
Постановка задачи. Вычислить приближенно с помощью дифференциала значение функции у = f(x) в точке х = а.
План решения. Если приращение 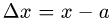
по абсолютной величине, то
1.Выбираем точку а, ближайшую к x и такую, чтобы легко вычислялись значения f(а) и f'(a).
2.Вычисляем 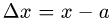
3.По формуле (1) вычисляем f(x).
Пример:
Вычислить приближенно с помощью дифференциала
значение функции 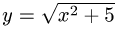
Решение:
1.Ближайшая к 1,97 точка, в которой легко вычислить значения
f(а) и f'(а), — это точка а = 2.
2.Вычисляем:
3.По формуле (1) имеем
Ответ.
Логарифмическое дифференцирование
Постановка задачи. Найти производную функции вида
План решения.
1.Логарифм данной функции имеет вид
2.Продифференцировав обе части этого равенства, получаем
Поэтому
3.Подставляя в последнее равенство выражение для у, получаем
ответ.
Пример:
Найти производную функции
Решение:
1.Логарифм данной функции имеет вид
2.Продифференцировав обе части этого равенства, получаем
Поэтому
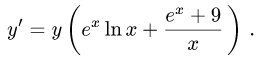
3.Подставляя в последнее равенство выражение для у, получаем
ответ.
Ответ.
Производная функции, заданной параметрически
Постановка задачи. Найти производную функции, заданной
параметрически.
План решения. Если зависимость у от х задана посредством
параметра t:
то зависимость у’ от х задается посредством параметра t формулами
Вычисляем f'(t) и g'(t), подставляем в формулу (1) и записываем
ответ.
Пример:
Найти производную 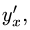
Решение:
Вычисляем:
Подставляя полученные результаты в формулу (1), получаем
Ответ.
Касательная и нормаль к кривой, заданной параметрически
Постановка задачи. Составить уравнения касательной и нормали к кривой
в точке А, соответствующей значению параметра
План решения. Если функция у(х) в точке а имеет конечную
производную, то уравнение касательной имеет вид
Если 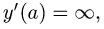
Если 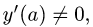
Если у'(а) = 0, то уравнение нормали имеет вид х = а.
1.Вычисляем координаты точки А:
2.Находим производную у’ в точке касания при
3.Подставляем полученные значения в уравнения касательной (1)
и нормали (2) и записываем ответ.
Пример:
Составить уравнения касательной и нормали к кривой
в точке А, соответствующей значению параметра t = 0.
Решение:
1.Вычисляем координаты точки А: а = 2, у(а) = 1.
2.Находим производную у’ в точке А:
Поскольку 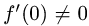
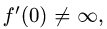
2.Подставляем полученные значения в уравнения касательной (1):
и нормали (2):
у=1+2(х-2).
Ответ. Уравнение касательной: х + 2у — 4 = 0. Уравнение нормали:
2х — у — 3 = 0.
Производные высших порядков
Постановка задачи. Найти производную п-го порядка функции y=f(x).
План решения.
Производной n-го порядка функции у = f(x) называют производную от производной порядка (n — 1), т.е.
1.Дифференцируем функцию у = f(x) последовательно несколько
раз, пока не станет ясной формула для производной n-ого порядка.
2.Доказываем эту формулу методом математической индукции.
Для этого проверяем, что она справедлива при n = 1, т.е. дает правильное значение f’, и что дифференцирование выражения для 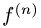
Пример:
Найти производную n-го порядка функции
Решение:
1.Найдем последовательно
Проанализировав эти выражения, делаем предположение, что
2.Докажем эту формулу методом математической индукции.
Проверим, что она справедлива при n = 1, т.е.
Дифференцирование 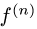
Ответ.
Формула Лейбница
Постановка задачи. Найти производную п-го порядка функции
у = u(x)v(x).
План решения. Если функции u(х) и v(x) имеют производные
до n-го порядка включительно, то справедливы следующие формулы:
где 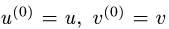
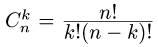
Формула (1) для n-й производной произведения называется
формулой Лейбница.
Следовательно, для определения производной n-го порядка функции вида у = u(x)v(x) нужно вычислить все производные (до n-го
порядка включительно) каждой из функций u(х) и v(x), биномиальные коэффициенты 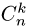
Пример:
Найти производную 4-го порядка функции
Решение:
1.Применяем формулу Лейбница (1). В данном случае
Имеем
Подставляя полученные результаты в формулу (1), получим
Ответ.
Вторая производная функции, заданной параметрически
Постановка задачи. Найти производную второго порядка
функции, заданной параметрически.
План решения. Если функция задана параметрически:
то ее первая производная определяется формулами
Дифференцируя 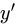
Пример:
Найти производную второго порядка функции, заданной параметрически:
Решение:
1.Вычисляем
и подставляем эти значения в формулу (1):
Дифференцируя 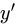
Ответ.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Таблица производных в алгебре нужна для решения целого ряда различных прикладных задач. Поскольку смысл производной иначе интерпретируется как “скорость изменения”, то, каждый раз, беря производную, мы находим величину на ступеньку более “быструю”, чем та, от которой мы берем производную. Например, беря производную от y(x) по x, мы фактически находим скорость изменения координаты y в зависимости от изменения координаты x, а беря производную от скорости изменения координаты y в зависимости от координаты x, мы находим ускорение.
Что такое производная функции
Например, при использовании производной в физике, мы знаем, что производная расстояния s по времени – это скорость. Потому что скорость – это величина, характеризующая быстроту изменения расстояния в зависимости от времени. А производная скорости – ничто иное как ускорение, так как ускорение – это величина, характеризующая быстроту изменения скорости.
Поскольку производная находится по формуле: , то бесконечное количество различных функций усложняют задачу дифференцирования, так как удобно функцию, которую можно представить из различных элементарных функций, дифференцировать основываясь на уже выведенных выражениях для производных этих элементарных функций.
Характеристика производной и ее смысл
Производная характеризует быстроту изменения функции в зависимости от изменения аргумента.
Таблица производных
Таким образом, чтобы работать с производными, необходима таблица производных элементарных функций. Руководствуясь этой таблицей, можно взять производную от какой угодно функции. Но прежде чем работать с таблицей – нужно знать как брать производную функции, есть определенные правила дифференцирования, которые представим в таблице.
Правила дифференцирования
| № правила | Название правила | Правило дифференцирования |
| 1 | Производная постоянной величины | |
| 2 | Производная суммы | |
| 3 | Производная произведения постоянной на функцию | |
| 4 | Производная переменной x | |
| 5 | Производная произведения двух функций | |
| 6 | Производная деления двух функций | |
| 7 | Производная сложной функции |
Таблица производных простых и сложных функций
Теперь таблица производных для элементарных и для сложных функций.
| Номер формулы | Название производной | Основные элементарные функции | Сложные функции |
| 1 | Производная натурального логарифма по x | ||
| 2 | Производная логарифмической функции по основанию a | ||
| 3 | Производная по x в степени n | ||
| 4 | Производная квадратного корня | ||
| 5 | Производная a в степени x | ||
| 6 | Производная e в степени x | ||
| 7 | Производная синуса | ||
| 8 | Производная косинуса | ||
| 9 | Производная тангенса | ||
| 10 | Производная котангенса | ||
| 11 | Производная арксинуса | ||
| 12 | Производная арккосинуса | ||
| 13 | Производная арктангенса | ||
| 14 | Производная арккотангенса |
Примеры нахождения производных
Пример 1
Пользуясь формулами и правилами дифференцирования, найти производную функции: .
Решение:
Мы использовали правило 2 дифференцирования суммы. Теперь найдем производную каждого слагаемого:
По формуле 3 “производная по x в степени n” (у нас в степени 2).
По правилам дифференцирования 3 и 4.
По первому правилу дифференцирования “производная постоянной равна нулю”
Итак, получим: .
Пример 2
Найти производную функции
Решение:
Находим производную, пользуясь правилам дифференцирования 6.
Ответ:
Пример 3
Найти производную функции
Решение: здесь все просто, мы возьмем производную из таблицы производных.
Ответ:
Пример 4
Найдите производную функции
Решение: Здесь мы уже имеем не простую функцию, а сложную функцию и брать производную мы будем по формуле 8 таблицы производных для сложных функций.
Ответ:
Пример 5
Пользуясь правилами дифференцирования и таблицей производных, найдите производную функции
Решение: У нас сложная функция, так как под корнем стоит не просто , а квадратная функция.
То есть мы имеем функцию вида .
Возьмем производную этой функции:
Ответ:
Пример 6
Найдите скорость тела, если траектория его движения задана уравнением м
Решение: скорость тела – это первая производная траектории по времени: . м/с.
Находим скорость тела:
Ответ: 3 м/с.
Итак, таблица производных и правила дифференцирования дают возможность легко брать производные и простых, и сложных функций.