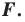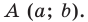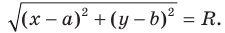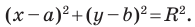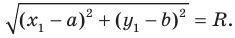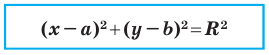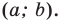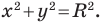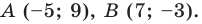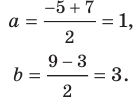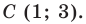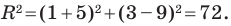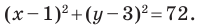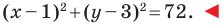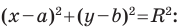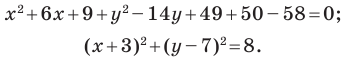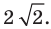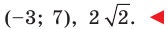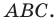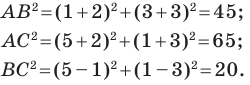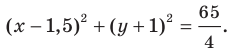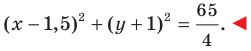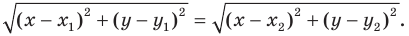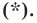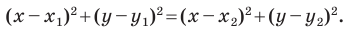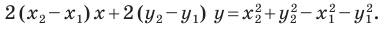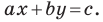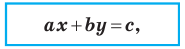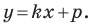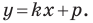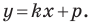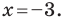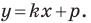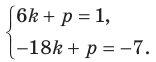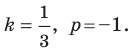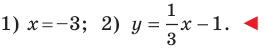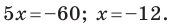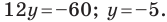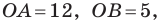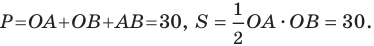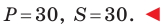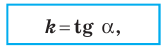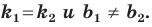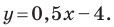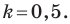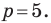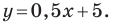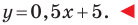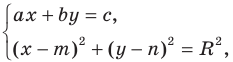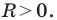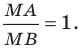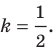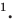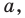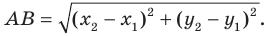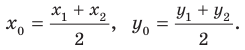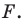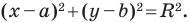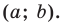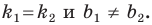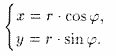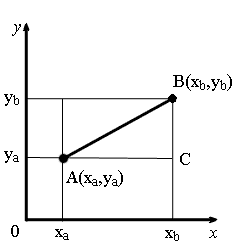Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
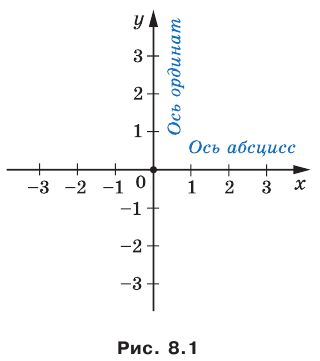
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
Договорились координатную плоскость с осью
Координаты точки на плоскости 
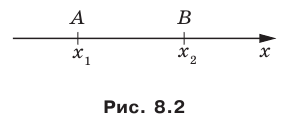
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 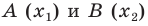
Научимся находить расстояние между точками 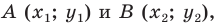
Рассмотрим случай, когда отрезок 
Через точки 
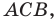
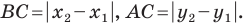
Тогда формулу расстояния между точками 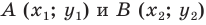
Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 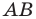
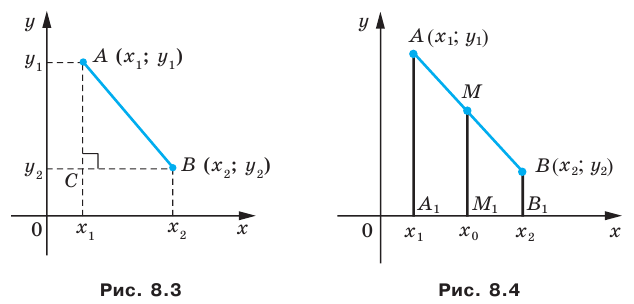
Пусть 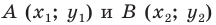
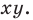
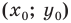
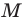
Рассмотрим случай, когда отрезок 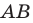
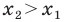
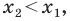
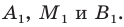
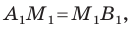
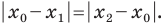
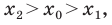
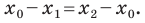

Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 
Пример №1
Докажите, что треугольник с вершинами в точках 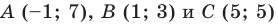
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
Следовательно, 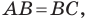
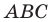
Поскольку 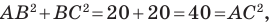
Пример №2
Точка 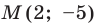
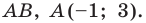
Решение:
Обозначим 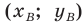
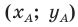
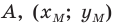
Поскольку 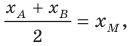
Аналогично
Ответ:
Пример №3
Докажите, что четырехугольник 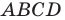
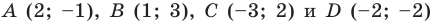
Решение:
Пусть точка 
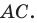
Следовательно,
Пусть точка 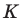
Следовательно,
Таким образом, точки 
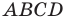
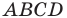
Найдем диагонали параллелограмма:
Следовательно, диагонали параллелограмма 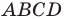
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 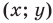
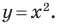
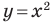
Определение. Уравнением фигуры 
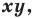
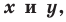
- если точка принадлежит фигуре
то ее координаты являются решением данного уравнения;
- любое решение
данного уравнения является координатами точки, принадлежащей фигуре
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 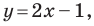
Если данное уравнение является уравнением фигуры 
Пользуясь этими соображениями, выведем уравнение окружности радиуса 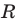
Пусть 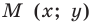
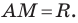
Отсюда
Мы показали, что координаты 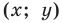
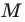
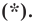
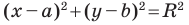
Пусть пара чисел 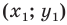
Тогда 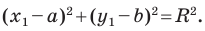
Это равенство показывает, что точка 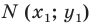
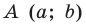
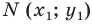
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 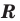
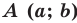
Верно и такое утверждение: любое уравнение вида 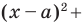
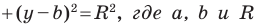
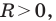
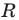
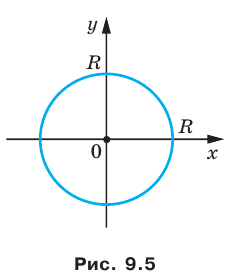
Если центром окружности является начало координат (рис. 9.5), то 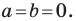
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 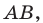
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 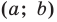
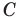
Следовательно,
Радиус окружности 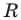
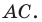
Следовательно, искомое уравнение имеет вид
Ответ:
Пример №5
Докажите, что уравнение 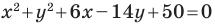
Решение:
Представим данное уравнение в виде
Следовательно, данное уравнение является уравнением окружности с центром в точке 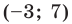
Ответ:
Пример №6
Докажите, что треугольник с вершинами в точках 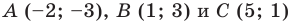
Решение:
Найдем квадраты сторон данного треугольника:
Поскольку 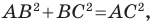
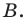
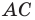
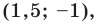
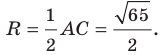
Ответ:
Уравнение прямой
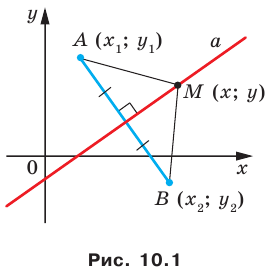
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
Пусть 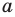
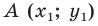
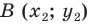
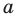
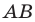
Пусть 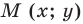
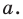
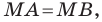
Мы показали, что координаты 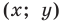
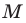
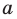
Теперь покажем, что любое решение уравнения 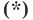
Пусть 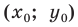
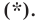
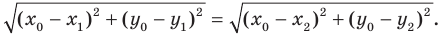
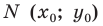
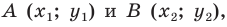
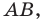
Итак, мы доказали, что уравнение 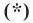
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 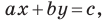
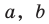
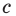
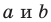
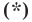
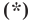
Раскроем скобки и приведем подобные слагаемые. Получим:
Обозначив 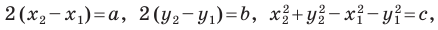
Поскольку точки 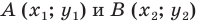
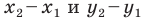
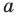
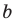
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где 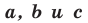
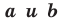
Верно и такое утверждение: любое уравнение вида 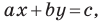
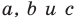
Если 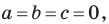
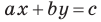
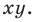
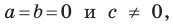
Из курса алгебры 7 класса вы знаете, что уравнение вида 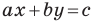
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 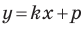
Перепишем уравнение 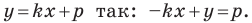
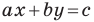
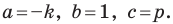
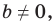
А любую ли прямую на плоскости можно задать уравнением вида 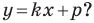
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой 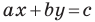
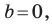
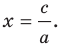
Если 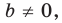
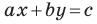
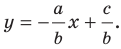
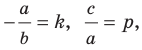
Следовательно, если 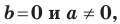
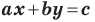
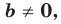
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.
Пример №7
Составьте уравнение прямой, проходящей через точки:
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 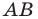
2) Поскольку данные точки имеют разные абсциссы, то прямая 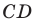
Подставив координаты точек 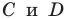
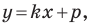
Решив эту систему уравнений, находим, что
Ответ:
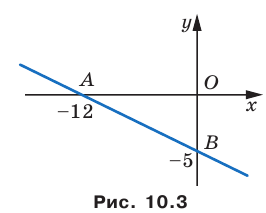
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 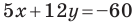
Решение:
Найдем точки пересечения данной прямой с осями координат.
С осью абсцисс: при 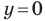
С осью ординат: при 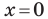
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 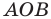
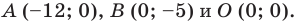
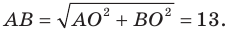
Ответ:
Угловой коэффициент прямой
Рассмотрим уравнение 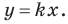
Покажем, что прямые 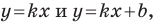
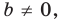
Точки 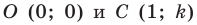
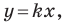
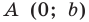
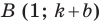
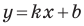
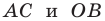
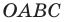
Теперь мы можем сделать такой вывод: если 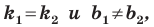
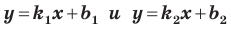
Пусть прямая 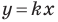
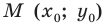
Если прямая 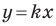
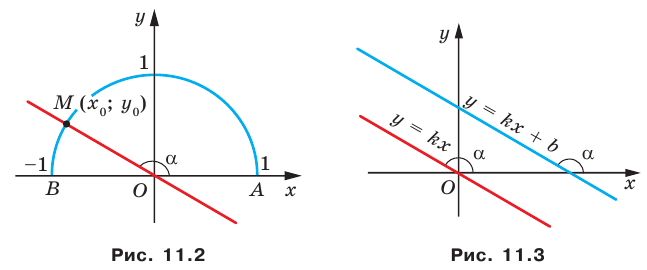
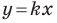
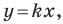
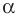
Рассмотрим прямую 
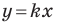
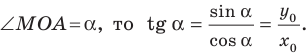
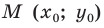
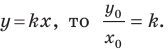
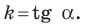
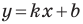
где 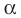
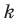
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 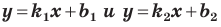
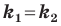
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 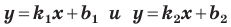
Пример №9
Составьте уравнение прямой, которая проходит через точку 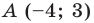
Решение:
Пусть уравнение искомой прямой 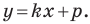
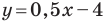
Следовательно, искомое уравнение имеет вид 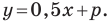
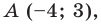
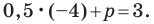
Искомое уравнение имеет вид
Ответ:
Метод координат
Мы часто говорим: прямая 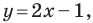
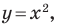
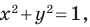
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
где числа 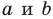
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
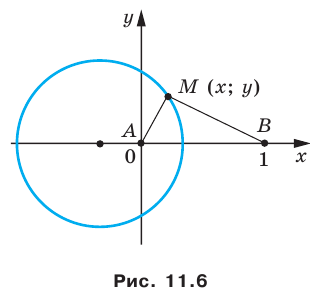
Отметим на плоскости две точки 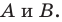
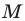
Это серединный перпендикуляр отрезка 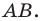
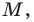
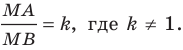
Плоскость, на которой отмечены точки 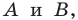
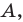
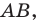
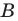
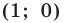
Пусть 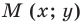
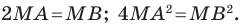
Следовательно, если точка 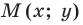
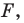
Пусть 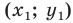
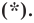
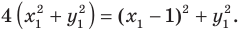
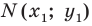
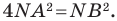
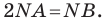
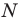
Таким образом, уравнением фигуры 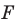
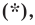
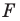
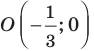
Мы решили задачу для частного случая, когда 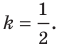
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 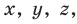
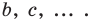
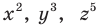
Справочный материал
Расстояние между двумя точками
Расстояние между точками 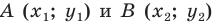
Координаты середины отрезка
Координаты 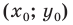
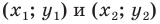
Уравнение фигуры
Уравнением фигуры 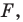
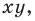
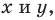
1) если точка принадлежит фигуре 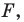
2) любое решение 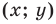
Уравнение окружности
Уравнение окружности радиуса 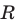
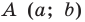
Любое уравнение вида 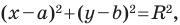
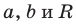
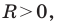
Уравнение прямой
Уравнение прямой имеет вид 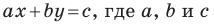
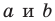
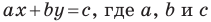
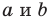
Если 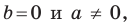
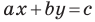
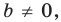
Угловой коэффициент прямой
Коэффициент 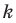
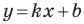
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 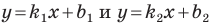
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
Математика
6 класс
Урок № 79
Декартова система координат на плоскости
Перечень рассматриваемых вопросов:
- прямоугольная система координат;
- координатная плоскость;
- координатная ось, координата точки;
- изображение точек с действительными координатами на плоскости.
Тезаурус
Координатная плоскость. Зададим на плоскости две оси координат, расположив их под прямым углом. Координатные оси пересекаются в точке, являющейся началом отсчёта для каждой из них.
Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.
Оси координат разделяют плоскость на 4 угла, которые называются координатными четвертями.
Координаты точки М (х; у), где х – абсцисса, у – ордината точки.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Зададим на плоскости две оси координат, расположив их под прямым углом. Единичные отрезки осей возьмём равными друг другу.
Ось х называют осью абсцисс – расположена горизонтально, направлена вправо. Ось у называют осью ординат – расположена вертикально, направлена вверх.
Положительное направление на осях указывается стрелкой.
Точку пересечения осей называют началом координат.
Оси взаимно перпендикулярны, поэтому заданную таким образом систему координат называют прямоугольной.
Оси координат разделяют плоскость на 4 угла – координатные четверти. Обозначают римскими цифрами как показано на рисунке.
Одним из первых, кто начал широко использовать прямоугольную систему координат в своих исследованиях, был французский философ и математик Рене Декарт, поэтому её часто называют декартовой системой координат.
Пусть A – произвольная точка координатной плоскости. Проведём через точку A прямые, параллельные осям координат. Прямая, параллельная оси y, пересечёт ось x в точке A1, а прямая, параллельная оси x, пересечёт ось y в точке A2. Координату точки A1 на оси x называют абсциссой точки A. Координату точки A2 на оси y называют ординатой точки A. Абсциссу x и ординату y точки A называют координатами точки A.
Координаты точки, записывают в круглых скобках рядом с буквой, обозначающей эту точку: М (х; у).
Важно!
х – первая координата
у – вторая координата
Поменять местами х и у нельзя – получится другая точка.
Поэтому пару координат (x; y) точки A называют упорядоченной парой чисел.
Если на плоскости задана прямоугольная система координат хOу, то:
– каждой точке плоскости поставлена в соответствие упорядоченная пара чисел (координаты точки);
– разным точкам плоскости соответствуют разные упорядоченные пары чисел;
– каждая упорядоченная пара чисел соответствует одной точке плоскости.
То есть установлено взаимно однозначное соответствие между точками плоскости и упорядоченными парами чисел.
Алгоритм построения точки на координатной плоскости
Построим точку А(3; 6).
Введём прямоугольную систему координат.
На каждой оси откладываем заданные координаты х и у (x > 0 и y > 0, значит, точка A расположена в I координатной четверти).
Проводим перпендикуляры к оси х и оси у.
Точка их пересечения – искомая точка.
В(– 4; 5) – имеет отрицательную абсциссу и положительную ординату, значит, расположена во II четверти.
С(– 8; – 4) – имеет обе отрицательные координаты, значит, расположена в III четверти.
D(9; – 2) – имеет положительную абсциссу и отрицательную ординату, значит, расположена в IV четверти.
F(6; 0), E(– 5; 0) – точки лежат на оси абсцисс.
H(0; – 5) – точка лежит на оси ординат.
O(0; 0) – начальная точка системы координат.
В географии положение объектов на земной поверхности определяется двумя координатами: широтой и долготой.
В концертном зале своё кресло можно найти по номеру ряда и места.
В шахматах каждой клетке соответствует буква столбца и цифра ряда.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте
Построить прямую АВ, если А(3; 2), В(– 3; – 4).
Найти:
1) координаты точек пересечения прямой AB с осями;
2) координаты середины отрезка AB.
Шаг 1. Строим точки А и В по их координатам.
Шаг 2. Проводим прямую АВ.
Шаг 3. Находим точки пересечения с осями координат, обозначаем их буквами M и N. Определяем их координаты:
М (1; 0), N (0; – 1).
Шаг 4. Находим по графику середину отрезка АВ, это точка N (0; – 1).
Ответ: координаты точек пересечения прямой AB с осями: М (1; 0), N (0; – 1), координаты середины отрезка AB: N (0; – 1).
Тип 2. Нарисуйте фигуру, последовательно соединяя точки
(0; 4), (– 2; – 2), (3; 2), (– 3; 2), (2; – 4), (0; 4).
Декартовы координаты — это (декартова система координат) система координат на плоскости или в пространстве, обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям прямоугольные декартовы координаты.
Содержание:
- Декартовы координаты на прямой
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
- Координаты середины отрезка
- Формула расстояния между точками
Декартовы координаты на прямой
В курсе алгебры постоянно приходится пользоваться прямоугольной системой координат. Рассмотрим прямоугольную систему координат на прямой. Хорошей иллюстрацией этой системы координат является термометр.
Пусть некоторой точке прямой ставится в соответствие число 0; положительные целые числа 1, 2, 3, … располагаются на равных расстояниях друг от друга с одной стороны от 0, отрицательные целые числа -1, -2, -3… — с противоположной стороны, а дробные числа вставляются между ними естественным образом. Смещение точки 

Стрелка показывает положительное направление отсчета координат. Прямую с установленной на ней системой координат называют координатной прямой. Точку О называют началом координат. Кроме этого, на координатной прямой вводится единичный отрезок ОЕ, его иногда называют масштабом.
Декартовы координаты на плоскости
Положение точки на плоскости может быть определено ее расстоянием до двух фиксированных взаимно перпендикулярных прямых — осей. В этом случае каждой точке плоскости будет соответствовать не одно число, а пара чисел. Соответствие между точками и парами чисел задается на плоскости: выбирают прямую, называемую осью Ох, вводят на ней систему координат. На оси Ох рисуют стрелку, чтобы указать ее положительное направление. Эта ось называется также осью абсцисс.
Проводят прямую Оу, перпендикулярную оси Ох и проходящую через точку О прямой Ох, имеющую координату 0, и вводят на прямой Оу систему координат так, чтобы точка с координатой 0 совпадала с точкой О. Прямая Оу называется осью Оу или осью ординат. Положительное направление на оси Оу также указывается стрелкой. Точка О пересечения прямых Ох и Оу (осей координат) называется началом координат (рис. 2.445).
На рисунке 2.446 изображена построенная прямоугольная система координат. Если дана точка Р, то из нее опускают перпендикуляр на ось Ох. Пусть основанием перпендикуляра будет точка М и х — координата точки М на прямой Ох (рис. 2.446). Тогда число х называют абсциссой точки Р. На рисунке 2.446 
Затем опускают из точки Р перпендикуляр на ось Оу. Пусть основанием этого перпендикуляра будет точка N и у — координата точки N на прямой Оу. Тогда число у называют ординатой точки Р. На рисунке 2.446 

Порядок, в котором записываются координаты точки, очень существенен. Координаты (1, 3) имеет точка 

Ниже приводится определение координат точки на плоскости.
Определение. Абсциссой точки Р называют координату основания перпендикуляра, опущенного из точки Р на ось Ох; ординатой точки Р называют координату основания перпендикуляра, опущенного из точки Р на ось Оу.
Если прямая разбивает плоскость на две полуплоскости, то две оси координат разбивают плоскость на четыре части, называемые четвертями. Четыре четверти нумеруются в порядке, изображенном на рисунке 2.448.

Таким образом, между точками плоскости и упорядоченными парами действительных чисел имеется взаимооднозначное соответствие. Такое соответствие называют прямоугольной системой координат.
Декартовы координаты в пространстве
Построим горизонтальную плоскость и введем на ней декартову систему координат хОу (рис. 2.449).
Если ввести также координатную прямую Oz, перпендикулярную плоскости хОу в точке О, то тем самым будет введена система координат в пространстве. Точка О будет началом этой системы координат.
Стрелки осей Ох, Оу и Oz на рисунках указывают положительное направление каждой оси.
В декартовой системе координат в пространстве мы имеем три оси: Ох — ось абсцисс, Оу — ось ординат, Oz — ось аппликат. Плоскости, проходящие через оси Ох и Оу, Оу и Oz, Ох и Oz — координатные плоскости. Их обозначают соответственно: ху, yz, xz (рис. 2.450). Координатные плоскости разбивают все пространство на восемь частей — октантов.
Если задана такая система координат, то каждой точке пространства можно поставить в соответствие упорядоченную тройку действительных чисел, а каждой тройке чисел — единственную точку.
Пусть дана точка А, расположенная в первом октанте. Опустим из нее на плоскости yz, xz, ху перпендикуляры 

На рисунке 2.452: точка Р лежит в плоскости хОу, так что ее проекция на ось Ог есть 0. Ее проекция на ось Ох совпадает с точкой, имеющей координату 2, а на ось Оу — с точкой, имеющей координату 3. Поэтому пишут Р(2, 3, 0).
Таким образом, нахождение координат точки в пространстве сводится к построению соответствующего прямоугольного параллелепипеда (иногда его воспроизводят частично, чтобы были видны координаты точки (рис. 2.453)).

Порядок записи этих трех чисел также существенен. На рисунке 2.452 изображены точки 
Можно иначе находить координаты точки пространства. Пусть дана точка М. Спроектируем точку М на оси Ох, Оу, Ог в точки 

Если есть три координаты — три числа 



Прямоугольная система координат носит имя Рене Декарта (1596—1650). В 1637 г. вышла книга с длинным по обычаю времен названием «Рассуждение о методе, позволяющем направлять разум и отыскивать истину в науках. Кроме того, Диоптрика, Метеоры и Геометрия, которые являются приложениями этого метода», с ней в науку вошел метод координат. Со времен Декарта алгебра и геометрия стали сотрудничать между собой к выгоде обеих дисциплин. Введенную систему координат с тех пор стали называть декартовой.
Координаты середины отрезка
Рассмотрим отрезок 



Дано, что
1. 
2. 
3. 
Эта формула годится и в случае, когда
Рассмотрим случай, когда отрезок 
1. Точка Р является серединой отрезка 
2. Построим проекции точек 

3. Точка М является серединой отрезка 
4. 
Аналогично можно получить, что 
Теорема 1. Даны точки 

Формула расстояния между точками
Пусть мы знаем координаты двух точек 
Теорема 2. Расстояние между точками 
Например, если 
Формула расстояния между точками верна и в пространстве. Пусть даны две точки 

Пример:
Докажите, что середина гипотенузы прямоугольного треугольника равноудалена от его вершин.
Решение:
Из условия задачи имеем:
1. 
2. CD = BD.
3. CD = AD (требуется доказать).
Мы хотим применить для решения задачи декартову систему координат, а значит, надо удачно выбрать расположение этой системы.
4. Для данной задачи удачный выбор системы координат показан на рисунке 2.460. Начало координат помещено в точку А, а оси проведены через точки Б и С так, чтобы эти точки лежали на положительных лучах осей (построение).
5. Точка В имеет координаты (

6. Середина отрезка СВ точка D имеет координаты 
7. 
8. 
9. CD = BD (7, 8).
Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
- Математика решение заданий и задач
Смотрите также дополнительные лекции по предмету «Математика»:
Лекции:
- Наибольшее значение функции
- Степенные ряды. Теорема Абеля
- Построить ряд по степеням
- Интегрирование рациональных дробей
- Модуль комплексного числа
- Найти область определения функции
- Возрастание и убывания функции на промежутке
- Интегрирование заменой переменной по частям. Неопределенный интеграл
- Степенные ряды
- Найти неопределённый интеграл: пример решения
-
Прямоугольные (декартовы) координаты на прямой, плоскости и в пространстве
Система
координат
– способ, позволяющий численно описать
положение точки на плоскости.
Прямоугольная
система координат (декартова)задается
2 взаимно перпендикулярными прямыми —
осями, на каждой из которых выбрано
положительное направление и задан
единичный (масштабный) отрезок. Единицу
масштаба обычно берут одинаковой для
обеих осей. Эти оси наз. осями координат,
точку их пересечения О – началом
координат. Ось абсцисс – Ох, ось ординат
– Оу. Оси делят плоскость на 4 области
– четверти
или квадранты.
Единичные векторы осей обозначают i
и j(
|i
| =| j
| = 1, i
┴j
) .
Произвольный
вектор ОМ называется радиус-вектором
точки М. Координатами точки М в системе
координат Оху (Oij)
наз. координаты радиуса-вектора ОМ. Если
ОМ (х; у), то М (х; у). Эти два числа х и у
полностью определяют положение точки
на плоскости – каждой паре х и у
соответствует единственная точка, и
наоборот.
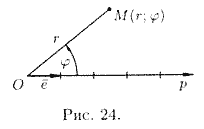
Полярная
система координат
задается точкой О, называемой полюсом,
лучом Ор, называемым полярной осью, и
единичным вектором е того же направления,
что и луч Ор.
Возьмем
на плоскости точку М, не совпадающую с
О. Положение точки М определяется двумя
числами: ее расстоянием г от полюса О и
углом φ, образованным отрезком ОМ с
полярной осью (отсчет углов против
движению часовой стрелки). Числа r и φ
называются полярными координатами
точки М, пишут М(r; φ), при этом r называют
полярным радиусом, φ — полярным углом.
Полярный
угол φ ограничивают промежутком (—π;
π] (или 0< φ< 2πr), а полярный радиус —
[0;∞).
Прямоугольные
координаты точки М выражаются через
полярные координаты точки следующим
образом:
Полярные
же координаты точки М выражаются через
ее декартовы координаты такими формулами:
Декартова
система координат в пространстве:
Прямоугольная
система координат в пространстве
образуется тремя взаимно перпендикулярными
осями координат Ох, Оу и Оz.
Оси координат пересекаются в точке О,
которая называется началом координат,
на каждой оси выбрано положительное
направление, указанное стрелками, и
единица измерения отрезков на осях.
Единицы измерения обычно одинаковы для
всех осей. Ох — ось абсцисс, Оу — ось
ординат, Оz
— ось аппликат.
-
Расстояние между двумя точками прямой, плоскости и в пространстве.
Расстояние
между двумя точками —
это длина отрезка, что соединяет эти
точки.
Формулы
вычисления расстояния между двумя
точками:
-
Формула
вычисления расстояния между двумя
точками A(xa, ya)
и B(xb, yb)
на плоскости:
AB =
√(xb — xa)2 + (yb — ya)2
-
Формула
вычисления расстояния между двумя
точками A(xa, ya, za)
и B(xb, yb, zb)
в пространстве:
AB =
√(xb — xa)2 + (yb — ya)2 +
(zb — za)2
Вывод
формулы для вычисления расстояния между
двумя точками на плоскости
Из
точек A и B опустим перпендикуляры на
оси координат.
Рассмотрим
прямоугольный треугольник ∆ABC. Катеты
этого треугольника равны:
AC
= xb —
xa;
BC
= yb —
ya.
Воспользовавшись
теоремой Пифагора, вычислим длину
отрезка AB:
AB =
√AC2 + BC2.
Подставив
в это выражение длины отрезков AC и BC,
выраженные через координаты точек A и
B, получим формулу для вычисления
расстояния между точками на плоскости.
Формула
для вычисления расстояния между двумя
точками в пространстве выводится
аналогично.
Соседние файлы в предмете Линейная алгебра
- #
- #
- #

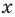
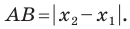
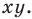
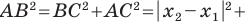

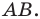
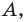
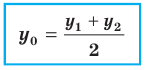
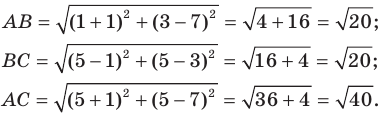

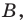
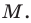
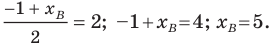
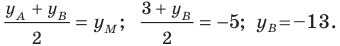
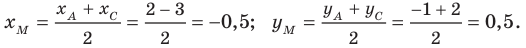
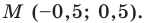
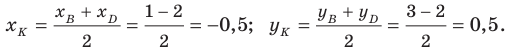
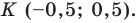
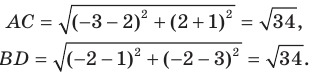

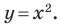
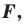 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;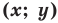 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре