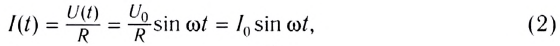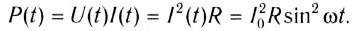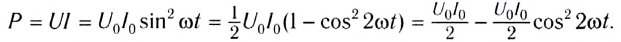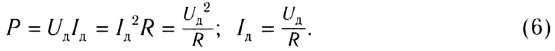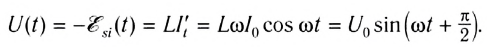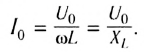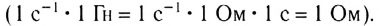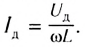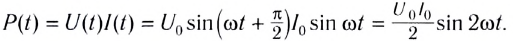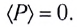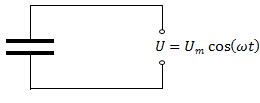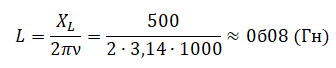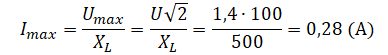Переменный электрический ток:
До сих пор рассматривались электрические цепи, содержащие в различных сочетаниях резисторы, конденсаторы и катушки, с источником постоянного тока либо без него. Теперь рассмотрим подключение таких цепей к источнику переменного тока.
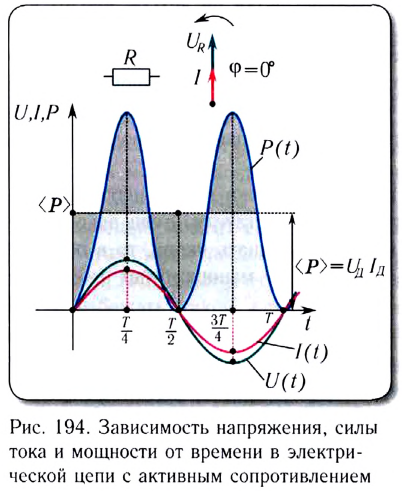
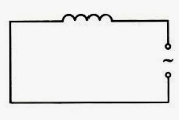
Пусть источник тока создает переменное гармоническое напряжение (рис. 194)
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
где 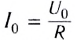
Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины 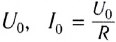
Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность 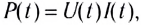
С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде
Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.
Перепишем формулу для мощности по-другому:
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рис. 194).
Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле
Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока 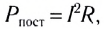
Аналогично можно ввести действующее значение и для напряжения
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе (см. рис. 194).
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии во внутреннюю. Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.
Катушка индуктивности в цепях переменного тока
Реальный соленоид (катушка индуктивности) обладает активным сопротивлением R и индуктивностью L. В цепях постоянного тока главную роль играет его сопротивление R, тогда как в цепях переменного тока — его индуктивность L.
Рассмотрим физические процессы, происходящие в идеальной катушке, у которой отсутствует активное сопротивление (R=0), при включении ее в цепь переменного тока.
В катушке индуктивностью L переменный ток 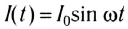
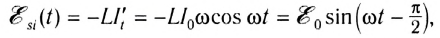
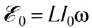
При возрастании силы тока ЭДС самоиндукции согласно правилу Ленца будет препятствовать его увеличению. Для идеальной катушки, активное сопротивление которой равно нулю (R=0), согласно закону Ома для полной цепи 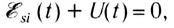
Следовательно, в любой момент времени внешнее напряжение на концах катушки равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:
Сравнивая выражения для мгновенных значений силы тока I(t) и напряжения U(t), видим, что для их амплитудных значений можно записать закон Ома в виде
Величину 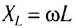
Обратите внимание на то, что фазы колебаний силы тока и напряжения не совпадают. Наличие сдвига фаз означает, что мгновенное значение напряжения U на катушке индуктивности опережает мгновенное значение силы I переменного тока по фазе на 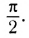
Закон Ома для цепи переменного тока, содержащей только катушку индуктивности, выполняется и для действующих значении силы тока 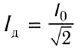
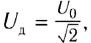
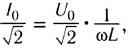
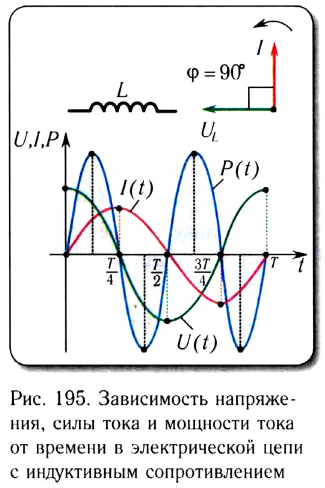
Таким образом, если в цепь переменного тока включена катушка индуктивности, то закон Ома выполняется для амплитудных и действующих значений силы тока и напряжения, но не выполняется для их мгновенных значений, так как мгновенные значения силы тока и напряжения не совпадают по фазе (см. рис. 195).
Мгновенная мощность, потребляемая катушкой индуктивности от источника переменного тока, определяется по формуле
Поскольку среднее за период значение функции 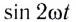
Как видно из рисунка 195, цепь с идеальной катушкой индуктивности в течение первой и третьей четвертей периода работает в режиме потребителя, запасая энергию магнитного поля 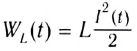
Поскольку потерь энергии в этом случае не происходит, то индуктивное сопротивление называют реактивным.
- Конденсатор в цепях переменного тока
- Электрический ток в различных средах
- Электромагнитная индукция в физике
- Правило Ленца для электромагнитной индукции
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Переменный электрический ток
Что такое катушка индуктивности
Что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь «фиговинка», на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC — метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
где
В — магнитное поле, Вб
I — сила тока, А
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
С научной же точки зрения, индуктивность — это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
где
I — сила тока в катушке , А
U — напряжение в катушке, В
R — сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух — это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей — это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Что влияет на индуктивность?
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
где
1 — это каркас катушки
2 — это витки катушки
3 — сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо «виток к витку».
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков — тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Замеряем индуктивность
15 микрогенри
Отдалим витки катушки друг от друга
Замеряем снова
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Замеряем
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от «витков в квадрате». Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек индуктивности
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:
Мощность переменного тока
-
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
-
Мощность тока через резистор
-
Мощность тока через конденсатор
-
Мощность тока через катушку
-
Мощность тока на произвольном участке
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: переменный ток, вынужденные электромагнитные колебания.
Переменный ток несёт энергию. Поэтому крайне важным является вопрос о мощности в цепи переменного тока.
Пусть и
— мгновенные значение напряжения и силы тока на данном участке цепи. Возьмём малый интервал времени
— настолько малый, что напряжение и ток не успеют за это время сколько-нибудь измениться; иными словами, величины
и
можно считать постоянными в течение интервала
.
Пусть за время через наш участок прошёл заряд
(в соответствии с правилом выбора знака для силы тока заряд
считается положительным, если он переносится в положительном направлении, и отрицательным в противном случае). Электрическое поле движущихся зарядов совершило при этом работу
Мощность тока — это отношение работы электрического поля ко времени, за которое эта работа совершена:
(1)
Точно такую же формулу мы получили в своё время для постоянного тока. Но в данном случае мощность зависит от времени, совершая колебания вместе током и напряжением; поэтому величина (1) называется ещё мгновенной мощностью.
Из-за наличия сдвига фаз сила тока и напряжение на участке не обязаны совпадать по знаку (например, может случиться так, что напряжение положительно, а сила тока отрицательна, или наоборот). Соответственно, мощность может быть как положительной, так и отрицательной. Рассмотрим чуть подробнее оба этих случая.
1. Мощность положительна: . Напряжение и сила тока имеют одинаковые знаки. Это означает, что направление тока совпадает с направлением электрического поля зарядов, образующих ток. В таком случае энергия участка возрастает: она поступает на данный участок из внешней цепи (например, конденсатор заряжается).
2. Мощность отрицательна: . Напряжение и сила тока имеют разные знаки. Стало быть, ток течёт против поля движущихся зарядов, образующих этот самый ток.
Как такое может случиться? Очень просто: электрическое поле, возникающее на участке, как бы «перевешивает» поле движущихся зарядов и «продавливает» ток против этого поля. В таком случае энергия участка убывает: участок отдаёт энергию во внешнюю цепь (например, конденсатор разряжается).
Если вы не вполне поняли, о чём только что шла речь, не переживайте — дальше будут конкретные примеры, на которых вы всё и увидите.
к оглавлению ▴
Мощность тока через резистор
Пусть переменный ток протекает через резистор сопротивлением
. Напряжение на резисторе, как нам известно, колеблется в фазе с током:
Поэтому для мгновенной мощности получаем:
(2)
График зависимости мощности (2) от времени представлен на рис. 1. Мы видим, что мощность всё время неотрицательна — резистор забирает энергию из цепи, но не возвращает её обратно в цепь.
Рис. 1. Мощность переменного тока через резистор
Максимальное значение нашей мощности связано с амплитудами тока и напряжения привычными формулами:
На практике, однако, интерес представляет не максимальная, а средняя мощность тока. Это и понятно. Возьмите, например, обычную лампочку, которая горит у вас дома. По ней течёт ток частотой Гц, т. е. за секунду совершается
колебаний силы тока и напряжения. Ясно, что за достаточно продолжительное время на лампочке выделяется некоторая средняя мощность, значение которой находится где-то между
и
. Где же именно?
Посмотрите ещё раз внимательно на рис. 1. Не возникает ли у вас интуитивное ощущение, что средняя мощность соответствует «середине» нашей синусоиды и принимает поэтому значение ?
Это ощущение совершенно верное! Так оно и есть. Разумеется, можно дать математически строгое определение среднего значения функции (в виде некоторого интеграла) и подтвердить нашу догадку прямым вычислением, но нам это не нужно. Достаточно интуитивного понимания простого и важного факта:
среднее значение квадрата синуса (или косинуса) за период равно .
Этот факт иллюстрируется рисунком 2.
Рис. 2. Среднее значение квадрата синуса равно
Итак, для среднего значения мощности тока на резисторе имеем:
(3)
В связи с этими формулами вводятся так называемые действующие (или эффективные) значения напряжения и силы тока (на самом деле это есть не что иное, как средние квадратические значения напряжения и тока. Такое у нас уже встречалось: средняя квадратическая скорость молекул идеального газа (листок «Уравнение состояния идеального газа»):
(4)
Формулы (3), записанные через действующие значения, полностью аналогичны соответствующим формулам для постоянного тока:
Поэтому если вы возьмёте лампочку, подключите её сначала к источнику постоянного напряжения , а затем к источнику переменного напряжения с таким же действующим значением
, то в обоих случаях лампочка будет гореть одинаково ярко.
Действующие значения (4) чрезвычайно важны для практики. Оказывается, вольтметры и амперметры переменного тока показывают именно действующие значения (так уж они устроены). Знайте также, что пресловутые вольт из розетки — это действующее значение напряжения бытовой электросети.
к оглавлению ▴
Мощность тока через конденсатор
Пусть на конденсатор подано переменное напряжение . Как мы знаем, ток через конденсатор опережает по фазе напряжение на
:
Для мгновенной мощности получаем:
График зависимости мгновенной мощности от времени представлен на рис. 3.
Рис. 3. Мощность переменного тока через конденсатор
Чему равно среднее значение мощности? Оно соответствует «середине» синусоиды и в данном случае равно нулю! Мы видим это сейчас как математический факт. Но интересно было бы с физической точки зрения понять, почему мощность тока через конденсатор оказывается нулевой.
Для этого давайте нарисуем графики напряжения и силы тока в конденсаторе на протяжении одного периода колебаний (рис. 4).
Рис. 4. Напряжение на конденсаторе и сила тока через него
Рассмотрим последовательно все четыре четверти периода.
1. Первая четверть, . Напряжение положительно и возрастает. Ток положителен (течёт в положительном направлении), конденсатор заряжается. По мере увеличения заряда на конденсаторе сила тока убывает.
Мгновенная мощность положительна: конденсатор накапливает энергию, поступающую из внешней цепи. Эта энергия возникает за счёт работы внешнего электрического поля, продвигающего заряды на конденсатор.
2. Вторая четверть, . Напряжение продолжает оставаться положительным, но идёт на убыль. Ток меняет направление и становится отрицательным: конденсатор разряжается против направления внешнего электрического поля.В конце второй четверти конденсатор полностью разряжен.
Мгновенная мощность отрицательна: конденсатор отдаёт энергию. Эта энергия возвращается в цепь: она идёт на совершение работы против электрического поля внешней цепи (конденсатор как бы «продавливает» заряды в направлении, противоположном тому, в котором внешнее поле «хочет» их двигать).
3. Третья четверть, . Внешнее электрическое поле меняет направление: напряжение отрицательно и возрастает по модулю. Сила тока отрицательна: идёт зарядка конденсатора в отрицательном направлении.
Ситуация полностью аналогична первой четверти, только знаки напряжения и тока — противоположные. Мощность положительна: конденсатор вновь накапливает энергию.
4. Четвёртая четверть, . Напряжение отрицательно и убывает по модулю. Конденсатор разряжается против внешнего поля: сила тока положительна.
Мощность отрицательна: конденсатор возвращает энергию в цепь. Ситуация аналогична второй четверти — опять-таки с заменой заменой знаков тока и напряжения на противоположные.
Мы видим, что энергия, забранная конденсатором из внешней цепи в ходе первой четверти периода колебаний, полностью возвращается в цепь в ходе второй четверти. Затем этот процесс повторяется вновь и вновь. Вот почему средняя мощность, потребляемая конденсатором, оказывается нулевой.
к оглавлению ▴
Мощность тока через катушку
Пусть на катушку подано переменное напряжение . Ток через катушку отстаёт по фазе от напряжения на
:
Для мгновенной мощности получаем:
Снова средняя мощность оказывается равной нулю. Причины этого, в общем-то, те же, что и в случае с конденсатором. Рассмотрим графики напряжения и силы тока через катушку за период (рис. 5).
Рис. 5. Напряжение на катушке и сила тока через неё
Мы видим, что в течение второй и четвёртой четвертей периода энергия поступает в катушку из внешней цепи. В самом деле, напряжение и сила тока имеют одинаковые знаки, сила тока возрастает по модулю; для создания тока внешнее электрическое поле совершает работу против вихревого электрического поля, и эта работа идёт на увеличение энергии магнитного поля катушки.
В первой и третьей четвертях периода напряжение и сила тока имеют разные знаки: катушка возвращает энергию в цепь. Вихревое электрическое поле, поддерживающее убывающий ток, двигает заряды против внешнего электрического поля и совершает тем самым положительную работу. А за счёт чего совершается эта работа? За счёт энергии, накопленной ранее в катушке.
Таким образом, энергия, запасаемая в катушке за одну четверть периода, полностью возвращается в цепь в ходе следующей четверти. Поэтому средняя мощность, потребляемая катушкой, оказывается равной нулю.
к оглавлению ▴
Мощность тока на произвольном участке
Теперь рассмотрим самый общий случай. Пусть имеется произвольный участок цепи — он может содержать резисторы, конденсаторы, катушки…На этот участок подано переменное напряжение .
Как мы знаем из предыдущего листка «Переменный ток. 2», между напряжением и силой тока на данном участке имеется некоторый сдвиг фаз . Мы записывали это так:
Тогда для мгновенной мощности имеем:
(5)
Теперь нам хотелось бы определить, чему равна средняя мощность. Для этого мы преобразуем выражение (5), используя формулу:
В результате получим:
(6)
Но среднее значение величины равно нулю! Поэтому средняя мощность оказывается равной:
(7)
Данную формулу можно записать с помощью действующих значений (4) напряжения и силы тока:
Формула (7) охватывает все три рассмотренные выше ситуации. В случае резистора имеем , и мы приходим к формуле (3). Для конденсатора и катушки
, и средняя мощность равна нулю.
Кроме того, формула (7) даёт представление о весьма общей проблеме, связанной с передачей электроэнергии. Чрезвычайно важно, чтобы у потребителя был как можно ближе к единице. Иначе потребитель начнёт возвращать значительную часть энергии назад в сеть (что ему совсем невыгодно), и к тому же возвращаемая энергия будет безвозвратно расходоваться на нагревание проводов и других элементов цепи.
С этой проблемой приходится сталкиваться разработчикам электрических схем, содержащих электродвигатели. Обмотки электродвигателей обладают большими индуктивностями, и возникает ситуация, близкая к «чистой» катушке. Чтобы избежать бесполезного циркулирования энергии по сети, в цепь включают дополнительные элементы, сдвигающие фазу — например, так называемые компенсирующие конденсаторы.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Мощность переменного тока» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Опишем колебания, которые происходят в цепи переменного тока при включении в нее конденсатора и катушки индуктивности. А также рассмотрим условия, при выполнении которых в цепи переменного тока наступает резонанс. Получим формулы для вычисления амплитуд напряжений, введем понятия емкостного и индуктивного сопротивления и выясним, какую роль играют эти величины.
Конденсатор в цепи переменного тока
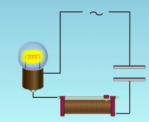
Постоянный ток не может существовать в цепи, содержащий конденсатор. Движению электронов препятствует диэлектрик, расположенный между обкладками. Но переменный ток в такой цепи существовать может, что доказывает опыт с лампой (см. рисунок ниже).
Пусть фактически такая цепь разомкнута, но если по ней течет переменный ток, конденсатор то заряжается, то разряжается. Ток, текущий при перезарядке конденсатора нагревает нить лампы, и она начинает светиться.
Найдем, как меняется сила тока в цепи, содержащей только конденсатор, если сопротивление проводов и обкладок конденсатора можно пренебречь (см. рис. выше). Напряжение на конденсаторе будет равно:
u=φ1−φ2=qC
Учтем, что напряжение на конденсаторе равно напряжению на концах цепи:
qC=Umaxcosωt
Следовательно, заряд конденсатора меняется по гармоническому закону:
q=CUmaxcosωt
Тогда сила тока, представляющая собой производную заряда по времени, будет равна:
i=q´=−CUmaxsinωt=CUmaxcos(ωt+π2)
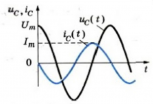
Следовательно, колебания силы тока опережают колебания напряжения на конденсаторе на π2 (см. график ниже). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того, как напряжение достигнет максимума, сила тока становится равной нулю и т.д.
Амплитуда силы тока равна:
Imax=UmaxCω
Примем, что:
1Cω=XC
Также будем использовать действующие значения силы тока и напряжения. Тогда получим, что:
Определение
I=UXC
Величина XC, равная обратному произведению циклической частоты на электрическую емкость конденсатора, называется емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Обратите внимание, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода (при разрядке конденсатора), эта энергия возвращается в сеть.
Пример №1. Максимальный заряд на обкладках конденсатора колебательного контура qmax=10−6 Кл. Амплитудное значение силы тока в контуре Imax=10−3 А. Определите период колебания (потерями на нагревание проводника пренебречь).
Согласно закону сохранения энергии максимальное значение энергии электрического поля конденсатора равно максимальному значения магнитного поля катушки:
q2max2C=LI2max2
Отсюда:
LC=q2maxI2max
√LC=qmaxImax
T=2π√LC=2πqmaxImax=2·3,1410−610−3≈6,3·10−3 (с)
Катушка индуктивности в цепи переменного тока
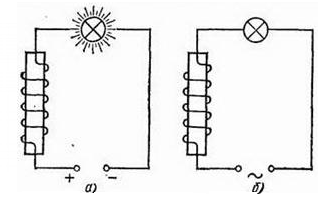
Соберем две электрических цепи, состоящих из лампы накаливания, катушки индуктивности и источника питания: в первом случае постоянного, во втором — переменного (см. рисунки «а» и «б» ниже).
Опыт покажет, что в цепи постоянного тока лампа светится ярче по сравнению с той, что включена в цепь переменного тока. Это говорит о том, что сила тока в цепи постоянного тока выше действующего значения силы тока в цепи переменного тока.
Результат опыта легко объясняется явлением самоиндукции. При подключении катушки к постоянному источнику тока сила тока нарастает постепенно. Возрастающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь спустя какое-то время сила тока достигает наибольшего значения, соответствующему данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не успевает достигнуть максимального значения. Поэтому максимальное значение силы тока в цепи переменного тока с катушкой индуктивности ограничивается индуктивность. Чем больше индуктивность и чем больше частота приложенного напряжения, тем меньше амплитуда силы переменного тока.
Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (см. рисунок ниже). Для этого найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.
Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна равняться нулю. Иначе, согласно закону Ома, сила тока была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля →Ei, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля →Eк, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.
Из равенства →Ei=−→Eк следует, что удельная работа вихревого поля (т.е. ЭДС самоиндукции ei) равна по модулю и противоположна по знаку удельной работе кулоновского поля.
Учитывая, что удельная работа кулоновского поля равна напряжения на концах катушки, можно записать:
ei=−u
Напомним, что сила переменного тока изменяется по гармоническому закону:
i=Imaxsinωt
Тогда ЭДС самоиндукции равна:
ei=−Li´=−LωImaxcosωt
Так как u=−ei, то напряжение на концах катушки оказывается равным:
u= LωImaxcosωt=LωImaxsin(ωt+π2)=Umax(ωt+π2)
Амплитуда напряжения равна:
Umax=LωImax
Следовательно, колебания напряжения на катушке опережают колебания силы тока на π2, или колебания силы тока отстают от колебаний напряжения на π2, что одно и то же.
В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (см. график ниже).
Но в момент, когда напряжение становится равным нулю, сила тока максимальна по модулю. Амплитуда силы тока в катушке равна:
Imax=UmaxLω
Введем обозначение:
Lω=XL
Также будем использовать вместо амплитуд действующие значения силы тока и напряжения. Тогда получим:
Определение
I=UXL
Величина XL, равная произведению циклической частоты на индуктивность, называется индуктивным сопротивлением. Индуктивное сопротивление зависит от частоты. Поэтому в цепи постоянного тока, в котором отсутствует частота, индуктивное сопротивление катушки равно нулю.
Пример №2. Катушка с индуктивным сопротивлениемXL=500 Ом присоединена к источнику переменного напряжения, частота которого ν = 1000 Гц. Действующее значение напряжения U = 100 В. Определите амплитуду силы тока Imax в цепи и индуктивность катушки L. Активным сопротивлением пренебречь.
Индуктивное сопротивление катушки выражается формулой:
XL=Lω=2πνL
Отсюда:
Так как амплитуда напряжения связана с его действующим значением соотношением Umax=U√2, то для амплитуды силы тока получаем:
Резонанс в электрической цепи
Механические и электромагнитные колебания имеют разную природу, но процессы, происходящие при этом, идентичны. Поэтому можно предположить, что резонанс в электрической цепи так же реален, как резонанс в колебательной системе, на которую действует периодическая сила.
Напомним, что в механической системе резонанс тем более заметен, чем меньше в колебательной системе трение между ее элементами. Роль трения в электрической цепи играет активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока во внутреннюю энергию проводника, который при этом нагревается. Следовательно, резонанс в электрической цепи будет отчетливо наблюдаться при малом активном сопротивлении R.
Если активное сопротивление мало, то собственная частота колебаний в колебательном контуре определяется формулой:
ω0=1√LC
Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру равна собственной частоте колебательного контура:
ω=ω0=1√LC
Определение
Резонанс в электрическом колебательном контуре — явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура.
После включения внешнего переменного напряжения резонансное значение силы тока в цепи устанавливается не моментально, а постепенно. Амплитуда колебаний силы тока возрастает до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:
I2maxR2=UmaxImax2
Упростив это уравнение, получим:
ImaxR=Umax
Следовательно, амплитуда установившихся колебаний силы тока при резонансе определяется уравнением:
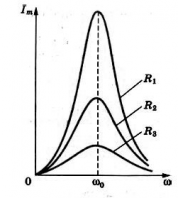
Imax=UmaxR
При сопротивлении, стремящемся к нулю, сила тока возрастает до бесконечно больших значений. При большом сопротивлении сила тока возрастает незначительно. Это хорошо видно на графике ниже.
Пример №3. В цепь переменного тока с частотой ν = 500 Гц включена катушка индуктивностью L = 10 мГн. Какой емкости конденсатор надо включить в эту цепь, чтобы наступил резонанс?
Электрическая цепь, описываемая в условии, представляет собой колебательный контур. Резонанс в этой цепи наступит, когда частота переменного тока будет равна собственной частоте колебательного контура (ν = ν0).
Но:
ν0=12π√LC
Тогда:
ν=12π√LC
Отсюда:
Задание EF22579
К колебательному контуру подсоединили источник тока, на клеммах которого напряжение гармонически меняется с частотой ν.
Индуктивность L катушки колебательного контура можно плавно менять от максимального значения Lmax до минимального Lmin, а ёмкость его конденсатора постоянна.
Ученик постепенно уменьшал индуктивность катушки от максимального значения до минимального и обнаружил, что амплитуда силы тока в контуре всё время возрастала. Опираясь на свои знания по электродинамике, объясните наблюдения ученика.
Алгоритм решения
1.Установить, что вызывает увеличение амплитуды силы тока.
2.Объяснить, какие изменения вызвало уменьшение индуктивности.
3.Объяснить, при каком условии в течение всего эксперимента амплитуда силы тока может только расти.
Решение
В колебательном контуре источником тока возбуждаются вынужденные колебания. Частота этих колебаний равна частоте источника — ν. Амплитуда колебаний зависит от того, как соотносятся между собой внешняя частота и частота собственных электромагнитных колебаний, которая определяется формулой:
ν0=12π√LC
По мере увеличения внешней частоты от нуля до ν0 амплитуда растет. Она достигает максимума тогда, когда происходит резонанс. При этом внешняя частота равна частоте собственных электромагнитных колебаний: ν = ν0. Затем амплитуда начинает убывать.
В данном случае, ученик меняет не внешнюю частоту, а частоту собственных электромагнитных колебаний. При плавном уменьшении индуктивности контура от максимального значения Lmax до минимального Lmin частота возрастает от ν0min до ν0max. Причем:
ν0min=12π√LminC
ν0max=12π√LmaxC
Из того факта, что амплитуда всё время увеличивалась, можем сделать вывод, что частота ν0 всё время приближалась к частоте источника тока, при этом ν > ν0max. В противном случае наблюдалось бы уменьшений амплитуды силы тока.
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22785
В колебательном контуре, состоящем из катушки индуктивности и конденсатора, происходят свободные незатухающие электромагнитные колебания.
Из приведённого ниже списка выберите две величины, которые остаются постоянными при этих колебаниях.
Ответ:
а) период колебаний силы тока в контуре
б) фаза колебаний напряжения на конденсаторе
в) заряд конденсатора
г) энергия магнитного поля катушки
д) амплитуда колебаний напряжения на катушке
Алгоритм решения
- Определить, от чего зависит каждая из перечисленных величин.
- Установить, какие величины меняются, а какие нет.
Решение
В колебательном контуре происходят гармонические колебания. Поэтому период колебаний силы тока в контуре — величина постоянная.
Фаза — это величина, которая определяет положение колебательной системы в любой момент времени. Поскольку в системе происходят колебания, фаза меняется.
Заряд конденсатора — колебания происходят за счет постоянной перезарядки конденсатора. Следовательно, эта величина тоже меняется.
Энергия магнитного поля катушки — в колебательном контуре происходят взаимные превращения энергии магнитного поля катушки в энергию электрического поля конденсатора, и обратно. Поэтому энергия магнитного поля катушки постоянно меняется.
В условии задачи сказано, что колебания незатухающие. Это значит, что полная механическая энергия колебательной системы сохраняется. Поскольку именно от нее зависит амплитуда колебаний напряжения на катушке, то эта величина также остается постоянной.
Ответ: ад
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18656
Алгоритм решения
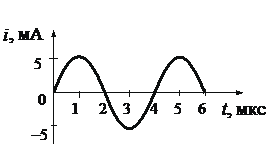
1.Записать исходные данные (определить по графику начальный период колебаний).
2.Перевести единицы измерения величин в СИ.
3.Записать формулу Томсона.
4.Выполнить решение в общем виде.
5.Установить, каким станет период колебаний после уменьшения емкости конденсатора.
Решение
Запишем исходные данные:
• Период колебаний (определяем по графику): T = 4 мкс.
• Емкость конденсатора в первом опыте: C1 = 4C.
• Емкость конденсатора во втором опыте: C2 = C.
4 мкс = 4∙10–6 с
Запишем формулу Томсона:
T=2π√LC
Применим формулу для обоих опытов и получим:
T1=2π√L4C=4π√LC
T2=2π√LC
Поделим первый период на второй:
T1T2=4π√LC2π√LC=2
Отсюда:
T2=T12=4·10−62=2·10−6 (с)=2 (мкс)
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 10k
Демьян Бондарь
Эксперт по предмету «Электроника, электротехника, радиотехника»
преподавательский стаж — 5 лет
Задать вопрос автору статьи
Катушка индуктивности
Катушки индуктивности делятся на два класса:
- Катушка индуктивности с магнитным сердечником.
- Катушка индуктивности с немагнитным сердечником.
В большинстве случаев используются сердечники из железных пластин и феррита. Сердечник способствует увеличению индуктивности в несколько раз. Для катушек средней индуктивности используются сердечники из феррита. Катушки большой индуктивности делаются, как трансформаторы с железным сердечником, но с одной обмоткой. К основным свойствам катушки индуктивности относятся:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
- Возрастание сопротивления с увеличением частоты электрического тока, который течет через катушку.
- Скорость изменения электрического тока, протекающего через катушку, ограничена и определяется ее индуктивностью.
- При протекании электрического тока катушка индуктивности запасает энергию в собственном магнитном поле.
Электрическая цепь с реальной катушкой индуктивности
Примером реальной катушки индуктивности являются линии электропередач, обмотки трансформатора и электрических машин. Отличие между идеальной и реальной катушками заключается в том, что переменный ток в реальной катушке индуктивности становится причиной не только изменения энергии в магнитном поле, но и преобразования электроэнергии в другой вид энергии. Переменный ток, протекая по катушке создает на активном и индуктивном сопротивлениях падение напряжения. Активная составляющая напряжения может быть определена при помощи включения катушки на постоянное напряжение, потому что при нулевой частоте сети составляющие напряжения также равняются нулю, рассмотрим цепь с реальной катушкой индуктивности, активным и реактивным сопротивлениями.
«Цепь с реальной катушкой индуктивности» 👇

Рисунок 1. Цепь с реальной катушкой индуктивности, активным и реактивным сопротивлениями. Автор24 — интернет-биржа студенческих работ
Так как активная составляющая напряжения совпадает с током по фазе, то можно записать:
$ua = Uamsinwt$
Реактивная составляющая опережает электрический ток по фазе на 90 градусов:
$uL = ULmsin(wt+90)$
В соответствии со вторым законом Кирхгофа мгновенное значение напряжения на зажимах рассматриваемой цепи является алгебраической суммой составляющих:
$u = ua+uL$
На рисунке ниже — а представлен график общего напряжения, который построен посредством слоения синусоид ua и uL
Рисунок 2. График. Автор24 — интернет-биржа студенческих работ
Из графика понятно, что напряжение, что напряжение опережает ток на угол ф по фазе. Мгновенное значение напряжения, которое прилагается к реальной катушке соответствует следующему выражению:
$u = Umsin(wt+ф)$
Действующее значение данного напряжения определяется, как геометрическая сумма действующих значений составляющих:
$U = Ua + UL$
Данное уравнение является основой для построения векторной диаграммы — рисунок б выше. Из прямоугольного треугольника следует:
Рисунок 3. Уравнение. Автор24 — интернет-биржа студенческих работ
Из представленного выше уравнения можно получить математическое выражение закона Ома в действующих значения для цепи с реальной катушкой индуктивности:
$I = U/z$
где z — полное сопротивление электрической цепи, измеряемое в омах.
Если треугольник напряжений уменьшить в I раз, то получится треугольник сопротивлений, который изображен на рисунке ниже.
Рисунок 4. Треугольник сопротивлений. Автор24 — интернет-биржа студенческих работ
Стоит помнить, что сопротивления не являются векторными величинами. Из треугольников сопротивлений и напряжений можно определить угол сдвига фаз между током и напряжением:
Рисунок 5. Угол сдвига. Автор24 — интернет-биржа студенческих работ
В данном случае активная мощность катушки может быть рассчитана по следующей формуле:
Рисунок 6. Формула. Автор24 — интернет-биржа студенческих работ
Реактивная мощность рассчитывается по формуле:
Рисунок 7. Формула. Автор24 — интернет-биржа студенческих работ
Чтобы рассчитать полную мощность используется формула:
$S = U*I$
Если треугольник напряжений увеличить в I раз, то получится треугольник мощностей.
Рисунок 8. Треугольник мощностей. Автор24 — интернет-биржа студенческих работ
Нужно учитывать, что стороны треугольника мощностей не являются векторными величинами, потому что реактивная, активная и полная мощности являются произведением действующих значений, а не функциями времени. Из выше представленного треугольника мощностей очевидны следующие зависимости:
Рисунок 9. Зависимости. Автор24 — интернет-биржа студенческих работ
Но если в цепи потребляется только некоторая часть полной мощности, а именно активная, то она преобразуется в другой вид энергии:
$cosф = Р/S$
Предположим, что в сеть, напряжение которой составляет 120 вольт, частота 50 герц, включена катушка индуктивностью 50 миллигенри и активным сопротивлением в 12 Ом. Необходимо определить полное и реактивное сопротивление цепи, ток цепи, реактивную и активную составляющую напряжения, коэффициент мощности, активную, реактивную и полную мощность и максимальную энергию магнитного поля катушки. Алгоритм решения выглядит следующим образом:
Рисунок 10. Алгоритм решения. Автор24 — интернет-биржа студенческих работ
Рисунок 11. Алгоритм решения. Автор24 — интернет-биржа студенческих работ
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме