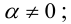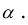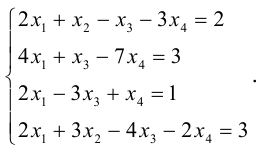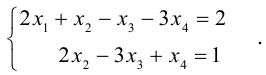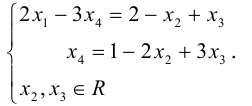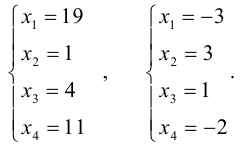|
0 / 0 / 0 Регистрация: 07.12.2012 Сообщений: 34 |
|
|
1 |
|
|
23.09.2013, 11:51. Показов 1589. Ответов 1
Вот задача
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
23.09.2013, 11:51 |
|
Ответы с готовыми решениями: Дан линейный массив. Получить действительную квадратную матрицу порядка n Даны действительные числа x1, …, x8. Получить действительную квадратную матрицу порядка 8
1 |
|
Rivory 148 / 114 / 21 Регистрация: 15.01.2013 Сообщений: 266 |
||||
|
23.09.2013, 12:25 |
2 |
|||
|
Решение
1 |
Примеры решения матриц с ответами
Простое объяснение принципов решения матриц и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Помощь в написании работы
Алгоритм решения матриц
Матрица – это математическая таблица с числовыми значениями. Обозначаются матрицы латинскими буквами.
Есть два отличия между матрицами:
- Комплексные матрицы. Это когда хотя бы одно число равно комплексному.
- Действительные матрицы. Это когда в матрице содержаться действительные числа.
С матрицей можно выполнять самые наипростейшие действия: умножение, деление, сложение, вычитание и трансформация.
Сложение и вычитание
Данные действия можно совершать тогда, когда матрицы равны между собой, чтобы в конце получилось выражение аналогичной размерности. Сложение и вычитание выполняются по аналогии друг друга.
Задание
Даны две матрицы, найдите их сумму.
Решение
Элемент первой строки складывается с элементом второй. Абсолютно также совершается вычитание, только вместо плюса, нужно поставить минус.
Задание
Даны две матрицы, найдите их разность.
Решение
Задание
Найдите C=2A +3B, если :
Решение
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Умножение
В математике умножать таблицу с числами можно абсолютно любую. В таком случае число умножается с показателем. Умножаем первое число на первой строке с числом второго столбца и так далее.
Задание
Даны две матрицы. Умножьте их друг на друга.
Решение
=
Матрицы можно перемножать друг на друга, только если количество столбцов в первой матрице, равно количеству строк второй. Элемент матрицы будет равняться сумме произведений (Aji), где i – строки в таблице; j – строки чисел второй таблицы.
Возведение матрицы в степень
Данную формулу используют лишь в случаях, если матрица стоит в квадратном выражении. Важно знать, что степень должна быть у таких выражений натуральной!
Если число не будет натуральным, то это усложняет возведение матрицы в степень, так как степень n придётся умножить саму на себя n количество раз. Но если у Вас такой случай, то используется следующая формула.
Задание
Найдите
матрицы.
Решение
В первую очередь найдём, для этого нужно будет просто умножить её саму на себя.
После по формуле подставляем числовые значения.
Расчёт определителя
В математике линейной есть два понятия – определитель и детерминант. Определитель – это какое-либо число, которое ставится в соответствии с квадратной матрицей. Определитель используется при решении многих задач. Найти его можно с помощью формулы.
А детерминант находиться с помощью перемножения простых матриц, используются числа только с побочной и главной диагоналях.
Есть вероятность, что произведения матрицы будут значительно отличаться друг от друга. Если индекс чётный, то число будет со знаком плюс, если нечётный, то число будет со знаком минус. Обозначается определитель det А, а круглые скобки меняются на квадратные.
Дано
Решение
Пользуемся свойствам степеней – A^{3}=A^{2}*A
Возведём А в A^{2}
Далее используем свойство степеней
Ответ
Задание
Найдите определитель матрицы А.
Решение
Обратная матрица
Перед тем, как речь непосредственно пойдёт о самой обратной связи матрицы, давайте разберём алгоритм трансформирования матрицы. Во время трансформации столбцы и строки меняются местами.
Задание
Найти обратную матрицу А.
Решение
Приписываем к матрице А матрицу третьего ряда.
Переводим всё в единичную матрицу.
Ответ
Обратная матрица
Обратная матрица схожа с алгоритмом нахождения обратных чисел. К примеру, если умножить матричную таблицу на обратную матрицу, то в итоге мы получаем A*A(-1)=E. Но чтобы перейти уже к нахождению обратной матрицы, нам придётся найти её определитель. Мы рассмотрим самый простой способ – алгебраических дополнений.
Задание
В пример возьмём квадратную матрицу, она находиться с помощью следующей формулы:
, где
-транспортированные матрицы;|А| – определитель.
Рассмотрим самый простейший пример, где размер таблицы 2*2.
Найти обратную матрицу
Решение
Для начала находим определитель матрицы.
Если ответ равен нулю, то обратной матрицы нет! Так как наш ответ равен -2, то всё в порядке. Следующим действием нам нужно будет рассчитать матрицу миронов. Таблица элементов при этом не изменяется. Где прописан нужным нам элемент, нужно вычеркнуть строчку или столбец, оставшееся число и будет являться мироном.
Подставляем числа, возвращаясь к матрица, которая указана выше.
Всегда начинаем с левого верхнего угла и делаем следующее:
← линиями показано, что нужно и как зачеркнуть.
Как итог, у нас остаётся число 4
Теперь мы переходим к нахождению алгебраических дополнений.
Первым делом нужно поменять знаки у двух чисел в мироне.
← подчёркнуты те числа, у которых мы будем менять знаки.
, вот что у нас получилось.
И наконец-то мы переходим к завершающему этапу, к нахождению транспортированной матрице.
, вспоминаем формулу нахождения, и подставляем числовые значения
В завершении желательно проверить правильно ли мы нашли числовую таблицу. Это делать не обязательно, но рекомендуется, чтобы удостовериться в том, то ответ верный.
Задание
Найдите матрицу А.
Решение
Начинаем с определения матрицы.
Дело осталось за малым – осталось начти алгебраическое дополнение матрицы А:
Не забываем записать союзную матрицу:
И уже из неё находим обратную матрицу:
Получаем ответ
Пусть А = 
Определение 7. Определителем матрицы А (определителем N-го порядка) Называется алгебраическая сумма n! слагаемых, каждое из которых есть произведение n элементов матрицы, взятых по одному из каждой строки и каждого столбца. При этом произведение берётся со знаком «+», если подстановка из индексов входящих в него элементов чётная, и со знаком «-» в противном случае.
Обозначение определителя: |А| = 
Например, при n = 6 произведение А21а13а62а34а46а55 является членом определителя, так как в него входит точно по одному элементу из каждой строки и из каждого столбца. Подстановка, составленная из его индексов будет . В ней 4-е инверсии в верхней строке и 2-е инверсии – в нижней. Общее число инверсий равно 6, т. е. подстановка чётная. Следовательно, данное произведение входит в разложение определителя со знаком «+».
Произведение А21а13а62а34а46а15 не является членом определителя, так как в него входят два элемента из первой строки.
Свойства определителей.
10. При транспонировании определитель не меняется (напомним, что транспонирование матрицы и определителя означает перемену строк и столбцов местами).
Действительно, если (-1)к является членом определителя, то все a1, a2, … , an различны и к – число инверсий в перестановке (a1, a2, … , an). При транспонировании номера строк станут номерами столбцов и наоборот. Следовательно, в произведении
Все множители будут из разных столбцов и строк, т. е. это произведение будет входить в транспонированный определитель. Знак его будет определяться числом инверсий в подстановке
. Но это число, очевидно равно к. Итак, (-1)к
будет членом транспонированного определителя. Так как мы брали любой член данного определителя, а число членов в данном и транспонированном определителях одинаково, то отсюда и следует их равенство. Из доказанного свойства следует, что всё, что будет доказано для строк определителя, будет верно и для его столбцов.
20. Если все элементы строки (или столбца) определителя равны нулю, то определитель равен нулю.
Это следует из того, что по одному элементу указанной строки (или столбца) будет входить в каждый член определителя.
30. Если все элементы какой-нибудь строки определителя имеют общий множитель, то его можно вынести за знак определителя.
Действительно, если все элементы к-ой строки имеют общий множитель l, то их можно записать в виде . Любой член определителя будет иметь вид (-1)s
. Следовательно, из всех членов определителя можно вынести множитель l.
40. Если две строки определителя поменять местами, то определитель сменит знак.
Действительно, если (-1)к любой член данного определителя, то в новом определителе номера строк р и q поменяются местами, а номера столбцов останутся прежними. Следовательно, в новом определителе это же самое произведение будет входить в виде (-1)s
. Так как в номерах строк произошла одна транспозиция, а номера столбцов не изменились, то к и s имеют противоположные чётности. Итак, все члены данного определителя изменили знак, следовательно, и сам определитель изменил знак.
50. Если две строки определителя пропорциональны, то определитель равен нулю.
Действительно, пусть все элементы к-ой строки равны соответствующим элементам р-ой строки, умноженным на l, т. е. |А| = 

60. Если в определителе все элементы к-ой строки есть суммы двух слагаемых, то определитель равен сумме двух определителей, в которых все строки, кроме к-ой, такие же как и в данном определителе. На месте элементов к-ой строки одного из них стоят первые слагаемые элементов к-ой строки данного определителя, а на месте элементов к-ой строки второго – вторые их слагаемые.
Пусть элементы к-ой строки будут + Ск1,
+ Ск2, …. ,
+ Скn. Тогда любой член определителя будет иметь вид
(-1)s= (-1)s
+ (-1)s
.
Собрав все первые слагаемые, мы получим определитель, отличающийся от данного только к-ой строкой. На месте к-ой строки будут стоять ,
, …. ,
. Собрав все вторые слагаемые, получим определитель тоже отличающийся от данного только к-ой строкой. В к-ой строке будут стоять Ск1, ск2, …. , Скn.
70. Если к одной строке определителя прибавить другую его строку, все элементы которой умножены на одно и то же число, то определитель не изменится.
Это свойство является следствием двух предыдущих.
Если в определителе |А| вычеркнуть к-ую строку и р-ый столбец, то останется определитель (n–1)-го порядка. Он называется Минором, дополнительным для элемента и обозначается Мкр. Число (-1)к+р×МКр Называется Алгебраическим дополнением для элемента
и обозначается Акр.
80. Дополнительный минор и алгебраическое дополнение не зависит от того, какой элемент стоит в к-ой строке и р-ом столбце определителя.
Лемма 1 D = 
Доказательство. Если А11 = 0, то равенство (8) очевидно. Пусть А11 ¹ 0. Так как в каждый член определителя входит точно один элемент из первой строки, то ненулевыми членами определителя могут быть только те, в которые входит А11. Все они имеют вид , где gк и к пробегают значения от 2 до N. Знак этого члена в определителе D определяется чётностью подстановки s =

Со знаками, определяемыми подстановкой s. Если в этой сумме вынести за скобки А11, то получим, что D = А11× S, где S Есть алгебраическая сумма слагаемых вида
, знак которых определяется подстановкой s. Этих слагаемых, очевидно, (N – 1)!. Но подстановка s и подстановка

Лемма 2. D = 
Доказательство. В определителе D переставим р-ую строку последовательно с каждой предыдущей. При этом р-ая строка займёт место первой строки, но минор, дополнительный к элементу Арк не изменится. Всего будет сделано (Р – 1) перестановка строк. Если новый определитель обозначить D1, то D1 = (-1)р-1×D. В определителе D1 переставим К-ый столбец последовательно с каждым предыдущим столбцом, при этом будет сделано (К – 1) перестановка столбцов и минор, дополнительный к Арк, не изменится. Получится определитель
D2 = 
Теорема 3. Определитель равен сумме произведений элементов некоторой строки на их алгебраические дополнения, т. е. D = Ак1Ак1 + ак2×Ак2 +…+аKn×АKn (10).
Доказательство. Пусть D = 
= 0 + 0 + …+ 0 + А
. Используя свойство 60, получим, что D =

А
(использовали лемму 2).
Теорема 4. Сумма произведений элементов одной строки определителя на алгебраические дополнения соответствующих элементов другой строки равна нулю.
Доказательство. Пусть D = 
D = . Если взять
, то в определителе Dбудет две одинаковые строки, т. е. D будет равен нулю. Следовательно, 0 =
, если р ¹ к.
Замечание. Теоремы 3 и 4 будут верны, если в их формулировках слово «строка» заменить на слово «столбец».
Способ вычисления определителя N-го порядка.
Для вычисления определителя N-го порядка достаточно в какой-нибудь строке (или столбце) получить как можно больше нулей, используя свойство 70, а потом использовать теорему 3. При этом вычисление определителя n-го порядка сведётся к вычислению определителя (N – 1)-го порядка.
Пример. Вычислите определитель D = 
Решение. Получим нули во второй строке. Для этого Второй столбец 1) умножим на (-2) и прибавим к первому столбцу; 2) прибавим к третьему столбцу; 3) умножим на (-4) и прибавим к четвёртому столбцу. Получим, что D = 

D = 
. Используя свойство 70, прибавим к первому столбцу второй, получим D = —
= -3×(23 – 40) = 51.
Некоторые определители (например, такие, в которых стоят «большие» миноры, целиком состоящие из нулей) удобно разлагать по нескольким строкам. Это позволяет делать теорема Лапласа. Пусть в определителе D выделен минор М s-го порядка, элементы которого стоят на строках с номерами К1,к2,…,кS И на столбцах с номерами Р1,р2,…,рS . Вычеркнем строки и столбцы с указанными номерами. После этого останется определитель (N – s)-го порядка. Его называют минором М1, дополнительным к минору М. Если s = К1+…+ кS + р1+…+рS, то
Алгебраическим дополнением к минору М Называется А = (-1)s×М1.
Теорема 5 (теорема Лапласа). Пусть в определителе N-го порядка выделены К строк (или столбцов). Определитель равен сумме произведений всех миноров, стоящих на выделенных строках, на их алгебраические дополнения.
Доказательство этой теоремы опустим.
Пример. 
Теорема 6 (теорема Крамера). Если в системе линейных уравнений число неизвестных равно числу уравнений и определитель D системы отличен от нуля, то система имеет решение и только одно. Это решение получается по формулам , где каждое Dк получается из D заменой к-го столбца столбцом свободных членов.
Доказательство. Пусть дана система 

+… … +
+ … +
=
Используя теоремы 3 и 4, получим Х1×0 + … + Хк×D + … + ХN×0 = DК , где DК = 
=
для всех К = 1, 2, …, N.
| < Предыдущая | Следующая > |
|---|
- Виды матриц.
- Матрица A размера m×n — это прямоугольная таблица чисел, расположенных в m строках и n столбцах
где aij (i =1, …, m; j =1, …, n) — это элементы матрицы A. Первый индекс i — это номер строки, второй индекс j — это номер столбца, на пересечении которых расположен элемент aij.
Сокращённое обозначение матрицы A=(aij)m×n. - Порядок матрицы — это число ее строк или столбцов.
- Главная диагональ квадратной матрицы — это диагональ, идущая из левого верхнего в правый нижний угол.
- Прямоугольная матрица — это матрица, у которой число строк не равно числу столбцов.
- Квадратная матрица — это матрица у которой число строк равно числу столбцов:
- Матрица-столбец — это матрица, у которой всего один столбец:
- Матрица-строка — это матрица, у которой всего одна строка:
- Диагональная матрица — это квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю.
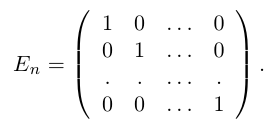
- Единичная матрица — это диагональная матрица, у которой все диагональные элементы равны единице:
- Матрица квадратная диагональная:
- Треугольная матрица — это квадратная матрица, у которой все элементы, расположенные по одну сторону главной диагонали, равны нулю.
- Матрица верхняя треугольная:
- Матрица нижняя треугольная:
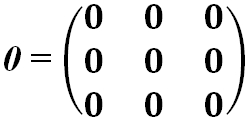
- Нулевая матрица — это матрица, все элементы которой равны 0:
- Операции над матрицами.
- Равенство матриц.
Две матрицы A (aij), B (bij) совпадают |A=B|, если совпадают их размеры и соответствующие элементы равны,
то есть при всех i, j aij=bij. - Сложение матриц.
Суммой двух матриц A=(aij)m×n и B=(bij) m×n одинаковых размеров называется матрица C=(cij)m×n=A+B тех же размеров, элементы которой определяются равенствами cij=aij+bij. Пример 1. - Умножение матрицы на число.
Произведением матрицы A=(aij)m×n на число λ ∈ R называется матрица B=(bij)m×n=λA, элементы которой определяются равенствами bij=λaij. Пример 2. - Умножение матриц.
Произведением матрицы A=(aij)m×k на матрицу B=(bij)k×n называется матрица C=(cij)m×n=A· B размера m×n, элементы которой cij определяются равенством
cij=ai1b1j+ai2b2j+ … aikbkj.
Таким образом, элемент матрицы C=A·B, расположенный в i-й строке и j-м столбце, равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B. Пример 3. - Транспонированные матрицы.
Транспонированием матрицы А называется замена строк этой матрицы ее столбцами с сохранением их номеров.
Полученная матрица обозначается через A’ или AT. Пример 4.
Квадратная матрица называется симметричной, если A=A’, то есть для элементов выполнены равенства aij=aji. - Обратная матрица.
Квадратная матрица n–го порядка называется вырожденной, если определитель этой матрицы равен нулю, |A| = 0, и невырожденной, если |A| ≠ 0.
Матрица А-1 называется обратной матрицей для некоторой квадратной матрицы А, если выполняется соотношение:
Если матрица А-1 не вырождена, то существует, и притом единственная, обратная матрица А-1, равная, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
1)
2)
3)
4) - Алгоритм нахождения А-1 заключается в следующих пунктах:
1) Находим det A, проверяем det A ≠ 0.
2) Находим Mij — все миноры матрицы A.
3) Определяем
4) Строим матрицу алгебраических дополненийи транспонируем:
5) Делим каждый элемент матрицы на det A:Пример 5.
- Элементарные преобразования строк (столбцов) матрицы:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число α ≠ 0;
3) прибавление к элементам строки (столбца) матрицы элементов другой строки (столбца), умноженных на некоторое число. - Решение матричных уравнений.
Матричное уравнение — это уравнение, содержащее неизвестную матрицу X и известные матрицы A, B, …, .
Простейшие типы матричных уравнений:
1). Матрица A – квадратная и невырожденная,
|A| ≠ 0, следовательно, существует обратная матрица A-1.
Умножим уравнение на A-1 слева:
2). Матрица A – квадратная, |A| ≠ 0.
Умножим уравнение на A-1 справа:.
3). Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
Умножим уравнение на A-1 слева:
Умножим уравнение на B-1 справа:.
- Ранг матрицы.
Ранг матрицы A — это число, равное максимальному порядку отличных от нуля миноров.
Mk этой матрицы:
Матрицы называются эквивалентными, что обозначается
A ∼ B, если.
Ранг матрицы A вычисляется методом окаймляющих миноров или методом элементарных преобразований. - Метод окаймляющих миноров.
Пусть в матрице A элемент aij ≠ 0, тогда M1 ≠ 0 и r(A) ≥ 1. Окаймляем этот элемент элементами соседнего столбца и соседней строки (например, (j+1)–го столбца и (i+1)–й строки), получаем минор 2-го порядка:.
Если M2, то присоединяем другие строки и столбцы, перебирая все возможные миноры 2-го порядка.
Если все миноры второго порядка равны нулю, то r(A) = 1; если же существует хотя бы один минор 2-го порядка, отличный от нуля, то r(A) ≥ 1.
Выбираем отличный от нуля минор 2-го порядка M2 и окаймляем его элементами соседних строк и столбцов до минора 3-го порядка и так до тех пор, пока не будет выполнено условие: Mr ≠ 0, но все Mr+1 = 0. Пример 6. - Метод элементарных преобразований.
Элементарные преобразования матрицы не меняют ее ранга.
К элементарным преобразованиям матрицы относятся следующие: транспонирование; перестановка строк (столбцов); умножение строки (столбца) на число α ≠ 0; прибавление к элементам строки (столбца) матрицы элементов другой строки, умноженных на некоторое число; отбрасывание нулевой строки (столбца) матрицы.
Для определения ранга матрицы A методом элементарных преобразований следует:
1) Переставить строки и столбцы так, чтобы в верхнем левом углу матрицы был ненулевой элемент.
2) Все элементы первого столбца, кроме a11, обратить в ноль с помощью элементарных преобразований строк:
3) Переставить строки со 2–й по m и столбцы со 2–го по n так, чтобы a22 ≠ 0. Повторить операцию (2) со вторым столбцом: во втором столбце все элементы, кроме a12 и a22, обратить в ноль.
Окончательно после многократного применения указанной процедуры и отбрасывания нулевых строк преобразованная матрица будет иметь вид:
Тогда ранг матрицы A равен: rang A = rang Ã.
- Свойства определителей.
- Определитель квадратной матрицы А не меняется при транспонировании: |AT|=|A|.
- При перестановке местами любых двух строк (столбцов) определитель |A| меняет знак:
- Определитель, содержащий две одинаковые строки (столбца), равен нулю.
- Умножение всех элементов некоторой строки (столбца) определителя |A| на число k равносильно умножению определителя на это число:
- Если все элементы некоторой строки (столбца) определителя |A| равны нулю, то и сам определитель равен нулю (вытекает из предыдущего свойства при (k = 0):
- Если все элементы двух строк (столбцов) определителя |A| пропорциональны, то определитель равен нулю.
- Если каждый элемент некоторой строки (столбца) определителя представляет собой сумму двух слагаемых, то такой определитель можно представить в виде суммы двух определителей:
- Если к элементам какой-нибудь строки (столбца) определителя |A| прибавить соответствующие элементы другой строки (столбца), умноженные на произвольный множитель k, то величина определителя не изменится:
- Определитель |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения:
- Определитель произведения матриц А и В равен произведению их определителей:
.
- Определители n–го порядка.
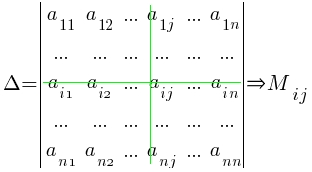
- Минор Мij или Δij элемента аij ( иначе – дополнительный минор элемента аij) определителя n-го порядка — это определитель (n–1) порядка, полученный из исходного вычеркиванием i–й строки и j–го столбца, на пересечении которых стоит элемент aij.
- Алгебраическое дополнение Аij элемента аij — это его минор со знаком (-1)i+j, где i – номер строки, а j – номер столбца, на пересечении которых стоит элемент aij, Аij=(-1)i+jMij или Аij=(-1)i+jΔij. Пример 8.
Для определителей n-го порядка имеют место все перечисленные выше свойства определителей. - Правило выбора знака перед минором в алгебраическом дополнении:
- Определитель n-го порядка |A| численно равен сумме произведений элементов любой его строки (столбца) на соответствующие алгебраические дополнения.
- Метод сведения к треугольному виду.
Используя свойства (1–9), определитель преобразуют к виду, когда элементы, лежащие по одну сторону от главной диагонали, становятся равными нулю. Преобразованный таким образом определитель равен произведению элементов, лежащих на главной диагонали.
Формулы, уравнения, теоремы, примеры решения задач
Содержание:
Линейная алгебра
Линейная алгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения, системы линейных уравнений, среди основных инструментов, используемых в линейной алгебре — определители, матрицы, сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры.
Матрицы и операции над ними
Основные определения:
В математике и ее приложениях наряду с числами часто бывает удобным использовать числовые таблицы, которые называются матрицами. Аппарат теории матриц эффективно применяется, например, при решении систем линейных уравнений, как мы скоро в этом убедимся. Перейдем к точным определениям.
Определение: Матрицей размерности m х n называется прямоугольная таблица действительных чисел, состоящая из m строк и n столбцов.
Числа, составляющие матрицу, называются ее элементами. Для доступа к элементам матрицы используются два индекса: первый указывает на номер строки, второй — на номер столбца, на пересечении которых расположен данный элемент.
Обозначаются матрицы, как правило, прописными латинскими буквами A, B, C,иногда указывается размерность, например, Amxn. В развернутой форме матрица записывается как таблица:
Более компактно с указанием элементов матрица записывается в виде:
Матрицы А и В одинаковой размерности считаются равными, если все элементы одной матрицы равны соответвующим элементам другой матрицы.
Рассмотрим некоторые специальные виды матриц.
Матрица, у которой все элементы равны нулю, называется нуль-матрицей и обозначается через O.
Матрица, у которой число строк равно числу столбцов, называется квадратной. Размерность квадратной матрицы часто называют ее порядком.
Числа 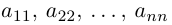
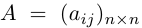
Квадратная матрица, диагональные элементы которой равны единице, а все остальные — нулю, называется единичной матрицей и обозначается через 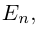
Таким образом,
Квадратная матрица называется треугольной, если все ее элементы, расположенные ниже (выше) главной диагонали, равны нулю. Например, треугольной является матрица
Матрица называется трапециевидной, если она представляет собой следующую таблицу:
Операции над матрицами
Введем сначала линейные операции над матрицами.
Произведением действительного числа 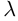
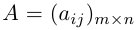
Суммой двух матриц 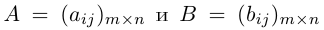
Таким образом, элементы суммы матриц равны суммам соответствующих элементов данных матриц.
Разность матриц А и B можно определить как А — В = А + (-1)В.
Свойства линейных операций над матрицами аналогичны соответствующим свойствам действительных чисел.
Пример №1
Даны матрицы
Найти матрицу -2А +3В.
Решение.
Тогда
Определим теперь операцию умножения матриц. Рассмотрим сначала матрицу-строку и матрицу-столбец с одинаковым числом элементов, т.е.
Произведением этих строки и столбца называется число1
Рассмотрим так называемые согласованные матрицы 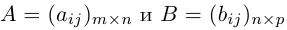
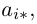
Произведением данных согласованных матриц А и B называется матрица
Часто для суммы n чисел 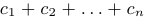
размерности m х p, элементы которой равны произведениям строк матрицы A на столбцы B.
Пример №2
Найти произведение согласованных матриц
Решение. Найдем произведение строк матрицы А на столбцы матрицы В.
Осталось записать искомое произведение матриц:
Отметим некоторые свойства произведения матриц1.
Первые три сразу следуют из определения произведения матриц. Докажем последнее свойство. Пусть заданы три матрицы 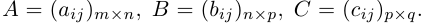
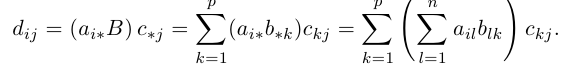
что представляет собой произведение Тем строки с номером i матрицы A на столбец с номером j матрицы ВС. Тем самым свойство 4 доказано.
Заметим, что в отличие от чисел матрицы, вообще говоря, не коммутируют (не перестановочны). Приведем соответствующий
Контрпример. Доказать, что матрицы
не коммутируют.
Действительно,
Таким образом, для этих матриц
Замечание. Пользуясь случаем, введем здесь определение n-мерного векторного пространства Rn, как множество упорядоченных совокупностей n действительных чисел. Каждую такую совокупность мы будем обозначать через и называть n-мерным вектором.
Мы предполагаем, что все матрицы в свойствах согласованы.
Очевидно, каждый вектор мы можем отождествить с соответствующей матрицей-строкой или матрицей-столбцом, поэтому на векторы автоматически переносятся линейные операции, которые мы определили выше для матриц.
Определитель матрицы и его свойства
Познакомимся теперь с такой важнейшей характеристикой матрицы, как определитель. Введем предварительно понятие перестановки и изучим некоторые ее свойства.
Перестановки
Перестановкой n натуральных чисел 1, 2, ….., n называется строка
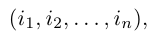
содержащая все эти числа.
Первым элементом перестановки может быть любое из чисел 1, 2, …., n, вторым — любое из оставшихся n — 1 чисел и так далее, следовательно, число различных перестановок данных чисел равно 
Два числа в перестановке находятся в инверсии, если большее из них имеет меньший номер. Число всех инверсий в перестановке (1) мы обозначим через
В связи с этим перестановка (1) называется четной, если в ней число 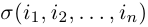
Отметим два свойства перестановок, которые мы будем использовать ниже.
Лемма 1. Характер четности перестановки изменится на противоположный, если в ней поменять местами какие-нибудь два элемента.
Доказательство. Предположим сначала, что меняются местами рядом стоящие элементы к и l перестановки. В этом случае число инверсий в новой перестановке изменится на единицу, а именно, увеличится на единицу, если к и l не находились в инверсии, или настолько же уменьшится, если они находились в инверсии. Таким образом, характер четности перестановки изменится на противоположный. Рассмотрим теперь случай, когда числа к и l разделяют s других элементов перестановки. Тогда поменять местами данные элементы мы можем последовательно переставляя число к с s промежуточными элементами, а затем переставляя число l в обратном порядке с элементом к и всеми s промежуточными. В результате мы выполним 2s + 1 обменов рядом стоящих элементов и, таким образом, характер четности исходной перестановки изменится нечетное число раз и, следовательно, он изменится на противоположный. Лемма доказана.
Из этой леммы сразу же следует, что количество четных перестановок равно количеству нечетных. В самом деле, поменяв местами любые два элемента в каждой из p четных перестановок, мы получим p нечетных и, следовательно, 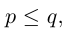
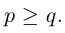
Лемма 2. Пусть
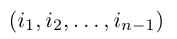
— перестановка чисел 1, 2, …, n — 1. Зафиксируем число j из множества {1, 2, … , n} и оставим его перестановку (2) на место с номером i, сдвинув вправо на одну позицию все ее элементы с номерами i, i + 1, … , n — 1 и увеличив на единицу все не меньшие, чем j элементы этой перестановки. В результате получим перестановку
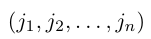
чисел 1, 2, …. , n. Четности перестановок (2) и (3) связаны равенством
Действительно, предположим сначало, что элемент j в перестановке (3) стоит на первом месте. Тогда, очевидно, количество инверсий в этой перестановке равно 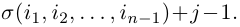
Определитель и его вычисление для матриц второго и третьего порядков
Рассмотрим квадратную матрицу порядка n :
Составим произведение элементов данной матрицы, взятых по одному из каждой строки и каждого столбца. Упорядочив элементы этого произведения по возрастанию номеров строк, мы можем записать его в виде:
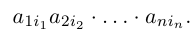
Номера столбцов в записанном произведении образуют перестановку чисел 1, 2, … , n.
Определение: Число, равное сумме всех n! произведений
называется определителем данной квадратной матрицы А (определителем n-го порядка) и обозначается через |А| или det А. В развернутой форме определитель записывается как
Найдем пользуясь этим определением выражение для определителей второго и третьего порядков.
Так как 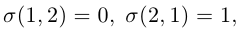
Аналогично, для вычисления определителя третьего порядка найдем число инверсий в каждой из перестановок чисел 1, 2, 3 :
Тогда
Для упрощения вычисления определителя третьего порядка можно использовать правило треугольников, согласно которому со знаком » + » следует брать произведения по схеме
а со знаком » — » — по схеме
Пример №3
Вычислить определитель
Решение. Воспользуемся правилом треугольников: 
Свойства определителя
1) Если какая-либо строка (столбец) определителя состоит из нулей, то и определитель равен нулю.
2) Общий множитель элементов какой-либо строки (столбца) можно выносить за знак определителя.
3) Если все элементы какой-нибудь строки (столбца) определителя равны суммам двух слагаемых, то данный определитель равен сумме двух определителей, в которых в указанной строке (столбце) стоят, соответственно, первые и вторые слагаемые, а остальные элементы обоих определителей такие же, как и в исходном определителе.
Эти свойства напрямую следуют из определения определителя.
4) Если переставить две какие-нибудь строки (столбца) определителя, то он поменяет знак на противоположный.
Действительно, переставим, например, две строки определителя. В результате получим определитель, каждое слагаемое которого отличается знаком от соответствующего слагаемого исходного определителя, так как по доказанной в пункте 1 лемме 1 четность соответствующей перестановки вторых индексов изменится па противоположную.
5) Если в определителе совпадают (пропорциональны) две какие-нибудь строки (столбцы), то этот определитель равен нулю.
В самом деле, если в определителе совпадают две каие-нибудь строки (столбцы), то, с одной стороны, определитель при этом не изменится, а, с другой стороны, по предыдущему свойству его знак поменяется на противоположный. Таким образом |A| = — |A| и, стало быть, |A| = 0. Если же в определителе имеются две пропорциональные строки (столбца), то после вынесения за его знак по свойству 2) общего множителя элементов строки (столбца), мы получим определитель с двумя одинаковыми строками (столбцами), который равен нулю.
6) Определитель не изменится, если к элементам какой-нибудь строки (столбца) добавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.
Это следует из свойств 3) и 5), так как в этом случае полученный определитель можно представить в виде суммы двух определителей, один из которых равен исходному, а в другом имеются пропорциональные строки (столбцы), и поэтому он равен пулю.
Прежде чем сформулировать очередное свойство, введем понятие алгебраического дополнения к элементу матрицы.
Алгеброическим дополнением элемента aij квадратной матрицы A = (aij)nxn мы будем называть число
где 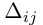
7) Разложение определителя по элементам строки (столбца).
Определитель матрицы равен сумме произведений элементов какой-нибудь строки (столбца) на соответствующие алгебраические дополнения. Таким образом,
или
Докажем, например, первую из этих формул. Убедимся в том, что правая часть данной формулы содержит все слагаемые определителя матрицы А. Выражение
содержит n(n — 1)! = n! различных произведений элементов определи теля матрицы A, взятых по одному из каждой строки и каждого столбца. Осталось проверить соответствие знаков.
Рассмотрим произвольное произведение
Каждое слагаемое определителя 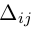
чисел 1, 2, … , n — 1. Умножив данное произведение на число 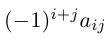
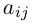
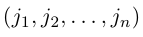
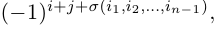
Таким образом, вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка.
Пример №4
Вычислить определитель.
Решение. Разложим этот определитель по элементам второй строки:
Пример №5
Вычислить определитель треугольной матрицы
Разлагая этот и следующие определители по первому столбцу, получим:
таким образом, определитель треугольной матрицы равен произведению диагональных элементов.

Это свойство является прямым следствием предыдущего.
9) Сумма произведений элементов какой-нибудь строки (столбца) на алгебраические дополнения к элементам какой-нибудь другой строки (столбца) определителя равна нулю.
Действительно, по предыдущему свойству эта сумма произведений равна определителю с двумя совпадающими строками (столбцами), а такой определитель по свойству 5) равен нулю.
10) Определитель произведения матриц равен произведению определителей этих матриц, т. е.
Достаточно громоздкое доказательство этого свойства мы приводить не будем.
Обратная матрица
Определение: Обратной к квадратной матрице 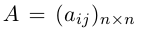
Из этого определения следует, что матрица А-1 также является квадратной той же размерности, что и матрица А.
Отметим некоторые свойства обратной матрицы, следующие из ее определения.
а) У матрицы не может существовать больше одной обратной.
Действительно, пусть для матрицы А имеются две обратные 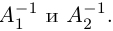
Умножив обе части первого равенства слева на матрицу 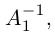
b) (A-1)-1 = A.
c) Если для квадратных матриц А и В одного порядка существуют обратные, то и у матрицы АВ также существует обратная , причем
Выясним условия, при которых обратная матрица существует.
Теорема (критерий существования обратной матрицы). Для того, чтобы существовала матрица, обратная данной, необходимо и достаточно, чтобы данная матрица была невырожденной, то есть чтобы ее определитель был не равен нулю.
Доказательство. Докажем сначала необходимость условия теоремы. Пусть для матрицы А существует обратная матрица. Тогда из равенства АА-1 = E, воспользовавшись свойством 10) определителя произведения матриц, получаем: det(AA-1) = det А 
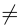
Убедимся теперь в том, что условие теоремы является и достаточным. Предположим, что матрица А является невырожденной. Проверим, что обратной к данной является матрица со следующей структурой 1:
Действительно, если
откуда, воспользовавшись свойствами 7) и 9) определителя (§2, пункт 3), заключаем:
т. е. АА-1 = Е. Аналогично убеждаем, что А-1А = Е. Теорема доказана.
В строках указанной ниже матрицы записаны алгебраические дополнения к элементам соответствующих столбцов.
Пример №6
Найти обратную к матрице
Решение. Найдем сначала определитель матрицы: 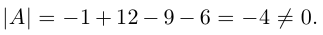
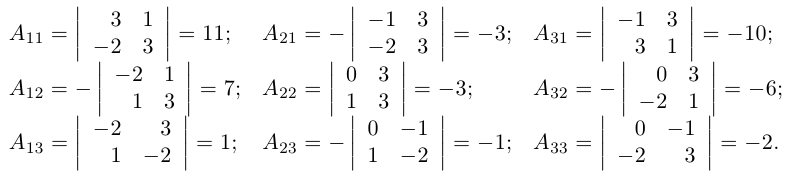
Обратную матрицу можно использовать при решении линейных матричных уравнений. Пусть, например, требуется решить матричное уравнение
AX = B
с известными матрицами А и B, причем матрица A является невырожденной. Умножая обе части данного матричного уравнения слева на обратную матрицу A-1, получим:
Аналогично, решением матричного уравнения XA = B является матрица X = BA-1, а решением матричного уравнения AXB = С с невырожденными матрицами A и B является матрица X = A-1CB-1.
Ранг матрицы и его вычисление
Рассмотрим произвольную матрицу
Минором порядка k матрицы A называется определитель, стоящий на пересечении выбранных k строк и k столбцов данной матрицы.
Определение: Рангом матрицы А называется максимальный из порядков ненулевых миноров этой матрицы. Обозначается ранг через rang A.
Естественно считать, что rang O = 0. Очевидно также, что
Пример №7
Найти ранг матрицы
Решение. Вычислим минор, находящийся на пересечении первых двух строк и первого и четвертого столбцов:
Все же миноры третьего порядка этой матрицы равны нулю, так как третья строка равна разности второй и первой строк. Следовательно, rang A = 2.
Как видно из определения, вычисление ранга матрицы через миноры является весьма трудоемкой задачей, особенно для матриц большой размерности. Значительно сократить объем вычислений позволяет другой метод, основанный на элементарных преобразованиях матрицы.
Элементарными преобразованиями матрицы называются следующие операции над ее строками или столбцами:
- перестановка двух строк (столбцов) матрицы;
- умножение строки (столбца) на ненулевое действительное число;
- добавление к строке (столбцу) другой строки (столбца), умноженной на действительное число.
Тот факт, что матрица В получена из матрицы А с помощью одного или нескольких последовательно выполненных элементарных преобразований, мы будем обе тачать как
Теорема. Ранг матрицы не меняется при ее элементарных преобразованиях.
Доказательство этого утверждения для первого и второго элементарных преобразований следует из того, что по свойствам 2) и 4) определителя (§2, пункт 3) миноры исходной матрицы могут отличаться от миноров преобразованной разве лишь знаком или ненулевым множителем, что. естественно, не отражается на ранге матрицы. Пусть теперь матрица А’ получена из матрицы А с помощью третьего элементарного преобразования, для определенности будем считать, что к строке с номером i добавлена строка с номером j, умноженная на действительное число 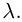
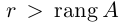
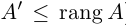
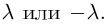
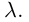
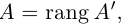
Из этой теоремы следует, что для вычисления ранга матрицы достаточно привести ее с помощью элементарных преобразований к более простой — трапециевидной, ранг которой легко находится. Изложим соответствующий алгоритм, который мы будем использовать ниже при решении систем линейных алгебраических уравнений.
Итак, рассмотрим матрицу
Если А = О, то rang A = 0. Пусть теперь 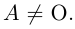
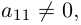
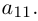
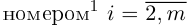
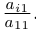
Повторяя теперь все рассуждения из предыдущего абзаца применительно к полученной матрице с вычеркнутыми из нее первой строкой и первым столбцом и всем последующим матрицам, после конечного числа шагов, не превышающего m — 1, мы придем к трапециевидной матрице
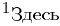
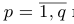
с r ненулевыми диагональными элементами a11, b22, . . . , crr. Ранг матрицы 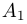

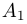
элементарных преобразований, то
Замечание. При практическом использовании приведенного алгоритма матрицу бывает
иногда удобно приводить к форме, которая отличается от трапециевидной порядком следования столбцов.
Пример №8
Найти ранг матрицы
Решение.
Приведем матрицу к трапециевидной с помощью элементарных преобразований:
Здесь вторая матрица получена из исходной вычитанием в ней из второй и третьей строк первой, умноженной на 4 и 3 соответственно, а затем вторая матрица преобразована в третью вычитанием из последней строки, умноженной на 5, второй строки. Перегнав в последней матрице четвертый столбец на первое место, получим трапециевидную матрицу с тремя ненулевыми элементами на диагонали. Следовательно, rang
Системы линейных алгебраических уравнений
Основные определения:
Определение: Системой m линейных алгебраических уравнений с n неизвестными (или, короче, линейной системой) называется система вида
где действительные числа 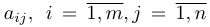
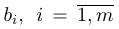
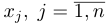
Числа 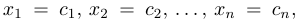
Для этого введем следующие обозначения:

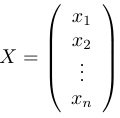
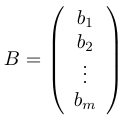
В этих обозначениях данная линейная система принимает вид:
AX = B.
Линейная система с нулевыми правыми частями, т.е. система АХ = О, называется однородной.
Решение невырожденных линейных систем
Рассмотрим линейную систему n уравнений с n неизвестными и невырожденной основной матрицей. Такая система называется невырожденной.
Рассмотрим два метода решения невырожденных систем.
Метод обратной матрицы
Так как определитель основной матрицы невырожденной системы линейных уравнений отличен от Iгуля. то решение этой системы мы можем найти как решение матричного линейного уравнения (§3)
по формуле
Полученное таким образом решение является единственным. Действительно, пусть 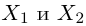
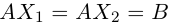
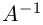
Пример №9
Решить систему линейных уравнений:
Решение.
Здесь
В §3 был вычислен определитель матрицы данной системы 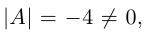
Тогда
Таким образом, 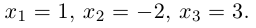
Формулы Крамера
Воспользовавшись представлением обратной матрицы через алгебраические дополнения, получим:
следовательно,
По свойству 
т. е. определителю, который может быть получен из определителя 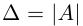
Пример №10
Решить систему линейных уравнений:
Решение. Для этой системы 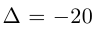
Тогда по формулам Крамера
Решение произвольных систем линейных уравнений. Метод исключения неизвестных (метод Гаусса)
Рассмотрим линейную систему общего вида:
Определим, как и для матриц, элементарные преобразования над уравнениями линейной системы. Таковыми являются:
- перестановка двух уравнений системы;
- умножение обеих частей уравнения на отличное от. нуля действительное число:
- добавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на действительное число.
Все эти преобразования, очевидно, обратимы и поэтому их результатом является система, эквивалентная исходной, т. е. система, множество решений которой, совпадает с множеством решений данной системы.
Упростим теперь систему, последовательно исключая неизвестные из ее уравнений с помощью элементарных преобразований. Для этого, расширенную матрицу системы
с помощью элементарных преобразований над ее строками приведем к трапециевидной форме с помощью алгоритма, изложенного в §4. В результате получим матрицу
где диагональные элементы 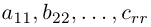
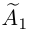
Очевидно, последняя система получена из исходной с помощью тех же элементарных преобразований, какими матрица 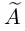
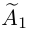
Рассмотрим два случая, которые здесь возможны.
a) 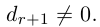
b)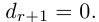
Здесь, в свою очередь, представляются две возможности.
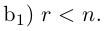
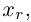
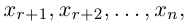
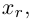
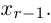
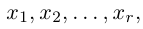
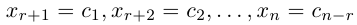
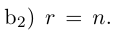
Приведенный алгоритм метода исключения неизвестных позволяет сформулировать критерий совместности линейной системы.
Теорема Кронекера. Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы системы равен рангу ее расширенной матрицы.
Доказательство немедленно следует из вида матрицы 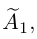
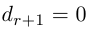
Из теоремы Кронекера следует, что если 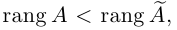
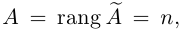
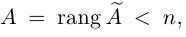
Пример №11
Решить систему линейных уравнений:
Решение. Приведем расширенную матрицу этой системы к трапециевидной с помощью элементарных преобразований над ее строками:
Вторая матрица получена из первой вычитанием из третьей строки второй и добавлением ко второй строке, умноженной на 2, первой строки. С точностью до перестановки столбцов, мы получили трапециевидную матрицу. Здесь, очевидно, rang 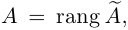
Придавая свободным неизвестным 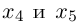
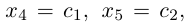
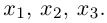
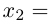
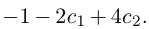
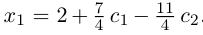
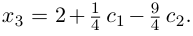
где 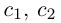
Замечание. Однородная система линейных уравнений всегда совместна, так как она имеет нулевое решение. Если rang A = n, то однородная система имеет единственное (нулевое) решение. а если 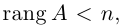
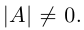
Обращение невырожденной матрицы с помощью элементарных преобразований
Рассмотрим невырожденную квадратную матрицу 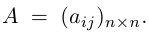
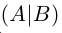
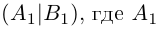
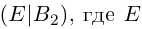
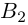
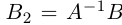
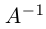
Таким образом, для того, чтобы найти матрицу, обратную к данной невырожденной матрице А, достаточно в расширенной матрице 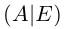
Пример №12
Найти обратную к матрице
Решение. Воспользуемся изложенным выше алгоритмом.
Следовательно,
Изложенный выше алгоритм нахождения обратной матрицы является более экономичным по сравнению с изложенным в §3, так как он требует гораздо меньшего объема вычислений. Заметим также, что программирование этого метода также не представляет трудностей.
Справочный материал по линейной алгебра
Этот раздел математики возник в связи с необходимостью решать системы линейных уравнений.
Рассмотрим систему линейных уравнений:
Чтобы решить ее, можно, например, выразить одну из переменных из первого уравнения, подставить во второе, после чего найти неизвестные x и y .
Однако можно найти решение быстрее: легко убедиться, что
Способ получения этого результата станет ясным, если рассмотреть таблицы, составленные из коэффициентов системы:
Такие таблицы называются матрицами второго порядка (так как в них две строки и два столбца), а соответствующие числа — определителями. Матрицы и определители играют важную роль при решении более сложных систем линейных уравнений, поэтому начнем изучение линейной алгебры с матриц.
Матрицы и действия над ними
Определение: Числовой матрицей размера 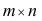
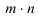
столбцов.
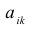
Определение: Если 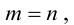
Элементы 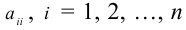
Матрица размера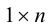
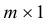
Пример №13
Определение: Две матрицы называются равными, если они имеют
одинаковый размер и равны их элементы, стоящие на одинаковых местах.
Пример №14
Определение: Квадратная матрица называется диагональной, если равны нулю все ее элементы, расположенные вне главной диагонали, то есть
На главной диагонали могут быть любые числа. Если все они равны 1, то диагональная матрица называется единичной и обозначается буквой E .
Пример №15
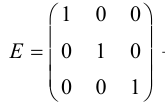
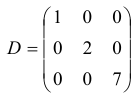
Определение: Квадратная матрица называется треугольной, если все ее элементы снизу (сверху) от главной диагонали равны нулю.
Пример №16
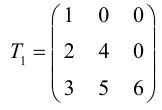
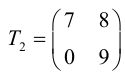
Линейные операции над матрицами
К числу линейных относятся операции сложения и умножения на число.
Определение: Пусть 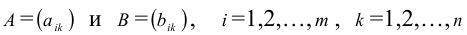
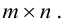
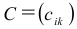
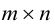
Пример №17
Определение: Произведением матрицы 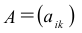
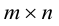
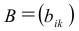
Пример №18
Определение: Нулевой матрицей O называется матрица, все элементы которой равны нулю.
Определение: Матрица (-1) * A называется противоположной для A и обозначается -A.
Очевидно, что 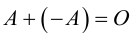
Определение: Разностью матриц A и B одного размера называется сумма 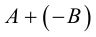
Определение: Результат конечного числа линейных операций над матрицами называется их линейной комбинацией.
Пример №19
Пусть
Матрица 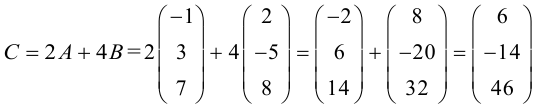
Свойства линейных операций
Если A , B , и C – матрицы одного размера, 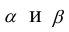
1. 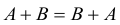
2. 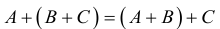
3. 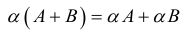
4. 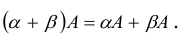
5.
Транспонирование и умножение матриц
Эти операции над матрицами не относятся к числу линейных.
Определение: Транспонированной матрицей 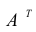
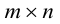
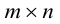
То есть, если
Пример №20
Определение: Если 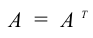
Все диагональные матрицы симметрические, так как равны их элементы,
симметричные относительно главной диагонали.
Очевидно, справедливы следующие свойства операции транспонирования:
Определение: Пусть 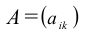
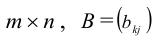
матрица размера 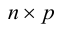
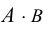
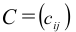
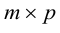
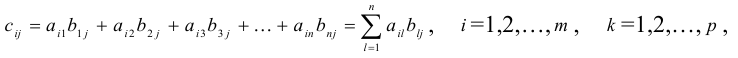
Пример №21
Произведение 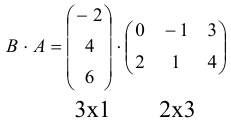
Свойства операции умножения матриц
1. 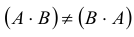
Пример №22
Определение: Матрицы A и B называются перестановочными, если 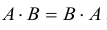
Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.
Пример №23
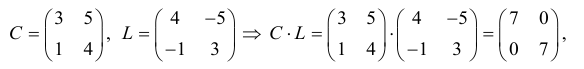
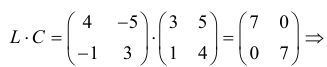
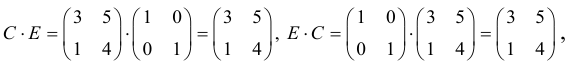
Вообще единичная матрица перестановочная с любой квадратной матрицей того же порядка, и для любой матрицы 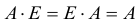
чисел таким свойством обладает число 1.
Если соответствующие произведения определены, то:
Пример №24
ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.
Пример №25
Определители и их свойства
Каждой квадратной матрице можно по определенным правилам поста-
вить в соответствие некоторое число, которое называется ее определителем.
Рассмотрим квадратную матрицу второго порядка:
Её определителем называется число, которое записывается и вычисляется так:
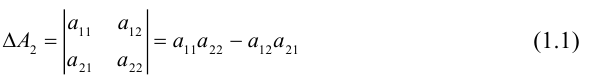
Такой определитель называется определителем второго порядка и может
обозначаться по-другому:
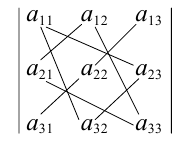
Определителем третьего порядка называется число, соответствующее квадратной матрице 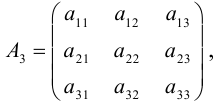
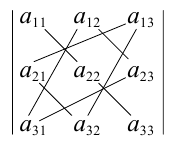
Это правило вычисления определителя третьего порядка называется правилом треугольников и схематически его можно представить так:

Пример №26
Если справа от определителя приписать первый, а затем второй столбец, то правило треугольников можно модифицировать:
Сначала умножаются числа на главной диагонали и двух ей параллельных диагоналях, затем – числа на другой (побочной) диагонали и ей параллельных. Из суммы первых трех произведений вычитается сумма остальных.
Группируя слагаемые в (1.2) и используя (1.1), заметим, что
То есть при вычислении определителя третьего порядка используются
определители второго порядка, причем 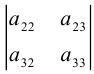
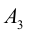
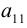
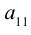
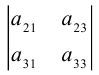
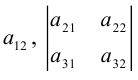
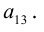
Определение: Дополнительным минором 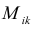
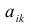
Пример №27
и так далее: матрица третьего порядка имеет 9 дополнительных миноров.
Определение: Алгебраическим дополнением элемента aik квадратной
матрицы A называется число
Пример №28
Для матрицы A2 :
Для матрицы A3: 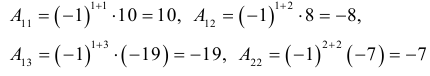
Итак, с учетом сформулированных определений (1.3) можно переписать в
виде: 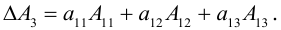
Перейдем теперь к общему случаю.
Определение: Определителем квадратной матрицы 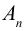
Равенство (1.4) называется разложением определителя по элементам первой строки. В этой формуле алгебраические дополнения вычисляются как определители 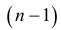
Пример №29
Рассмотрим (без доказательства) свойства определителей:
1. Определитель можно разложить по элементам первого столбца:
Пример №30
ЗАМЕЧАНИЕ. Рассмотренные примеры позволяют сделать вывод: определитель треугольной матрицы равен произведению элементов главной диагонали.
2. При транспонировании матрицы величина ее определителя не меняется:
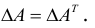
Отсюда следует, что строки и столбцы определителя равноправны.
3. Если в определителе поменять местами две строки (два столбца), то
определитель изменит свой знак, не изменившись по абсолютной вели-
чине.
4. Определитель, имеющий две равные строки (столбца), равен нулю.
5. Если все элементы некоторой строки (столбца) определителя умножить на число 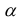
Отсюда, в частности, следует, что общий множитель любой строки (столбца) можно выносить за знак определителя. Кроме того, определитель, имеющий нулевую строку или нулевой столбец, равен нулю.
6. Определитель, имеющий пропорциональные строки (столбцы), равен нулю.
7. Определитель можно разложить по элементам любой строки (любого
столбца):
или
Равенство (1.6) называется разложением определителя по элементам i -й строки.
Равенство (1.7) называется разложением определителя по элементам k -го столбца.
8. Сумма произведений всех элементов некоторой строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) равна нулю, то есть при
9. Определитель не изменится от прибавления ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца),умноженных на одно и то же число.
10. Определитель произведения двух матриц одного порядка равен произведению определителей этих матриц: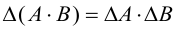
Пример №31
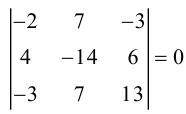
Особенно часто при вычислении определителей используется свойство 9, так как оно позволяет в любом определителе получать строку или столбец, где все элементы, кроме одного, равны нулю.
Пример №32
Определение обратной матрицы
Определение: Матрица 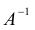
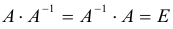
Из определения следует, что A и 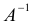
Определение: Квадратная матрица A называется невырожденной, если 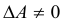
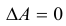
Пример №33
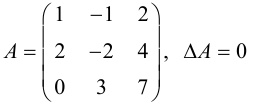
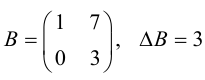
Теорема: Всякая невырожденная матрица имеет обратную, причем одну.
Доказательство: Рассмотрим для определенности квадратную матрицу A третьего порядка:
Покажем, что матрица вида 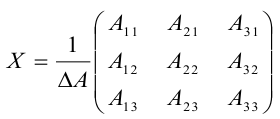
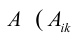
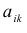
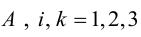
По условию A – невырожденная, т.е. 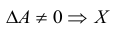
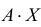
Аналогично доказывается, что 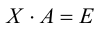
Следовательно, по определению матрица X является обратной для A .
Докажем единственность обратной матрицы.
Пусть невырожденная матрица A имеет две обратные: 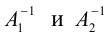
Умножим (1.8) слева на
Используя свойство 2 умножения матриц и равенство (1.9), получим:
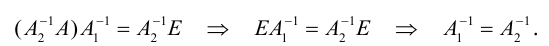
Таким образом, обратная матрица единственна, что и требовалось доказать.
Обратная матрица для матрицы A n — го порядка имеет вид:
Пример №34
Найти матрицу, обратную для
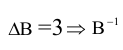
Проверка:
Пример №35
Найти матрицу, обратную для 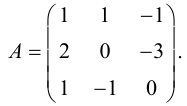
существует.
Проверка:
Аналогично проверяется, что
Крамеровские системы уравнений
Рассмотрим систему n линейных уравнений с n неизвестными:
Матрица, составленная из коэффициентов системы (1.10)
называется основной матрицей системы (1.10), 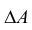
Определение: Система линейных уравнений называется Крамеровской, если
1) число уравнений равно числу неизвестных;
2) основной определитель не равен нулю.
Рассмотрим матрицы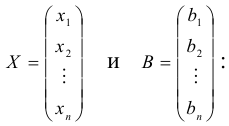
В – столбец правых частей. Очевидно, что система (1.10) может быть записана
в виде матричного уравнения
Определение: Совокупность n чисел 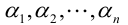
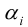
Теорема: Всякая Крамеровская система имеет решение, причем одно.
Доказательство: По условию 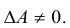
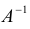
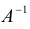
По формуле (1.12) определяется каждое из неизвестных 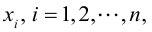
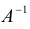
ЗАМЕЧАНИЕ. Способ решения системы (1.10) по формуле (1.12) называется матричным способом решения системы линейных уравнений.
Пример №36
Решить систему уравнений матричным способом:
В предыдущем примере было показано, что 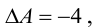
Таким образом, 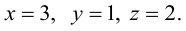
ЗАМЕЧАНИЕ. Матричный способ удобен, когда надо решить несколько Крамеровских систем, которые отличаются только правыми частями.
Вернемся к равенству (1.12). Из него следует, что
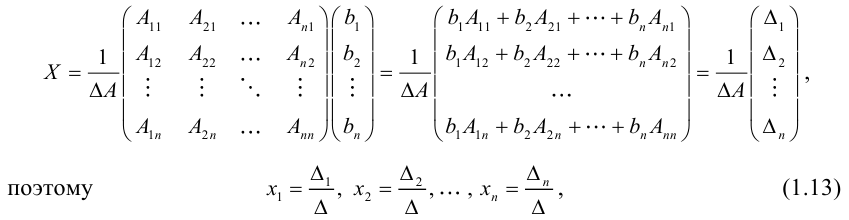
где 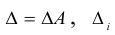
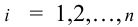
Ранг матрицы и элементарные преобразования
Определение: Минором порядка k матрицы А называется определитель k -го порядка, составленный из элементов матрицы А, стоящих на пересечении произвольно выбранных k строк и k столбцов без изменения порядка их следования.
Пример №37
Рассмотрим матрицу
Миноры первого порядка – каждый элемент матрицы A .
Миноры второго порядка: 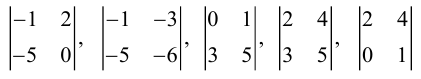
Матрица A имеет всего 18 миноров второго порядка.
Миноры третьего порядка:
Миноров четвертого порядка у этой матрицы нет.
Теорема: Если все миноры k -го порядка матрица А равны нулю, то равны нулю и все миноры старших порядков, если они существуют.
Доказательство: Рассмотрим минор порядка (k+1) . Это определитель (k-1) -го порядка, который ( по свойству 7 ) можно разложить по элементам некоторой строки (столбца ). В разложении будут алгебраические дополнения, которые с точностью до знака совпадают с минорами k — го порядка и по условию равны нулю. Поэтому равен нулю и рассматриваемый минор порядка k( 1 ). Аналогично равны нулю и миноры старших порядков 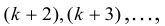
Определение:. Рангом матрицы А называется такое целое число r ,
что среди ее миноров r -го порядка есть хотя бы один ненулевой, а все миноры
порядка (r+1) равны нулю.
Из доказанной теоремы следует, что, другими словами, ранг матрицы – это наивысший порядок отличного от нуля минора.
Будем обозначать 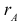
Ранг матрицы равен нулю тогда и только тогда, когда ее миноры равны
нулю, то есть если матрица нулевая.
Пример №38
Матрица F , очевидно, имеет ненулевой минор второго порядка, например,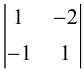
поэтому 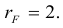
Определение: Элементарными преобразованиями матрицы называются следующие действия:
- умножение любой строки на число
;
- перемена местами двух строк;
- прибавление ко всем элементам строки соответствующих элементов другой строки, умноженных на одно и то же число
;
- отбрасывание нулевой строки;
- отбрасывание одной из двух пропорциональных строк;
- те же преобразования со столбцами.
Теорема: Элементарные преобразования не изменяют ранга матрицы.
С их помощью всякую матрицу можно привести к диагональному виду, и ее ранг равен количеству ненулевых элементов на главной диагонали (без доказательства).
Покажем теперь, что ранг матрицы F из последнего примера равен 2.
При переходе от F к 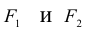
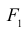
Вычислить 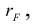
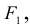
Исследование произвольных систем линейных уравнений
Рассмотрим систему m линейных уравнений с n неизвестными.
Матрица 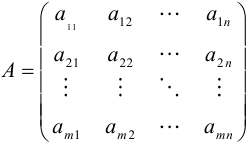
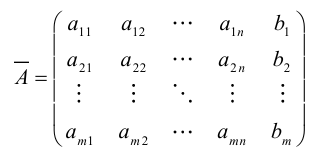
Определение: Система линейных уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она решений не имеет.
Определение: Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений у нее более одного.
Пример №39
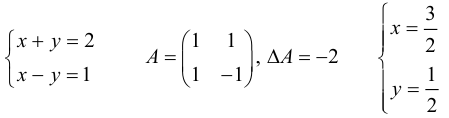
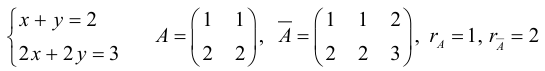
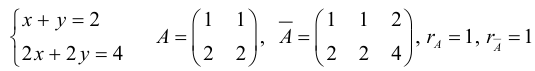
Теорема: (Кронекера-Капелли, критерий совместности системы линейных уравнений) Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг ее основной матрицы был равен рангу расширенной (без доказательства).
Теорема: (о числе решений). Пусть выполнены условия совместности системы линейных уравнений. Тогда, если 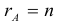
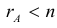
Однородные системы линейных уравнений
Система линейных уравнений вида
называется однородной.
Однородная система всегда совместна, так как 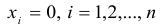
Теорема: Для того чтобы система линейных однородных уравнений (1.15) имела нетривиальное решение, необходимо и достаточно, чтобы ранг ее основной матрицы r был меньше числа неизвестных n .
Доказательство:
- Достаточность:
(1.15) имеет нетривиальное решение. По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные.
- Необходимость: (1.15) имеет нетривиальное решение
Пусть r = n, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и r > n.
Следствие: Для того чтобы однородная система n уравнений с n неизвестными имела ненулевое решение, необходимо и достаточно, чтобы ее основной определитель был равен нулю.
Доказательство:
- Достаточность:
система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r < n, значит, нетривиальное решение существует.
- Необходимость: система имеет нетривиальное решение
Если
то не равен нулю минор n -го порядка основной матрицы, значит, r = n и решение единственно, что противоречит условию.
Метод Гаусса
Этим методом можно решить любую систему линейных уравнений (1.14) или доказать, что она несовместна. Он состоит в последовательном исключении неизвестных системы (1.14) по следующей схеме: выписывается расширенная матрица системы 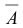
- перемена местами двух строк (уравнений);
- умножение любой строки (уравнения) на число
- отбрасывание одной из двух равных или пропорциональных строк (уравнений) ;
- прибавление к любой строке (уравнению) другой строки (уравнения), умноженной на число
После выполнения преобразований возможны три случая:
а)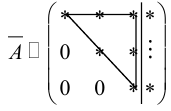
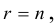
б) 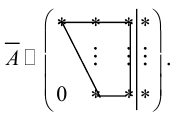
в) 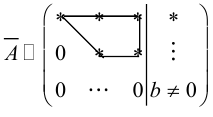
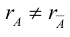
Пример №40
Решить систему линейных уравнений:
Выпишем расширенную матрицу и системы и упростим ее с помощью элементарных преобразований над строками:
Очевидно, что 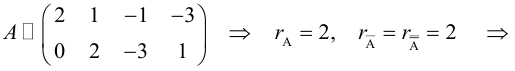
Кронекера-Капелли система совместна.
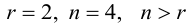
Выпишем систему, соответствующую матрице 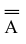
Перенесем в правую часть переменные 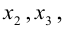
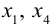
Теперь подставим 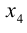
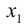
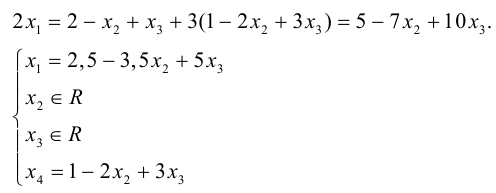
Определение: Общим решением системы (1.14) называется решение, содержащее информацию обо всех неизвестных, в котором зависимые переменные выражаются как функции свободных.
Решение, полученное из общего при конкретных значениях свободных переменных, называется частным решением.
Например, частными решениями этой системы являются:
Сделаем проверку частного решения (для всех уравнений исходной системы!):
Лекции по предметам:
- Математика
- Алгебра
- Векторная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика


 Даны действительные числа a1.a64. Получить действительную квадратную матрицу порядка 8
Даны действительные числа a1.a64. Получить действительную квадратную матрицу порядка 8
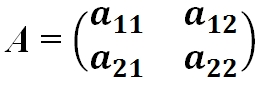
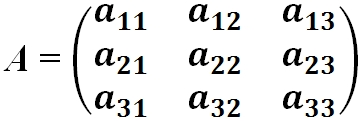
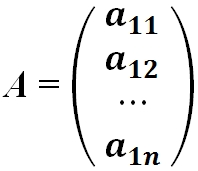
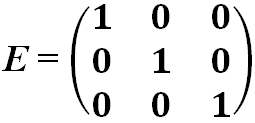
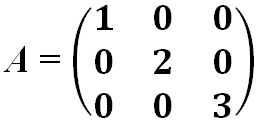
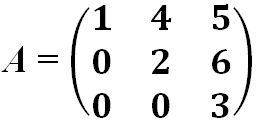
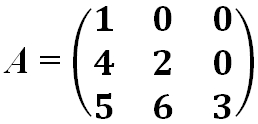

 , где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).
, где АV = Aij — присоединенная матрица (матрица, составленная из алгебраических дополнений элементов исходной матрицы, стоящих на тех же местах).




 и транспонируем:
и транспонируем: 
 Пример 5.
Пример 5. . Матрица A – квадратная и невырожденная,
. Матрица A – квадратная и невырожденная,
 . Матрица A – квадратная, |A| ≠ 0.
. Матрица A – квадратная, |A| ≠ 0. .
. . Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
. Матрицы A и B – квадратные, |A| ≠ 0, |B| ≠ 0.
 .
.
 .
. .
.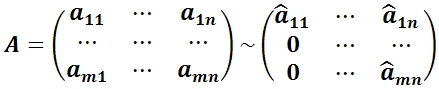
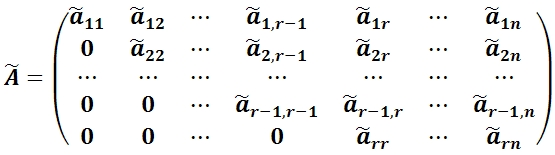







 .
.


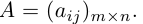

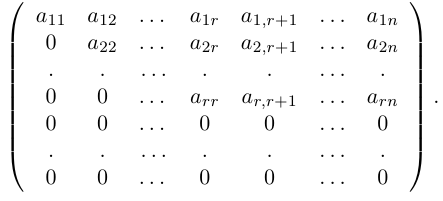
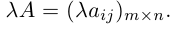
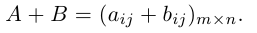
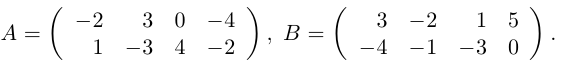
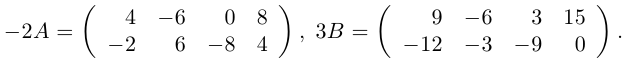
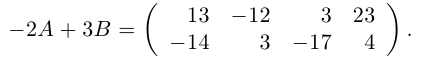
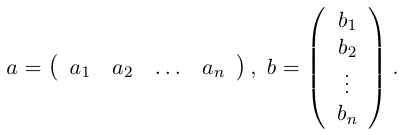
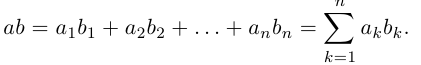
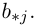
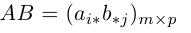
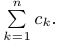
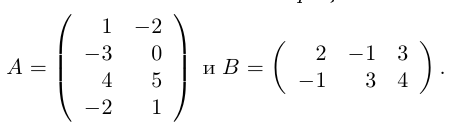
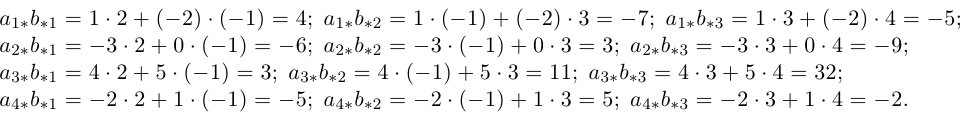
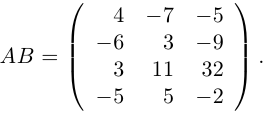
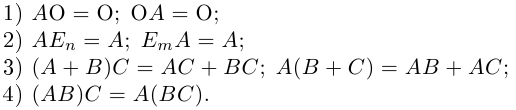
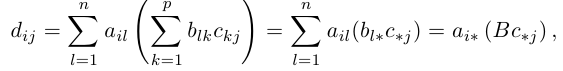
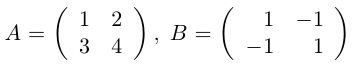
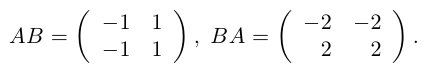
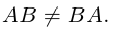
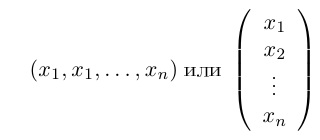
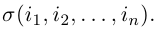
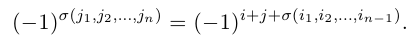
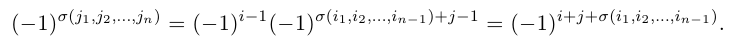

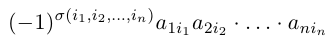

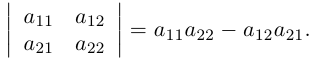
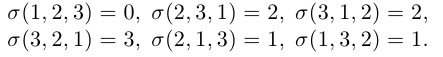
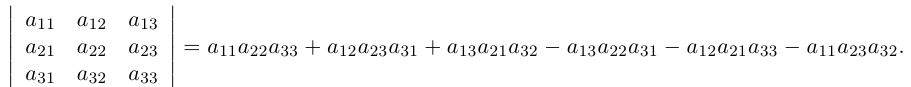

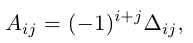
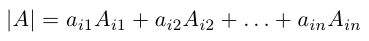
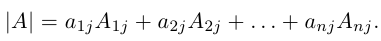
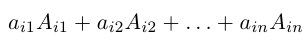
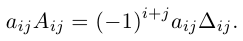

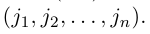
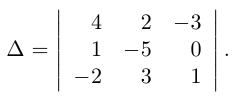
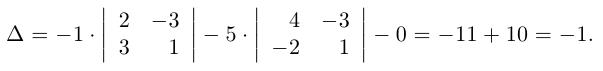

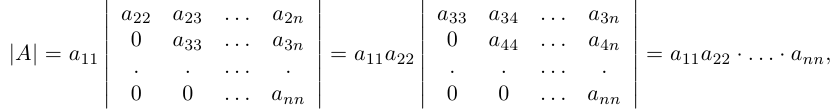
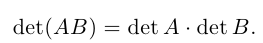
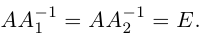
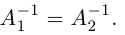
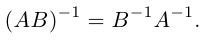
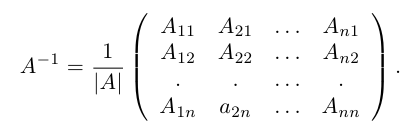
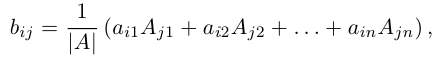
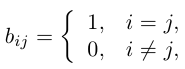
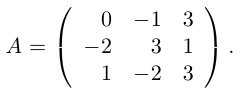
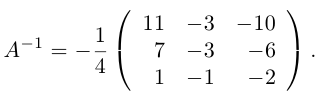
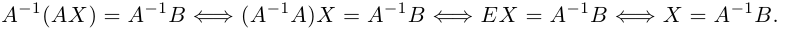
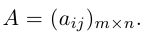
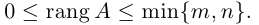
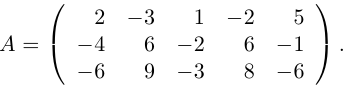
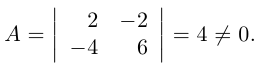
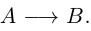

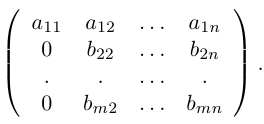
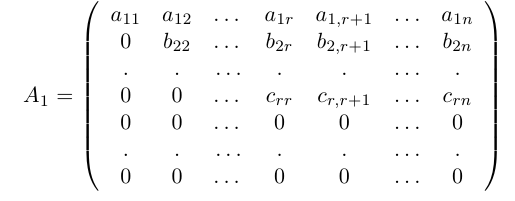
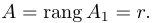
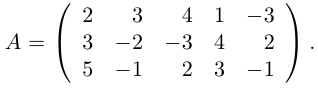
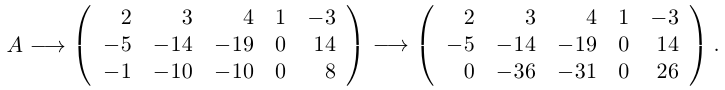
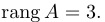
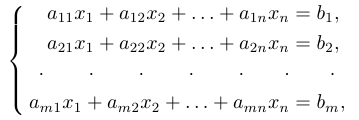
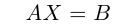
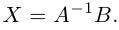
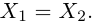
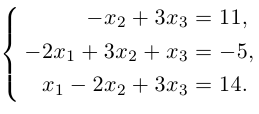
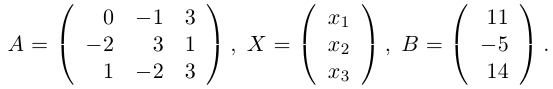
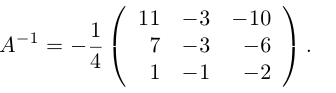
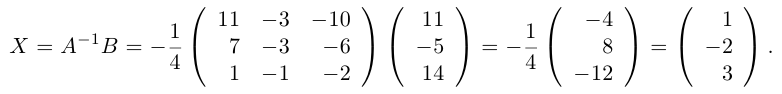

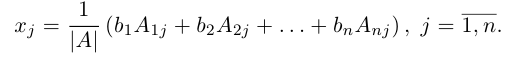
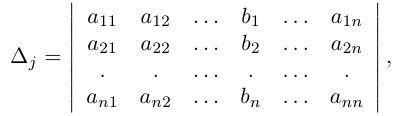
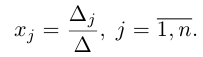
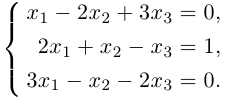
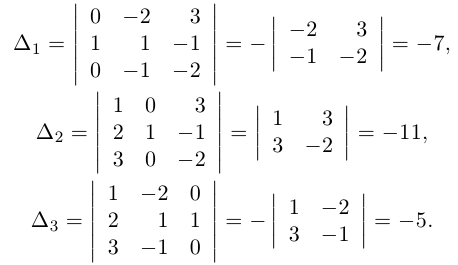
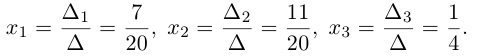
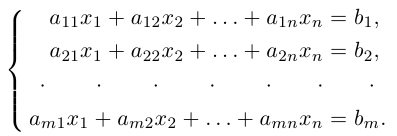
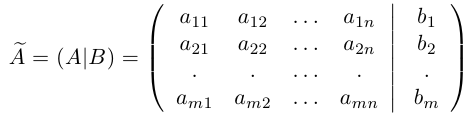
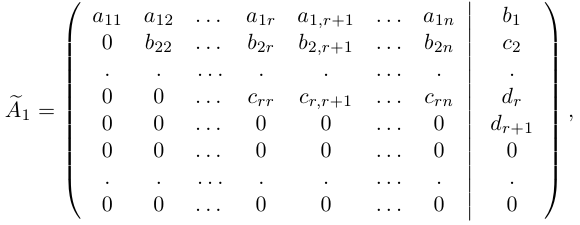
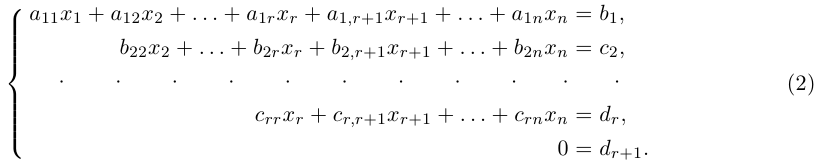
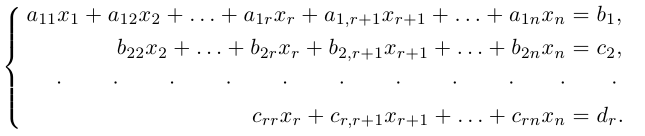
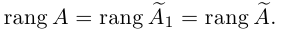
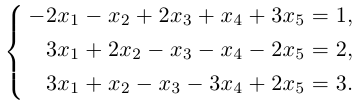

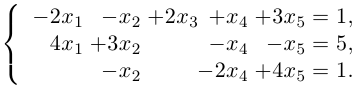
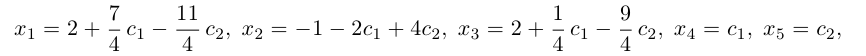
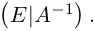
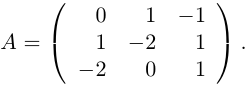

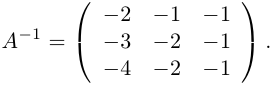
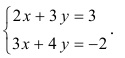
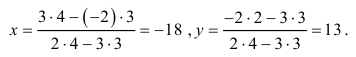
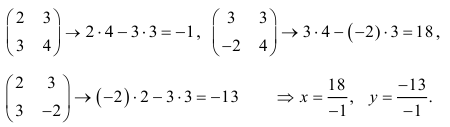
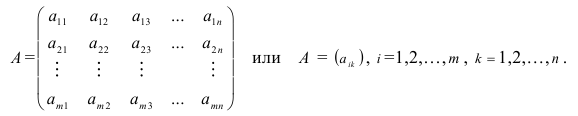
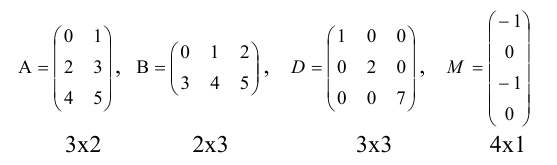
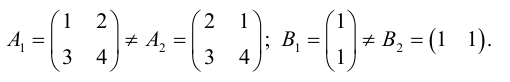
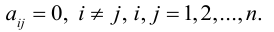
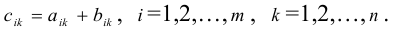
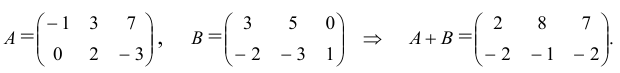
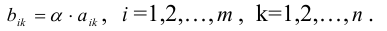

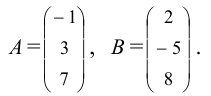
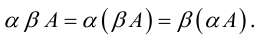
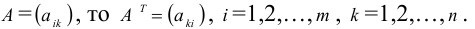
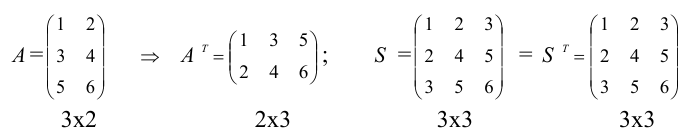
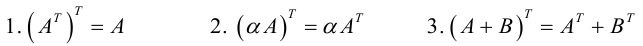
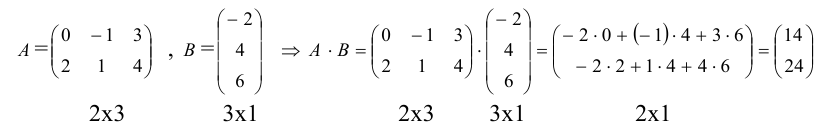
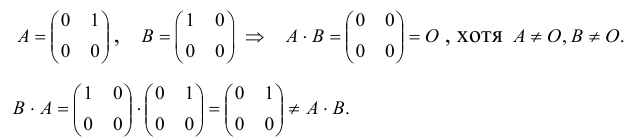
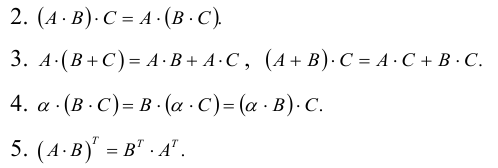
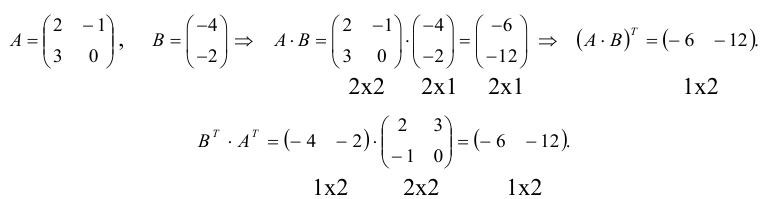
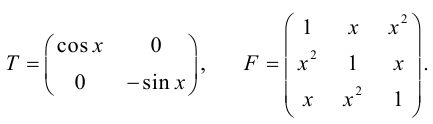
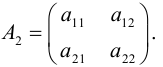
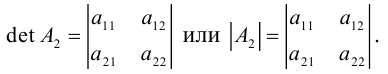
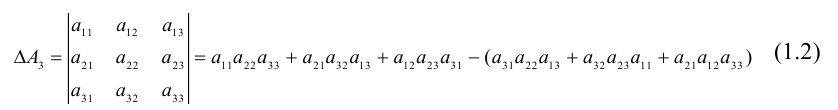
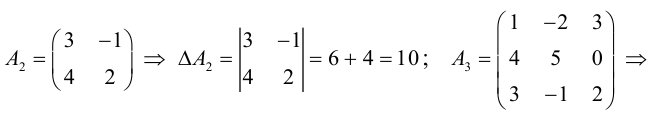
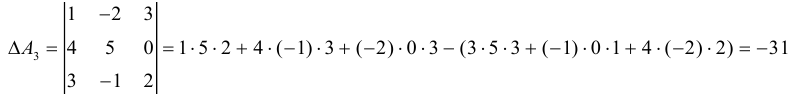
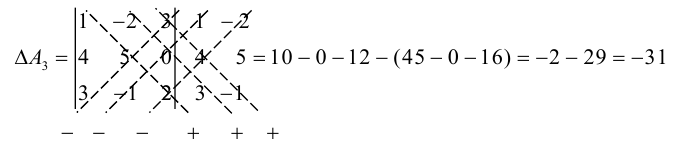
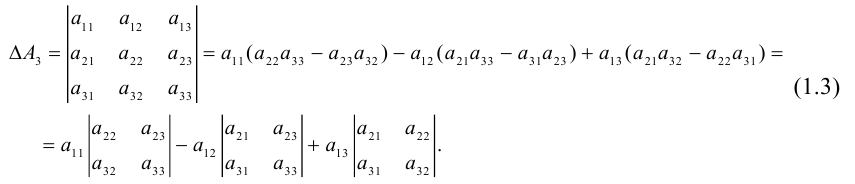
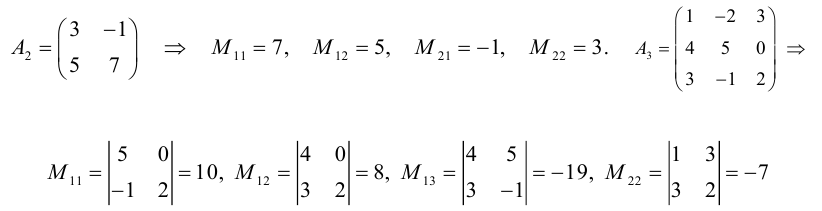
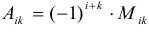
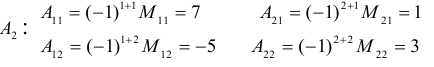
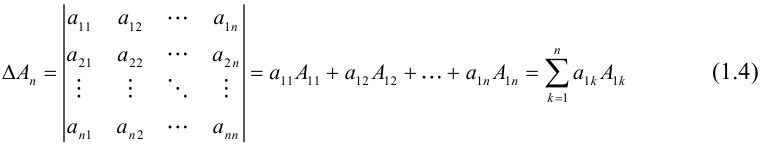
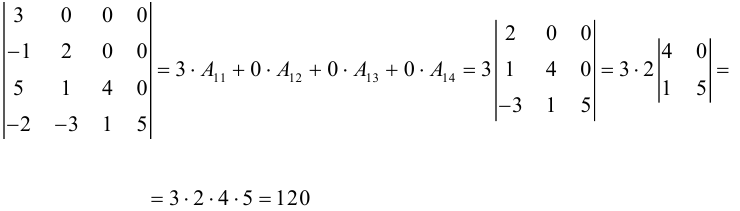
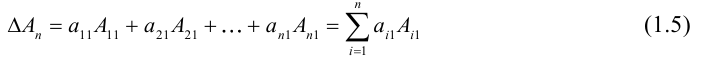
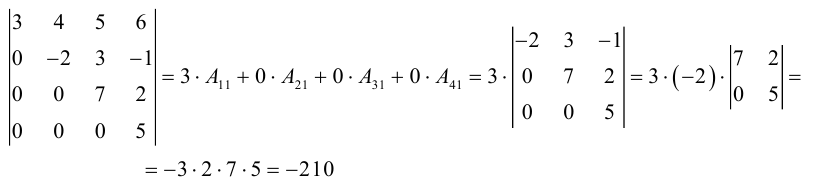
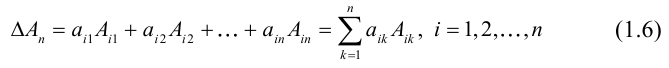
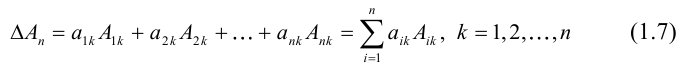
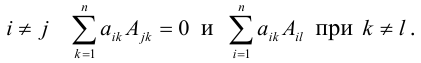

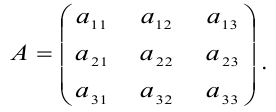
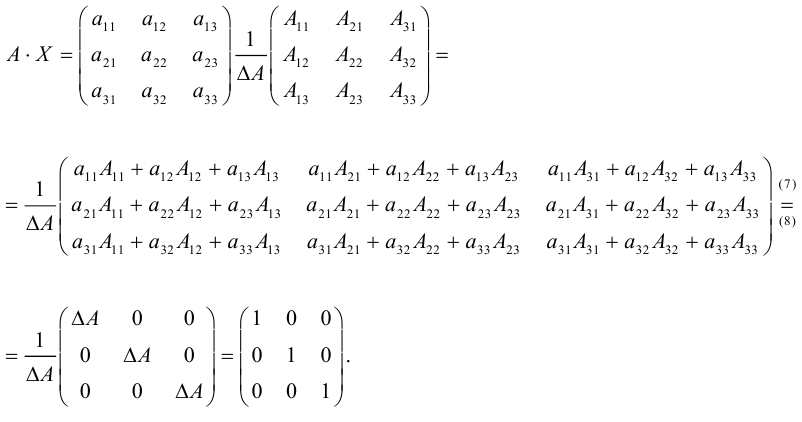

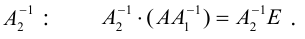

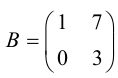
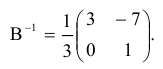
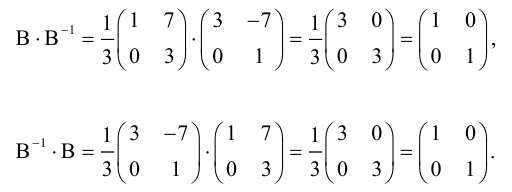
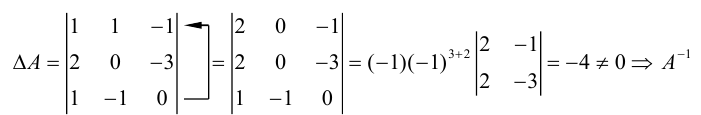
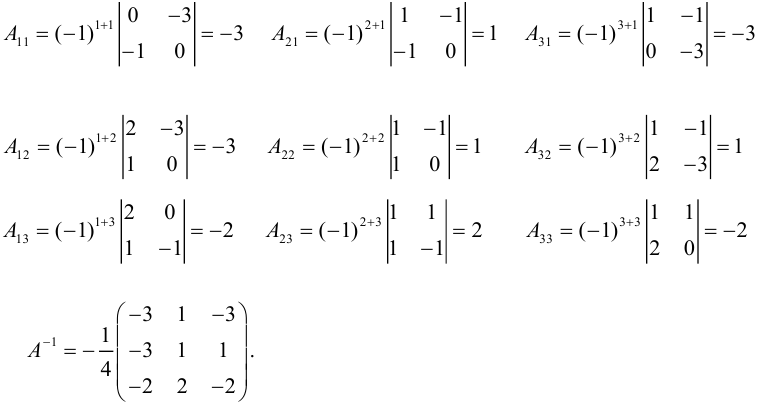
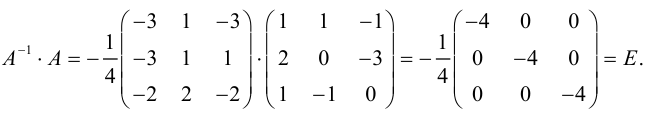
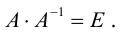
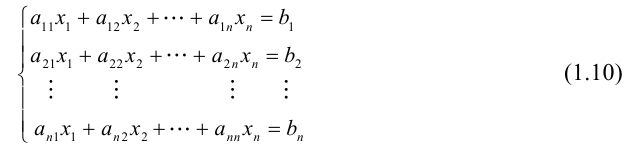
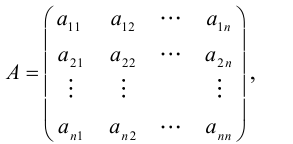

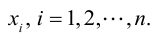
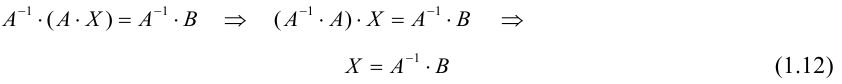
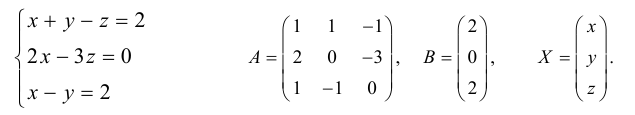
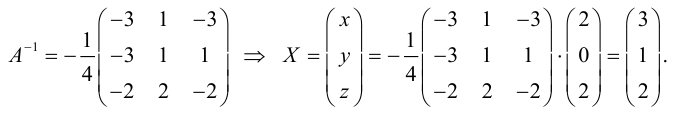
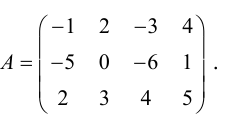
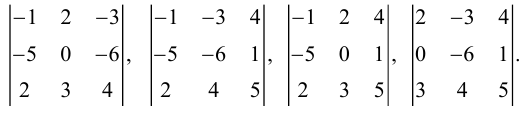
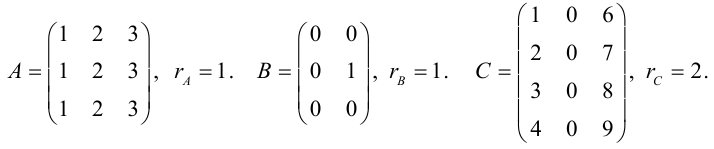
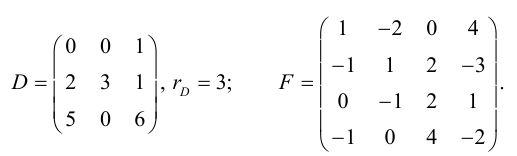
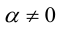 ;
; 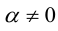 ;
; 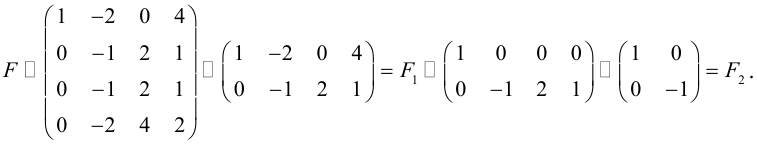
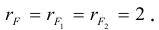
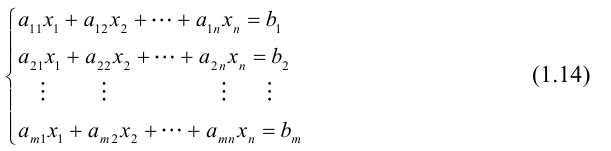
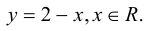
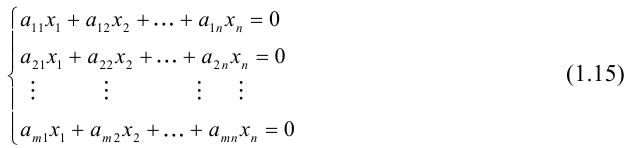
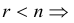 (1.15) имеет нетривиальное решение. По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные.
(1.15) имеет нетривиальное решение. По теореме о числе решений система в этом случае имеет бесконечное множество решений, среди которых содержатся и нетривиальные. 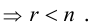 Пусть r = n, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и r > n.
Пусть r = n, тогда по теореме о числе решений система (1.15) имеет единственное решение. Это решение тривиальное, что противоречит условию. Поэтому сделанное предположение неверно и r > n.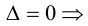 система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r < n, значит, нетривиальное решение существует.
система имеет нетривиальное решение. Так как единственный минор n -го порядка равен нулю, то r < n, значит, нетривиальное решение существует. 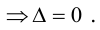 Если
Если 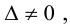 то не равен нулю минор n -го порядка основной матрицы, значит, r = n и решение единственно, что противоречит условию.
то не равен нулю минор n -го порядка основной матрицы, значит, r = n и решение единственно, что противоречит условию.