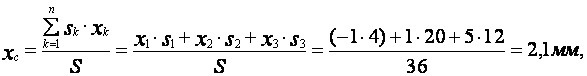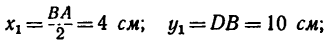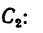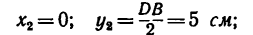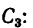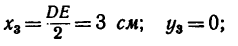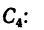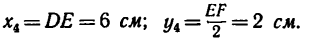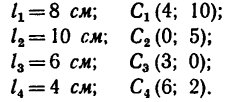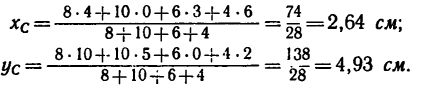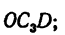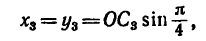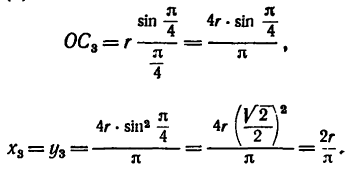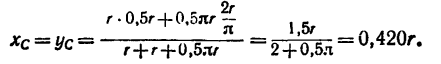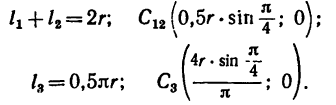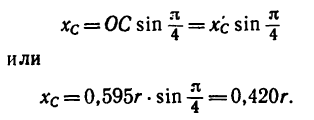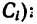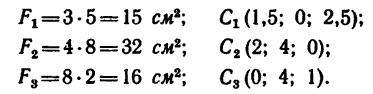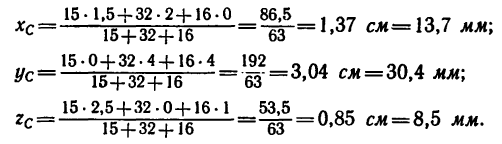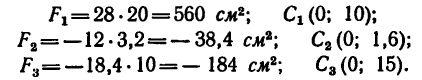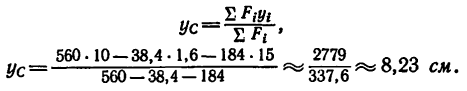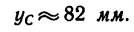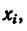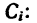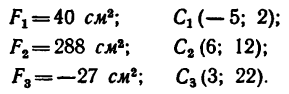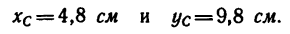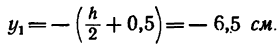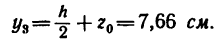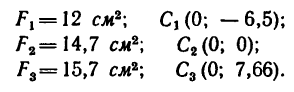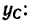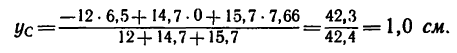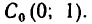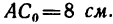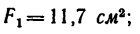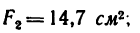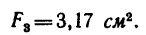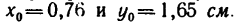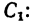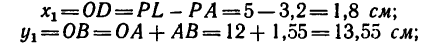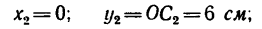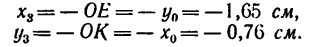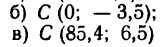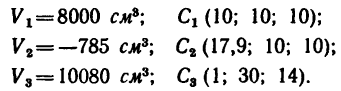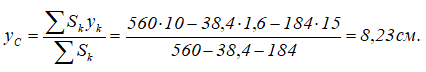Приведем пример
определения центра массы тела методом разделения его на отдельные тела, центры
масс которых известны.
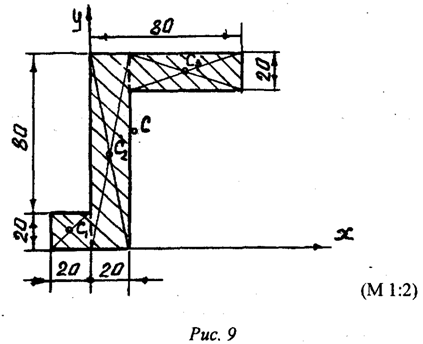
Пример 1. Определить координаты центра массы однородной
пластины (рис.9). Размеры заданы в миллиметрах на рисунке 9.
Решение: Показываем оси координат и
. Разбиваем пластину на части,
которые образованы тремя прямоугольниками. Для каждого прямоугольника проводим
диагонали, точки пересечения которых и
определяют положения центров массы
каждого прямоугольника. В принятой системе координат несложно найти значения
координат этих точек. А именно:
(-1;
1), (1;5),
(5;9).
Площади каждого тела соответственно равны:
;
;
.
Площадь всей пластины равна:
.
Для определения
координат центра массы заданной пластины применяем выражения (21). Подставим
значения всех известных величин в данном уравнении, получим
Согласно полученных
значений координат центра массы пластины укажем точку С на рисунке. Как видно,
центр массы (геометрическая точка) пластины находится за ее пределами.
Способ дополнения. Этот способ есть частичным случаем способа
разделения. Он может применяться к телам, которые имеют вырезы (пустоты).
Причем, без вырезанной части, положение центра массы тела известно. Рассмотрим
например применение такого метода.
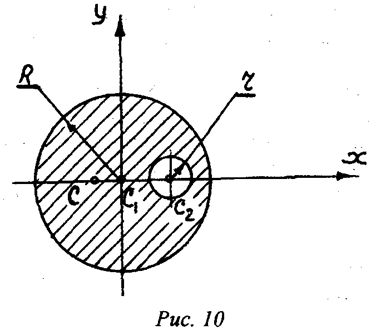
Пример 2. Определить положение центра массы веса круглой
пластины радиусом R, в которой есть вырез радиусом r (рис.10). Расстояние .
Решение: Как видим, из рис.10 центр массы пластины лежит на
оси симметрии пластины, то есть на прямой ,
поскольку эта прямая есть осью симметрии. Таким образом, для определения
положения центра массы этой пластины необходимо определить только одну
координату , поскольку вторая координата
будет расположена на оси симметрии и
уравновешивает нулевые. Покажем оси координат ,
. Примем, что
пластина складывается из двух тел – из полного круга (как будто без выреза) и
тела, которое как будто выполнено с вырезом. В принятой системе координат
координаты для указанных тел будут равны:
.Площади тел равны:
;
.
Общая площадь всего тела будет равна разнице между площадями первого и
второго тела, а именно
.
Теперь,
для определения неизвестной координаты центра массы заданной пластины
применяем первое уравнение выражения (21). Подставим значения всех известных
величин в это уравнение, получаем
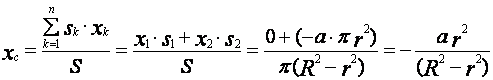
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание — внизу страницы.
Определение положения центра тяжести тела, составленного из тонких однородных стержней
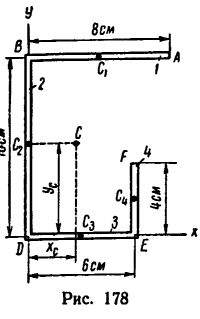
Задача 122-23. Определить положение центра тяжести плоской фигуры (рис. 178), изогнутой из тонкой проволоки.
Решение.
1. Фигура состоит из четырех прямых отрезков:
2. Оси координат расположим так, чтобы они совпали с отрезками DE (ось х) и DB (ось у). Так как фигура плоская, третья ось здесь не нужна.
3. Для центров тяжести 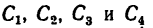
а Обозначив 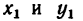
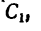
координаты
координаты
координаты
Для удобства, а также ввиду того, что координаты центров тяжести можно определить непосредственно по рисунку, данные для подстановки в формулы следует представлять в таком виде:
4. Подставим значения 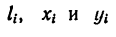
5. Отложив вдоль осей х и у найденные координаты, отметим на рис. 178 положение центра тяжести С данной фигуры.
Задача 123-23. Определить положение центра тяжести плоской фигуры ОАВ, изогнутой из тонкой проволоки в виде квадранта (рис. 179).
Решение 1.
1. Фигура состоит из трех частей: двух прямолинейных отрезков 1 и 2 длиной r и дуги 3, равной четверти окружности.
2. Совместив оси координат с прямолинейными отрезками ОА и ОВ (рис. 179, а), приведем данные для подстановки в формулы:
Координаты 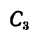
но по формуле (5)
поэтому
3. Подставим значение 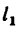
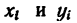
Решение 2.
1. Так как фигура имеет одну ось симметрии, проходящую по биссектрисе прямого угла, одну из осей координат целесообразно совместить с осью симметрии (рис. 179, б)
В этом случае общий центр тяжести отрезков ОА и ОВ (точка 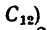
2. Определим исходные данные для подстановки в формулы (2):
3. Найденные значения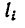
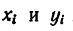
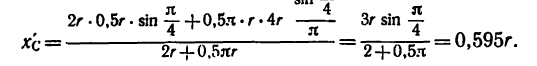
Сравнивая 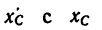
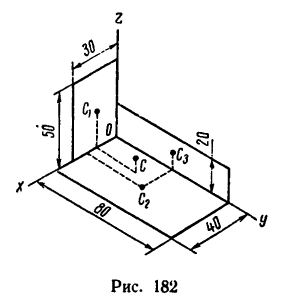
Задача 124-23. Определить положение центра тяжести пространственно изогнутой проволочной фигуры (рис. 180); размеры — в мм.
Решение.
1. Расположив проволочную фигуру в осях координат как показано на рис. 180, разделим ее на пять прямолинейных участков 1, 2, 3, 4 и 5 и отметим точками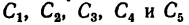
2. Найдем исходные данные для подстановки в формулы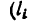
3. Найденные исходные данные подставим в формулы (2) и вычислим координаты центра тяжести всей фигуры:
4. Таким образом, центр тяжести фигуры расположен в точке С (55,0; 62,2; 7,2).
Следующую задачу рекомендуется решить самостоятельно.
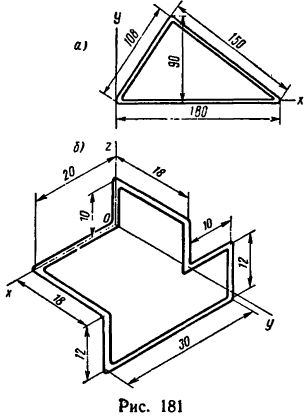
Задача 125-23. Определить положение центров тяжести плоской и пространственной проволочных фигур, показанных на рис 181
(размеры в мм).
Ответ (в осях, показанных на рис. 181);
а) С (85,5; 26,5);
б) С (6; 9,95; -2,19).
Определение положения центра тяжести фигур, составленных из пластинок
Задача 126-24. Определить положение центра тяжести фигуры, составленной из трех тонких плоских пластинок прямоугольной формы, пересекающихся друг с другом под прямыми углами (рис. 182); размеры —в мм.
Решение.
1. Поместим начало координат в вершине трехгранного угла и расположим оси координат вдоль линий пересечения пластинок.
Фигура состоит из трех прямоугольников с центрами тяжести 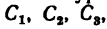
2. Исходя из размеров фигуры, определим необходимые данные для подстановки в формулы (3): 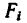
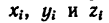
3. Подставим эти данные в формулы (4) и вычислим искомые координаты центра тяжести фигуры:
Центр тяжести фигуры расположен в точке С (13,7; 30,4; 8,5).
В последней задаче, а также в задачах, приведенных в предыдущем параграфе, расчленение фигур на составные части не вызывает особых затруднений. Но иногда фигура имеет такой вид, который позволяет разделить ее на составные части несколькими способами, например тонкую пластинку прямоугольной формы с треугольным вырезом (рис. 183). При определении положения центра тяжести такой пластинки ее площадь можно разделить на четыре прямоугольника (1, 2, 3 и 4) и один прямоугольный треугольник 5 — несколькими способами. Два варианта показаны на рис. 183, а к б.
Наиболее рациона.льным является тот способ деления фигуры на составные части, при котором образуется наименьшее их число. Если в фигуре есть вырезы, то их можно также включать в число составных частей фигуры, но площадь вырезанной части считать отрицательной. Поэтому такое деление получило название способа отрицательных площадей.
Пластинка на рис. 183,в делится при помощи этого способа всего на две части: прямоугольник 1 с площадью всей пластинки, как будто она целая, и треугольник 2 с площадью, которую считаем отрицательной.
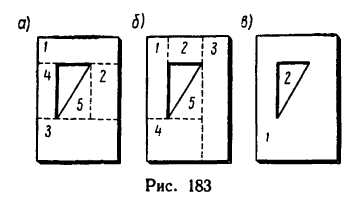
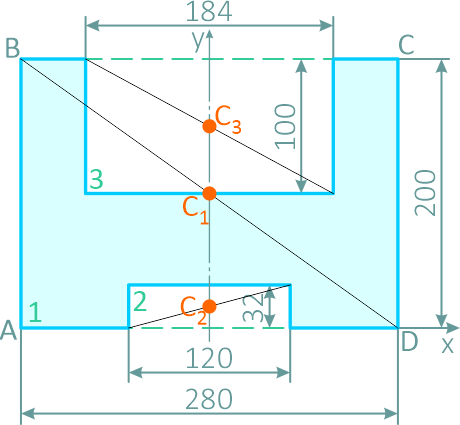
Задача 127-24. Определить положение центра тяжести тонкой однородной пластинки, имеющей ось симметрии. Формаш размеры пластинки показаны на рис. 184.
Решение.
1. Пластинка имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось у, а ось х — с нижним краем пластинки.
2. Дополнив пластинку до прямоугольника ABCD, разобьем ее тем самым на три части: 1, 2 и 3.
3. Определим площади каждой части в 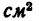
4. Определим ординату центра тяжести пластинки, подставив найденные значения во вторую формулу системы (3):
Таким образом, центр тяжести 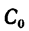
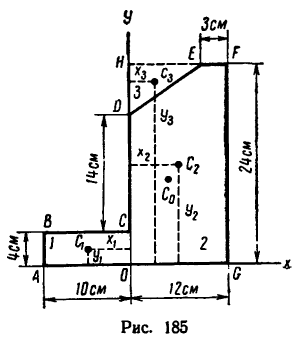
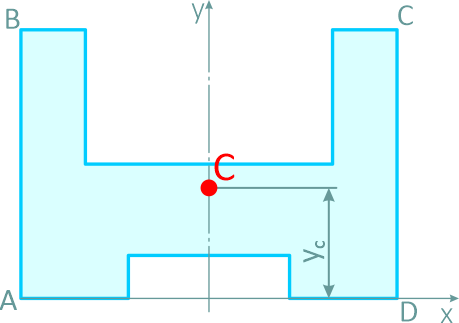
Задача 128-24. Определить положение центра тяжести плоской однородной пластинки ABCDEFG, размеры которой в см указаны на рис. 185.
Решение.
1. Разбиваем пластинку на два прямоугольника АВСО и OHFG и на треугольник DHE, площадь которого считаем отрицательной.
2. Начало координат помещаем в точке О, ось х совмещаем с прямой AG, ось у — с прямой CD.
3. Определяем площади 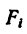
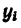
4. Подставляем найденные значения площадей и координат в две первые формулы (3) и производим .вычисление:
Таким образом, центр тяжести пластинки находится в точке 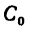
Следующую задачу рекомендуется решить самостоятельно.
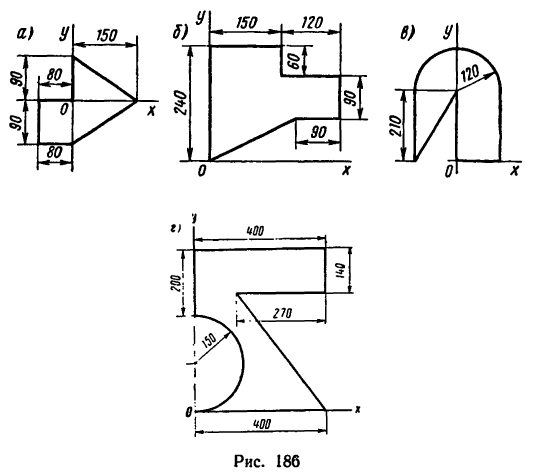
Задача 129-24. Определить положение центров тяжести тонких однородных пластинок, форма и размеры которых показаны на рис 186.
Ответ:
§ 28-8. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ЦЕНТРА ТЯЖЕСТИ СЕЧЕНИЙ, СОСТАВЛЕННЫХ ИЗ ПРОФИЛЕЙ СТАНДАРТНОГО ПРОКАТА
При решении задач, приведенных в этом параграфе, нужно пользоваться таблицами из ГОСТа на прокатную сталь (табл. 1—4).
Эти таблицы для каждого профиля содержат их размеры и площадь, а для уголков и швеллера, кроме того, — координаты центров тяжести.
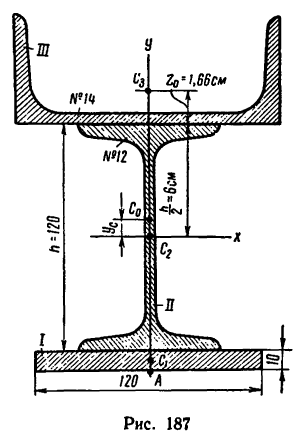
Задача 130-25. Определить положение центра тяжести симметричного сечения, составленного, как показано на рис. 187, из полосы размером 120×10 мм, двутавра № 12 (ГОСТ 8239—56) и швеллера 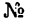
Решение.
1. Разбиваем сечение на три части: / — полоса, //—двутавр и /// — швеллер.
2. Находим площади каждой части, выражая их в 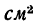
Площадь сечения полосы
Площадь сечения двутавра № 12
Площадь сечения швеллера № 14
3. Данное сечение имеет вертикальную ось симметрии. Совместим с этой осью ось у, а ось х проведем через середину двутавра через точку 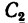
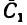
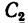
Центр тяжести швеллера 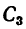
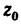
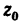
Таким образом,
4. Подставляем эти значения в расчетную формулу для ординаты
В выбранных осях положения центра тяжести сечения выражены координатами
Это значит, что центр тяжести сечения находится от его нижнего края (от точки А) на расстоянии
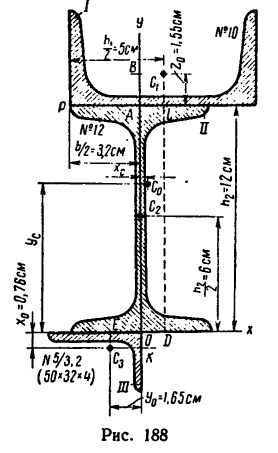
Задача 131-25. Определить положение центра тяжести сечения, составленного, как показано на рис 188, из трех профилен стандартного проката: швеллера 
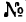
Решение.
1. Разбиваем сечение на три части: / — швеллер, //-двутавр и ///—неравнобокий уголок.
2. Начало координат поместим в вершине прямого угла неравнобокого уголка; ось х совместим с нижней полкой двутавра,
а ось у — с его вертикальной осью симметрии.
3 При помощи таблиц из ГОСТа находим:
площадь сечения швеллера 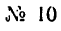
площадь сечения двутавра № 12
площадь сечения уголка 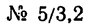
4. В таблицах из ГОСТа положение центра тяжести 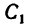
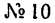
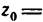
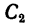
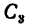
Располагаем центры тяжести 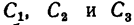
координаты центра тяжести
координаты центра тяжести
5. Таким образом,
6. Подставляем эти значения в расчетные формулы:
7. Центр тяжести данного составного сечения имеет координаты (в мм) 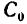
Следующую задачу рекомендуется решить самостоятельно.
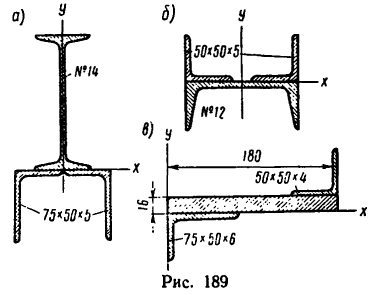
Задача 132-25. Определить положение центра тяжести трех сечений, составленных из профилей стандартного проката, как показано на рис. 189.
Ответ (в мм):
а) С (0; 31,1);
Определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму
Чтобы решать задачи на определение положения центра тяжести тела, составленного из частей, имеющих простую геометрическую форму, необходимо иметь навыки определения координат
центра тяжести фигур, составленных из линий или площадей.
Задача 133-26. Определить положение центра тяжести тела, составленного из куба /, имеющего горизонтальную цилиндрическую канавку //, и прямоугольного параллелепипеда 
Решение.
1. Тело состоит из куба /, полуцилиндра //, объем которого считаем отрицательным, так как он вырезан из объема куба /, и прямоугольного параллелепипеда
2. Отметив на рисунке положение центра тяжести составных частей 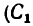
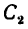
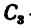
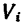
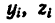
3. После подстановки в расчетные формулы имеем:
Таким образом, центр тяжести данного тела находится в точке 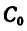
Эту точку рекомендуется отметить на рис. 190 самостоятельно.
Задача 134-26 (для самостоятельного решения). Определить положение центра тяжести тела, форма и размеры (в мм) которого показаны на рис. 191.
Ответ. С (122; 184; 80).
РАЗДЕЛ ВТОРОЙ
КИНЕМАТИКА
В кинематике изучаются законы движения материальных точек и твердых тел с чисто геометрической стороны. Законом движения точки или тела можно назвать такую совокупность математических образов и уравнений, которая в любой момент времени позволяет установить, где находится точка или тело, куда и как они движутся. При этом в кинематике не рассматриваются вопросы, почему точка или тело двигается именно так, а не иначе. Эти вопросы изучаются в разделе «Динамика».
Прежде чем решить задачи но кинематике, необходимо выяснить следующее:
а) можно ли данный в задаче движущийся предмет рассматривать как материальную точку или его нужно считать твердым телом;
б) в какой форме закон движения задан в задаче.
Необходимость выяснения первого положения вызывается тем,
что законы движения материальных точек (предметов, формой и размерами которых можно пренебречь) и законы движения твердых тел (предметов, состоящих из множества материальных точек), как правило, отличаются друг от друга.
От способа задания закона движения зависит ход решения задачи.
- Равномерное прямолинейное движение точки
- Равномерное криволинейное движение точки
- Равнопеременное движение точки
- Неравномерное движение точки по любой траектории
- Равновесие сходящихся сил
- Равновесие трех непараллельных сил
- Сочлененные системы
- Равновесие пространственной системы сходящихся сил
Центр тяжести плоской однородной
пластины, т.е. координаты точки С,
определяется по формулам
;
,
где S – площадь всей пластины; Sk
– площадь одной из частей пластины; xk
и yk – координаты центров
тяжести отдельных частей пластины;
n – число частей.
Если плоская фигура имеет вырезы или
отверстия, ее центр тяжести определяется
методом отрицательных площадей. Сущность
метода заключается в том, что из
геометрических характеристик
рассматриваемой площади вычитаются
параметры вырезов (отверстий). Координаты
центра тяжести в этом случае
;
,
где F1 – площадь всей фигуры;
F2 – площадь выреза или
отверстия; F1x1 и F1y1
– статические моменты площади фигуры
относительно осей x и y
соответственно; F2x2
и F2y2 – статические
моменты выреза или отверстия относительно
осей x и y.
Пример 1.5. Найти положение
центра тяжести фигуры с вырезом
(рис.1.50, а).
Размеры на рисунке указаны в сантиметрах.
Решение. Применим метод
отрицательных площадей. Для этого
разобьем фигуру на четыре части: 1 –
треугольник AFH; 2 – прямоугольник
OADB, который считаем сплошным; 3 –
круг с отрицательной площадью; 4 –
треугольник BDE, также имеющий
отрицательную площадь (рис.1.50, б).
Площадь каждой части фигуры вычислим
общепринятым способом:
см2;
cм2;
см2;
cм2.
Теперь найдем координаты центров тяжести
частей 1-4, на которые разбита фигура.
Вычисления произведем по формулам
;
,
используя при этом данные табл.1.1.
Таблица 1.1
|
Номер фигуры |
Si, |
xi, |
yi, |
Si |
Si |
|
|
1 |
900 |
20 |
70 |
18000 |
63000 |
|
|
2 |
6000 |
50 |
30 |
300000 |
180000 |
|
|
3 |
–1250 |
30 |
30 |
–37500 |
–37500 |
|
|
4 |
–900 |
90 |
30 |
–81000 |
–27000 |
|
|
|
4750 |
– |
– |
199500 |
178500 |
В результате
вычислений получим xC = 42,0
cм и yC = 37,6 см,
которые являются координатами центра
тяжести фигуры.
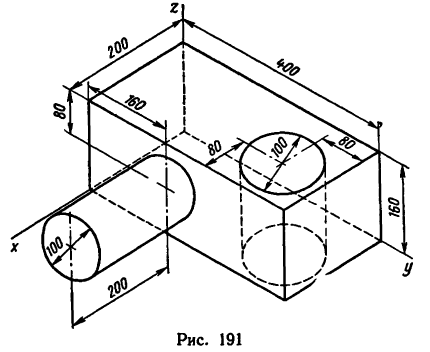
Задача 1.48. В однородной
квадратной доске ABCD со стороной
АВ = 2 м вырезано квадратное
отверстие EFGH, стороны которого
соответственно параллельны сторонам
ABCD и равны 0,7 м каждая (рис.1.51).
Определить координаты x и y центра
тяжести оставшейся висящей доски, зная,
что ОК = О1К = 0,5
м, где О и О1 –центры
квадратов, ОК и О1К
параллельны сторонам квадратов.
Ответ: x = y = –7 см.
З
Определить положение центра тяжести С
однородного диска с круговым отверстием.
Радиус диска r1, радиус отверстия
r2 и центр этого отверстия
находится на расстоянии r1/2
от центра диска (рис.1.52).
Ответ:
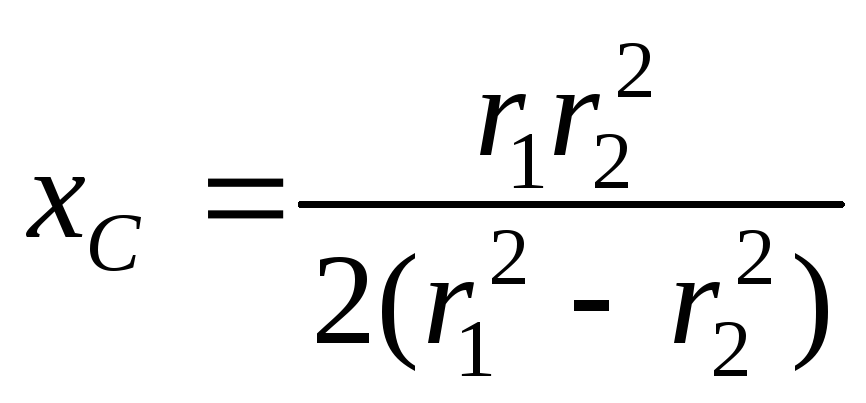
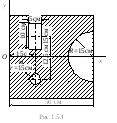
Задача 1.50. В квадратной однородной
пластине сделаны три выреза: полукруглый,
прямоугольный и круглый (рис.1.53).
Размеры указаны на чертеже. Определить
положение центра тяжести пластины.
Ответ: x = 22,17 см;
y =
= –0,243 см.
З
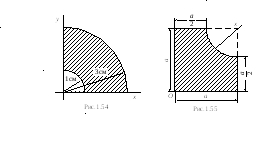
Определить координаты центра тяжести
четверти кольца (рис.1.54).
Ответ: x = y = 1,38 см.
Задача 1.52. Найти координаты центра
тяжести фигуры (рис.1.55).
Ответ: x = 0,61а, y = 0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Приложения кратных интегралов в механике
Краткая теория
Масса и статистические моменты пластики
Если
– область плоскости
, занятая пластинкой, и
– поверхностная плотность пластики в точке
, то масса
пластинки и ее статистические моменты
и
относительно осей
и
выражаются двойными интегралами:
Если
пластика однородна, то
Координаты центра тяжести пластики
Если
– центр тяжести пластики, то
где
– масса пластинки и
– ее статистические моменты относительно осей
координат.
Моменты инерции пластики
Моменты
инерции пластинки относительно осей
и
соответственно равны:
Момент инерции пластики относительно
начала координат:
Полагая
, получаем геометрические моменты инерции плоской
фигуры.
Масса тела, занимающего область
![]() и статистические моменты тела относительно
и статистические моменты тела относительно
координатных плоскостей
где
– плоскость тела в точке
Координаты центра тяжести
Если тело
однородно, то формулах для координат центра тяжести можно положить
.
Моменты инерции относительно
осей координат
Полагая в
этих формулах
, получаем геометрические
моменты инерции тела.
Примеры решения задач
Задача 1
Вычислить
массу материальной пластины, занимающей область
плоскости
, если поверхностная
плотность
и границы области
заданы уравнениями.
Решение
Сделаем
чертеж области
:
Искомая
масса материальной пластины:
Ответ:
Задача 2
Найти
статистический момент фигуры, ограниченной линиями
и
относительно оси абсцисс.
Решение
Сделаем
чертеж:
Статистический
момент относительно оси
:
Ответ:
Задача 3
Вычислить
координаты центра масс однородной
материальной пластины
, ограниченной данными
линиями:
Решение
Сделаем
чертеж:
Масса
пластинки:
Статистические
моменты:
Искомые
координаты центра масс:
Ответ:
.
Задача 4
Вычислить массу тела
, ограниченного заданными поверхностями
-плотность в
точке
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Изобразим
тело на рисунке:
С боков
тело будет ограничено цилиндром
и плоскостями
. Сверху плоскостью
Проекция на плоскость
:
Ответ:
Задача 5
Найти
момент инерции однородного шара
с массой
относительно оси
.
Решение
Момент
инерции относительно оси
можно найти по формуле:
Шар
однородный, поэтому плотность:
Перейдем
к сферическим координатам:
Получаем:
Ответ:
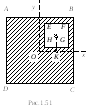
Пример решения задачи по определению координат положения центра тяжести тонкой однородной симметричной пластины методом отрицательных площадей.
Задача
Определить положение центра тяжести тонкой однородной пластинки, имеющей ось симметрии (рисунок 2.6).
Рисунок 2.6
Другие примеры решений >
Помощь с решением задач >
Решение
Пример определения координат центра тяжести для несимметричных фигур рассмотрен в нашем коротком видео:
Другие видео
Пластина симметрична, т.е. имеет ось симметрии, на которой находится центр тяжести. Совместим с осью симметрии ось y, а ось x – с нижним краем пластинки (абсцисса центра тяжести плоской фигуры xC= 0).
Дополнив пластинку до прямоугольника ABCD, разобьем ее на три части. Определим площади каждой части в см2 и координаты их центров тяжести в см:
S1= 28∙20 = 560 см2; C1(0;10);
S2= 12∙3,2 = 38,4 см2; C2(0;1,6);
S3= 18,4∙10 = 184 см2; C3(0;15).
Определим ординату центра тяжести плоской фигуры с помощью метода отрицательных площадей:
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее