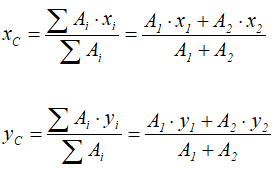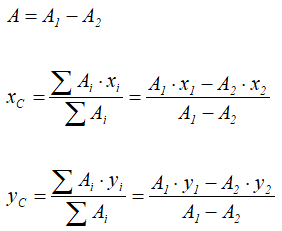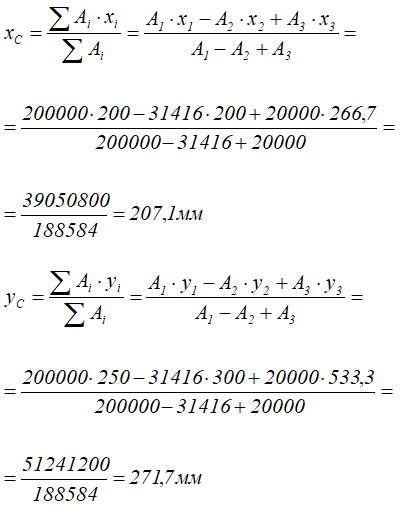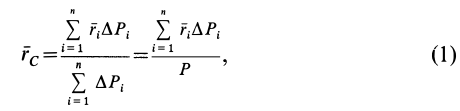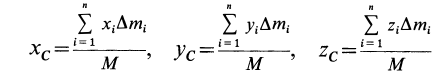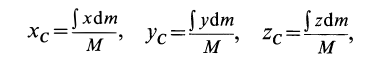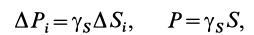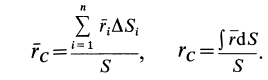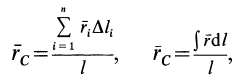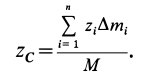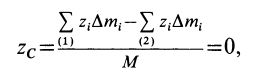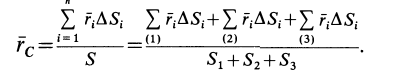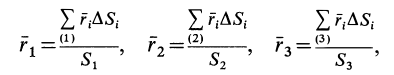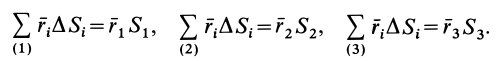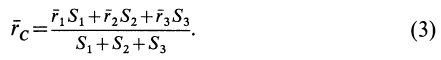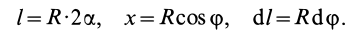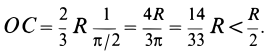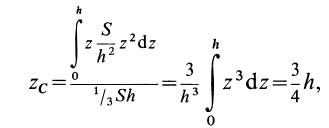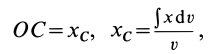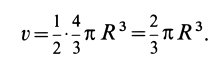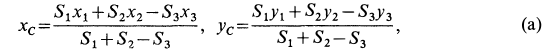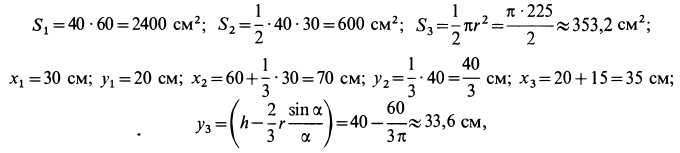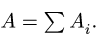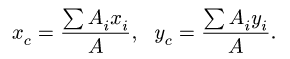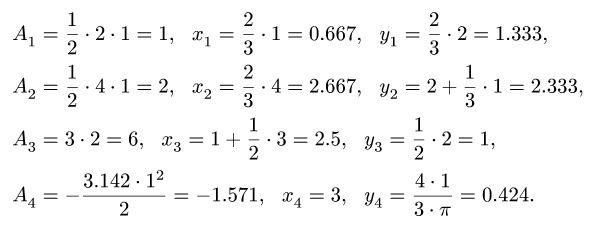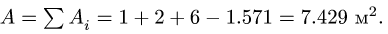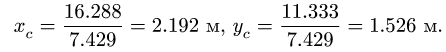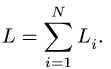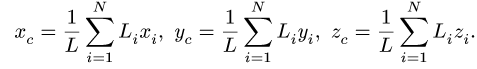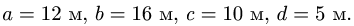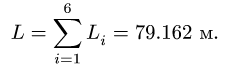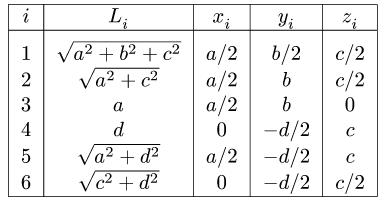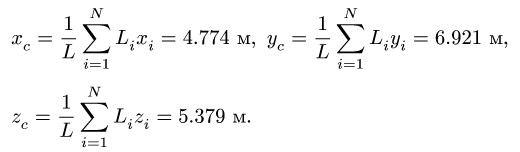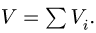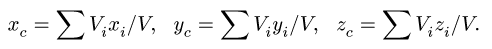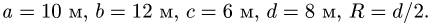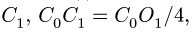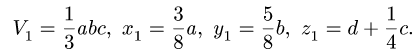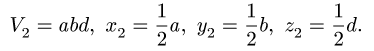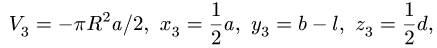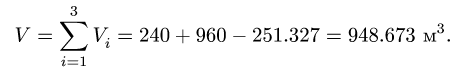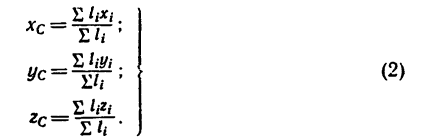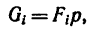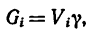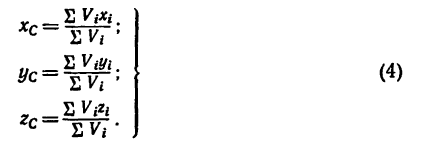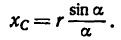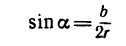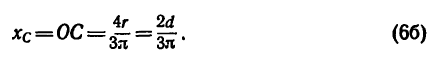
И. В. Богомаз. Механика
Рис. 5.7
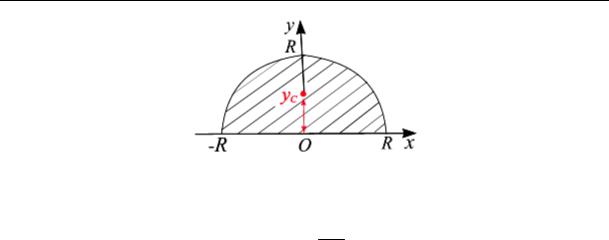
Центр тяжести полукруга yC = 43Rπ .
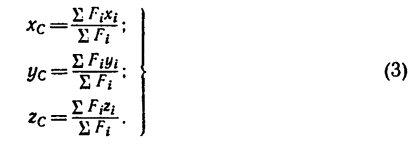
Метод разбиения на части. Некоторые тела сложной формы можно разбить на части, положение центра тяжести которых известно. В таких случаях центр тяжести составного тела вычисляют по формуле
|
n |
n |
|||
|
∑Ai xi |
∑Ai yi |
|||
|
x = |
i=1 |
, y = |
i=1 |
. |
|
C |
A |
C |
A |
|
Здесь A = ∑Ai – площадь сечения; xi, yi – центр тяжести i-го сечения; Ai – площадь i-го сечения.
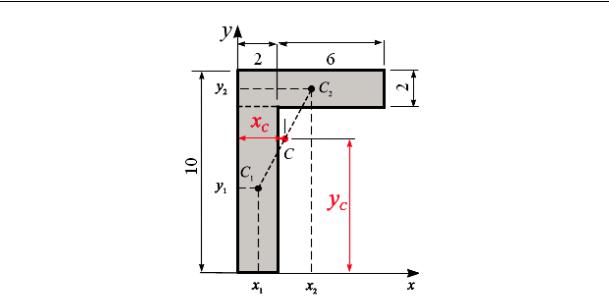
Пример 5.1. Вычислить координаты центра тяжести однородного сечения, составленного из двух прямоугольников (рис. 5.8). Размеры прямоугольников показаны на рис. 5.8 в см.
Решение. Разбиваем сечение на два прямоугольника (линии разреза показаны пунктиром) и проводим оси координат (рис. 5.8).
Вычислим координаты центров тяжести и площадь каждого из прямоугольников:
|
x =1cм, |
x = 4 см, |
|||
|
1 |
2 |
|||
|
y1 = 4 см, |
y2 = 9 см, |
|||
|
А = 2 8 =16cм2 |
; |
А =8 2 =16см2. |
||
|
1 |
2 |
112
5. Центр тяжести
Рис. 5.8
Площадь всего сечения
|
3 |
|||||||
|
А= ∑Аk = А1 + А2 =16 +16 = 32 см2. |
|||||||
|
Тогда |
k=1 |
||||||
|
x1 A1 + x2 A2 |
= 1 16 + 4 16 = 80 = 2,5см; |
||||||
|
x |
= |
||||||
|
С |
A |
32 |
32 |
||||
|
y |
= |
y1 A1 + y2 A2 |
= 4 16 +9 16 = 64 +144 = 6,5см. |
||||
|
С |
A |
32 |
32 |
||||
Положение центра тяжести совпадает с точкой С {2,5; 6,5}
(рис. 5.7).
Метод отрицательных площадей. В данном методе вырезан-
ные сечения заменяют отрицательными площадями. Проиллюстрируем этот метод на примере сечения.
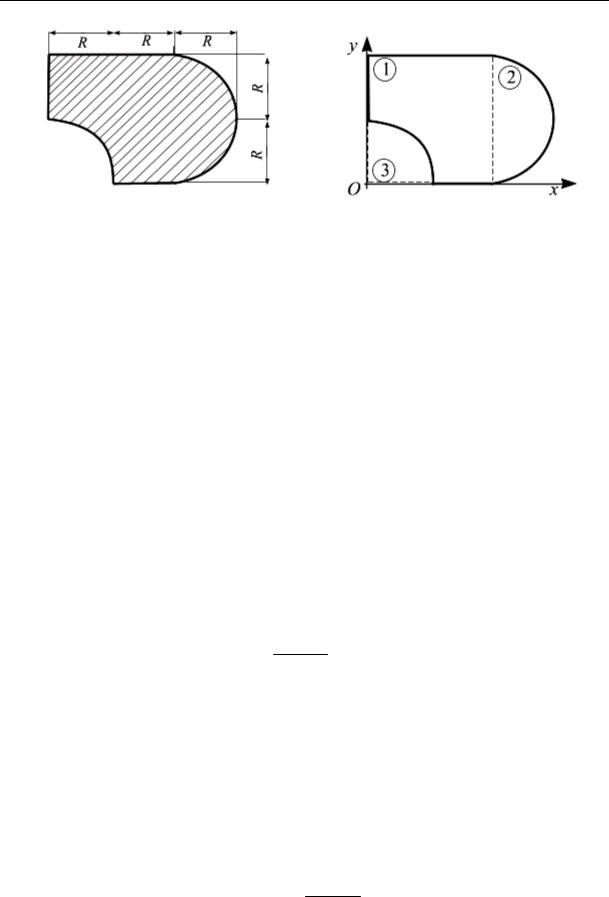
Пример 5.2. Задано сечение (рис. 5.9, а). Дано: R = 6 см. Вычислить центр тяжести сечения.
Решение. Разобьем сечение на простые фигуры: дополним квадрат – сечение 1, полукруг – сечение 2 и четверть круга – сечение 3 (рис. 5.9, б). За вспомогательную систему координат выберем стороны квадрата: Oxy. Вычислим площадь и координаты центров тяжести каждого сечения.
113
И. В. Богомаз. Механика
Рис. 5.9
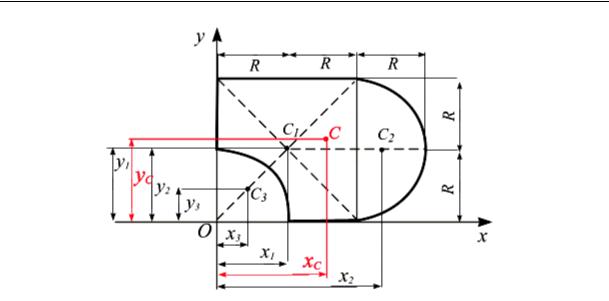
Имеем (рис. 5.10) 1. Квадрат:
A1 = 2R 2R = 4R2 = 4 62 = 4 36 =144 см2;
x1 = R = 6 см; y1 = R = 6 см.
2. Полукруг:
A2 = πR2 2 = 3,142 62 = 56,52 см2;
x2 = 2R + 43Rπ = 2 6 + 343,146 =12 + 2,55 =14,55см;
y2 = R = 6 см.
3. Четверть круга:
A3 = − πR4 2 = −3,144 62 = −28,26 см2; xC = yC = 43Rπ = 3 43.146 = 2,6 см.
114
5. Центр тяжести
Рис. 5.10
|
Итак, |
|||||
|
x |
= x1 A1 + x2 A2 + x3 A3 |
= 6 144 +14,55 56,52 −2,6 28,26 = |
|||
|
С |
A1 + A2 + A3 |
144 |
+56,52 −28,26 |
||
|
= 864 +822,37 −73,5 |
= 9, 4см; |
||||
|
172, 26 |
|||||
|
y |
= y1 A1 + y2 A2 + y3 A3 = 6 144 +6 56,52 −2,6 28,26 = |
||||
|
С |
A1 + A2 + A3 |
144 |
+56,52 −28,26 |
||
|
= 864 +339,12 −73,5 |
= 6,6см. |
||||
|
172, 26 |
Положение центра тяжести совпадает с точкой С {9,4; 6,6}
(рис. 5.11).
Статические моменты. Статические моменты сечения Sx и Sy определим, как сумму произведений элементарных площадей dAi на кратчайшее расстояния до осей Ox, Oy соответственно (рис. 5.11), т. е.
S x = ∑Ai yi → Sx = ∫y dA, Sy = ∑Ai xi → Sy = ∫x dA.
A A
115

И. В. Богомаз. Механика
Рис. 5.11
Статические моменты имеют размерность см3 или м3.
При параллельном переносе осей (Oxy → O1x1 y1 ) значения ста-
тических моментов изменяются и могут иметь как положительное, так и отрицательное значение. Следовательно, существует ось, относительно которой статический момент равен нулю.
Ось, относительно которой статический момент равен нулю, называется центральной. Точка пересечения центральных осей совпадает с точкой центра тяжести сечения.
Координаты центра тяжести тела через статические моменты будут вычисляться следующим образом:
|
x |
= |
Sy |
= ∑Ai xi →, |
y |
= |
Sx |
= ∑Ai yi . |
|
C |
A A |
C |
A |
A |
|||
Пример 5.3. Для заданного несимметричного поперечного сечения, составленного из швеллера № 20 и неравнополочного уголка № 10/6,5 (рис. 5.12), найти положение центральных осей.
Рис. 5.12
116

I – момент инерции;
5. Центр тяжести
Решение. Из сортамента выберем геометрические характеристики швеллера № 20 и неравнополочного уголка № 10/6,5 (табл. 5.1) и построим чертеж в масштабе (рис. 5.13).
Таблица 5.1
Сталь горячекатаная. Швеллеры. Сортамент (ГОСТ 8240–89)
|
I – момент инерции; |
||||||||
|
h – высота швеллера; |
z0 – расстояние от оси y до на- |
|||||||
|
b – ширина полки |
ружной грани стенки; |
|||||||
|
А – площадь поперечного сече- |
||||||||
|
ния |
||||||||
|
Номер |
Размеры, |
|||||||
|
швел- |
мм |
А, см2 |
Ix, см4 |
Iy, см4 |
x0, см |
|||
|
лера |
h |
b |
||||||
|
20 |
200 |
76 |
23,4 |
1530 |
134 |
2,3 |
Уголки стальные горячекатаные неравнополочные. Сортамент (ГОСТ 8510–86)
В – ширина
большей полки; z0 – расстояние от оси y до наружной b – ширина грани стенки;
меньшей полки А – площадь поперечного сечения
|
Но- |
Разме- |
|||||||
|
мер |
ры, мм |
А, см2 |
Ix, см4 |
Iy, см4 |
Ixy, см4 |
x0, см |
||
|
угол- |
В |
b |
||||||
|
ка |
||||||||
|
10/6,5 |
200 |
65 |
15,67 |
155,52 |
51,68 |
51,18 |
2,3 |
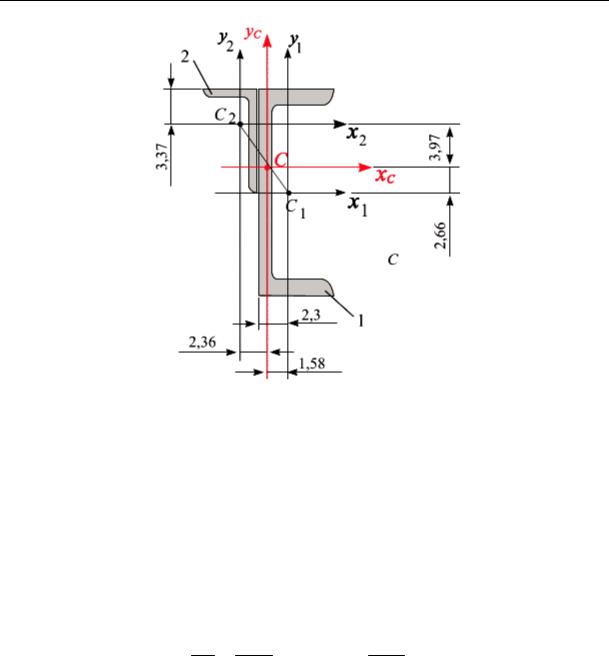
Для вычисления положения центра тяжести заданного сечения за вспомогательные оси примем центральные оси швеллера C1x1y1
(рис. 5.13).
Вычислим координаты центра тяжести сечения осей C1x1y1:
|
y |
= ∑Sxi |
= |
S1x1 |
+ S2x1 |
= |
А1 уС1 + А2 уС2 |
= |
0 +15,67 6,63 |
= 2,66; |
||||||||
|
A1 |
+ A2 |
А1 + А2 |
23,4 +15,67 |
||||||||||||||
|
C |
∑Ai |
||||||||||||||||
|
х |
= |
∑Sуi = |
S1у1 + S2 у1 |
= |
А1 хС1 + А2 хС2 |
= |
0 +15,67 (−3,94) |
= −1,58. |
|||||||||
|
23,4 +15,67 |
|||||||||||||||||
|
C |
∑Ai |
A1 + A2 |
А1 + А2 |
117
И. В. Богомаз. Механика
Рис. 5.13
Откладываем на схеме координаты точки центра тяжести сечения С{xC , yC }. Координаты центра тяжести сечения «легли» на отре-
зок С1С2, соединяющий центры тяжести частей (профилей), составляющих заданное сечение. Проверим правильность расчета. Соотношение отрезков должно быть равно соотношению площадей. Измеряем отрезки С1С и С2С, уточняем правильность соотношения
A2 = C1C →15,67 = C1C = 0,67.
A1 C2C 23,4 C2C
Проводим центра центральные оси CxCyC (рис. 5.13).
118
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подборка по базе: Практическое задание 3 Открытие наследства Решение.docx, ипз решение на проверку.docx, 1. Расчет изменений энтропии (теория и решение задач).doc, 9. Центральная Россия состав, географическое положение.ppt, Практическая работа 3 Решение кейсовой задачи по теме Качество о, 6F2E5EBF-6E49-4D28-9891-48278A22D182+18. Решение псих проб в пед, 2.1 Определение понятия скважины.pdf, ЗАДАЧИ РЕШЕНИЕ.docx, Государственный бюджет как централизованный денежный фонд.docx, Тест на определение готовности педагога к работе с одаренными д
Найти площадь (в ми координаты центра тяжести плоской фигуры (в м. Отметки на осях даны в метрах. Криволинейный участок контура является дугой половины или четверти окружности.
Решение:
Определение центра тяжести плоской несимметричной фигуры проводится в следующем порядке
1) сложное сечение разбиваем на простые, положение центра тяжести которых известно, либо легко может быть определено
2) выбираем произвольно координатные оси
3) определяем площади простых сечений
4) определяем координаты центров тяжести простых сечений относительно выбранных осей координат
5) найденные значения подставляем в формулы
𝑋
∑ 𝐴 𝑥
∑ 𝐴
; 𝑌
∑ 𝐴 𝑦
∑ где А, А … А — площади простых сечений x
1
, x
2
… x k
, y
1
, y
2
… yk
– координаты центра тяжести простых сечений
6) значения X
C
,Y
C
откладываем от выбранных осей координат с учетом знака, те. от точки О в положительном направлении координаты со знаком плюс ив отрицательном направлении координаты со знаком минус. Разбиваем плоскую фигуру на типовые геометрические фигуры. Площадь заштрихованной области можно представить в виде разности
площади основного прямоугольника O со сторонами b = 9 и h = 6 метров и площадей сектора круга I радиусом R = 2 метра, прямоугольного треугольника
II с катетами b = 5 и h = 2 метра, прямоугольного треугольника III с катетами b = 2 и h = 4 метра и прямоугольника IV со сторонами b = 2 и h = 5 метров. Координаты центра тяжести входящих простых плоских фигур в выбранной системе координат 9
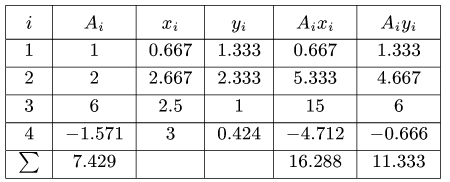
2 4,5 мм мм мм мм мм мм мм мм Тогда положение центра тяжести составного сечения запишется так
𝑋
∑ 𝐴 𝑥
∑ 𝐴
54 ∙ 4,5 3,14 ∙ 0,85 5 ∙ 3,67 4 ∙ 6,33 10 ∙ 8 31,86 3,66 мм. Ответ
𝑋
3,66 мм м .
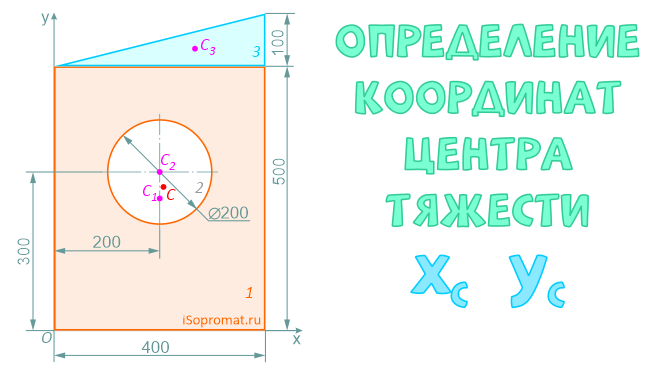
Определение координат центра тяжести xC и yC плоских фигур нестандартной формы выполняется при решении задач для последующих расчетов остальных геометрических характеристик, например, таких как радиусы и осевые моменты инерции поперечных сечений.
Рассмотрим способы и пример определения координат положения центра тяжести фигуры нестандартной формы.
Способы определения координат центра тяжести
Способы определения координат центров тяжести твердых объёмных тел и плоских фигур можно получить исходя из полученных ранее общих формул для расчета положения центра тяжести.
Существует 5 способов расчета координат положения центра тяжести:
- Аналитический (путем интегрирования).
- Метод симметрии. Если тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
- Экспериментальный. (метод подвешивания тела).
Этот способ подходит в основном для плоских и линейных тел. - Разбиение. Тело или фигура разбивается на конечное число частей (простых тел или фигур), для каждой из которых положение центра тяжести C и площадь A известны.
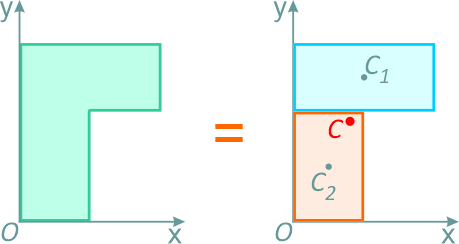
Например, проекцию тела на плоскость xOy (рисунок 1.8) можно представить в виде двух плоских фигур с площадями A1 и A2 (A = A1+ A2).
Рисунок 1.8
Центры тяжести этих фигур находятся в точках C1(x1, y1) и C2(x2, y2). Тогда координаты центра тяжести тела равны:
- Дополнение (Метод отрицательных площадей или объемов).
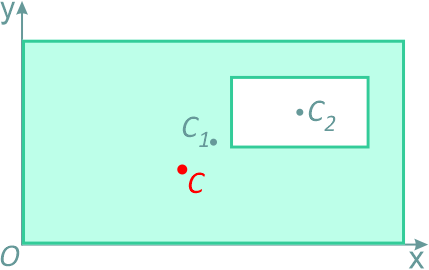
Это частный случай предыдущего способа разбиения. Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны.Например, необходимо найти координаты центра тяжести плоской фигуры (рисунок 1.9):
Рисунок 1.9
Тогда координаты центра тяжести фигуры с отверстием можно определить по формулам:
При решении задач по определению координат центра тяжести плоских фигур и объемных тел применяются последние два способа (разбиение и дополнение).
Пример определения координат центра тяжести сложной фигуры в нашем коротком видео:
Другие видео
Пример определения координат центра тяжести плоской фигуры
Задача
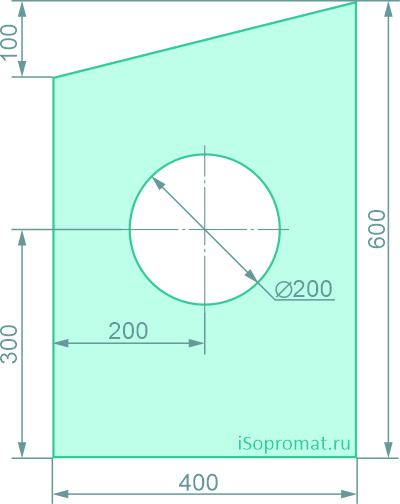
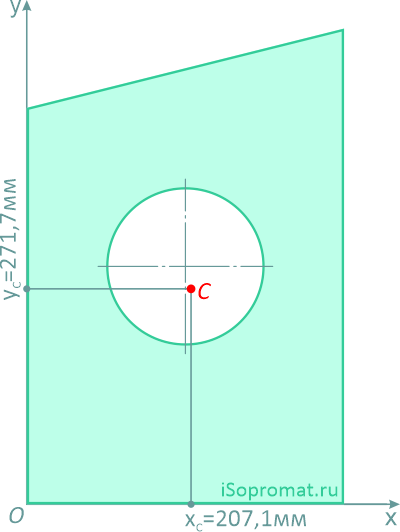
Определить координаты центра тяжести плоской фигуры с круглым отверстием
Решение
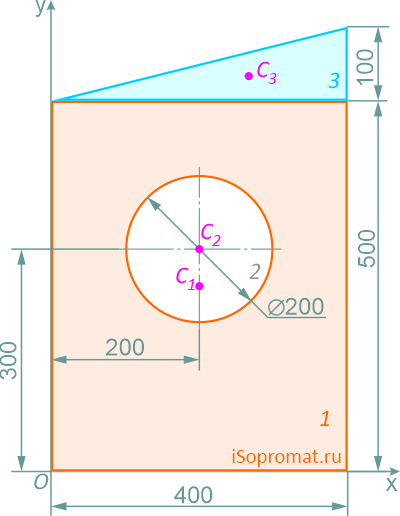
Разделим заданное сечение на простые фигуры – прямоугольник, круг и прямоугольный треугольник.
Через нижнюю левую точку фигуры проведем координатные оси x и y.
Рассчитаем необходимые для решения задачи площади A и координаты x,y центров тяжести Ci отдельных фигур:
Прямоугольник (фигура 1)
Площадь
A1=400×500=200000 мм2
Положение центра тяжести
x1=200мм
y1=250мм
Круг (2) (вычитаемая фигура)
Площадь
A2=π×2002/4=31416 мм2
Центр тяжести
x2=200мм
y2=300мм
Прямоугольный треугольник (3)
Площадь
A3=400*100/2=20000 мм2
Положение центра тяжести треугольника находится на пересечении его медиан (на расстоянии 1/3 высоты от основания или 2/3 высоты от его вершин)
x3=400×2/3=266,7мм
y3=500+100×1/3=533,3мм
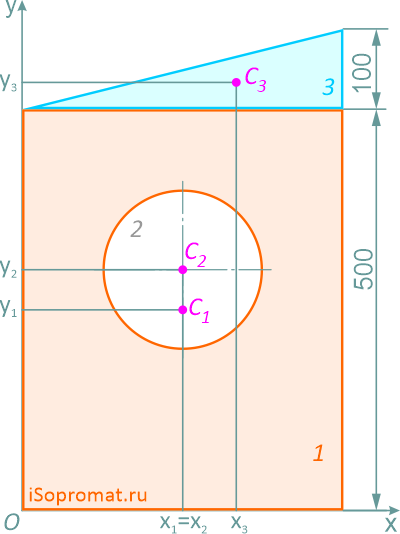
Координаты x и y центра тяжести C всей плоской фигуры определим по формулам:
Ответ: Таким образом, центр тяжести заданной фигуры находится в точке C с координатами xC=207,1мм, yC=271,7мм.
Другие примеры решения задач >
Центры тяжести простейших фигур >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
РГР
№ 3 «Определение центра тяжести плоской фигуры»
Методические
указания
Положения центров
тяжести простых геометрических фигур могут быть рассчитаны по известным
формулам (рис. 8.3: а) — круг; б) — квадрат, прямоугольник; в)
— треугольник; г) — полукруг).
 |
Примечание.
Центр тяжести симметричной фигуры находится на оси симметрии.
Центр тяжести
стержня находится на середине высоты. При решении задач используются следующие
методы:
1.
метод симметрии: центр тяжести
симметричных фигур находится на оси симметрии;
2.
метод разделения: сложные сечения
разделяем на несколько простых частей, положение центров тяжести которых легко
определить;
3.
метод отрицательных площадей: полости
(отверстия) рассматриваются как часть сечения с отрицательной площадью.
Достаточно удачно
определение координат центра тяжести плоских фигур разобрано в учебнике
Вереиной «Техническая механика» (тот, которым Вы пользуетесь в классе).
Рекомендую использовать табличную форму решения задачи на определение координат
центра тяжести.
Обратите внимание,
на формулы и рисунки для нахождения центра тяжести треугольника и полукруга:
они вам понадобятся для расчета.
Не пугайтесь
отрицательных площадей: увидели отверстие (или вырез) можете приписать этой
площади знак «минус» — всего делов-то!
На защите кроме
четкого понимания решения своего варианта, необходимо знать формулы для
основных случаев (см. выше), уметь графически находить центр тяжести плоской
фигуры, понимать суть методов нахождения координат центра тяжести.
Алгоритм
выполнения работы
Алгоритм
выполнения РГР «Определение координат центра тяжести»
1.
Вычерчиваем заданную фигуру: масштаб 1:1. (то есть если написано 120 мм, то вы
и вычерчиваете отрезок 12 см, в 10 варианте придется даже немного выйти за
рамки, не переживайте, пусть так и будет).
2.
Выбираем координатные оси: так как у Вас фигура несимметричная, понадобятся оси
Ох и Оу, ну и задавайте начало координат в левом нижнем углу.
3.
Расставляем размеры фигуры – не обязательно по правилам черчения, главное,
чтобы Вы сами
понимали,
где какие размеры (см. рисунок на следующей странице).
4.
Пользуясь правилами нахождения координат основных фигур (прямоугольника,
треугольника,
полуокружности
(см. Пояснения к выполнению РГР), показываете на вашем чертеже, где находятся эти
координаты, попутно заполняя табличку (она ниже приведена). Для треугольника
рассчитывайте 1/3 размера стороны от прямого угла. Для полуокружности
отсчитывайте значение 4*R/(3*π ) от центра окружности. Не забывайте, где у Вас
начало координат! На моем примере взят рисунок е) и численные значения варианта
1.
5.
Заполняйте таблицу (приведена ниже) найденными значениями координат элементов.
Смотрите на примечание внизу страницы!!!
6.
Вычислите площади элементов (для прямоугольника, треугольника, полуокружности).
Смотрите на примечание внизу страницы!!!
7.
Не забудьте приписать отрицательные площади элементам (вырезам и отверстиям!!!)
8.
По табличке рассчитываете координаты центра тяжести фигуры (хотите посчитать
быстрее? Тогда не ленитесь, Excel Вам в помощь).
9.
Вычисляем координаты центра тяжести фигуры:
10. Укажите положение найденного центра тяжести фигуры
на чертеже.
11. Не забывайте, что все расчетно-графические работы
выполняются на листах с рамками: первый лист – большая, остальные маленькие!
Сама
фигура – на следующей странице!
Содержание:
Центр тяжести:
При рассмотрении движения тел, особенно таких, как самолеты, ракеты, космические корабли, важное значение имеет понятие центра тяжести.
Определения и формулы для вычисления центров тяжести
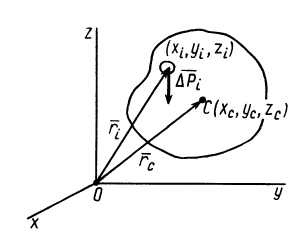
Для введения понятия центра тяжести разобьем мысленно рассматриваемое тело на достаточно большое число малых по сравнению с телом или элементарных его частей произвольной формы. Силу тяжести элементарной частицы тела с индексом
Радиус-вектор центра тяжести тела 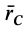
где 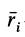

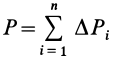

Рис. 88
Если в (1) перейти к пределу, увеличивая число элементарных частей 

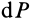
где 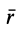
где 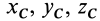
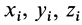
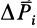
Используя понятие центра тяжести тела, введем понятие его центра масс. Силы тяжести элементарных частей тела и всего тела можно выразить через их массы 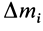
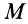

Подставляя эти значения сил тяжести в (1) и (1′) после сокращения на 
и соответственно
По формулам (2) и (2′) определяют радиус-вектор центра масс тела. Центр масс обычно определяют независимо от центра тяжести как геометрическую точку, радиус-вектор, которой вычисляется по формулам (2) или (2′). В проекциях на оси координат из (2) и (2′) получаем:
и
где 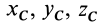
Для однородного тела силу тяжести элементарной частицы тела и ее массу можно вычислить по формулам
где 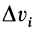


где 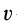


по которым определяют центр тяжести объема тела.
Если тело имеет форму поверхности, т. е. один из размеров мал по сравнению с двумя другими, как, например, у тонкого листа железа, то имеем
где 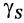
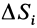
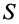
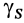
Для однородных тел типа проволоки, у которых два размера малы по сравнению с третьим, можно определить радиус-вектор центра тяжести длины линии по формулам
где 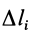
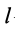
Методы определения центров тяжести (Центров масс)
Метод симметрии
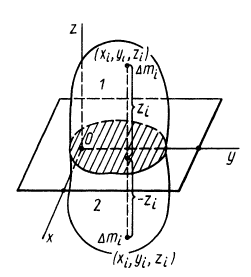
При определении центров тяжести широко используется симметрия тел. Докажем, что для однородного тела, имеющего плоскость симметрии, центр тяжести находится в плоскости симметрии. Для доказательства выберем начало координат в плоскости симметрии тела и одну из осей координат, ось 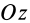
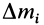
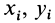
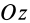
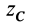
Разбивая сумму в числителе на две по симметричным частям тела, получаем, что
так как симметричные части тела 1 и 2 одинаковы.
Таким образом, центр масс расположен в плоскости симметрии и для его определения достаточно вычислить только две его координаты 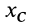
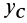
Аналогично доказывается, что для однородного тела, имеющего ось или центр симметрии, центр масс находится соответственно на оси симметрии или в центре симметрии.
Рис. 89
Метод разбиения на части (метод группировки)
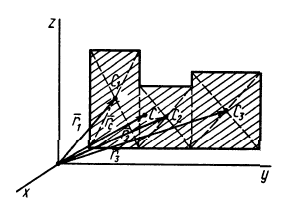
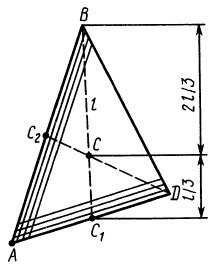
Некоторые тела сложной формы можно разбить на части, центры тяжести которых известны или предварительно могут быть определены. В таких случаях центры тяжести сложных тел вычисляются по общим формулам, определяющим центр тяжести, только вместо элементарных частиц тела берутся его конечные части, на которые оно разбито. Покажем это на частном примере плоской фигуры, изображенной на рис. 90. Плоскую фигуру можно разбить на три части, центры тяжести которых 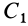
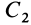
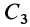
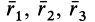
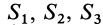
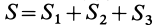
Используя определение центра тяжести и производя группировку слагаемых под знаком суммы по частям фигуры, на которые она разбита, получим
Радиусы-векторы центров тяжести частей тела выразятся в такой форме:
или
Используя эти формулы для радиуса-вектора всей фигуры, имеем
Полученная формула имеет ту же структуру, что и формула, определяющая радиус-вектор центра тяжести тела при разбиении его на элементарные частицы, только в нее входят величины для конечных частей тела.
Рис. 90
Метод отрицательных масс
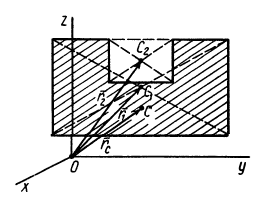
Видоизменением метода разбиения на части является метод отрицательных масс. Проиллюстрируем его тоже на примере плоской фигуры (рис. 91). Для определения центра тяжести этой фигуры ее можно разбить на три части. Можно поступить по-другому. Для этого дополним нашу фигуру до прямоугольника и примем, что этот прямоугольник с площадью 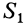
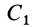
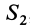
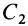
В отличие от обычного метода разбиения на части в формуле (4) массы и, следовательно, площади входят со знаком минус.
Метод отрицательных масс особенно удобен при вычислении положения центров тяжести тел, имеющих отверстия.
Рис. 91
Центры тяжести простейших тел
Для определения центров тяжести тел сложной формы методом разбиения на части или методом отрицательных масс необходимо уметь вычислять центры тяжести простейших тел, на которые разбивается тело сложной формы. Рассмотрим некоторые из тел, для определения центров тяжести которых известны простые способы их нахождения или вычисления по формулам.
Прямолинейный отрезок
Центр тяжести прямолинейного однородного отрезка располагается на его середине, а неоднородного— на самом отрезке и не может находиться вне отрезка.
Площадь треугольника
Для определения центра тяжести площади треугольника разобьем его прямыми линиями, параллельными одной из его сторон 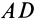

Затем разобьем треугольник на полоски прямыми линиями, параллельными другой стороне 
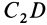

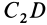
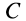

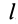
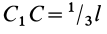
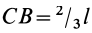
Рис. 92
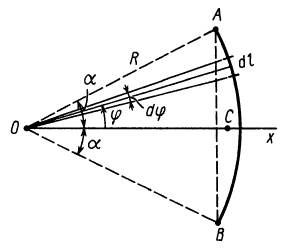
Дуга окружности
Дуга окружности 
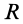
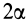
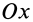

Рис. 93
В рассматриваемом случае
Подставляя эти значения в формулу для 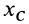
Таким образом,
Для полуокружности 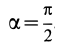
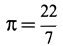
Площадь кругового сектора
Центр тяжести площади кругового сектора с радиусом 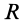
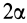
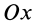
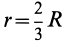
Рис. 94
Используя формулу для центра тяжести дуги окружности, получим
или
Для площади полукруга 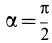
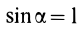
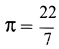
Объем пирамиды и конуса
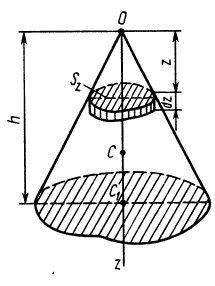
Определим положение центра тяжести объема конуса (рис. 95). Для простоты рассмотрим прямой конус, у которого высота является осью симметрии. Высотой конуса является отрезок, соединяющий его вершину 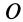
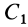
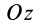
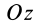
Разобьем конус плоскостями, перпендикулярными оси 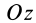
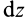
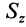
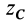
Отношения линейных размеров сечений к соответствующим размерам основания конуса пропорциональны их расстояниям до вершины конуса. Отношения площадей пропорциональны квадратам расстояний. Приняв 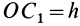
Учитывая, что
имеем
или
Таким образом, центр тяжести прямого конуса находится на расстоянии 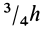
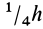
Рис. 95
Это справедливо для объема любого конуса и любой пирамиды, как прямых, так и наклонных, т. е. центр тяжести объема пирамиды или конуса находится на расстоянии 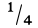
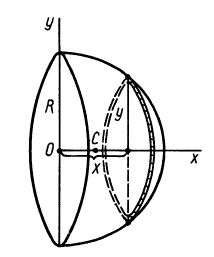
Объем полушара
Полушар имеет ось симметрии, которую примем за координатную ось 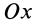
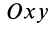
где 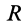
где 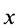
Объем элементарного диска
так как радиус диска 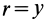
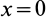
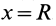
Таким образом, центр тяжести объема полушара находится от его центра на расстоянии
Это расстояние меньше половины радиуса полушара.
Рис. 96
Задача №1
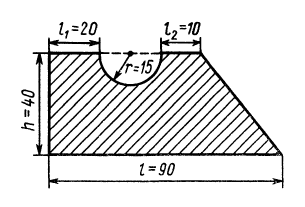
Определить координаты центра тяжести площади плоской фигуры, имеющей размеры, указанные на рис. 97.
Рис.97
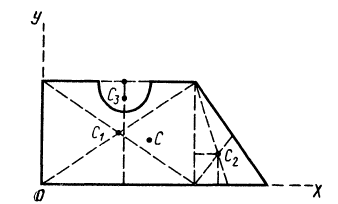
Рис. 98
Решение. Присоединим к заданной фигуре дополнительно полукруг 3 и разобьем полученную фигуру на прямоугольник 1 и треугольник 2. Получили три фигуры, две из которых имеют положительные площади (прямоугольник 1 и треугольник 2) и одна — отрицательную (полукруг 3). В выбранной системе координат для координат центра тяжести заданной фигуры имеем
где 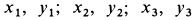
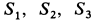
Вычислим площади и координаты центров тяжести отдельных фигур, учитывая рис. 98 Имеем:
так как 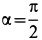
Подставляя полученные значения в (а), получим:
Центр тяжести плоской фигуры
постановка задачи. Найти площадь и координаты центра тяжести плоской фигуры.
План решения:
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
2. Выбираем систему координат. Вычисляем площади и координаты 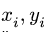
3. Находим общую площадь фигуры по формуле
4. Определяем координаты центра тяжести фигуры:
Задача №2
Найти площадь и координаты центра тяжести плоской фигуры. Криволинейный участок контура является половиной окружности с центром на оси Ох (рис. 74). Размеры на рисунке даны
Решение
1. Разбиваем фигуру на простые отдельные части, положение центров тяжести которых известны.
Центр тяжести прямоугольника находится в его геометрическом центре, положение центра тяжести других фигур, встречающихся в задачах, изображено на рис. 75
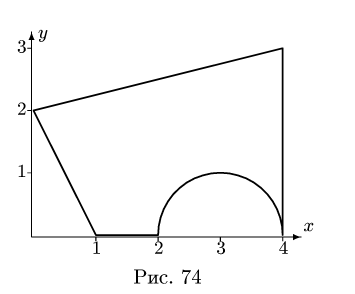
Представляем фигуру в виде двух треугольников 1,2, прямоугольника 3 и выреза 4 в виде полукруга (рис. 76).
2. Вычисляем площадь (в 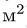
Площадь выреза берем со знаком минус.
3.Площадь фигуры
4. Находим координаты центра тяжести всей фигуры:
Вычисления удобно свести в таблицу:
Сначала заполняем столбцы 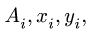
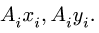
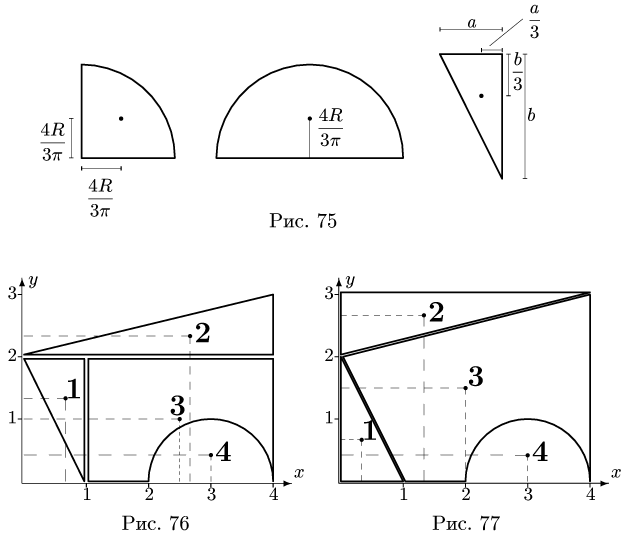
Замечание 1. Большинство задач на определение центра тяжести допускает несколько способов разбиения фигуры. Это можно использовать для проверки решения. Второй вариант разбиения фигуры в данном примере состоит из прямоугольника 3 с размерами 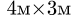
Замечание 2. Решение задачи в системе Maple V методом контурного интегрирования.
- Заказать решение задач по теоретической механике
Пространственная стержневая система
Постановка Задачи. Найти координаты центра тяжести пространственной фигуры, состоящей из N однородных стержней.
План решения:
1. Разбиваем фигуру на отдельные стержни.
2. Выбираем систему координат. Вычисляем длины и координаты 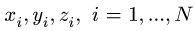
3. Находим суммарную длину стержней системы
4. Определяем координаты центра тяжести тела по формулам
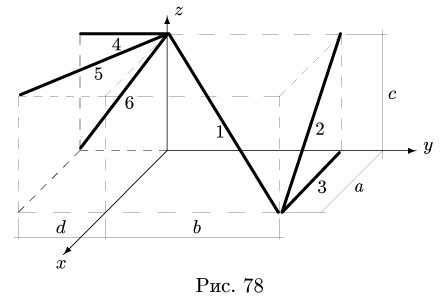
Задача №3
Найти координаты центра тяжести пространственной фигуры, состоящей из шести однородных стержней (рис. 78). Даны размеры:
Решение
1. Разбиваем фигуру на шесть стержней.
2. Выбираем систему координат (рис. 78). Вычисляем длины и координаты 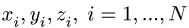
3. Находим суммарную длину стержней системы:
Промежуточные результаты удобно занести в таблицу:
4. Определяем координаты центра тяжести тела по формулам
Постановка задачи. Найти координаты центра тяжести однородного объемного тела.
План решения:
1. Разбиваем тело на простые части, положение центров тяжести которых известно.
2. Выбираем систему координат. Вычисляем объемы 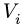
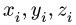
3. Находим общий объем тела по формуле
4. Определяем координаты центра тяжести тела:
Задача №4
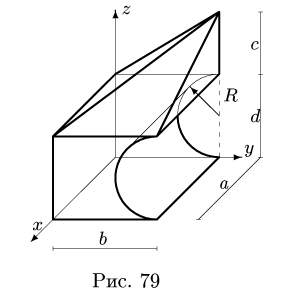
Найти координаты центра тяжести однородного объемного тела (рис.79);
Решение
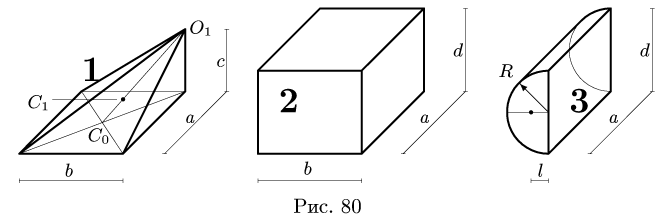
1. Разбиваем тело на пирамиду 1, параллелепипед 2 и половину цилиндра 3 (рис. 80).
2. Выбираем систему координат. Вычисляем объемы 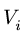
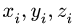
Центр тяжести параллелепипеда 2 совпадает с его геометрическим центром:
Объем половины цилиндра 3 берем со знаком минус:
где 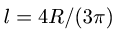
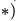
3. Находим общий объем тела:
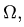
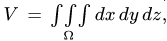
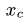
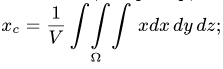
4. Определяем координаты центра тяжести тела:
Центр тяжести
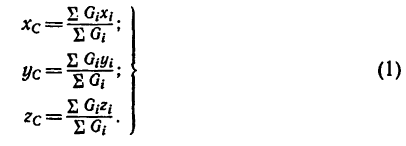
Центр тяжести — точка, через которую проходит линия действия равнодействующей элементарных сил тяжести. Он обладает свойством центра параллельных сил. Поэтому формулы для определения положения центра тяжести различных тел имеют вид:
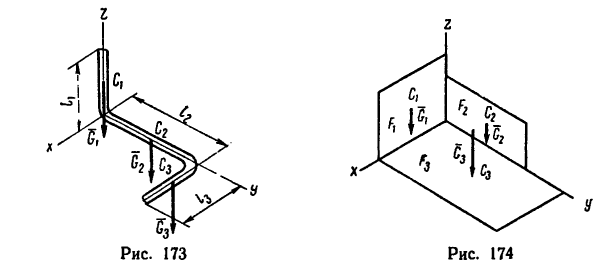
Если тело, центр тяжести которого нужно определить, можно отождествить с фигурой, составленной из линий (например, замкнутый или незамкнутый контур, изготовленный из проволоки, как на рис. 173), то вес 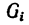
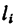
где d — постоянный для всей фигуры вес единицы длины материала.
После подстановки в формулы (1) вместо 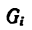
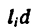
Если тело имеет вид фигуры, составленной из расположенных различным образом плоскостей или кривых поверхностей (рис. 174),
то вес каждой плоскости (поверхности) можно представить так:
где 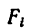
После подстановки этого значения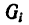
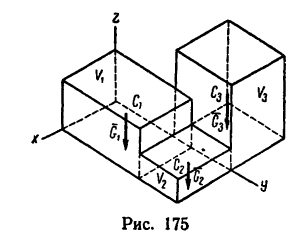
Если же однородное тело можно разделить на простые части определенной геометрической формы (рис. 175), то вес каждой части
где 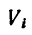
После подстановки значений 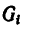
При решении некоторых задач на определение положения центра тяжести тел иногда необходимо знать, где расположен центр тяжести дуги окружности, кругового сектора или треугольника.
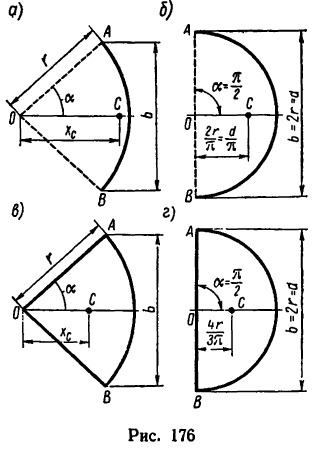
Если известен радиус дуги г и центральный угол 2а, стягиваемый дугой и выраженный в радианах, то положение центра тяжести С (рис. 176, а) относительно центра дуги О определится формулой
Если же задана хорда 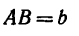
и тогда
В частном случае для полуокружности обе формулы примут вид (рис. 176, б)
Положение центра тяжести кругового сектора, если задан его радиус r (рис. 176, в), определяется при помощи формулы
Если же задана хорда сектора, то
В частном случае для полукруга обе последние формулы примут вид (рис. 176, г)
Центр тяжести площади любого треугольника расположен от любой стороны на расстоянии, равном одной трети соответствующей высоты.
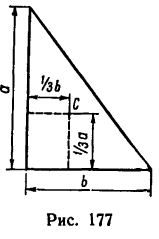
У прямоугольного треугольника центр тяжести находится на пересечении перпендикуляров, восставленных к катетам из точек, расположенных на расстоянии одной трети длины катетов, считая от вершины прямого угла (рис. 177).
При решении задач на определение положения центра тяжести любого однородного тела, й составленного либо из тонких стержней (линий), либо из пластинок (площадей), либо из объемов, целесообразно придерживаться следующего порядка:
- выполнить рисунок тела, положение центра тяжести которого нужно определить. Так как все размеры тела обычно известны, при этом следует соблюдать масштаб;
- разбить тело на составные части (отрезки линий или площади, или объемы), положение центров тяжести которых определяется исходя из размеров тела;
- определить или длины, или площади, или объемы составных частей;
- выбрать расположение осей координат;
- определить координаты центров тяжести составных частей;
- найденные значения длин или площадей, или объемов отдельных частей, а также координат их центров тяжести подставить в соответствующие формулы и вычислить координаты центра тяжести всего тела;
- по найденным координатам указать на рисунке положение центра тяжести тела.
- Кинематика точки
- Плоское движение твердого тела
- Мгновенный центр скоростей
- Мгновенный центр ускорений
- Условия равновесия системы сил
- Плоская система сил
- Трение
- Пространственная система сил