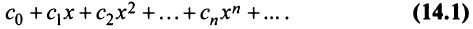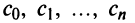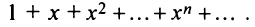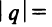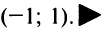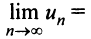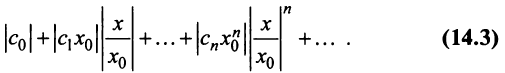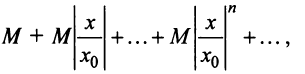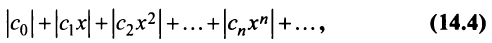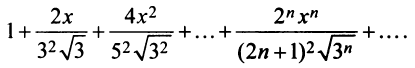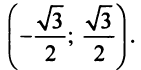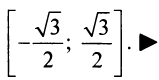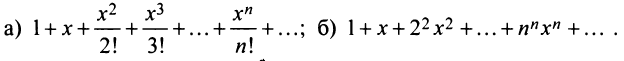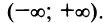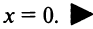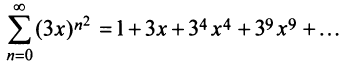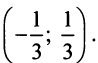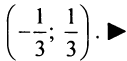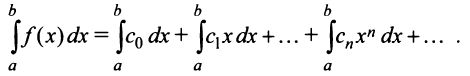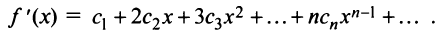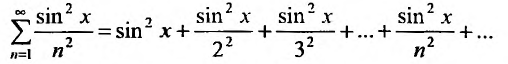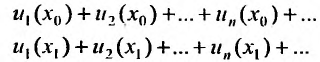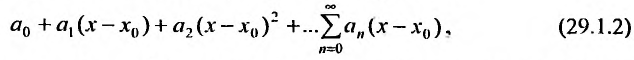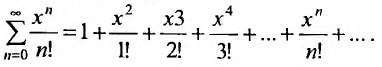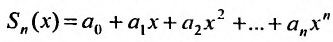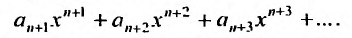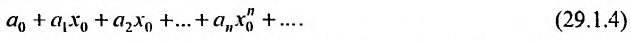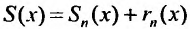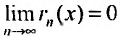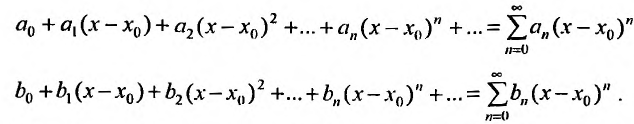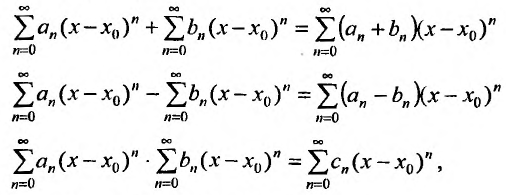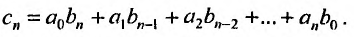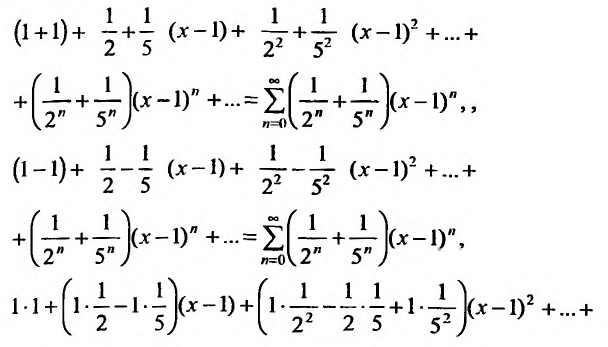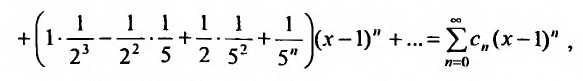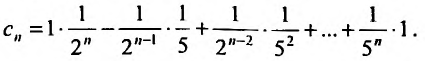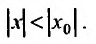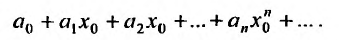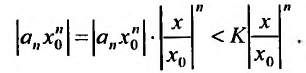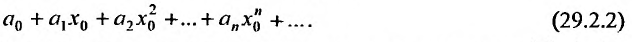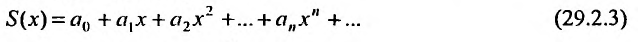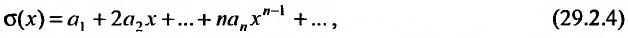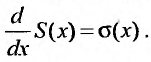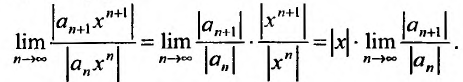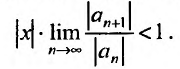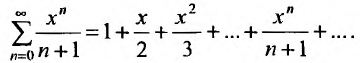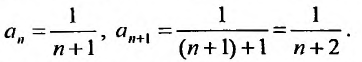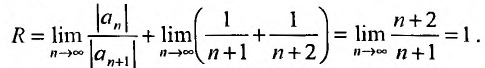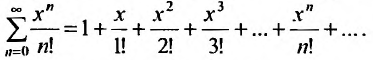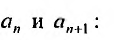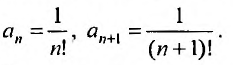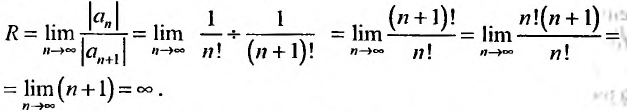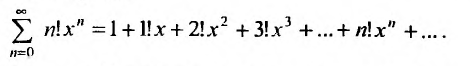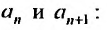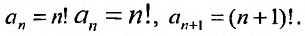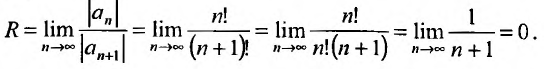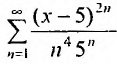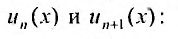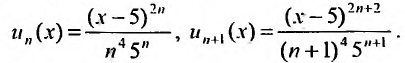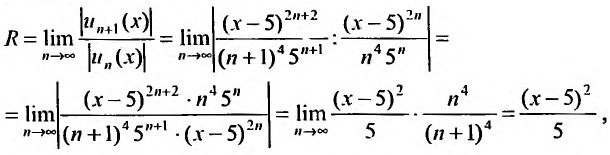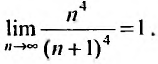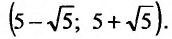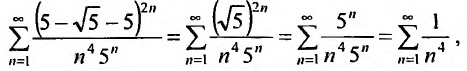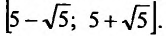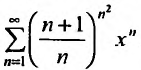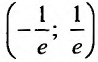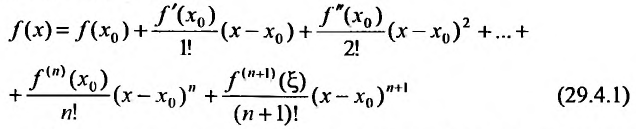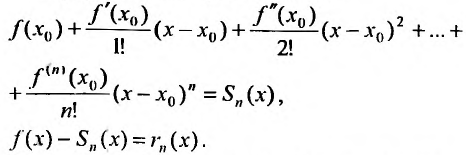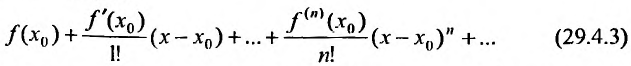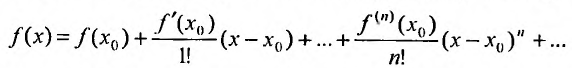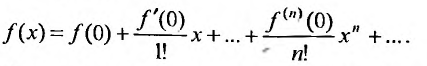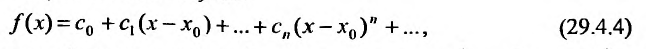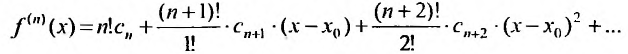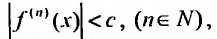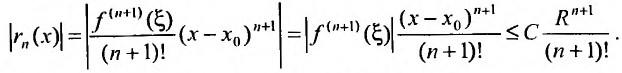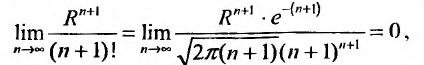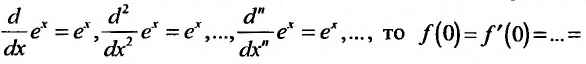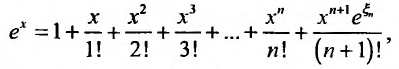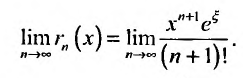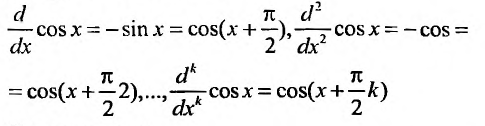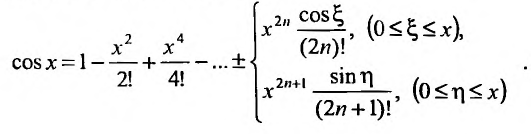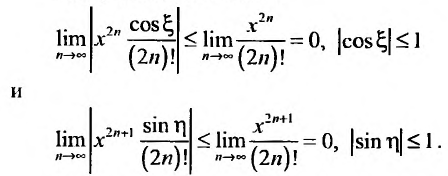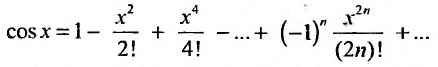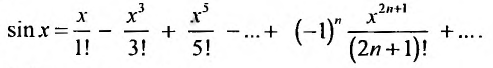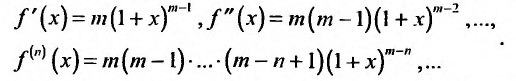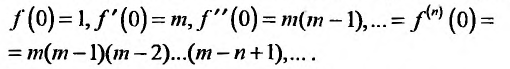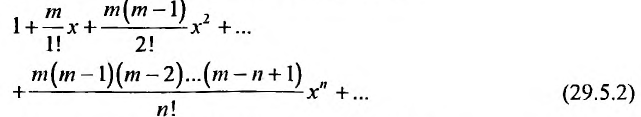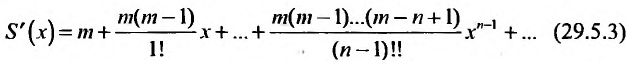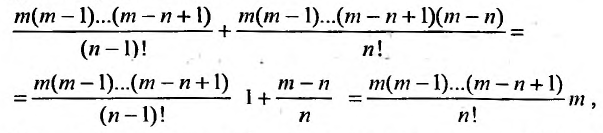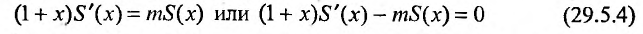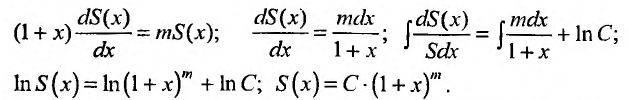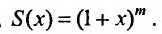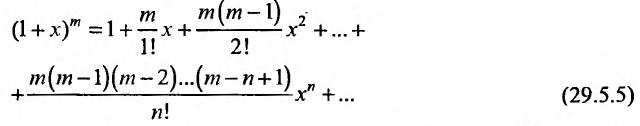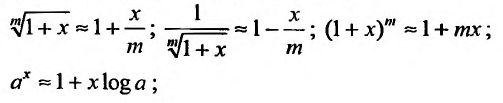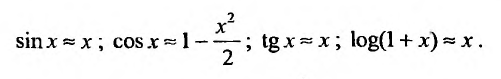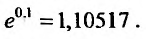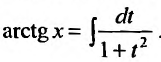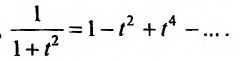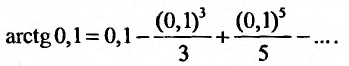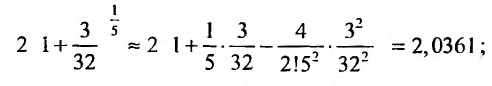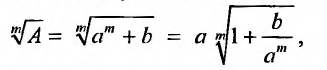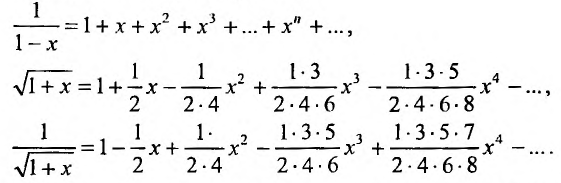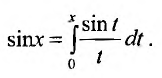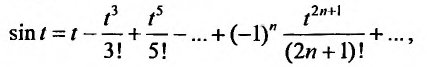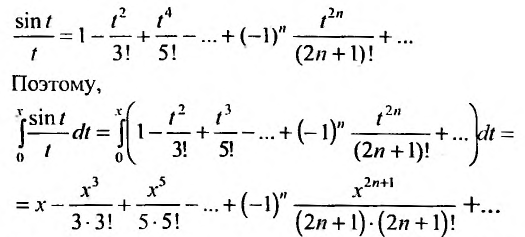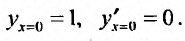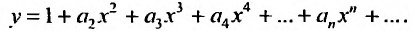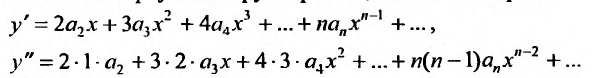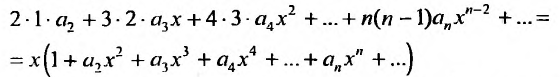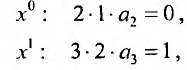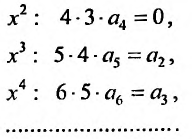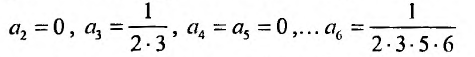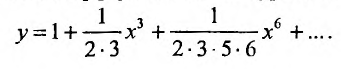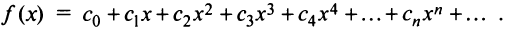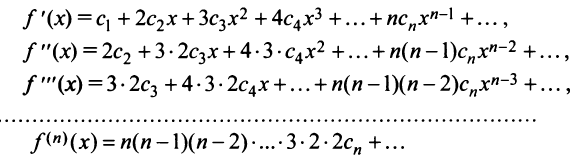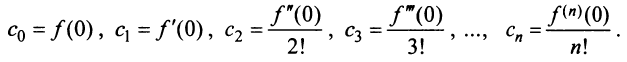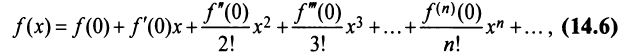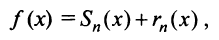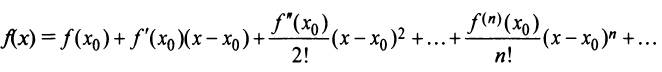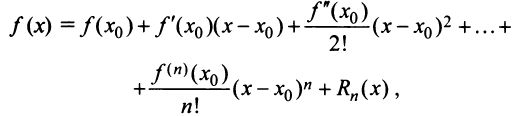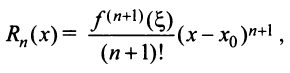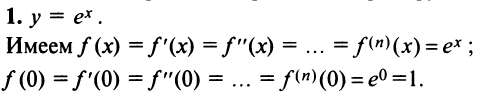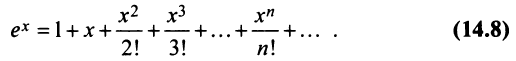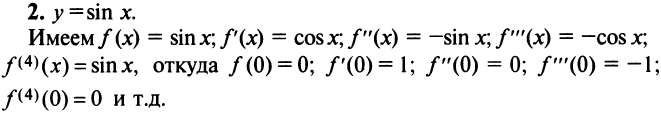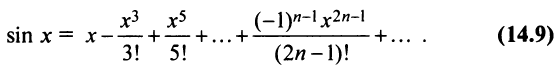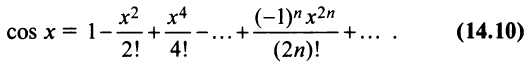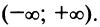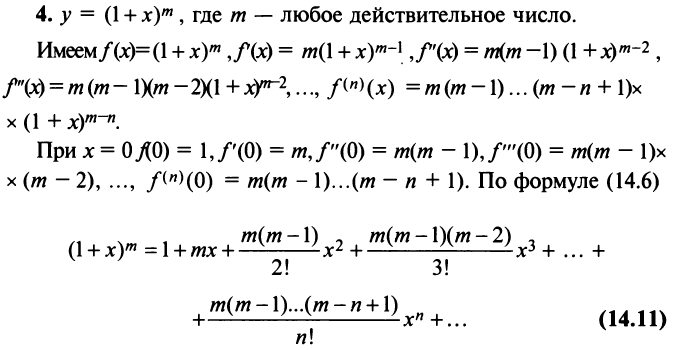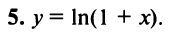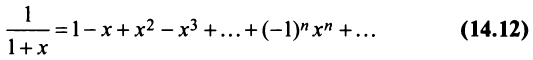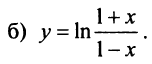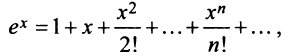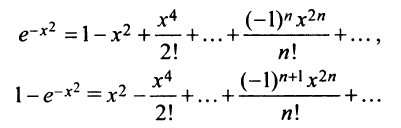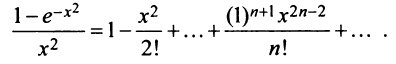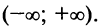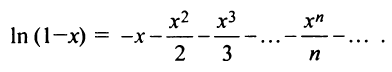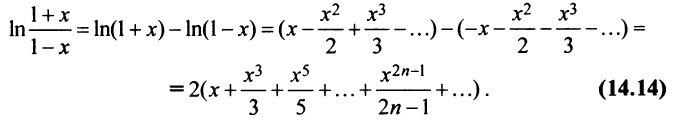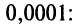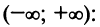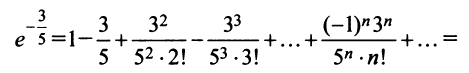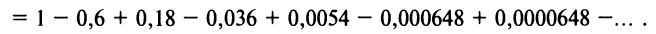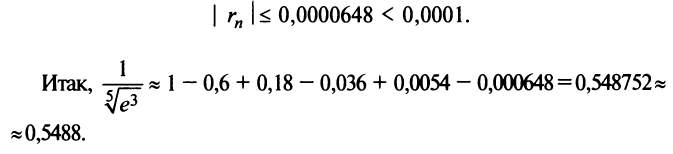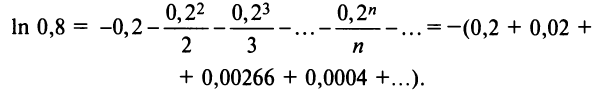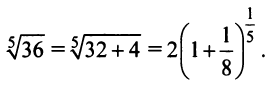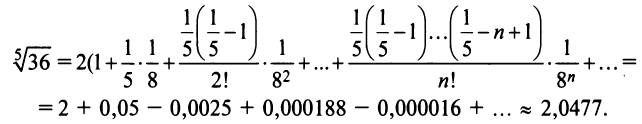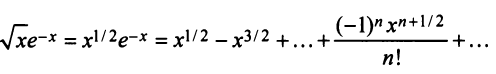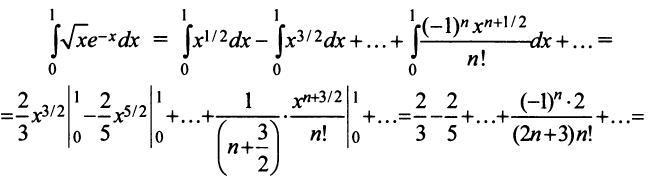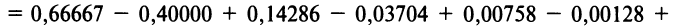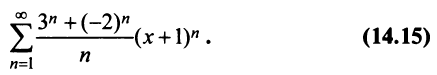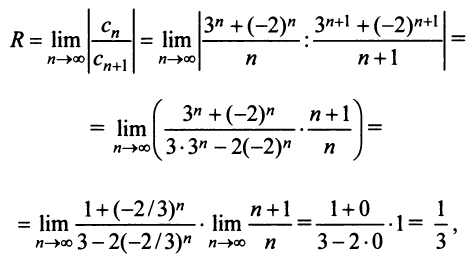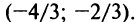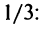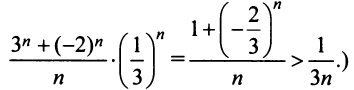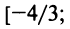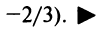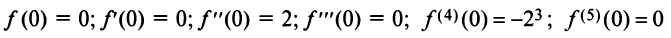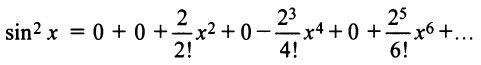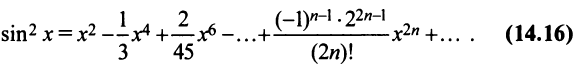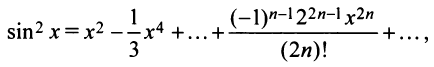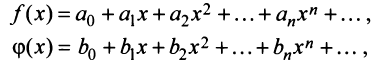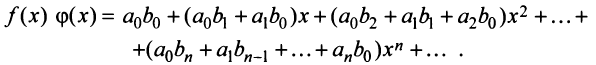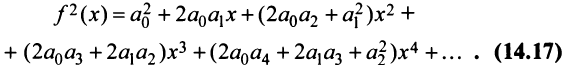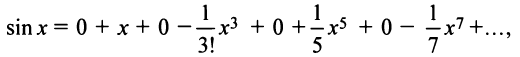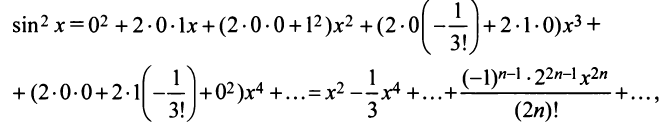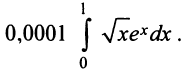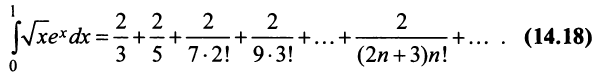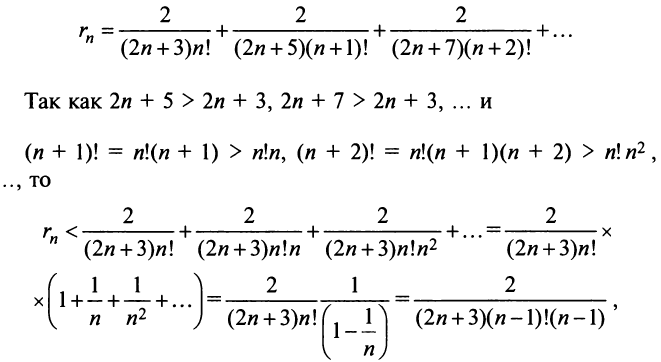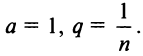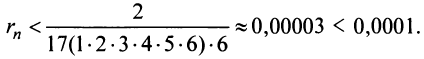Степенные ряды
Частным
случаем функциональных рядов являются
степенные ряды.
Определение
Степенным
рядом
называется функциональный ряд
, (15)
члены
которого являются произведениями
постоянных
,
,
…,,…
на степенные функции от разностис целыми неотрицательными показателями
степеней.
Точка
x0
называется
центром
степенного ряда.
Пример
20
Ряд
– степенной ряд с центром в точке
.
Ряд
– степенной ряд с центром в точке
.
Ряд
– функциональный ряд.
Исследование
степенного ряда на сходимость, а именно
нахождение области сходимости степенного
ряда, является важной задачей теории
рядов. Ее решение основано на теореме
Абеля.
ТЕОРЕМА
11 (Теорема Абеля)
-
Если
степенной ряд сходится при
,
то он сходится, и притом абсолютно, для
всех,
удовлетворяющих неравенству
.
-
Если
степенной ряд расходится при
,
то он расходится для всех,
удовлетворяющих неравенству
.
Доказательство
1)
Введем замену
.
Тогда получаем степенной ряд,
точка сходимости которого,
а неравенство, описывающее область
сходимости, примет вид.
По
условию
числовой
ряд
сходится,
следовательно общий член
при
,
но любая последовательность, имеющая
предел ограничена, т.е. существует такое,
чтодля всех
.
Рассмотрим
общий член степенного ряда
.
,
,
так как
.
Получили
новый ряд
,
который является геометрической
прогрессией со знаменателем,
следовательно, он сходится. Так как,
то из первого признака сравнения следует
абсолютная сходимость исходного
степенного ряда.
2)
Вторую часть теоремы можно доказать
аналогично.
Геометрическая
интерпретация этой теоремы
Если
ряд (1) сходится в точке
,
то он сходится и во всех точках,
расположенных ближе к центру степенного
ряда
,
чем.
Если же ряд расходится при
,
то он расходится и во всех более удаленных
от центра ряда точках.
Опираясь
на теорему Абеля, можно доказать, что
существует такое положительное число
,
что для всех,
удовлетворяющих неравенству
,
ряд сходится абсолютно и расходится
при всех
,
для которых
.
Число
называетсярадиусом
сходимости
ряда
,
а интервал
–интервалом
сходимости.
В
частном случае интервал сходимости
степенного ряда может совпадать со всей
числовой осью (в этом случае
)
или может превращаться в точку (в этом
случае).
Заметим, что интервал сходимости всегда
симметричен относительно центра
степенного ряда.
Пример
21.
Найти интервал сходимости степенного
ряда
.
Решение
Первый
способ решения
Рассмотрим
ряд, составленный из абсолютных величин
членов данного ряда:
.
Применим признак Даламбера:
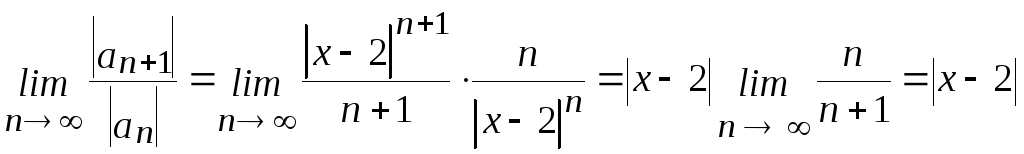
Если
,
то ряд сходится. Итак,,
–
интервал сходимости данного ряда.
Поведение данного ряда на концах
интервала сходимости, т.е. в точкахи
,
исследуется отдельно.
При
из данного ряда получаем ряд
,
который условно сходится.
При
получаем гармонический ряд
,
который расходится.
Второй
способ решения
Если
для степенного ряда (2) существует
,
то радиус сходимости степенного ряда
можно вычислить по формуле
В
нашем случае
и
,
поэтому
.
Так
как
– центр степенного ряда, то
– интервал сходимости данного ряда.
Сходимость
ряда на концах интервала сходимости
исследована выше.
Итак,
данный ряд сходится абсолютно при
и условно при
.
Соседние файлы в предмете Высшая математика
- #
- #
- #
- #
- #
Содержание:
Степенные ряды:
До сих пор мы рассматривали ряды, членами которых были числа, т.е. числовые ряды. Теперь перейдем к рассмотрению рядов, членами которых являются функции, в частности степенные функции
Такие ряды называются степенными, а числа
Область сходимости степенного ряда
Совокупность тех значений 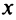
Пример:
Найти область сходимости степенного ряда
Решение:
Данный ряд можно рассматривать как геометрический ряд со знаменателем 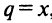
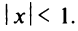
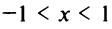
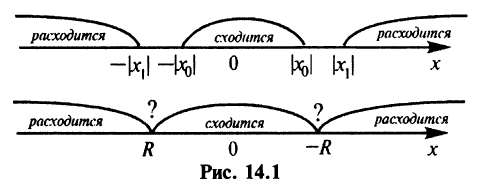
Структура области сходимости степенного ряда устанавливается с помощью теоремы Абеля.
Теорема Абеля. 1) Если степенной ряд сходится при значении 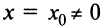
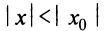
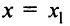
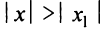
1) По условию ряд (14.1) сходится при 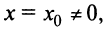
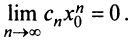
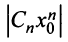
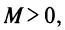
Рассмотрим ряд, составленный из абсолютных величин членов ряда (14.1) 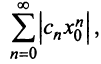
Члены ряда (14.3) согласно неравенству (14.2) меньше соответствующих членов ряда
представляющего геометрический ряд, который сходится, когда его знаменатель 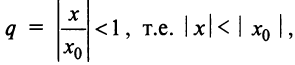
2) По условию ряд (14.1) расходится при 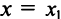
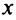
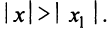
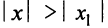
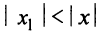
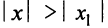
Из теоремы Абеля (см. рис. 14.1) следует, что существует такое число 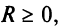
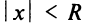
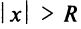
Число 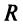
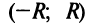
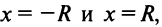
Найдем выражение радиуса сходимости степенного ряда (14.1) через его коэффициенты. Рассмотрим ряд, составленный из абсолютных величин его членов
в котором все коэффициенты 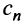
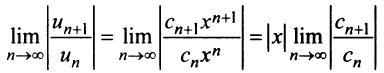
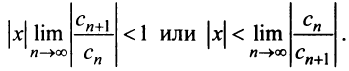
Замечание. Следует отметить, что у некоторых рядов интервал сходимости вырождается в точку 
Пример:
Найти область сходимости степенного ряда
Решение:
Найдем радиус сходимости ряда по формуле (14.5) 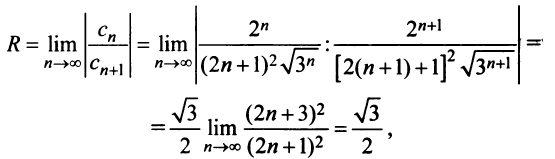
Теперь выясним поведение ряда на концах интервала сходимости. На левом конце при 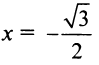
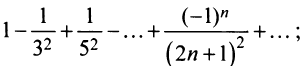
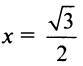
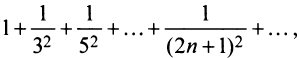
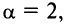
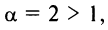
Следует отметить, что сходимость ряда на левом конце ин-тервала сходимости при 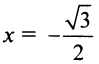
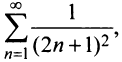
Итак, область сходимости данного ряда
Замечание. При исследовании сходимости на концах интервала сходимости для получающегося ряда с положительными членами применять признак Даламбера не имеет смысла, так как в этом случае всегда будем получать 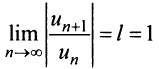
Пример:
Найти области сходимости степенных рядов:
Решение:
а) Радиус сходимости ряда по (14.5)
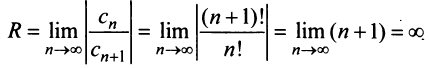
б) Задачу можно решать аналогично предыдущим. Решение упрощается, если заметить, что 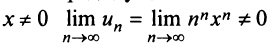
Итак, область сходимости ряда состоит из одной точки
Пример:
Найти область сходимости ряда
Решение:
Найти радиус сходимости по формуле (14.5) в данном случае не представляется возможным, так как коэффициенты ряда 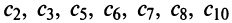
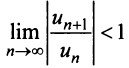
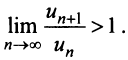
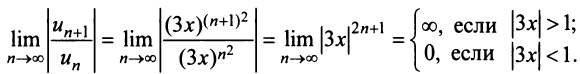
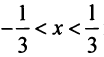
Исследуем сходимость на концах интервала сходимости: при 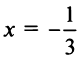
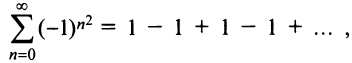
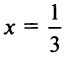
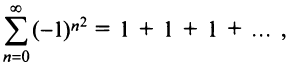
Итак, область сходимости ряда
Свойства степенных рядов. Пусть функция 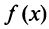
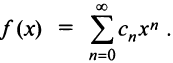
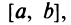
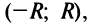
Кроме того, в интервале сходимости степенной ряд можно почленно дифференцировать:
При этом после интегрирования или дифференцирования полученные ряды имеют тот же радиус сходимости
Определение степенного ряда и его сходимости
Понятое функциональной зависимости является одним из важнейших в математике. Всякая функция осуществляет некоторое соответствие между объектами, составляющими область задания этой функции, и объектами, составляющими область её значений. Так можно рассматривать функции, которые ставят в соответствие числам — ряды. Эти функции называются функциональными рядами, т.е. функциональный ряд это выражение
членами которого являются некоторые функции переменной х. Например, ряд
является функциональным рядом.
Придавая в выражении (29.1.1) переменной х некоторые значения 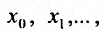
которые могут оказаться, как сходящимися, так и расходящимися.
В простейших случаях для определения сходимости ряда (29.1.1) можно применять к нему известные признаки сходимости числовых рядов, считая х фиксированным.
Определение 29.1.1. Совокупность всех значений переменной х, для которых соответствующие числовые ряды сходятся, называется областью сходимости функционального ряда (29.1.1). Определение 29.1.2. Функциональный ряд вида
где 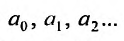
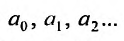
Если в ряде (29.1.2) сделать замену переменного, положив
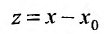
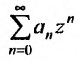
Очевидно, что исследование сходимости ряда (29.1.2) эквивалентно исследованию сходимости ряда (29.1.3). Примером степенного ряда может служить ряд
Сумма п первых членов ряда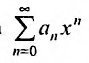
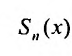
Для степенного ряда можно составить последовательность частичных сумм 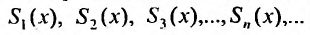
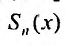
Остатком степенного ряда после n -го его члена (или n -ым остатком) называется ряд, полученный из заданного исключением n его первых членов:
Определение 29.1.3. Степенной ряд называется сходящимся на некотором множестве, если он сходится в любой точке этого множества.
Степенной ряд называется абсолютно сходящимся на некотором множестве, если в каждой точке этого множества сходится ряд из модулей его членов:
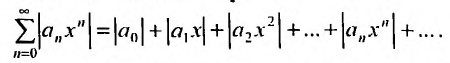
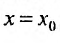
Соответствующий числовой ряд а0 +о,л:0 +… сходится абсолютно, если сходится ряд 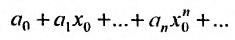
Так как каждой точке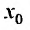
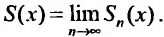
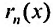
Для сходящегося степенного ряда предел остатка равен нулю:
Степенные ряды можно складывать, вычитать, умножать. Пусть заданы два степенных ряда:
Сумма, разность и произведение заданных степенных рядов определяется формулами:
где
Например, сумма, разность и произведение степенных рядов:
имеет вид:
где
Радиус сходимости, интервал сходимости
Области сходимости степенных рядов устроены довольно просто. Они описываются следующей теоремой.
Теорема 29.2.1 (теорема Абеля). Если степенной ряд
сходится при некотором 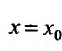
Если же степенной ряд (29.2.1) расходится при 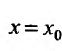
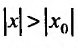
Доказательство. Предположим сначала, что степенной ряд (29.2.1) сходится в точке 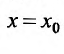
Тогда, в силу необходимого признака сходимости, 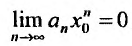
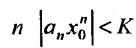
Если 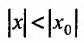
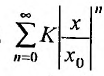
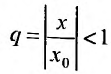
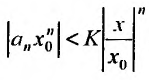
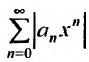
Предположим теперь, что степенной ряд (29.2.1) расходится, при 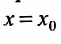
Возьмём тогда некоторое значение х, для которого 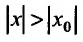
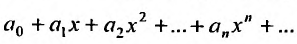
сходится. Но тогда из сходимости этого ряда, в силу первой части доказательства теоремы, вытекает сходимость ряда (29.2.2), что противоречит предположению, о его расходимости. Полученное противоречие означает, что для всех 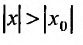
Если ряд (29.2.1) имеет вещественные коэффициенты и переменная х принимает только вещественные значения, то справедливо следующее определение, вытекающее из теоремы Абеля.
Определение 29.2.1. Величина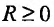
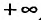
такая, что при всех х, у которых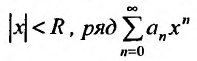
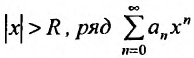
Множество точек х удовлетворяющих соотношению 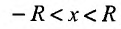
Итак, из определения 29.2.1 и теоремы Абеля следует, что областью сходимости степенного ряда — является интервал сходимости. И если значение 
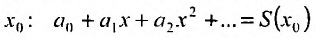
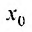
Свойства степенных рядов
Для степенных рядов справедливы следующие свойства:
1) Степенной ряд сходится равномерно внутри интервала сходимости.
2) Внутри интервала сходимости ряда сумма его является непрерывной функцией.
3) Если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то последовательность интегралов от частичных сумм ряда сходится к интегралу от суммы ряда.
4) Если степенной ряд
имеет радиус сходимости R , то и ряд
получаемый в результате почленного дифференцирования ряда (29.2.3) также имеет радиус сходимости R. Производная суммы ряда (29.2.3) равна сумме ряда (29.2.4), т.е.
Вычисление интервала сходимости
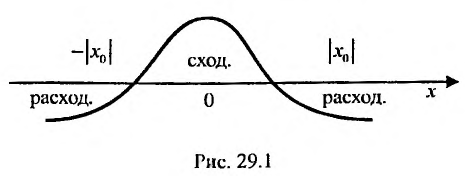
Как уже было сказано в и. 2 областью сходимости степенного ряда является интервал сходимости. Более того, из теоремы Абеля следует, что областью сходимости степенного ряда является интервал с центром в начале координат (рис 29.1).
Действительно, если 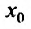
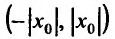
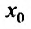
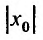
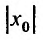
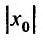
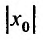
Заметим, что на концах интервала вопрос о сходимости или расходимости решается индивидуально в каждом конкретном случае. У некоторых рядов интервал сходимости может вырождаться в точку, у других охватывать всю ось Ох.
Укажем теперь способ вычисления радиуса сходимости степенного ряда.
Пусть задан степенной ряд 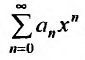
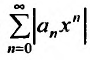
вычислим предел
Если этот предел меньше единицы, то, как следует из признака Д’Аламбера, ряд, составленный из модулей членов ряда (29.2.1) сходится, т.е. ряд сходится если
Если же 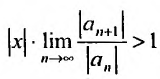
А это означает, что если 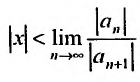
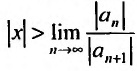
Учитывая определение радиуса сходимости степенного ряда, получим, что радиус сходимости можно вычислить по формуле:
Рассуждая аналогичным образом можно получить еще одну формулу для определения радиуса сходимости:
Если степенной ряд содержит только четные или нечетные степени х, то применяем признак Д’Аламбсра или Коши к ряду, составленному из модулей членов данного ряда.
Пример №1
Найти радиус и интервал сходимости степенного ряда:
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.1):
Итак, степенной ряд сходится для |х| 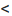
Исследуем сходимость ряда на концах интервала сходимости.
Пусть х =—1. Тогда получим знакочередующийся ряд 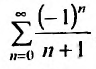
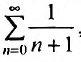
Суммируя вышесказанное, получим интервал сходимости
Пример №2
Найти радиус и интервал сходимости степенного ряда
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.2):
Так как 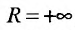
Пример №3
Найти радиус и интервал сходимости степенного ряда:
Решение:
Выпишем вначале значения
Для определения радиуса сходимости воспользуемся формулой (29.3.1):
Так как радиус сходимости равен нулю, то ряд сходится только в одной точке x= 0.
Пример №4
Найти радиус и интервал сходимости степенного ряда
Решение:
Данный ряд содержит только четные степени (а- — 5), коэффициенты при нечетных степенях равны нулю. Поэтому воспользоваться формулами (29.3.1) и (29.3.2) не представляется возможным.
Считая х фиксированным, применим признак Д’Аламбера к ряду, составленному из модулей членов данного ряда. Выпишем значения
Тогда
так как
Ряд сходится, если 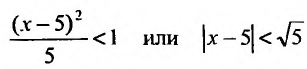
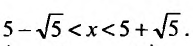
Исследуем сходимость ряда на концах интервала сходимости. Пусть 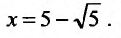
который сходится, как ряд Дирихле, для которого а = 4. При 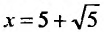
Пример №5
Найти радиус и интервал сходимости степенного ряда
Решение:
Выпишем значение 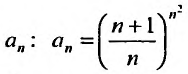
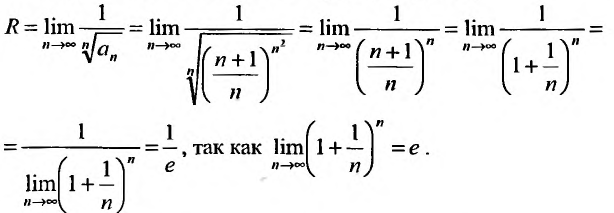
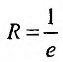
Исследуем его сходимость на концах интервала.
Пусть 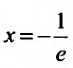
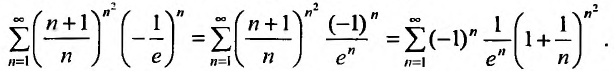
Следовательно, данный ряд расходится. И при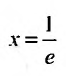
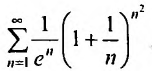
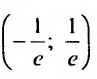
Ряды Тейлора и Маклорена
Как уже отмечалось, сумма сходящегося степенного ряда является некоторой функцией, определенной внутри интервала сходимости. В связи с этим мы рассмотрим задачу разложения некоторой функции в ряд, т.е. будем по заданной функции искать сходящийся ряд того или иного типа, сумма которого в интервале сходимости равнялась бы заданной функции.
Известно, что если функция f имеет на некотором отрезке производные всех порядков, то можно написать формулу Тейлора для любого значения n:
где 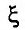
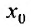
В формуле Тейлора обозначим:
пункта 27.2 (теорема 27.2.1) следует, что если
то степенной ряд
сходится и его суммой будет функция f(х), так как 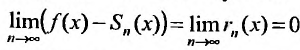
Справедливо и обратное утверждение, что если степенной ряд (29.4.3) сходится, то выполняется (29.4.2).
Определение 29.4.1. Представление функции f в виде ряда
называется разложением этой функции в ряд Тейлора. Если же 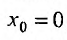
Следует заметить, что остаточный член в формуле Тейлора для функции J не обязательно является остатком ряда Тейлора для этой функции. Поэтому из сходимости ряда Тейлора для функции f , еще не следует сходимость именно к этой функции. При разложении функции в ряд Тейлора необходимо проверять условие (29.4.2). Однако сели разложение функции в какой-либо степенной ряд вообще возможно, то оно является разложением в ряд Тейлора, т.е. справедлива следующая теорема.
Теорема 29.4.1. Пусть
и стоящий справа ряд сходится в интервале 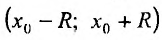
Доказательство. Так как степенной ряд в интервале сходимости можно почленно дифференцировать, то n-ую производную функции (29.4.4) можно представить в виде:
Полагая в последнем тождестве 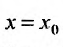
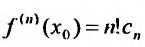
Из доказанной теоремы вытекает, что в одной и той же области, для одной и той же функции существует единственное разложение.
На практике, для разложения функции в ряд Тейлора, удобно пользоваться следующей теоремой.
Теорема 29.4.2. Если при любых х, удовлетворяющих неравенству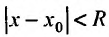
то ряд Тейлора, для этой функции, сходится в интервале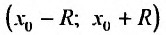
Доказательство. Из условия теоремы следует, что функцию f можно представить формулой Тейлора с остаточным членом в форме Лагранжа, т.е.
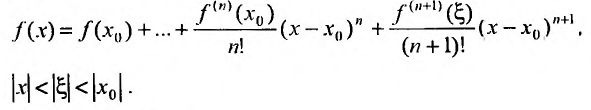
Переходя к пределу при
Воспользовавшись асимптотической формулой Стерлинга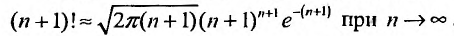
так как стспснно-показательная функция 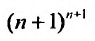
Тогда из неравенства (29.4.6) получим: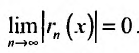
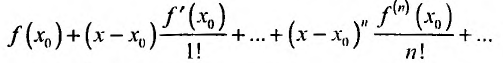
Разложение некоторых элементарных функций в ряд Маклорена
Из пункта 29.4 следует, что для того чтобы некоторая функция разлагалась в ряд Тейлора нужно, чтобы она имела производные любого порядка и чтобы либо 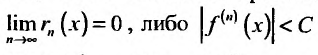
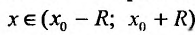
1. Разложение функции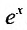
Находим производные данной функции и их значения при х=0. Так как
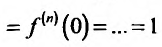
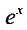
где 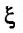
Вычислим предел остаточного члена, для любого х:
Выражение 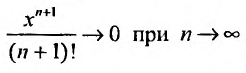
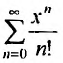
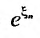
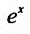
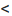
Следовательно, ряд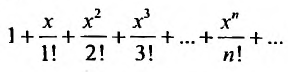
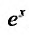
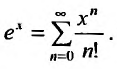
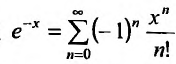
2. Разложение функций cos х и sin х. Для функции cos x имеем:
Следовательно,
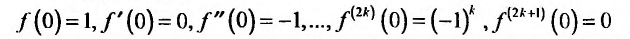
Маклорена с остаточным членом в форме Лагранжа для функции cosx имеет вид:
Ясно, что для любого X
Поэтому, функция cos л- разлагается в ряд Маклорена вида:
Аналогично получается разложение в ряд Маклорена функции sinx:
3. Биномиальный ряд.
Найдем разложение в степенной ряд функции
где m -произвольное действительное число.
Дифференцируя равенство (29.5.1) n раз, получим:
Значения функции и се производных при х = 0 равны:
Следовательно, ряд Маклорена имеет вид:
Если m- целое, то выражение (29.5.2) содержит конечное число членов. Если же m- нецелое, то выражение (29.5.2)- бесконечный ряд, называемый биномиальным.
Определим вначале радиус сходимости этого ряда, для чего применим признак Д’Аламбсра к ряду, составленному из модулей его членов:
Следовательно, при |х| 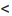
Покажем теперь, что ряд (29.5.2) сходится к функции 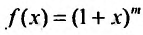
Умножим обе части (29.5.3) на 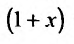
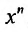
Эта сумма, как показано, равна произведению коэффициента при 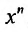
С другой стороны, вычисляя производную отношения
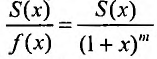
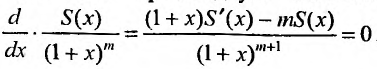
Решая дифференциальное уравнение 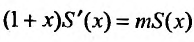
Пусть x = 0, тогда S(0) = С. Из (29.5.2) следует, что S(0) = 1, тогда С = 1.
Следовательно,
Итак, разложение
имеет место при всех х, удовлетворяющих условию 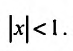
Применение рядов в приближенных вычислениях
Разложения функций в ряд Маклорена позволяют во многих случаях вычислить с большой степенью точности значения этих функций, заменяя ее конечным числом членов разложения. Чем меньше х, тем меньше членов можно брать в этом разложении для вычисления f(х) с желаемой точностью. Если х весьма мало, то достаточно ограничится первыми двумя членами, отбросив все остальные. Например, при х близких к нулю можно пользоваться следующими приближенными формулами:
Например, вычислим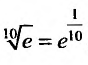
Имеем, 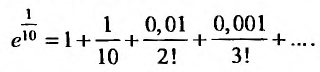
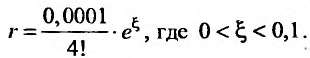
Иногда при вычислении значений функций удобно пользоваться почленным дифференцированием или интегрированием рядов.
Например, известно, что
С другой стороны,
Следовательно,
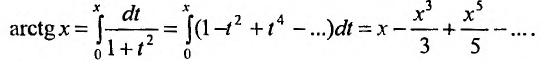
Этот ряд знакочередующийся. Поэтому, его остаток не превосходит первого «отброшенного» члена. Удерживая в разложении первых два слагаемых, получим значение arctg 0,1 = 0,09967 с пятью верными знаками.
При помощи биномиальною ряда можно быстро и довольно точно вычислять значение корней из чисел.
Пример №6
Вычислить 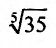
Решение:
Представим, этот корень в виде
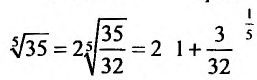
следующим член 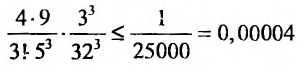
В общем случае можно записать:
где 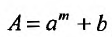
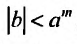
Кроме того, биномиальный ряд является основой многих дальнейших разложений функций в ряды. Например, можно найти разложение в ряд Маклорена функции:
При помощи рядов можно вычислять определенные интегралы.
Например, вычислим интегральный синус:
Имеем
тогда
Подставляя вместо x, те или иные конкретные значения переменной, мы можем вычислять интересующие нас значения интегрального синуса.
При помощи разложении в степенные ряды можно приближенно интегрировать разнообразные дифференциальные уравнения.
Например, найдем решение уравнения 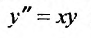
Будем искать решение этого уравнения в виде степенного ряда: 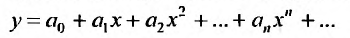
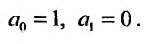
Вычислим первую и вторую производные от этого ряда:
и подставив у, 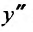
приравняем коэффициенты при равных степенях .г, предварительно умножив правую часть на х:
Получаем систему уравнений, из которой находим:
Замечаем, что отличными от нуля будут лишь те коэффициенты, у которых индекс и степень делятся на 3. Получим решение заданного дифференциального уравнения в виде:
- Заказать решение задач по высшей математике
Ряд Маклорена
Предположим, что функция 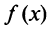
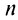
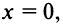
Выразим коэффициенты ряда через 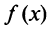
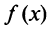
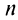
Полагая в полученных равенствах 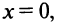
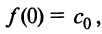
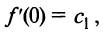
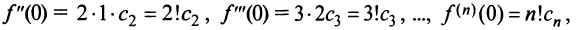
Подставляя значения коэффициентов 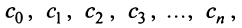
называемый рядом Маклорена.
Следует отметить, что не все функции могут быть разложены в ряд Маклорена. Может оказаться, что ряд Маклорена, составленный формально для функции 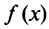
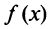
Так же как и для числовых рядов, сумму 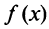
где 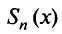
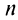
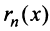
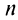
Тогда на основании свойства 4 сходящихся рядов (см. §13.1) можно сформулировать теорему.
Теорема. Для того чтобы ряд Маклорена сходился к функции 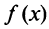
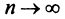
для всех значений 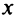
Можно доказать, что если функция 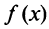
Замечание. Ряд Маклорена является частным случаем ряда Тейлора:
при
Ряд Тейлора тесно связан с формулой Тейлора.
где 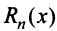
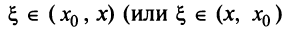
Очевидно, что при выполнении условия (14.7) остаток 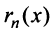
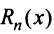
Разложение в ряд Маклорена некоторых функций
По формуле (13.6)
Область сходимости ряда 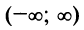
Очевидно, что производные четного порядка 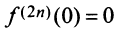
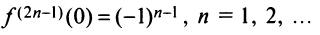
Область сходимости ряда
Область сходимости ряда
Интервал сходимости ряда 
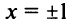
Ряд (14.11) называется биномиальным. Если 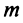
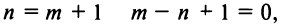
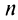
Получить разложение для этой функции можно проще, не вычисляя непосредственно коэффициенты ряда (14.6) с помощью производных.
Рассмотрим геометрический ряд
со знаменателем 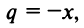
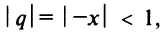
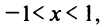
Интегрируя почленно равенство (14.12) в интервале 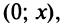
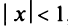
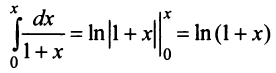
Область сходимости ряда (после выяснения сходимости на концах интервала сходимости) есть
Можно доказать, что ряды, приведенные в формулах (14.8) — (14.13), сходятся к функциям, для которых они составлены.
При разложении более сложных функций используют непосредственно формулу (14.6) либо таблицу простейших разложений (14.8) — (14.13).
Пример №7
Разложить в ряд функции:
Решение:
а) Так как по (14.8)
то, заменяя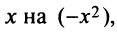
и, наконец,
Область сходимости ряда
б) В разложении 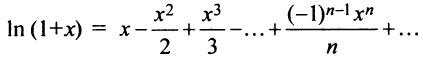
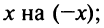
Теперь
Область сходимости ряда
Применение рядов в приближенных вычислениях
Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «неберущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения.
Пример №8
Вычислить приближенно с точностью до
Решение:
а) Для вычисления 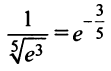
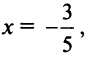
Взяв первые шесть членов разложения, на основании следствия из теоремы Лейбница (см. § 13.4) для сходящегося знакочередующегося ряда мы допустим погрешность 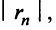
б) Для вычисления 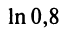
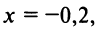
Если в качестве 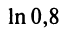
(Мы учли, что сумма сходящегося геометрического ряда в
скобках равна 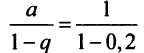
Следует отметить, что для вычисления логарифмов более удобным является ряд (14.14), который сходится быстрее ряда (14.13). Действительно, пусть 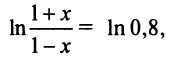
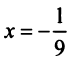
т.е. для вычисления 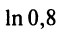
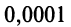
в) Представим 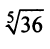
Так как 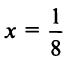
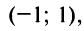
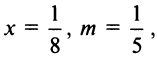
(Для обеспечения данной точности расчета необходимо взять 4 члена, так как по следствию из признака Лейбница для сходящегося знакочередующегося ряда погрешность 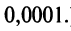
г) Для вычисления 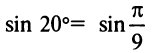
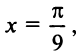
(Необходимо взять два члена, так как при этом погрешность
д)«Точное» интегрирование здесь невозможно, так как интеграл «неберущийся». Заменив 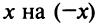
Умножая полученный ряд на
и почленно интегрируя в интервале 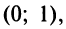
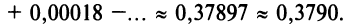
Пример №9
Исследовать сходимость ряда
Решение:
Радиус сходимости ряда (14.15), заданного по степеням 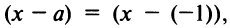
т.е. 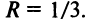
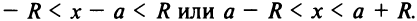
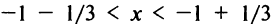
Исследуем сходимость ряда (14.15) на концах этого интервала. При 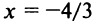
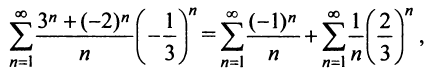
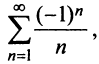
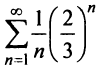
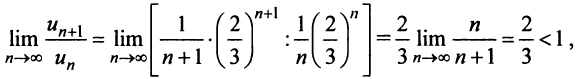
При 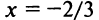
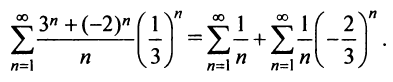
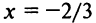
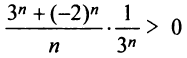
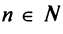
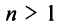
Итак, область сходимости степенного ряда (14.15)
Пример №10
Разложить в ряд Маклорена функцию
Решение:
Первый способ. Применим метод непосредственного разложения по формуле (14.6).
Вначале найдем производные до «-го порядка и вычислим их значения при
При 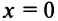
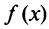
и т.д. Теперь по формуле (14.6) запишем ряд
или
Второй способ. Учитывая, что 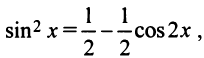
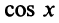
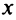

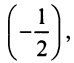
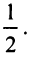
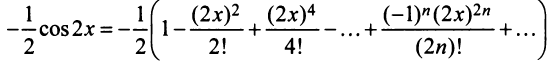
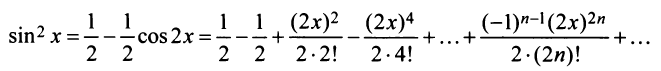
т.е. то же разложение (14.16).
Третий способ. Разложение функции 
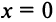
то произведение функций разлагается в той же окрестности в степенной ряд
В частности, при 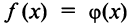
Для функции 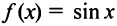
находим по формуле (14.17)
т.е. получили то же разложение (14.16).
Область сходимости ряда, как нетрудно убедиться, есть 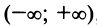
Пример №11
Вычислить с точностью до
Решение:
Выражение данного интеграла в виде числового ряда находится
Вычисление интеграла свелось не к нахождению суммы сходящегося знакочередующегося ряда, при вычислении которой погрешность оценивается с помощью следствия из теоремы Лейбница, а к определению суммы ряда с положительными членами с неизвестной оценкой погрешности.
Поступим следующим образом. Предположим, что для оценки суммы ряда мы взяли 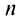
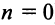
ибо выражение в круглых скобках представляет сумму сходящегося геометрического ряда (13.5) при
При
(Легко вычислить, что при любых 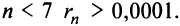
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
$begingroup$
How to find the center of the power series.
$sum _{ n=0 }^{ infty }{ frac { 2n(x+1)^ n }{ 3^ n } } $
I think it to be (x-(-1))= so, the center is -1
asked May 7, 2018 at 13:29
$endgroup$
1
$begingroup$
By definition a power series $Sigma a_n(x-x_0)^n$ is centered at $x_0$. So in your problem it’s indeed centered at -1
answered May 7, 2018 at 13:32
MacrophageMacrophage
1,4856 silver badges18 bronze badges
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Функциональные и степенные ряды
Возьмем последовательность натуральных чисел n{n} и поставим каждому n{n} в соответствие функцию fn(x)f_n (x). Если функции fn(x)f_n (x) определены на некотором множестве x∈Ex in E, E⊂RE subset R, то на множестве EE определено выражение:
f1(x)+f2(x)+f3(x)+…+fn(x)+…,f_1 (x)+f_2 (x)+f_3 (x)+ ldots +f_n (x)+ ldots,
состоящее из функций fn(x)f_n (x), которое называется функциональным рядом.
В общем виде функциональный ряд записывается как:
∑n=1∞fn(x)sumlimits_{n=1}^{infty} f_n(x)
Примеры функциональных рядов
1+cosx2!+cos2×3!+cos3×4!+…+cosnx(n+1)!+…=∑n=1∞cosnx(n+1)!1+frac{cos x}{2!}+frac{cos 2x}{3!}+frac{cos 3x} {4!} +ldots +frac{cos nx}{(n+1)!}+ldots=sumlimits_{n=1}^{infty}frac{cos nx} {(n+1)!}
ex−ex+13+ex+29−ex+327+…+(−1)nex+n3n+…=∑n=0∞(−1)nex+n3ne^{x}-frac{e^{x+1}}{3}+frac{ e^{x+2}}{9}-frac{e^{x+3}}{27} +ldots +(-1)^nfrac{ e^{x+n}}{3^n}+ldots=sumlimits_{n=0}^{infty} (-1)^n frac{ e^{x+n}}{3^n}
Степенные ряды являются одним из видов функциональных рядов и в общем виде записываются как:
a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)n+…=∑k=0∞ak(x−x0)ka_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n+ldots=sumlimits_{k=0}^{infty} a_k(x-x_0)^k
где a0,a1,…,an,…a_0, a_1, ldots, a_n, ldots – постоянные, коэффициенты ряда,
x0x_0 – центр интервала сходимости ряда ∣x−x0∣<R|x-x_0|<R,
RR – радиус сходимости степенного ряда.
Примеры степенных рядов
12+2!(x−5)4+3!(x−5)28+…+(n+1)!(x−5)n2n+1+…=∑n=0∞(n+1)!(x−5)n2n+1frac{1}{2}+frac{2!(x-5)}{4}+frac{3!(x-5)^2}{8}+ldots +frac{(n+1)!(x-5)^n}{2^{n+1}}+ldots =sum limits_{n=0} ^{infty} frac{(n+1)!(x-5)^n}{2^{n+1}}
ex−ex+13+ex+29−ex+327+…+(−1)nex+n3n+…=∑n=0∞(−1)nex+n3ne^{x}-frac{e^{x+1}}{3}+frac{ e^{x+2}}{9}-frac{e^{x+3}}{27} +ldots +(-1)^nfrac{ e^{x+n}}{3^n}+ldots=sumlimits_{n=0}^{infty} (-1)^n frac{ e^{x+n}}{3^n}
Сходимость степенных рядов
Сумму SnS_n первых nn членов степенного ряда называют nn–й частичной суммой:
Sn(x)=a0+a1(x−x0)+a2(x−x0)2+…+an(x−x0)nS_n(x)= a_0+a_1(x-x_0)+a_2(x-x_0)^2+ldots+a_n(x-x_0)^n
Если при определенном значении x∈Ex in E существует конечный предел:
limn→∞Sn(x)=S(x)limlimits_{n to infty } S_n (x) = S (x)
то ряд называется сходящимся, а значение S(x)S(x) называют суммой ряда. Если сходится ряд, составленный из абсолютных величин его членов, то такой ряд называется абсолютно сходящимся.
Если степенной ряд сходится в точке x=x1x=x_1, то он сходится абсолютно и при:
∣x∣<∣x1∣|x|<|x_1 |
Если степенной ряд расходится в точке x=x2x=x_2, то он расходится и при:
∣x∣>∣x2∣|x|>|x_2 |
Интервалом сходимости степенного ряда является:
(x0−R,x0+R)(x_0-R,x_0+R)
Здесь RR – радиус сходимости степенного ряда. Степенной ряд расходится при:
∣x−x0∣>R|x-x_0 |>R
Для граничных точек интервала
∣x−x0∣>R|x-x_0 |>R
степенной ряд может, как сходится, так и расходится, для чего требуется дополнительное изучение.
Основные признаки сходимости
Приведем основные признаки, используемые для определения сходимости степенных рядов.
1-й признак сравнения
Пусть даны два ряда с положительными членами:
∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
причем, un≤vnu_n le v_n для всех номеров, начиная с некоторого nn. Тогда:
-
Если ряд ∑n=1∞vnsum limits_{n=1} ^{infty} v_n сходится, то сходится и ряд ∑n=1∞unsum limits_{n=1} ^{infty} u_n
-
Если ряд ∑n=1∞unsum limits_{n=1} ^{infty} u_n расходится, то расходится и ряд ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
2-й признак сравнения
Пусть даны два ряда с положительными членами:
∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
и существует конечный и отличный от нуля предел:
limn→∞unvn≠0limlimits_{n to infty } dfrac{ u_n }{ v_n }ne 0
Тогда ряды
∑n=1∞unsum limits_{n=1} ^{infty} u_n и ∑n=1∞vnsum limits_{n=1} ^{infty} v_n
сходятся или расходятся одновременно.
Признак Лейбница для знакочередующихся рядов
При исследовании степенных рядов на сходимость часто используется признак Лейбница для знакочередующихся рядов. Ряд, содержащий как положительные, так и отрицательные члены, называют знакопеременным.
Ряд вида:
b1−b2+b3−b4+…+(−1)n+1bn+1+…=∑k=1∞(−1)k+1bk+1b_1-b_2+b_3-b_4+ ldots +{(-1)}^{n+1}b_{n+1}+ldots=sumlimits_{k=1} ^ {infty}{(-1)}^{k+1}b_{k+1},
когда любые два соседних члена имеют противоположные знаки, называется знакочередующимся.
Очевидно, каждый знакочередующийся ряд является знакопеременным.
В случае, когда выполняется два условия:
b1>b2>b3>b4>…>bn>…b_1>b_2>b_3>b_4> ldots >b_{n}> ldots, т.е когда члены ряда по модулю монотонно убывают
и
limn→∞an=0limlimits_{n to infty }{a_n}=0, т.е. когда общий член ряда стремится к нулю при n→∞n to infty, ряд сходится. Если, помимо этого, сходится ряд
b1+b2+b3+b4+…+bn+1+…=∑k=1∞bk+1b_1+b_2+b_3+b_4+ ldots + b_{n+1}+ldots=sumlimits_{k=1} ^ {infty} b_{k+1}
составленный из модулей исходного ряда, то такой ряд называют абсолютно сходящимся. Если признак Лейбница выполняется, но, при этом, ряд из абсолютных значений не сходится, то такой ряд называют условно сходящимся.
Признак Даламбера
Пусть дан ряд с положительными членами
∑n=1∞unsum limits_{n=1} ^{infty} u_n
и существует конечный предел
limn→∞un+1un=1limlimits_{n to infty } dfrac{ u_{n+1} }{ u_n }=1
Тогда, если l<1l<1, то данный ряд сходится; если же l>1l>1, то – расходится. Если l=1l=1 , то ряд может сходиться или расходиться; в этом случае требуется исследовать ряд с помощью других методов.
Признак Коши
Пусть дан ряд с положительными членами
∑n=1∞unsum limits_{n=1} ^{infty} u_n
такой, что существует конечный предел
limn→∞unn=1limlimits_{n to infty } sqrt [n] { u_n }=1
Тогда, если l<1l<1, то ряд сходится. В случае, если l>1l>1, то ряд расходится. Если же l=1l=1, то вопрос о сходимости рядя требует дополнительного исследования.
Интегральный признак сходимости
Пусть дан ряд с положительными членами
∑n=1∞unsum limits_{n=1} ^{infty} u_n
для которого существует положительная, непрерывная и монотонно убывающая на промежутке [1,+∞)[1, +infty) функция f(x)f(x) такая, что f(n)=an,n=1,2,…f(n)=a_n, n=1,2, ldots
Тогда данный ряд и несобственный интеграл ∫0∞f(x)dxintlimits_0^infty f(x) dx сходятся или расходятся одновременно.
Примеры исследования степенных рядов
Пример 1
Найти область сходимости ряда
∑n=1∞(x−1)n+12n(n+1)sum limits_{n=1} ^{infty} dfrac{(x-1)^{n+1}}{2^n {(n+1)}}
Используем признак Даламбера. Учитывая, что
∣an+1an∣=∣(x−1)(n+1)+12n+1(n+1+1):(x−1)n+12n(n+1)∣=∣(x−1)n+2(x−1)n+1⋅2n2n+1⋅n+1n+2∣=∣x−1∣2⋅n+1n+2Bigl| dfrac{a_{n+1}}{a_n} Bigr|= Bigl| dfrac {(x-1)^{(n+1)+1}}{2^{n+1}(n+1+1)}: dfrac {(x-1)^{n+1}}{2^n(n+1)}Bigr|= Bigl| dfrac {(x-1)^{n+2}}{(x-1)^{n+1}}cdot dfrac {2^n}{2^{n+1}}cdot dfrac {n+1}{n+2}Bigr|=dfrac {|x-1|}{2} cdot dfrac{n+1}{n+2}
находим:
limn→∞∣an+1an∣=limn→∞(∣x−1∣2⋅n+1n+2)=∣x−1∣2⋅limn→∞1+1n1+2n=∣x−1∣2limlimits_{n to infty }Bigl| dfrac{a_{n+1}}{a_n} Bigr|= limlimits_{n to infty} left(dfrac {|x-1|}{2} cdot dfrac{n+1}{n+2}right)= dfrac {|x-1|}{2} cdot limlimits_{n to infty }dfrac{1+dfrac{1}{n}}{1+dfrac{2}{n}}=dfrac {|x-1|}{2}
Для определения требуемых значений xx решаем неравенство:
∣x−1∣2<1⇔−1<x−12<1⇔−2<x−1<2⇔−1<x<3dfrac{|x-1|}{2}<1 Leftrightarrow -1<dfrac{x-1}{2}<1 Leftrightarrow -2<x-1<2 Leftrightarrow -1<x<3
Таким образом, при x∈(−1,3)x in (-1,3) ряд сходится абсолютно, а при $ x notin (-1,3) $ ряд расходится. Это означает, что (−1,3)(-1,3) – интервал сходимости данного ряда.
Для полного решения задачи необходимо исследовать сходимость ряда на концах интервала, при x=−1x=-1 и x=3x=3.
При x=3x=3 получаем ряд
∑n=1∞(x−1)n+12n(n+1)=∑n=1∞(3−1)n+12n(n+1)=∑n=1∞2n+12n(n+1)=∑n=1∞2n+1sum limits_{n=1}^{infty} dfrac{(x-1)^{n+1}}{2^n(n+1)}=sum limits_{n=1} ^{infty} dfrac{(3-1)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{2^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{2}{n+1}
Применим 2-й признак сравнения и проведем сравнение этого ряда с гармоническим:
∑n=1∞1nsum limits_{n=1} ^{infty} dfrac{1}{n}
Получаем:
limn→∞(2n+1:1n)=limn→∞(2nn+1)=limn→∞(21+1n)=2≠0limlimits_{n to infty }left( dfrac{2}{n+1}:dfrac{1}{n}right)= limlimits_{n to infty }left( dfrac{2n}{n+1}right)=limlimits_{n to infty }left( dfrac{2}{1+dfrac{1}{n}}right)=2 ne 0
Как известно, гармонический ряд расходится. Так как полученный предел отличен от нуля, то ряды
∑n=1∞2n+1sum limits_{n=1} ^{infty} dfrac{2}{n+1} и ∑n=1∞1nsum limits_{n=1} ^{infty} dfrac{1}{n}
сходятся или расходятся одновременно. В данном случае, они расходятся, и, следовательно, исходный ряд при x=2x=2 расходится.
При x=−1x=-1 получаем ряд
∑n=1∞(x−1)n+12n(n+1)=∑n=1∞(−1−1)n+12n(n+1)=∑n=1∞(−2)n+12n(n+1)=∑n=1∞(−1)n+1⋅(2)n+12n(n+1)=∑n=1∞(−1)n+1⋅2n+1sum limits_{n=1}^{infty} dfrac{(x-1)^{n+1}}{2^n(n+1)}=sum limits_{n=1} ^{infty} dfrac{(-1-1)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{(-2)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{(-1)^{n+1}cdot (2)^{n+1}}{2^n (n+1)}= sum limits_{n=1} ^{infty} dfrac{ (-1)^{n+1}cdot 2}{n+1}
Как было показано, этот ряд не является абсолютно сходящимся, так как ряд, составленный из абсолютных значений:
∑n=1∞∣(−1)n+1⋅2n+1∣=∑n=1∞2n+1sum limits_{n=1} ^{infty}Bigl| dfrac{ (-1)^{n+1}cdot 2}{n+1} Bigl|=sum limits_{n=1} ^{infty} dfrac {2}{n+1}
расходится.
Используя признак Лейбница, выясним сходимость данного знакочередующегося ряда. Очевидно, что неравенство:
bn>bn+1⇔2n+1>2(n+1)+1⇔2n+1>2n+2b_n>b_{n+1} Leftrightarrow dfrac{2}{n+1}>dfrac{2}{(n+1)+1} Leftrightarrow dfrac{2}{n+1}>dfrac{2}{n+2}
выполнено для всех n=1,2,3,…n=1,2,3, ldots
Выполняется и второе условие:
limn→∞an=limn→∞3n+2=0limlimits_{n to infty } a_n = limlimits_{n to infty } dfrac{3}{n+2}=0
Оба условия признака Лейбница выполнены. Это означает, что знакочередующийся ряд
∑n=1∞(−1)n+13n+2sum limits_{n=1} ^{infty} (-1)^{n+1} dfrac {3}{n+2}
сходится. Так как этот ряд не является абсолютно сходящимся, то знакочередующийся ряд сходится условно.
Таким образом, областью сходимости исходного ряда является промежуток:
x∈[−1,3)x in [-1,3)
Пример 2
Найти область сходимости ряда
∑n=2∞(x+3)nnln3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}
Используем признак Даламбера. Учитывая, что
∣an+1an∣=∣(x+3)n+1(n+1)ln3(n+1):(x+3)nnln3n∣=∣(x+3)n+1(x+3)n⋅nn+1⋅ln3nln3(n+1)∣=∣x+3∣⋅nn+1⋅ln3nln3(n+1)Bigl| dfrac{a_{n+1}}{a_n} Bigr|= Bigl| dfrac {(x+3)^{n+1}}{(n+1)ln^3{(n+1)}}: dfrac {(x+3)^n}{nln^3{n}}Bigr|= Bigl| dfrac {(x+3)^{n+1}}{(x+3)^n}cdot dfrac {n}{n+1}cdot dfrac {ln^3{n}}{ln^3{(n+1)}}Bigr|=|x+3| cdot dfrac{n}{n+1} cdot dfrac{ln^3{n}}{ln^3{(n+1)}}
находим c помощью правила Лопиталя:
limn→+∞∣an+1an∣=limn→+∞(∣x+3∣⋅nn+1⋅ln3nln3(n+1))=∣x+3∣⋅limn→∞11+1n⋅(limn→∞lnnln(n+1))3=∣x+3∣⋅limn→∞1n1n+1=∣x+3∣limlimits_{n to +infty } Bigl| dfrac {a_{n+1}}{a_n}Bigr| = limlimits_{n to +infty } left( |x+3| cdot dfrac {n}{n+1}cdot dfrac{ln^3{n}}{ln^3{(n+1)}} right)=|x+3| cdot limlimits_{n to infty } dfrac {1}{1+dfrac{1}{n}} cdot {left(limlimits_{n to infty } dfrac {ln{n}}{ln{(n+1)}}right)}^3= |x+3| cdot limlimits_{n to infty } dfrac{dfrac{1}{n}}{dfrac{1}{n+1}}=|x+3|
Для определения требуемых значений x решаем неравенство:
∣x+3∣<1⇔−1<x+3<1⇔−4<x<−2|x+3|<1 Leftrightarrow -1<x+3<1 Leftrightarrow -4<x<-2
Таким образом, при x∈(−4,−2)x in (-4,-2) ряд сходится абсолютно, а при x∉(−4,−2)x notin (-4,-2) ряд расходится. Это означает, что (−4,−2)(-4,-2) – интервал сходимости данного ряда.
Для полного решения задачи необходимо исследовать сходимость ряда на концах интервала, при x=−4x=-4 и x=−2x=-2.
При x=−4x=-4 получаем ряд
∑n=2∞(x+3)nnln3n=∑n=2∞(−4+3)nnln3n=∑n=2∞(−1)nnln3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-4+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-1)^n}{nln^3{n}}
Воспользуемся интегральным признаком. Возьмем функцию:
f(x)=1xln3xf(x)=dfrac{1}{x ln^3{x}}
Очевидно, что для любых x1>x2>2x_1>x_2>2:
1x2ln3×2>1x1ln3×1⇒f(x2)>f(x1)dfrac{1}{x_2 ln^3{x_2}}>dfrac{1}{x_1 ln^3{x_1}} quad Rightarrow quad f(x_2 )>f(x_1 )
Найдем неопределенный интеграл
∫dxxln3x=∫d(lnx)xln3x=(−12)(lnx)−2+C=−12ln2x+Cint dfrac {dx}{x ln^3 {x}}=int dfrac {d(ln{x})}{x ln^3 {x}}=left( -dfrac{1}{2}right)(ln{x})^{-2}+C= -dfrac{1}{2 ln^2{x}}+C
Далее:
∫2∞f(x)dx=∫2∞dxxln3x=limd→+∞∫2ddxxln3x=limd→+∞(−12ln2x∣2d)=limd→+∞(−12ln2d+12ln22)=12ln22intlimits_2^infty f(x) dx=intlimits_2^infty dfrac {dx}{x ln^3 {x}}=limlimits_{d to +infty }intlimits_2^d dfrac{dx}{xln^3 {x}}=limlimits_{d to +infty }left( -dfrac{1}{2 ln^2{x}}Bigr|_2^d right) = limlimits_{d to +infty } left(-dfrac{1}{2 ln^2{d}}+dfrac{1}{2 ln^2{2}} right) = dfrac{1}{2 ln^2{2}}
Таким образом, несобственный интеграл сходится. Это значит, что ряд
∑n=2∞1nln3nsum limits_{n=2} ^{infty} dfrac{1}{nln^3{n}}
также сходится, а ряд
∑n=2∞(−1)nnln3nsum limits_{n=2} ^{infty} dfrac{(-1)^n}{nln^3{n}}
сходится абсолютно.
При x=−2x=-2 получим ряд
∑n=2∞(x+3)nnln3n=∑n=2∞(−2+3)nnln3n=∑n=2∞1nln3nsum limits_{n=2} ^{infty} dfrac{(x+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{(-2+3)^n}{nln^3{n}}=sum limits_{n=2} ^{infty} dfrac{1}{nln^3{n}}
Как было показано, этот ряд сходится абсолютно. Следовательно, область сходимости исходного ряда – промежуток [−4,−2][-4, -2].