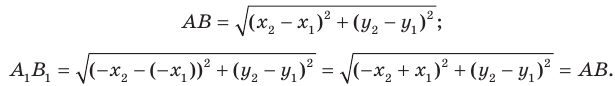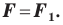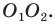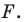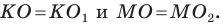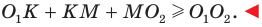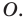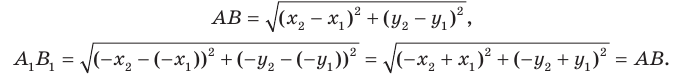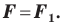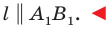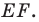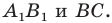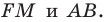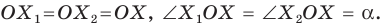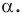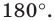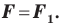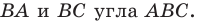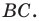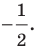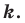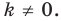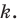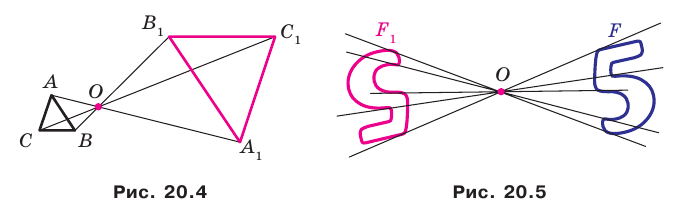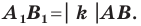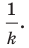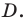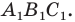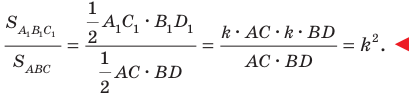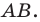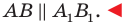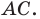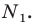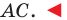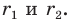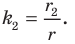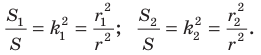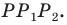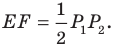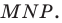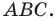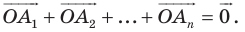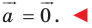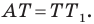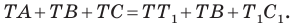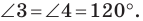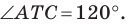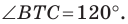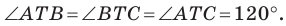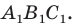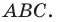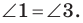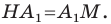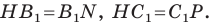Содержание:
Геометрические преобразования:
В этой лекции вы узнаете, что такое преобразование фигуры. Ознакомитесь с такими видами преобразований, как параллельный перенос, центральная симметрия, осевая симметрия, поворот, гомотетия, подобие.
Вы научитесь применять свойства преобразований при решении задач и доказательстве теорем.
Движение (перемещение) фигуры. Параллельный перенос
Пример:
На рисунке 17.1 изображены отрезок
Мы указали правило, с помощью которого каждой точке 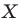
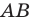
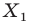
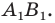
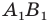
Пример:
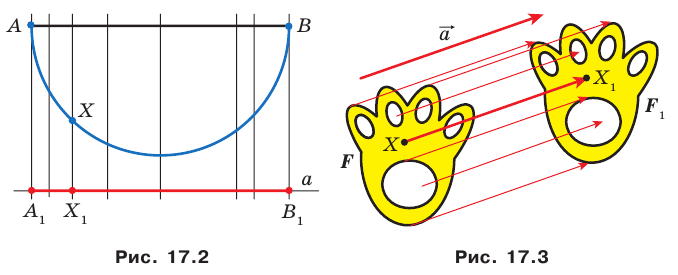
На рисунке 17.2 изображены полуокружность 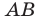
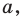
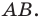
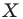
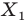
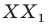
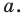
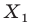
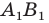
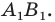
Пример:
Пусть даны некоторая фигура 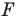
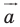
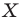
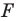
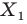
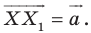
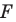
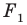
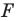
Обобщим приведенные примеры.
Пусть задана некоторая фигура 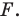
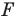
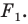
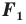
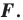
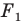
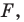
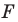
Так, в примере 1 отрезок 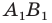
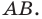
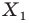
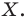
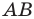
Обратим внимание на то, что в примере 3 фигура 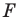
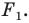
Какими же свойствами должно обладать преобразование, чтобы образ и прообраз были равными фигурами? Оказывается, что достаточно лишь одного свойства: преобразование должно сохранять расстояние между точками, то есть если 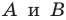
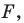
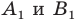
Что такое преобразование фигур
Определение. Преобразование фигуры 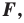
Если каждой точке 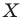
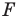
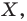
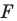
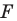
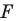
Мы давно используем понятие «равенство фигур», хотя не давали ему строгого определения.
На то, что движение связано с равенством фигур, указывают следующие свойства движения.
Если преобразование является движением, то:
- образом прямой является прямая,
- образом отрезка является отрезок, равный данному;
- образом угла является угол, равный данному,
- образом треугольника является треугольник, равный данному.
Доказательство этих свойств выходит за рамки рассматриваемого курса геометрии.
Свойства движения подсказывают следующее определение.
Определение. Две фигуры называют равными, если существует движение, при котором одна из данных фигур является образом другой.
Запись 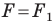
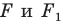
Если существует движение, при котором фигура 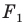
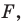
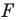
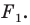
Замечание. Ранее равными фигурами мы называли такие фигуры, которые совпадали при наложении. Термин «наложение» интуитивно понятен, и в нашем представлении он связывается с наложением реальных тел. Но геометрические фигуры нельзя наложить в буквальном смысле этого слова. Теперь наложение фигуры 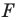
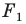
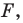
Термин «движение» также ассоциируется с определенным физическим действием: изменением положения тела без деформации.
Именно с этим связано появление этого термина в математике. Однако в геометрии предметом исследования является не процесс, происходящий во времени, а лишь свойства фигуры и ее образа.
То, что изображенные на рисунке 17.3 фигуры 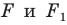
Теорема 17.1 (свойство параллельного переноса). Параллельный перенос является движением.
Доказательство: Пусть 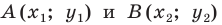
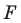
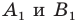
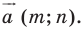
Имеем: 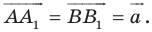
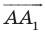
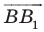
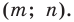
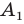
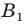
Найдем расстояние между точками
Найдем расстояние между точками
Следовательно, мы показали, что 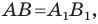
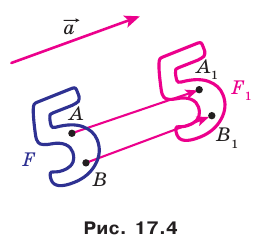
Следствие. Если фигура 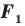
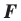
Это свойство используется при создании рисунков на тканях, обоях, покрытиях для пола и т. п. (рис. 17.5).
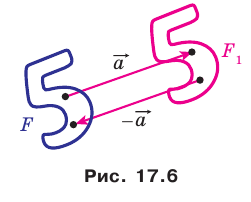
Если фигура 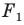
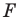
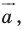
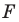
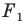
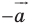
Параллельные переносы на векторы 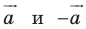
Пример №1
Каждой точке 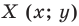
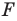
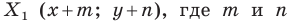
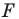
Решение:
Рассмотрим вектор 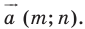
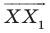
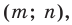
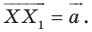
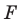
Пример №2
Точка 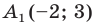
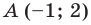
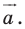
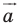
Решение:
Из условия следует, что 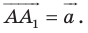
Пусть 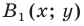
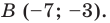
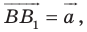
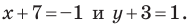
Ответ:
Пример №3
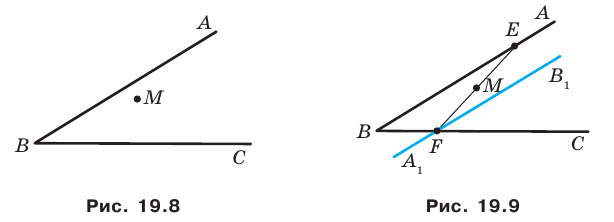
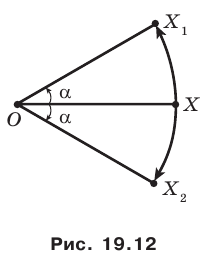
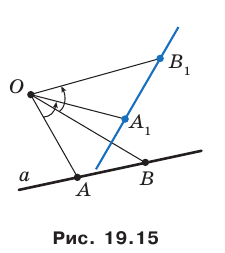
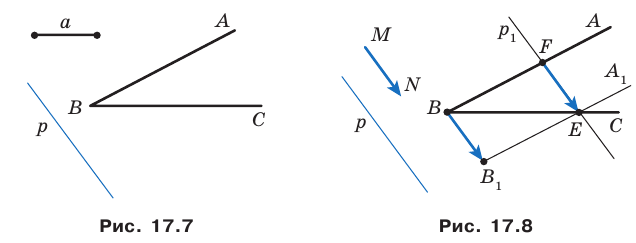
Даны угол 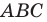
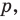
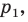
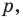
Решение:
Рассмотрим вектор 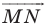

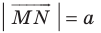
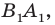
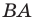
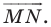
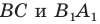
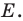
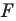
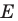
Приведенные рассуждения подсказывают следующий алгоритм построения:
- найти образ луча
при параллельном переносе на вектор
- отметить точку пересечения луча
с построенным образом;
- через найденную точку провести прямую
параллельную прямой
Прямая
будет искомой.
Осевая симметрия
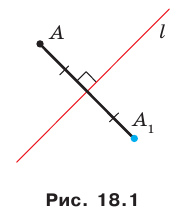
Определение. Точки 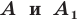
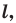
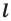
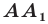
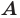
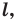
Например, точки 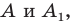
Рассмотрим фигуру 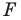
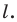
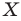
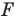
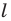
В результате такого преобразования фигуры 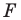
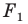
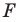
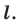
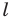
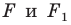
Теорема 18.1 (свойство осевой симметрии). Осевая симметрия является движением.
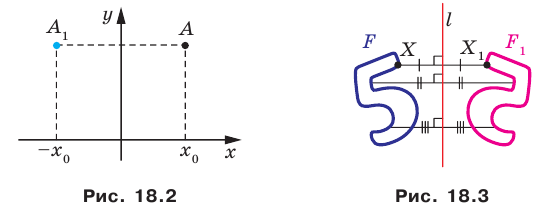
Доказательство: Выберем систему координат так, чтобы ось симметрии совпала с осью ординат. Пусть 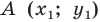
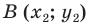
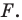
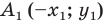
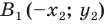
Мы получили, что 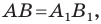
Следствие. Если фигуры 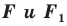
Определение. Фигуру называют симметричной относительно прямой 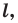
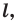
Прямую 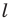
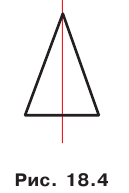
Приведем примеры фигур, имеющих ось симметрии. На рисунке 18.4 изображен равнобедренный треугольник. Прямая, содержащая его высоту, проведенную к основанию, является осью симметрии треугольника.
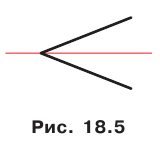
Любой угол имеет ось симметрии — это пря-Рис. 18.5 мая, содержащая его биссектрису (рис. 18.5).
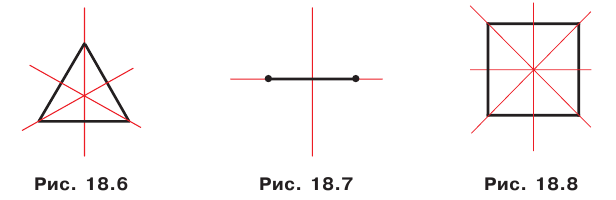
Равносторонний треугольник имеет три оси симметрии (рис. 18.6). Две оси симметрии имеет отрезок: это его серединный перпендикуляр и прямая, содержащая этот отрезок (рис. 18.7).
Квадрат имеет четыре оси симметрии (рис. 18.8).
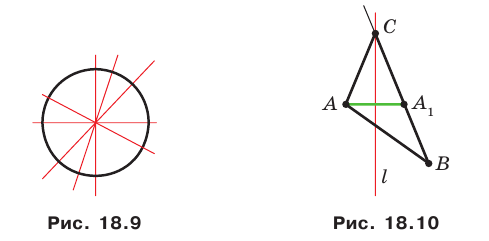
Существуют фигуры, имеющие бесконечно много осей симметрии, например окружность. Любая прямая, проходящая через центр окружности, является ее осью симметрии (рис. 18.9).
Бесконечно много осей симметрии имеет и прямая: сама прямая и любая прямая, ей перпендикулярная, являются ее осями симметрии.
Пример №4
Начертили неравнобедренный треугольник 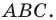
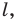
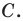
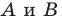
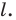
Решение:
Поскольку прямая 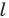
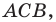
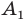
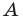
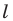
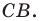
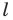
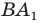
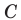
Эти соображения подсказывают, как построить искомый треугольник: строим точку 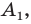
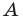
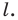
Пример №5
Точка 
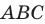
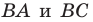
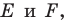
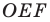
Решение:
Пусть точки 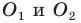
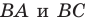
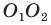
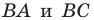
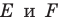
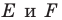
Заметим, что отрезки 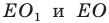
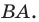
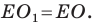
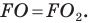
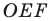
Покажем, что построенный треугольник имеет наименьший периметр из возможных.
Рассмотрим треугольник 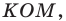
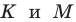
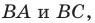
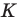
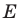
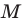
Понятно, что
Тогда периметр треугольника 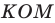
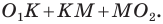
Центральная симметрия. Поворот
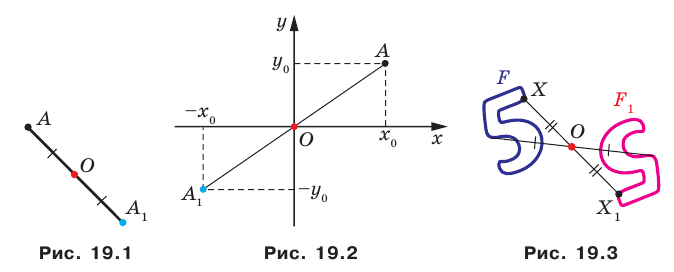
Определение. Точки 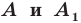
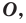
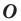
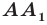
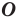
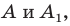
Рассмотрим фигуру 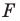
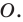
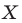
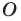
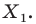
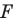
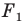
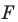
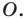
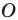
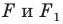
Теорема 19.1 (свойство центральной симметрии). Центральная симметрия является движением.
Доказательство: Выберем систему координат так, чтобы центр симметрии совпал с началом координат. Пусть 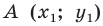
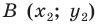
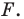
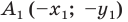
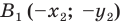
Мы получили, что 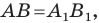
Следствие. Если фигуры 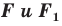
Определение. Фигуру называют симметричной относительно точки 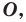
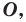
Точку 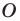
Приведем примеры фигур, имеющих центр симметрии.
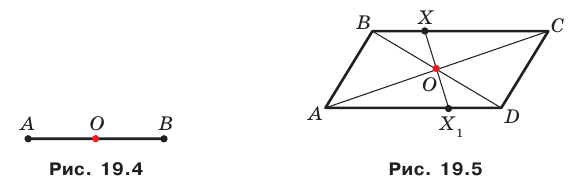
Центром симметрии отрезка является его середина (рис. 19.4).
Точка пересечения диагоналей параллелограмма является его центром симметрии (рис. 19.5).
Существуют фигуры, имеющие бесконечно много центров симметрии. Например, каждая точка прямой является ее центром симметрии.
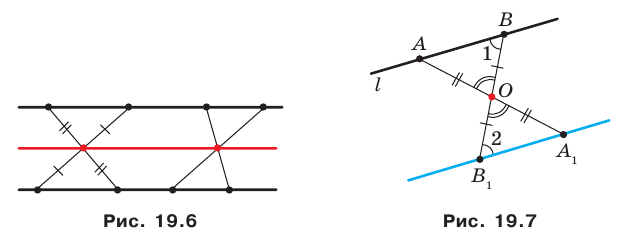
Также бесконечно много центров симметрии имеет фигура, состоящая из двух параллельных прямых. Любая точка прямой, равноудаленной от двух данных, является центром симметрии рассматриваемой фигуры (рис. 19.6).
Пример №6
Докажите, что образом данной прямой 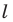
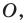
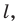
Решение:
Поскольку центральная симметрия — это движение, то образом прямой 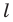
Выберем на прямой 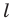
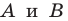
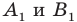
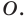
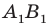
Поскольку 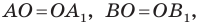
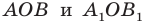
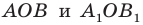
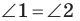
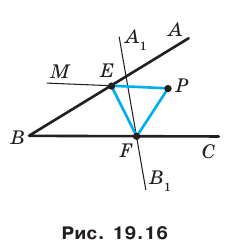
Пример №7
Точка 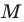
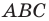
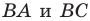
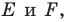
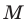
Решение:
Пусть прямая 
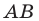
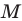
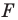
Найдем прообраз точки 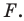
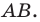
Обозначим эту точку буквой 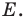
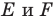
Изучая окружающий мир, мы часто видим примеры проявления симметрии в природе (рис. 19.10). Объекты, имеющие ось или центр симметрии, легко воспринимаются и радуют взгляд. Недаром в Древней Греции слово «симметрия» служило синонимом слов «гармония», «красота».
Идея симметрии широко используется в изобразительном искусстве, архитектуре и технике (рис. 19.11).
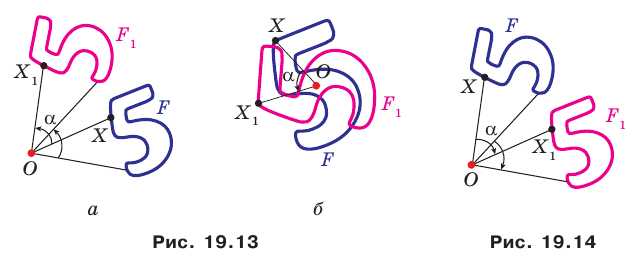
На рисунке 19.12 изображены точки 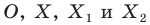
Говорят, что точка 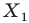
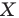
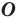
Так же говорят, что точка 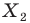
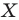
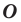
Точку 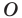
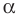
Рассмотрим фигуру 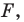
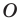
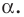
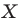
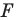
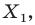
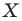
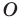
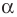
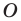
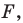
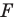
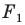
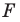
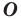
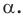
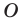
Аналогично определяют преобразование поворота фигуры 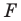
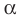
Заметим, что центральная симметрия является поворотом вокруг центра симметрии на угол
Теорема 19.2 (свойство поворота). Поворот является движением.
Докажите эту теорему самостоятельно.
Следствие. Если фигура 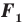
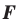
Пример №8
Даны прямая 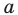
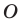
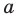
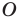
Решение:
Поскольку поворот — это движение, то образом прямой 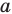
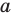
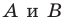
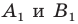
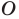
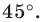
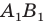
Пример №9
Точка 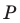
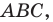
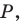
Решение:
Пусть прямая 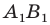
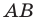
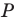
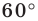
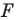
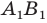
Пусть точка 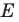
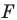
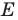
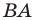
Эти соображения подсказывают, как построить искомый треугольник.
Строим прямую 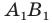
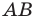
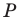
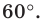
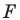
Строим угол 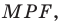
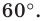
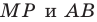
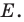
Имеем: 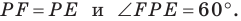
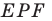
Подобие фигур
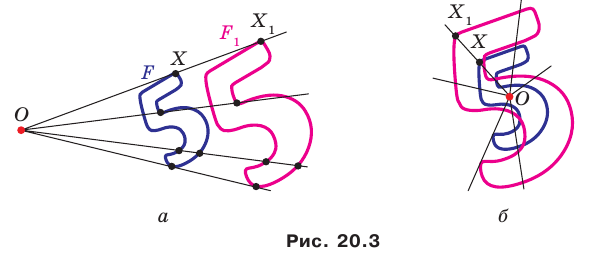
На рисунке 20.1 изображены точки 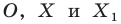
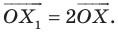
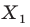
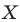
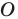
На рисунке 20.2 изображены точки 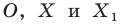
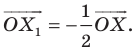
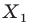
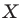
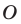
Вообще, если точки 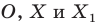
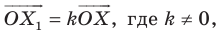
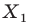
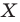
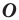
Точку 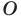
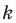
Рассмотрим фигуру 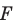
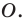
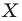
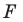
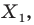
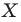
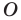
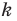
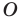
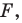
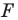
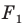
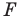
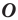
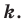
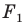
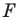
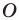
Например, на рисунке 20.4 треугольник 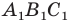
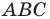
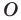
можно сказать, что треугольник 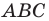
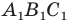
Отметим, что при 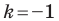
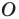
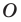
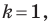
Очевидно, что при 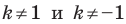
Теорема 20.1. При гомотетии фигуры 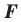
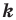
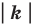
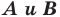
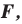
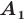
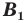
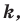
Доказательство: Пусть точка 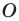
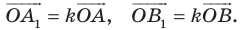
Следствие. Если треугольник 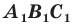
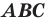
Для доказательства этого утверждения достаточно воспользоваться теоремой 20.1 и третьим признаком подобия треугольников.
Гомотетия обладает целым рядом других свойств.
При гомотетии:
Эти свойства вы можете доказать на занятиях математического кружка.
Перечисленные свойства гомотетии указывают на то, что это преобразование может изменить размеры фигуры, но не меняет ее форму, то есть при гомотетии образ и прообраз являются подобными фигурами. Заметим, что в курсе геометрии 8 класса, говоря о подобии фигур, мы давали определение только подобных треугольников. Сейчас определим понятие подобия для произвольных фигур.
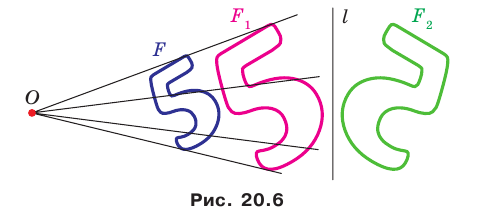
На рисунке 20.6 фигура 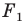
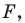
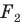
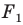
Говорят, что фигура 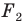
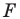
Поскольку 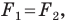
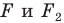
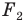
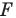
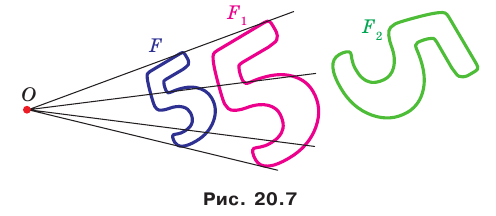
На рисунке 20.7 фигура 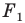
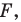
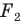
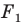
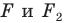
Из сказанного следует, что целесообразно принять такое определение.
Определение. Две фигуры называют подобными, если одну из них можно получить из другой в результате композиции двух преобразований: гомотетии и движения.
Это определение иллюстрирует схема, изображенная на рисунке 20.8.
Запись 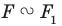
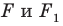
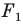
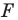
Из приведенного определения следует, что при преобразовании подобия фигуры 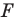
Так как тождественное преобразование является движением, то из схемы, изображенной на рисунке 20.8, следует, что гомотетия — частный случай преобразования подобия.
Пусть 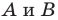
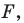
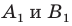
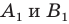
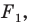
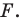
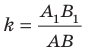
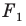
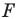
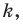
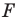
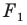
Заметим, что преобразование подобия с коэффициентом 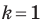
С преобразованием подобия мы часто встречаемся в повседневной жизни (рис. 20.9). Например, в результате изменения масштаба карты получаем карту, подобную данной. Фотография — это преобразование негатива в подобное изображение на фотобумаге. Перенося в свою тетрадь рисунок, сделанный учителем на доске, вы также выполняете преобразование подобия. 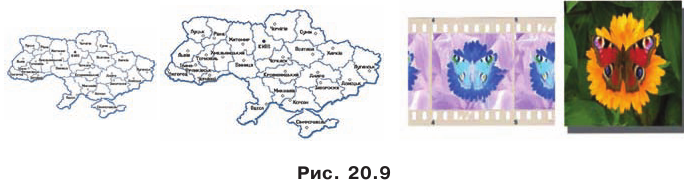
Доказательство этой теоремы выходит за рамки рассматриваемого курса геометрии. Мы докажем ее для частного случая, рассмотрев подобные треугольники.
Доказательство: Пусть треугольник 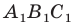
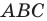
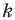
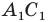
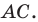
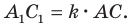
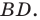
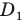
Поскольку при преобразовании подобия сохраняются углы, то отрезок 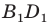
Тогда 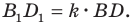
Пример №10
Докажите, что образом прямой 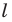
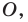
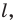
Решение:
Из свойств гомотетии следует, что образом прямой 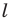
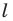
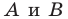
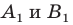
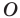
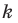
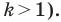
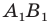
При доказательстве теоремы 20.1 мы показали, что 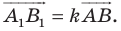
Пример №11
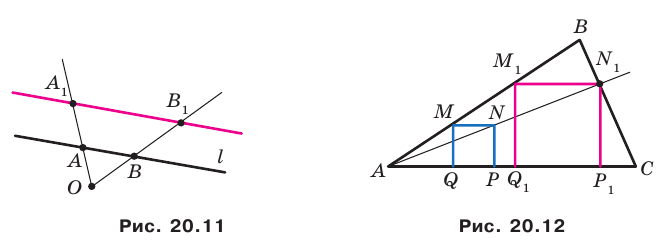
В остроугольный треугольник 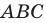
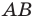
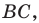
Решение:
Из произвольной точки 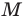
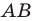
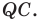
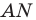
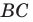
Рассмотрим гомотетию с центром 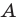
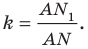
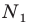
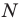
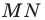
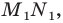
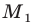
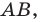
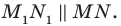
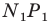
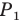
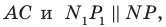
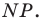
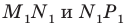
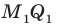
Пример №12
Отрезок 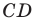
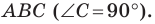
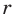

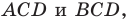
Решение:
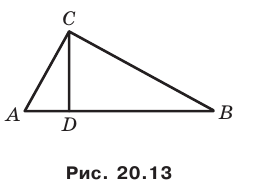
Поскольку угол 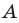
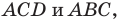
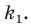
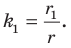
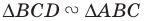
Обозначим площади треугольников 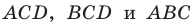
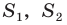
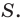
Отсюда 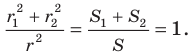
Ответ:
Применение преобразований фигур при решении задач
Преобразование фигур — эффективный метод решения целого ряда геометрических задач. Проиллюстрируем это на примерах.
Пример №13
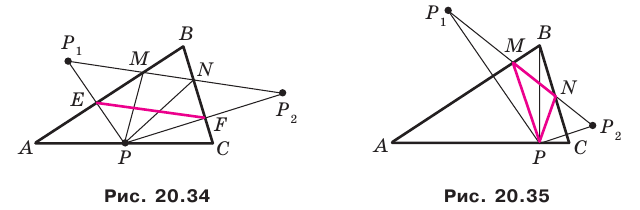
На сторонах 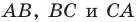
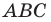
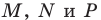
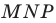
Решение:
Пусть 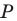
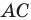
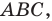
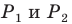
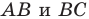
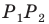
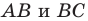
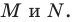
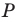
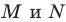
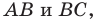
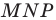
Заметим, что отрезок 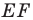
Тогда
Поскольку 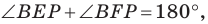
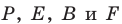
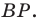
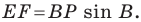
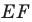
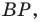
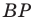
На рисунке 20.35 отрезок 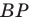
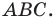
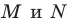
Из построения следует, что периметр любого другого треугольника, вершины которого лежат на сторонах треугольника 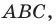
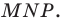
Можно показать (сделайте это самостоятельно), что точки 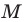
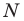
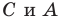
Следовательно, вершины искомого треугольника — это основания высот данного треугольника 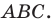
Пример №14
Точка 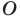
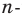
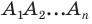
Решение:
Пусть 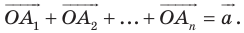
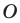
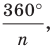
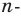
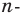
Пример №15
Внутри треугольника 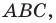
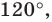
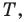
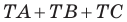
Решение:
Пусть 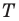
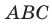
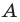
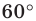
Имеем:
Понятно, что сумма 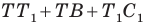
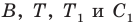
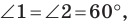
Так как угол 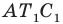
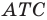
Итак, точки 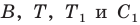
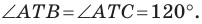
Таким образом, сумма 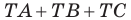
Найти точку 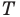
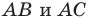
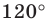
Понятно, что если один из углов треугольника 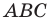
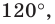
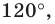
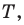
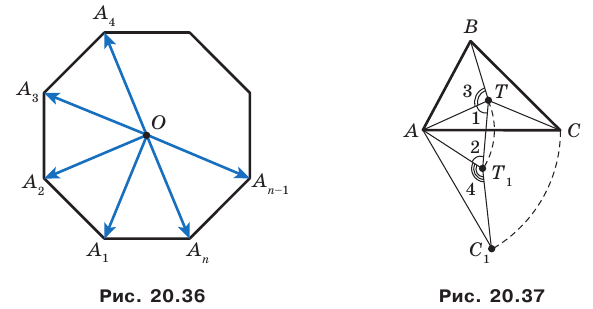
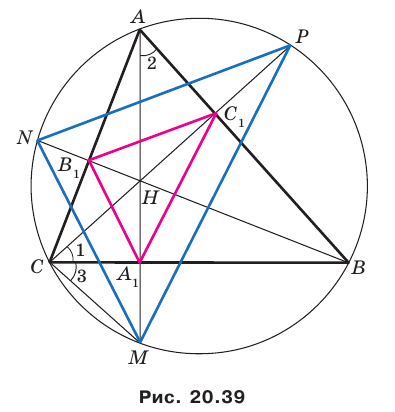
Пример №16
Отрезки 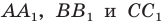
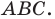
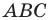
Решение:
Пусть прямые 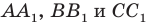
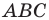
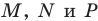
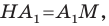
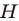
Имеем:
Углы 2 и 3 равны как вписанные, опирающиеся на дугу 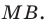
Тогда в треугольнике 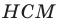
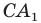
Аналогично можно доказать, что
Теперь понятно, что треугольник 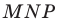
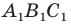
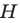
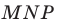
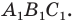
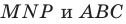
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Возникновение геометрии
- Призма в геометрии
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
- Декартовы координаты на плоскости
- Декартовы координаты в пространстве
Как найти центр симметрии
Одним из видов симметрии является центральная. Центр симметрии — некоторая точка O, относительно которой вращают плоскость, поворачивая ее на 180°. Каждая точка A переходит в такую точку A’, что O — середина отрезка AA’.

Инструкция
Если даны две точки, центром симметрии между ними, по определению, будет середина отрезка, соединяющего их. Сложнее обстоит дело с геометрической фигурой: здесь уже надо рассмотреть все точки, составляющие ее. Любая произвольная точка должна переходить в центрально симметричную ей, иначе принцип симметрии будет нарушен.
Если даны две фигуры, про которые сказано, что они являются симметричными относительно неизвестного центра, попробуйте мысленно вращать каждую из фигур. В итоге вы должны представить переход на 180° (пол-окружности). Найдите любые две симметричные точки, проведите между ними отрезок. В его центре будет располагаться центр симметрии и этих двух точек, и всей фигуры.
Пусть надо построить окружность, симметричную данной относительно точки O. Центр окружности пусть обозначен точкой C. Проведите прямую от точки C через точку O. Ножками циркуля отмерьте расстояние OC, отложите такое же расстояние на прямой от точки O в другую сторону. Зафиксируйте результат, это будет центр новой окружности. Измерьте циркулем радиус исходной окружности и достройте симметричную.
Чтобы построить многоугольник, симметричный данному относительно центра O, найдите образ каждой из его вершин. Исходная точка называется «прообразом», конечная – «образом». Последовательно соедините точки между собой. Мысленно повращайте фигуры, оцените, правильным ли получился результат.
Если дана пространственная фигура, и необходимо найти центр симметрии между какими-либо двумя точками, вспомните свойства этого объемного тела. Возможно, центр симметрии лежит на пересечении диагоналей, биссектрис, медиан, перпендикуляров. Докажите, что указанная вами точка является именной центром симметрии, используя свойства фигуры, другие данные в задаче условия и определение симметричности.
Видео по теме
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
ВИДЕОУРОК
Симметрия – слово греческого происхождения. Оно означает соразмерность, наличие
определённого порядка, закономерности в расположении частей.
Люди с давних времён
использовали симметрию в рисунках, орнаментах, предметах быта, в архитектуре,
художестве, строительстве.
Симметрия широко распространена и в природе, где
не было вмешательства человеческой руки. Её можно наблюдать в форме листьев и
цветов растений, в расположении различных органов животных, в форме кристаллических
тел, в порхающей бабочке, загадочной снежинке, морской звезде.
Симметрия
в геометрии – свойство геометрических фигур.
Рассмотрим две симметрии на плоскости относительно точки и прямой.
ОСЕВАЯ СИММЕТРИЯ
Ось симметрии.
Две
точки, лежащие на одном перпендикуляре к данной плоскости (или прямой) по
разные стороны и на одинаковом расстоянии от неё, называются симметричными
относительно этой плоскости (или прямой). Фигура (плоская или пространственная)
симметрична относительно прямой (оси симметрии) или плоскости (плоскости
симметрии), если её точки попарно обладают указанным свойством.
Фигура симметрична
относительно прямой, если для каждой точки фигуры симметричная ей точка
относительно прямой также принадлежит этой фигуре. Прямая – ось симметрии фигуры, а фигура обладает
осевой симметрией.
Фигура, обладающая
осевой симметрией – это неразвёрнутый угол, который имеет одну ось симметрии –
прямую на которой расположена биссектриса угла.
Осевая симметрия – это симметрия относительно проведённой
прямой (оси).
Две точки А
и В
симметричны относительно прямой а (оси симметрии), если эта прямая проходит через середину отрезка
АВ и перпендикулярна
к нему.
Проведем прямую
ЕF через
середины Е и F сторон АВ и СD прямоугольника АВСD.
Эта прямая делит прямоугольник пополам. Если прямоугольник перегнуть по этой
прямой, то обе две половины совпадут. Говорят, что прямоугольник симметричный относительно
прямой ЕF, а прямую ЕF называют осью симметрии прямоугольника. У
прямоугольника АВСD есть другая ось симметрии – прямая NК.
Вообще, фигуру называют симметричной относительно прямой l, если эта прямая делит фигуру на две части, которые совпадают при перегибании
по этой прямой. Прямую l называют осью симметрии этой фигуры.
Две
точки А и В, которые совпадают при перегибании плоскости по
прямой l, называют симметричными относительно этой
прямой. Если точки А и В симметричные относительно прямой l, то:
1) отрезок АВ
перпендикулярен прямой l.
2) прямая l делит этот отрезок пополам.
Окружность имеет бесконечное количество осей симметрии. Любая прямая, которая
проходит через центр окружности, будет его осью симметрии.
Ось симметрии имеют изображения многих фигур (предметов), которые часто
встречаются в природе и технике.
Каждая точка прямой а симметрична самой себе.
ПРИМЕР:
АО
= ОВ, АВ ⊥
а.
Точка А
симметрична сама себе.
Фигура симметрична относительно прямой – если для каждой точки фигуры симметричная ей точка
относительно прямой также принадлежит этой фигуре.
Прямая – ось симметрии фигуры, а
фигура обладает осевой симметрией.
Фигуры, симметричные относительно прямой, равны.
Иногда у фигур несколько осей симметрии.
Фигуры, обладающие осевой симметрией.
ПРИМЕР:
Неразвёрнутый угол имеет одну ось симметрии –
прямую, на которой расположена биссектриса угла.
Равнобедренный
треугольник имеет одну ось симметрии.
Равносторонний
треугольник имеет три оси симметрии.
Квадрат имеет четыре оси
симметрии.
Прямоугольник имеет две
оси симметрии
Ромб имеет две оси
симметрии
Окружность имеет
бесконечно много осей симметрии – любая прямая, проходящая через центр,
является осью симметрии.
Примером фигур, у которых нет ни одной оси симметрии, являются
параллелограмм и треугольник, все стороны которого различны.
Алгоритм построения фигуры, симметричной относительно некоторой прямой.
ПРИМЕР:
Построим треугольник А1В1С1, симметричный треугольнику АВС
относительно красной прямой линии (ось симметрии).
Для этого проведём из вершины
треугольника АВС прямые,
перпендикулярные оси симметрии, и продолжим их дальше на другой стороне оси.
Измерим расстояние от вершин треугольника
до получившихся точек на прямой и отложим с другой стороны прямой такие же
расстояния.
Соединим получившиеся точки отрезками и
получим треугольник А1В1С1, симметричный данному треугольнику АВС.
ЗАДАЧА:
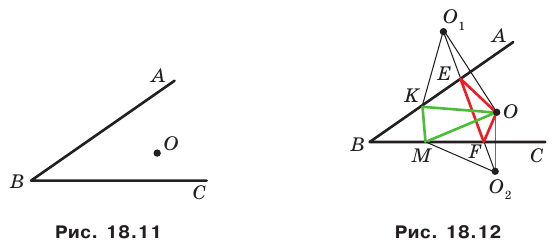
Дан отрезок АВ.
Построить его симметрию относительно прямой
l,
не пересекающий данный отрезок.
РЕШЕНИЕ:
Изобразим схематически условие задачи.
Так как осевая симметрия
является движением, то отрезок АВ
отобразится на равный ему отрезок
А’В’.
Для его построения сделаем
следующее: проведём через точки А и В прямые m и n перпендикулярно
прямой l.
Пусть
m ∩ l = Х, n ∩ l = Y.
Далее проведём отрезки
А’Х
= АХ и
В’Y = ВY.
ЗАДАЧА:
Построить симметричный
треугольник для данного треугольника относительно какой-либо его стороны.
РЕШЕНИЕ:
Пусть нам дан треугольник АВС. Будем строить его
симметрию относительно стороны ВС.
Сторона ВС при осевой симметрии перейдёт в саму себя (следует из
определения). Точка А перейдёт в точку А1 следующим образом:
АА1 ⊥ ВС, АН = НА1.
Треугольник АВС перейдёт в треугольник А1ВС.
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
Симметрию относительно точки называют центральной
симметрией.
Две точки А и В
симметричны относительно точки О, если О – середина отрезка АВ. Точка О называется центром симметрии.
Точка О симметрична самой
себе.
Фигура
симметрична относительно точки (центр симметрии), если её точки попарно лежат
на прямых, проходящих через центр симметрии, по разные стороны и на равных
расстояниях от него.
Фигура симметрична относительно точки, если для каждой точки фигуры симметричная ей точка
относительно данной точки также принадлежит этой фигуре. Данная точка – центр симметрии фигуры, а фигура обладает центральной симметрией.
Фигуры, симметричные относительно некоторой точки, равны.
Фигуры, обладающие центром симметрии.
ПРИМЕР:
Окружность, центр окружности
является её центром симметрии.
Параллелограмм, его центром
симметрии является точка пересечения диагоналей.
Прямая имеет бесконечно много
центров симметрии, так как любая точка прямой является её центром симметрии.
Примером фигуры, не имеющей центра симметрии, является треугольник.
Алгоритм построения центрально-симметричных фигур.
ПРИМЕР:
Построим треугольник А1В1С1, симметричный треугольнику АВС
относительно центра (точки) О.
Для этого соединим точки А,В,С с центром О и продолжим эти отрезки.
Измерим отрезки АО,
ВО, СО и отложим с
другой стороны от точки О равные им отрезки
АО
= ОА1, ВО = ОВ1, СО = ОС1.
Соединим получившиеся точки
отрезками и получим треугольник
А1В1С1, симметричный данному треугольнику АВС.
ЗАДАЧА:
Дан отрезок АВ.
Построить его симметрию относительно точки
С, лежащей на прямой l.
РЕШЕНИЕ:
Изобразим схематически условие задачи.
Так как центральная симметрия
является движением, то отрезок АВ
отобразится на равный ему отрезок
А»В».
Для его построения сделаем
следующее: проведём прямые АС и ВС. Далее проведём отрезки
А»С = АС и В»С = ВС.
ЗАДАЧА:
Построить симметричный
треугольник для данного треугольника относительно какой-либо его вершины.
РЕШЕНИЕ:
Пусть нам дан треугольник АВС. Будем строить его
симметрию относительно вершины А.
Вершина А при центральной симметрии перейдёт в саму
себя (следует
из определения). Точка В перейдёт
в точку В1 следующим образом ВА = АВ1, а точка С перейдёт
в точку С1 следующим образом СА = АС1. Треугольник
АВС перейдёт
в треугольник АВ1С1.
Некоторые повороты и осевые симметрии на координатной плоскости.
Пусть на плоскости дана прямоугольная система координат хОу. Ознакомимся с координатной записью некоторых
перемещений.
1) При осевой симметрии
относительно оси Оу точка Р(х, у) отображается на
точку Р’
с координатами:
х‘ =
–х,
у‘ =
у.
2) При осевой симметрии относительно оси Ох точка Р(х, у) отображается на
точку Р’
с координатами:
х‘ =
х,
у‘ =
–у.
3) При повороте на 90° вокруг начала координат ось Ох
переходит в ось Оу так, что положительное направление переходит
в положительное, а ось Оу отображается на ось Ох так, что
положительное направление переходит в отрицательное. Поэтому Р(х, у) отображается на
точку Р’
с координатами:
х‘ =
–у,
у‘ =
х.
4) При центральной симметрии
каждая из осей координат
отображается на себя, но так, что положительное направление оси переходит в
отрицательное и наоборот: отрицательное в положительное. Поэтому
Объединим результаты в таблицу
Задания к уроку 32
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Точка и прямая
- Урок 2. Угол
- Урок 3. Параллельные и перпендикулярные прямые
- Урок 4. Окружность
- Урок 5. Угол и окружность
- Урок 6. Треугольник (1)
- Урок 7. Треугольник (2)
- Урок 8. Прямоугольный треугольник (1)
- Урок 9. Прямоугольный треугольник (2)
- Урок 10. Равнобедренный треугольник (1)
- Урок 11. Равнобедренный треугольник (2)
- Урок 12. Периметр треугольника
- Урок 13. Периметр равнобедренного (равностороннего) треугольника
- Урок 14. Треугольник и окружность
- Урок 15. Прямоугольный треугольник и окружность
- Урок 16. Равнобедренный треугольник и окружность
- Урок 17. Четырёхугольники
- Урок 18. Параллелограмм
- Урок 19. Периметр параллелограмма
- Урок 20. Прямоугольник
- Урок 21. Периметр прямоугольника
- Урок 22. Квадрат
- Урок 23. Ромб
- Урок 24. Периметр ромба
- Урок 25. Трапеция
- Урок 26. Равнобедренная трапеция
- Урок 27. Периметр трапеции
- Урок 28. Четырёхугольник и окружность (1)
- Урок 29. Четырёхугольник и окружность (2)
- Урок 31. Правильный многоугольник
Если середину отрезка провести перпендикулярную прямую, то она будет осью симметрии данного отрезка.
Есть утверждения, что если через этот отрезок провести прямую, то она будет второй осью симметрии для данного отрезка.
Давайте рассмотрим более подробнее этот случай и для начала ознакомимся с определением некоторых вещей
Определение точки
Определение линии
Определение прямой
Определение отрезка
Отрезок — это часть прямой линии, он имеет длину, но не имеет ширины и толщины, следовательно — разделить его вдоль никак нельзя и поэтому, он имеет только одну ось симметрии.
Теперь рассмотрим случай с прямой.
Проведем две перпендикулярных прямых к прямой а — одну посередине отрезка АА1, который лежит на этой прямой, другую немного правее
Первая прямая будет осью симметрии и для отрезка АА1 и для прямой а, вторая — только для прямой а (для любых точек А и А1 всегда найдем симметричные).
Прямая линия имеет бесконечное количество осей симметрии, но все они должны быть к ней перпендикулярны.

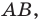
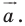
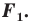
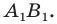
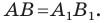
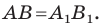
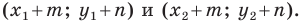
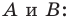
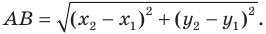
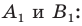
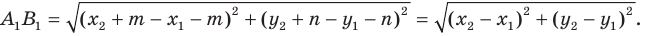

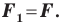

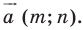

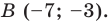
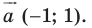
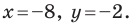
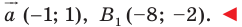
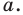
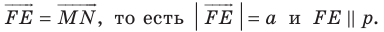
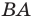 при параллельном переносе на вектор
при параллельном переносе на вектор 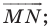
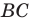 с построенным образом;
с построенным образом;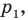 параллельную прямой
параллельную прямой 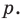 Прямая
Прямая 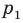 будет искомой.
будет искомой.