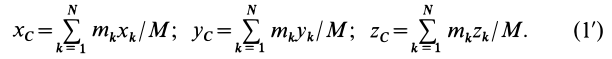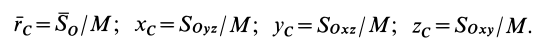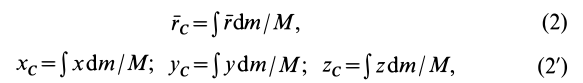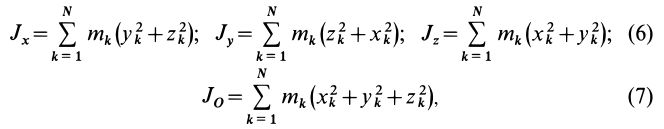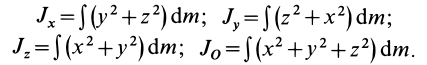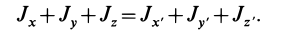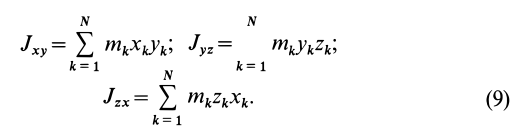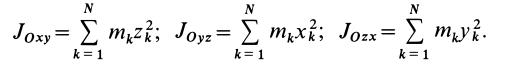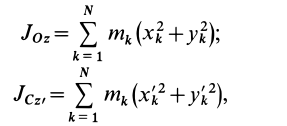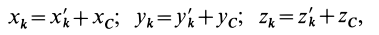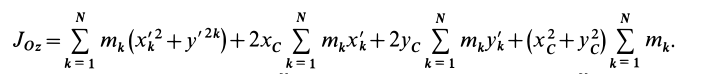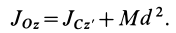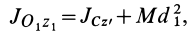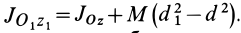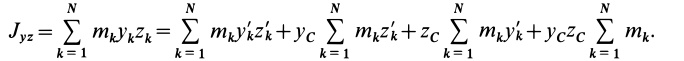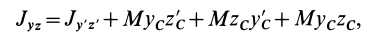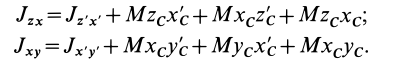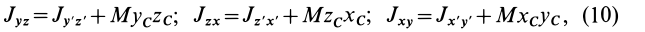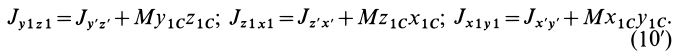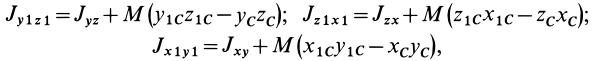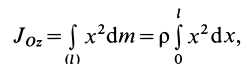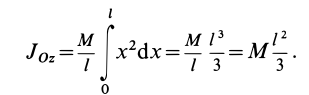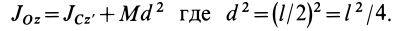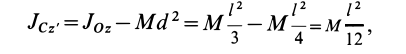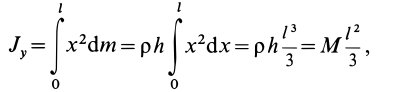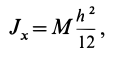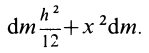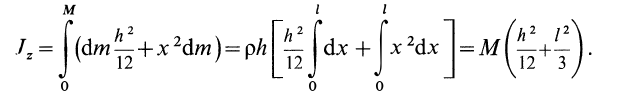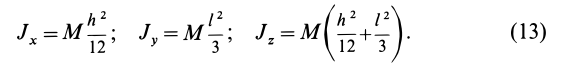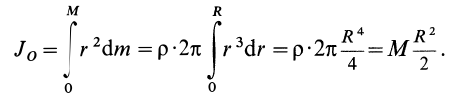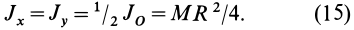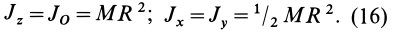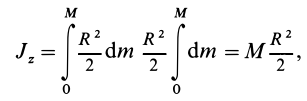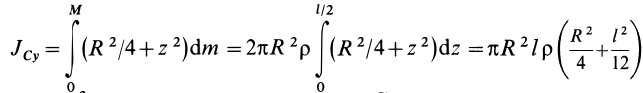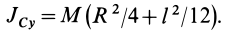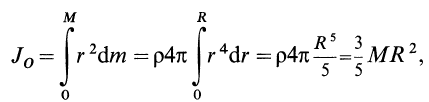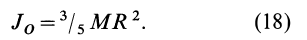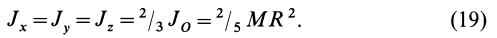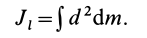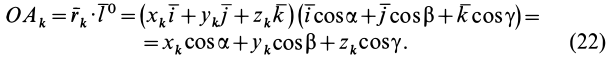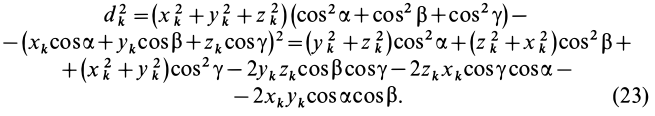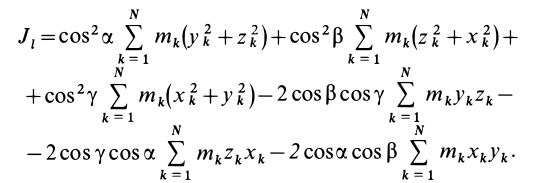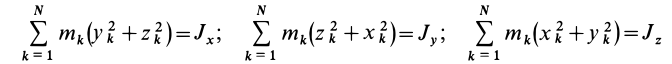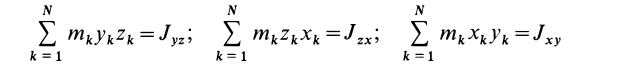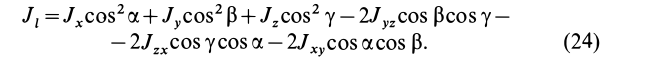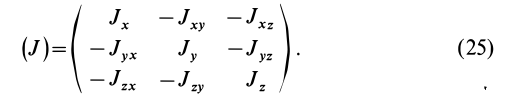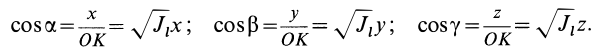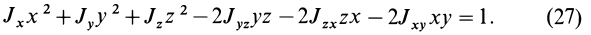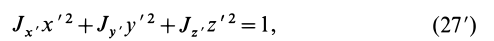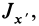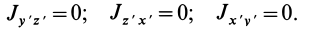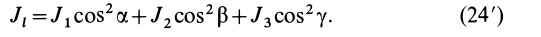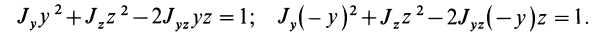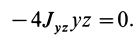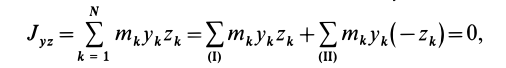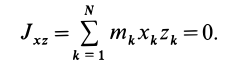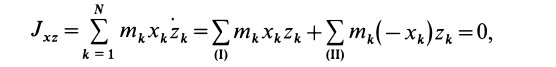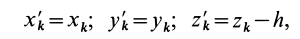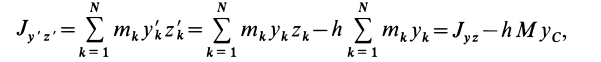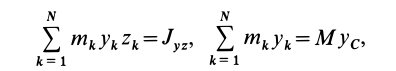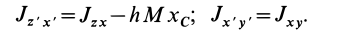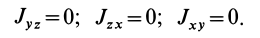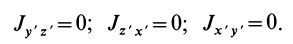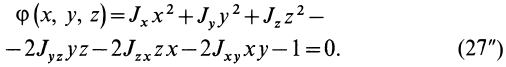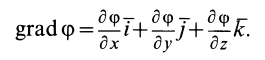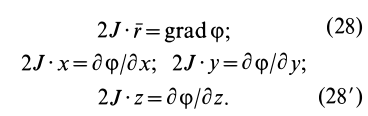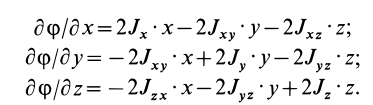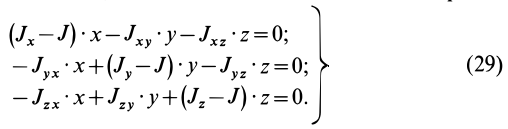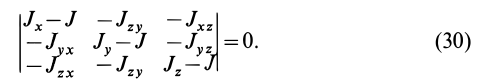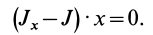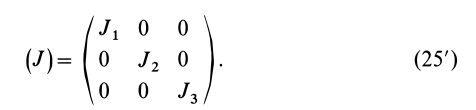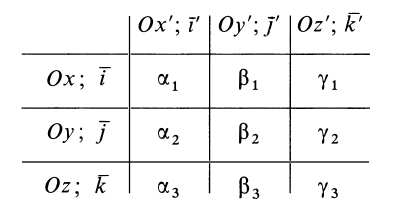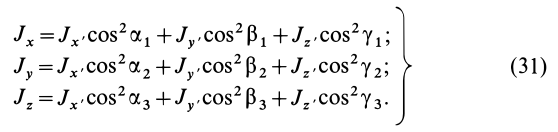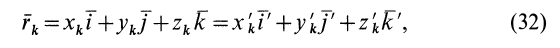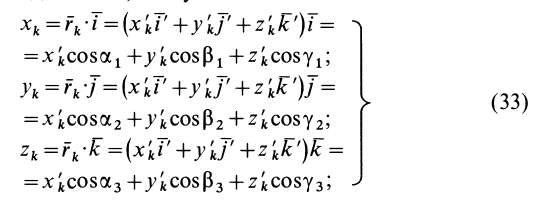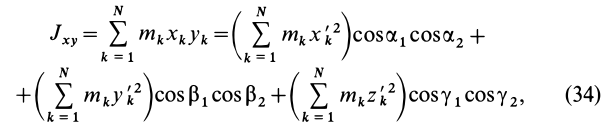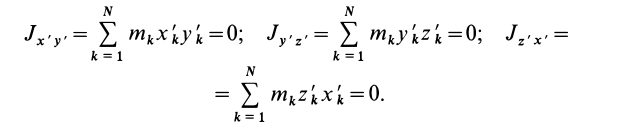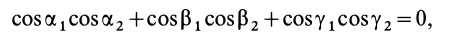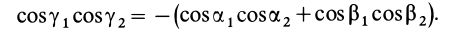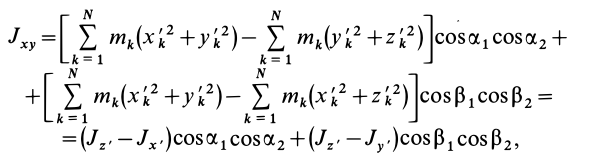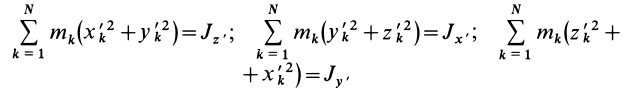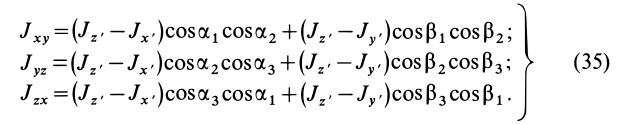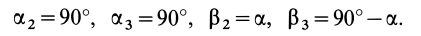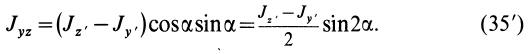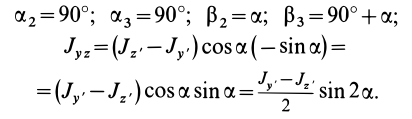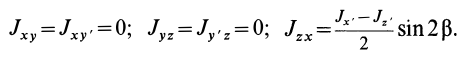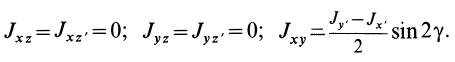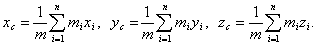Если система
не замкнута, то записав уравнения
движения для каждой материальной точки
системы, сложив их и учтя, что векторная
сумма внутренних тел равна нулю, придем
к уравнению
(5.1)
где
–
импульс системы n
материальных точек, F
– векторная сумма всех внешних сил,
действующих на точки системы. Таким
образом, скорость изменения импульса
системы материальных точек равна
результирующей всех внешних сил,
действующих на точки системы, и направлена
вдоль этой результирующей силы.
Уравнение (5.1)
является обобщением соответствующего
уравнения для одной материальной точки
и называется уравнением движения
системы. Умножив это уравнение на dt,
и проинтегрировав обе части полученного
равенства по времени между моментами
t1
и t2,
придем к теореме об изменении импульса
системы:
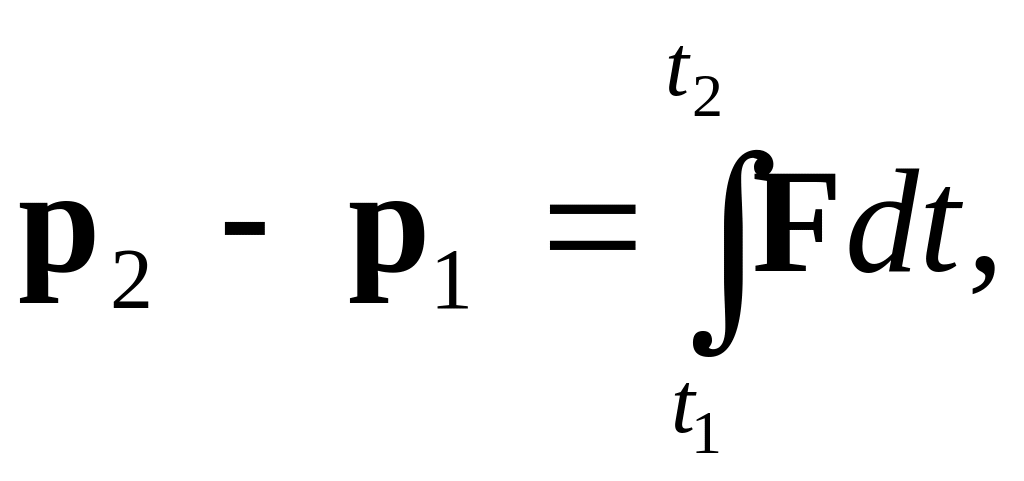
аналогичное
соответствующей теореме для одной
материальной точки. Здесь p1
и p2
– импульсы системы в моменты времени
t1
и t2.
Следовательно, изменение импульса
системы материальных точек за промежуток
времени от t1
до t2
равно
импульсу всех внешних сил, действующих
на точки системы за этот промежуток
времени. Теорему об изменении импульса
можно рассматривать как более общую
формулировку закона сохранения импульса
системы, так как в ней указана причина
изменения импульса – действие других
тел (посредством внешних сил F).
В любой системе
материальных точек имеется одна
замечательная геометрическая точка С,
называемая центром инерции или центром
масс системы. Ее положение в заданной
системе координат определяется
радиус-вектором
(5.2)
где
–
масса системы, ri
– радиус-вектор i-ой
материальной точки. Декартовы координаты
центра инерции системы определятся
так:
(5.3)
В случае однородного
поля сил тяжести центр инерции совпадает
с центром тяжести, т.е. с точкой приложения
силы тяжести, являющейся равнодействующей
параллельных сил, приложенных к
материальным точкам в однородном поле
силы тяжести.
Продифференцировав
выражение (5.2) по времени, найдем скорость
движения центра инерции:
(5.4)
где
–
импульс системы. Откуда,
p
= mvC.
(5.5)
Следовательно,
импульс системы материальных точек
можно определить как произведение массы
системы на скорость движения ее центра
инерции.
Если система
замкнута, то p =
const,
а значит, vС
= const.
Следовтельно, центр инерции замкнутой
системы движется равномерно и прямолинейно,
в частности, он может покоится. Этот
вывод есть обобщение закона инерции и
понятия покоя на случай системы
материальных точек. Скорость vС
имеет смысл скорости движения системы
как целого. Если система замкнута и ее
центр инерции вначале покоился (vС
= 0) или двигался равномерно и прямолинейно,
то никакие движения точек системы под
действием внутренних сил не изменят
этого состояния центра инерции. Это –
так называемый закон сохранения центра
инерции.
Если система
не замкнута, то импульс системы будет
изменяться со временем. Продифференцировав
соотношение (5.5) и учтя, что
где F
– результирующая всех внешних сил,
действующих на систему, получим
maC
= F,
(5.6)
где aC
= dvC/dt
– ускорение центра инерции системы.
Уравнение (5.6) выражает собой, так
называемую теорему о движении центра
инерции: произведение массы системы на
ускорение ее центра инерции равно
геометрической сумме всех действующих
на систему внешних сил. Сравнивая это
уравнение с уравнением второго основного
уравнения динамики материальной точки,
можно дать другую формулировку этой
теоремы: центр инерции системы движется
как материальная точка, масса которой
равна массе всей системы и к которой
приложены все внешние силы, действующие
на систему. Эта теорема объясняет, почему
поступательно движущееся тело можно
рассматривать как материальную точку
с массой, равной массе тела и оправдывает
введение самого понятия материальной
точки. Практическое значение этой
теоремы состоит в том, что она позволяет
при определении закона движения центра
масс любой системы исключить из
рассмотрения все наперед неизвестные
внутренние силы. Другими словами, она
позволяет свести движение системы к
движению одной материальной точки.
5.2.2.
Реактивное движение. Формула Циолковского
Закон сохранения
импульса как один из фундаментальных
законов природы проявляется в целом
ряде явлений. В частности, он лежит в
основе реактивного движения. Используя
этот закон, найдем зависимость скорости
ракеты от изменения ее массы.
При движении
ракеты ее масса уменьшается, так как
запасенное в ней топливо сгорает, и
продукты сгорания вылетают из соп-
|
Рис. 5. |
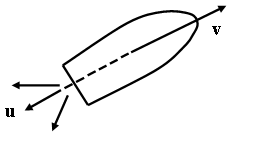
ла в виде выхлопных газов.
Обозначим
скорость ракеты в момент времени t
через v,
а массу через m.
Пусть в этот момент времени начинают
выходить выхлопные газы, скорость
которых относительно ракеты равна u
(рис. 4.). Через время dt
масса ракеты уменьшится и станет равной
m + dm,
где –dm
– масса вышедшего газа, а скорость
увеличится и станет равной v
+ dv.
Сравним теперь импульсы системы «ракета
+ выхлопные
газы» в моменты времени t
и t + dt.
Первоначальный импульс равен, очевидно,
mv.
Импульс ракеты в момент времени t
+ dt
будет (m + dm)(v
+ dv)1,
а импульс выхлопного газа будет –dm(v
– u),
так как скорость газа относительно
Земли равна, очевидно, v
– u. В соответствии
с законом сохранения импульса мы должны
приравнять величины импульсов в оба
момента времени:
mv = (m
+ dm)(v
+ dv) – dm(v
– u),
Откуда, пренебрегая
(бесконечно малой второго порядка dmdv,
находим
mdv
+ udm
= 0,
(5.7)
или
Будем считать, что
скорость истечения газа не меняется с
течением времени. Тогда последнее
равенство можно переписать в виде
Откуда следует,
что
где
–
постоянная интегрирования. Значение
постоянной C
определяется из условия, что в начале
движения ракеты, т.е. при v
= 0, масса ракеты
равнялась начальному значению m0:
C = lnm0.
Подставляя это значение С
в полученное соотношение, будем иметь
откуда окончательно
получим
Эта формула
определяет скорость ракеты в зависимости
от изменения ее массы и носит название
формулы Циолковского.
Формулу
Циолковского часто записывают в виде
В такой форме она
определяет начальную массу ракеты для
сообщения ей скорости v.
Если ракете, имеющей массу m,
требуется сообщить скорость v,
то начальная масса ракеты должна быть
равна m0.
С увеличением расчетной скорости v
начальная масса m0
экспоненциально возрастает. При v
>> u
отношение m0
/ m
получается очень большим. Это и создает
основные технические трудности при
построении космических ракет, достигающих
скорости порядка 10 км/с. Увеличение
скорости выхлопных газов позволяет
значительно уменьшить стартовую массу
и тем самым облегчает задачу конструкторов.
Разделив обе
части равенства (5.7) получим
(5.8)
Величина
определяет скорость изменения массы
ракеты (ежесекундный расход выхлопных
газов). Видим, что произведение
имеет размерность силы; ее называют
реактивной силой.
Она возникает вследствие того, что
частицам газа сообщается скорость u.
Предположим, что частицы газа находятся
в покое относительно ракеты. Затем
некоторой силой F
им сообщено ускорение относительно
ракеты, вследствие чего они получают
скорость u.
Сила, противодействующая этой силе F,
по третьему закону динамики приложена
к ракете и направлена в сторону,
противоположную скорости выброшенного
газа: она и есть реактивная сила, двигающая
ракету.
5.3. Закон сохранения
момента импульса
Из уравнения
моментов следует, что если момент силы,
действующий на материальную точку равен
нулю, то вектор момента ее импульса
будет сохраняться: L
= const.
Момент силы
будет равен нулю либо если сила F
равна нулю, либо если линия ее действия
проходит через точку, относительно
которой определяется момент импульса.
Последнее имеет место, если сила F
– центральная. Покажем, что момент
импульса замкнутой системы будет
сохраняться и для системы материальных
точек. Как и прежде, рассмотрим сначала
систему, состоящую из двух точек. Запишем
уравнение моментов для каждой из них:
Здесь L1,
M12,
M1
и L2,
M21,
M2
– моменты импульса и моменты внутренних
и внешних сил, действующих на первую и
вторую точки соответственно. Сложив
эти уравнения, получим
где L
= L1
+ L2
– момент импульса системы,
– суммарный момент внешних сил,
действующий на точки системы. Если
система замкнута, то
= 0, и в этом случае
скорость изменения момента импульса
системы будет
По свойству
изотропии пространства правая часть
этого равенства равна нулю. Действительно,
если рассматриваемую систему
|
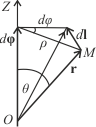
Рис. 5.1 |
как целое повернуть на угол
dφ
(рис. 5.1), то в силу изотропии пространства
ни в состоянии системы, ни в ее внутренних
движениях ничего не изменится. Поэтому
полная работа внутренних сил при
указанном повороте должна быть равна
нулю:
где dl1
и dl2
– элементарные векторы перемещения
точек 1 и 2 при повороте системы как
целого на угол dφ.
Элементарный
угол поворота dφ
будем считать вектором
dφ,
модуль которого равен самому углу dφ,
а направление совпадает с осью (на рис.
5.1 c
осью Z),
вокруг которой происходит поворот так,
что если смотреть навстречу этому
вектору, будем видеть направление
поворота против часовой стрелки (по
правилу правого винта).
Найдем связь
вектора перемещения dl
с углом поворота dφ.
Из рис. 5. 1 видно, что
(5.9)
Как видно из рис.
5.1, вектор dl
перпендикулярен плоскости, содержащей
векторы r
и dφ,
и образует с ними правовинтовую систему
(правую тройку) векторов, поэтому
равенство (5.9) представляет собой модуль
векторного произведения
Это соотношение
и определяет связь вектора перемещения
с вектором угла
поворота
.
С учетом этого получим
Левая часть этого
равенства представляет собой сумму
смешанных произведений трех векторов.
Произведя циклическую перестановку
этих векторов по формуле
,
будем иметь
Вследствие
произвольности угла поворота δφ
должно выполняться равенство M12
+ M21
= 0. Тогда
а значит, L = L1
+ + L2
= const.
Обобщить закон
сохранения момента импульса на системы
с числом материальных точек, больших
2, можно аналогично тому, как это было
сделано в случае закона сохранения
импульса.
Если система
не замкнута, то для момента импульса
системы материальных точек будем иметь
где
– векторная сумма всех внешних сил,
действующих на систему.
С помощью этого
соотношения можно получить и математическое
выражение теоремы об изменении момента
импульса системы:
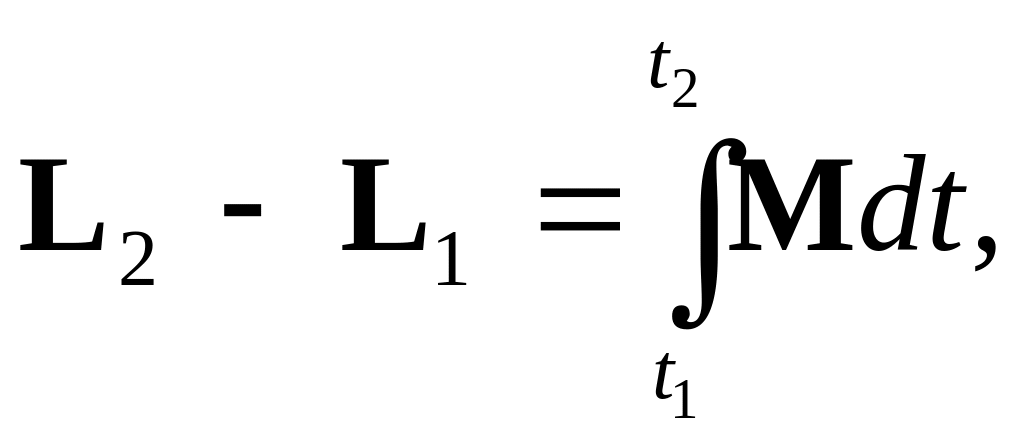
где L1
и L2
– моменты импульса системы в моменты
времени t1
и t2
соответственно.
Таким
образом, изменение момента импульса
системы материальных точек за промежуток
времени от t1
до t2
равно импульсу момента силы за этот
промежуток времени.
Аналогичным
образом можно показать, что закон
сохранения имеет место и для проекций
вектора момента импульса на любую ось,
проходящую через полюс: если вдоль
какой-либо оси, например оси Z,
момент силы Mz
= 0, то соответствующая
проекция момента импульса Lz
= const.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
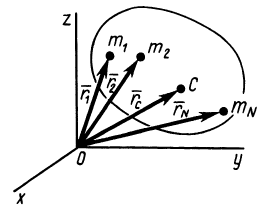
Геометрия масс:
Центр масс
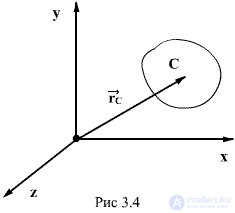
При рассмотрении движения твердых тел и других механических систем важное значение имеет точка, называемая центром масс. Если механическая система состоит из конечного числа материальных точек
где 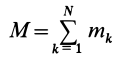
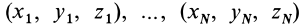
Рис. 21
Центр масс является не материальной точкой, а геометрической. Он может не совпадать ни с одной материальной точкой системы, как, например, в случае кольца. Центр масс системы характеризует распределение масс в системе.
Векторная величина 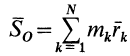
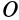
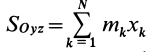
массы относительно координатной плоскости 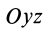
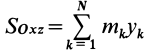
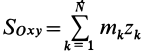
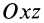
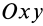
Радиус-вектор и координаты центра масс через статические моменты массы выражаются формулами
Если механическая система представляет собой сплошное тело, то его разбивают на элементарные частицы с бесконечно малыми массами 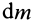
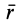
Суммы в пределе переходят в интегралы. Формулы (1) и (Г) принимают форму
где 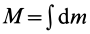
Для однородных сплошных тел 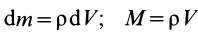
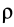
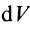
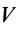
Для тел типа тонкого листа, которые можно принять за однородные материальные поверхности, 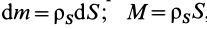
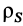
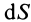
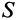
Для тонкой проволоки, которую можно принять за отрезок линии, 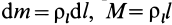
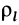
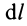
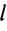
В этих случаях определение центра масс тел сводится к вычислению центра масс объемов, площадей и длин линий соответственно.
Моменты инерции
Для характеристики распределения масс в телах при рассмотрении вращательных движений требуется ввести понятия моментов инерции.
Моменты инерции относительно точки и оси
Моментом инерции механической системы, состоящей из 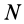
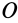
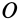
Момент инерции относительно точки часто называют полярным моментом инерции. В случае сплошного тела сумма переходит в интеграл и для полярного момента инерции имеем
где 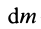
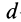
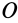
Моментом инерции 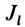
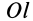
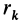
Рис. 22
В частном случае сплошного тела сумму следует заменить интегралом:
Моменты инерции одинаковых по форме однородных тел, изготовленных из разных материалов, отличаются друг от друга. Характеристикой, не зависящей от массы материала, является радиус инерции. Радиус инерции 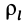
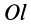
где 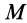
Момент инерции относительно оси через радиус инерции относительно этой оси определяется выражением
В справочниках по моментам инерции приводят таблицы значений радиусов инерции различных тел.
Формула (5′) позволяет считать радиус инерции тела относительно оси расстоянием от этой оси до такой точки, в которой следует поместить массу тела, чтобы ее момент инерции оказался равным моменту инерции тела относительно рассматриваемой оси.
Моменты инерции относительно оси и точки имеют одинаковую размерность — произведение массы на квадрат длины 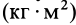
Кроме моментов инерции относительно точки и оси используются также моменты инерции относительно плоскостей и центробежные моменты инерции. Эти моменты инерции удобно рассмотреть относительно координатных плоскостей и осей декартовой системы координат.
Моменты инерции относительно осей координат
Моменты инерции относительно декартовых осей координат 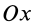
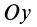
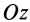
где 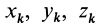
Из приведенных формул следует зависимость
Если через точку 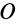
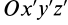
Из сравнения (8) и (8′) следует, что
Рис. 23
Сумма моментов инерции относительно декартовых осей координат не зависит от ориентации этих осей в рассматриваемой точке, т. е. является величиной, инвариантной по отношению к направлению осей координат.
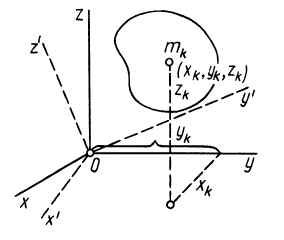
Для осей координат 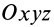
Центробежные моменты инерции часто называют произведениями инерции.
Моменты инерции относительно осей и точек — величины положительные, так как в них входят квадраты координат. Центробежные моменты инерции содержат произведения координат и могут быть как положительными, так и отрицательными.
Центробежные моменты инерции имеют важное значение при рассмотрении давлений на подшипники при вращении твердого тела вокруг неподвижной оси и в других случаях.
Кроме рассмотренных моментов инерции иногда используются моменты инерции относительно координатных плоскостей 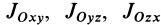
Теорема о моментах инерции относительно параллельных осей (теорема Штейнера)
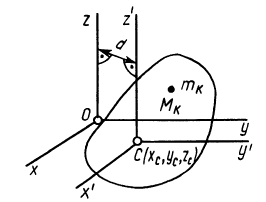
Установим зависимость между моментами инерции системы относительно параллельных осей, одна из которых проходит через центр масс. Пусть имеем две системы прямоугольных, взаимно параллельных осей координат 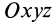
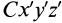
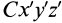
Рис. 24
По определению момента инерции относительно оси имеем
где 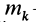
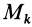
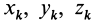
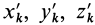
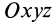
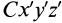
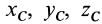
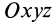
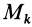
Подставим эти значения координат в выражение момента инерции 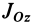
В этом соотношении 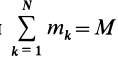
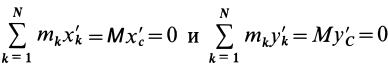
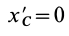
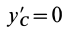
того, что по условию центр масс находится в начале координат этой системы координат.
Величина 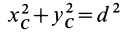
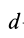
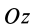
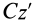
Связь моментов инерции относительно двух параллельных осей, одна из которых проходит через центр масс, составляет содержание так называемой теоремы Штейнера или Гюйгенса— Штейнера: момент инерции системы относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр масс, плюс произведение массы системы на квадрат расстояния между этими осями.
Из теоремы Штейнера следует, что для совокупности параллельных осей момент инерции является наименьшим относительно оси, проходящей через центр масс.
Если взять ось 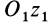
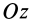
где 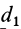
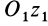
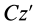
Исключая момент инерции 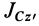
Установим изменение центробежных моментов инерции при параллельном переносе осей координат. Имеем
Учитывая, что 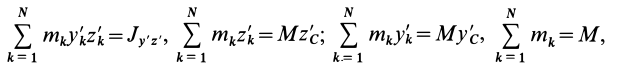
где 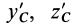
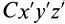
Так как начало системы координат 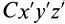
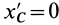
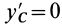
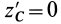
т. е. центробежные моменты инерции при параллельном переносе осей координат из любой точки в центре масс изменяются в соответствии с (10).
Если производится параллельный перенос осей 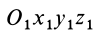
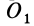
Исключая из (10) и (10′) центробежные моменты инерции Л’з» Лу, получим формулы для изменения центробежных моментов инерции при параллельном переносе осей координат из точки 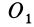
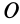
где 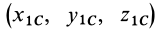
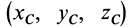
Моменты инерции простейших однородных тел
Моменты инерции тел сложной формы часто удается вычислить, если их предварительно разбить на тела простой формы. Моменты инерции сложных тел получают суммируя моменты инерции частей этих тел. Получим формулы для вычисления моментов инерции некоторых однородных простейших тел.
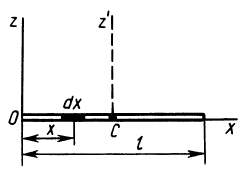
Однородный стержень
Имеем однородный стержень длиной 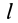
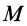
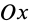
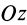
так как 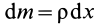
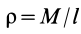
Вычисляя интеграл, получаем
Рис. 25
Таким образом,
Момент инерции стержня относительно оси 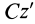
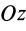
Следовательно,
т. е.
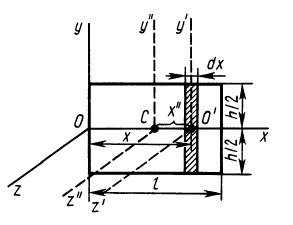
Прямоугольная пластина
Прямоугольная тонкая пластина имеет размеры 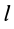
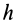
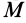
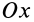
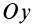
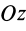
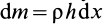
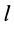
так как 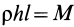
Аналогичные вычисления для оси 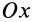
так как эта ось 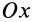
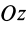
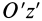
Рис. 26
Интегрируя это выражение в пределах от 0 до 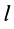
Итак, для моментов инерции пластины относительно осей координат получены следующие формулы:
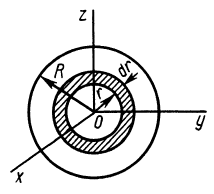
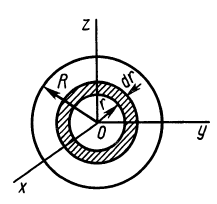
Круглый диск
Имеем тонкий однородный диск радиусом 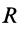
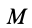
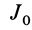
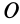
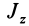
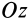
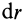
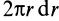
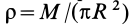
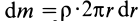
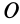
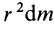
Таким образом,
Рис. 27
Для осей координат 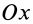
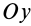
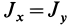
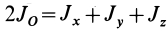
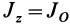
В случае тонкого проволочного кольца или круглого колеса, у которых масса распределена не по площади, а по его ободу, имеем
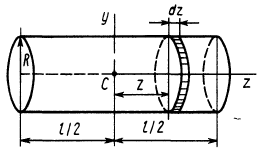
Круглый цилиндр
Рис. 28
Для круглого однородного цилиндра, масса которого 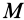
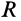
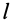
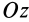
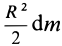
т.е.
Вычислим момент инерции цилиндра относительно его поперечной оси симметрии 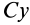
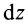
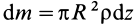
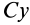
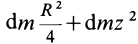
Чтобы получить момент инерции всего цилиндра относительно оси 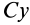
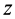
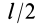
Но 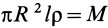
Таким образом, момент инерции цилиндра относительно его поперечной оси симметрии получается как сумма моментов инерции относительно этой оси диска и стержня, массы которых равны по отдельности массе цилиндра. Диск получается из цилиндра симметричным сжатием его с торцов до срединной плоскости при сохранении радиуса, а стержень — сжатием цилиндра в однородный стержень, расположенный по оси цилиндра, при сохранении длины.
Шар
Пусть масса шара 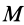
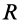
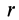
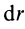
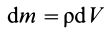
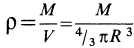
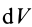
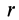
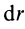
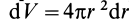
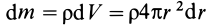
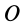
т.е.
Рис. 29
Для осей координат, проходящих через центр шара, в силу симметрии 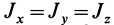
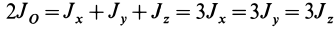
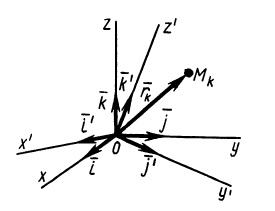
Моменты инерции относительно осей, проходящих через заданную точку
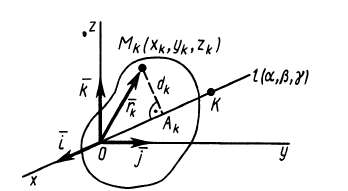
В заданной точке 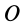
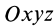
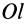
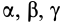
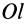
или для сплошных тел
В дальнейшем используется определение (20). Сплошные тела считаются разбитыми на 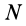
Из прямоугольного треугольника 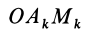
где 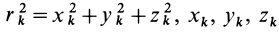
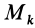
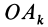
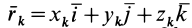
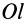
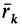
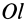
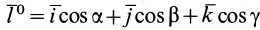
Умножая в (21) 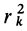
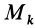
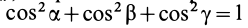
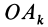
Подставляя (23) в (20) и вынося косинусы углов за знаки сумм, имеем
Учитывая, что
— моменты инерции относительно осей координат, а
— центробежные моменты инерции относительно тех же осей, получим
Для определения момента инерции 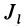
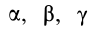

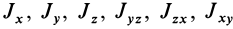
Матрица, или таблица (25), составленная из осевых и центробежных моментов инерции относительно декартовых осей координат, называется тензором инерции в точке 
Для определения момента инерции относительно какой-либо оси, проходящей через заданную точку, для рассматриваемого тела необходимо иметь тензор инерции в этой точке и углы, определяющие направление оси с осями координат.
Рис. 30
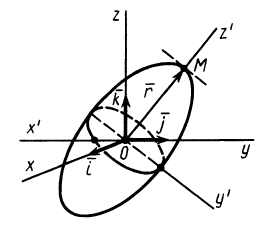
Эллипсоид инерции
Для характеристики распределения моментов инерции тела относительно различных осей, проходящих через заданную точку, используется поверхность второго порядка — эллипсоид инерции. Для построения этой поверхности на каждой оси 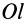

Геометрическое место концов отрезков 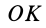
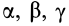
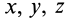
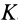
Подставляя эти значения косинусов углов в (24) и сокращая на 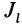
Это действительно уравнение эллипсоида, так как отрезок 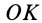

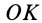
Для каждой точки 
В случае эллипсоида вращения все прямые, расположенные в экваториальной плоскости эллипсоида, перпендикулярной оси вращения, будут главными осями инерции. Для шара любая прямая, проходящая через его центр, есть главная ось инерции.
Моменты инерции относительно главных осей инерции называются главными моментами инерции, а относительно главных центральных осей инерции — главными центральными моментами инерции.
Если уравнение эллипсоида инерции отнести к его главным осям 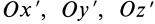
где 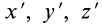
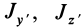
Справедливо и обратное утверждение: если центробежные моменты инерции относительно трех взаимно перпендикулярных осей равны нулю, то эти оси являются главными осями инерции. Обращение в нуль трех центробежных моментов инерции является необходимым и достаточным условием того, что соответствующие прямоугольные оси координат есть главные оси инерции.
Главные моменты инерции часто обозначают 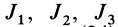
- Заказать решение задач по теоретической механике
Свойства главных осей инерции
Теорема 1. Если одна из декартовых осей координат, например 

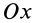
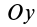

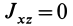
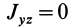
Главная ось инерции 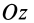
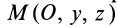
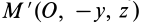
Вычитая из первого уравнения второе, имеем
Так как всегда можно выбрать точки, для которых 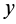
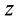
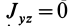
Рис. 31
Аналогичные рассуждения для двух симметричных относительно оси 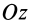
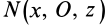
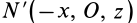
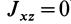
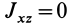
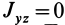

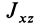
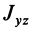


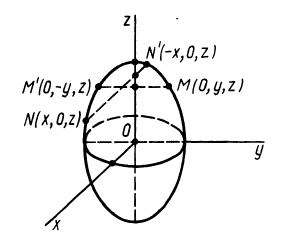
Теорема 2. Если однородное тело имеет плоскость симметрии, то для любой точки, лежащей в этой плоскости, одна из главных осей инерции перпендикулярна плоскости симметрии, а две другие главные оси инерции расположены в этой плоскости.
Рис. 32
Для доказательства теоремы выберем в плоскости симметрии 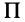

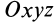

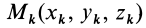
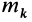
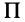
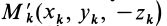
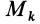
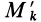
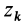
Для центробежного момента инерции 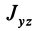
так как часть тела (I), соответствующая точкам с положительными координатами 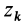
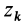
Так как центробежные моменты инерции 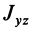
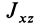



Центр масс однородного симметричного тела находится в плоскости симметрии. Поэтому одна из главных центральных осей инерции перпендикулярна плоскости симметрии, а две другие расположены в этой плоскости.
Доказанная теорема справедлива и для неоднородного тела, имеющего плоскость материальной симметрии.
Теорема 3. Если однородное тело имеет ось симметрии или неоднородное тело имеет ось материальной симметрии, то эта ось является главной центральной осью инерции.
Теорема доказывается аналогично предыдущей. Для каждой точки тела 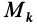
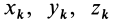
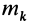
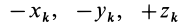

так как суммы по симметричным относительно оси частям тела (I) и (II) отличаются друг от друга только знаком у координаты 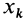
Аналогично доказывается, что 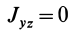
Таким образом, ось 
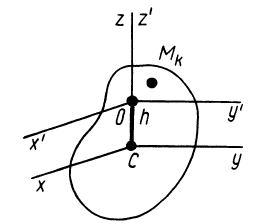
Теорема 4. Главные оси инерции для точки 
Выберем в точке 
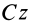
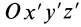
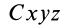
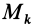
где 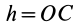
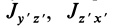
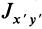
так как
где 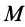
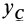
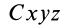
Если 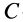
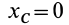
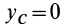
Используя полученные формулы при этих условиях, имеем:
Рис. 33
Следовательно, оси 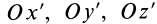
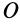
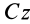
Из доказанной теоремы в качестве следствия получаем: главная центральная ось инерции является главной осью инерции для всех своих точек. Действительно, главная ось инерции 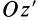
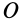
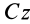
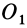
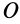
Определение главных моментов инерции и направления главных осей
Пусть известны компоненты тензора инерции в точке 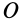
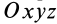
Если оси координат 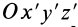
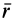
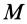
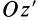
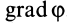
Параллельные векторы отличаются друг от друга скалярным множителем, который обозначим 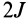
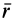
Рис. 34
В этих уравнениях 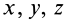
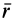
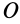
Для частных производных из (27′) получаем:
Подставляя их значения в (28′) и перенося все слагаемые в левую часть, после объединения и сокращения на общий множитель получим следующую систему уравнений для определения координат 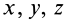
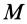
Так как (29) является однородной системой линейных уравнений, то отличные от нуля решения для координат 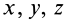
Это кубическое уравнение для определения 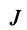
В общем случае имеется три различных действительных корня кубического уравнения 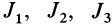
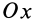
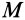
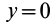
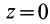
Так как 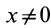
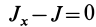
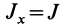
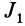
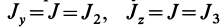
Подставляя в (29) 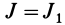
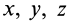
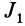
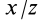
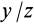
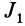
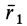
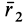
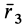
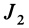
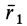
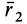
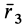
Таким образом, если известен тензор инерции для осей 
Выражение компонентов тензора инерции через главные моменты инерции
Определим компоненты тензора инерции в точке 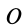

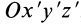
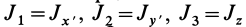

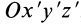
Осевые моменты инерции относительно осей 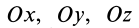
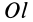
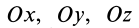
Для выражения центробежных моментов инерции через главные моменты инерции используем формулы преобразования координат точек тела при повороте осей координат вокруг точки 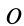

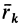
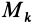
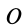
где 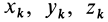
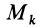
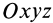
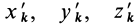
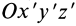
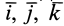
Рис. 35
Используя (33) для центробежного момента инерции 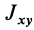
так как центробежные моменты инерции относительно главных осей инерции равны нулю, т. е.
Оси координат 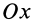
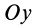
или
Используя это соотношение для исключения величины 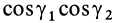
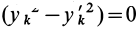
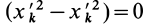
где
— главные моменты инерции. Аналогично получаются выражения для 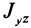
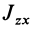
Формулы (31) и (35) дают выражения всех компонентов тензора инерции для осей координат 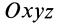
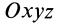
Если ось 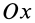
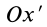
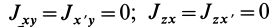
Из (35) имеем
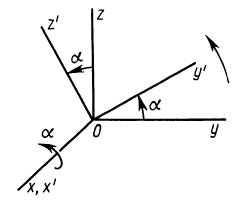
В формуле (35′) с полюсом следует брать главный момент инерции с индексом той оси, на положительное направление которой указывает дуговая стрелка поворота осей 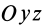
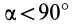
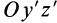
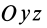
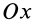
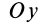
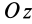
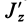
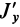
Рис. 36
Если оси расположены, как показано на рис. 37, то дуговая стрелка поворота осей 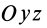
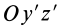
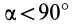
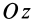
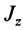
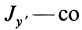
= 90°; р2 = а; Р3 = 90° + а;
Рис. 37
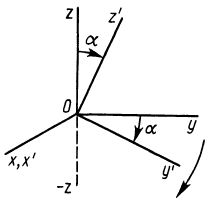
Аналогично при совпадении осей 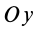
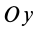
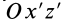
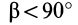
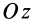
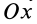
При совпадении осей 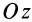
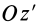
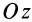
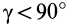
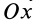
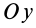
- Свойства внутренних сил системы
- Дифференциальное уравнение движения системы
- Теоремы об изменении количества движения и о движении центра масс
- Теорема об изменении кинетического момента
- Прямолинейное движение точки
- Криволинейное движение материальной точки
- Движение несвободной материальной точки
- Относительное движение материальной точки
Сразу хочу сказать, что здесь никакой воды про центр инерции системы, и только нужная информация. Для того чтобы лучше понимать что такое
центр инерции системы , настоятельно рекомендую прочитать все из категории Физические основы механики.
. Об этом говорит сайт https://intellect.icu
В рассматриваемом выше уравнении Ньютона предполагалось, что тело имеет настолько малые размеры, что его можно считать материальной точкой. Движение любого недеформируемого тела конечных размеров может быть описано уравнениями, аналогичными (3.6), если ввести понятие «центра масс» («центра инерции») тела. Если тело состоит из n материальных точек с массами 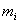
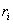
 |
(3.7) |
где 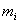
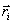
Соответственно соотношения между декартовыми координатами центра инерции и всех точек системы имеют вид:
Скорость центра инерции:
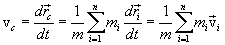 |
(3.8) |
Импульс системы. Геометрическую сумму импульсов всех материальных точек системы называют импульсом системы и обозначают буквой 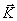
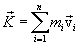
тогда скорость центра масс
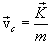 |
(3.9) |
Таким образом, из (3.9) следует, что импульс системы равен произведению массы всей системы на скорость ее центра инерции:
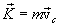 |
(3.10) |
Статью про центр инерции системы я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое центр инерции системы
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Физические основы механики
Из статьи мы узнали кратко, но емко про центр инерции системы