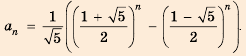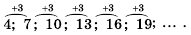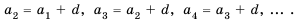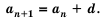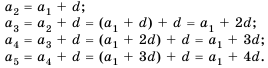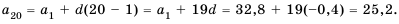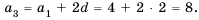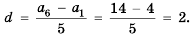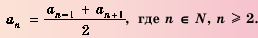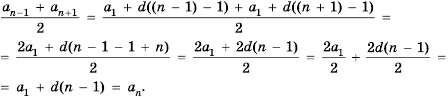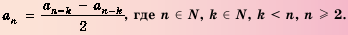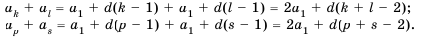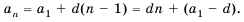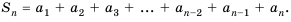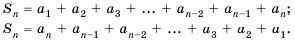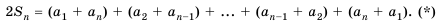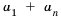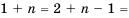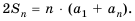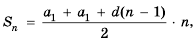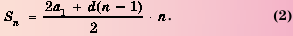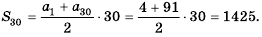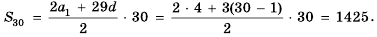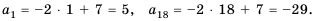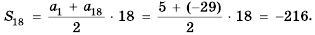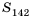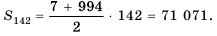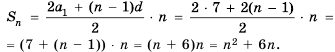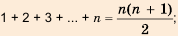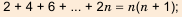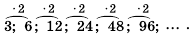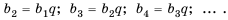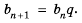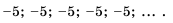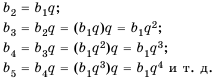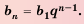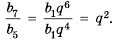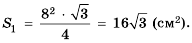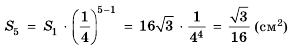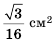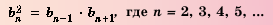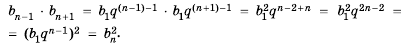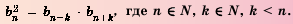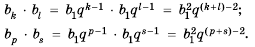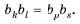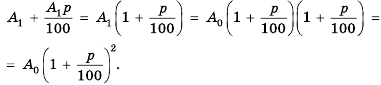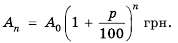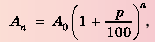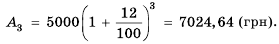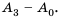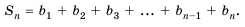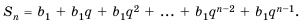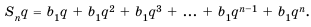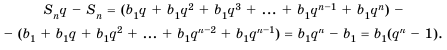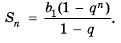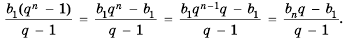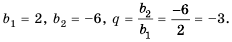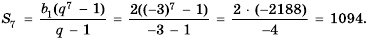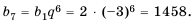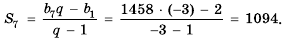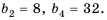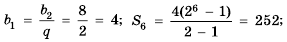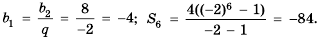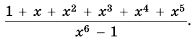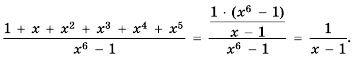По просьбам читателей возобновляем рубрику «Математика для чайников». Говорим о числовых последовательностях и вычислении их пределов. Выясняем, чем последовательность отличается от простого набора чисел и как ее можно задать.
Нужно больше полезной и интересной информации? Этого добра много не бывает! Присоединяйтесь к нам в телеграм.
Последовательности чисел
Мы сталкиваемся с последовательностями чисел каждый день. Вот только встреча с последовательностями на экзамене может быть не самой приятной.
Чтобы было иначе, читаем эту статью, а если что-то непонятно, смело обращаемся к нашим консультантам за помощью.
Одна из самых интересных и известных последовательностей – числа Фибоначчи. Эта последовательность имеет удивительные свойства и часто встречается в природе. Например, семечки у подсолнуха упорядочены в две спирали. Числа, обозначающие количество семечек в каждой из них, являются членами последовательности Фибоначчи.
Что такое числовая последовательность?
Последовательность – это набор элементов множества, который удовлетворяет следующим условиям:
- для каждого натурального числа существует элемент данного множества;
- это число является номером элемента и обозначает позицию данного элемента в последовательности;
- для любого элемента последовательности можно указать следующий за ним элемент.
Числовая последовательность – это функция переменной n, которая принадлежит множеству натуральных чисел N.
Существованием функции, по которой можно вычислить любой член последовательности, она и отличается от случайного набора чисел.
На словах звучит громоздко и сложно. Но на то это и математика, чтобы записывать все буквами и числами. Обычно последовательность обозначают буквой x, хотя можно применять и другие.
Какие бывают последовательности
Различают:
- постоянную, или монотонную последовательность: 1, 1, 1, 1, 1…
- возрастающую последовательность, в которой каждый следующий элемент больше предыдущего
- убывающую последовательность, в которой каждый следующий элемент меньше предыдущего
Также последовательности делятся на сходящиеся и расходящиеся. Сходящаяся последовательность имеет конечный предел. А предел расходящейся последовательности равен бесконечности, либо последовательность вообще не имеет предела. Но о пределах немного позже.
Рассмотрим самые известные примеры последовательностей. Еще со школы всем знакомы арифметическая и геометрическая прогрессии.
Арифметическая прогрессия
Посмотрим на числа:
Что у них общего? Они все нечетные и каждое следующее можно получить из предыдущего, прибавляя к нему одно и то же число. Назовем его d. В данном случае d=2.
Описанная выше последовательность – арифметическая прогрессия. Приведем основные формулы для нее:
Элемент a с номером n называется общим членом последовательности. А число d – разностью афифметической прогрессии.
Сумма первых n членов прогрессии вычисляется по формуле:
Также африфметическая прогрессия обладает характреристическим свойством:
Геометрическая прогрессия
Геометрической прогрессией называется последовательность чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число q – знаменатель прогрессии. Элементы геометрической прогрессии задаются соотношением:
Основные формулы для геометрической прогрессии приведены ниже. Формула n-го члена прогрессии:
Сумма первых n членов прогрессии:
Характеристическое свойство геометрической прогрессии:
Способы задания последовательностей
Последовательность можно задать несколькими способами:
- Аналитически или, проще говоря, формулой.
- Реккурентно. Здесь известно несколько первых членов прогрессии и есть формула, которая позволяет вычислить последующие.
- Описательно, простым перечислением всех элементов последовательности.
Предел последовательности
Мы уже говорили о пределах функций и способах их вычисления. Из определения последовательности следует, что последовательность – это и есть некоторая функция. Так что, вычисление пределов последовательностей будет во многом схоже с вычислением пределов функций. Правда, со своими особенностями.
Предел последовательности – это такой объект, к которому стремятся члены последовательности с ростом порядкового номера n.
Скажем иначе. Это число, в окрестности которого лежат все члены последовательности, начиная с некоторого.
Переменная n в последовательностях всегда стремится к бесконечности, в сторону увеличения натуральных чисел.
Что нужно помнить, вычисляя пределы последовательностей
Кстати! Также полезно помнить, что для всех наших читателей сейчас действует скидка 10% на любой вид работы.
- Последовательность может иметь только один предел.
- Если последовательность имеет предел, то она ограничена. Обратное верно не всегда!
- Если члены некоторой последовательности zn заключены между соответствующими членами двух последовательностей xn, yn, сходящихся к одному пределу, то и эта последовательность сходится к тому же пределу.
- Предел постоянной последовательности равен ее постоянному.
- Если две последовательности x и y равны между собой, то пределы этих последовательностей также равны между собой, если они существуют.
- Если каждый член сходящейся последовательности не превосходит соответствующего члена другой сходящейся последовательности, то и предел первой не превосходит предела второй.
- Предел суммы (разности) двух последовательностей равен сумме (разности) их пределов. При условии, что обе последовательности имеют пределы.
- Предел произведения двух последовательностей, имеющих пределы, существует и равен произведению пределов последовательностей.
- Постоянный множитель можно выносить за знак предела.
- Предел частного двух последовательностей, имеющих пределы, равен частному пределов этих последовательностей, если предел знаменателя не равен нулю.
Для проверки своих решений при вычислении пределов не обязательно нести работу на проверку преподавателю. Достаточно воспользоваться онлайн калькулятором.
Тема последовательностей разрабатывалась многими математиками на протяжении веков. Охватить ее в одной статье просто невозможно. Здесь мы дали лишь поверхностное представление. Если у вас есть вопросы или нужна консультация – обращайтесь к специалистам студенческого сервиса, которые помогут быстро прийти к понимаю.
Содержание:
Числовые последовательности
Термин «последовательность» используют, когда говорят о расположении учеников в шеренге, очередности дней недели, расположении команд в турнирной таблице и т. п. В этом параграфе мы выясним, что такое числовая последовательность, в частности, что такое арифметическая и геометрическая прогрессии, каковы их свойства, научимся использовать свойства упомянутых прогрессий при решении прикладных задач.
- 1; 1; 2; 3; 5; 8;… — последовательность
- 2; 5; 8; 11; 14;… — арифметическая прогрессия (каждое число, начиная со второго, на 3 больше предыдущего)
- 2; 6; 18:54; 162:. . — геометрическая прогрессия (каждое число, начиная со второго, в три раза больше предыдущего)
Рассмотрим несколько примеров.
Пример:
Один подсолнух за лето «выпивает» в среднем 250 л воды. Сколько воды «выпьют» за лето 1 ,2 ,3 ,4 ,5 подсолнухов?
Решение:
Во второй строке получили несколько чисел, записанных в определенном порядке, говорят, получим последовательность чисел: 250; 500; 750: 1000; 1250, в которой на первом месте стоит число 250, на втором — 500, на пятом — 1250. В этом примере каждому натуральному числу от 1 до 5 включительно соответствует одного число из указанной последовательности. Итак, имеем функцию, областью определения которой является множество чисел 1.2.3.4.5.
Пример:
3аписать в порядке возрастания натуральные числа запись которых оканчивается цифрой 2.
Решение:
Получим последовательность чисел 2; 12; 22; 32; 42; …. в которой на первом месте стоит число 2, на втором — 12. на третьем — 22 и т. д.
В этом примере каждому натуральному числу 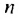
Определение:
Последовательностью называют функцию, заданную на множестве всех или первых 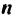
Числа образующие последовательность. называют членами последовательности. Если последовательность имеет конечное число членов, тогда ее называют конечной последовательностью (пример 1). Если последовательность имеет бесконечное число членов, то ее называют бесконечной последовательностью (пример 2), а в записи это показывают многоточием после последнего записанною члена последовательности.
Приведем еще примеры последовательностей:
- 4; 8; 12; 16;… — последовательность натуральных чисел, кратных 4;
— последовательность правильных дробей с числителем 1;
- -1: -2 ; -3 ; -4 ;… — последовательность отрицательных целых чисел;
- 0.1; 1.1; 2.1: 3,1 — последовательность, состоящая из четырех членов;
- 7 :7 ; 7 :7 :… — последовательность, все члены которой равны 7.
- Четвертая последовательность конечная, остальные — бесконечные.
В общем случае члены последовательности, как правило, обозначают маленькими буквами с индексами внизу. Каждый индекс указывает порядковый номер члена последовательности. Например, первый член последовательности обозначают 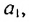
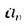
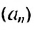
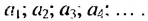
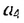
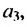
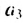
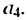
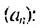
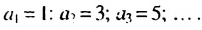
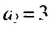
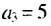
Способы задании последовательностей
Чтобы задать последовательность, нужно указать способ, при помощи которого можно найти любой ее член. Существуют различные способы задания последовательностей.
1. Последовательность можно задать описанием способа определения ее членов. Например, пусть задана последовательность, членами которой являются делители числа 15, записанные в порядке возрастания. Эту последовательность, описанную словами, можно записать так; 1 ; 3; 5: 15.
2. Конечную последовательность можно задать, перечислив ее члены. Например,
3. Последовательность можно задать таблицей, в которой напротив каждого члена последовательности указывают его порядковый номер. Например.
4. Последовательность можно задать формулой, по которой можно найти любой член последовательности, зная его номер. Например, последовательность натуральных чисел, кратных 3, можно задать формулой 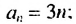
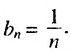
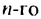
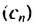
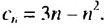
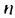
Поэтому 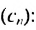
5. Последовательность можно задать так: сначала указать первый или несколько первых членов последовательности, а потом — условие, по которому можно определить любой член последовательности, зная предыдущие. Такой способ задания последовательности называют рекуррентным. Например, найдем несколько членов последовательности 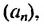
Условия, определяющие эту последовательность, можно записать так: 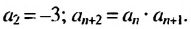
Рассмотренные выше последовательности являются числовыми последовательностями, так как их элементами являются числа. Существуют и другие последовательности. Например, последовательность передач на канале телевидения, последовательность футбольных команд в турнирной таблице и т. п.
В дальнейшем будем рассматривать только числовые последовательности.
Пример:
Записать шесть первых членов последовательности натуральных чисел, которые при делении на 3 дают остаток 2.
Решение:
Первым натуральным числом, которое при делении па 3 дает остаток 2, является число 2. Следующим является число 5 — оно на 3 больше 2, дальше 8 — на 3 больше 5 и т. д. Поэтому получим: 2; 5; 8; I I ; 14; 17.
Ответ. 2 ;5 ;8 ; 11; 14; 17
Пример:
Записать формулу 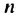
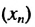
Решение:
Первым натуральным числом, которое больше 8 и при делении на 9 дает остаток 7, является число 16. Его можно записать так: 16 = 9 •1 + 7 . Вторым будет число 25, которое можно записать гак: 25 = 9 • 2 + 7, третьим — 34 = 9 • 3 + 7 и т. д. Тогда формула 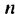
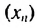
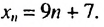
Пример:
Последовательность задана формулой 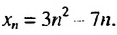
Решение:
Число 6 будет членом этой последовательности, если найдется такой номер 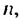
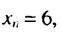
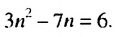
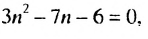
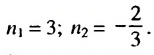
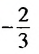
Ответ. Да.
Пример:
Записать три первых члена последовательности 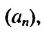
Решение:
При 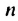
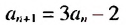
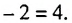
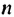
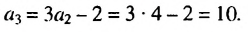
Арифметическая прогрессия и ее свойства
Среди числовых последовательностей важную роль играют последовательности, которые называют арифметической и геометрической прогрессиями.
Пример:
Группа туристов поднималась на гору в течение 4 ч. За первый час туристы прошли 2,5 км, а та каждый следующий — на 0,5 км меньше, чем за предыдущий. Какой путь проходили туристы за каждый час движения?
Решение:
За первый час туристы прошли 2.5 км. за второй — 2,5 — 0,5 = 2 (км), за третий — 2 — 0,5 = 1,5 (км), за четвертый — 1 км. Получили конечную последовательность чисел: 2,5; 2; 1,5; 1, в которой каждый последующий член, начиная со второю, равен предыдущему, сложенному с одним и тем же числом -0.5.
Пример:
3аписать последовательность натуральных чисел, которые при делении на 3 дают остаток 1.
Решение:
Получим: 1;4 ;7 ; 10; 13; 16; 19; 22 ;…. В этой последовательности любой член, начиная со второго, равен предыдущему, сложенному с одним и тем же числом 3. Каждая из рассмотренных последовательностей является примером арифметической прогрессии.
Определение:
Арифметической прогрессией называют последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом.
Это число называют разностью арифметической прогрессии и обозначают буквой d (d — начальная буква латинского слова differentia — разность). Итак, если имеется арифметическая прогрессия 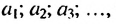
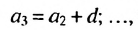
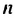
Из определения арифметической прогрессии следует, что разность между любым ее членом, начиная со второго, и предыдущим членом равна одному и тому же числу — разности d, то есть 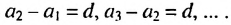
Верно и наоборот: если в некоторой числовой последовательности разность между любым ее членом, начиная со второго, и предыдущим членом равна одному и тому же числу, то такая последовательность является арифметической прогрессией.
Арифметические прогрессии могут быть конечными (пример 1) и бесконечными (пример 2).
Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность. Тогда каждый последующий член можно вычислить по предыдущему по рекуррентной формуле 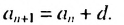
Рассмотрим свойства арифметической прогрессии.
1. В арифметической прогрессии 1; 3; 5: 7; 9 ;… каждый член, начиная со второго, является средним арифметическим двух соседних с ним членов:
Покажем, что такое свойство имеет любая арифметическая прогрессия. Пусть имеется арифметическая прогрессия 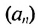
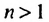
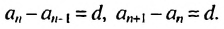
Свойство 1. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух соседних с ним членов. С этим свойством арифметической прогрессии и связано ее название.
2. Рассмотрим конечную арифметическую прогрессию 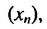
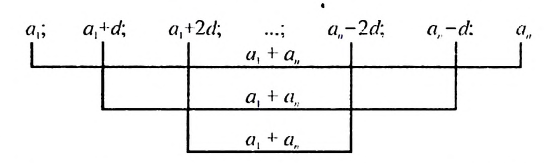
Сумма любых двух членов арифметической прогрессии, равноотстоящих от ее крайних членов, равна сумме крайних членов.
Используем эти соображения для произвольной конечной арифметической прогрессии 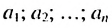
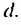
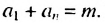
Свойство 2. Сумма любых двух членов конечной арифметической прогрессии, равноотстоящих от ее крайних членов, равна сумме крайних членов этой прогрессии.
Пример:
Найти разность и третий член арифметической прогрессии
Решение:
В этой прогрессии 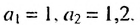
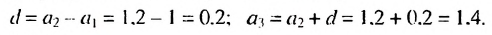
Пример:
Является ли последовательность чисел 3: 0: -3 : -6 ; -9 арифметической прогрессией?
Решение:
Обозначим члены заданной последовательности:
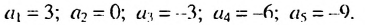
Так как полученные разности равны одному и тому же числу — 3, то эта последовательность является арифметической прогрессией.
Пример:
Между числами 7 и 15 вставить такое число, чтобы все три числа образовали арифметическую прогрессию.
Решение:
Пусть 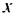
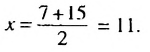
Формула n-го члена арифметической прогрессии
Чтобы задать арифметическую прогрессию, достаточно указать ее первый член и разность, а последующие члены можно найти по формуле
Например, найдем несколько первых членов арифметической прогрессии, в которой 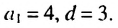
Далее можно найти 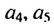
Чтобы найти член этой прогрессии с большим порядковым номером, например, 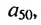
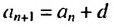
По определению арифметической прогрессии получим:
Замечаем, что в этих формулах коэффициент при d на 1 меньше порядкового номера искомого члена прогрессии. Так, 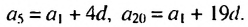
Полученную формулу называют формулой 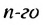
Пример:
Найти девятый член арифметической прогрессии
Решение:
Имеем: 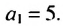
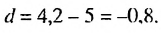
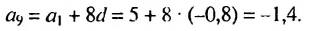
Пример:
Найти первый член арифметической прогрессии 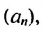
Решение:
Используя формулу 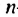
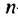
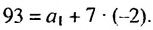
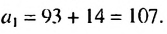
Пример:
Является ли число 181 членом арифметической прогрессии, в которой
Решение:
Число 181 будет членом прогрессии, если существует такое натуральное число 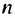
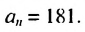
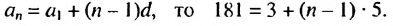
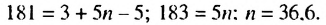
Пример:
Найти первый член и разность арифметической прогрессии 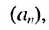
Решение:
По условию имеем: 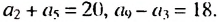
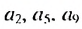
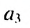
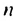
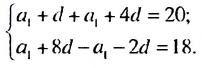
Ответ. 2.5;3 .
Формула суммы первых п членов арифметической прогрессии
Пример:
Найти сумму натуральных чисел от 1 до 100 включительно.
Решение:
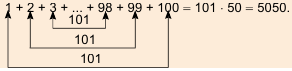
Запишем суму 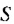
Суммы пар чисел, расположенных друг под другом в правых частях этих равенств, равны одному и тому же числу 101; таких нар 100. Поэтому
Отсюда
Итак, сумма всех натуральных чисел от 1 до 100 включительно равна 5050. Отметим, что последовательность натуральных чисел I; 2; …; 99: 100 является арифметической прогрессией 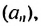
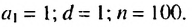
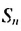
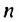
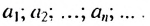
Сложим почленно эта равенства, получим:
По свойству 2 арифметической прогрессии сумма каждых двух членов, взятых в скобки, равна 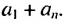
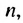
Отсюда
Если в этой формуле вместо 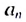
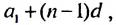
Итак,
Формулы (1) и (2) называют формулами суммы первых 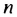
Пример:
Найти сумму первых девяти членов арифметической прогрессии
Решение:
1-й способ. Имеем: 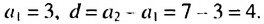
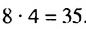
2-й способ. Зная, что 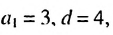
Ответ. 171.
Пример:
Найти сумму нечетных натуральных чисел, не превышающих 71.
Решение:
Нечетные натуральные числа образуют арифметическую прогрессию 1; 3: 5;……. в которой 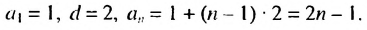
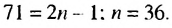
Ответ. 1296.
Пример:
Найти сумму натуральных чисел не больше 105, которые при делении на 9 дают остаток 1.
Решение:
Натуральные числа, которые при делении на 9 дают остаток 1, образуют арифметическую прогрессию 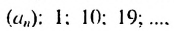
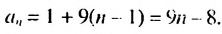
Следовательно, нужно искать сумму первых двенадцати членов прогрессии. Имеем: 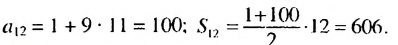
Пример:
Найти первый член арифметической прогрессии 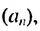
Решение:
По условию имеем: 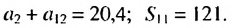
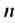
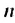
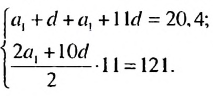
Ответ. 15.
Пример:
Сколько нужно взять первых членов арифметическом прогрессии 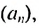
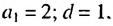
Решение:
Используя формулу суммы первых 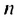
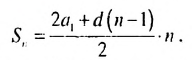
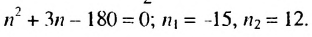
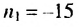
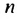
Геометрическая прогрессия и ее свойства
В благоприятных условиях некоторые бактерии размножаются так, что их количество удваивайся каждые 30 минут. Поэтому, если первоначально была одна бактерия, то их будет:
- через 0,5 ч 2
- через I ч 4
- через 1,5 ч 8
- через 2 ч 16
- …………………..
Во втором столбце получили последовательность чисел: 2: 4; 8; 16; каждый член которой, начиная со второго, равен предыдущему, умноженному на число 2. Такая последовательность является примером геометрической прогрессии.
Определение:
Геометрической прогрессией называют последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число.
Это число называют знаменателем геометрической прогрессии и обозначают буквой q (начальная буква французского слова qwoti — частное). Итак, если имеем геометрическую прогрессию 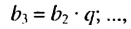
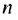
Из определения геометрической прогрессии следует, что частное от деления любого ее члена, начиная со второго, на предыдущий член равно одному и тому же числу — знаменателю то есть: 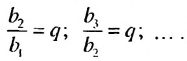
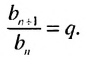
Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель. Тогда каждый последующий член по предыдущему можно вычислить по рекуррентной формуле
В таблице прицелены примеры геометрических прогрессий для некоторых значений
Рассмотрим свойства геометрической прогрессии.
1. В геометрической прогрессии 1; 3: 9, 27; 81;… квадрат каждого члена, начиная со второго, равен произведению двух соседних с ним членов:
Покажем, что такое свойство имеет любая геометрическая прогрессия. Пусть имеется геометрическая прогрессия 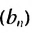
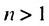
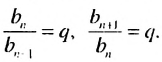
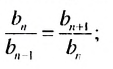
Свойство 1
Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних с ним членов.
Если все члены геометрической прогрсссии являются положительными числами, то из равенства 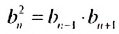
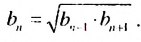
2. Рассмотрим конечную геометрическую прогрессию 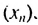
Видим, что произведения членов профессии, равноотстоящих от ее крайних членов, одинаковы и равны произведению крайних членов.
Используем эти соображения для произвольной конечной геометрической прогрессии 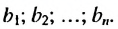
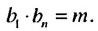
Свойство 2
Произведение любых двух членов конечной геометрической прогрессии, равноотстоящих от ее крайних членов, равно произведению крайних членов.
Пример:
Найти знаменатель и третий член геометрической npoгpеcсии
Решение:
В этой прогрессии 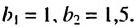
Ответ. 1,5; 2,25.
Пример:
Доказать, что последовательность 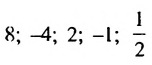
Решение:
Обозначим члены последовательности: 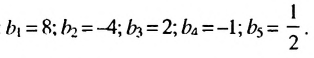
Так как полученные частные равны одному и тому же числу 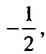
Пример:
Найти второй член геометрической прогрессии:
Решение:
Согласно свойству 1 геометрической прогрессии 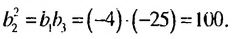
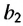
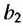
Формула n-го члена геометрической прогрессии
Чтобы задать геометричсскую прогрессию 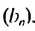
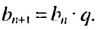
Далее можно найти 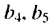
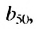
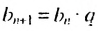
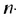
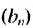
Замечаем, что в этих формулах показатель степени числа q на единицу меньше порядкового номера искомого члена прогрессии. Так, 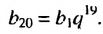
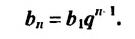
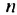
Пример:
Найти шестой член геометрической прогрессии
Решение:
Имеем: 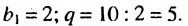
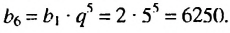
Пример:
Найти первый член геометрической прогрессии 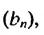
Решение:
Используя формулу 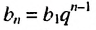
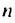
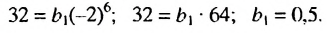
Пример:
Найти знаменатель геометрической прогрессии 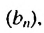
Решение:
Используя формулу 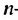
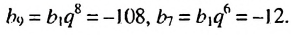
Ответ. -3 или 3.
Формула суммы первых n членов геометрической прогрессии
Пусть 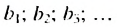
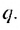
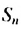
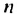
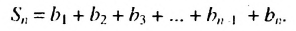
Умножив обе части этого равенства на q получим:
Пo определению геометрической прогрессии: 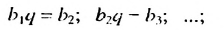
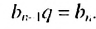
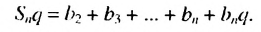
Вычтем почленно из равенства (1) равенство (2), получим:
Если 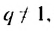
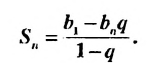
Учитывая, что 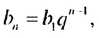
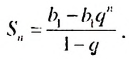
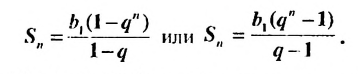
Формулы (3) и (4) называют формулами суммы первых 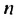
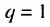
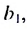
Пример:
Найти сумму восьми первых членов геометрической прогрессии
Решение:
Имеем : 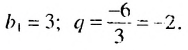
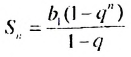
Ответ. -255.
Пример:
Найти первый член геометрической прогрессии 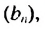
Решение:
Так как 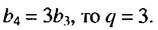
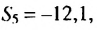
Ответ. -0,1.
Сумма бесконечной геометрической прогрессии, в которой [q] меньше 1
Сумма бесконечной геометрической прогрессии, в которой
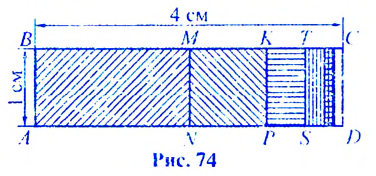
Пусть стороны прямоугольника 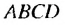
Найдем площадь этою прямоугольника иначе. Отрезком MN. соединяющим середины противоположных сторон ВС и 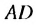
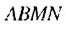
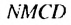
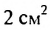
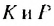
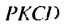
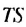
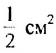
Найдем сумму площадей прямоугольников 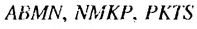
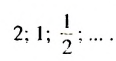
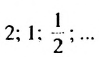
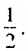
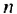
Если число 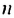
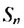
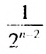
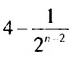
Итак, сумма площадей прямоугольников ABMN, NMKP, PKTS и т. д. равна 4 см2, то есть равна площади прямоугольника ABCD. Обобщим рассмотренный пример. Пусть 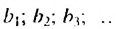
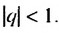
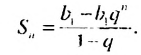
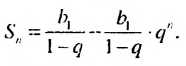
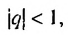
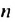
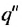
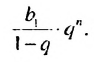
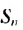
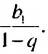
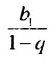
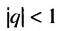
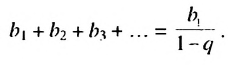
Полученную формулу называют формулой суммы бесконечной геометрической прогрессии, в которой
Пример:
Найти сумму бесконечной геометрической прогрессии 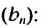
Решение:
По условию 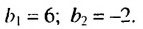
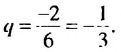
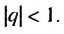
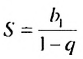
Ответ. 4,5.
Решение задач, связанных с арифметической и геометрической прогрессиями
Вычисление сумм
Изучая арифметическую и геометрическую прогрессии, мы вычисляли суммы первых 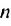
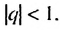
Пример 1. Найти сумму
Решение:
Обозначим эту сумму через 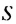
В первых скобках записана сумма членов арифметической прогрессии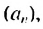
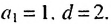
Итак, в первых скобках записана сумма первых семи членов арифметической прогрессии. Во вторых скобках записана сумма первых семи членов геометрической прогрессии 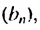
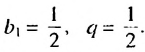
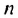
Ответ:
Обращение бесконечных периодических десятичных дробей в обыкновенную дробь
Рассмотрим пример.
Пример:
Записать число 0,(7) в виде обыкновенной дроби.
Решение:
Бесконечную десятичную дробь 0,(7) = 0,777… запишем в виде такой суммы: 0,(7) = 0.7 + 0,07 + 0,007 + …. Слагаемые 0,7; 0,07; 0.007;… — члены бесконечной геометрической прогрессии с первым членом 0,7 и знаменателем 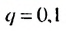
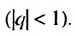
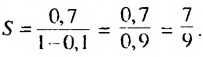
Ответ:
Решение уравнении
Рассмотрим пример.
Пример:
Решить уравнение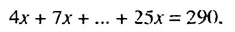
Решение:
Запишем уравнение так:
В скобках записана сумма первых членов арифметической прогрессии. в которой 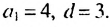
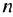
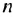
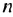
Итак, в скобках записана сумма первых 8 членов арифметической прогрессии. Тогда получим:
Ответ. 2,5.
Пример:
Записать число 3.1(23) в виде обыкновенной дроби.
Решение:
Число 3.1(23) = 3,12323… запишем в виде такой суммы:
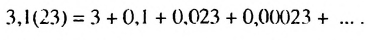
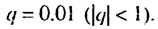
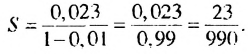
Ответ:
Пример:
Решить уравнение:
Решение:
Запишем уравнение в виде:
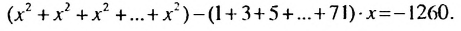
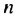
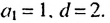
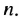
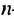
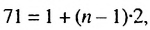
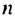
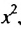
Ответ. 1; 35.
Пример:
Найти сумму
Решение:
Обозначим данную сумму через S. Записав слагаемые в виде 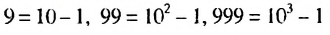
В скобках записана сумма первых 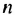
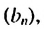
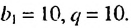
Ответ.
ИНТЕРЕСНО ЗНАТЬ
Слово «прогрессия» происходит от латинского слона «prcigrcssio» и значит «движение вперед» (как и слово «прогресс»). Впервые этот термин встречается в работах римского ученого Боэция (V -V I в.). Прогрессии как частные виды числовых последовательностей встречаются в папирусах II тысячелетия до н. э. Первые задачи на прогрессии, дошедшие до нас, связаны с хозяйственной деятельностью, а именно — с распределением продуктов, разделом наследства и т. п. Древнейшей задачей на прогрессии считают задачу из египетского папируса Ахмеса Райнда о распределении 100 мер хлеба между пятью людьми так, чтобы второй получил на столько больше первого, на сколько третий получил больше второго и т. д. В этой задаче речь идет об арифметической прогрессии, сумма первых пяти членов которой равна 100. В одной из задач этого папируса представлена формула первого члена арифметической прогрессии, которую в современной символике записывают так:
где а — первый член, 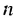
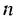
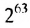
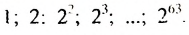
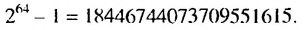
————
Числовые последовательности
♦ Множество чисел в котором каждое число имеет свой номер 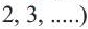
♦ Числа, образующие последовательность, называются соответственно первым, вторым, третьим, четвертым и т.д. членами последовательности. Члены последовательности, обычно обозначаются буквами, индекс буквы показывает порядковый номер члена. Например, первый член 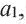
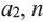
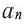
♦ Последовательности бывают конечные и бесконечные. Например, множество двузначных чисел может быть примером конечной последовательности. А последовательность натуральных чисел — бесконечна.
♦ Обычно последовательность задают с помощью формулы определящей функцию 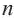
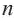
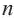
Например: 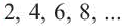
Наблюдается взаимосвязь многих природных явлений с последовательностью Фибоначчи.
Фибоначчи родился в итальянском городе Пиза: Его произведение «Книга вычислений» (Liber Abaci) оказала огромное влияние на распространение математических знаний в Европе, служила учебником — справочником европейских ученых. Особенно неоценима его роль в быстром распространении в Европе индийско-арабской десятичной системы. В то время в Европе при записи и вычислениях пользовались Римскими цифрами. В этом произведении Фибоначчи также уделил большое внимание задаче о размножении кроликов, которая дает последовательность чисел 1,1, 2, 3, 5, 8, 13, 21,… Для членов этого ряда (при 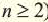
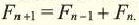
Рекуррентный и экспилитический способы задания последовательности
Формула, выражающая любой член последовательности, начиная с некоторого, через один или несколько предыдущих членов называется рекуррентной формулой, (от латинского слова recirro — возвращаться). Например, в последовательности 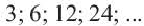
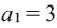
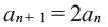
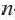
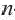
Например,
Арифметическая прогрессия, рекуррентное правило
Определение. Числовая последовательность, в которой каждый член, начиная со второго равен предыдущему, сложенному с одним и тем же для данной последовательности числом называется арифметической прогрессией. То есть арифметическая прогрессия — это такая последовательность, в которой 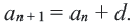
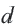
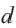
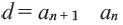
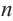
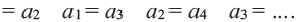
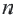
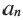
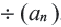
Пример 1. Определите, какие из последовательностей являются арифметической прогрессией.
а) 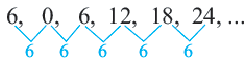
b) 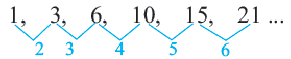
Разность арифметической прогрессии может быть положительным, отрицательным числом или нулем. При 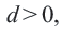
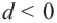
Пример 2. а) При 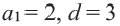
b) При условии 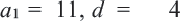
При 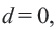
Формула n-го члена арифметической прогрессии
Каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же для данной последовательности числом. Согласно этому правилу:
По этому правилу можно записать:
Формула 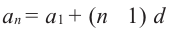
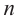
Пример 1. В арифметической прогрессии 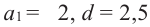
Отметим, что 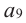
Вообще, 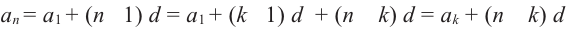
Отсюда, получаем формулу для разности прогресии:
Пример 2. В арифметической прогрессии
Решение:
Замечание. Переписав формулу 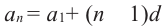
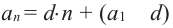
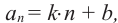
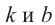
Арифметическая прогрессия и среднее арифметическое
Свойство. Любой член арифметической прогрессии, начиная со второго, равен среднему арифметическому соседних с ним членов.
Действительно, из 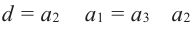
Так как в общем случае, 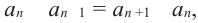
Это свойство можно обобщить таким образом. Каждый член арифметической прогрессии (начиная со второго) равен среднему арифметическому равноудаленных от него членов:
Это свойство поясняет причину названия арифметической прогрессии. Верно и обратное. Если любой член последовательности, начиная со второго, равен среднему арифметическому предыдущего и последующего членов, то эта последовательность является арифметической прогрессией.
В конечной арифметической прогрессии сумма членов, расположенных на одинаковом расстоянии от концов, равна сумме крайних членов.
В общем, если
Сумма n-первых членов арифметической прогрессии
Обозначим через 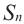
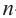
Попарные суммы 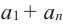
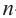
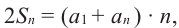
Сумма 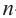
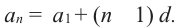
Пример 1. Найдите сумму 12-ти первых членов арифметической прогрессии заданной формулой 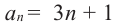
Решение:
Пример 2. Найдите сумму 10-ти первых членов арифметической прогрессии 3; 5; 13;… .
Решение.
Пример 3. В зале заседаний 30 рядов. В первом ряду 24 места, а в каждом следующем ряду на одно место больше, чем в предыдущем. Сколько всего мест в зале?
Решение:
В последнем ряду: 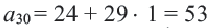
Пример 4. Сколько членов арифметической прогрессии 5; 7; 9… нужно сложить, чтобы получить 320 ?
Решение:
Так как количество членов не может быть отрицательным, то сумма 16-ти первых членов этой прогрессии равна 320. Перепишем сумму первых 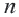
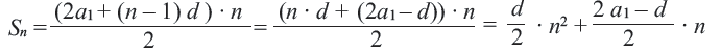
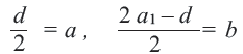
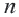
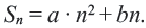
Пример 5. Найдем первый член и разность арифметической прогрессии, сумма 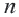
Решение:
Внимание! При решении некоторых задач для определения 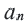
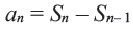
Члены геометрической прогрессии, рекуррентное правило
Определение. Геометрической прогрессией называется числовая последовательность, члены которой отличны от нуля, а каждый член, начиная со второго, равен предыдущего члену, умноженному на одно и то же, не равное нулю, число. То есть если для любого натурального числа 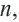
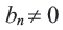
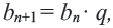
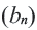
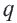
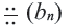
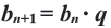
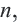
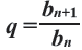
Пример 1. а) Если 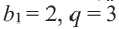
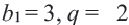
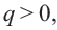
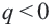
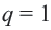
Пример 2. Какая из данных числовых последовательностей геометрическая прогрессия?
а) 4, 12, 22, 34, 48; b) 625, 125, 25, 5, 1.
Отношение каждого члена геометрической прогрессии на предыдущий всегда остается постоянной. Проверим это условие для обеих прогрессий.
а)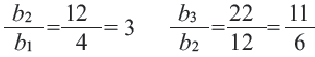
b)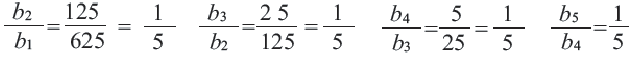
Формула n-го члена геометрической прогрессии
Вообще, чтобы в геометрической прогрессии найти 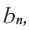
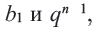
Это выражение называется формулой 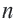
Пример 1. Если в геометрической прогрессии 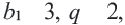
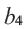
Указание. Можно было бы вычислить следующем способом
Вообще, справедливо равенство,
Пример 2. Найдем 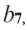
Решение: 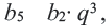
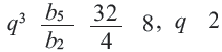
Заключение: Если известны какие-либо два члена, то можно задать геометрическую прогрессию, 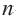
Если перемножить почленно эти 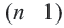
Сократив одинаковые члены в левой и правой частях, получим формулу
Заключение: Записав 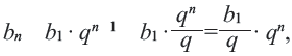
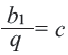
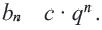
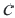
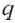
Члены геометрической прогрессии и среднее геометрическое
В геометрической профессии с положительными членами, начиная со второго, каждый член равен среднему геометрическому соседних с ним членов. Это свойство поясняет причину названия геометрической прогрессии. Например, в последовательности, 2, 6, 18, 54, 162,… число 18 является средним геометрическим 6 и 54. Среднее геометрическое-можно ясно увидеть, записывая отношения, выражающие знаменатель профессии. Из определения геометрической прогрессии получатся равенства:

Взяв попарно эти равенства, получим: 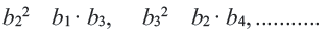
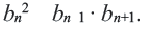
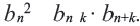
Еще одно свойство членов геометрической профессии: Если 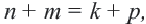
Сумма n-первых членов геометрической прогрессии
Обозначим через 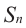
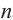
При 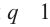
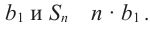
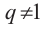
Умножим обе части (1 )-го равенства на 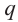
Отнимем от (2)-го равенства (1)-е. Получим:
Отсюда S
(3)-я формула называется формулой 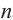
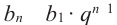
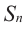
Пример. В геометрической прогрессии 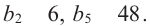
Решение. 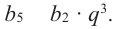
Из формулы 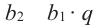
Тогда
Сумма бесконечной геометрической прогрессии при
Если число членов геометрической прогрессии бесконечно, то ее называют бесконечной геометрической профессией. Преобразуем формулу суммы 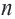
Если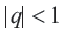
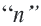
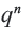
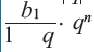
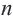
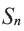
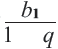
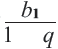
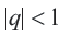
Если обозначить эту сумму через 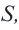
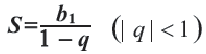
Пример. Примените формулу суммы бесконечной геометрической профессии в преобразовании периодической дроби 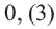
Так как 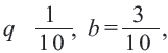
Геометрические преобразования. Движение
Параллельный перенос
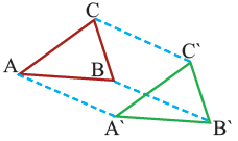
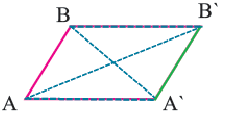
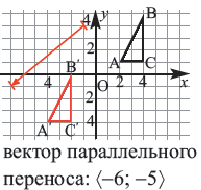
При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и тоже расстояние и фигура переходит в фигуру конгруэнтную себе. Треугольник 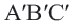
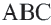
В координатной плоскости каждая точка данного треугольника 
Применяя формулу расстояния между двумя точками, получим: 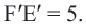
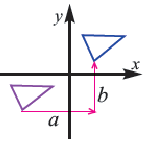
При параллельном переносе фигуры произвольная точка 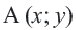
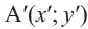
На координатной плоскости при параллельном переносе перемещение по осям координат направо и наверх выражаегся положительными, налево и вниз отрицательными единицами. Это определяется числами 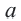
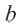
Действительно, при параллельном переносе произвольные точки 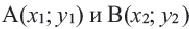
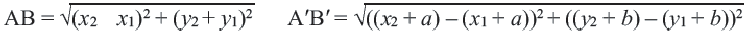
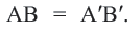
Координаты середины отрезка
Координаты середины отрезка 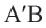
Значит, диагонали четырехугольника 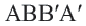
- Заказать решение задач по высшей математике
Параллельный перенос и векторы
Каждый параллельный перенос определяет один вектор. То есть при параллельном переносе перемещение всех точек фигуры выполняется по одному вектору. Выражение параллельного переноса вектором упрощает запись. Компоненты вектора 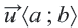
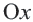
На картине изображен параллельный перенос 
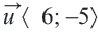
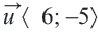
Длина вектора
Движение и конгруэнтные фигуры
Пусть каждой точке фигуры 
Теорема. При движении отрезок преобразуется в отрезок.
Доказательство. Пусть при движении концы отрезка 
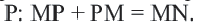
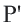
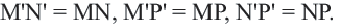
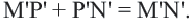
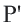
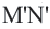
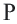
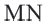
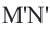
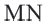
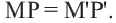
Следствие. При движении каждая сторона треугольника переходит в конгруэнтный отрезок, и поэтому по признаку 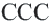
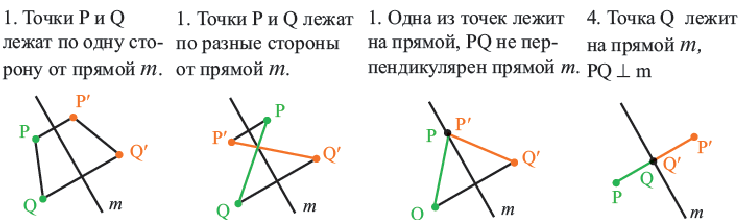
Теорема. Осевая симметрия (отражение) есть движение.
На рисунке изображено отражение отрезка 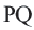
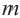
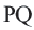
Докажем теорему для первого случая:
Текстовое доказательство
В этом случае точки 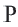
Из определения отражения следует, что, так как отрезок 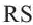
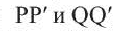
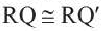
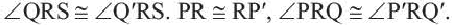
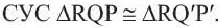
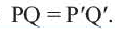
——
Числовые последовательности
В этой лекции вы:
Пример №356
Запишем в порядке возрастания четные натуральные числа: 2; 4; 6; 8; 10; … .
Получим последовательность четных натуральных чисел. На первом месте в ней число 2, на втором — число 4, на пятом — 10. Если и далее записывать четные натуральные числа, то, например, на десятом месте окажется число 20, на сотом — число 200. Вообще, для любого натурального числа 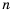
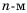
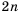
Числа, образующие последовательность, называют соответственно первым, вторым, третьим, четвертым и т. д. членами последовательности. Члены последовательности принято обозначать буквами с индексами, указывающими порядковый номер члена последовательности. Например: 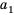
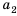
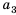
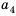
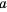
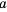
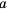
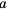
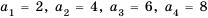
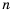
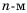
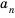
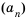
Рассмотрим два соседних члена последовательности с номерами 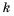
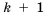
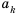
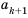
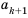
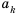
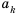
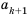
Поскольку в последовательности четных натуральных чисел на 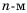
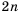
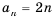

Эта последовательность содержит бесконечное число членов. Такую последовательность называют бесконечной. В записи бесконечной последовательности после перечисления нескольких ее первых членов ставят многоточие. Если же последовательность содержит конечное число членов, то ее называют конечной.
Пример №357
Последовательность двузначных натуральных чисел 10; 11; 12; …; 98; 99 является конечной. Она содержит 90 членов и может быть задана формулой 
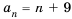
Зная формулу 
Пример №358
Последовательность задана формулой 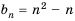
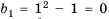
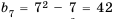
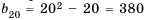
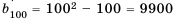
Формула 
Пример №359
Конечную последовательность можно задать перечислением ее членов. Например, 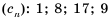
Пример №360
Последовательность можно задать описанием ее членов. Например, последовательность натуральных делителей числа 18, записанных в порядке возрастания, выглядит так: 1; 2; 3; 6; 9; 18.
Пример №361
Конечную последовательность можно задать и в виде таблицы. Например:
Последовательность можно задавать, указав первый или несколько первых членов последовательности, а затем — формулу, позволяющую найти остальные члены последовательности через предыдущие. Такую формулу называют рекуррентной, а способ задания последовательности — рекуррентным.
Пример №362
Пусть первый член последовательности 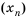
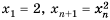
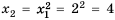
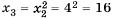
Получим последовательность: 2; 4; 16; 256; 65 536; … .
Пример №363
Найдем третий, четвертый и пятый члены последовательности 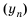
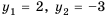
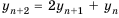
Получим:
Последовательности, рассмотренные выше, являются числовыми последовательностями, так как состоят из чисел. Иногда рассматривают последовательности, членами которых являются выражения, функции и т. п. В дальнейшем будем рассматривать только числовые последовательности.

- 1, 2, 3, 4, 5,… — последовательность натуральных чисел;
- 2, 4, 6, 8, 10,… — последовательность четных чисел;
- 1, 3, 5, 7, 9,… — последовательность нечетных чисел;
- 1,4,9,16,25,… — последовательность квадратов натуральных чисел;
- 2, 3, 5, 7, 11,… — последовательность простых чисел;
— последовательность чисел, обратных натуральным.
Для всех этих последовательностей, кроме пятой, можно записать формулу 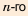
Одной из наиболее известных является числовая последовательность, которую называют последовательностью Фибоначчи в честь итальянца Л. Пизанского (Фибоначчи) (ок. 1170 — ок. 1250). Он первым рассмотрел последовательность чисел, два первых члена которой — единицы и каждый член которой, начиная с третьего, равен сумме двух предыдущих:
1; 1; 2; 3; 5; 8; 13; 21; 34; 55; 89; 144 ….
Лишь несколько веков спустя была найдена формула 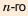
Арифметическая прогрессия, ее свойства. формула n-го члена арифметической прогрессии
Рассмотрим числовую последовательность, первый член которой равен 4, а каждый следующий, начиная со второго, равен предыдущему, сложенному с числом 3:
Такую последовательность называют арифметической прогрессией.
Последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом, называют арифметической прогрессией.
Это число называют разностью арифметической прогрессии и обозначают буквой 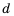
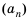
Таким образом, для любого натурального 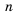
Тогда: 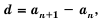
разность арифметической прогрессии можно найти, если от любого члена прогрессии, начиная со второго, отнять предыдущий.
Пусть первый член арифметической прогрессии равен 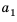
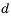
Заметим, что в каждой из полученных формул коэффициент у разности 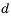
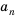
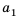
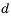

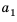
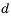
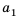
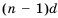
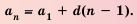

Рассмотрим несколько примеров применения этой формулы.
Пример №364
Последовательность 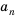
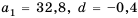
Решение:
Ответ. 25,2.
Пример №365
Принадлежит ли арифметической прогрессии 7; 10; 13; … число: 1) 82; 2) 102?
Решение:
В данной прогрессии 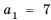
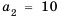
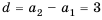

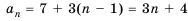
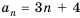
1) Допустим, число 82 является членом прогрессии 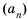
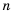
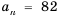
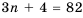
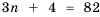
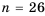
Следовательно, число 82 является двадцать шестым членом арифметической прогрессии, то есть 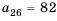
2) Рассуждая аналогично, имеем: 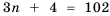
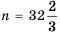
Полученное число 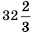
Ответ. 1) Да; 2) нет.
Пример №366
Кубики сложены рядами так, что в верхнем ряду 4 кубика, а в каждом следующем ниже ряду — на одно и то же количество кубиков больше, чем в предыдущем. Известно, что в шестом ряду 14 кубиков. Сколько кубиков в третьем ряду?
Решение:
Так как в каждом следующем ряду на одно и то же количество кубиков больше, чем в предыдущем, то числа, равные количеству кубиков в рядах, образуют арифметическую прогрессию, в которой 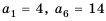
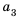
Для начала найдем разность 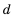
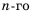
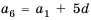
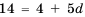
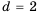
Теперь, зная значение 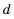
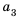
Следовательно, в третьем ряду 8 кубиков.
Заметим, что найти 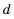
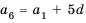
Ответ. 8 кубиков.
Докажем несколько важных свойств арифметической прогрессии.
1. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух соседних с ним членов, то есть
Доказательство: Используем формулу 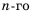
По одной из версий именно с этим свойством арифметической прогрессии связано ее название.
2. Любой член арифметической прогрессии, начиная со второго, является средним арифметическим двух равноудаленных от него членов, то есть
Свойство доказывается аналогично предыдущему свойству.
3. Если 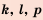
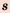
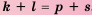

Доказательство: Используем формулу 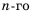
Но 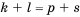
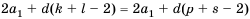
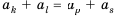
4. Любую арифметическую прогрессию можно задать формулой 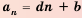
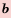
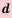
Доказательство: По формуле 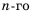
Обозначив 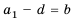
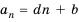
5. Последовательность 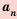
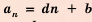
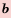
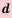
Доказательство: Рассмотрим разность 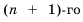
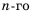
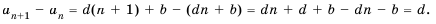
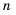
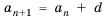
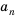
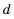


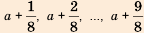
Задачи на арифметические прогрессии есть и в древнекитайском трактате «Математика в девяти книгах».
Первые из дошедших до нас задач на прогрессии связаны с запросами хозяйственной жизни и общественной практики, как, например, распределение продуктов, деление наследства и т. п.
У древних греков теория арифметических прогрессий была связана с так называемой непрерывной арифметической пропорцией:
Здесь числа 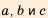
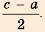
Сумма n первых членов арифметической прогрессии
Рассмотрим 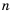
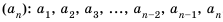
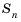
Найдем формулу для вычисления этой суммы. Запишем эту сумму дважды, разместив в первом случае слагаемые в порядке возрастания их номеров, а во втором — в порядке убывания:
Теперь сложим эти равенства почленно и получим:
Но по свойству 3 из предыдущего параграфа: 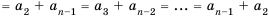
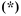
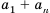

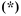
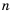
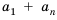
Разделив обе части этого равенства на 2, получим формулу суммы 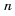
Если в формуле 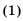
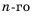
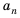
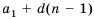
или
Получили еще одну формулу для вычисления суммы п первых членов арифметической прогрессии, которой удобно пользоваться, если известны первый член и разность прогрессии.
Применим формулы 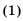
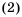
Пример №367
Найти сумму тридцати первых членов арифметической прогрессии 4; 7; 10; … .
Решение:
1-й способ. Так как 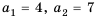
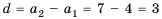
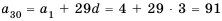
Тогда по формуле 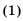
2-й способ. Так как 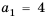
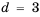
Ответ. 1425.
Пример №368
Найти сумму восемнадцати первых членов последовательности 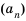
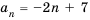
Решение:
Поскольку последовательность задана формулой 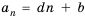
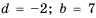
Имеем:
Найдем 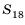
Ответ. -216.
Пример №369
Найти сумму всех натуральных чисел, кратных числу 7 и не превышающих 999.
Решение:
Натуральные числа, кратные числу 7, образуют арифметическую прогрессию: 7; 14; 21; 28; …, которую можно задать формулой 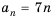
Найдем, сколько членов этой прогрессии не превышают числа 999. Для этого решим неравенство 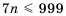
что 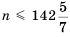
Следовательно, 142 члена прогрессии не превышают 999. Найдем их сумму, то есть
Имеем: 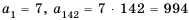
Ответ. 71 071.
Пример №370
Из двух точек, расстояние между которыми 100 м, одновременно навстречу друг другу начинают двигаться два объекта. Первый движется равномерно со скоростью 9 м/с, а второй за первую секунду проходит 7 м, а за каждую следующую на 2 м больше, чем за предыдущую. Через сколько секунд они встретятся?
Решение:
Пусть объекты встретятся через 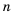
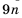
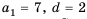
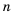
По условию 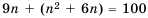
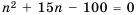
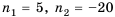
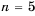
Ответ. 5 с.

1)
2)
3) 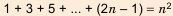
С вычислением суммы арифметической прогрессии связана интересная история, произошедшая с выдающимся немецким математиком Карлом Гауссом (1777-1855), который, еще учась в школе, проявил чрезвычайные математические способности. Однажды учитель предложил ученикам найти сумму ста первых натуральных чисел. Юный Гаусс мгновенно получил результат. Он заметил, что значения сумм 1 + 100, 2 + 99, 3 + 98, … одинаковы, а количество таких сумм равно 50:
Геометрическая прогрессия, ее свойства. формула n-го члена геометрической прогрессии
Рассмотрим числовую последовательность, первый член которой равен 3, а каждый следующий, начиная со второго, равен предыдущему, умноженному на число 2:
Такую последовательность называют геометрической прогрессией.
Геометрической прогрессией называют последовательность отличных от нуля чисел, каждое из которых, начиная со второго, равно предыдущему, умноженному на одно и то же число.
Это число называют знаменателем геометрической прогрессии и обозначают буквой 
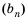
Следовательно, для любого натурального 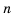
Тогда 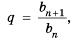
знаменатель геометрической прогрессии можно найти, ли любой член прогрессии, начиная со второго, разделить на предыдущий.
Заметим, что поскольку члены геометрической прогрессии отличны от нуля, то и знаменатель 
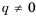
Если 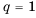
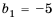
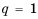
Заметим, что полученную последовательность можно также считать и арифметической прогрессией, первый член которой равен -5, а разность равна нулю.
Пусть первый член геометрической прогрессии равен 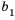

Заметим, что в каждой из полученных формул показатель степени числа 
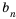
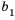


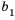

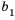
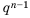
Получили формулу 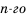
Рассмотрим несколько примеров применения этой формулы.
Пример №371
Последовательность 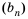
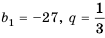
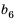
Решение:
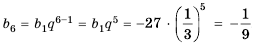
Ответ. 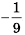
Пример №372
Найти знаменатель 
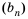
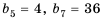
Решение:
1-й способ. 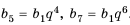
При этом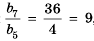
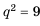
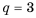
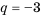
2-й способ. 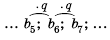
Так как 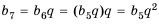
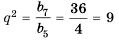
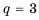
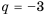
Ответ. 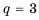
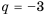
Пример №373
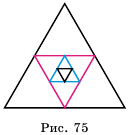
Дан равносторонний треугольник со стороной 8 см. Середины его сторон являются вершинами второго треугольника, а середины сторон второго являются вершинами третьего и т. д. (рис. 75). Найти площадь пятого треугольника, построенного по тому же принципу.
Решение:
Пусть 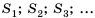
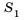
Поскольку стороны каждого следующего треугольника являются средними линиями предыдущего, то длина стороны каждого следующего треугольника будет вдвое меньше длины стороны предыдущего. Тогда сторона второго треугольника равна 4 см, а его площадь 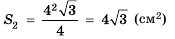
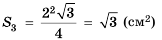
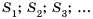
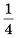
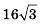
Ответ.
Докажем некоторые важные свойства геометрической прогрессии.
1. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних с ним членов, то есть
Доказательство. Воспользуемся формулой 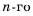
Если все члены геометрической прогрессии являются положительными числами, то 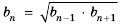
По одной из версий именно с этим свойством геометрической прогрессии и связано ее название.
2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух равноудаленных от него членов, то есть
Свойство доказывается аналогично предыдущему свойству.
3. Если 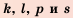

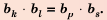
Доказательство: Воспользуемся формулой 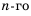
Нo 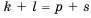
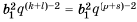

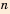
В своей работе «Псаммит» Архимед впервые сопоставил арифметическую и геометрическую прогрессии:
и указал на связь между ними, например: 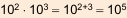
У древних греков теория геометрических прогрессий была связана с так называемой непрерывной геометрической пропорцией:
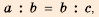
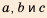
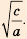
Формула сложных процентов
Бухгалтерам и работникам банков часто приходится решать задачи на проценты. Рассмотрим задачу о начислении процентного дохода. С экономической точки зрения процентный доход можно считать вознаграждением, которое платит лицо или учреждение (заемщик) за пользование в течение определенного времени определенной суммой средств, полученных от другого лица или учреждения (кредитора). Размер этого вознаграждения зависит от суммы средств и срока пользования ими.
Пример №374
Вкладчик открыл в банке депозит в размере 10 ООО грн под 11 % годовых (то есть банк обязан выплатить процентный доход в размере 11 % в год от начальной суммы вклада). Какой процентный доход получит вкладчик через год?
Решение:
11 % = 0,11, поэтому вкладчик получит 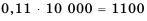
Ответ. 1100 грн.
Если вкладчик решил держать средства в банке более года, не добавляя новых средств и не забирая вложенных, то определить сумму средств на счету вкладчика через несколько лет можно с помощью формулы сложных процентов.
Пусть вкладчик положил в банк 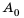
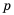
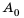
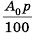
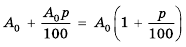
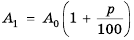
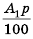
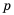
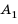
Рассуждая аналогично и применяя формулу 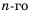
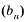
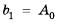
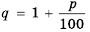
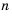
Таким образом,
начальный капитал 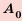
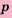
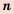
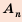
которую называют формулой сложных процентов.
Пример №375
Вкладчик открыл в банке депозит на 5000 грн под 12 % годовых. Сколько средств будет на счету вкладчика через 3 года? Какой процентный доход получит вкладчик через 3 года?
Решение:
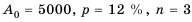
Процентный доход можно найти как разность
Таким образом, 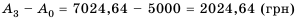
Ответ. 7024,64 грн, 2024,64 грн.
По формуле сложных процентов можно решать и другие задачи, не связанные с наращиванием капитала.
Пример №376
Население города составляет 30 000 жителей. Каждый год количество населения уменьшается на 0,2 %. Сколько жителей будет в этом городе через 10 лет?
Решение:
Так как население города ежегодно уменьшается на один и тот же процент, и это процент от количества населения каждого предыдущего года, а не от начального количества жителей, то можно воспользоваться формулой сложных процентов.
Имеем, 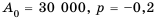
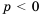
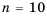
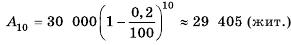
Ответ. 29 405 жителей.
Сумма n первых членов геометрической прогрессии
Рассмотрим 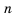
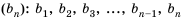
Обозначим через 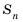
Найдем формулу для вычисления этой суммы. Имеем (учитывая формулу 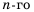
Умножим обе части этого равенства на 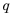
Вычтем почленно из этого равенства предыдущее:
Таким образом, 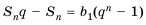
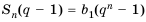
Если 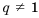
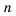
Если 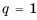
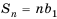
Заметим, что полученную формулу 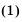
Так как 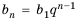
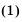
Таким образом,
Получили еще одну формулу для вычисления суммы 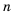
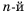
Пример №377
Найти сумму первых семи членов геометрической прогрессии 2; -6; 18; … .
Решение:
1-й способ. По условию:
Тогда по формуле 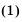
2-й способ. Известно, что 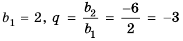
По формуле 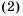
Ответ. 1094.
Пример №378
Найти сумму первых шести членов геометрической прогрессии 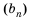
Решение:
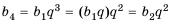
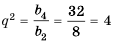
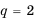
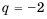
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи:
1) если 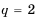
2) если 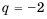
Ответ. 252 или -84.
Пример №379
Сократить дробь
Решение:
Слагаемые в числителе дроби являются последовательными членами геометрической прогрессии 1, 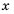
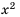
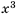
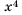
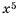
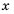
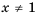
Найдем сумму всех шести членов этой прогрессии по формуле 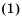
Ответ. 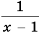

Царь удивился, что изобретатель пожелал столь мало, и приказал придворным математикам подсчитать необходимое количество зерен. Каково же было изумление царя, когда он узнал, что не сможет выдать обещанную награду, так как необходимое число зерен равно
Чтобы получить столько зерен, потребовалось бы собрать урожай с площади, в 2000 раз превышающей всю поверхность Земли. А для хранения такого урожая понадобился бы амбар, который при высоте 4 м и ширине 10 м тянулся бы на 300 000 000 км, то есть вдвое дальше, чем от Земли до Солнца.
- Предел числовой последовательности
- Предел и непрерывность числовой функции одной переменной
- Функции, их свойства и графики
- Параллельность в пространстве
- Рациональные выражения
- Квадратные корни
- Квадратные уравнения
- Неравенства
Числовой последовательностью называют ряд чисел, полученных по некоторому правилу или формуле.
Например, правило «все положительные четные числа по возрастанию начиная с двойки» задает последовательность: (2; 4; 6; 8; 10…) А правило «первое число равно (3), а каждое следующее число в два раза больше предыдущего» формирует последовательность: (3; 6; 12; 24; 48….)
Ниже разобраны несколько разных способов задания числовых последовательностей.
Числа, образующие последовательность, называются ее членами
(или элементами). И каждое из этих чисел имеет свой порядковый номер.
Например, в последовательности (3; 6; 12; 24; 48…) тройка является первым членом (порядковый номер – один), шестерка – вторым (ее номер по порядку равен двум), двенадцать – третьим и т.д.
В математике последовательность обозначают маленькой латинской буквой, а каждый отдельный ее элемент – той же буквой с числовым индексом равным порядковому номеру этого элемента.
То есть, если последовательность (3; 6; 12; 24; 48…) обозначить как (a_n), то можно записать, что (a_1=3), (a_2=6), (a_3=12), (a_4=24) и так далее.
Иными словами, для последовательности (a_n={ 3;: 6; :12; : 24; : 48; : 96; : 192; : 384…}).
|
порядковый номер элемента |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
… |
|
обозначение элемента |
(a_1) |
(a_2) |
(a_3) |
(a_4) |
(a_5) |
(a_6) |
(a_7) |
(a_8) |
… |
|
значение элемента |
(3) |
(6) |
(12) |
(24) |
(48) |
(96) |
(192) |
(384) |
… |
Отметим, что членами последовательности необязательно должны быть различные числа. Она может состоять из одних и тех же чисел, например, выглядеть вот так: (1; : 1; : 1; : 1…) .
Способы задания числовых последовательностей
Все способы формирования числовых последовательностей можно разделить на три большие группы:
— I способ: словесный. Здесь все просто – в буквальном смысле словами описывается каким образом можно вычислить элементы искомой последовательности.
Пример: Напишите первые пять членов последовательности квадратов натуральных чисел.
Решение: Натуральными называют числа, возникающие естественным образом при счете количества предметов, то есть: (1; : 2; : 3; : 4; : 5) и т.д. Нашу же последовательность формируют квадраты этих чисел, то есть (1^2;: 2^2; : 3^2; : 4^2; : 5^2…) . Таким образом, имеем ответ: (1; : 4; : 9; : 16; : 25…)
Ответ: (1; : 4; : 9; : 16; : 25…)
Отметим, что последовательности в начале статьи заданы именно словесным способом.
— II способ: аналитический (формулой энного члена). Тут значение каждого элемента последовательности вычисляется по некоторой формуле, в которую подставляется порядковый номер этого элемента.
Пример: Последовательность задана формулой: (b_n=frac{n-1}{n^2}). Вычислите первые пять членов этой последовательности.
Решение: Вычислим (b_1). Это первый член последовательности, то есть его порядковый номер (n) равен единице. Тогда его значение равно (b_1=frac{1-1}{1^2} =frac{0}{1}=0).
У второго члена (n=2), то есть его значение равно (b_2=frac{2-1}{2^2} =frac{1}{4}).
Третий ((n=3)): (b_3=frac{3-1}{3^2} =frac{2}{9}).
Четвертый ((n=4)): (b_4=frac{4-1}{4^2} =frac{3}{16}).
Пятый ((n=5)): (b_5=frac{5-1}{5^2} =frac{4}{25}) .
Готово. Можно писать ответ.
Ответ: (b_n= {0; : frac{1}{4}; : frac{2}{9}; : frac{3}{16}; : frac{4}{25}…}).
Обратите внимание, что при таком задании последовательности, значение каждого элемента зависит только от его порядкового номера. И поэтому, если нам нужно вычислить, например, пятнадцатый элемент, мы можем это сделать сразу, не вычисляя предыдущие четырнадцать.
Пример: Последовательность задана формулой: (a_n=8+5n-n^2). Вычислите (a_9).
Решение: Нужно вычислить значение девятого элемента, то есть порядковый номер (n=9). Подставляем в формулу: (a_9=8+5·9-9^2=8+45-81=-28).
Ответ: (a_9=-28).
III способ: рекуррентное соотношение. Звучит страшно, но суть проста – здесь дается начало последовательности (один или несколько первых элементов) и правило, по которому из предыдущего (или нескольких предыдущих) членов последовательности можно вычислить следующий.
Пример: Последовательность задана условиями: (c_1=4), (c_{n+1}=c_n+3). Вычислите первые пять членов этой последовательности.
Решение: Первый член нам известен: (c_1=4).
Второй мы получим, подставив в формулу вместо (n) единицу: (c_{1+1}=c_1+3)
(c_2=c_1+3=4+3=7)
Третий ((n=2)): (c_{2+1}=c_2+3 )
(c_3=c_2+3=7+3=10).
Четвертый ((n=3)): (c_{3+1}=c_3+3)
(c_4=c_3+3=10+3=13).
Пятый ((n=4)): (c_{4+1}=c_4+3)
(c_5=c_4+3=13+3=16).
Нужные пять элементов вычислены. Теперь можно записывать ответ.
Ответ: (c_n={4; : 7; : 10; : 13; : 16…}).
В этом примере мы по сути получали следующий элемент из предыдущего путем прибавления к предыдущему тройки. Логично, ведь формула (c_{n+1}=c_n+3) требовала именно этого. В ней (c_n) – это предыдущий элемент, а (c_{n+1}) – следующий за ним (ведь его номер на единицу больше).
На практике могут встречаться более сложные формулы, в которых следующий элемент вычисляется из двух, трех или даже большего количества предыдущих.
Пример: У последовательности известны первые два элемента (z_1=2;) (z_2=5). Так же известна формула следующего элемента (z_{n+2}=3z_{n+1}-z_n). Вычислите значения третьего, четвертого и пятого членов.
Решение: Слева будем писать текущую последовательность, а справа вести вычисления очередного элемента.
|
Последовательность на данный момент: |
Вычисления: |
||||||||||||
|
Так как формула дана для элемента с номером (n+2), то чтобы найти (z_3) нужно подставлять вместо (n) единицу:
|
||||||||||||
|
Теперь найдем (z_4), подставив вместо (n) двойку: (z_{2+2}=3z_{2+1}-z_2) (z_4=3z_3-z_2=3·13-5=34) |
||||||||||||
|
Наконец вычисляем (z_5), подставляя вместо (n) тройку: (z_{3+2}=3z_{3+1}-z_3) (z_5=3z_4-z_3=3·34-13=89) |
||||||||||||
|
Готово. Можно писать ответ. |
Ответ: (c_3=13); (c_4=34); (c_5=89).
Важное отличие рекуррентного способа задания последовательности от аналитического – при рекуррентном мы не можем посчитать следующий элемент, не зная предыдущих. То есть, если нам нужно вычислить, например, пятнадцатый элемент, придется сначала вычислить все, что идут до него.
Как определить является ли число элементом последовательности?
Во всех предыдущих примерах мы находили значения элементов последовательности – чему равен третий, пятый или девятый член. Иначе говоря, выясняли какое именно число стоит в последовательности на таком-то месте.
Но в практике встречается также обратная задача – значение известно и надо выяснить, есть ли оно среди элементов некоторой последовательности? А если есть, то на каком месте?
Пример (ОГЭ): Какое из чисел ниже есть среди членов последовательности (a_n=n^2-n):
а) (1) б) (3) в) (6) г) (10) ?
Решение: Из условия задачи понятно, что одно из этих чисел точно является элементом последовательности. Поэтому мы можем просто вычислять элементы по очереди, пока не найдем нужный:
(a_1=1^2-1=0) – мимо.
(a_2=2^2-2=2) – тоже не то.
(a_3=3^2-3=6) – есть!
Нужный элемент найден.
Ответ: (6).
Такой метод решения годится только если заранее известно, что элемент точно в последовательности есть. Потому что если его вдруг там нет – это можно проверять вечность, последовательность ведь бесконечна!
Поэтому в такой ситуации пользуются следующим алгоритмом:
-
Подставляют заданное число в формулу (n) -го члена вместо (a_n);
-
Решая полученное уравнение, находят неизвестное (n);
-
Если (n) – натуральное, то данное число — член последовательности.
Пример: Выяснить, является ли число (3) членом последовательности (a_n=)(frac{51+2n}{n+4}) ?
Решение:
|
(a_n=)(frac{51+2n}{n+4}) |
Если число (3) – член последовательности, то значит при некотором значении (n), формула (frac{51+2n}{n+4}) должна дать нам тройку. Найдем это (n) по алгоритму выше. |
|
(3=)(frac{51+2n}{n+4}) |
Решаем это уравнение. Умножаем левую и правую части на знаменатель ((n+4)). |
|
(3cdot (n+4)=51+2n) |
Получилось линейное уравнение. Раскрываем скобки слева. |
|
(3n+12=51+2n) |
Собираем неизвестные слева, числа справа… |
|
(3n-2n=51-12) |
…и приводим подобные слагаемые. |
|
(n=39) |
Готово. Найденное значение – это то число, которое надо подставить вместо (n) в формулу (frac{51+2n}{n+4}), чтоб получилось тройка (можете проверить это сами). Значит (39)-ый член последовательности равен трем. |
Ответ: Да, число (3) является элементом данной последовательности.
Смотри также:
Арифметическая прогрессия
Геометрическая прогрессия
На этой странице вы узнаете
- Как мы привыкаем к последовательностям на протяжение нашей жизни?
- Что такое золотое сечение?
Что значит “действовать последовательно”? Мы делаем что-то по определенным принципам, не нарушаем правила. Все наши действия будут иметь логику, которую мы сможем отследить. В математике также можно составлять числа в строгом порядке. Называться такие ряды будут последовательностями.
Понятие последовательности
Посмотрим на несколько рядов чисел и порассуждаем.
По какому принципу составлен ряд чисел 1, 2, 3, 4, 5 и т.д.? Всё просто: к каждому новому числу прибавляют единицу.
А какой принцип в ряде чисел 2, 4, 6, 8 и т.д.? Здесь к каждому новому числу прибавляют 2.
Что можно сказать про ряд 2, 4, 8, 16, 32 и т.д.? Каждое новое число умножают на 2.
Все приведенные выше ряды чисел будут называться последовательностью. Как описать ее одним термином?
Ненадолго вспомним функции чисел. Разберем функцию f(x)=x+1.
Если x = 0, то f(x) = 1.
Если x = 1, то f(x) = 2.
Если x = 2, то f(x) = 3.
Если x = 3, то f(x) = 4.
Внимательно посмотрим на значения функции: это и будет наша первая последовательность 1, 2, 3, 4, 5. Мы можем сделать вывод, что последовательность можно задать с помощью функции.
На самом деле, любая последовательность и есть функция. Теперь дадим определение.
Последовательность — функция, заданная на множестве натуральных чисел или его части.
То есть подставлять в такую функцию можно только натуральные числа.
Подробнее про функцию, ее значение, область определения и другие свойства можно прочесть в статье «Определение и график функции».
Аргумент будет обозначать порядковый номер числа в последовательности. Первое число в последовательности будет задаваться х = 1, второе число х = 2, n число как х = n.
Числа, которые образуют последовательность, — это члены последовательности. И у каждого члена последовательности есть свой порядковый номер.
Как же обозначаются члены последовательности? Не будем же мы каждый раз писать “двадцатый член последовательности” или что-то подобное?
Для членов последовательности существует свое обозначение: an, где индекс после буквы а обозначает порядковый номер члена последовательности.
Например,
- а1 — первый член последовательности,
- а20 — двадцатый член последовательности,
- а100 — сотый член последовательности и так далее.
Таким образом можно обозначить любой член последовательности.
Вспомним считалочки, которые мы использовали в играх в детстве: “Раз, два, три, четыре, пять, вышел зайчик погулять”. Первая строчка многих подобных считалочек — это последовательность натуральных чисел 1, 2, 3, 4, 5.
Дальше в школе на уроках физкультуры нас распределяют по командам, присваивая каждому свой номер. И это тоже последовательность.
Потом мы поступаем в вуз и попадаем в списки абитуриентов, тоже — в ещё одну последовательность.
Способы задания числовой последовательности
Рассмотрим, каким способами можно задать числовую последовательность.
Первый способ — это указать все члены последовательности. Однако он не всегда удобен, поскольку в последовательности может быть бесконечное количество членов.
Второй способ мы уже использовали — это задать общую формулу. Тогда можно будет найти любой член последовательности. В этом случае нужно будет подставить порядковый номер члена последовательности в формулу.
Допустим, дана последовательность an = 3n + 40, и нам нужно найти третий член последовательности. Тогда нужно подставить n = 3 в формулу:
a3 = 3 * 3 + 40 = 9 + 40 = 49.
Аналогичным способом можно будет найти любой член в данной последовательности.
Рассмотрим ещё пример. Что мы можем сказать про последовательность чисел 2, 4, 12, 32, 88 и так далее? Определенный закон здесь вывести достаточно сложно. Всё потому, что следующий член последовательности зависит от предыдущего.
Обратим внимание на третий член последовательности: 12 = 2 * 6 = 2(2 + 4). А если посмотреть на четвертый член последовательности? 32 = 2 * 16 = 2(4 + 12).
И так с каждым членом последовательности: он равен удвоенной сумме двух предыдущих членов.
Это еще один способ задания последовательности, когда используется рекуррентная формула. Ее особенность в том, что каждый член последовательности выражен с помощью предыдущих членов последовательности.
Одним из примеров такой последовательности будут числа Фибоначчи. Это последовательность, в которой первые два члена равны 1, а все следующие являются суммой двух предшествующих им.
Числа Фибоначчи выглядят так: 1, 1, 2, 3, 5, 8, 13, 21 и так далее.
Как задать их с помощью рекуррентной формулы? Допустим, мы хотим найти член an в этой последовательности. Мы знаем, что для этого нужно сложить два предыдущих члена, то есть an-1 и an-2. Вот мы и получили формулу.
an = an-1 + an-2.
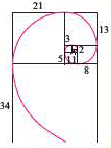
Золотое сечение — это пропорциональное деление отрезка на неравные части. При этом весь отрезок относится к большей части, как меньшая часть этого отрезка относится в большей его части.
Золотое сечение можно представить в виде “завитка”, который вписан в прямоугольник. Прямоугольник будет делиться на квадраты, стороны которых равны числам Фибоначчи.
Принципы золотого сечения позволяет построить гармоничную композицию, а значит, применяются в архитектуре и искусстве. Более того, их можно встретить в природе. Форма ракушек, завитки ростков, семена подсолнуха, шишки, даже ураган (если посмотреть на него сверху) имеют форму золотого сечения или приближенную к нему.

Виды числовых последовательностей
Возьмем обычную последовательность натуральных чисел 1, 2, 3, 4, 5, …, an. Мы можем сказать, что каждый следующий член последовательности больше, чем предыдущий. Такие последовательности называются возрастающими.
Если перевернуть ее и получить последовательность 5, 4, 3, 2, 1, …, an — последовательность будет называться убывающей. Для такой последовательности обязательно, чтобы каждый следующий член был меньше, чем предыдущий.
Что, если мы просто будем менять знак числа? Например, −1, 1, −1, 1 и так далее? Тогда последовательность будет ни убывающей и ни возрастающей.
Такую последовательность можно задать с помощью формулы an = (-1)n.
Разумеется, не все последовательности бывают бесконечными. Ранее мы рассматривали только бесконечные последовательности: в них можно было подставить любое значение n.
Возьмем последовательность простых однозначных чисел: 2, 3, 5, 7. Больше однозначных чисел нет — продолжить последовательность мы не можем.
Последовательность, в которой ограничено количество членов, будет называться конечной последовательностью. Если же в последовательности не ограничено количество членов, и их можно задавать до бесконечности, то такая последовательность будет называться бесконечной последовательностью.
Фактчек
- Последовательность — функция, заданная на множестве натуральных чисел или его части.
- Каждый член последовательности имеет свой номер, который отображается в индексе. Например, a1 — первый член последовательности, а a25 — двадцать пятый.
- Последовательность можно задать несколькими способами. Во-первых, выписать все члены последовательности. Во-вторых, задать общую формулу. В-третьих, задать рекуррентную формулу.
- Рекуррентная формула — это формула, в которой каждый следующий член последовательности зависит от предыдущих. Ярким примером такой последовательности являются числа Фибоначчи, где каждое число является суммой двух предыдущих.
- Последовательности бывают возрастающими и убывающими. В возрастающих последовательностях каждый следующий член больше предыдущего, а в убывающей каждый следующий член последовательности меньше предыдущего. В бесконечных последовательностях не ограничено количество членов. А в конечных последовательностях количество членов ограничено.
Проверь себя
Задание 1.
Выберите конечную числовую последовательность.
- Числа Фибоначчи.
- Четные положительные числа.
- Нечетные трехзначные числа.
- Нечетные отрицательные числа.
Задание 2.
Выберите убывающую последовательность.
- 10, 9, 8, 7, 6, 5, …, an
- Числа Фибоначчи
- 1, 2, 3, 4, 5, …, an
- 1, 3, 5, 7, 9, …, an
Задание 3.
Выберите возрастающую последовательность.
- 100, 90, 80, …, an
- (frac{1}{2}), (frac{1}{3}), (frac{1}{4}), …, an
- Числа Фибоначчи
- −1, −2, -3, …, an
Задание 4.
Какая последовательность является числами Фибоначчи?
- 1, 2, 3, 4, 5, …
- 1, 1, 2, 3, 5, 8, …
- 1, 4, 9, 16, 25, …
- 1, (frac{1}{2}), (frac{1}{3}), (frac{1}{4}), …
Ответы: 1. — 3 2. — 1 3. — 3 4. — 2
Последовательности. Числовые последовательности
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Понятие числовой последовательности
Введем два определения числовой последовательности:
Определение 1
Числовая функция, у которой область определения совпадает с натуральным рядом чисел, будет называться числовой последовательностью.
Определение 2
Отображения натурального ряда чисел на множество действительных чисел будет называться числовой последовательностью.
Математически это можно записать следующим образом:
$f:N→R$
Числовая последовательность обозначается следующим образом:
${p_k }={p_1,p_2,…,p_k,…}$
где $p_1,p_2,…,p_k,…$ — действительные числа.
Способы задания
Есть три различных способа для задания числовых последовательностей. Опишем их.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
-
Аналитический.
В этом способе последовательность задается в виде формулы, с помощью которой можно найти любой член этой последовательности, подставляя в нее вместо переменной натуральные числа.
Пример: $p_k=frac{k^2+2k+7}{k-6}$.
-
Рекуррентный.
Данный способ задания последовательности заключается в следующем: Дается первый (или несколько первых) член данной последовательности, а затем формула, которая связывает любой член ее с предыдущим членом или предыдущими членами.
Пример: $p_1=10,p_2=1,p_{k+1}=2p_{k-1}+p_k$.
-
Словесный.
При этом способе числовая последовательность просто описывается без введения каких-либо формул.
Пример: Последовательность абсолютных значений отрицательных чисел.
Примеры задач
Пример 1
Найти первые $5$ членов последовательности, которая задана аналитически
$p_k=frac{k^2+2k+7}{k-6}$
Решение.
Для этого нам необходимо в данное аналитическое выражение числа $1, 2, 3, 4 и 5$.
$k=1$.
$p_1=frac{1^2+2+7}{1-6}=-2$
$k=2$.
$p_2=frac{4+4+7}{2-6}=frac{-15}{4}=-3.75$
$k=3$.
$p_3=frac{9+6+7}{3-6}=frac{-22}{3}$
$k=4$.
$p_4=frac{16+8+7}{4-6}=frac{-31}{2}=-15.5$
$k=5$.
$p_5=frac{25+10+7}{5-6}=-42$
Ответ: $-2$, $-3.75$, $frac{-22}{3}$, $-15.5$, $-42$.
«Последовательности. Числовые последовательности» 👇
Пример 2
Найти первые $5$ члена последовательности, которая задана рекуррентно
$p_1=10,p_2=1,p_{k+1}=2p_{k-1}-p_k$
Решение.
Первые два члена уже даны. Найдем из рекуррентной формулы $3$ и $4$члены:
Третий член по данной формуле равен
$p_3=2p_1-p_2=20-1=19$.
Четвертый член по данной формуле равняется
$p_4=2p_2-p_3=2-19=-17$.
Пятый член по данной формуле равняется
$p_5=2p_3-p_4=38+17=55$.
Ответ: $10, 1, 19, -17, 55$.
Пример 3
Записать последовательность, которая задана словесно, рекуррентным способом и записать ее: Первые два числа равняются двум и единице, а остальные равняются произведению двух предыдущих.
Решение.
Очевидно, что
$p_1=2,p_2=1$
Условию далее, можно записать следующее рекуррентное соотношение:
$p_{k+2}=p_{k+1}cdot p_k$
Тогда последовательность имеет вид:
$2,1,2,2,4,8,32,…$
Ответ: $p_1=2,p_2=1,p_{k+2}=p_{k+1}cdot p_k$.
$2,1,2,2,4,8,32,….$
Пример 4
Записать последовательность, которая задана словесно, аналитическим способом и записать ее: Последовательность чисел, в которой натуральное число складывается с тройкой и делится на $2$.
Решение.
Обозначим произвольное натуральное число через $k$. Тогда формула аналитической записи описанной выше последовательности имеет вид:
$p_k=frac{k+3}{2}$
Тогда последовательность имеет вид:
$2,2.5,3,3.5,4,…$
Ответ: $p_k=frac{k+3}{2}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 17.06.2022

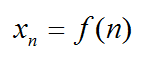
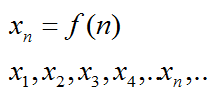
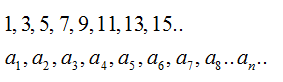
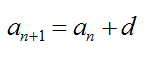
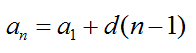
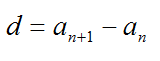
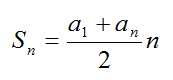

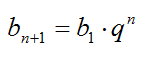
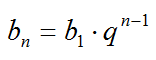
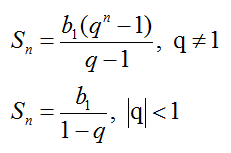
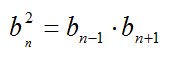


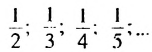 — последовательность правильных дробей с числителем 1;
— последовательность правильных дробей с числителем 1;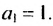
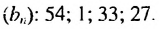

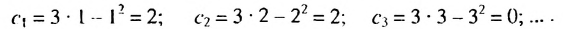
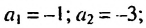
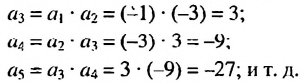
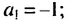
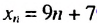
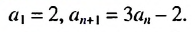
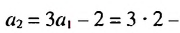
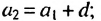
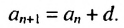
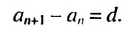
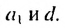

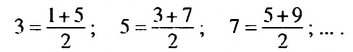
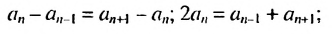
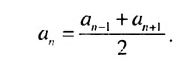
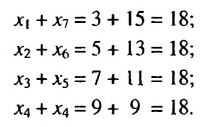
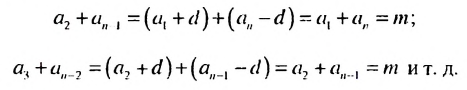
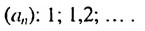
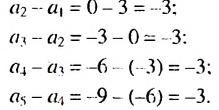
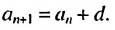
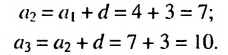
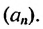
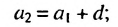
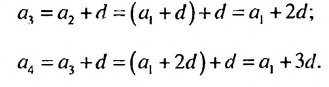
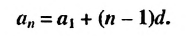
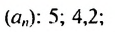
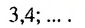
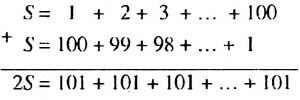
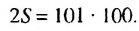
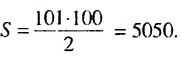
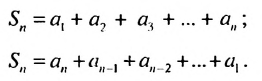
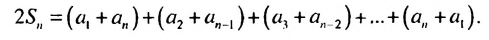
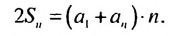

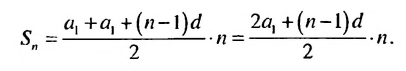
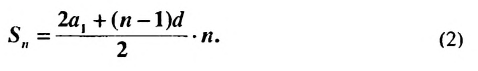
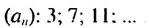
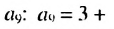
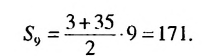
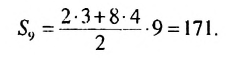
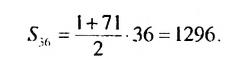
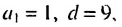
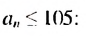
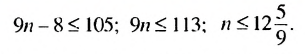
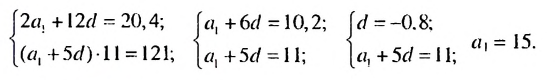
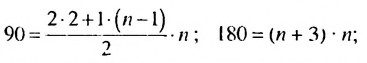
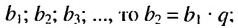
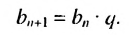
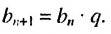
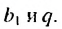

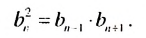
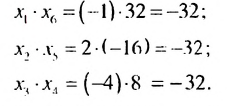
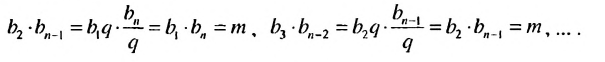
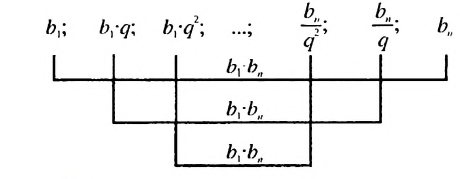
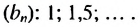
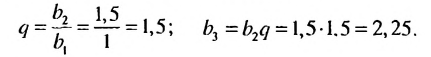
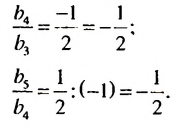
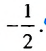
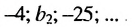
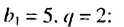
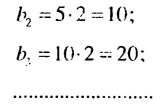
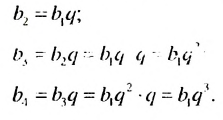
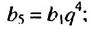
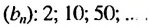
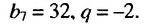
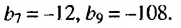
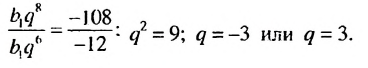
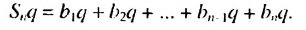
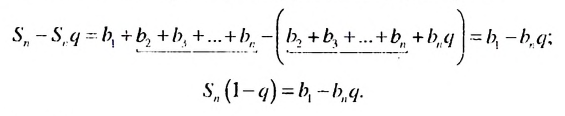
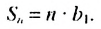
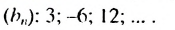
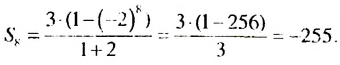
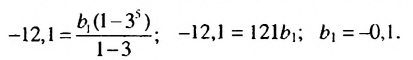
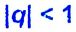
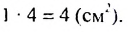
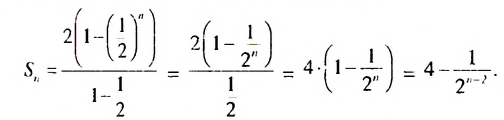
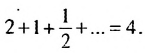
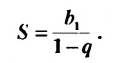
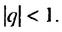
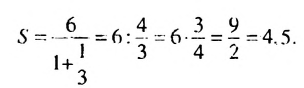
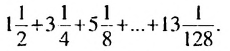
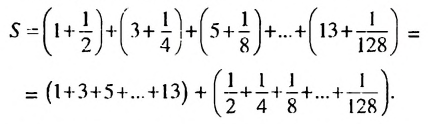
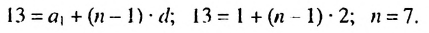
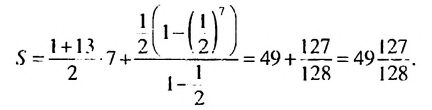
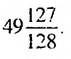
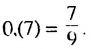
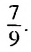
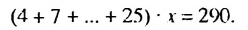
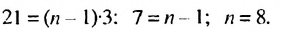
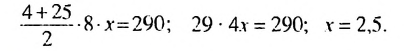
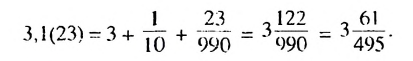
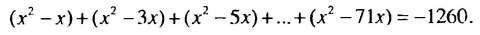
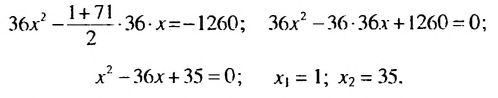
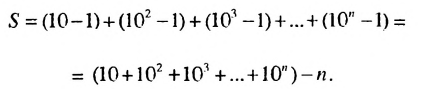
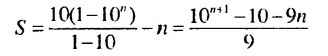
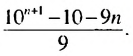
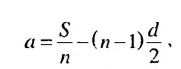
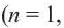
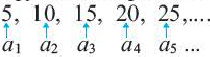
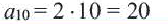

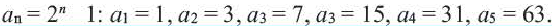
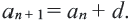
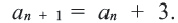
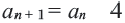
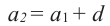
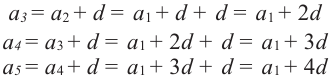
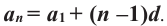
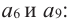
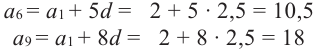
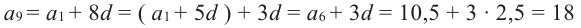
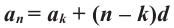
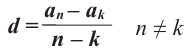
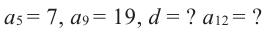
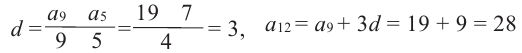
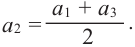
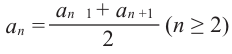
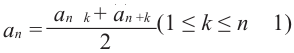
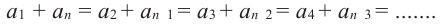
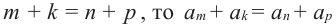
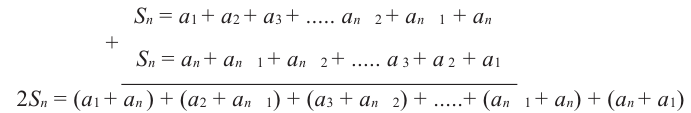
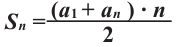
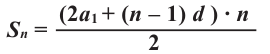

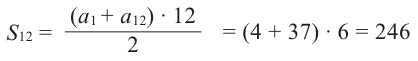
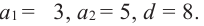
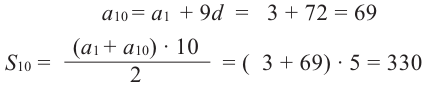
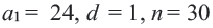
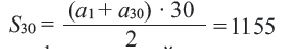
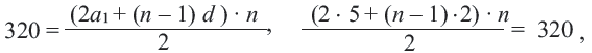
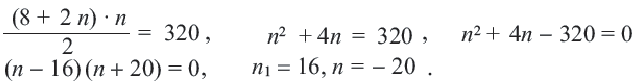
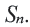
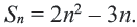
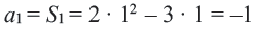
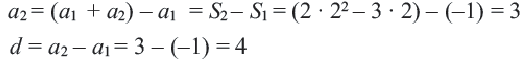
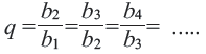
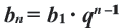

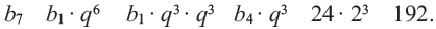
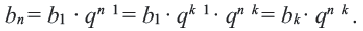
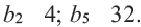
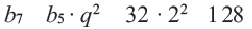
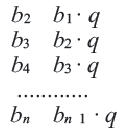
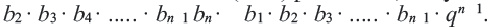
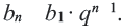

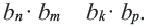
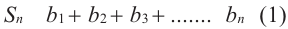
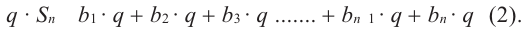
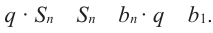
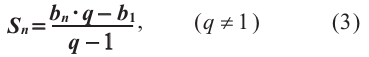
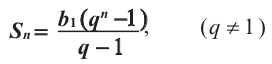
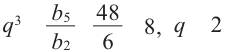
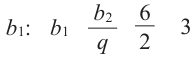
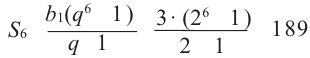

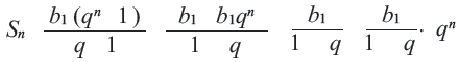

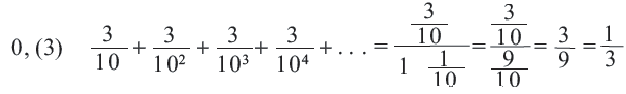
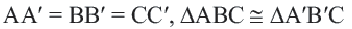
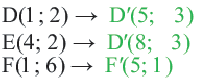
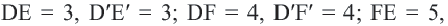

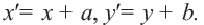
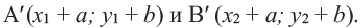
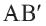
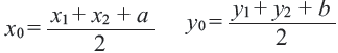
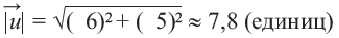

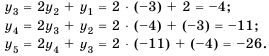
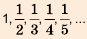 — последовательность чисел, обратных натуральным.
— последовательность чисел, обратных натуральным.