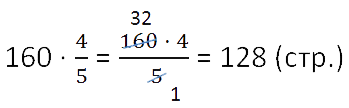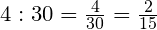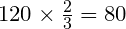Как найти часть от числа, выраженную дробь? Вычисли:
7
8
от 240 О;
5
6
от 90 Е;
9
7
от 56 Р;
17
12
от 84 С;
14% от 4000 Ж;
134% от 800 Д.
Расположив ответы примеров в порядке убывания и сопоставив им соответствующие буквы, ты узнаешь имя египетского фараона, в честь которого была построена самая первая пирамида.
reshalka.com
ГДЗ учебник по математике 4 класс Петерсон. 1 урок. Сравнение углов. Номер №10
Решение
Чтобы найти часть от числа, выраженную дробью от целого, нужно целое разделить на знаменатель этой дроби и умножить на числитель.
240 : 8 * 7 = 30 * 7 = 210 О;
90 : 6 * 5 = 15 * 5 = 75 Е;
56 : 7 * 9 = 8 * 9 = 72 Р;
84 : 12 * 17 = 7 * 17 = 119 С;
4000 : 100 * 14 = 40 * 14 = 560 Ж;
800 : 100 * 134 = 8 * 134 = 1072 Д.
1072(Д) > 560(Ж) > 210(О) > 119(С) > 75(Е) > 72(Р)
Ответ: ДЖОСЕР
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Нахождение дроби от числа
Поддержать сайт
Дроби используют в математике, чтобы кратко обозначить часть
рассматриваемой величины.
Но если есть часть, то обязательно есть и целое (то, отчего
была взята эта часть).
Зная целое, можно найти его часть, указанную соответствующей дробью.
Запомните!
Чтобы найти дробь (часть) от числа, нужно это число
умножить на данную дробь.
Пример. Рассмотрим задачу.
В книге 160 страниц. Юра прочитал
книги. Сколько страниц
прочитал Юра?
Прежде всего найдём в задаче целое. Это — вся книга и в ней всего
160 страниц.
Посмотрим на дробь (часть) от целого:
.
Знаменатель равен 5, значит, целое разделили
на 5 частей и мы можем найти сколько страниц составляет
часть.
- 160 : 5 = 32 (стр.) — составляет часть страниц.
- Числитель дроби равен 4, значит взято 4 части.
- 32 · 4 = 128 (стр.) — составляют книги.
Оба действия можно записать кратко, в соответствии с правилом нахождения части от целого.
Ответ: Юра прочитал 128 страниц.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
а) Чтобы найти дробь от числа необходимо данное число умножить на числитель искомой дроби и разделить на ее знаменатель.
16 * 5 : 8 = 10;
б) Чтобы найти процент от числа необходимо данное число умножить на искомый процент и разделить на 100.
900 * 7 : 100 = 63;
в) Чтобы найти число по его дроби необходимо данное число умножить на знаменатель и разделить на числитель известной дроби.
8 * 9 : 2 = 36;
г) Чтобы найти число по его проценту необходимо данное число умножить на 100 и разделить на известный процент.
35 * 100 : 5 = 700.
Полоску длиной (10) см разделили на (10) частей и закрасили
410
части.
Найдём длину одной части полоски:
см.
Вся закрашенная часть — в (4) раза больше:
·1= 4
см.
Длину закрашенной части можно найти более простым путём:
·4= 4
см.
Чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель дроби.
Пример:
от (20) будет
20:4
·3=15
.
от года будет
12:4
·3=9
месяцев.
от килограмма будет
1000:100
·3=30
грамм.
Задачи на дроби
- Выражение части в долях целого
- Нахождение дроби от числа
- Нахождение числа по его дроби
Выражение части в долях целого
Чтобы выразить часть в долях целого, нужно часть разделить на целое.
Задача. В классе 30 учащихся, отсутствуют четверо. Какая часть учащихся отсутствует?
Решение:
Ответ: В классе отсутствует 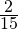
Нахождение дроби от числа
Для решения задач, в которых требуется найти часть целого справедливо следующее правило:
Если часть целого выражена дробью, то чтобы найти эту часть, можно целое разделить на знаменатель дроби и результат умножить на её числитель.
Задача 1. Было 600 рублей, 
Решение: Чтобы найти 
600 : 4 = 150 (р.).
Ответ: Истратили 150 рублей.
Задача 2. Было 1000 рублей, 
Решение: Из условия задачи мы знаем, что 1000 рублей состоит из пяти равных частей. Сначала найдём сколько рублей составляет одна пятая часть от 1000, а затем узнаем сколько рублей составляют две пятых:
1) 1000 : 5 = 200 (р.) — одна пятая часть.
2) 200 · 2 = 400 (р.) — две пятых части.
Эти два действия можно объединить:
1000 : 5 · 2 = 400 (р.).
Ответ: Было истрачено 400 рублей.
Второй способ нахождения части целого:
Чтобы найти часть целого, можно умножить целое на дробь, выражающую эту часть целого.
Задача 3. По уставу кооператива, для правомочности отчётного собрания на нём должно присутствовать не менее 
Решение:
Ответ: Отчётное собрание может состояться при наличии 80 членов организации.
Нахождение числа по его дроби
Для решения задач, в которых требуется найти целое по его части справедливо следующее правило:
Если часть искомого целого выражена дробью, то чтобы найти это целое, можно данную часть разделить на числитель дроби и результат умножить на её знаменатель.
Задача 1. Потратили 50 рублей, это составило 
Решение: Из описания задачи мы видим, что 50 рублей в 6 раз меньше первоначальной суммы, т. е. первоначальная сумма в 6 раз больше, чем 50 рублей. Чтобы найти эту сумму, надо 50 умножить на 6:
50 · 6 = 300 (р.).
Ответ: Первоначальная сумма — 300 рублей.
Задача 2. Потратили 600 рублей, это составило 
Решение: Будем считать, что искомое число состоит из трёх третьих долей. По условию две трети числа равны 600 рублей. Сначала найдём одну треть от первоначальной суммы, а затем сколько рублей составляют три третьих (первоначальная сумма):
600 : 2 · 3 = 900 (р.).
Ответ: Первоначальная сумма — 900 рублей.
Второй способ нахождения целого по его части:
Чтобы найти целое по величине выражающей его часть, можно разделить эту величину на дробь, выражающую данную часть.
Задача 3. Отрезок AB, равный 42 см, составляет 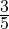
Решение:
Ответ: Длина отрезка CD 70 см.
Задача 4. В магазин привезли арбузы. До обеда магазин продал 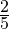
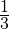
Решение: Сначала узнаем, какую часть от привезённых арбузов составляет число 80. Для этого примем за единицу общее количество привезённых арбузов и вычтем из неё то количество арбузов, которое получилось реализовать (продать):
Итак, мы узнали, что 80 арбузов составляет 

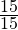
2) 80 : 4 · 15 = 300 (арбузов).
Ответ: Всего в магазин привезли 300 арбузов.