Как найти биссектрисы в остроугольном треугольнике - Autoru.top

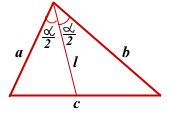
L— биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b — стороны треугольника

с — сторона на которую опущена биссектриса

d, e — отрезки полученные делением биссектрисы

γ — угол ABC , разделенный биссектрисой пополам

p — полупериметр, p=(a+b+c)/2

Длина биссектрисы через две стороны и угол, (L):

Длина биссектрисы через полупериметр и стороны, (L):

Длина биссектрисы через три стороны, (L):

Длина биссектрисы через стороны и отрезки d, e, (L):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

Подробности

Опубликовано: 06 октября 2011

Обновлено: 13 августа 2021

Источник

Все формулы биссектрисы в треугольнике

L — биссектриса, отрезок |OB|, который делит угол ABC пополам

a, b — стороны треугольника

с — сторона на которую опущена биссектриса

d, e — отрезки полученные делением биссектрисы

γ — угол ABC , разделенный биссектрисой пополам

p — полупериметр, p =(a+b+ c )/2

Длина биссектрисы через две стороны и угол, ( L ):

Длина биссектрисы через полупериметр и стороны, ( L ):

Длина биссектрисы через три стороны, ( L ):

Длина биссектрисы через стороны и отрезки d , e , ( L ):

Точка пересечения всех трех биссектрис треугольника ABC, совпадает с центром О, вписанной окружности.

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Треугольник – это геометрическая фигура, состоящая из трех точек на плоскости, которые не лежат на одной прямой, и трех последовательно соединяющих их отрезков.

Точки называют вершинами треугольника, а отрезки – сторонами. Вершины треугольника обозначают заглавными латинскими буквами.

Виды треугольников по углам

Треугольники классифицируются по углам: остроугольные; тупоугольные; прямоугольные.

Виды треугольников по сторонам

Треугольники классифицируются по сторонам: разносторонний; равнобедренный; равносторонний.

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.

В любом треугольнике можно провести три медианы, так как сторон – три. На рисунке показаны медианы треугольника АВС: AF, EC, BD.

По данному рисунку также видно, что медианы треугольника пересекаются в одной точке – точке О. Это справедливо для любого треугольника.

Биссектриса

Биссектрисой треугольника называется луч, исходящий из вершины угла треугольника и делящий его пополам.

В любом треугольнике можно провести три биссектрисы, так как углов – три. На рисунке показаны биссектрисы треугольника ЕDC: DD₁, EE₁ и CC₁.

По рисунку также видно, что биссектрисы имеют одну точку пересечения. Это справедливо для любого треугольника.

Высота

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к противоположной стороне.

На рисунке показаны высоты треугольника АВС: АН₁, ВН₂ и СН₃.

По рисунку видно, что высоты треугольника пересекаются в одной точке. Это также справедливо для любого треугольника.

Средняя линия

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.

Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. На рисунке показаны три средние линии треугольника АВС: MN, KN и MK.

Средняя линия обладает следующими свойствами: она параллельна противоположной стороне; она равна половине противоположной стороны. Так, на данном рисунке MN параллельна АС, KN параллельна АВ, MK параллельна ВС. Также MN=0,5АС, KN=0,5АВ и MK=0,5ВС. Например, если известно, что сторона АС=20 см, то средняя линия МN равна половине АС, то есть МN=10 см. Или, например, если средняя линия МК=12 см, то сторона ВС будет в два раза больше, то есть ВС=24 см.

Выполним чертеж окружности, описанной около треугольника АВС, покажем на нём все дополнительные элементы.

При построении прямой АО образовалась точка пересечения этой прямой с окружностью, обозначим её буквой Е и соединим с точкой В и с точкой С. Получим вписанные углы АВЕ и АСЕ, опирающиеся на диаметр АЕ, следовательно угол АВЕ и АСЕ равны по 90 0 .

Рассмотрим треугольники АВЕ и АВF: у них углы АВЕ и АFВ прямые, угол ЕАВ – общий, следовательно, эти треугольники подобны.

Составим отношение сторон:

A E A B . . = A B A F . . откуда по свойству пропорции АВ 2 =АЕ ∙ АF

Рассмотрим треугольники АСЕ и ADF, у которых углы АСЕ и AFD прямые, а угол FAD – общий. Значит, треугольники АСЕ и ADF подобны.

Составим отношение сторон:

A E A D . . = A C A F . . ; откуда выразим AD= A E ∙ A F А C . . = A E ∙ A F A C . .

Теперь рассмотрим наши два полученных равенства: АВ 2 =АЕ ∙ АF и AD= A E ∙ A F A C . .

Видим, что 36 2 =АЕ ∙ АF (подставили вместо АВ значение 36), также у нас известно, что АС=54. Найдем из второго равенства AD= A E ∙ A F A C . . = 36 2 54 . . = 24

Теперь найдем CD=AC-AD=54-24=30

pазбирался: Даниил Романович | обсудить разбор | оценить

На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.

Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.

pазбирался: Даниил Романович | обсудить разбор | оценить

В треугольнике АВС известно, что угол ВАС равен 84 0 , АD – биссектриса. Найдите угол ВАD. Ответ дайте в градусах.

Ключевое слово в данной задаче – биссектриса. Вспоминаем, что она делит угол пополам. Нам надо найти величину угла ВАD, следовательно он равен половине угла ВАС, то есть 84 0 :2=42 0

pазбирался: Даниил Романович | обсудить разбор | оценить

Определение и свойства биссектрисы угла треугольника

В данной публикации мы рассмотрим определение и основные свойства биссектрисы угла треугольника, а также приведем пример решения задачи, чтобы закрепить представленный материал.

Определение биссектрисы угла треугольника

Биссектриса угла – это луч, который берет начала в вершине угла и делит данный угол пополам.

Биссектриса треугольника – это отрезок, соединяющий вершину угла треугольника с противоположной стороной и делящий этот угол на две равные части. Такая биссектриса, также, называется внутренней.

Основание биссектрисы – точка на стороне треугольника, которую пересекает биссектриса. Т.е. в нашем случае – это точка D.

Внешней называется биссектриса угла, смежного с внутренним углом треугольника.

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Биссектриса угла треугольника делит его противоположную сторону в пропорции, равной отношению прилежащих к данному углу сторон. Т.е. для нашего треугольника (см. самый верхний рисунок):

Свойство 2

Точка пересечения трех внутренних биссектрис любого треугольника (называется инцентром) является центром вписанной в фигуру окружности.

Свойство 3

Все биссектрисы треугольника в точке пересечения делятся в отношении, равном сумме прилежащих к углу сторон, деленной на противолежащую сторону (считая от вершины).

Свойство 4

Если известны длины отрезков, образованных на стороне, которую пересекает биссектриса, а также две другие стороны треугольника, найти длину биссектрисы можно по формуле ниже (следует из теоремы Стюарта):

BD 2 = AB ⋅ BC – AD ⋅ DC

Свойство 5

Внешняя и внутренняя биссектрисы одного и того же угла треугольника перпендикулярны друг к другу.

CD – внутренняя биссектриса ∠ACB;
CE – биссектриса угла, смежного с ∠ACB;
∠DCE равен 90°, т.е. биссектрисы CD и CE перпендикулярны.

Пример задачи

Дан прямоугольный треугольник с катетами 6 см и 8 см. Найдите длину биссектрисы, проведенной к гипотенузе.

Решение
Нарисуем чертеж согласно условиям задачи.

Применив теорему Пифагора мы можем найти длину гипотенузы (ее квадрат равен сумме квадратов двух катетов).
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
Следовательно, BC = 10 см.

Далее составляем пропорцию согласно Свойству 1, условно приняв отрезок BD на гипотенузе за “a” (тогда DC = “10-a”):

Избавляемся от дробей и решаем получившееся уравнение:
8a = 60 – 6a
14a = 60
a ≈ 4,29

Таким образом, BD ≈ 4,29 см, CD ≈ 10 – 4,29 ≈ 5,71 см.

Теперь мы можем вычислить длину биссектрисы, использую формулу, приведенную в Свойстве 4:
AD 2 = AB ⋅ AC – BD ⋅ DC = 6 ⋅ 8 – 4,29 ⋅ 5,71 ≈ 23,5.

источники:

Треугольник. Медиана, биссектриса, высота, средняя линия.

Определение и свойства биссектрисы угла треугольника

Источник

Длина биссектрисы треугольника может быть найдена разными способами, в зависимости от исходных данных.

I. Через длины двух сторон и отрезки, на которые биссектриса делит третью сторону.

Утверждение 1

Квадрат биссектрисы треугольника равен разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

Соответственно, длина биссектрисы равна квадратному корню из разности между произведением двух его сторон и произведением отрезков, на которые эта биссектриса делит третью сторону.

$[ l = sqrt {ab - a_1 b_1 } ]$

Дано:

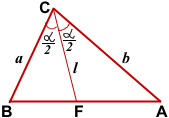
ΔABC,

СF — биссектриса ∠ABC

Доказать:

Доказательство:

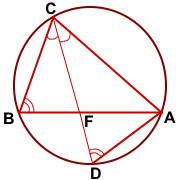
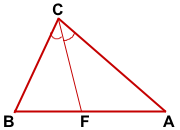
Опишем около треугольника ABC окружность и продлим биссектрису CF до пересечения с окружностью в точке D. Соединим точки A и D отрезком.

Рассмотрим треугольники BCF и DCA.

∠BCF=∠DCA (по условию);

∠CBF=∠CDA (как вписанные углы, опирающиеся на одну дугу AC).

Значит, треугольники BFC и DCA подобны (по двум углам).

Из подобия треугольников следует пропорциональность соответствующих сторон:

$[ frac{{BC}}{{CD}} = frac{{CF}}{{AC}}, Rightarrow CD = frac{{BC cdot AC}}{{CF}}. ]$

$[ FD = CD - CF = frac{{BC cdot AC}}{{CF}} - CF. ]$

По свойству пересекающихся хорд

Отсюда

$[ BF cdot AF = CF cdot (frac{{BC cdot AC}}{{CF}} - CF) ]$

Что и требовалось доказать.

II. Через три стороны треугольника

Утверждение 2

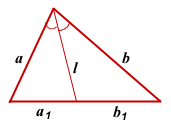
Длина биссектрисы треугольника выражается через длины его сторон a, b и c по формуле

$[ l_c = frac{1}{{a + b}}sqrt {ab(a + b + c)(a + b - c)} . ]$

Доказательство:

По свойству биссектрисы треугольника:

$[ [ frac{a}{{a_1 }} = frac{b}{{b_1 }}, Rightarrow a_1 b = ab_1 . ]$

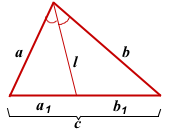
a₁+b₁=c, b₁=c-a₁, поэтому

$[ a_1 = frac{{ac}}{{a + b}}. ]$

Согласно утверждению 1,

$[ l^2 = ab - a_1 (c - a_1 ) = ab - frac{{ac}}{{a + b}}(c - frac{{ac}}{{a + b}}) = ]$

$[ = ab - frac{{ac^2 }}{{a + b}} + frac{{a^2 c^2 }}{{(a + b)^2 }} = frac{{ab(a + b)^2 - ac^2 (a + b) + a^2 c^2 }}{{(a + b)^2 }} = ]$

$[ = frac{{ab(a + b)^2 - a^2 c^2 - abc^2 + a^2 c^2 }}{{(a + b)^2 }} = frac{{ab(a + b)^2 - abc^2 }}{{(a + b)^2 }} = ]$

$[ = frac{{ab}}{{(a + b)^2 }}((a + b)^2 - c^2 ) = frac{{ab}}{{(a + b)^2 }}((a + b) + c)((a + b) - c) = ]$

$[ = frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c), ]$

откуда

$[ l = sqrt {frac{{ab}}{{(a + b)^2 }}(a + b + c)(a + b - c)} , ]$

$[ l_c = frac{1}{{a + b}}sqrt {ab(a + b + c)(a + b - c)} . ]$

Что и требовалось доказать.

Аналогично,

$[ l_a = frac{1}{{b + c}}sqrt {bc(b + c + a)(b + c - a)} , ]$

$[ l_b = frac{1}{{a + c}}sqrt {ac(a + c + b)(a + c - b)} . ]$

III Через две стороны треугольника и угол между ними.

Утверждение 3

Длина биссектрисы треугольника через две стороны, образующие угол, из вершины которого исходит биссектриса, и угол между этими сторонами выражается по формуле

$[ l_c = frac{{2abcos frac{alpha }{2}}}{{a + b}} ]$

Доказательство:

Найдем площади треугольников BCF, ACF и ABC.

$[ S_{Delta BCF} = frac{1}{2}BC cdot CF cdot sin angle BCF, ]$

$[ S_{Delta ACF} = frac{1}{2}AC cdot CF cdot sin angle ACF, ]$

$[ S_{Delta ABC} = frac{1}{2}AC cdot BC cdot sin angle BCA. ]$

Так как

$[ S_{Delta ABC} = S_{Delta BCF} + S_{Delta ACF} , ]$

то

$[ frac{1}{2}AC cdot BC cdot sin angle BCA = ]$

$[ = frac{1}{2}BC cdot CF cdot sin angle BCF + frac{1}{2}AC cdot CF cdot sin angle ACF, ]$

$[ ab cdot sin alpha = al cdot sinfrac{alpha }{2} + bl cdot sinfrac{alpha }{2}, ]$

$[ ab cdot sin alpha = l cdot sinfrac{alpha }{2}(a + b), ]$

$[ l = frac{{ab cdot sin alpha }}{{sinfrac{alpha }{2}(a + b)}} = frac{{ab cdot sin (2 cdot frac{alpha }{2})}}{{sinfrac{alpha }{2}(a + b)}} = frac{{ab cdot 2sin frac{alpha }{2}cos frac{alpha }{2}}}{{sinfrac{alpha }{2}(a + b)}} = frac{{2abcos frac{alpha }{2}}}{{a + b}}. ]$

Что и требовалось доказать.

Источник

Остроугольный треугольник, элементы, свойства, признаки и формулы.

Остроугольный треугольник – это треугольник, у которого все углы острые.

Остроугольный треугольник (понятие и определение)

Элементы остроугольного треугольника

Свойства остроугольного треугольника

Формулы остроугольного треугольника

Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник

Остроугольный треугольник (понятие и определение):

Остроугольный треугольник – это треугольник, у которого все углы острые, т.е. меньше 90°.

Остроугольный треугольник – это треугольник, у которого все три угла острые. В свою очередь, острый угол – это угол, градусная мера которого составляет менее 90 градусов.

Рис. 1. Остроугольный треугольник

∠ АВС, ∠ BАC, ∠ BСA – острые углы треугольника

По определению, каждый правильный (равносторонний) треугольник также является остроугольным, но не каждый остроугольный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем остроугольного треугольника. У равностороннего треугольника каждый угол составляет 60 °.

Рис. 2. Равносторонний треугольник

АВ = ВС = АС – стороны треугольника,

∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника

Остроугольный треугольник также может быть одновременно равнобедренным треугольником.

Рис. 3. Равнобедренный треугольник

АВ = ВС – боковые стороны, АС – основание,

∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании

Хотя в остроугольном треугольнике каждый угол меньше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.

Элементы остроугольного треугольника:

Кроме сторон и углов у одностороннего треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. остроугольного, 6 внешних углов, по 2 на каждый внутренний. Любой внешний угол остроугольного треугольника всегда будет тупым углом.

Рис. 4. Остроугольный треугольник и внешний угол

∠ ВСD – внешний угол

Медиана остроугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.

Рис. 5. Остроугольный треугольник и медиана остроугольного треугольника

MС – медиана остроугольного треугольника

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Рис. 6. Остроугольный треугольник и высота остроугольного треугольника

MС – высота остроугольного треугольника

Высота остроугольного треугольника находится внутри треугольника. Все 3 высоты остроугольного треугольника (как и любого треугольника) пересекаются в одной точке, называемой ортоцентром.

Биссектриса в остроугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.

Рис. 7. Остроугольный треугольник и биссектриса угла остроугольного треугольника

MС – биссектриса угла остроугольного треугольника

Кроме того, биссектриса остроугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника

Свойства остроугольного треугольника:

Свойства остроугольного треугольника аналогичны свойствам обычного треугольника:

1. Против большей стороны лежит больший угол, и наоборот.

Рис. 8. Остроугольный треугольник

2. Против равных сторон лежат равные углы, и наоборот.

Рис. 9. Остроугольный треугольник с равными боковыми сторонами

АВ = ВС

3. Сумма углов остроугольного треугольника равна 180°.

4. Любая сторона остроугольного треугольника меньше суммы двух других сторон и больше их разности:

- a < b + c;
- a > b – c;
- b < a + c,
- b > a – c;
- c < a + b;
- c > a – b.

Квадрат

Овал

Остроугольный треугольник

Полукруг

Прямой угол

Прямоугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Ромб

Трапеция

Тупой угол

Шестиугольник

Коэффициент востребованности
16 589

Источник

2 апреля 2023 19:36

744

определение медианы,биссектрисы и высоты треугольника. Построение их в остроугольном,прямоугольном и тупоугольном треугольниках

Посмотреть ответы

· Для того, чтобы построить высоту остроугольного треугольника, проведите из его вершины прямую, перпендикулярную противолежащей стороне. Отрезок, соединяющий точку пересечения перпендикулярных прямых и вершину, и будет являться вершиной треугольника, опущенной из заданной высоты. При этом все три высоты остроугольного треугольника должны лежать внутри треугольника.

· В случае тупоугольного треугольника, для того, чтобы построить высоты, опущенные из двух его острых углов, необходимо продолжить прямые, содержащие стороны, прилегающие к тупому углу. Высота, опущенная из острого угла тупоугольного треугольника, лежит на продолжении противолежащей вершине стороны, за пределами треугольника.

· Если один из углов треугольника прямой, то стороны треугольника, прилегающие к прямому углу (катеты) уже являются его высотами (совпадают с высотами треугольника). Третья высота прямоугольного треугольника, проведенная к его гипотенузе, лежит внутри пределов сторон треугольника.

Перпендикуляр, проведённый из вершины треугольника к прямой, являющейся противоположной стороной, называется выстой треугольника.
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется бессиктрисой треугольника.
Отрезок, соединяющий вершину треугольника с серидиной противоположной стороны, называется медианой треугольника.
О построение я незнаю

Еще вопросы по категории Алгебра

Источник

Все формулы биссектрисы в треугольнике

Треугольник. Медиана, биссектриса, высота, средняя линия.

теория по математике 📈 планиметрия

Виды треугольников по углам

Виды треугольников по сторонам

Медиана, биссектриса, высота, средняя линия треугольника

Медиана

Биссектриса

Высота

Средняя линия

Определение и свойства биссектрисы угла треугольника

Определение биссектрисы угла треугольника

Свойства биссектрисы треугольника

Свойство 1 (теорема о биссектрисе)

Свойство 2

Свойство 3

Свойство 4

Свойство 5

Пример задачи

Остроугольный треугольник, элементы, свойства, признаки и формулы.

Остроугольный треугольник (понятие и определение):

Элементы остроугольного треугольника:

Свойства остроугольного треугольника:

определение медианы,биссектрисы и высоты треугольника. Построение их в остроугольном,прямоугольном и тупоугольном треугольниках

Не пропустите также: