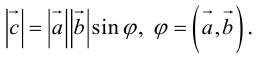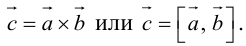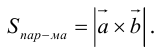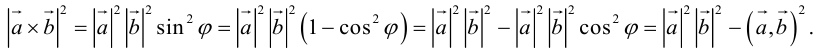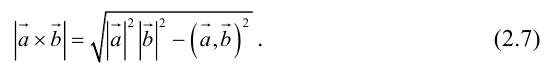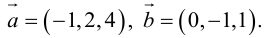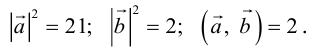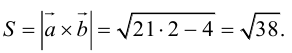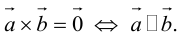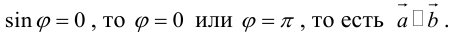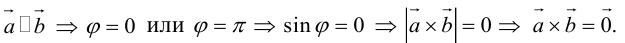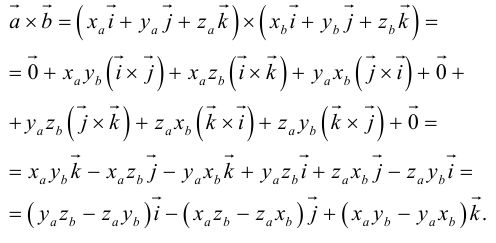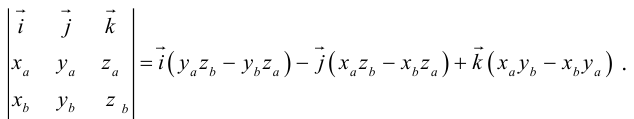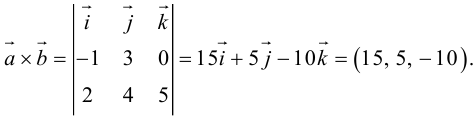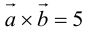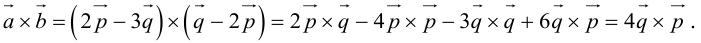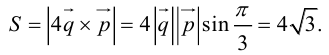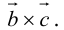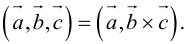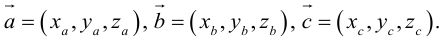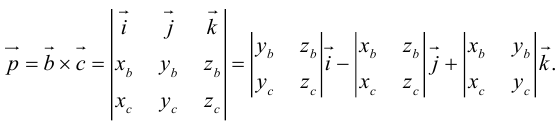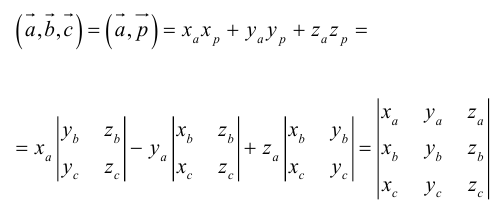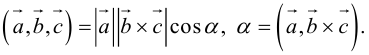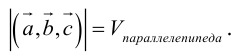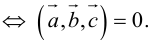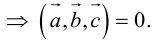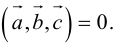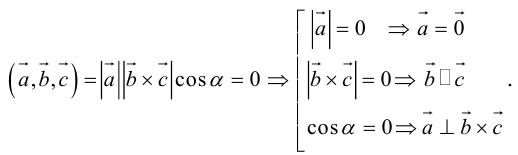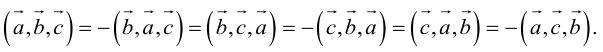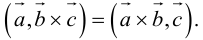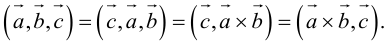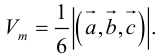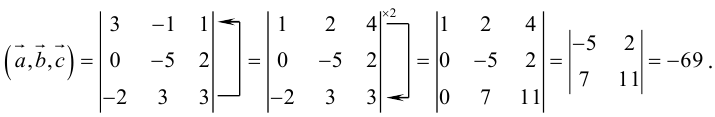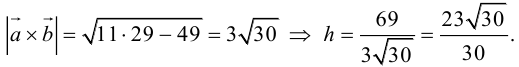Уравнение биссектрисы угла
Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.
Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0.
Расстояние от точки (xo;yo) до прямой ax+by+c=0 определяется по формуле
По свойству биссектрисы угла любая точка, лежащая на биссектрисе угла, равноудалена от его сторон.
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0, находится от этих прямых на одинаковом расстоянии, то есть
Это равенство можно записать в виде
Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.
Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.
В формулу уравнения биссектрис подставляем данные прямых:
Уравнение биссектрисы в треугольнике — формула, свойства и решение задач
Прямая на плоскости
Задачи по геометрии могут относиться к одному из двух принципиально отличающихся случаев. Это следующие:
- На плоскости, где достаточно двух координат для описания любых геометрических объектов.
- В трехмерном пространстве, где любая точка имеет три координаты.
Когда рассматривают треугольники и их элементы, то в ряде ситуаций речь идет именно о двумерном пространстве. В нем всякая прямая линия может быть выражена в виде нескольких математических форм или уравнений. Чаще всего используются следующие типы:
- Общий. Он также называется универсальным. Прямая представляет собой следующую математическую запись: A*x + B*y + C = 0. Здесь A, B, C — числовые коэффициенты, x и y — переменные, являющиеся координатами. Сразу нужно отметить, что эта форма представления прямой используется для составления уравнения биссектрисы угла. Для удобства геометрического изображения общую форму записи часто представляют в виде y = f (x). Нужно понимать, что указанной форме в пространстве соответствует не прямая, а плоскость.
- Канонический или уравнение в отрезках. Имеет оно такой вид: y/p + x/q = 1. Здесь p, q — это координаты, в которых прямая пересекает оси y и x, соответственно, поэтому удобно ее изображать в координатной системе.
- Векторный. Это один из важных типов представления прямой как на плоскости, так и в пространстве. По сути, он является исходным представлением, из которого можно получить все остальные. Математически он записывается так: (x, y) = (x0, y0) + α*(v1, v2). Где (x0, y0) — координаты произвольной точки, которая лежит на прямой, (v1, v2) — направляющий вектор, он параллелен заданной прямой, α — произвольное число, параметр.
- Параметрический. Этот тип представляет собой систему уравнений, которую удобно использовать во время преобразования одного вида прямой в другой. Представляет он собой следующую математическую запись: x = x0 + α*v1; y = y0 + α*v2. Несложно понять, что, выражая параметр α, можно получить уравнения общего вида и в отрезках. Объединяя же систему уравнений в одно выражение, получается векторная форма записи прямой.
Делящая пополам угол линия
Каждый школьник, который знаком с азами геометрии, знает, что прямая, делящая на две равные части произвольный угол, называется биссектрисой. Этот элемент присутствует для любой фигуры, которая в своем составе содержит какой-либо угол.
Другое определение биссектрисы гласит, что она представляет собой геометрическое расположение точек, которые равноудалены от соответствующих сторон углового объекта. Например, если имеется угол dac, то любая из точек биссектрисы находится на одинаковом расстоянии как от отрезка da, так и от отрезка ac.
Способы построения
В классах общеобразовательных школ рассматривают два основных способа построения биссектрисы. Это следующие:
- С помощью транспортира. Для этого следует измерить заданный угол в градусах, разделить его пополам. Полученное значение отметить в виде точки. Затем соединить вершину угла и поставленную точку внутри него. Получится искомый элемент.
- С использованием циркуля и линейки. Эти инструменты еще проще применять для построения биссектрисы, чем транспортир. Сначала необходимо установить в вершину угла ножку циркуля и отметить дугами пересечение окружности со сторонами. Затем, в точки пересечения поставить ножку циркуля и провести две окружности. Соединив две точки их пересечения одной прямой, можно получить биссектрису.
Имеется еще один метод, который позволяет просто начертить изучаемый линейный элемент. Для его использования нужна линейка со шкалой. С помощью нее следует от вершины угла отмерить два одинаковых отрезка любой длины. Затем соединить концы этих отрезкой, получится равнобедренный треугольник.
В нем любая биссектриса также является высотой и медианой. Поэтому, разделив его ровно пополам линейкой, и соединив полученную точку с вершиной, можно получить требуемую линию.
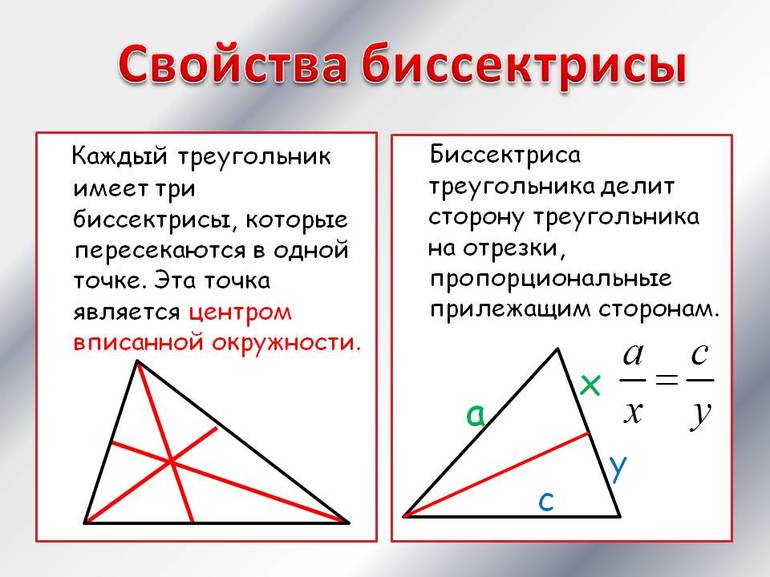
Основные свойства
Чтобы найти по координатам вершин длину биссектрисы треугольника, следует знать некоторые свойства этого геометрического объекта. Главным из них является существование двух линий, которые делят пополам исходный угол. Нужно понимать, что угол бывает не только внутренний, но и внешний. По сути, оба типа образуются при пересечении двух прямых. Нетрудно доказать, что биссектрисы каждого из них пересекаются всегда под углом 90 °.
Еще одним важным свойством является тот факт, что пересекаются в одной точке биссектрисы треугольника. Она представляет собой центр вписанной в фигуру окружности. Чтобы это доказать, следует вспомнить, что каждая точка биссектрисы равноудалена от соответствующих сторон угла.
Пусть имеется треугольник ABC. У него две биссектрисы пересекаются в точке O. Пусть это будут линии для углов A и B. Расстояние от O до AC должно быть равно таковому от O до AB. С другой стороны, расстояния от O до AB и до BC также одинаковые. Поэтому дистанции от O до BC и до AB также равны, а значит, точка O лежит на биссектрисе угла C и центром вписанной окружности является.
В треугольнике рассматриваемый геометрический элемент используется часто для решения задач благодаря применению так называемой теоремы биссектрис. Чтобы ее сформулировать максимально простым языком, следует представить, что имеется треугольник произвольного типа ABC. В нем проведена биссектриса AD, где точка D лежит на прямой BC. Тогда справедливо следующее выражение:
Это равенство не является очевидным, однако, оно было известно еще древнегреческим мыслителям. Эту теорему в несколько иной форме можно встретить в знаменитом труде по геометрии Евклида, который называется «Элементы». Доказательство равенства несложно провести с использованием небольших дополнительных построений и применением признаков подобия треугольников.
Наконец, отрезок биссектрисы, который заключен между вершиной и противоположной стороной треугольника, имеет определенную длину. Вычислить ее можно с использованием следующего равенства:
Это равенство прописано для угла A треугольника ABC, в котором противоположная A сторона имеет длину a. Стороны AB и AC имеют длины c и b, соответственно. Буквой p обозначен полупериметр фигуры.
Важно понимать, если нарисовать прямоугольный параллелепипед (или иную фигуру) в пространстве, и построить биссектрису для его граней, она будет представлять собой не прямую, а плоскость.
Уравнение биссектрисы треугольника
Когда известно, как математически записывать выражения для прямых, и что такое биссектриса, и какими свойствами она обладает, можно переходить к непосредственному нахождению ее уравнения.
В общем случае задача решается в результате применения следующей последовательности действий (существуют онлайн-ресурсы, позволяющие решить данную проблему):
- Сначала требуется определить уравнения двух сторон угла по их координатам. Это легко сделать в векторной форме, а затем, преобразовать ее в выражение общего типа.
- Далее, необходимо найти уравнение биссектрис первого координатного угла, прировняв расстояния от ее точек до соответствующей стороны. Рабочая формула имеет вид: |A1*x + B1*y + C|/(A1 2 + B1 2 )^0,5 = |A2*x + B2*y + C|/(A2 2 + B2 2 )^0,5. Следует обратить внимание на наличие двух различных решений этого равенства, поскольку в числителе стоит модульное выражение. Два полученных уравнения говорят о наличии взаимно перпендикулярных биссектрис для углов треугольника внутреннего и внешнего.
- Для внутреннего угла искомое уравнение можно найти, если определить точку пересечения соответствующей прямой с противоположной исходному углу стороной треугольника. Та точка, сумма расстояний от которой до концов отрезка будет равна длине стороны, принадлежит искомой биссектрисе.
Пример решения задачи
Пусть, треугольник задан координатами A (1, -1), B (0, -2), C (3,0). Следует уравнение биссектрисы найти для угла B и ее длину вычислить.
Сначала нужно написать уравнения прямых для сторон AB и CB, получается:
- AB: (x, y) = (1, -1) + α*(-1, -1) ==> y — x + 2 = 0;
- CB: (x, y) = (3, 0) + α*(-3, -2) ==> 3*y — 2*x + 6 = 0.
Составить уравнения биссектрис можно так:
| y — x + 2 |/(2)^0,5 = | 3*y — 2*x + 6 |/(13)^0,5.
Решение этого уравнения приводит к следующим двум выражениям для взаимно перпендикулярных биссектрис:
- y*(6−3*3 0,5 ) + x*(3*3 0,5 −4)+12−6*3 0,5 = 0;
- y*(3*3 0,5 +6) -x*(4+3*3 0,5 )+12+6*3 0,5 = 0.
Чтобы определить, какая из двух прямых является искомой для треугольника заданного, следует точку пересечения каждой из них со стороной AC найти. Уравнение для AC имеет вид:
Подставляя его в каждое из выражений для биссектрис, можно получить две точки пересечения:
При этом длина основания AC составляет 2,236 единицы через единичный вектор. Расстояние от точек D1 и D2 до A, C равно:
- D1A = 1,4; D1C = 3,635;
- D2A = 0,621; D2C = 1,614.
Видно, что точка пересечения второй прямой D2 лежит между A и C, поэтому соответствующее ей уравнение биссектрисы является ответом на задачу. Ее длину можно вычислить по формуле для модуля вектора BD2:
BD2 = 2,014 единицы.
Таким образом, для определения в треугольнике биссектрисы уравнения по координатам следует уметь находить векторную форму выражений для прямой по координатам двух точек. Также нужно знать свойства делящей пополам угол линии.
Составить уравнение биссектрис углов образованных двумя прямыми
Составить уравнение биссектрисы острого угла между прямыми
Решение
Найдем точку пересечения двух прямых
Направляющий вектор первой прямой есть 



Направляющий вектор биссектрисы угла равен сумме нормированных направляющих векторов сторон
Так как точка 
Задание 8
Составить уравнение плоскости, которая проходит через точку 
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Увлечёшься девушкой-вырастут хвосты, займёшься учебой-вырастут рога 9987 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Составить уравнение биссектрисы угла можно с помощью свойства биссектрисы угла.
Выведем уравнения биссектрис углов, образованных двумя пересекающимися прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0.
Расстояние от точки (xo;yo) до прямой ax+by+c=0 определяется по формуле
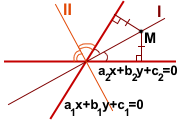
Следовательно, любая точка M(x;y), лежащая на биссектрисе угла, образованного прямыми a1x+b1y+c1=0 и a2x+b2y+c2=0, находится от этих прямых на одинаковом расстоянии, то есть
Это равенство можно записать в виде
Получили уравнения двух биссектрис углов, образованных пересекающимися прямыми.
Написать уравнения биссектрис углов, образованного прямыми 4x-3y-10=0 и 9x-12y-7=0.
В формулу уравнения биссектрис подставляем данные прямых:
Что ты хочешь узнать?
Ответ
Проверено экспертом
Даны прямые: 11x-2y+5=0 и 4x+8y-7=0
Уравнения биссектрис углов между прямыми Ax + By + C = 0 и A₁x + B₁y + C₁ = 0:
Знак + или – выбирается в зависимости от того, нужно уравнение биссектрисы острого или тупого углов.
Подставив коэффициенты заданных прямых в приведенную формулу, получим уравнения биссектрис:
В приближённом варианте у ≈ 1,3541х + 1,3772.
http://nauka.club/matematika/geometriya/uravnenie-bissektrisy-v-treugolnike.html
http://4apple.org/sostavit-uravnenie-bissektris-uglov-obrazovannyh/
Содержание:
Векторная алгебра
Векторная алгебра — это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая — конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор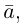
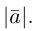
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
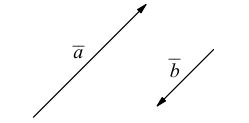
Два вектора 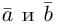
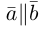
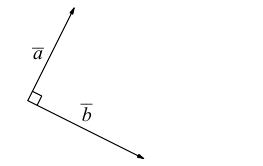
Аналогично, векторы а и b называются ортогональными (обозначение 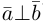
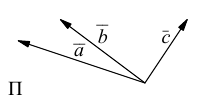
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
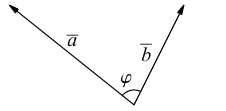
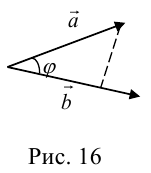
Углом между векторами 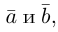
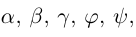
Два ненулевых вектора 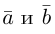
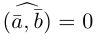
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 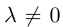
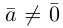
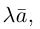
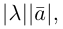
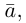
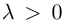
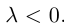
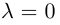
В частности, вектор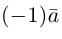
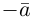
Если 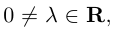
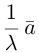
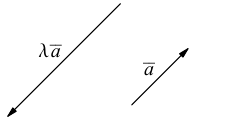
Из приведенного определения сразу же следует, что коллинеарные векторы 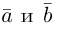
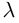
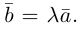
взять число 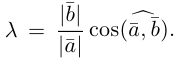
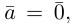
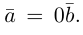
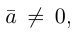
b) Сложение векторов.
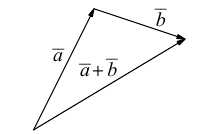
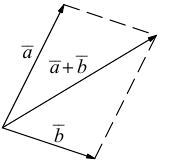
Суммой двух векторов 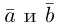
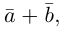
или по равносильному ему правилу параллелограмма
Вектор 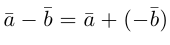
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
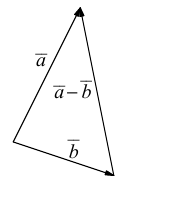
Проекцией вектора 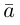
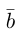
Геометрически очевидны следующие свойства проекции:
Пример №1
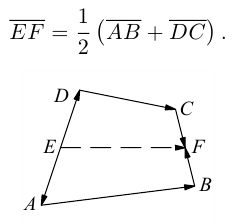
Пусть Е и F — середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 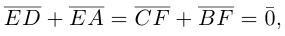
что и требовалось.
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 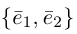
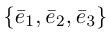
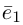
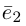
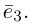
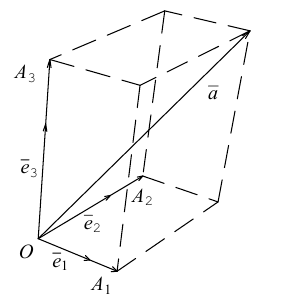
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 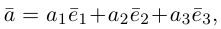
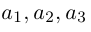
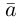
Приведем геометрическое доказательство этого утверждения.
Вектор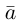
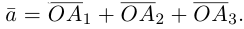
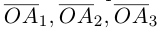
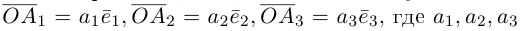
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 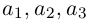
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 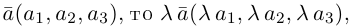
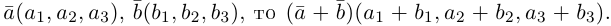
Рассмотрим теперь ортонормированный базис 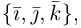
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 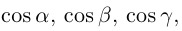
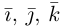
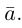
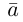
Очевидно также, что
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 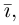
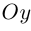
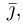
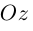
В выбранной системе координат координаты радиуса-вектора 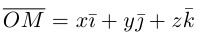
Если известны координаты начальной 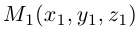
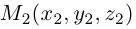
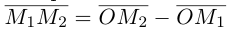
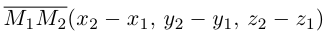
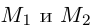
Найдем теперь координаты точки М, делящей отрезок с концами в точках 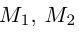
отношении 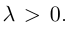
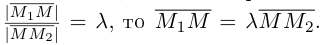
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
Пример №2
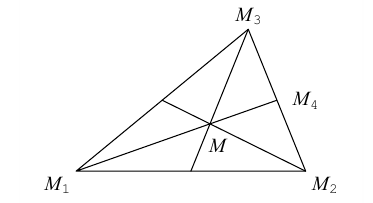
Треугольник задан координатами своих вершин 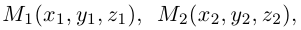
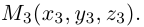
Пусть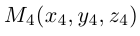
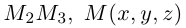
По известному свойству точки пересечения медиан 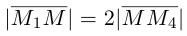
Подставив сюда найденные координаты точки 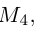
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 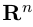
обладающая тем свойством, что любой вектор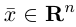
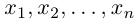
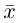
В качестве базиса в 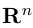
так как, очевидно, любой вектор 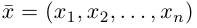
Скалярное произведение векторов
Определение: Скалярным произведением векторов 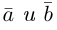
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое — из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 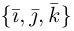
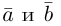
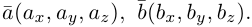
перемножим векторы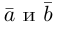
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
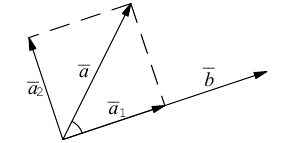
Пример №3
Разложить вектор 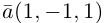
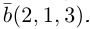
Решение.
Из чертежа следует, что 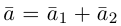
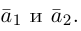
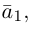
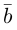
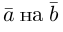
Тогда вторая ортогональная составляющая вектора 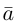
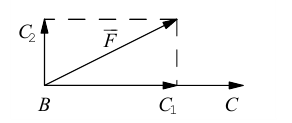
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 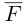
Найдем работу этой силы. Для этого разложим вектор силы 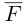
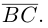
Составляющая 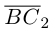
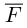
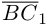
Окончательно, работа силы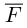
Замечание. Скалярным произведением векторов 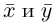
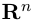
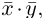
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 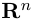
Длиной вектора 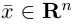
Векторы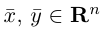
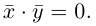
составляют ортонормированный базис пространства 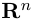
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 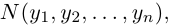
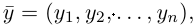
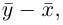
Таким образом переопределенное пространство 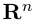
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R». Точка 0(0,0,… ,0) называется, естественно, началом координат.
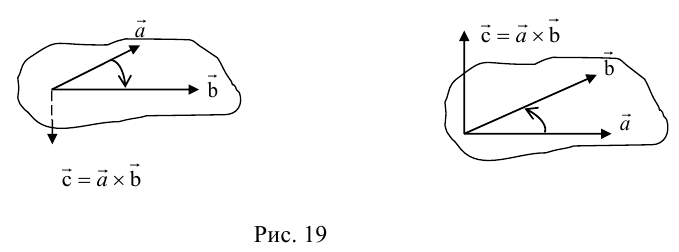
Векторное произведение векторов
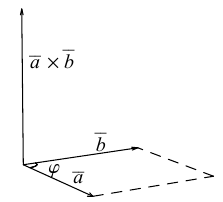
Определение: Векторным произведением некоялинеарных векторов 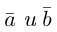

Из этого определения следует, что площадь параллелограмма, построенного на векторах 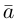
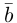

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 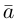
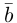
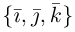
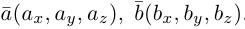
раскроем скобки в векторном произведении 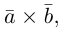
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
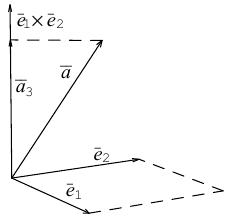
Пример №4
Найти составляющую вектора 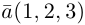
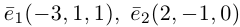
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 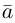

Переходим к вычислениям:
Тогда
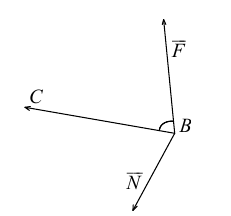
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 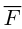
Смешанное произведение векторов
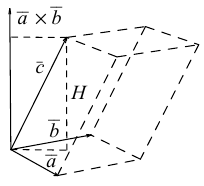
Определение: Смешанным произведением трех векторов 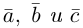
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
Поскольку 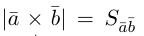
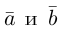
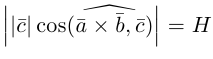
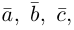
— объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 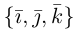
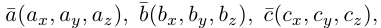
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 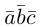
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 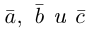
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 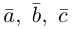
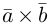
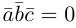
Следствие. Три вектора 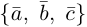
Заметим, кроме того, что, если 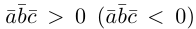
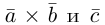
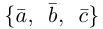
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 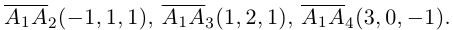
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 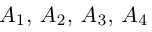
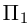
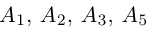
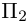
так как первая и третья строки в определителе пропорциональны. Плоскости 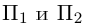
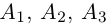
Векторы и линейные операции над ними
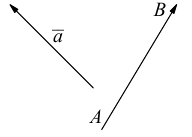
Определение: Вектором называется направленный отрезок (рис. 1).
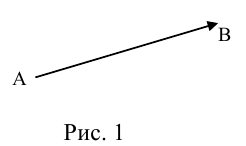
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 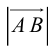
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
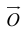
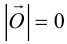
Определение: Векторы 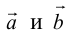
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
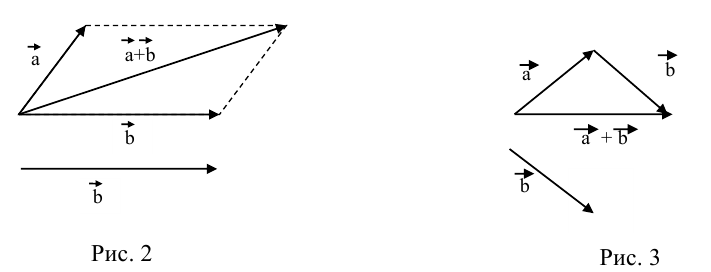
Сложение
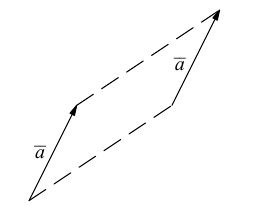
а) Правило параллелограмма (рис.2): начала 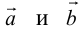
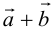
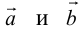
б) Правило треугольника (рис. 3): начало 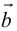
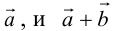
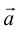
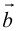
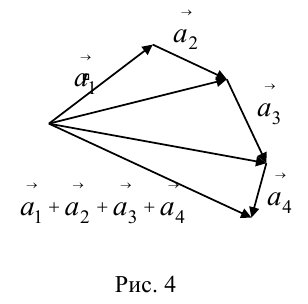
в) Правило сложения нескольких векторов (рис. 4).
Вектор 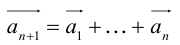
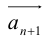
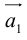
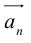
Умножение на число
Определение: Произведением вектора 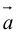
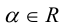
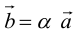
а) 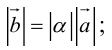
б) 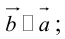
в)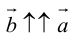
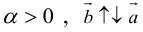
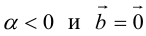
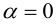
Произведение 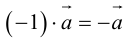
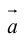
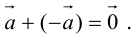
Определение: Разностью 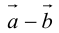
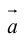
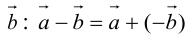
Начала 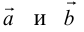
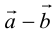
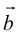
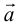
Свойства линейных операций
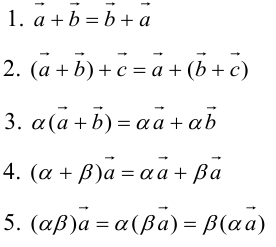
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: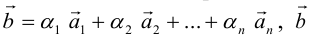
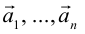
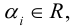
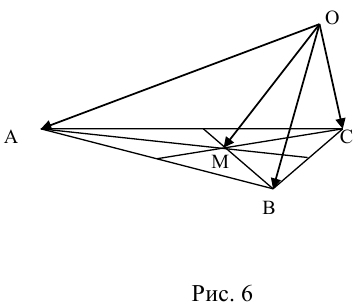
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 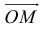
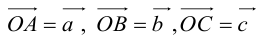
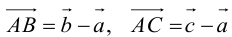
По правилу треугольника 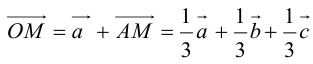
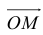
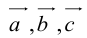
Теорема: Пусть 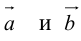
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 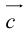
Доказательство:
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
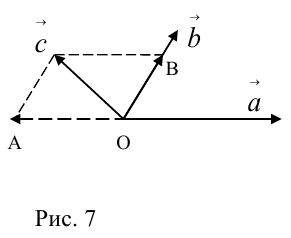
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 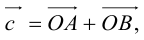
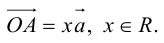
Докажем единственность разложения. Предположим, что 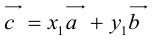
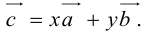
Если 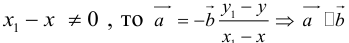
Теорема: Пусть 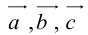
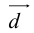
причем единственным образом.
Представление вектора 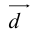
Доказать самостоятельно.
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 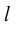
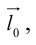
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 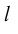
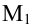
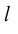
Определение: Ортогональной проекцией вектора 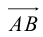
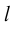
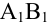
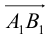
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
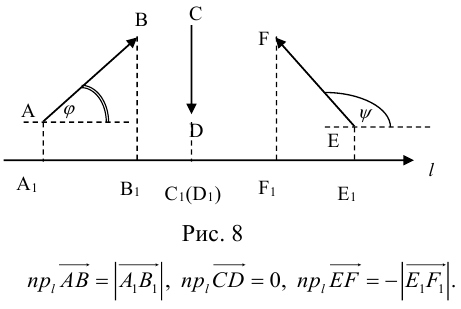
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
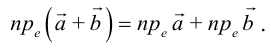
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 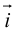
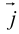

Аналогично в пространственной системе OXYZ 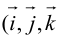
– разложение 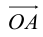
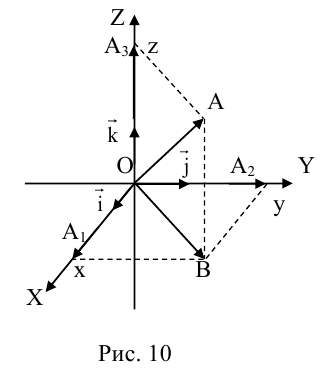
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 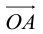
Определение: Координатами вектора 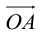
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 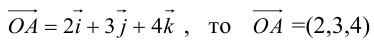
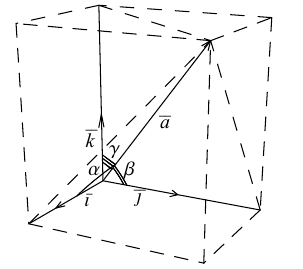
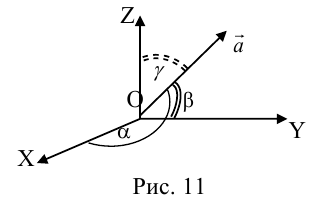
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
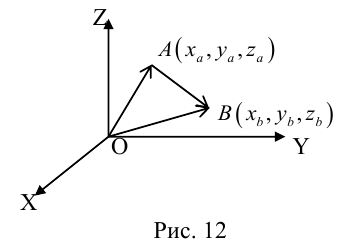
Если известны длина 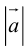
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
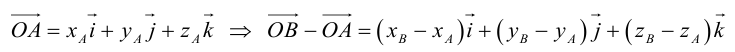
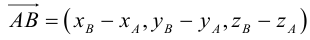
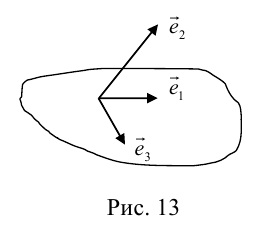
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 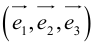
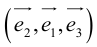
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 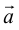
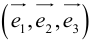
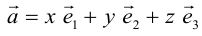
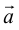
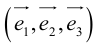
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 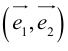
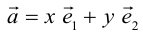
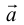
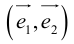
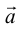
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
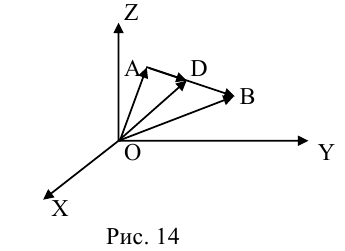
Деление отрезка в данном отношении
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 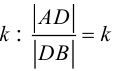
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
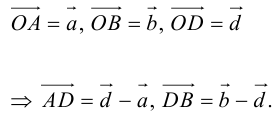
Так как 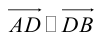
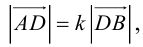
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
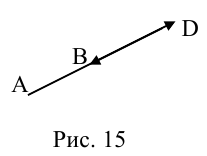
ЗАМЕЧАНИЕ 2. Если k < 0, 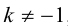
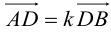
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 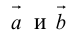
Скалярное произведение обозначается так: 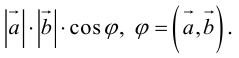
Так как 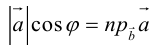
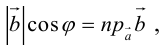
Свойства скалярного произведения
1.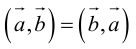
2.
Доказательство:
3.
Доказательство:
а) 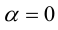
б)
в) 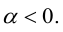
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 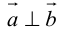
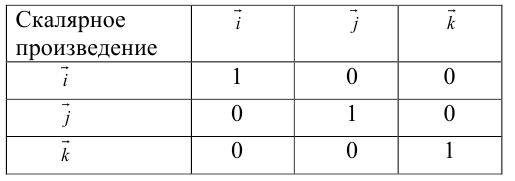
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 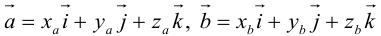
Таким образом,
Пример №8
Найти, при каком значении x векторы 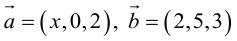
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 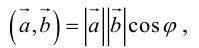
то
Найдем координаты векторов 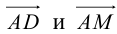
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 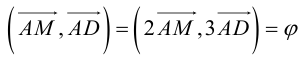
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 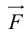
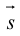
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 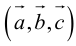
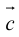
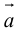
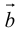
Определение: Векторным произведением вектора 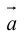
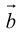
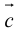
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 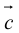
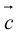
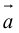
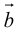
Свойства векторного произведения
1.
Доказательство:
а)пусть 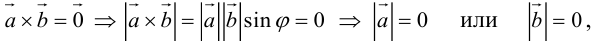
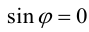
Его направление не определено, поэтому можно считать, что 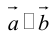
б)пусть
2. 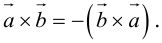
Доказательство: По определению направления векторов 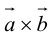
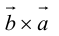
3.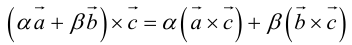
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 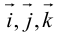
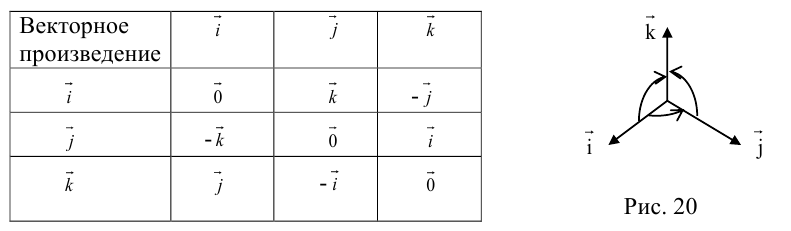
Пусть в некоторой пдск 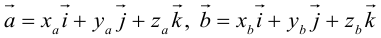
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
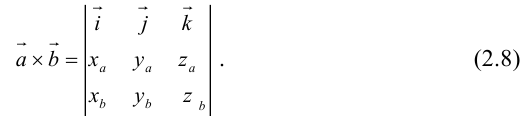
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 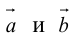
или
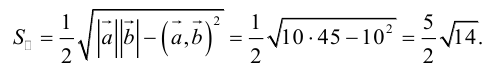
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 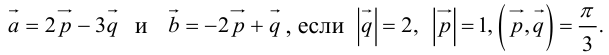
Так как 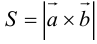
Отсюда
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 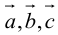
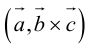
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
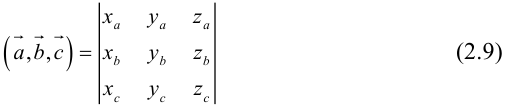
По определению скалярного произведения
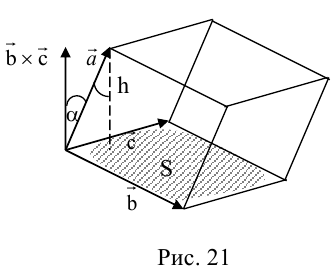
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
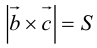
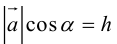
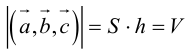
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 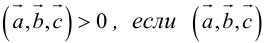
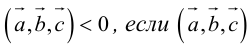
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 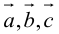
Доказательство: а) 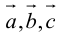
Если 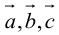
б)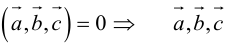
Во всех трех случаях 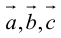
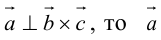
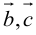
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
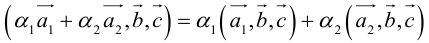
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
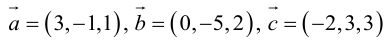
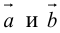
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 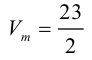

Чтобы найти высоту, воспользуемся формулой
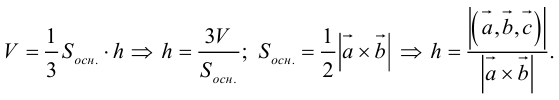
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
2.1. Даны уравнения
двух прямых. Составить
уравнение биссектрисы тупого угла,
образованного этими прямыми.
Общие
сведения и расчётные формулы:по представленному заданию.
Пусть
имеем две прямые:
:
x+
y+
=0
и
:
x+
y+
=0.
Уравнением
определяется вектор нормали
,
уравнением
вектор нормали
.
Так как векторы
и
–
свободные, то изобразим их так, чтобы
их начала принадлежали соответствующим
плоскостям, а сами они располагались
внутри одного из углов, образованных
пересекающимися прямыми. Важно помнить
также, что уравнение прямой можно
умножать на произвольное, не равное
нулю число. Это значит, что, по необходимости,
мы можем разместить векторы
и
как внутри тупого, так и внутри острого
угла. Пусть векторы
и
разместились внутри тупого угла, как
показано на рисунке. Умножим уравнение
на число (-1). Вектор нормали этой прямой
станет равным
,
и пара векторов
и
расположится внутри острого угла.
Видим,
когда векторы нормалей плоскостей
располагаются внутри тупого угла угол
между ними острый. И наоборот, если
векторы расположились внутри острого
угла, то угол между ними тупой. Какой из
случаев реализуется в конкретном
примере, легко определить при помощи
скалярного произведения:
а)
∙
> 0 – векторы расположены в области
тупого угла;
б)
∙
< 0 – векторы расположены в области
острого угла.
Так как от случая
а) легко перейти к случаю б), то для
определённости будем считать, что всегда
нужно строить биссектрису тупого угла.
О
факт: рассматриваемую задачу относят
кклассическим
задачам аналитической геометрии. Важно
также то, что существует несколько
способов решения этой задачи, причём
существенно различающихся как по
теоретическим основам, так и технологии
применяемых вычислений!
Способ–1.
Пусть
∙
> 0: векторы
и
располагаются в области тупого угла.
Воспользуемся
свойством биссектрисы: каждая принадлежащая
ей точка одинаково удалена от сторон
угла, который биссектриса делит пополам.
Для
эффективного (и удобного) использования
понятия расстояние
от точки до прямой,
каждое из уравнений заданных прямых
необходимо нормализовать. Нормированное
уравнение прямой удобно как для
вычисления отклонения точки от плоскости,
так и для вычисления расстояния от
точки до плоскости. В нашем случае задача
упрощается, так как отклонения
и
произвольной точки биссектрисы от
прямых
и
имеют одинаковые знаки и можно записать:
=
.
Это значит уравнение биссектрисы, как
геометрическое место точек, равноудалённых
от сторон угла, которому эта биссектриса
принадлежит, можно записать в виде:
=
. (B1)
Если бы теперь
нужно было построить биссектрису острого
угла, то её уравнение должно быть записано
в виде:
=
–. (B2)
Замечание:
Если
бы векторы
и
располагались в области острого угла,
то биссектриса острого угла определялась
бы выражением (B1),
а биссектриса тупого – выражением
(B2).
С
В этом случае примем схему решения
задачи: а) находим точку M0(x0,y0)
пересечения прямых
и
;
б) находим направление биссектрис
;
в) проводим прямую через заданную точку
в заданном направлении.
Для
определения направления биссектрис
lВ
построим единичные векторы:
и
,
затем суммы:
=
+
– этот вектор определяет направление
биссектрисы угла, содержащего векторы
,
;
=
–
–
определяет направление биссектрисы
угла, смежного первому.
Используя
угловой коэффициент вектора
,
строим биссектрису угла, содержащего
векторы
,
;
если использовать угловой коэффициент
вектора
,
построим биссектрису смежного угла.
Замечание: на
самом деле, достаточно найти только
один вектор:
для первой биссектрисы он играет роль
направляющего вектора, а для второй –
роль вектора нормали.
Способ–3.
Воспользуемся уравнением пучка прямых:
:
и вектором
.
Параметр
прямой
выбирается из условия:
.
Интересно рассмотреть
один и тот же пример, решив его сразу
всеми тремя способами: это позволит
сравнить их трудоёмкости!
Пример
(и образец оформления):
Общая часть.
Составить уравнение
биссектрисы тупого угла, образованного
пересекающимися прямыми:и
.
Задачу
решим, применяя все рассмотренные
способы.
Способ–1.
Используем равенство отклонений=
каждой точки биссектрисы от сторон
тупого угла, которому она принадлежит.
Решение:
1). Запишем векторы:
,
.
Вычислим:∙
=3·12+(-4)·5>0.
Это значит, что векторыи
располагаются в области тупого угла.
2). Общая запись
уравнения биссектрисы имеет вид:
=
,
а в нашем случае:=
,
откуда получаем уравнение искомой
биссектрисы:.
Ответ:.
Способ–2.
В этом случае применим схему решения
задачи: а) находим точкупересечения прямых
и
;
б) находим направление биссектрис;
в) проводим прямую через заданную точку
в заданном направлении.
Решение:
1). Координаты
находим из системы уравнений:
→
=
.
2). Так как
и
,
тои
.
Тогда:=
–
=–
(3,11).
Векторможно принять в качестве нормали искомой
биссектрисы. Удобнее принять коллинеарный
ему вектор:.
3). Общее уравнение
биссектрисы запишем в виде:
.
В нашем примере: 3+11
=0,
или.
Ответ:.
Способ–3.
Воспользуемся уравнением пучка прямых:,
или в виде:и направляющим вектором
=(11,–3)..
Решение:
1). Вычислим угловой
коэффициент прямой пучка:
.
2). Вычислим угловой
коэффициент направляющего вектора: –.
3). Воспользуемся
равенством:
=–
,
откуда получаем:.
4). Подставляем
значение
в уравнение:
.
Окончательно записываем уравнение
искомой биссектрисы:.
Ответ:.
Выводы: 1).
В рассматриваемой задачеСпособ–1демонстрирует великолепные возможности
использования нормальных уравнений
прямой!
2). Применение
Способа–3демонстрирует эффективность использования
конструкциипучок.
3). Применение
Способа–2также полезно, так как требует минимум
специальных знаний. Это может сработать
при выполнении контрольной работы!
Замечание:
при оформлении задания использование
рисунка (в карандаше, с использованием
чертёжных инструментов)обязательно!
Варианты
индивидуальных заданий:
|
Вар. |
Задание: |
Вар. |
Задание: |
|
1. |
|
16. |
|
|
2. |
|
17. |
|
|
3. |
|
18. |
|
|
4. |
|
19. |
|
|
5. |
|
20. |
|
|
6. |
|
21. |
|
|
7. |
|
22. |
|
|
8. |
|
23. |
|
|
9. |
|
24. |
|
|
10. |
|
25. |
|
|
11. |
|
26. |
|
|
12. |
|
27. |
|
|
13. |
|
28. |
|
|
14. |
|
29. |
|
|
15. |
|
30. |
|
2.2. Даны координаты
вершин
и
треугольника
и точка
пересечения его высот. Найти координаты
вершинытреугольника.
Общие
сведения и расчётные формулы:по представленному заданию.
Пусть
прямая
:
x+
y+
=0
определяет сторону
треугольника, а прямая
:
x+
y+
=0
сторону
.
Тогда вектор
можем принять в качестве нормали прямой
,
а вектор
в качестве нормали прямой
.
Остаётся воспользоваться уравнением
прямой, для которой задан вектор нормали
и точка, принадлежащая прямой! Как только
будут построены уравнения прямых,
нетрудно найти их точку пересечения .
Пример
(и образец оформления):
Общая часть.
Пусть вершиныи
треугольника
:
=(-10,2),
=(6,4)
и точка пересечения его высот:=(5,2).
Найти координаты вершины.
Р
1)
Вычислим: =
–
=(5,2)–(6,4)=(-1,-2)=
;
=
–
=(5,2)–(-10,2)=(15,0)=
.
2). Заменим полученные
векторы нормалей коллинеарныvми
им, но более простые в записи:
=(1.2),
=(1,0).
3). Воспользуемся
общим уравнение прямой для случая, когда
задан вектор нормали прямой и точка,
принадлежащая прямой:
.
Тогда получим:
:
→
;
:
→
.
4). Вычислим
координаты точки
:
откуда
,
.
Ответ:=
.
Замечание:
при оформлении задания использование
рисунка (в карандаше, с использованием
чертёжных инструментов)обязательно!
Варианты
индивидуальных заданий:
|
Вар. |
Задание: |
Вар. |
Задание: |
||||
|
1. |
|
|
|
16. |
|
|
|
|
2. |
|
|
|
17. |
|
|
|
|
3. |
|
|
|
18. |
|
|
|
|
4. |
|
|
|
19. |
|
|
|
|
5. |
|
|
|
20. |
|
|
|
|
6. |
|
|
|
21. |
|
|
|
|
7. |
|
|
|
22. |
|
|
|
|
8. |
|
|
|
23. |
|
|
|
|
9. |
|
|
|
24. |
|
|
|
|
10. |
|
|
|
25. |
|
|
|
|
11. |
|
|
|
26. |
|
|
|
|
12. |
|
|
|
27. |
|
|
|
|
13. |
|
|
|
28. |
|
|
|
|
14. |
|
|
|
29. |
|
|
|
|
15. |
|
|
|
30. |
|
|
|
2.3. Даны координаты
вершин треугольника
.
Составить уравнения:
стороны ,высоты, биссектрисы
и медианы, проведённых из вершины A.
Общие
сведения и расчётные формулы:по представленному заданию.
Для решения задачи
необходимо вспомнить формулы, определяющие
уравнение прямой, для случаев:
1*.
Заданы две точки, принадлежащие прямой.
Тогда уравнение прямой, проходящей
через две заданные точки записывают в
форме
:
,
где
=
.
2*.
Заданы: точка A,
принадлежащая прямой, и направление
прямой. Для построения уравнения прямой,
содержащей высоту, опущенную на
,
учтём:
.
Это значит:
.
Так как
после построения уравнения
будет известно, то уравнение прямой
может быть записано в виде :
,
где
=
.
3*.
Тремя точками
задан угол с вершиной в точке .
Прямая
проходит через точку
и делит угол:
пополам. Эту задачу можно решить двумя
вариантами:
а).
Используем равенство углов: =
.
Обозначив угловой коэффициент прямой
через
,
запишем:
=
,
причём угловые коэффициенты сторон
заданного угла вычисляют по формулам:
,
.
Для искомой прямой уравнение принимает
вид:
:
.
б
Определим направление стороны
угла
единичным вектором:
,
стороны –
единичным
вектором:
.
Тогда направляющий вектор прямой,
совпадающей с биссектрисой может быть
записан в виде:
.
После этого остаётся воспользоваться
каноническим уравнением прямой:
=
.
4*.
Заданы : точка
,
принадлежащая прямой, и концы отрезка
точками
и
.
Прямая
совпадает с медианой, проведённой из
точки
к середине отрезка
–
точке
.
Далее задача совпадает с задачей 1*:
записываем уравнение прямой, проходящей
через две заданные точки записывают в
форме
:
,
где
=
.
Пример
(и образец оформления):
Общая часть.
Пусть задан треугольникего вершинами:
,
,
.
Составить уравнения:
стороны ,высоты, медианы и
биссектрисы, проведённые из вершины A.
Решение
задачи 1*.
1). Уравнение прямой
,
содержащей точкии
:
,
где=
.
2). Вычислим
=
=
=4.
3). Запишем уравнение
прямой
:
,
или в виде:.
Ответ:.
Решение
задачи 2*.
1). Уравнение прямой
,
содержащей высоту,
опущенную на :
,
где=
.
2). Учитывая результат
задачи 1*, вычислим
=
=
.
3). Запишем уравнение
прямой
:
,
или в виде:.
Ответ:.
Решение
задачи 3*.
1). Уравнение
биссектрисы
определим двумя способами.
Способ-1.
Общая запись уравнения::y–
=
(x–
),
гдевычисляем
из выражения:=
,
причём,
.
1). Вычислим
,
.
Тогда=0.
2). Уравнение
принимает вид:
.
Ответ:.
Способ-2.
Общая запись канонического уравнения:
=
,
где=
,
причём,
=
=
;
=
=
=
.
1). Вычислим:
=
=(4,-3)
–(1,1)=(3,-4);=5
→=
(3,–4);
=
=(7,
9) –(1, 1)=(6,8);=10
→=
(3,4).
2). Тогда:
=
(3,–4)+
(3,4)=
(3,0)
→ принимаем:=(1,0).
3). Получили уравнение
в виде:
=
,
или:.
Ответ:.
Решение
задачи 4*.
1). Уравнение прямой
,
содержащей медиану,
проведённую из точкик середине отрезка
–
точке,
имеет вид:,
где=
.
2). Вычислим
координаты точки M
из условия: =
,
илиM==
=
.
3). Тогда:
=
=
и уравнение
принимает вид:
,
или:.
Ответ:.
Замечание:
при оформлении задания использование
рисунка (в карандаше, с использованием
чертёжных инструментов)обязательно!
Варианты
индивидуальных заданий:
|
Вар. |
Задание: |
Вар. |
Задание: |
||||
|
1. |
|
|
|
16. |
|
|
|
|
2. |
|
|
|
17. |
|
|
|
|
3. |
|
|
|
18. |
|
|
|
|
4. |
|
|
|
19. |
|
|
|
|
5. |
|
|
|
20. |
|
|
|
|
6. |
|
|
|
21. |
|
|
|
|
7. |
|
|
|
22. |
|
|
|
|
8. |
|
|
|
23. |
|
|
|
|
9. |
|
|
|
24. |
|
|
|
|
10. |
|
|
|
25. |
|
|
|
|
11. |
|
|
|
26. |
|
|
|
|
12. |
|
|
|
27. |
|
|
|
|
13. |
|
|
|
28. |
|
|
|
|
14. |
|
|
|
29. |
|
|
|
|
15. |
|
|
|
30. |
|
|
|
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #











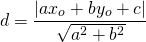
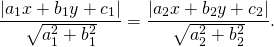
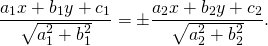
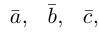
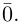
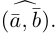
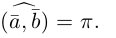
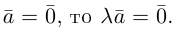
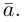
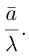
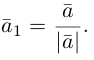
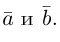
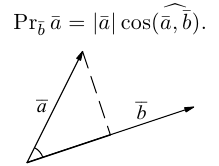
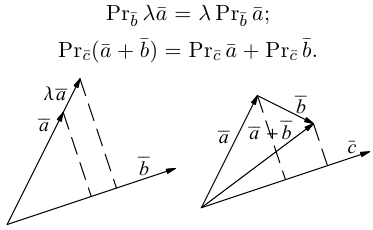
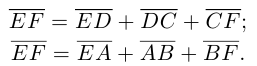
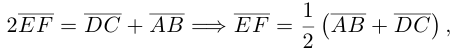
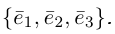
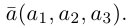
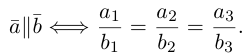
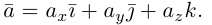
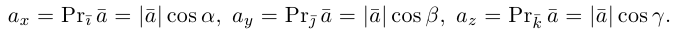
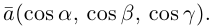
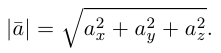
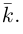

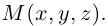
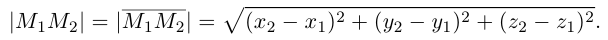
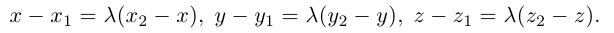
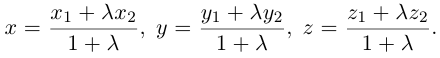
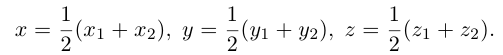
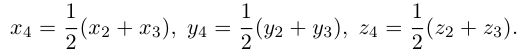
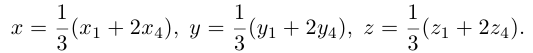
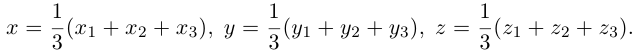


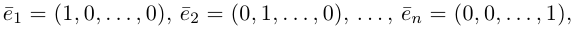
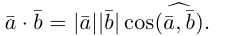
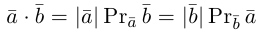
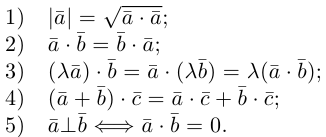
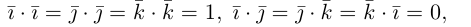
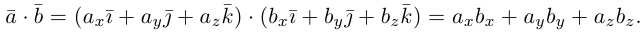
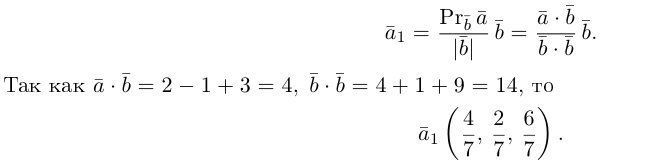
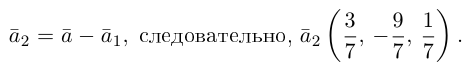
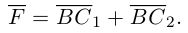
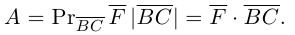
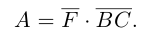
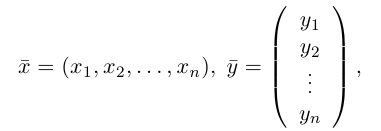
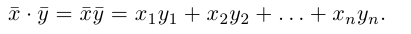
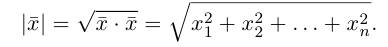
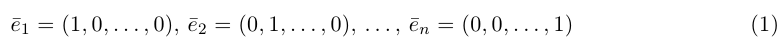
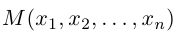

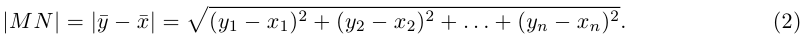
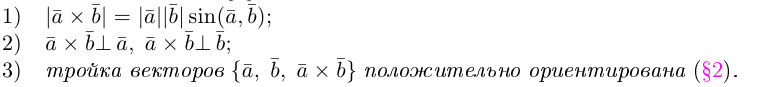
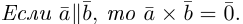
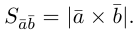
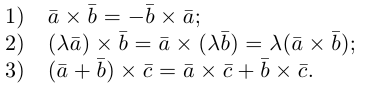
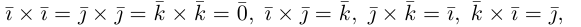
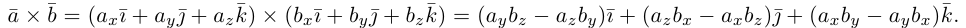
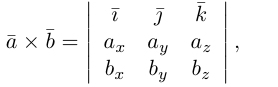
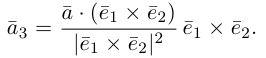
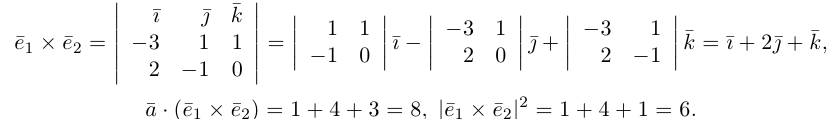
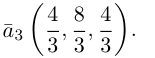
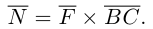
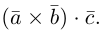
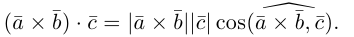
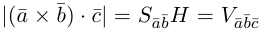
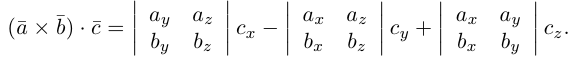
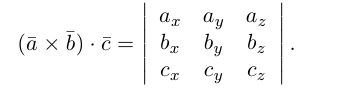
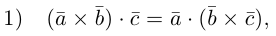
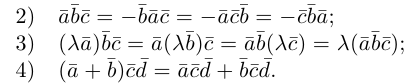
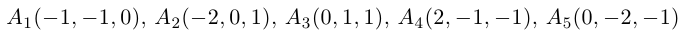
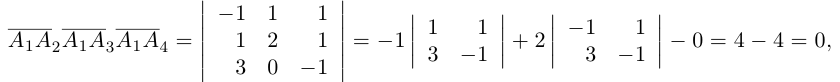
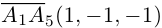
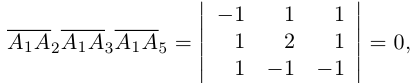
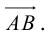
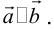

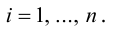
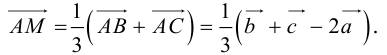
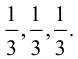
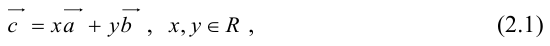
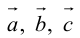 есть два коллинеарных, например:
есть два коллинеарных, например: 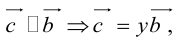
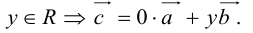
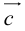 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 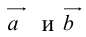 (рис. 7).
(рис. 7). 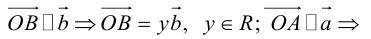
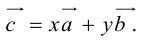
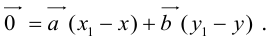
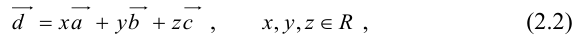
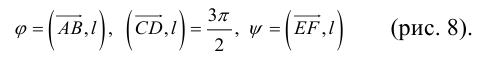
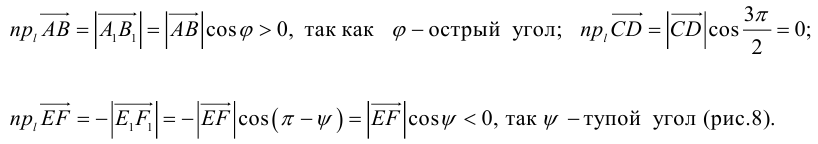
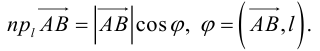
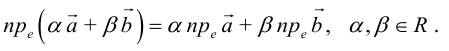
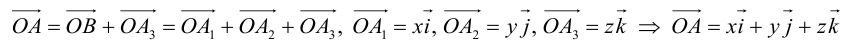
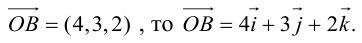
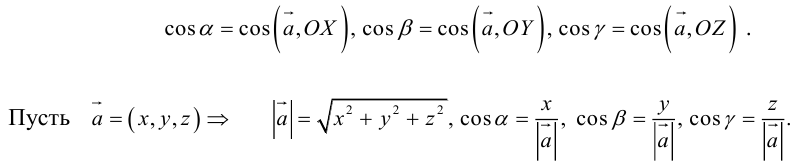
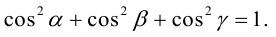
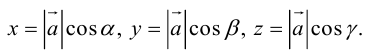
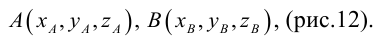
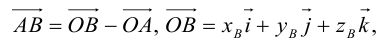
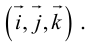
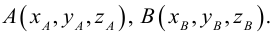

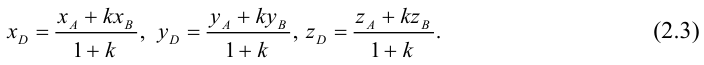
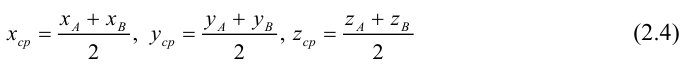
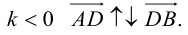
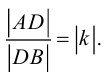
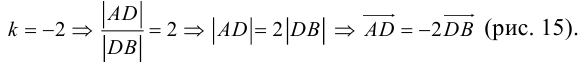
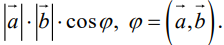
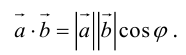
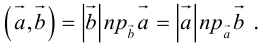
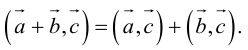
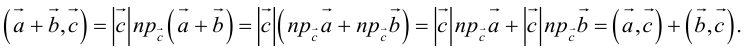
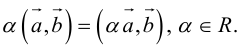
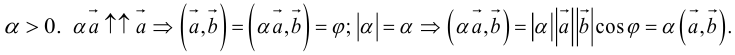
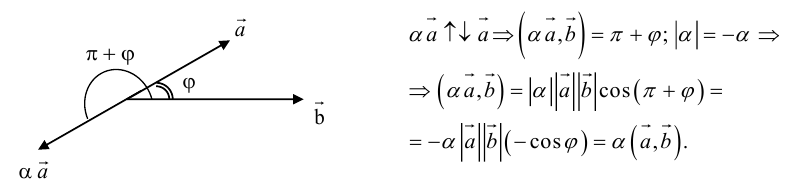
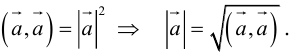
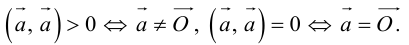
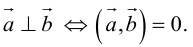
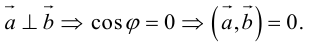
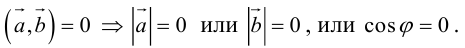
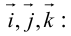
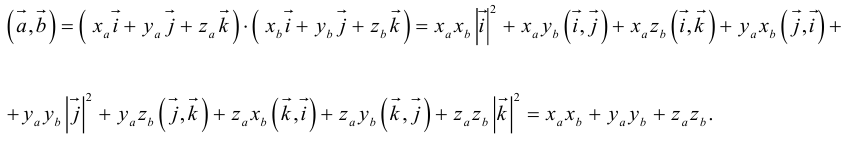

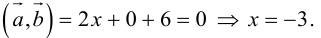
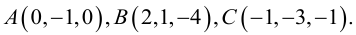

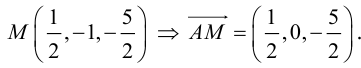
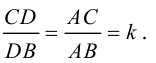
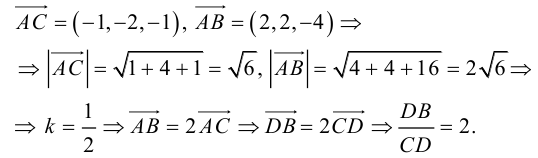
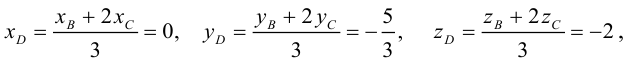
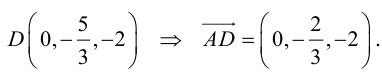
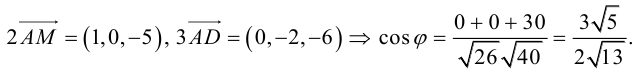
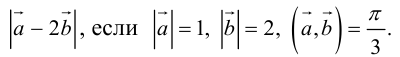
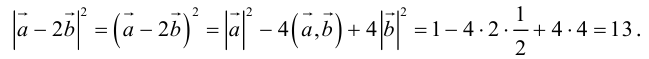
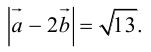
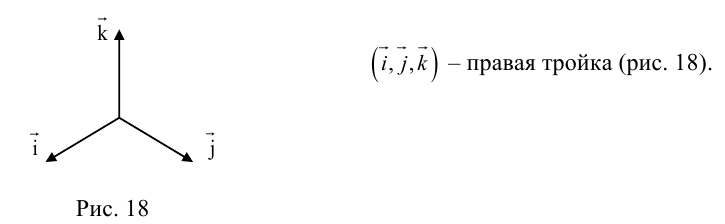
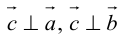 (
(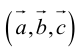 – правая.
– правая.