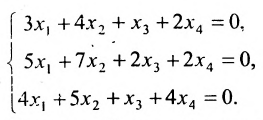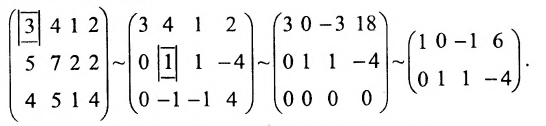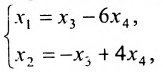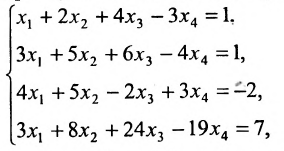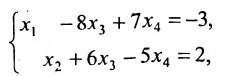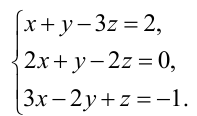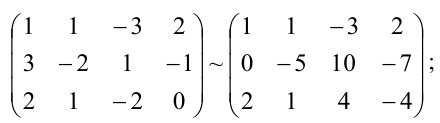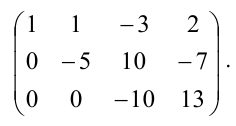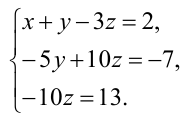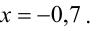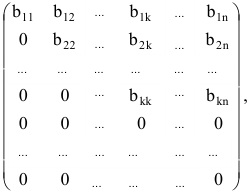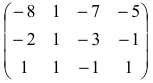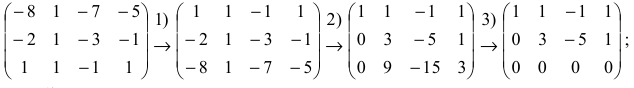Базисные (основные) и свободные (неосновные) переменные. Общее и базисное решения системы линейных алгебраических уравнений. Первая часть.
В теме «Теорема Кронекера-Капелли» было указано, что если ранг расширеной матрицы системы $widetilde{A}$ и ранг матрицы системы $A$ равны между собой, то заданная система линейных алгебраических уравнений (СЛАУ) совместна, т.е. имеет решение. Вопрос о количестве этих решений разрешим с помощью следствия из теоремы Кронекера. Согласно ему, если $rang A=rangwidetilde{A} = n$ ($n$ – количество неизвестных), то СЛАУ имеет единственное решение. Если же $rang A=rangwidetilde{A} < n$, то количество решений заданной СЛАУ бесконечно.
Особый интерес представляет именно случай $rang A=rangwidetilde{A} < n$, которым и займёмся в этой теме. Так как $rang A=rangwidetilde{A}$, то обозначим эти ранги просто буквой $r$, т.е. $rang A=rangwidetilde{A}=r$. Итак, $r < n$ и система неопределена, т.е. имеет бесконечное количество решений.
Что означает фраза «ранг матрицы равен $r$»? Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют.
Если коэффициенты при $r$ переменных совместной СЛАУ образуют базисный минор матрицы системы $A$, то эти $r$ переменных называют базисными или основными. Остальные $n-r$ переменных именуют свободными или неосновными.
Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.
Решение СЛАУ, в котором все свободные переменные равны нулю, называется базисным.
Во всех изложенных ниже примерах матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde{A}$.
Пример №1
Решить СЛАУ $
left { begin{aligned}
& 3x_1-6x_2+9x_3+13x_4=9\
& -x_1+2x_2+x_3+x_4=-11;\
& x_1-2x_2+2x_3+3x_4=5.
end{aligned} right.$. Если система является неопределённой, указать базисное решение.
Решение
Итак, мы имеем СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$
left( begin{array} {cccc|c}
3 & -6 & 9 & 13 & 9 \
-1 & 2 & 1 & 1 & -11 \
1 & -2 & 2 & 3 & 5 end{array} right) rightarrow
left|begin{aligned}
& text{поменяем местами первую и третью}\
& text{строки, чтобы первым элементом}\
& text{первой строки стала единица.}
end{aligned}right| rightarrow \
rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
-1 & 2 & 1 & 1 & -11 \
3 & -6 & 9 & 13 & 9
end{array} right)
begin{array} {l} phantom{0} \ r_2+r_1\ r_3-3r_1 end{array} rightarrow
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 3 & 4 & -6
end{array}right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-r_2end{array} rightarrow \
rightarrowleft( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)
$$
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.
И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde{A} = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на «ступеньках». Что это за «ступеньки» показано на рисунке:
На «ступеньках» стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Примечание. показатьскрыть
Базисные переменные выбраны: это $x_1$ и $x_3$. Остальные $n-r=2$ переменных (т.е. $x_2$ и $x_4$) являются свободными. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6 \
0 & 0 & 0 & 0 & 0
end{array}right)$ от нулевой строки:
$$
left( begin{array} {cccc|c}
1 & -2 & 2 & 3 & 5\
0 & 0 & 3 & 4 & -6
end{array}right)
$$
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:
Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 3 & -6 & 0 & -4
end{array}right)
begin{array} {l} phantom{0} \ 1/3cdot{r_2} end{array} rightarrow
left( begin{array} {cc|ccc}
1 & 2 & 5 & 2 & -3\
0 & 1 & -2 & 0 & -4/3
end{array}right)
begin{array} {l} r_1-2r_2 \ phantom{0} end{array} rightarrow \
rightarrow left(begin{array} {cc|ccc}
1 & 0 & 9 & 2 & -1/3\
0 & 1 & -2 & 0 & -4/3
end{array}right).
$$
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Если вспомнить, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, то получим:
$$
left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.
$$
Нами получено общее решение заданной СЛАУ. Чтобы найти базисное решение, нужно все свободные переменные приравнять к нулю. Т.е. полагая $x_2=0$ и $x_4=0$, будем иметь:
$$
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.
$$
Решение $x_1=9$, $x_2=0$, $x_3=-2$, $x_4=0$ и является базисным решением данной СЛАУ. В принципе, задавая свободным переменным иные значения, можно получить иные частные решения данной системы. Таких частных решений бесконечное количество. Например, принимая $x_2=-4$ и $x_4=1$, получим такое частное решение: $left{begin{aligned}
& x_1=frac{2}{3};\
& x_2=-4;\
& x_3=-frac{10}{3};\
& x_4=1.
end{aligned}right.$. Базисное решение, которые мы нашли ранее – лишь одно из бесконечного множества частных решений заданной СЛАУ.
Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=9+2x_2-frac{1}{3}x_4$ и $x_3=-2-frac{4}{3}x_4$ в левую часть первого уравнения, получим:
$$
3x_1-6x_2+9x_3+13x_4=3cdot left(9+2x_2-frac{1}{3}x_4right)-6x_2+9cdot left(-2-frac{4}{3}x_4right)+13x_4=9.
$$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Ответ: Общее решение: $left{begin{aligned}
& x_1=9+2x_2-frac{1}{3}x_4;\
& x_2in R;\
& x_3=-2-frac{4}{3}x_4;\
& x_4 in R.
end{aligned}right.$, базисное решение: $
left{begin{aligned}
& x_1=9;\
& x_2=0;\
& x_3=-2;\
& x_4=0.
end{aligned}right.$.
Пример №2
Решить СЛАУ
$$left{begin{aligned}
& x_1-2x_2+4x_3+2x_5=0;\
& 4x_1-11x_2+21x_3-2x_4+3x_5=-1; \
& -3x_1+5x_2-13x_3-4x_4+x_5=-2.
end{aligned}right.$$
Если система является неопределённой, указать базисное решение.
Решение
Похожий пример уже был решен в теме «метод Крамера» (пример №4). Переменные $x_4$ и $x_5$ были перенесены в правые части, а дальше применялись стандартные операции метода Крамера. Однако такой метод решения не гарантирует достижения результата. Например, мы переносим некие переменные в правую часть, а оставшийся определитель оказывается равным нулю, – что тогда? Решать перебором? 
$$
left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
4 & -11 & 21 & -2 & 3 & -1\
-3 & 5 & -13 & -4 & 1 & -2
end{array} right)
begin{array} {l} phantom{0} \r_2-4r_1\r_3+3r_1end{array} rightarrow
left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -3 & 5 & -2 & -5 & -1\
0 & -1 & -1 & -4 & 7 & -2
end{array} right) rightarrow \
rightarrow left|begin{aligned}
& text{поменяем местами вторую и третью}\
& text{строки, чтобы диагональным элементом}\
& text{второй строки стало число (-1).}
end{aligned}right|rightarrow
left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & -3 & 5 & -2 & -5 & -1
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\r_3-3r_1end{array} rightarrow \
rightarrow left( begin{array} {ccccc|c}
1 & -2 & 4 & 0 & 2 & 0\
0 & -1 & -1 & -4 & 7 & -2\
0 & 0 & 8 & 10 & -26 & 5
end{array} right).
$$
Матрица системы и расширенная матрица системы приведены к трапециевидной форме. Ранги этих матриц равны между собой и равны числу 3, т.е. $rang A=rangwidetilde{A} = 3$. Так как ранги равны между собой и меньше, чем количество переменных, то согласно следствию из теоремы Кронекера-Капелли данная система имеет бесконечное количество решений.
Количество неизвестных $n=5$, ранги обеих матриц $r=3$, поэтому нужно выбрать три базисных переменных и $n-r=2$ свободных переменных. Применяя тот же метод «ступенек», что и в предыдущем примере, выберем в качестве базисных переменных $x_1$, $x_2$, $x_3$, а в качестве свободных переменных – $x_4$ и $x_5$.
Столбцы №4 и №5, которые соответствуют свободным переменным, перенесём за черту. После этого разделим третью строку на 8 и продолжим решение методом Гаусса:
$$
left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 8 & 5 & -10 & 26
end{array} right)
begin{array} {l} phantom{0} \ phantom{0}\1/8cdot{r_3}end{array} rightarrow
left( begin{array} {ccc|ccc}
1 & -2 & 4 & 0 & 0 & -2\
0 & -1 & -1 & -2 & 4 & -7\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1-4r_3 \r_2+r_3\ phantom{0}end{array} rightarrow \
left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & -1 & 0 & -11/8 & 11/4 & -15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l} phantom{0} \ -1cdot{r_2}\ phantom{0}end{array} rightarrow
left( begin{array} {ccc|ccc}
1 & -2 & 0 & -5/2 & 5 & -15\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
begin{array} {l}r_1+2r_2 \ phantom{0}\ phantom{0}end{array} rightarrow\
rightarrowleft( begin{array} {ccc|ccc}
1 & 0 & 0 & 1/4 & -1/2 & -15/2\
0 & 1 & 0 & 11/8 & -11/4 & 15/4\
0 & 0 & 1 & 5/8 & -5/4 & 13/4
end{array} right)
$$
Из последней матрицы имеем общее решение заданной СЛАУ: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$. Базисное решение получим, если приравняем свободные переменные к нулю, т.е. $x_4=0$, $x_5=0$:
$$
left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.
$$
Ответ: Общее решение: $left{begin{aligned}
& x_1=frac{1}{4}-frac{1}{2}x_4-frac{15}{2}x_5;\
& x_2=frac{11}{8}-frac{11}{4}x_4+frac{15}{4}x_5;\
& x_3=frac{5}{8}-frac{5}{4}x_4+frac{13}{4}x_5;\
& x_4 in R;\
& x_5 in R.
end{aligned}right.$, базисное решение: $left{begin{aligned}
& x_1=frac{1}{4};\
& x_2=frac{11}{8};\
& x_3=frac{5}{8};\
& x_4=0;\
& x_5=0.
end{aligned}right.$.
Продолжение этой темы рассмотрим во второй части, где разберём ещё два примера с нахождением общего решения.
Системой
уравнений называется общим решением
совместная система A1x1+A2x2+…+Anxn=B (1), если
выполняется следующее
условие:
A1’x1+A2’x2+…+An’xn=B (2)
система
(2) общее решение сист. (1)
условия:1)система
(1) и (2) должны быть равносильны
2)система
векторов A1,A2,..,An в сист. уравнений (2) явл.
Разрешённой системой векторов
Набор
неизвестных системы уравнения (1)
называются базисными,
если векторы при этих неизвестных
образуют базис системы A1A2…An
не
базисные неизвестные принято называть
свободными.
21)
Однородные
СЛУ. Свойства однородной СЛУ.
Система
линейных уравнений называется однородной,
если все свободные члены=0
однородная
система в векторной форме: A1x1+A2x2+…+Anxn=
θ
вектороно-матричная:AX=
θ
свойства;
1)если k1,k2-решение
ОС,то сумма решений явл. Решением (k1+k2)
2)линейная комбинация векторов k1…kn
также будет решенеием
Утверждения:
1)
если r(A)=n, то система имеет единственное
решение(θ)
2) если r(A)<n, то система
имеет множество решений ≠ 0
Однородная
система — всегда
совместна, так как x1=x2=x3=…=xn=0 является
решением
системы.
22)Теорема о нулевом
и ненулевом решении однородной
СЛУ(док-во). Теорема о числе линейно-независимых
решений однородной СЛУ.
Теоремы о
ненулевых решениях однородной системы :
-
Для того, чтобы система однородных
уравнений имела ненулевые решения,
необходимо и достаточно, чтобы ранг r
ее основной матрицы был меньше числа
n неизвестных, т. е. r<n.
Допустим,
система, ранг которой равен, имеет
ненулевое решение. Очевидно, что
не
превосходит
.
В случае
система
имеет единственное решение. Поскольку
система однородных линейных уравнений
всегда имеет нулевое решение, то именно
нулевое решение и будет этим единственным
решением. Таким образом, ненулевые
решения возможны только при
.
Следствие
1: Однородная система уравнений, в которой
число уравнений меньше числа неизвестных,
всегда имеет ненулевое решение.
Доказательство:
Если у системы уравнений
,
то ранг
системы
не превышает числа уравнений
,
т.е.
.
Таким образом, выполняется условие
и,
значит, система имеет ненулевое решение.
Следствие
2: Однородная система
уравнений
с
неизвестными
имеет ненулевое решение тогда и только
тогда, когда ее определитель равен нулю.
Доказательство:
Допустим, система
линейных
однородных уравнений, матрица которой
с
определителем
,
имеет ненулевое решение. Тогда по
доказанной теореме
,
а это значит, что матрица
вырожденная,
т.е.
-
Для того, чтобы однородная
система n линейных
уравнений с n неизвестными имела
ненулевые решения, необходимо и
достаточно, чтобы ее определитель D был
равен нулю, т. е. D=0.
Теорема
о числе линейно независимых решений
однородной СЛУ
Число линейно-независимых
решений однородной СЛУ не превосходит
числа n-r(A).
23)Фундаментальная
система решений однородной СЛУ. Теорема
об условиях существования фундаментальной
системы решений однородной СЛУ(док-во).
Фундаментальная
система решений (ФСР) представляет
собой набор линейно
независимых решений
однородной системы
уравнений.
Система F1,F2…Fk
называется ФСР, если выполняются условия:
а) вектора F1,F2..Fk
линейно-независимы
б) k=n*r(A)
– число решений равно разности количества
неизвестных и ранга системы
Теорема
об условии существования ФСР однородной
СЛУ
Однородная система
уравнений имеет фундаментальную систему
решений n-r(A)=0
Д-во: Если r(A)=r, то базис
сист. векторов, состоящий из матр. А,
состоит из r-векторов. Для определённости
первые r векторов образуют базис системы
A1…An.Каждый вектор,не вошедший в базис
разложим по базису
A1…Ar.
Ar+1=A1k1r+1+…+Arkrr+1
Ar+2=A1k1r+2+…+Arkrr+2
……………………………
An=A1k1n+…+Arkrn
-
Перепишем эти
разложения в следующем
виде:-A1k1r+1-…-Arkrr+1+Ar+1*1+Ar+1*0+…+An*0=
θ-A1k1r+2-…-Arkrr+2+Ar+1*0+Ar+2*1+…+An*0=
θ………………………………………………………
-A1k1n-…-Arkrn+Ar+1*0+Ar+2*0+…+An*1=
θF1=(-k1r+1;…;-krr+1;1;0;…;0)
F2=(-k1r+2;…;-krr+2;0;1;…;0)
……………………………
Fn=(-k1n;…;-krn;0;0;…;1)
Вектора
F1…Fn явл. Решением ОСУ
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Базисные и свободные переменные:
Пусть задана система
Элементарными преобразованиями системы линейных уравнений называются следующие преобразования:
- исключение из системы уравнения вида
- умножение обеих частей одного из уравнений системы на любое действительное число
;
- перестановка местами уравнений системы;
- прибавление к обеим частям одного из уравнений системы соответствующих частей другого уравнения, умноженных на любое действительное число не равное нулю.
Элементарные преобразования преобразуют данную систему уравнений в эквивалентную систему, т.е. в систему, которая имеет те же решения, что и исходная.
Для решения системы т линейных уравнений с т неизвестными удобно применять метод Гаусса, называемый методом последовательного исключения неизвестных, который основан на применении элементарных преобразований системы. Рассмотрим этот метод.
Предположим, что в системе (6.1.1)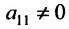
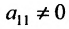
На первом шаге метода Гаусса исключим неизвестное 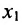
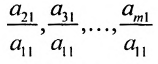
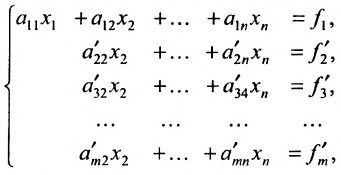
в которой коэффициенты 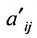
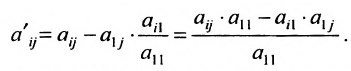
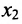
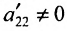
чтобы это условие было выполнено). Для исключения неизвестного 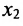
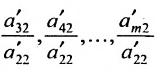
в которой коэффициенты 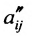
Продолжая аналогичные преобразования, систему (6.1.1) можно привести к одному из видов:
или
Совокупность элементарных преобразований, приводящих систему (6.1.1) к виду (6.1.4) или (6.1.5) называется прямым ходом метода Гаусса.
Отметим, что если на каком-то шаге прямого хода метода Гаусса получим уравнение вида:
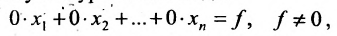
Итак, предположим, что в результате прямого хода метода Гаусса мы получили систему (6.1.4), которая называется системой треугольного вида. Тогда из последнего уравнения находим значение 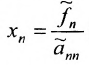
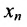
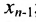
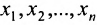
Если же в результате прямого хода метода Гаусса мы получим систему (6.1.5), которая называется системой ступенчатого вида, то из последнего уравнения этой системы находим значение неизвсстного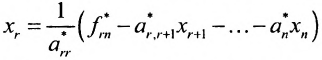
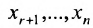
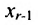
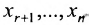
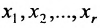
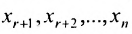
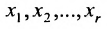
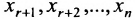
Таким образом, если система (6.1.1) путём элементарных преобразований приводится к треугольному виду (6.1.4), то она имеет единственное решение, если же она приводится к системе ступенчатого вида (6.1.5), то она имеет бесконечное множество решений. При этом неизвестные 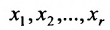
Практически удобнее преобразовывать не саму систему уравнений (6.1.1), а расширенную матрицу системы, соединяя последовательно получающиеся матрицы знаком эквивалентности
Формализовать метод Гаусса можно при помощи следующего алгоритма.
Алгоритм решения системы m линейных уравнений с n неизвестными методом Гаусса
1. Составьте расширенную матрицу коэффициентов системы уравнений так, чтобы 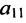
2. Выполните первый шаг метода Гаусса: в первом столбце начиная со второй строки, запишите нули, а все другие элементы вычислите по формуле
Матрица после первого шага примет вид
3. Выполните второй шаг метода Гаусса, предполагая, что 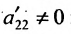
После второго шага матрица примет вид
4. Продолжая аналогичные преобразования, придёте к одному из двух случаев:
а) либо в ходе преобразований получим уравнение вида
тогда данная система несовместна;
б) либо придём к матрице вида:
где 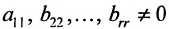
связано с тем, что в процессе преобразований матрицы исключаются строки, состоящие из нулей.
5. Использовав конечную матрицу, составьте систему, при этом возможны два случая:
5.1. r=n:
Система имеет единственное,решение 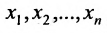
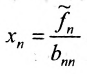
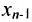
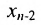
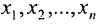
5.2. 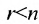
Тогда r неизвестных будут базисными, а остальные (n-r) — свободными. Из последнего уравнения выражаете неизвестное 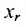
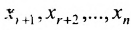
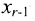
Система имеет в этом случае бесконечное множество решений.
Приведенный алгоритм можно несколько видоизменить и получить алгоритм полного исключения, состоящий в выполнении следующих шагов. На первом шаге:
- составляется расширенная матрица;
- выбирается разрешающий элемент расширенной матрицы
(если
, строки матрицы можно переставить так, чтобы выполнялось условие
);
- элементы разрешающей строки (строки, содержащей разрешающий элемент) оставляем без изменения; элементы разрешающего столбца (столбца, содержащего разрешающий элемент), кроме разрешающего элемента, заменяем нулями;
- все другие элементы вычисляем по правилу прямоугольника: преобразуемый элемент равен разности произведений элементов главной диагонали (главную диагональ образует разрешающий элемент и преобразуемый) и побочной диагонали (побочную диагональ образуют элементы, стоящие в разрешающей строке и разрешающем столбце):
— разрешающий элемент (см. схему).
Последующие шаги выполняем по правилам:
1) выбирается разрешающий элемент 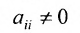
2) элементы разрешающей строки оставляем без изменения;
3) все элементы разрешающего столбца, кроме разрешающего элемента, заменяем нулями; • •
4) все другие элементы матрицы пересчитываем по правилу прямоугольника.
На последнем шаге делим элементы строк на диагональные элементы матрицы, записанные слева от вертикальной черты, и получаем решение системы.
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Из последней матрицы находим следующее решение системы
уравнении:
Ответ:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
Система привелась к ступенчатому виду (трапециевидной форме):
в которой неизвестные 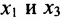
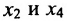
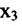
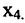
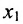
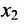
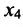
в котором 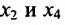
Если в общем решении положить 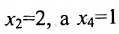
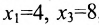
Ответ: система имеет бесконечное множество решений, общее решение которой записывается в виде:
Пример:
Решить систему уравнений:
Решение:
Составим расширенную матрицу системы, и применим алгоритм полного исключения, обозначая разрешающий элемент символом
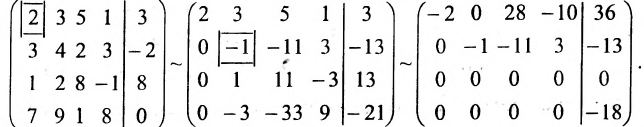
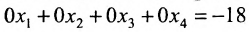
Ответ: система несовместна.
Замечание 1. Если дана система уравнений (6.1.1), в которой число уравнений m равно числу неизвестных n (m=n) и определитель этой системы 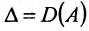
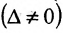
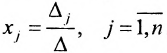
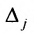
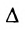
Если же такую систему (m-n) записать в матричной форме AX=F, то её решение можно найти по формуле 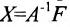
Замечание 2. Используя метод Гаусса, тем самым и алгоритм полного исключения, можно находить обратную матрицу. Для этого составляется расширенная матрица, в которой слева от вертикальной черты записана матрица А, а справа — единичная матрица. Реализовав алгоритм полного исключения, справа от вертикальной черты получаем обратную матрицу, а слева — единичную.
Пример:
Найти обратную матрицу для матрицы:
Решение:
Так как
то обратная матрица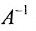
тогда
Покажем, что
ответ
Исследование совместности и определённости системы. Теорема Кронекера-Капелли
Рассмотрим систему (6.1.1) m линейных уравнений с n неизвестными при любых m и n (случай m=n не исключается). Вопрос о совместности системы решается следующим критерием.
Теорема 6.2.1. (критерий Кронкера-Капелли). Для того, чтобы система линейных уравнений(6.1.1) была совместна, необходимо и достаточно, чтобы ранг матрицы А системы был равен рангу расширенной матрицы 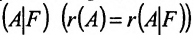
Доказательство и Необходимость:
Предположим, что система (6.1.1) совместна и 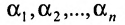
Из этих равенств следует, что последний столбец матрицы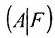
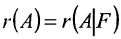
Достаточность. Пусть 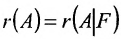
столбцов матрицы А, которые одновременно будут базисными столбцами и матрицы 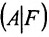
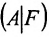
где 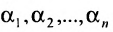
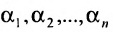
эта система совместна.
Совместная система линейных уравнений (6.1.1) может быть либо определенной, либо неопределенной.
Следующая теорема даст критерий определенности.
Теорема 6.2.2. Совместная система линейных уравнений имеет единственное решение тогда и только тогда, когда ранг матрицы А системы равен числу п ее неизвестных.
Таким образом, если число уравнений m системы (6.1.1) меньше числа ее неизвестных n и система совместна, то ранг матрицы системы 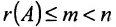
В случае 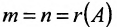
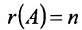
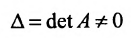
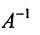
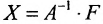
Следует отметить, что, решая систему (6.1.1) методом Гаусса, мы определяем и совместность, и определённость системы.
Пример:
Исследовать на совместность и определённость следующую систему линейных уравнений:
Решение:
Составим расширенную матрицу заданной системы. Определяя её ранг, находим тем самым и ранг матрицы системы. Для нахождения ранга матрицы применим алгоритм метода Гаусса.
Из последней матрицы следует, что ранг расширенной матрицы 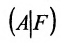
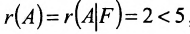
- Заказать решение задач по высшей математике
Однородные системы линейных уравнений
Система линейных уравнений (6.1.1) называется однородной, если все свободные члены 
Эта система всегда совместна, так как очевидно, что она имеет нулевое решение
Для однородной системы важно установить, имеет ли она ненулевые решения. Этот факт устанавливается следующей теоремой.
Теорема 6.3.1. Для того, чтобы однородная система имела ненулевые решения, необходимо и достаточно, чтобы ранг г матрицы А системы был меньше числа неизвестных n (r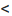
Доказательство. Необходимость. Пусть система (6.3.1) имеет ненулевое решение. Тогда она неопределённая, т.к. имеет еще и нулевое решение. В силу теоремы 6.2.2 ранг матрицы неопределённой системы не может равняться n потому что при r(А)=n система определённая. Следовательно, 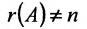
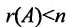
Достаточность. Если 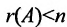
Следствие 1. Если число неизвестных в однородной системе больше числа уравнений, то однородная система имеет ненулевые решения.
Доказательство. Действительно, ранг матрицы системы (6.3.1) не может превышать m. Но так как по условию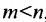
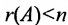
Следствие 2. Для того, чтобы однородная система с квадрат-ной матрицей имела ненулевые решения, необходимо и достаточно, чтобы её определитель 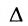
Доказательство. Рассмотрим однородную систему с квадратной матрицей:
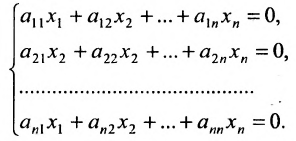
Если определитель матрицы системы 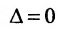
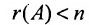
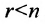
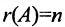
Пример:
Решить систему однородных линейных уравнений:
Решение:
Составим матицу системы и применим алгоритм полного исключения:
Из последней матрицы следует, что 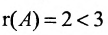
Используя последнюю матрицу, последовательно находим общее решение:
Неизвестные 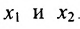
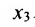
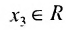
Фундаментальная система решений. Общее решение неоднородной системы линейных уравнений
Рассмотрим систему однородных линейных уравнений
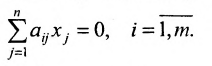
Любое решение
системы m линейных однородных уравнений с n неизвестными можно рассматривать как вектор-строку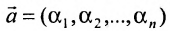
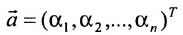
1) сумма двух решений также является решением системы, т.е.
если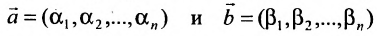
(6.4.1), то и 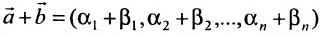
2) произведение решений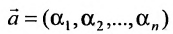
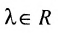
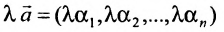
Из приведенных свойств следует, что
3) линейная комбинация решений системы (6.4.1) является решением этой системы.
В частности, если однородная система (6.4.1) имеет хотя бы одно ненулевое решение, то из него умножением на произвольные числа, можно получить бесконечное множество решений.
Определение 6.4.1. Фундаментальной системой решений для системы однородных линейных уравнений (6.4.1) называется линейно независимая система решений, через которую линейно выражается любое решение системы (6.4.1).
Заметим, что если ранг матрицы системы (6.4.1) равен числу неизвестных n (r(А)=n), то эта система не имеет фундаментальной системы решений, так как единственным решением будет нулевое решение, составляющее линейно зависимую систему. Существование и число фундаментальных решений определяется следующей теоремой.
Теорема 6.4.1. Если ранг матрицы однородной системы уравнений (6.4.1) меньше числа неизвестных (r(А)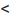
Сформулируем алгоритм построения фундаментальной системы решений:
- Выбираем любой определитель
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
- Свободным неизвестным придаём поочерёдно значения, равные элементам первой, второй и т.д. строк определителя
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
- Из полученных n-r решений составляют фундаментальную систему решений.
Меняя произвольно определитель 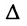
Пример:
Найти общее решение и фундаментальную систему решений для однородной системы уравнений:
Решение:
Составим матрицу системы и применим алгоритм полного исключения.
Для последней матрицы составляем систему:
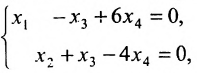
, из которой находим общее решение:
в котором 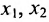
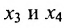
Построим фундаментальную систему решений. Для этого выбираем определитель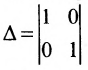
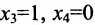
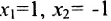
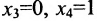
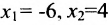
Таким образом, построенные два решения (1; -1; 1; 0) и (-6; 4; 0; 1) составляют фундаментальную систему решений.
Если ранг матрицы системы однородных линейных уравнений (6.4.1) на единицу меньше числа неизвестных: 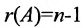
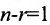
Рассмотрим теперь неоднородную систему m линейных уравнений с n неизвестными (6.1.1). Если в системе (6.1.1) положить 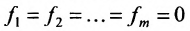
Решения системы (6.1.1) и её приведенной системы удовлетворяют свойствам:
- Сумма и разность любого решения системы (6.1.1) и любого решения её приведенной системы является решением неоднородной системы.
- Все решения неоднородной системы можно получить, прибавляя к одному (любому) её решению поочерёдно все решения её приведенной системы.
Из этих свойств следует теорема.
Теорема 6.4.2. Общее решение неоднородной системы (6.1.1.) определяется суммой любого частного решения этой системы и общего решения её приведенной системы.
Пример:
Найти общее решение системы:
Решение:
Составим расширенную матрицу (A|F) заданной системы и применим алгоритм полного исключения:
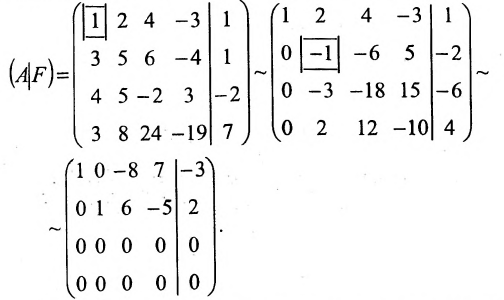
Преобразованной матрице соответствует система уравнений:
из которой находим общее решение системы:
, где 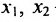
Покажем, что это общее решение определяется суммой любого частного решения заданной системы и общего решения приведенной системы.
Подставляя вместо свободных неизвестных 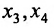
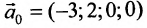
Очевидно, что общее решение приведенной системы имеет вид:
Суммируя частное решение заданной системы и общее решение приведенной системы, получим общее решение (6.4.2) исходной системы.
Отметим, что общее решение системы (6.1.1) можно представить в векторном виде:
где 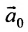
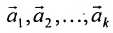
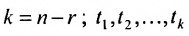
Формула (6.4.4) называется общим решением системы (6.1.1) в векторной форме.
Запишем общее решение системы примера 6.4.1 в векторной форме. Для этого определим фундаментальную систему решений приведенной системы. Возьмём определитель 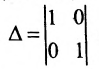
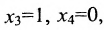
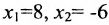
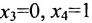
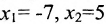
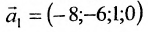
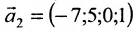
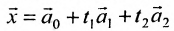
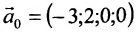
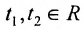
Определение метода Гаусса
Исторически первым, наиболее распространенным методом решения систем линейных уравнений является метод Гаусса, или метод последовательного исключения неизвестных. Сущность этого метода состоит в том, что посредством последовательных исключений неизвестных данная система превращается в ступенчатую (в частности, треугольную) систему, равносильную данной. При практическом решении системы линейных уравнений методом Гаусса удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу этой системы, выполняя элементарные преобразования над ее строками. Последовательно получающиеся в ходе преобразования матрицы обычно соединяют знаком эквивалентности.
Пример:
Решить систему уравнений методом Гаусса:
Решение:
Выпишем расширенную матрицу данной системы 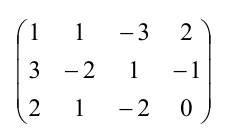
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
б) третью строку умножим на (-5) и прибавим к ней вторую:
В результате всех этих преобразований данная система приводится к треугольному виду:
Из последнего уравнения находим 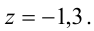
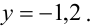
Вычисление метода Гаусса
Этот метод основан на следующей теореме.
Теорема:
Элементарные преобразования не изменяют ранга матрицы.
К элементарным преобразованиям матрицы относят:
- перестановку двух параллельных рядов;
- умножение какого-нибудь ряда на число, отличное от нуля;
- прибавление к какому-либо ряду матрицы другого, параллельного ему ряда, умноженного на произвольное число.
Путем элементарных преобразований исходную матрицу можно привести к трапециевидной форме
где все диагональные элементы 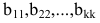
Пример:
Найти ранг матрицы
1) методом окаймляющих миноров;
2 ) методом Гаусса.
Указать один из базисных миноров.
Решение:
1. Найдем ранг матрицы методом окаймляющих миноров. Выберем минор второго порядка, отличный от нуля. Например,
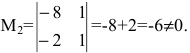
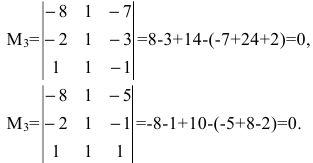
2. Найдем ранг матрицы методом Гаусса. Производя последовательно элементарные преобразования, получим:
- переставили первую и третью строки;
- первую строку умножили на 2 и прибавили ко второй, первую строку умножили на 8 и прибавили к третьей;
- вторую строку умножили на -3 и прибавили к третьей.
Последняя матрица имеет трапециевидную форму и ее ранг равен двум. Следовательно, ранг исходной матрицы также равен двум.
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Функция одной переменной
- Производная функции одной переменной
- Дифференциальные уравнения с примерами
- Обратная матрица — определение и нахождение
- Ранг матрицы — определение и вычисление
- Определители второго и третьего порядков и их свойства




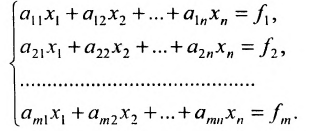
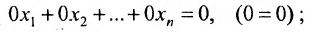
 ;
;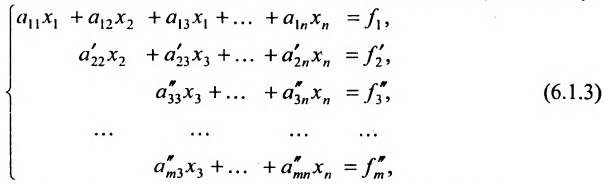
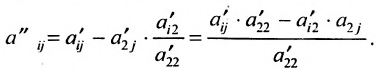
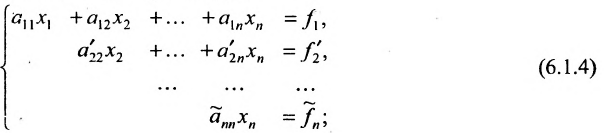
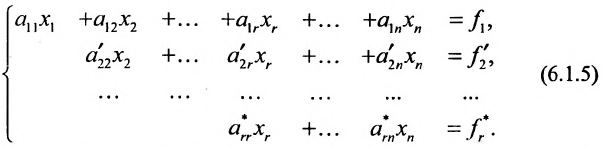

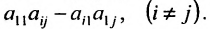
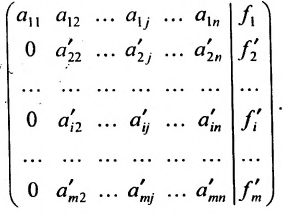
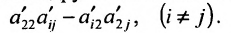

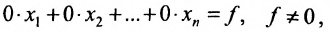
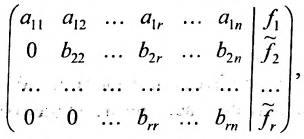
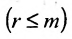
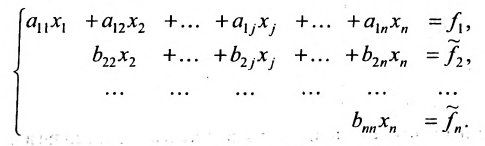
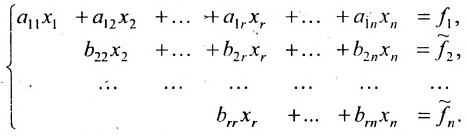
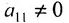 (если
(если 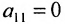 , строки матрицы можно переставить так, чтобы выполнялось условие
, строки матрицы можно переставить так, чтобы выполнялось условие 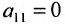 );
);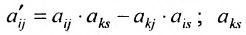 — разрешающий элемент (см. схему).
— разрешающий элемент (см. схему).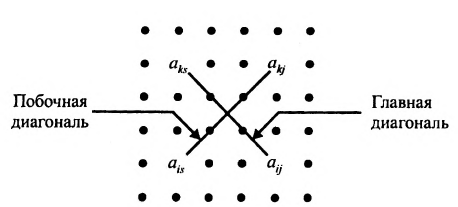
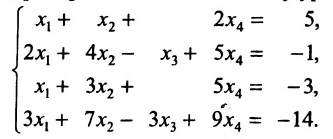


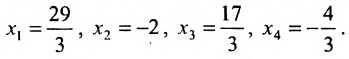
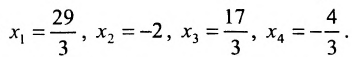
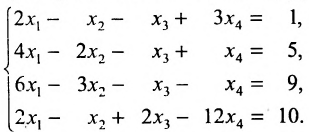

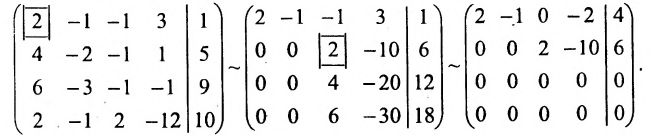

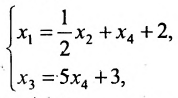
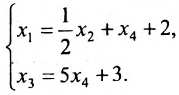
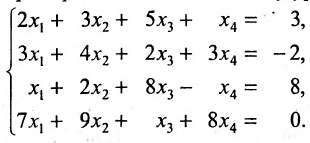
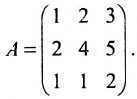
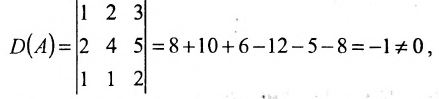

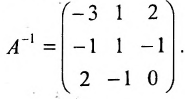
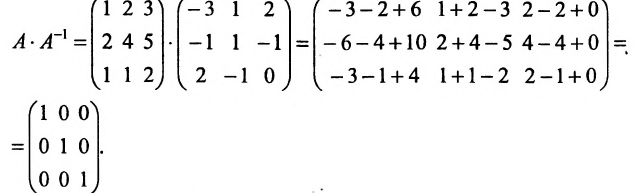
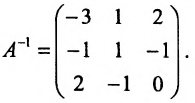
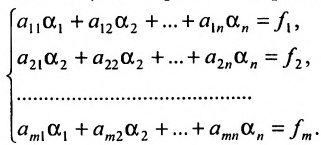
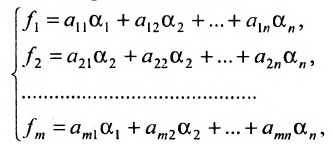
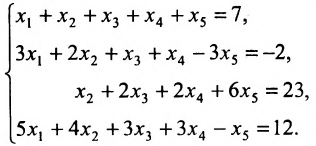

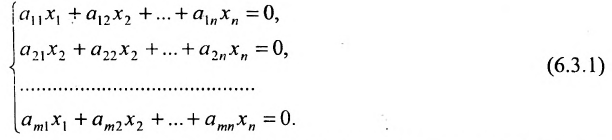
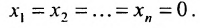
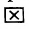
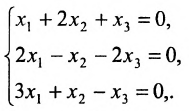
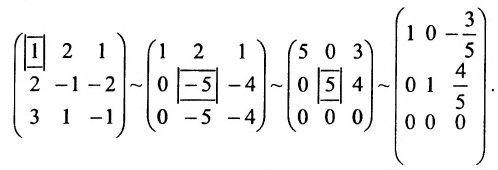
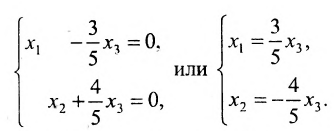
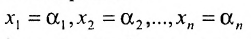
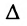 порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.
порядка n-r, отличный от нуля, в частности, определитель порядка n-r, у которого элементы главной диагонали равны единице, а остальные — нули.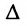 , и каждый раз из общего решения находим соответствующие значения базисных неизвестных.
, и каждый раз из общего решения находим соответствующие значения базисных неизвестных.