Как найти барометрическую высоту

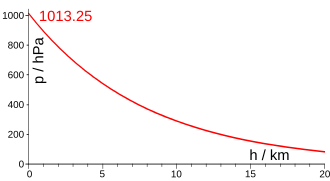
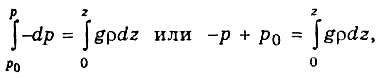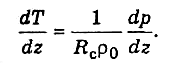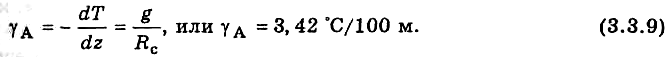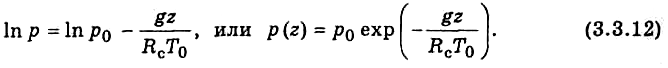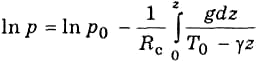Существует множество различных способов решения задачи по измерению высоты архитектурных сооружений и многоэтажных зданий. Курьезная история произошла с известным датским физиком, лауреатом нобелевской премии Нильсом Бором, который в студенческие годы на экзамене решал именно эту задачу при помощи барометра. При этом он предложил более двадцати вариантов решения. Помимо вполне разумных способов были и такие, которые вызывают улыбку, показывая остроумие и незаурядность мышления знаменитого ученого, например: «Закопать башню в землю. Вынуть башню. Полученную яму заполнить барометрами. Зная диаметр башни и количество барометров, приходящееся на единицу объема, рассчитать высоту башни». Если бы на месте Нильса Бора был Галилео Галилей, то он сбросил бы барометр с башни и по времени свободного падения определил бы высоту башни. Правда, в этом случае барометр пришел бы в негодность. Если бы нашу задачу решал математик, то он измерил бы длину тени от башни и от барометра и, зная размер барометра, при помощи пропорций определил бы высоту башни. Однако, ни один из этих способов не годится, чтобы измерить высоту горы или местности над уровнем моря. Давайте попробуем разобраться, как можно при помощи барометра измерить высоту горы.

Прямое назначение барометра – измерять атмосферное давление. Его существование открыл еще в XVII веке итальянский физик и математикЭванджелиста Торричелли, он же и создал первый барометр. Несколько позднее французский физик Блез Паскаль не только подтвердил существование атмосферного давления, но и обнаружил его уменьшение с высотой, что и позволяет определять высоту при помощи барометра. Зависимость давления от высоты определяется так называемой барометрической формулой:

где – атмосферное давление на высоте , – атмосферное давление на высоте , – молярная масса воздуха, – ускорение свободного падения¸ – универсальная газовая постоянная, – температура воздуха. После небольших математических преобразований, приравнивая к 0, получаем:

Например, если летом при температуре 27⁰С давление у подножия горы было 750 мм.рт.ст. (торр), а на вершине – 650 мм.рт.ст. (торр), то высота горы будет примерно 1255 м. Барометрическая формула достаточно громоздка и не очень удобна для быстрых расчетов, поэтому при измерении относительно невысоких гор лучше пользоваться хоть и менее точным, но более удобным соотношением: при подъеме на каждые 12 м атмосферное давление уменьшается примерно на 1 мм.рт.ст.

Следует также отметить еще один интересный факт. В связи с тем, что при увеличении высоты над уровнем моря атмосферное давление уменьшается, вместе с ним уменьшается и температура кипения воды. Так на высоте 5000 м атмосферное давление уменьшается примерно до 400 мм.рт.ст., поэтому температура кипения воды на этой высоте немногим больше 80⁰С, в то время как при нормальном давлении атмосферы вода кипит при 100⁰С. Об этом нужно помнить, собираясь в горы.

Предлагаем вам найти свой оригинальный способ решения задачи по измерению высоты.

Автор: Матвеев К.В., методист ГМЦ ДО г.Москвы

Источник

Вопрос может показаться странным, но я слышал, что в физике измеряют высо́ты зданий именно при помощи барометра. Так что эта процедура применяется ещё с древних времён. Ну, может быть, вернее сказать — со Средних веков.

Даже сэр Эрнест Резерфорд на экзамене задавал подобный вопрос Нильсу Бору, и последний сходу выпалил сразу пять способов, как можно точно измерить высоту любого дома с помощью барометра. Согласитесь, Нильс Бор был далеко не глупым парнем, а Резерфорд, конечно, был великим физиком и не стал бы задавать глупые вопросы. А я прочёл об этом где-то в одной занимательной книге. Но конкретно способы там не указывались. Мне стало интересно, что же мог ответить Бор.

Итак, как определить высоту дома, если у нас есть барометр? Допустим, стандартный безжидкостный барометр-анероид без всякой электроники.

Чем больше способов, тем лучше.

Дополнительный вопрос: сгодятся ли эти методы для любого здания, будь то крошечная хижина (хата, халупа, халабуда, бунгало и т. п.) или же Бурдж-Халифа?

Да, действительно, с помощью барометра можно измерить высоту здания. Ниже перечислены пять способов, которые мог бы назвать Нильс Бор:

С помощью формулы Барометрической высоты: Для этого нужно измерить атмосферное давление на уровне моря и на уровне здания. Разница между этими значениями позволит определить барометрическую высоту здания. Например, если на уровне моря давление составляет 1013 гектопаскалей, а на уровне здания — 950 гектопаскалей, то барометрическая высота здания составит 63 метра.
С помощью формулы Гайдера: Эта формула учитывает не только атмосферное давление, но и температуру воздуха. Для ее использования необходимо измерить температуру на уровне моря и на уровне здания, а также давление на этих высотах. Формула позволяет вычислить барометрическую высоту здания с учетом влияния температуры.
С помощью метода розы: Этот метод основан на наблюдении за тем, как меняется угол наклона ствола розы в зависимости от высоты. Чем выше мы поднимаемся, тем меньше угол наклона ствола розы. Измерив этот угол на уровне моря и на уровне здания, можно определить разницу в высоте.
С помощью метода термобарических уровней: Этот метод основан на наблюдении за тем, как меняется давление воздуха при движении вверх и вниз по зданию. Измерив эти изменения, можно вычислить высоту здания.
С помощью метода пульсаций атмосферы: Этот метод основан на наблюдении за пульсациями атмосферы, которые возникают при прохождении звуковой волны между зданием и местом, где находится барометр. Измерив время, за которое звуковая волна проходит расстояние между зданием и барометром, можно вычислить высоту здания.

alexm12
[257K]

3 месяца назад

1.Бросаем барометр с крыши здания и закаем время падения. По формуле 0.5gt^2 считаем высоту здания.

2.Вечером, ставим барометр на землю рядом со зданием, находим отношение высоты барометра к длине его тени, измеряем длину тени здания, считаем высоту здания.

3.Бросаем барометр с крыши здания, засекаем время его касания земли время когда до нас доходит звук удара. Скорость звука 340 м/с. Считаем высоту.

4.В обмен на барометр узнаем у коменданта (или кто там им командует) здания высоту здания.

5.Отходим от здания, держа барометр на вытянутой руке на такое расстояние, когда барометр будет размером со здание. Измеряем размер барометра, измеряем расстояние от глаза до барометра, измеряем расстояние от глаза до здания, вычисляем размер здания

Источник

Барометрическая формула высоты

Основное уравнение статики выводится из предположения равновесия воздуха по вертикали. В действительности этого может и не быть. Всегда существует некоторая разница между силой тяжести и силой вертикального барического градиента, отличная от нуля. Эта разность незначительна, но основное уравнение статики с учётом этого при использовании в расчётах будет выполняться не абсолютно строго, но с большой степенью точности.

С помощью барометрических формул можно решать ряд задач статики атмосферы:

зная давление на одном уровне атмосферы и среднюю температуру столба воздуха, можно найти давление на другом уровне (задача приведения давления к уровню моря);
зная давление воздуха на двух уровнях и среднюю температуру столба воздуха, можно найти разность уровней (задача барометрического нивелирования);
зная разность уровней и величины давления на них, можно найти среднюю температуру столба воздуха.

Барометрическая формула высоты показывает, как меняется атмосферное давление с высотой в зависимости от температуры воздуха:

где z₁ и z₂ — ограниченный слой поверхности атмосферы в виде высоты уровней нижележащего и вышележащего слоёв; Тm — среднее значение температуры воздуха между уровнями z₁ и z₂.

Быстрые подсчёты, связанные с оценкой изменения давления с высотой, можно сделать с помощью так называемой барической ступени.

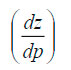
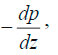
Барическая ступень — это величина, обратная вертикальному барическому градиенту составляющая прирост высоты, при котором атмосферное давление падает на единицу.

Под барической ступенью или барометрической ступенью понимается высота, на которую нужно подняться или опуститься, чтобы давление воздуха изменилось на 1 мбар или 1 гПа, исходя из расчёта по формуле

Барическая ступень прямо пропорциональна температуре воздуха и обратно пропорциональна величине самого давления. Чем больше высота и, следовательно, чем ниже давление атмосферы, тем больше барическая ступень. При одном и том же давлении барическая ступень будет больше при более высокой температуре воздуха, чем при более низкой. Кроме того, видно, что с увеличением высоты барическая ступень растёт, поскольку ρ уменьшается с высотой.

Сама барическая ступень оценивается приростом высоты, на котором давление падает на 1 мбар или 1 гПа. При температуре воздуха 0 ºC и давлении 1000 гПа барическая ступень равна 8 м/гПа. Следовательно, у поверхности Земли нужно подняться примерно на 8 м, чтобы давление воздуха упало на 1 гПа. С приростом температуры воздуха барическая ступень растёт на 0,4 % на каждый градус. На больших высотах барическая ступень может достигать значений 15–30 м/гПа.

Литература

Гидрометеорологическое Обеспечение Мореплавания — Глухов В.Г., Гордиенко А.И., Шаронов А.Ю., Шматков В.А. [2014]

MirMarine – образовательный морской сайт для моряков.
На нашем сайте вы найдете статьи по судостроению, судоремонту и истории мирового морского флота. Характеристики судовых двигателей, особенности устройства вспомогательных механизмов и систем.

Морская история

Основное уравнение гидростатики

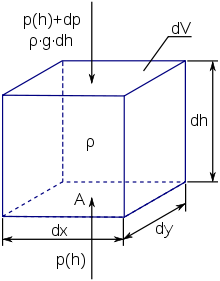
Элемент объема с решающим влиянием

Изменение давления и плотности атмосферы с высотой описывается основным уравнением гидростатики . Чтобы вывести это, рассмотрим кубический элемент объема с основанием и бесконечно малой высотой , который содержит воздух плотности . Снизу на основание действует только сила атмосферного давления . Сила, действующая на основание сверху, складывается из веса воздушной массы, содержащейся в объеме, и силы, оказываемой атмосферным давлением на верхней стороне. На этом уровне атмосферное давление на величину отличается от давления, действующего на нижней стороне; власть, которую он осуществляет, следовательно .
А , rho , п ,

Все воздушные потоки пришли в состояние гидростатического равновесия. Чтобы равновесие сохранялось и рассматриваемый элемент объема оставался в покое, сумма всех сил, действующих на него, должна быть равна нулю:

p cdot A- rho g , { mathrm {d}} h cdot A- (p + { mathrm {d}} p) cdot A = 0

Сокращайте и переставляйте расходные материалы

${ frac {{ mathrm {d}} p} {{ mathrm {d}} h}} = - rho g$

После закона идеального газа плотность может быть выражена как ,
rho , ${ displaystyle rho = { tfrac {pM} {RT}}}$

так что в конечном итоге результат:

${ frac {{ mathrm {d}} p} {{ mathrm {d}} h}} = - { frac {pMg} {RT}}$

это

Основное уравнение гидростатики указывает величину изменения атмосферного давления при небольшом изменении высоты . Как показывает отрицательный знак , отрицательный, когда положительный; давление уменьшается с увеличением высоты. Например, при среднем давлении воздуха на уровне моря ( = 1013 гПа) при температуре 288 K (= 15 ° C) давление снижается на 0,12 гПа при перепаде высот в один метр или на 1 гПа при перепаде высот в 1 метр. 8,3 метра. Перепад высот, соответствующий перепаду давления в 1 гПа, является уровнем барометрической высоты . На более высоких (более низких ) высотах и при более высоких температурах давление воздуха изменяется медленнее, и уровень барометрической высоты увеличивается.

Как правило, для заданных высот требуются явные значения давления и плотности. При необходимости отсюда также можно определить разницу давлений для большей разницы в высоте. Искомое решение основного уравнения получается разделением переменных

${ frac {{ mathrm {d}} p} {p}} = - { frac {Mg} {RT}} , { mathrm {d}} h$

и последующее интегрирование между искомыми высотами или соответствующими давлениями:

$int _ {{p (h_ {0})}} ^ {{p (h_ {1})}} { frac {{ mathrm {d}} p} {p}} = - int _ {{ h_ {0}}} ^ {{h_ {1}}} { frac {Mg} {RT}} , { mathrm {d}} h$

Интеграция левых дает . Чтобы интегрировать правую сторону, необходимо знать зависимость высоты от и . Ускорение свободного падения можно считать постоянным для не слишком больших высот. Температура меняется сложным и непредсказуемым образом с высотой. Поэтому необходимо сделать упрощающие предположения о температурном профиле .
$ln left ({ frac {p (h_ {1})} {p (h_ {0})}} right)$ Т (ч)

Изотермическая атмосфера

Классическая формула барометрической высоты, которая чаще всего цитируется во вводной литературе и на школьных уроках, применяется к частному случаю, когда температура одинакова на каждой высоте, то есть атмосфера изотермическая .

Вывод из основного уравнения гидростатики

Интегрирование основного уравнения гидростатики дает при постоянном значении :

${ displaystyle { begin {align} && int _ {p (h_ {0})} ^ {p (h_ {1})} { frac { mathrm {d} p} {p}} & = - { frac {Mg} {RT}} , int _ {h_ {0}} ^ {h_ {1}} mathrm {d} h \ iff && ln left ({ frac {p ( h_ {1})} {p (h_ {0})}} right) & = - { frac {Mg} {RT}} (h_ {1} -h_ {0}) = - { frac {Mg } {RT}} Delta h \ iff && { frac {p (h_ {1})} {p (h_ {0})}} & = mathrm {e} ^ {- { frac {Mg } {RT}} Delta h} \ iff && p (h_ {1}) & = p (h_ {0}) mathrm {e} ^ {- { frac {Mg} {RT}} Delta h} end {выровнено}}}$

Вводя масштаб высоты , формула высоты упрощается до
${ displaystyle h_ {s} = { tfrac {RT} {Mg}}}$

${ displaystyle p (h_ {1}) = p (h_ {0}) mathrm {e} ^ {- { frac { Delta h} {h_ {s}}}}}$

С каждым увеличением высоты давление воздуха уменьшается в раз . Таким образом, высота шкалы является естественной мерой высоты атмосферы и профиля давления в ней. В принятой здесь модели атмосферы она составляет около 8,4 км при температуре 15 ° C.
$ч_ {s}$

Следующее относится к плотности:

${ displaystyle rho (h_ {1}) = rho (h_ {0}) mathrm {e} ^ {- { frac { Delta h} {h_ {s}}}}}$

Для наблюдателя, спускающегося с горы, давление воздуха постоянно увеличивается, поскольку все более тяжелый столб воздуха давит на него. Увеличение экспоненциально, потому что воздух сжимаем : на каждый метр разницы в высоте вес столба воздуха, который весит на измерительной поверхности, увеличивается на вес объема столба, добавленного на это расстояние. Однако этот вес зависит от плотности воздуха, которая, в свою очередь, зависит от давления воздуха. Чем выше давление воздуха, тем быстрее давление воздуха растет (тем ниже спускается наблюдатель). Если переменная всегда изменяется на величину, пропорциональную самой переменной, изменение происходит экспоненциально.

Хотя давление не является постоянным, столб воздуха находится в механическом равновесии : отрицательный градиент давления равен силе тяжести на элемент объема. ${ displaystyle - partial _ {z} p (z) = g rho (z)}$

Вывод из статистической механики

В системе частиц, которая находится в тепловом равновесии при температуре (которая, следовательно, имеет одинаковую температуру повсюду) и частицы которой могут занимать непрерывно или дискретно распределенные уровни энергии , вероятность того, что частица в настоящее время находится на уровне энергии, дается формулой Больцмана распределение $E_ {j}$ $E_ {j}$

$P_ {j} = { frac {{ mathrm {e}} ^ {{- { frac {E_ {j}} {k _ {{{ mathrm {B}}}} T}}}}} { Z}}$

Тем самым это постоянная Больцмана и нормировочный множитель (так называемая сумма состояний ), который гарантирует , что сумма всех вероятностей равна 1. Если система состоит из частиц, количество частиц на уровне энергии является средним .
$к _ { mathrm {B}}$ $E_ {j}$ $n_ {j} = NP_ {j}$

Частица газа с массой обладает потенциальной энергией в гравитационном поле Земли и из-за своей температуры в среднем имеет тепловую энергию, то есть полную энергию . Если вы посмотрите на два элемента объема одинакового размера на высоте или , то частицы на высоте имеют энергию, которая на величину выше . Вероятность встречи с частицей в элементе большего объема связана с вероятностью встречи с ней в элементе меньшего объема как
$E _ {{ mathrm {pot}}} = mgh$ $E _ {{ mathrm {th}}}$ $E (h) = mgh + E _ {{ mathrm {th}}}$ h_0 $ч_ {1}$ $ч_ {1}$

${ frac {P (h_ {1})} {P (h_ {0})}} = { frac {{ mathrm {e}} ^ {{- { frac {E (h_ {1})} {k _ {{{ mathrm {B}}}} T}}}}} {{ mathrm {e}} ^ {{- { frac {E (h_ {0})} {k _ {{{ mathrm {B}}}} T}}}}}} = { mathrm {e}} ^ {{- { frac { Delta E} {k _ {{{ mathrm {B}}}} T }}}} = { mathrm {e}} ^ {{- { frac { Delta E _ {{ mathrm {pot}}}} {k _ {{{ mathrm {B}}}} T} }}}$

Для достаточно большого числа частиц плотности частиц ведут себя как вероятности их местоположения.
п (ч)

${ displaystyle { frac {n (h_ {1})} {n (h_ {0})}} = { frac {NP (h_ {1})} {NP (h_ {0})}} = mathrm {e} ^ {- { frac { Delta E _ { mathrm {pot}}} {k _ { mathrm {B}} T}}}}$

и из-за закона идеального газа то же соотношение
следует и для давления $p (h) = n (h) , k _ {{{ mathrm {B}}}} Т$

${ frac {p (h_ {1})} {p (h_ {0})}} = { mathrm {e}} ^ {{- { frac { Delta E _ {{ mathrm {pot}}) }} {k _ {{{ mathrm {B}}}} T}}}} = { mathrm {e}} ^ {{- { frac {mg Delta h} {k _ {{{ mathrm) {B}}}} T}}}} = { mathrm {e}} ^ {{- { frac {Mg} {RT}} Delta h}}$

где молярная масса и константа газа получаются путем умножения массы частицы или постоянной Больцмана со стороны постоянная Авогадро .
$к _ { mathrm {B}}$

Однако при рассмотрении энергии здесь предполагается принцип равного распределения . Это требование обычно выполняется только в плотной атмосфере, потому что только там происходит обмен энергиями между различными степенями свободы посредством столкновений между молекулами газа. Причина, по которой теорема о равномерном распределении обычно не применяется к энергии на высоте, заключается в том, что теорема о равномерном распределении может применяться непосредственно только к потенциалам, которые включены в функцию Гамильтона в виде квадрата. Поскольку высотная энергия входит в функцию Гамильтона только линейно, нельзя просто принять теорему однородности в очень тонких газах.

Атмосфера с линейным температурным профилем

Строго линейный температурный профиль состоит только в идеализированной идее спокойной атмосферы без конвекции без выравнивания температурного градиента за счет теплопроводности. Чтобы сделать это более удобным, была введена потенциальная температура . Хотя адиабатический градиент представляет собой градиент температуры, потенциальная температура постоянна; ЧАС. баланс. Это не имеет ничего общего с потенциальной энергией частицы в гравитационном поле ( ). Это становится особенно ясно по количеству степеней свободы . Частицы одинаковой массы, но разного числа степеней свободы имеют разные градиенты температуры.

Поскольку теплопроводность не должна играть роль в поддержании линейного температурного профиля, в действительности постоянный «перенос тепла» (теплопроводность) посредством быстрой циркуляции может иметь лишь незначительное влияние. Поскольку отсутствие конвекции и циркуляции не может происходить одновременно, линейный ход всегда слегка изменяется из-за переноса тепла всех видов, наиболее известным из которых является конденсация водяного пара, которая приводит к более низкому перепаду температуры («влажно-адиабатический» «, термин, вводящий в заблуждение).

Распределение температуры (адиабатическая атмосфера)

Из уравнения изменения давления

${ frac {{ mathrm {d}} p} {p}} = - { frac {Mg} {RT}} , { mathrm {d}} h$

и уравнение адиабатического изменения состояния, записанное с использованием логарифмических производных

${ frac {{ mathrm {d}} p} {p}} = { frac { kappa} { kappa -1}} { frac {{ mathrm {d}} T} {T}}$

линейное понижение температуры следует сразу в соответствии с

${ mathrm {d}} T = - { frac {Mg} {R kappa / ( kappa -1)}} { mathrm {d}} h$

При средней молекулярной массой атмосферного газа
М = 0,02896 кг моль ^-1 , то ускорение силы тяжести
г = 9,807 м с ^-2 , то универсальная газовая постоянная
R = 8,314 Дж К ^-1 моль ^-1 ,
а показатель адиабаты из (сухой) air = 1,402 получается градиент температуры

${ frac {{ mathrm {d}} T} {{ mathrm {d}} h}} = - , { frac {0 {,} 979 , { mathrm {K}}} {100 , { mathrm {m}}}}$

Это примерно соответствует температурному градиенту, указанному ниже. Однако это в основном определяется влажным адиабатическим расширением: показатель влажной адиабаты меньше, чем показатель сухой адиабаты. В случае атмосферы с чистым водяным паром градиент температуры будет

$left. { frac {{ mathrm {d}} T} {{ mathrm {d}} h}} right | _ {{{ mathrm {H_ {2} O}}}} = - { гидроразрыв {0 {,} 562 , { mathrm {K}}} {100 , { mathrm {m}}}}$

Дополнительные ограничения адиабатического подхода: если воздух становится очень холодным, показатель адиабаты изменяется, даже если воздух сухой. На очень больших высотах (низкая плотность) длина свободного пробега также очень велика, так что уравнения для газа практически не применимы. Кроме того, парниковый эффект также нарушает адиабатический подход (отсутствие обмена энергией с окружающей средой).

Распределение плотности и давления

Как правило, температура непостоянна, но меняется с высотой. Самый простой подход к объяснению такой изменчивости предполагает линейное уменьшение с высотой. Постоянный градиент температуры следует из адиабатического соотношения, описанного выше.

${ displaystyle a = - { frac { mathrm {d} T} { mathrm {d} h}} = { frac { kappa -1} { kappa}} { frac {Mg} {R} }}$

так что к температуре применимо следующее:
Т (ч)

$T (h) = T (h_ {0}) - a cdot (h-h_ {0}) qquad Rightarrow qquad T (h) = T (h_ {0}) cdot left (1- { frac {a (h-h_ {0})} {T (h_ {0})}} right) = T (h_ {0}) cdot left (1 - { frac {a Delta h}) {T (h_ {0})}} вправо)$

где — (положительная) величина вертикального градиента температуры атмосферы , которая указывает, на сколько Кельвинов температура воздуха понижается на метр разницы высот. Таким образом, интеграл по правой части основного уравнения равен

$- int _ {{h_ {0}}} ^ {{h_ {1}}} { frac {Mg} {RT}} , { mathrm {d}} h = - int _ {{h_ { 0}}} ^ {{h_ {1}}} { frac {Mg} {R , (T (h_ {0}) - a cdot (h-h_ {0}))}} , { mathrm {d}} h = - { frac {Mg} {R}} int _ {{h_ {0}}} ^ {{h_ {1}}} { frac {1} {(T (h_ { 0}) + ah_ {0}) - ah}} , { mathrm {d}} h$

Потому что

$int { frac {1} {b-ax}} , { mathrm {d}} x = - { frac {1} {a}} , ln (b-ax)$

является решением интеграла

$- { frac {1} {a}} ln (, (T (h_ {0}) + ah_ {0}) - ah) vert _ {{h_ {0}}} ^ {{h_ {1 }}} = - { frac {1} {a}} ln left ({ frac {T (h_ {0}) - a (h_ {1} -h_ {0})} {T (h_ { 0})}} справа)$

так что в целом из интеграла по основному уравнению

${ displaystyle ln left ({ frac {p (h_ {1})} {p (h_ {0})}} right) = + { frac {Mg} {R}} , { frac {1} {a}} ln left ({ frac {T (h_ {0}) - a (h_ {1} -h_ {0})} {T (h_ {0})}} right) = + { frac {Mg} {R}} , { frac {1} {a}} ln left (1 - { frac {a Delta h} {T (h_ {0})}} Правильно)}$

барометрическая формула для линейной кривой температуры выглядит следующим образом:

${ displaystyle p (h_ {1}) = p (h_ {0}) mathrm {e} ^ {+ { frac {Mg} {R}} { frac {1} {a}} ln left (1 - { frac {a Delta h} {T (h_ {0})}} right)}}$

или из-за ${ mathrm {e}} ^ {{y cdot ln (x)}} = x ^ {y}$

${ displaystyle p (h_ {1}) = p (h_ {0}) left (1 - { frac {a Delta h} {T (h_ {0})}} right) ^ { frac { Mg} {Ra}} = p (h_ {0}) left (1 - { frac { kappa -1} { kappa}} { frac {Mg Delta h} {RT (h_ {0})) }} right) ^ { frac { kappa} { kappa -1}}}$

То же самое и с плотностью

${ displaystyle rho (h_ {1}) = rho (h_ {0}) left (1 - { frac {a Delta h} {T (h_ {0})}} right) ^ { frac {Mg} {Ra kappa}} = rho (h_ {0}) left (1 - { frac { kappa -1} { kappa}} { frac {Mg Delta h} {RT ( h_ {0})}} right) ^ { frac {1} { kappa -1}}}$

Показатель здесь делится на, потому что соотношение плотность / давление является результатом адиабатического отношения между двумя величинами.

Эта расширенная формула барометрической высоты составляет основу функции барометрической высоты стандартной атмосферы в авиации . Во-первых, атмосфера делится на подслои, каждый с линейно интерполированным температурным профилем. Затем, начиная с самого нижнего слоя, рассчитываются температура и давление на верхнем пределе соответствующего подслоя и используются для нижнего предела верхнего слоя. Таким образом индуктивно создается модель всей атмосферы.

Типичные температурные градиенты

Как показывают измерения профилей температуры в атмосфере, предположение о линейном понижении температуры в среднем является хорошим приближением, даже если в отдельных случаях могут иметь место значительные отклонения, например, в погодных условиях инверсии . Основная причина снижения температуры с высотой — прогрев нижних слоев воздуха поверхностью земли, нагретой солнцем, в то время как верхние слои воздуха излучают тепло в космос. Кроме того, существуют сухие адиабатические или влажные адиабатические изменения температуры отдельных поднимающихся или падающих частиц воздуха и дополнительные модификации за счет процессов смешения между воздушными массами различного происхождения.

В горячих воздушных массах и во время процессов скольжения вверх градиент температуры принимает значения от 0,3 до 0,5 К на 100 м, в холодном воздухе обычно от 0,6 до 0,8 К на 100 м, в среднем при любых погодных условиях 0,65 К на 100 м. 100 м. В долинах частые инверсии почвы могут снизить средний градиент температуры до 0,5 К на 100 м, в зимние месяцы даже до 0,4 К на 100 м.

Описанные условия ограничиваются тропосферой . В стратосфере , температура падает значительно медленнее, в большинстве случаев это даже вновь возрастает, в основном из-за поглощения УФ — излучения в озоновом слое .

Для температурного градиента 0,65 К на 100 м показатель степени принимает значение 5,255:
${ Displaystyle mathrm { tfrac {Mg} {Ra}}}$

$p (h_ {1}) = p (h_ {0}) left (1 - { frac {0 {,} 0065 cdot Delta h} {T (h_ {0})}} right) ^ { {5 {,} 255}}$

Если показатель степени выражается изоэнтропическим коэффициентом, то:

$5 {,} 255 = { frac { kappa} { kappa -1}} quad Rightarrow quad kappa = 1 {,} 235$

Это означает 8,5 степеней свободы .

Средняя теплоемкость воздуха при любых погодных условиях определяется градиентом температуры:

${ displaystyle { frac { mathrm {d} T} { mathrm {d} h}} = { frac {0 {,} 65 , mathrm {K}} {100 , mathrm {m} }} = { frac {g} {c_ {p}}} = { frac {9 {,} 81 , { frac { mathrm {m}} { mathrm {s} ^ {2}}} } {c_ {p}}} quad Rightarrow quad c_ {p} = 1509 , { frac { mathrm {m} ^ {2}} { mathrm {K} ~ mathrm {s} ^ { 2}}} = 1509 , { frac { mathrm {Ws}} { mathrm {кг ~ K}}}}$

Это значение находится между значениями сухого воздуха (1005 Вт / (кг K)) и водяного пара (2034 Вт / (кг K)).

В следующей таблице показано соотношение между высотой и давлением (в среднем):

Температурный профиль атмосферы как функция барометрической высоты (поверхность земли = 1,013 бар) — тропопауза лучше всего аппроксимируется показателем изоэнтропы 0,19.

Высота в м	Давление в гПа
0	1013,25
500	954,61
1000	898,76
1500	845,58
2000 г.	794,98
2500	746,86
3000	701,12
3500	657,68
4000	616,45
4500	577,33
5000	540,25
6000	471,87
7000	410,66
8000	356,06
9000	307,48
10 000	264,42
11000	226,37

В этой форме формула высоты подходит для частого случая, когда температура и давление воздуха известны на одной из двух высот, но не существующий в настоящее время градиент температуры.

Уровни высоты

Уровень барометрической высоты — это расстояние по вертикали, которое необходимо преодолеть, чтобы добиться изменения давления воздуха на 1 гПа. У земли барометрическая высота составляет около 8 метров, 5,5 километров на высоте 16 метров и 11 километров на высоте 32 метра.

Формула высоты дает следующую таблицу для зависимости высоты и температуры от барометрического уровня высоты:

Уровень барометрической высоты в м / гПа
ЧАС	−15 ° С	0 ° C	15 ° С	30 ° С
0 мес.	7,5	7.9	8,3	8,8
500 м	7.9	8,3	8,7	9.2
1000 м	8,3	8,7	9.2	9,6
2000 м	9,3	9,7	10.1	10,6
3000 м	10,4	10,8	11.2	11,6

Практическое правило для средних высот и температур — «1 гПа / 30 футов». Авиаторы часто используют это округление для грубых расчетов.

Международная формула высоты

Если исходная высота установлена на уровне моря и предполагается среднее состояние атмосферы там, как описано в Международном стандарте атмосферы (температура 15 ° C = 288,15 K, давление воздуха 1013,25 гПа, градиент температуры 0,65 K на 100 м), международная формула высоты для тропосферы получается (срок действия до высоты 11 км):
h_0

${ displaystyle p (h) = 1013 {,} 25 cdot left (1 - { frac {0 {,} 0065 { frac { mathrm {K}} { mathrm {m}}} cdot h } {288 {,} 15 mathrm {K}}} right) ^ {5 {,} 255} mathrm {hPa}}$

${ displaystyle { color {White} p (h)} = p_ {0} cdot left (1 - { frac {0 {,} 0065 { frac { mathrm {K}} { mathrm {m) }}} cdot h} {T_ {0} }} right) ^ {5 {,} 255}}$

Эта формула позволяет рассчитать давление воздуха (в форме так называемого нормального давления ) на заданной высоте без знания температуры и температурного градиента. Однако точность в конкретном приложении ограничена, поскольку расчет основан только на средней атмосфере, а не на текущем ее состоянии .

Международная формула высоты, разрешенная в соответствии с высотой в рамках Международной стандартной атмосферы, для преобразования атмосферного давления p (h) (нормальное давление) в соответствующую высоту в метрах (м):

${ displaystyle h = { frac {288 {,} 15 mathrm {K}} {0 {,} 0065 { frac { mathrm {K}} { mathrm {m}}}}} cdot left (1- left ({ frac {p (h)} {1013 {,} 25 , mathrm {hPa}}} right) ^ { frac {1} {5 {,} 255}} Правильно)}$

Общий случай

Решение основного уравнения гидростатики является общим

${ displaystyle ln left ({ frac {p (h_ {1})} {p (h_ {0})}} right) = - int _ {h_ {0}} ^ {h_ {1}) } { frac {Mg} {RT}} , mathrm {d} h}$

соответственно

$p (h_ {1}) = p (h_ {0}) , { mathrm {e}} ^ {{- int _ {{h_ {0}}}} ^ {{h_ {1}}} { гидроразрыв {Mg} {RT}} , { mathrm {d}} h}}$

с интегралом, который еще предстоит решить.

Виртуальная температура

Газовая постоянная — это естественная постоянная, и ее можно нарисовать перед интегралом. Средняя молярная масса атмосферных газов , если не учитывать сильно изменяющееся содержание водяного пара, также практически постоянна в тропосфере и может быть помещена перед интегралом. Различная высота атмосферных газов с разным весом приведет к частичной сегрегации в спокойной атмосфере, так что более тяжелые компоненты будут накапливаться в нижних слоях, а более легкие компоненты — в верхних слоях; Однако вызванное погодой интенсивное перемешивание тропосферы препятствует этому. Изменяющееся содержание водяного пара и, в более общем плане, другие незначительные изменения M (особенно в верхних слоях атмосферы) можно учесть , используя соответствующую виртуальную температуру вместо фактической температуры . Следовательно, значение сухого воздуха на уровне моря можно использовать
для M.

Геопотенциальные высоты

Ускорение свободного падения уменьшается с высотой, что необходимо учитывать в случае большой разницы высот или требований высокой точности. Однако переменное ускорение свободного падения в подынтегральном выражении значительно затруднит интегрирование. Этого можно избежать, используя геопотенциал вместо геометрических высот. Представьте себе испытательную массу с переменной высотой от уровня моря . Поскольку она уменьшается с высотой, получаемая потенциальная энергия меньше, чем если бы она всегда имела значение уровня моря . Геопотенциальная высота равна высота, измеренная в геопотенциальных метрах, который должен быть преодолен математически для того , чтобы добавить такое же потенциальную энергию к массе с постоянным гравитационным ускорением (другими словами: он будет разделен гравитационным потенциалом Области то же самое. геопотенциальная высота — это эквипотенциальные поверхности в гравитационном поле).
ЧАС $Delta E _ {{ mathrm {pot}}}$ $г_ {0}$ h_p $г_ {0}$ $Delta E _ {{ mathrm {pot}}}$ h_p $г_ {0}$

Для геопотенциальной высоты, относящейся к геометрической высоте , должно применяться следующее :
ЧАС h_p

$Delta E _ {{ mathrm {pot}}} = int _ {0} ^ {h} mg (h) , { mathrm {d}} h = mg_ {0} cdot h_ {p}$

Из чего следует:

$g (h) , { mathrm {d}} h = g_ {0} , { mathrm {d}} h_ {p}$

Для отношения ускорения свободного падения на высоте к ускорению свободного падения на уровне моря применяется следующее, поскольку гравитационное поле уменьшается квадратично с расстоянием до центра Земли:
ЧАС $г_ {0}$

${ frac {g (h)} {g_ {0}}} = left ({ frac {R _ {{ mathrm {E}}}} {R _ {{ mathrm {E}}} + h }} right) ^ {2}$

с радиусом земли . Интеграция
$R _ {{ mathrm {E}}}$

${ mathrm {d}} h_ {p} = { frac {g (h)} {g_ {0}}} , { mathrm {d}} h = left ({ frac {R _ {{ mathrm {E}}}} {R _ {{ mathrm {E}}} + h}} right) ^ {2} { mathrm {d}} h$

запасы

$int _ {0} ^ {{h_ {p}}} { mathrm {d}} h_ {p} = int _ {0} ^ {h} left ({ frac {R _ {{ mathrm {E}}}} {R _ {{ mathrm {E}}} + h}} right) ^ {2} { mathrm {d}} h$

${ displaystyle iff h_ {p} = { frac {R _ { mathrm {E}} cdot h} {R _ { mathrm {E}} + h}}}$

$R _ {{ mathrm {E}}}$ следует установить на значение 6356 км. При необходимости следует также учитывать, что ускорение свободного падения на уровне моря зависит от географической широты.
$г_ {0}$

Таким образом, желаемые геометрические высоты должны быть преобразованы в геопотенциальные высоты только один раз перед расчетом; Вместо переменного ускорения свободного падения можно просто использовать постоянное значение уровня моря в формуле высоты. Для не слишком больших высот разница между геометрической и геопотенциальной высотами мала и часто незначительна:

геометрический	геопотенциал
0 мес.	0,0 м
500 м	500,0 м
1000 м	999,8 м
5000 м	4996,1 кв.м.
10000 м	9984,3 м

С учетом ускорения свободного падения на уровне моря , геопотенциальных высот и виртуальной температуры общая высота формулы упрощается до
$г_ {0}$ $h _ {{p0}}$ $h _ {{p1}}$

$p (h_ {1}) = p (h_ {0}) cdot exp left (- { frac {Mg_ {0}} {R}} int _ {{h _ {{p0}}}}) ^ {{h _ {{p1}}}} { frac {1} {T_ {v} (h_ {p})}} , { mathrm {d}} h_ {p} right)$

Остается решить интеграл , для которого необходимо знать только температурный профиль . Его можно определить в реальной атмосфере, например, по восхождениям радиозонда . Для упрощенных модельных атмосфер с постоянной или линейно изменяющейся температурой снова получаются формулы высоты типа, описанного в начале.
$1 / T_ {v}$ $Т_ {v} (h_ {p})$

Приложения

Понижение до уровня моря

теория

Давление воздуха ( QFE ) измеряется с помощью барометра зависит от метеорологического состояния атмосферы и высоты. Если информация от разных барометров должна сравниваться друг с другом в метеорологических целях (например, для определения местоположения области низкого давления или фронта), влияние высоты должно быть исключено из данных измерений. Для этого измеренные значения давления преобразуются в общую эталонную высоту, обычно на уровне моря . Это преобразование выполняется с использованием формулы высоты. Преобразование также называется уменьшением (даже если численное значение увеличивается), поскольку измеренное значение освобождается от нежелательных эффектов помех. В результате давление воздуха ( QNH ) снижается на уровне моря .

В зависимости от требований к точности необходимо использовать подходящую формулу высоты. В случае более низких требований фиксированный коэффициент преобразования может быть получен из формулы высоты для постоянной температуры, для которой необходимо выбрать репрезентативную температуру:

${ displaystyle p_ {0} = p (h) , mathrm {e} ^ {{ frac {Mg} {RT}} h}}$

Для высоты площадки 500 м и использования средней годовой температуры 6 ° C результат будет, например, B. коэффициент уменьшения 1,063, на который следует умножить измеренные значения.

Если требования несколько выше, можно учитывать текущую температуру воздуха. Их влияние показано в следующем примере, в котором давление воздуха 954,3 гПа, измеренное на высоте 500 м, уменьшено с помощью формулы высоты для линейного профиля температуры ( a = 0,0065 К / м), предполагающей различные температуры станции на уровне моря. :
Т (ч)

${ displaystyle p_ {0} = p (h) , left ({ frac {T (h)} {T (h) +0 {,} 0065 mathrm { frac {K} {m}} , h}} right) ^ {- 5 {,} 255} = p (h) , left ({ frac {T (h)} {T_ {0}}} right) ^ {- 5 { ,} 255}}$

	−10 ° С	0 ° C	10 ° C	20 ° C	30 ° С
$п_ {0}$	1017,9	1015,5	1013,3	1011,2	1009,3

T (h) = t (h) +273 {,} 15 , { mathrm {K}}

Если требуется более высокая точность, доступны текущие температуры воздуха и точность и калибровка используемого барометра оправдывают усилия, уменьшение всегда следует производить с использованием текущей температуры воздуха. Вариант линейной температурной кривой можно использовать как формулу высоты. Также можно использовать вариант с постоянным температурным профилем при условии, что используется текущая температура на половине высоты станции:

${ displaystyle p_ {0} = p (h) , mathrm {e} ^ {{ frac {Mg} {R , left (T (h) + a { frac {h} {2}}) right)}} h}}$

Этот вариант теоретически менее точен, поскольку не учитывает изменчивость температуры с высотой, а линейный вариант учитывает это приблизительно. Однако различия в высоте и температуре для метеостанций незначительны.

Формула снижения, рекомендованная Метеорологической службой Германии, соответствует варианту с постоянной температурной кривой. По температуре, измеренной на высоте площадки, температура на половине высоты площадки оценивается с помощью стандартного температурного градиента. Влажность воздуха учитывается через переход к соответствующей виртуальной температуре.

${ displaystyle p_ {0} = p (h) , mathrm {e} ^ {x}, quad x = { frac {g_ {0}} {R ^ {*} , (T (h) + C_ {h} cdot E + a { frac {h} {2}})}} , h}$

с участием

$п_ {0}$		Давление воздуха снижено до уровня моря
		Давление воздуха на высоте барометра (в гПа, с точностью до 0,1 гПа)
$г_ {0}$	= 9.80665 м / с²	Стандартное ускорение
$R ^ {*}$	= 287,05 м ² / (с²K)	Газовая постоянная сухого воздуха (= R / M)
		Высота барометра (в м с точностью до дм; высоту до 750 м можно рассчитать с геометрической высотой, выше которой должны использоваться геопотенциальные высоты)
		Температура в салоне (в К, где )
		Температура в салоне (в ° C)
	= 0,0065 К / м	вертикальный градиент температуры
		Давление паров фракции водяного пара (в гПа)
${ displaystyle C_ {h}}$	= 0,12 К / гПа	Коэффициент для учета изменения среднего давления пара с высотой (фактически зависит от станции, здесь как фиксированное среднее значение)

Если измеренная влажность воздуха недоступна, можно также использовать следующее приближение, основанное на долгосрочных средних значениях температуры и влажности:

$t (h) <9 {,} 1 , ^ {{ circ}} { mathrm {C}}: { tilde E} = 5 {,} 6402 cdot (-0 {,} 0916 + { mathrm {e}} ^ {{0 {,} 06 cdot t (h)}})$

$t (h) geq 9 {,} 1 , ^ {{ circ}} { mathrm {C}}: { tilde E} = 18 {,} 2194 cdot (1 {,} 0463 - { mathrm {e}} ^ {{- 0 {,} 0666 cdot t (h)}})$

упражняться

Сравнение нескольких барометров показывает ограниченную абсолютную точность имеющихся в продаже устройств.

Повышенные здесь требования к точности измерения атмосферного давления и высоты барометра обычно не могут быть выполнены метеорологом-любителем. С барометров Hobby метеостанций , систематические ошибки , по крайней мере 1 до 2 гПа , следует ожидать. Такая неопределенность соответствует неопределенности высоты площадки от десяти до двадцати метров через уровень барометрической высоты. Стремление определить высоту более точно, скорее всего, не приведет к более точному результату. В связи с этим следует также учитывать необходимость или избыточность учета влажности воздуха.

При необходимости рекомендуется использовать не фактическую высоту, а фиктивную высоту, которая наилучшим образом соответствует пониженному атмосферному давлению с информацией от ближайшего эталонного барометра (официальная метеостанция, аэропорт и т. Д.). Возможная систематическая погрешность барометра может быть в значительной степени компенсирована с помощью такой калибровки . Для этого рекомендуется сначала использовать приблизительный уровень снижения и сравнить свои собственные результаты со справочными данными за более длительный период времени (особенно при разных температурах). Если обнаружена систематическая разница, разность высот может быть рассчитана с использованием подходящей формулы высоты, которая на основе приблизительной высоты местоположения сдвигает уменьшенные высоты на желаемую величину. Исправленная таким образом сумма затем используется для будущих сокращений. Если температура не принимается во внимание во время снижения, калибровка должна основываться на ситуации при представительной температуре.

Типичный барометр для гостиной

Простые барометры в гостиной обычно настраиваются таким образом, чтобы сразу отображать пониженное давление воздуха. Обычно это делается с помощью винта на задней стороне корпуса, с помощью которого можно изменить предварительную нагрузку пружины ячейки давления . Таким образом, калибровка соответствует смещению шкалы отображения. Строго говоря, это неверно. Как показывают формулы для измерения высоты над уровнем моря, уменьшение должно производиться путем умножения на коэффициент калибровки, а не путем простого добавления константы: пониженное давление воздуха изменяется немногим более чем на один гПа, если давление воздуха на высоте объекта изменяется на один гПа. Следовательно, в дополнение к сдвигу пришлось бы немного растянуть шкалу. Однако ошибка, вызванная этим, меньше, чем ошибка, возникающая из-за того, что эти устройства игнорируют влияние температуры на снижение. Поскольку у вас нет возможности ввести высоту, калибровку можно выполнить только путем сравнения с эталонным барометром, что, в свою очередь, одновременно снижает систематические ошибки нулевой точки прибора. Калибровка должна выполняться для местоположения барометра (или местоположения на сопоставимой высоте). Нет смысла «правильно настраивать» устройство у дилера, если его потом повесили в совершенно другом месте. Если барометр используется на основании изменений атмосферного давления для получения краткосрочного прогноза погоды, точная калибровка менее важна.

Пределы

В общем, при сокращении измерений давления воздуха следует иметь в виду, что арифметически сложенный столб воздуха для большинства мест в действительности не может существовать, и поэтому не может быть «истинного» значения для « давления на уровне моря в данном месте». то есть точным путем достаточно сложных вычислений можно было бы приблизиться. Формулы сокращения частично основаны только на условных обозначениях и, помимо специальных научных приложений, в основном служат для того, чтобы сделать измеренные значения метеостанций максимально сопоставимыми. Пример фиктивности добавленного столба воздуха: На ровной местности, по которой холодный воздух не течет, воздух у земли может заметно остывать в ясные ночи из-за теплового излучения земли ( инверсия земли ). Расположенная там метеостанция зарегистрирует эту пониженную температуру и математически продолжит работу с обычным градиентом температуры вниз. Однако, если бы местность находилась на уровне моря, этот воздух не охладился бы из-за недостатка почвы, а фактически существующий столб воздуха имел бы значительно более высокую температуру, чем расчетная. Поэтому расчет предполагает слишком высокую плотность добавленного столба воздуха и приводит к более высокому пониженному давлению воздуха, чем было бы в той же погодной ситуации, если бы вся территория находилась на уровне моря.

Измерение барометрической высоты

Зависимость атмосферного давления от высоты также может использоваться для измерения высоты . Измерения барометрической высоты выполняются быстро и относительно легко, но их точность ограничена. Барометр, предназначенный для определения высоты, называется высотомером или высотомером . Процедура зависит от предполагаемого использования и требований к точности. Этот метод используется, среди прочего, для пеших прогулок и, с несколько более высокими требованиями к точности, при топографической съемке.

литература

Рихард Рюльманн : Измерения барометрической высоты и их значение для физики атмосферы. Лейпциг 1870, стр. 10-12, 21-24 ( цифровой ). (об истории)

W. Roedel: Физика нашей окружающей среды: Атмосфера. 3. Издание. Springer-Verlag, Берлин / Гейдельберг / Нью-Йорк 2000, ISBN 3-540-67180-3 .

Смотри тоже

Над уровнем моря

веб ссылки

Онлайн-программа для расчета международной формулы высоты

Индивидуальные доказательства

^ Эдмонд Галлей : Изложение правила уменьшения высоты ртути в барометре . В кн . : Филос. Транзакции , 1686 и 1687, т. 16, с. 104
↑ К.-Х. Альхейм [ред.]: Как это работает? Погода и климат. Meyers Lexikonverlag, Мангейм / Вена / Цюрих 1989, ISBN 3-411-02382-1 , стр. 46
↑ Руководство наблюдателя (BHB) для метеорологических пунктов синоптико-климатологической сети измерений и наблюдений . Проверено 20 января 2016 г.

Источник

Уравнение статики
является одним из важнейших уравнений
метеорологии, на основе которого
устанавливаются закономерности
распределения давления, плотности и
массы воздуха по высоте. В своем
дифференциальном виде уравнение статики
(3.2.4) позволяет выполнить расчет изменения
давления лишь для малых приращений
высоты dz.

На практике всегда
необходимо иметь данные о распределении
давления в слоях атмосферы конечной
толщины или определить толщину таких
слоев по измеренным значениям давления.
Для этой цели уравнение статики следует
записать в конечном (интегральном)
виде, т. е. найти его интегралы. Интегралы
уравнения статики атмосферы, полученные
при разных предположениях относительно
изменения температуры и плотности
воздуха с высотой, носят общее
название барометрических
формул. На
основе барометрических формул
решаются такие важные практические
задачи, как расчет распределения
давления и плотности по высоте,
определение высоты различных летательных
аппаратов по измеренному давлению,
приведение давления к уровню моря и
др.

Для получения
интегральной формы уравнения статики
проинтегрируем левую и правую части
(3.2.4) в пределах от уровня моря 2=0 (или
земной поверхности), где давление р0,
до произвольной высоты г, где давление
р. Имеем

Откуда

Здесь ρ = ρ(z)
– функция
высоты

Другую интегральную
форму уравнению статики можно придать,
если воспользоваться уравнением
состояния влажного воздуха (1.4.12) из
главы 1. Подставив найденное отсюда
значение р, перепишем (3.2.4) в виде

Интегрируя в
пределах от 0 до z
и от р₀
до р, получаем:

Интегральные
формы (3.3.1) и (3.3.3) уравнения статики в
дальнейшем широко используются для
получения различных барометрических
формул. Заметим, что p₀
в формулах (3.3.1) и (3.3.3) может обозначать
давление как на уровне моря, так и на
поверхности Земли. Различие будет
состоять лишь в начале отсчета высоты
г. В общем случае температура, а вместе
с ней и плотность воздуха являются
достаточно сложными функциями высоты,
установить аналитический вид которых
не всегда представляется возможным.
Поэтому прежде чем перейти к общему
случаю, рассмотрим несколько частных
случаев, отличающихся один от другого
различными предположениями
относительно вида функций Т = T(z) или р
= р(z),
с помощью которых описывается
распределение температуры или плотности
по высоте.

Однородная
атмосфера.
Предположим, что плотность воздуха в
пределах всей атмосферы

не изменяется с
высотой, т. е.

Здесь р₀—
плотность воздуха при z
= 0. Такая атмосфера носит название
однородной.
Пренебрежем зависимостью ускорения
свободного падения от высоты. Тогда
на основании (3.3.1) получаем барометрическую
формулу однородной атмосферы:

Согласно этой
формуле, давление в однородной атмосфере
убывает с высотой по линейному закону
(рис. 3.2).

Отметим,
что в приложении к атмосфере формула
(3.3.5) дает заведомо далекое от реальных
условий распределение давления. Однако
для гидросферы, плотность которой
изменяется в очень узких пределах
(плотность воды близка к 1 г/см3), формула
(3.3.5) дает вполне удовлетворительные
результаты. Поэтому ее можно назвать
барометрической формулой гидросферы
(высота в этом случае отсчитывается от
дна моря или океана).

Поставим вопрос
о высоте однородной атмосферы, т. е.
такой высоте, на которой давление
обращается в нуль (р = 0).

Обозначим ее
через Н. Согласно (3.3.5), имеем

Поскольку в
соответствии с уравнением (1.3.8) р₀/ρ₀
= R_cT₀
(T₀—
температура воздуха при z = 0), формула
(3.3.6) принимает вид

Отсюда следует,
что высота однородной атмосферы конечна
и зависит только от

температуры
воздуха на поверхности Земли. При Т = О
°С она составляет

Поскольку плотность
в однородной атмосфере постоянна, а
давление быстро убывает с высотой,
температура ее, равная в соответствии
с уравнением состояния

должна понижаться.
Если взять производную по высоте от
левой и правой части (3.3.8), то получим:

Привлекая (3.2.5),
находим следующее выражение для
вертикального градиента температуры

у_А
в однородной атмосфере:

Таким образом, в
однородной атмосфере температура
убывает с высотой по линейному закону:

при этом скорость
понижения температуры (градиент)
значительно больше среднего значения
у в пределах тропосферы.

Изменение плотности
воздуха с высотой. Рассмотрим вопрос
об изменении плотности воздуха с высотой
в общем случае. С этой целью сначала
прологарифмируем, а затем продифференцируем
по высоте левую и правую часть уравнения
состояния (1.3.8):

Заменив dp/dz в
соответствии с (3.2.5) и подставив в
полученное выражение р из уравнения
(1.3.8), найдем:

Формула (3.3.11)
справедлива для любого распределения
температуры воздуха по высоте. На
основе ее можно сделать выводы
относительно изменения плотности
воздуха с высотой. Возможны три различных
случая.

1. Если γ > γ_А=
3,42 ^oС/100
м, то dρ/dz > 0, т. е. плотность воздуха
возрастает с высотой. Вертикальные
градиенты температуры γ, превышающие
3,42 ^oС/100
м, в реальных условиях атмосферы могут
наблюдаться лишь в дневные часы (летом)
в приземном слое атмосферы. При таких
условиях плотность в этом слое
увеличиваетсяс высотой.

2. Если γ = γ_А,
то dρ/dz = 0, т. е. плотность воздуха не
изменяется с высотой (постоянна): ρ
= ρ₀
= const. Это случай однородной атмосферы.

3. Если γ < γ_А,
то dρ/dz < 0, т. е. плотность воздуха
убывает с высотой. Этот случай является
абсолютно преобладающим в условиях
атмосферы. Прежде всего, выше приземного
слоя γ < γ_А
при любых состояниях атмосферы. В
приземном слое случаи γ < γ_А
наблюдаются также значительно чаще,
чем случаи γ > γ_А.
Таким образом, наиболее характерным
состоянием атмосферы является такое,
когда плотность воздуха убывает с
высотой.

Изотермическая
атмосфера.
Атмосфера называется изотермической,
если температура не изменяется с
высотой, т. е.

Т = То = const,

где То — температура
на уровне моря или поверхности Земли.
Изотермическая атмосфера по своим
свойствам во многом противоположна
однородной атмосфере. Считая атмосферу
сухой и пренебрегая зависимостью
ускорения свободного падения от высоты,
на основании (3.3.3) и последнего соотношения
получаем барометрическую формулу
изотермической атмосферы:

Давление в
изотермической атмосфере убывает с
высотой по экспоненциальному
(показательному) закону

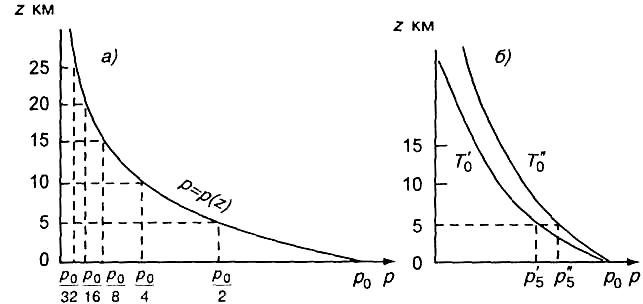
Графически
зависимость давления р от высоты z в
изотермической атмосфере представлена
на рис. 3.3. Рисунок 3.3 а поясняет вытекающую
из формулы (3.3.12) закономерность: если
высота возрастает в прогрессии
арифметической, то давление убывает в
прогрессии геометрической. Кривые
на рис. 3.3 б соответствуют различным
температурам атмосферы (постоянным по
высоте): T^′′₀
> T^′₀.
Из этого рисунка и анализа формулы
(3.3.12) следует, что при одном и том же
давлении у земной поверхности давление
на высотах (например 5, 10, 15 км) при
температуре T^′′₀
больше, чем при T^′₀.
Одно и то же значение давления наблюдается
при температуре T^′′₀
на более высоких уровнях, чем при
температуре T^′₀.
Это означает, что при более высокой
температуре давление в изотермической
атмосфере убывает с высотой медленнее,
чем при более низкой температуре.

Абсолютное значение
убывания давления в слоях равной
толщины в нижней части атмосферы
больше, чем в верхней. Так, в слое от О
до 5 км давление при средних условиях
падает на p₀
— p₀/2
= p₀/2,
т. е. примерно на 500 гПа (при р₀
= 1000 гПа); в слое от 5 до 10 км падение
давления составляет р₀/2
— р₀/4
= р₀/4
т. е. около 250 гПа, а в слое от 20 до 25 км
давление уменьшается всего лишь на
р₀/16
— р₀/32
= р₀/32,
т. е. примерно на 31—32 гПа. Таким образом,
чем выше расположен слой атмосферы
определенной толщины, тем меньше
падение давления в этом слое.

Рис. 3.3. Распределение
давления по высоте в изотермической
атмосфере.

а — общая
закономерность падения давления, б —
падение давления при разных температурах
(T^′′₀
> T^′₀).

Высота изотермической
атмосферы равна бесконечности, т. е. р
→ 0 только при z
→ ∞.

Формула для
плотности воздуха может быть получена,
если обратиться к уравнению состояния,
согласно которому

Поскольку в
изотермической атмосфере Т/Т₀
=1, то на основании (3.3.12) получаем

Величина δ = ρ/ρо
носит название относительной плотности.

Политропная
атмосфера.
Политропной называют такую атмосферу,
которая характеризуется линейным
изменением температуры с высотой
(или постоянным значением вертикального
градиента температуры):

Считая атмосферу
сухой (T_υ
= Т) и подставляя Т в соответствии с
(3.3.14) в формулу (3.3.3), получаем:

Выполнив
интегрирование (в предположении g —
const), приходим к барометрической
формуле политропной атмосферы:

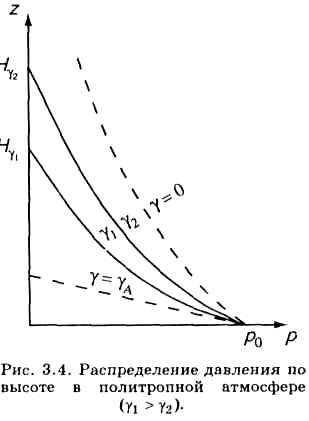
Графически
зависимость р от z изображена на рис.
3.4. Кривые соответствуют одним и тем же
значениям р₀
и T₀,
но различным значениям вертикального
градиента температуры: γ₁
и γ₂.
Давление при большем значении
вертикального градиента температуры
(γ₁)
убывает с высотой быстрее, чем при
меньшем (γ₂).
Для сравнения на рис. 3.4 приведены
кривые изменения давления в однородной
и изотермической атмосферах (штриховые
кривые). Высота политропной атмосферы
конечна. В самом деле, согласно (3.3.15),
давление обращается в нуль на такой
высоте z = Н_γ,
на которой

Высота политропной
атмосферы изменяется в широких пределах;
при Т₀
= 288 К и γ = 0,65 К/100 м значение Нγ
составляет 44,3 км.

Формула для
плотности воздуха в политропной
атмосфере имеет вид

Полная
барометрическая формула (формула
Лапласа).

Рассмотрим общий
случай, т. е. случай произвольного
распределения температуры по высоте.
Учтем также, что реальный воздух
влажный, а ускорение свободного падения
— функция широты и высоты. Привлекая
соотношение (3.1.2) и учитывая, что

уравнение (3.3.2)
перепишем в виде

Поскольку

(вследствие
малости слагаемых а₁
cos 2φ> и a₂z
по сравнению с единицей), то формулу
(3.3.18) приведем к виду

где H₀
= 273R_c/g₀
— высота однородной атмосферы при t =
0 °С.

Проинтегрируем
(3.3.19) в пределах от высоты z₁,
где давление равно p₁,
до высоты z₂,
где давление равно р₂.
Для величин t, s и z
в правой части (3.3.19) при интегрировании
введем средние значения (на основании
известной теоремы о среднем). Выполнив
интегрирование, получим:

Поскольку

полная барометрическая
формула (формула Лапласа) окончательно
принимает вид

Величина В = 2,30Н₀
≈ 18 400 м называется барометрической
постоянной, а средние значения
иносят название средних барометрических
(температуры и доли водяного пара
соответственно).

В таком полном
виде барометрическая формула на практике
используется лишь при барометрическом
нивелировании. При решении подавляющего
большинства метеорологических задач
такой высокой точности, какую может
обеспечить формула Лапласа, не требуется.
К тому же следует иметь в виду, что
точность измерения исходных данных
(температуры, влажности, давления),
необходимых для выполнения расчетов
по формуле (3.3.21), как правило, значительно
меньше тех уточнений, которые дает
формула Лапласа по сравнению с приводимой
ниже барометрической формулой реальной
атмосферы. Последняя получается из
формулы (3.3.21), если считать воздух сухим
(s = 0) и пренебречь зависимостью ускорения
свободного падения от широты и высоты:

Возвращаясь к
натуральным логарифмам и абсолютной
температуре, формулу (3.3.22) можно
переписать в виде

где
=
273(1 + a)
— средняя барометрическая температура
слоя воздуха, заключенного между
уровнямиz₁
и z₂.
Из сравнения последней формулы с
формулой (3.3.3) следует, что средняя
барометрическая температура связана
с температурой воздуха следующим
образом:

Средняя
барометрическая температура — это
такая постоянная в пределах слоя
температура, которая обеспечивает
значения давления на границах его,
наблюдаемые при реальном распределении
температуры по высоте. Практически Т
нередко отождествляют со средней
арифметической температурой, т. е.
полагают

где Т₁
и Т₂
— температуры воздуха на нижней и
верхней границах слоя. Если уровень z₁
совпадает с поверхностью Земли (z₁
= 0), а уровень z₂
— произвольный (z₂
= z),
то формула (3.3.23) принимает вид

Эта формула имеет
такой же вид, как и барометрическая
формула (3.3.12) изотермической атмосферы.
Принципиальное различие состоит в том,
что формулы (3.3.20), (3.3.23) и (3.3.25) всегда
справедливы лишь для слоя заданной
конечной толщины, для которого температура
должна быть каждый раз определена
прежде, чем по формулам можно начинать
выполнять расчет. Вместе с изменением
толщины слоя изменяется и величина.
В случае же изотермической атмосферы
температура является независимой
(задаваемой) величиной. Поскольку
барометрическая формула реальной
атмосферы является показательной
функцией, на основе ее анализа можно
сделать такие же выводы относительно
закономерностей изменения давления
с высотой, какие были сделаны в случае
изотермической атмосферы. Роль
температуры T₀
в реальной атмосфере играет средняя
барометрическая температура
.
Все выводы в случае реальной атмосферы
относятся к слою конечной толщины.
Поэтому вывод о бесконечной
протяженности атмосферы, сделанный на
основе формулы (3.3.12), здесь отпадает.

Если необходимо
учесть влияние влажности на плотность
воздуха и распределение давления
по высоте, то в формулах (3.3.22) — (3.3.25)
средняя барометрическая температура
должна быть заменена средней
виртуальной барометрической температурой_υ.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Барометрическая формула высоты

Литература

Категории

Морская история

Популярные теги

Основное уравнение гидростатики

Изотермическая атмосфера

Вывод из основного уравнения гидростатики

Вывод из статистической механики

Атмосфера с линейным температурным профилем

Распределение температуры (адиабатическая атмосфера)

Распределение плотности и давления

Типичные температурные градиенты

Уровни высоты

Международная формула высоты

Общий случай

Виртуальная температура

Геопотенциальные высоты

Приложения

Понижение до уровня моря

теория

упражняться

Пределы

Измерение барометрической высоты

литература

Смотри тоже

веб ссылки

Индивидуальные доказательства

Не пропустите также: