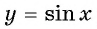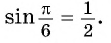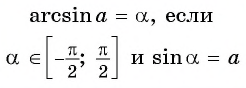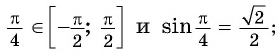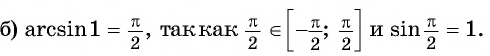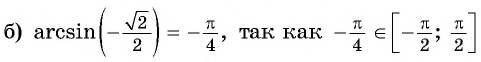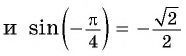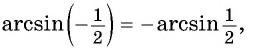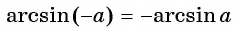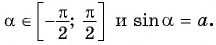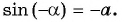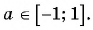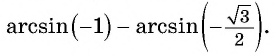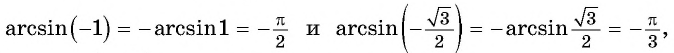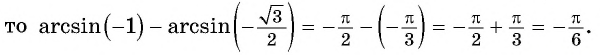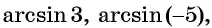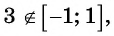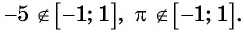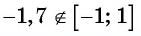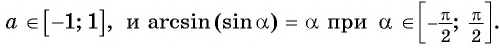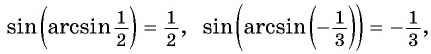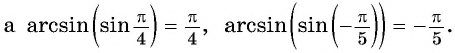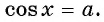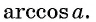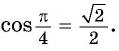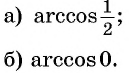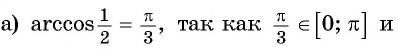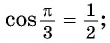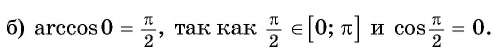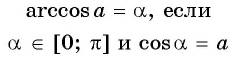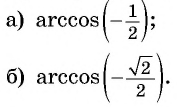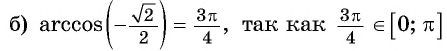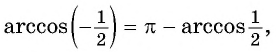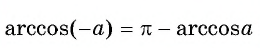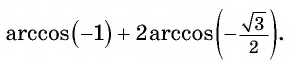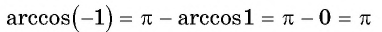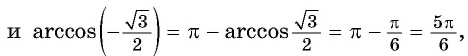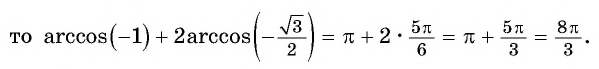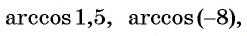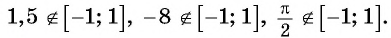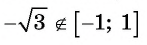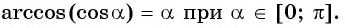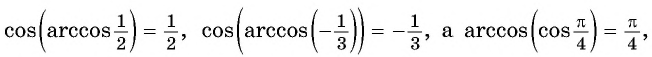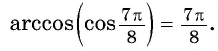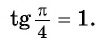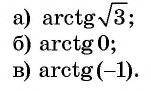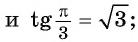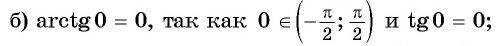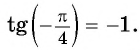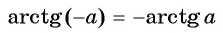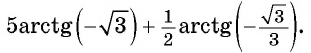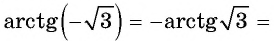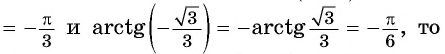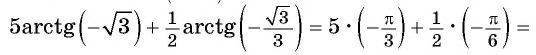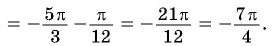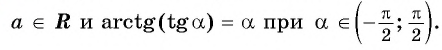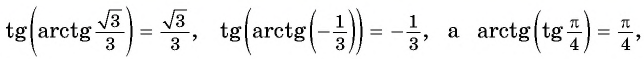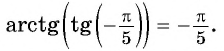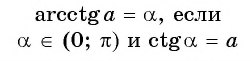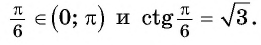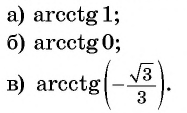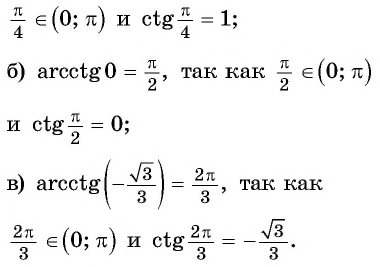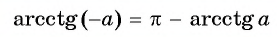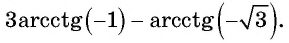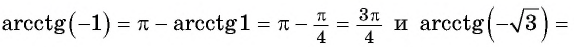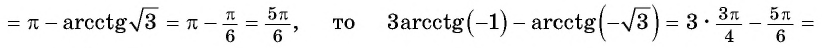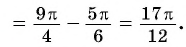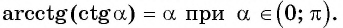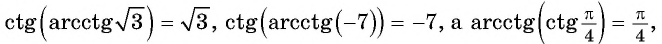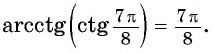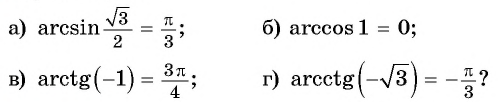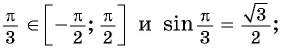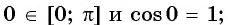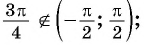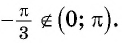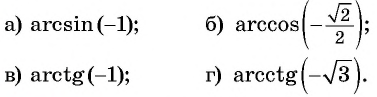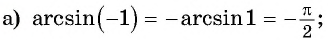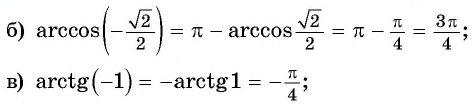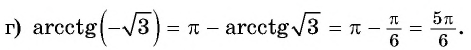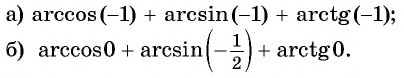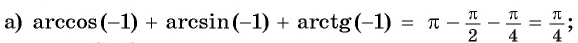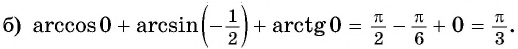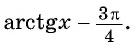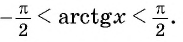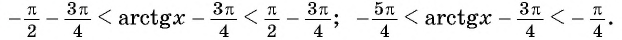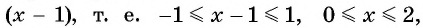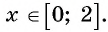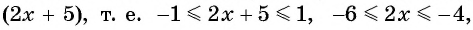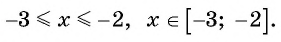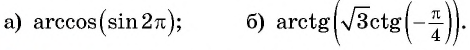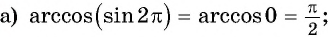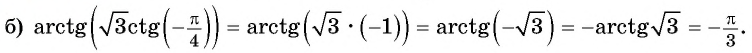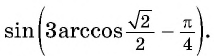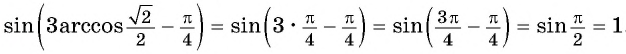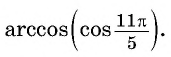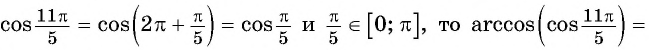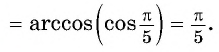Арксинус(y = arcsin(x)) – это обратная тригонометрическая функция к синусу x = sin(y). Область определения -1 ≤ x ≤ 1 и множество значений -π/2 ≤ y ≤ +π/2.
График пересекает оси в начале координат.
| arcsin(0) = 0° | arcsin(0.8660254038) = 120° | arcsin(-0.8660254038) = 240° |
| arcsin(0.01745240644) = 1° | arcsin(0.8571673007) = 121° | arcsin(-0.8746197071) = 241° |
| arcsin(0.0348994967) = 2° | arcsin(0.8480480962) = 122° | arcsin(-0.8829475929) = 242° |
| arcsin(0.05233595624) = 3° | arcsin(0.8386705679) = 123° | arcsin(-0.8910065242) = 243° |
| arcsin(0.06975647374) = 4° | arcsin(0.8290375726) = 124° | arcsin(-0.8987940463) = 244° |
| arcsin(0.08715574275) = 5° | arcsin(0.8191520443) = 125° | arcsin(-0.906307787) = 245° |
| arcsin(0.1045284633) = 6° | arcsin(0.8090169944) = 126° | arcsin(-0.9135454576) = 246° |
| arcsin(0.1218693434) = 7° | arcsin(0.79863551) = 127° | arcsin(-0.9205048535) = 247° |
| arcsin(0.139173101) = 8° | arcsin(0.7880107536) = 128° | arcsin(-0.9271838546) = 248° |
| arcsin(0.156434465) = 9° | arcsin(0.7771459615) = 129° | arcsin(-0.9335804265) = 249° |
| arcsin(0.1736481777) = 10° | arcsin(0.7660444431) = 130° | arcsin(-0.9396926208) = 250° |
| arcsin(0.1908089954) = 11° | arcsin(0.7547095802) = 131° | arcsin(-0.9455185756) = 251° |
| arcsin(0.2079116908) = 12° | arcsin(0.7431448255) = 132° | arcsin(-0.9510565163) = 252° |
| arcsin(0.2249510543) = 13° | arcsin(0.7313537016) = 133° | arcsin(-0.956304756) = 253° |
| arcsin(0.2419218956) = 14° | arcsin(0.7193398003) = 134° | arcsin(-0.9612616959) = 254° |
| arcsin(0.2588190451) = 15° | arcsin(0.7071067812) = 135° | arcsin(-0.9659258263) = 255° |
| arcsin(0.2756373558) = 16° | arcsin(0.6946583705) = 136° | arcsin(-0.9702957263) = 256° |
| arcsin(0.2923717047) = 17° | arcsin(0.6819983601) = 137° | arcsin(-0.9743700648) = 257° |
| arcsin(0.3090169944) = 18° | arcsin(0.6691306064) = 138° | arcsin(-0.9781476007) = 258° |
| arcsin(0.3255681545) = 19° | arcsin(0.656059029) = 139° | arcsin(-0.9816271834) = 259° |
| arcsin(0.3420201433) = 20° | arcsin(0.6427876097) = 140° | arcsin(-0.984807753) = 260° |
| arcsin(0.3583679495) = 21° | arcsin(0.629320391) = 141° | arcsin(-0.9876883406) = 261° |
| arcsin(0.3746065934) = 22° | arcsin(0.6156614753) = 142° | arcsin(-0.9902680687) = 262° |
| arcsin(0.3907311285) = 23° | arcsin(0.6018150232) = 143° | arcsin(-0.9925461516) = 263° |
| arcsin(0.4067366431) = 24° | arcsin(0.5877852523) = 144° | arcsin(-0.9945218954) = 264° |
| arcsin(0.4226182617) = 25° | arcsin(0.5735764364) = 145° | arcsin(-0.9961946981) = 265° |
| arcsin(0.4383711468) = 26° | arcsin(0.5591929035) = 146° | arcsin(-0.9975640503) = 266° |
| arcsin(0.4539904997) = 27° | arcsin(0.544639035) = 147° | arcsin(-0.9986295348) = 267° |
| arcsin(0.4694715628) = 28° | arcsin(0.5299192642) = 148° | arcsin(-0.999390827) = 268° |
| arcsin(0.4848096202) = 29° | arcsin(0.5150380749) = 149° | arcsin(-0.9998476952) = 269° |
| arcsin(0.5) = 30° | arcsin(0.5) = 150° | arcsin(-1) = 270° |
| arcsin(0.5150380749) = 31° | arcsin(0.4848096202) = 151° | arcsin(-0.9998476952) = 271° |
| arcsin(0.5299192642) = 32° | arcsin(0.4694715628) = 152° | arcsin(-0.999390827) = 272° |
| arcsin(0.544639035) = 33° | arcsin(0.4539904997) = 153° | arcsin(-0.9986295348) = 273° |
| arcsin(0.5591929035) = 34° | arcsin(0.4383711468) = 154° | arcsin(-0.9975640503) = 274° |
| arcsin(0.5735764364) = 35° | arcsin(0.4226182617) = 155° | arcsin(-0.9961946981) = 275° |
| arcsin(0.5877852523) = 36° | arcsin(0.4067366431) = 156° | arcsin(-0.9945218954) = 276° |
| arcsin(0.6018150232) = 37° | arcsin(0.3907311285) = 157° | arcsin(-0.9925461516) = 277° |
| arcsin(0.6156614753) = 38° | arcsin(0.3746065934) = 158° | arcsin(-0.9902680687) = 278° |
| arcsin(0.629320391) = 39° | arcsin(0.3583679495) = 159° | arcsin(-0.9876883406) = 279° |
| arcsin(0.6427876097) = 40° | arcsin(0.3420201433) = 160° | arcsin(-0.984807753) = 280° |
| arcsin(0.656059029) = 41° | arcsin(0.3255681545) = 161° | arcsin(-0.9816271834) = 281° |
| arcsin(0.6691306064) = 42° | arcsin(0.3090169944) = 162° | arcsin(-0.9781476007) = 282° |
| arcsin(0.6819983601) = 43° | arcsin(0.2923717047) = 163° | arcsin(-0.9743700648) = 283° |
| arcsin(0.6946583705) = 44° | arcsin(0.2756373558) = 164° | arcsin(-0.9702957263) = 284° |
| arcsin(0.7071067812) = 45° | arcsin(0.2588190451) = 165° | arcsin(-0.9659258263) = 285° |
| arcsin(0.7193398003) = 46° | arcsin(0.2419218956) = 166° | arcsin(-0.9612616959) = 286° |
| arcsin(0.7313537016) = 47° | arcsin(0.2249510543) = 167° | arcsin(-0.956304756) = 287° |
| arcsin(0.7431448255) = 48° | arcsin(0.2079116908) = 168° | arcsin(-0.9510565163) = 288° |
| arcsin(0.7547095802) = 49° | arcsin(0.1908089954) = 169° | arcsin(-0.9455185756) = 289° |
| arcsin(0.7660444431) = 50° | arcsin(0.1736481777) = 170° | arcsin(-0.9396926208) = 290° |
| arcsin(0.7771459615) = 51° | arcsin(0.156434465) = 171° | arcsin(-0.9335804265) = 291° |
| arcsin(0.7880107536) = 52° | arcsin(0.139173101) = 172° | arcsin(-0.9271838546) = 292° |
| arcsin(0.79863551) = 53° | arcsin(0.1218693434) = 173° | arcsin(-0.9205048535) = 293° |
| arcsin(0.8090169944) = 54° | arcsin(0.1045284633) = 174° | arcsin(-0.9135454576) = 294° |
| arcsin(0.8191520443) = 55° | arcsin(0.08715574275) = 175° | arcsin(-0.906307787) = 295° |
| arcsin(0.8290375726) = 56° | arcsin(0.06975647374) = 176° | arcsin(-0.8987940463) = 296° |
| arcsin(0.8386705679) = 57° | arcsin(0.05233595624) = 177° | arcsin(-0.8910065242) = 297° |
| arcsin(0.8480480962) = 58° | arcsin(0.0348994967) = 178° | arcsin(-0.8829475929) = 298° |
| arcsin(0.8571673007) = 59° | arcsin(0.01745240644) = 179° | arcsin(-0.8746197071) = 299° |
| arcsin(0.8660254038) = 60° | arcsin(0) = 180° | arcsin(-0.8660254038) = 300° |
| arcsin(0.8746197071) = 61° | arcsin(-0.01745240644) = 181° | arcsin(-0.8571673007) = 301° |
| arcsin(0.8829475929) = 62° | arcsin(-0.0348994967) = 182° | arcsin(-0.8480480962) = 302° |
| arcsin(0.8910065242) = 63° | arcsin(-0.05233595624) = 183° | arcsin(-0.8386705679) = 303° |
| arcsin(0.8987940463) = 64° | arcsin(-0.06975647374) = 184° | arcsin(-0.8290375726) = 304° |
| arcsin(0.906307787) = 65° | arcsin(-0.08715574275) = 185° | arcsin(-0.8191520443) = 305° |
| arcsin(0.9135454576) = 66° | arcsin(-0.1045284633) = 186° | arcsin(-0.8090169944) = 306° |
| arcsin(0.9205048535) = 67° | arcsin(-0.1218693434) = 187° | arcsin(-0.79863551) = 307° |
| arcsin(0.9271838546) = 68° | arcsin(-0.139173101) = 188° | arcsin(-0.7880107536) = 308° |
| arcsin(0.9335804265) = 69° | arcsin(-0.156434465) = 189° | arcsin(-0.7771459615) = 309° |
| arcsin(0.9396926208) = 70° | arcsin(-0.1736481777) = 190° | arcsin(-0.7660444431) = 310° |
| arcsin(0.9455185756) = 71° | arcsin(-0.1908089954) = 191° | arcsin(-0.7547095802) = 311° |
| arcsin(0.9510565163) = 72° | arcsin(-0.2079116908) = 192° | arcsin(-0.7431448255) = 312° |
| arcsin(0.956304756) = 73° | arcsin(-0.2249510543) = 193° | arcsin(-0.7313537016) = 313° |
| arcsin(0.9612616959) = 74° | arcsin(-0.2419218956) = 194° | arcsin(-0.7193398003) = 314° |
| arcsin(0.9659258263) = 75° | arcsin(-0.2588190451) = 195° | arcsin(-0.7071067812) = 315° |
| arcsin(0.9702957263) = 76° | arcsin(-0.2756373558) = 196° | arcsin(-0.6946583705) = 316° |
| arcsin(0.9743700648) = 77° | arcsin(-0.2923717047) = 197° | arcsin(-0.6819983601) = 317° |
| arcsin(0.9781476007) = 78° | arcsin(-0.3090169944) = 198° | arcsin(-0.6691306064) = 318° |
| arcsin(0.9816271834) = 79° | arcsin(-0.3255681545) = 199° | arcsin(-0.656059029) = 319° |
| arcsin(0.984807753) = 80° | arcsin(-0.3420201433) = 200° | arcsin(-0.6427876097) = 320° |
| arcsin(0.9876883406) = 81° | arcsin(-0.3583679495) = 201° | arcsin(-0.629320391) = 321° |
| arcsin(0.9902680687) = 82° | arcsin(-0.3746065934) = 202° | arcsin(-0.6156614753) = 322° |
| arcsin(0.9925461516) = 83° | arcsin(-0.3907311285) = 203° | arcsin(-0.6018150232) = 323° |
| arcsin(0.9945218954) = 84° | arcsin(-0.4067366431) = 204° | arcsin(-0.5877852523) = 324° |
| arcsin(0.9961946981) = 85° | arcsin(-0.4226182617) = 205° | arcsin(-0.5735764364) = 325° |
| arcsin(0.9975640503) = 86° | arcsin(-0.4383711468) = 206° | arcsin(-0.5591929035) = 326° |
| arcsin(0.9986295348) = 87° | arcsin(-0.4539904997) = 207° | arcsin(-0.544639035) = 327° |
| arcsin(0.999390827) = 88° | arcsin(-0.4694715628) = 208° | arcsin(-0.5299192642) = 328° |
| arcsin(0.9998476952) = 89° | arcsin(-0.4848096202) = 209° | arcsin(-0.5150380749) = 329° |
| arcsin(1) = 90° | arcsin(-0.5) = 210° | arcsin(-0.5) = 330° |
| arcsin(0.9998476952) = 91° | arcsin(-0.5150380749) = 211° | arcsin(-0.4848096202) = 331° |
| arcsin(0.999390827) = 92° | arcsin(-0.5299192642) = 212° | arcsin(-0.4694715628) = 332° |
| arcsin(0.9986295348) = 93° | arcsin(-0.544639035) = 213° | arcsin(-0.4539904997) = 333° |
| arcsin(0.9975640503) = 94° | arcsin(-0.5591929035) = 214° | arcsin(-0.4383711468) = 334° |
| arcsin(0.9961946981) = 95° | arcsin(-0.5735764364) = 215° | arcsin(-0.4226182617) = 335° |
| arcsin(0.9945218954) = 96° | arcsin(-0.5877852523) = 216° | arcsin(-0.4067366431) = 336° |
| arcsin(0.9925461516) = 97° | arcsin(-0.6018150232) = 217° | arcsin(-0.3907311285) = 337° |
| arcsin(0.9902680687) = 98° | arcsin(-0.6156614753) = 218° | arcsin(-0.3746065934) = 338° |
| arcsin(0.9876883406) = 99° | arcsin(-0.629320391) = 219° | arcsin(-0.3583679495) = 339° |
| arcsin(0.984807753) = 100° | arcsin(-0.6427876097) = 220° | arcsin(-0.3420201433) = 340° |
| arcsin(0.9816271834) = 101° | arcsin(-0.656059029) = 221° | arcsin(-0.3255681545) = 341° |
| arcsin(0.9781476007) = 102° | arcsin(-0.6691306064) = 222° | arcsin(-0.3090169944) = 342° |
| arcsin(0.9743700648) = 103° | arcsin(-0.6819983601) = 223° | arcsin(-0.2923717047) = 343° |
| arcsin(0.9702957263) = 104° | arcsin(-0.6946583705) = 224° | arcsin(-0.2756373558) = 344° |
| arcsin(0.9659258263) = 105° | arcsin(-0.7071067812) = 225° | arcsin(-0.2588190451) = 345° |
| arcsin(0.9612616959) = 106° | arcsin(-0.7193398003) = 226° | arcsin(-0.2419218956) = 346° |
| arcsin(0.956304756) = 107° | arcsin(-0.7313537016) = 227° | arcsin(-0.2249510543) = 347° |
| arcsin(0.9510565163) = 108° | arcsin(-0.7431448255) = 228° | arcsin(-0.2079116908) = 348° |
| arcsin(0.9455185756) = 109° | arcsin(-0.7547095802) = 229° | arcsin(-0.1908089954) = 349° |
| arcsin(0.9396926208) = 110° | arcsin(-0.7660444431) = 230° | arcsin(-0.1736481777) = 350° |
| arcsin(0.9335804265) = 111° | arcsin(-0.7771459615) = 231° | arcsin(-0.156434465) = 351° |
| arcsin(0.9271838546) = 112° | arcsin(-0.7880107536) = 232° | arcsin(-0.139173101) = 352° |
| arcsin(0.9205048535) = 113° | arcsin(-0.79863551) = 233° | arcsin(-0.1218693434) = 353° |
| arcsin(0.9135454576) = 114° | arcsin(-0.8090169944) = 234° | arcsin(-0.1045284633) = 354° |
| arcsin(0.906307787) = 115° | arcsin(-0.8191520443) = 235° | arcsin(-0.08715574275) = 355° |
| arcsin(0.8987940463) = 116° | arcsin(-0.8290375726) = 236° | arcsin(-0.06975647374) = 356° |
| arcsin(0.8910065242) = 117° | arcsin(-0.8386705679) = 237° | arcsin(-0.05233595624) = 357° |
| arcsin(0.8829475929) = 118° | arcsin(-0.8480480962) = 238° | arcsin(-0.0348994967) = 358° |
| arcsin(0.8746197071) = 119° | arcsin(-0.8571673007) = 239° | arcsin(-0.01745240644) = 359° |
Как найти арксинус: формула, свойства, функция
Содержание:
- Понятие арксинуса
- Зачем нужен арксинус
- Получение функции arcsin с пояснением на примерах
- Свойства функции arcsin
- График арксинуса
Понятие арксинуса
Обратные тригонометрические функции называют по соответствующим им тригонометрическим функциям. Формулировка наименования заключается в приписывании приставки «арк», что является производным от латинского слова «дуга» (arcus).
Такая методика объясняется тем, что в геометрии функцию, обратную тригонометрической, связывают с длиной, которую имеет дуга единичной окружности, равной какому-то отрезку, либо с углом, стягивающим данную дугу. В результате с помощью синуса можно, учитывая дугу окружности, определить хорду, которая ее стягивает.
Обратная функция под названием арксинус призвана решить противоположную задачу. Арксинус обозначают (arcsin x) и определяют, как угол с синусом, равным х.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для тригонометрических функций характерна периодичность. В связи с этим, обратные тригонометрические функции являются многозначными. Аркфункция обладает значением в виде множества из углов, для которых прямая тригонометрическая функция соответствует заданному числу.
Пример 1
Рассмотрим функцию: (arcsin ½). Данная аркфункция обозначает множество из углов:
(left ( frac{pi}{6}, frac{5 pi}{6}, frac{13 pi}{6}, frac{17 pi}{6} dots ~ (30^circ, 150^circ, 390^circ, 510^circ dots) right ))
Значение синуса при этом: ½
Как правило, под обратными тригонометрическими функциями понимают ключевые значения каждой аркфункции, выделенные из ее множества значений.
Если (-1leqslant alpha leqslant 1), то любое решение уравнения (sin x=alpha) записывают в такой форме: ( x=(-1)^{n}arcsin alpha +pi n,~n=0,pm 1,pm 2,dots )~
Арксинус числа х — значение для угла у, определенного в радианах, для которого (sin y=x,quad -{frac {pi }{2}}leqslant yleqslant {frac {pi }{2}},quad |x|leqslant 1).
Зачем нужен арксинус
С помощью аркфункций, в том числе — арккосинуса, арктангенса, арккотангенса, арксинуса — определяют углы треугольника. Подобное действие доступно при наличии информации о сторонах данной геометрической фигуры.
В том случае, когда имеется некий прямоугольный треугольник, обратные тригонометрические функции от отношений сторон позволяют определить угол. Например, длина катета составляет «а». Этот катет определяется, как противолежащий для угла (alpha), то:
(alpha =arcsin(a/c)=arccos(b/c)=operatorname {arctg} (a/b)=operatorname {arccosec} (c/a)=operatorname {arcsec}(c/b)=operatorname {arcctg} (b/a))
Получение функции arcsin с пояснением на примерах
Предположим, что существует некая функция:
(y=sin x)
Записанная функция обладает областью определения. В ее рамках она приобретает кусочно-монотонный вид. По этой причине обратное выражение y=arcsin x нельзя причислить к функциям.
В результате целесообразно проанализировать отрезок, где наблюдается строгое возрастание функции, и все значения относятся к ряду из области значений:
(left[-{frac {pi }{2}};{frac {pi }{2}}right])
Функция (y=sin x ) на отрезке (left[-{frac {pi }{2}};{frac {pi }{2}}right]) обладает следующей особенностью: какое-либо из значений этой функции возможно только при одном значении аргумента. По этой причине на данном интервале может существовать обратная функция с формулой (y=arcsin x.)
График обратной функции является симметричным графику функции (y=sin x) в рамках интервала (left[-{frac {pi }{2}};{frac {pi }{2}}right]) по отношению к прямой y=x. Можно наблюдать симметричность в расположении графиков функций, которые являются взаимно обратными, по отношению к биссектрисе первого и третьего координатных углов на плоскости координат Oxy.
Пример 2
Определим значение выражение:
(arcsin 0,4)
По определению обратной тригонометрической функции можно сделать вывод, что запись означает угол с синусом, равным 0,4. В данном выводе заключается смысл понятия арксинус.
Пример 3
Требуется найти, что означает (arcsin 0,5).
Если знать определение, эта простая обратная тригонометрическая функция является обозначением угла с синусом, равным 0,5. Таким синусом обладает угол в 30°. Таким образом:
(arcsin 0,5 = 30°)
Общий ответ можно высчитать не в градусах, а в радианах:
Свойства функции arcsin
Рассмотрим функцию (y=arcsin x). Она является непрерывной в тригонометрии и ограничивается на протяжении всей своей области определения. Данная функция строго возрастает.
Область определения, в которой функцию можно вычислить:
(D(arcsin x)=[-1;1]qquad) (от минус единицы до плюс единицы)
Область значений:
(E(arcsin x)=left[-{frac {pi }{2}};{frac {pi }{2}}right]qquad )
Значения функций можно посчитать таким образом:
- (sin(arcsin x)=xqquad), если (-1leqslant xleqslant 1)
- (arcsin(sin y)=yqquad), если (-{frac {pi }{2}}leqslant yleqslant {frac {pi }{2}})
Функция arcsin обладает следующими свойствами:
- (arcsin(-x)=-arcsin xqquad )(нечетная функция);
- (arcsin x>0, когда 0<xleqslant 1);
- (arcsin x=0, когда x=0);
- (arcsin x<0, если -1leqslant x<0);
- (arcsin x=left{{begin{matrix}arccos {sqrt {1-x^{2}}},qquad 0leqslant xleqslant 1\-arccos {sqrt {1-x^{2}}},qquad -1leqslant x<0end{matrix}}right.)
- (arcsin x=operatorname {arctg}{frac {x}{{sqrt {1-x^{2}}}}});
- (arcsin x=left{{begin{matrix}operatorname {arcctg},{frac {{sqrt {1-x^{2}}}}{x}},qquad 0<xleqslant 1\operatorname {arcctg},{frac {{sqrt {1-x^{2}}}}{x}}-pi ,qquad -1leqslant x<0end{matrix}}right.)
График арксинуса
График функции (y=arcsin x):
- Определение
- График арксинуса
- Свойства арксинуса
-
Таблица арксинусов
Определение
Арксинус (arcsin) – это обратная тригонометрическая функция.
Арксинус x определяется как функция, обратная к синусу x, при -1≤x≤1.
Если синус угла у равен х (sin y = x), значит арксинус x равняется y:
arcsin x = sin-1 x = y
Примечание: sin-1x означает обратный синус, а не синус в степени -1.
Например:
arcsin 1 = sin-1 1 = 90° (π/2 рад)
График арксинуса
Функция арксинуса пишется как y = arcsin (x). График в общем виде выглядит следующим образом (-1≤x≤1, -π/2≤y≤π/2):
Свойства арксинуса
Ниже в табличном виде представлены основные свойства арксинуса с формулами.
Таблица арксинусов
| x | arcsin x (рад) | arcsin x (°) |
| -1 | -π/2 | -90° |
| -√3/2 | -π/3 | -60° |
| -√2/2 | -π/4 | -45° |
| -1/2 | -π/6 | -30° |
| 0 | 0 | 0° |
| 1/2 | π/6 | 30° |
| √2/2 | π/4 | 45° |
| √3/2 | π/3 | 60° |
| 1 | π/2 | 90° |
microexcel.ru
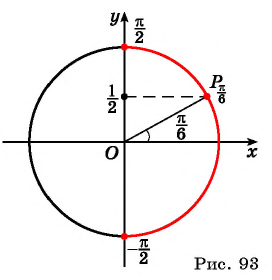
Арксинусом числа (a) ((a∈[-1;1])) называют число (x∈[-frac{π}{2};frac{π}{2}]) синус которого равен (a) т.е.
(arcsin a=x) (<=>) (sin x=a)
Примеры:
(arcsin{frac{sqrt{2}}{2}}=frac{π}{4}) потому что (sin frac{π}{4}=frac{sqrt{2}}{2}) и (frac{π}{4}∈[-frac{π}{2}; frac{π}{2}])
(arcsin 1=frac{π}{2}) потому что (sinfrac{π}{2}=1) и (frac{π}{2}∈[-frac{π}{2};frac{π}{2}])
(arcsin 0=0) потому что (sin 0=0) и (0∈[-frac{π}{2};frac{π}{2}] )
(arcsinsqrt{3}) – не определен, потому что (sqrt{3}>1)
Проще говоря, арксинус обратен синусу.
На круге это выглядит так:


Как вычислить арксинус?
Чтобы вычислить арксинус — нужно ответить на вопрос: синус какого числа (лежащего в пределах от (-frac{π}{2}) до (frac{π}{2}) ) равен аргументу арксинуса?
Например, вычислите значение арксинуса:
а) (arcsin(-frac{1}{2}))
б) (arcsin(frac{sqrt{3}}{2}))
в) (arcsin(-1))
а) Синус какого числа равен (-frac{1}{2})? Или в более точной формулировке можно спросить так: если (sin x=-frac{1}{2}), то чему равен (x)? Причем, обратите внимание, нам нужно такое значение, которое лежит между (-frac{π}{2}) и (frac{π}{2}). Ответ очевиден:
(arcsin(-frac{1}{2})=-frac{π}{6})
б) Синус какого числа равен (frac{sqrt{3}}{2})? Кто-то вспоминает тригонометрический круг, кто-то таблицу, но в любом случае ответ (frac{π}{3}).
(arcsin(-frac{sqrt{3}}{2})=-frac{π}{3})
в) Синус от чего равен (-1)?
Иначе говоря, (sin x=-1), (x=) ?
(arcsin(-1)=-frac{π}{2})
Тригонометрический круг со всеми стандартными арксинусами:

Зачем нужен арксинус? Решение уравнения (sin x=a)
Чтобы понять зачем придумали арксинус, давайте решим уравнение: (sin x=frac{1}{2}).
Это не вызывает затруднений:

( left[ begin{gathered}x=frac{π}{6}+2πn, n∈Z\ x=frac{5π}{6}+2πl, l∈Zend{gathered}right.)
Внимание! Если вдруг затруднения всё же были, то почитайте здесь о решении простейших уравнений с синусом.
А теперь решите уравнение: (sin x=frac{1}{3}).

Что тут будет ответом? Не (frac{π}{6}), не (frac{π}{4}), даже не (frac{π}{7}) — вообще никакие привычные числа не подходят, однако при этом очевидно, что решения есть. Но как их записать?
Вот тут-то на помощь и приходит арксинус! Значение правой точки равно (arcsinfrac{1}{3}), потому что известно, что синус равен (frac{1}{3}). Длина дуги от (0) до правой точки тогда тоже будет равна (arcsinfrac{1}{3}). Тогда чему равно значение второй точки? С учетом того, что правая точка находится на расстоянии равному (arcsinfrac{1}{3}) от (π), то её значение составляет (π- arcsinfrac{1}{3}).
Ок, значение этих двух точек нашли. Теперь запишем полный ответ: ( left[ begin{gathered}x=arcsin frac{1}{3}+2πn, n∈Z\ x=π-arcsin frac{1}{3}+2πl, l∈Zend{gathered}right.) Без арксинусов решить уравнение (sin x=frac{1}{3}) не получилось бы. Как и уравнение (sin x=0,125), (sin x=-frac{1}{9}), (sin x=frac{1}{sqrt{3}}) и многие другие. Фактически без арксинуса мы можем решать только (9) простейших уравнений с синусом:

С арксинусом – бесконечное количество.
Пример. Решите тригонометрическое уравнение: (sin x=frac{1}{sqrt{3}}).
Решение:

Ответ: ( left[ begin{gathered}x=arcsin frac{1}{sqrt{3}}+2πn, n∈Z\ x=π-arcsin frac{1}{sqrt{3}}+2πl, l∈Zend{gathered}right.)
Пример. Решите тригонометрическое уравнение: (sin x=frac{1}{sqrt{2}}).
Решение:
Кто поторопился написать ответ ( left[ begin{gathered}x=arcsin frac{1}{sqrt{2}}+2πn, n∈Z\ x=π-arcsin frac{1}{sqrt{2}}+2πl, l∈Zend{gathered}right.), тот на ЕГЭ потеряет 2 балла. Дело в том, что в отличии от прошлых примеров (arcsin frac{1}{sqrt{2}}) — вычислимое значение, но чтобы это стало очевидно нужно избавиться от иррациональности в знаменателе аргумента. Для этого умножим и числитель и знаменатель дробь на корень из двух (frac{1}{sqrt{2}} = frac{1 cdot sqrt{2}}{sqrt{2} cdot sqrt{2}}= frac{sqrt{2}}{2}). Таким образом, получаем:
(arcsin frac{1}{sqrt{2}} = arcsin frac{sqrt{2}}{2}=frac{π}{4})
Значит в ответе вместо арксинусов нужно написать (frac{π}{4}).
Ответ: ( left[ begin{gathered}x=frac{π}{4}+2πn, n∈Z\ x=frac{3π}{4}+2πl, l∈Zend{gathered}right.)
Пример. Решите тригонометрическое уравнение: (sin x=frac{7}{6}).
Решение:
И вновь тот, кто поторопился написать ( left[ begin{gathered}x= arcsin frac{7}{6}+2πn, n∈Z\ x=π- arcsinfrac{7}{6}+2πl, l∈Zend{gathered}right.) на ЕГЭ потеряет (2) балла. Что не так? – спросите вы. Ведь точно не табличное значение, почему нельзя написать (arcsinfrac{7}{6})? Пролистайте до самого верха, туда, где было определение арксинуса. Там написана маленькая, но очень важная деталь – аргумент арксинуса должен быть меньше или равен (1) и больше или равен (-1). Ведь синус не может выходить за эти пределы! И если решить уравнение с помощью круга, а не бездумно пользоваться готовыми формулами, то станет очевидно, что у такого уравнения решений нет.

Ответ: решений нет.
Думаю, вы уловили закономерность.
Если (sin x) равен не табличному значению между (1) и (-1), то решения будут выглядеть как: ( left[ begin{gathered}x= arcsin a +2πn, n∈Z\ x=π- arcsin a +2πl, l∈Zend{gathered}right.)
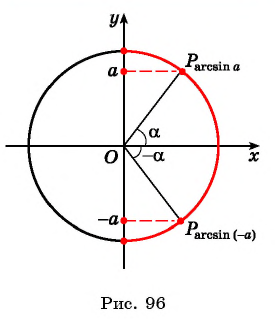
Арксинус отрицательного числа
Прежде чем научиться решать тригонометрические уравнения с отрицательным синусом советую запомнить формулу:
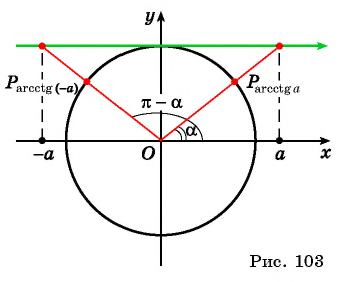
(arcsin({-a})=-arcsin a)
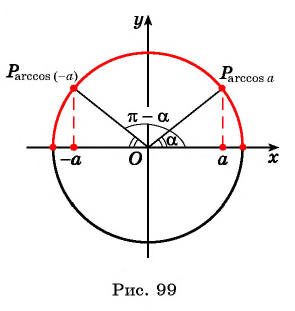
Если хотите понять логику этой формулы, внимательно рассмотрите картинку ниже:

Примеры:
(arcsin(-0,7)=-arcsin 0,7)
(arcsin(-frac{sqrt{3}}{2})=-arcsinfrac{sqrt{3}}{2}=-frac{π}{6})
(arcsin(-frac{sqrt{7}}{2}) neq -arcsinfrac{sqrt{7}}{2})
Удивил последний пример? Почему в нем формула не работает? Потому что запись (arcsin(-frac{sqrt{7}}{2})) в принципе неверна, ведь (-frac{sqrt{7}}{2}<-1), а значит арксинус от (-frac{sqrt{7}}{2}) взять нельзя – он не вычислим, не существует, точно также как (sqrt{-5}) или (frac{3}{0}).
Пример. Решите тригонометрическое уравнение: (sin x=-frac{1}{sqrt{3}}).
Решение:
Можно воспользоваться готовой формулой и написать:
( left[ begin{gathered}x=arcsin (-frac{1}{sqrt{3}})+2πn, n∈Z\ x=π-arcsin (-frac{1}{sqrt{3}})+2πl, l∈Zend{gathered}right.)
( left[ begin{gathered}x=-arcsin (frac{1}{sqrt{3}})+2πn, n∈Z\ x=π+arcsin (frac{1}{sqrt{3}})+2πl, l∈Zend{gathered}right.)
Но я фанатка круга, поэтому:

Ответ: ( left[ begin{gathered}x=-arcsin frac{1}{sqrt{3}}+2πn, n∈Z\ x=π+arcsin frac{1}{sqrt{3}}+2πl, l∈Zend{gathered}right.)
На всякий случай, уточню, что при решении уравнений написанное синим писать не обязательно – это скорее пояснения, как надо рассуждать.
Смотрите также:
Синус
Тригонометрические уравнения
Содержание:
При изучении тригонометрических функций часто возникает вопрос о нахождении значения аргумента, при котором значение функции равно заданному числу.
Нахождение значения аргумента
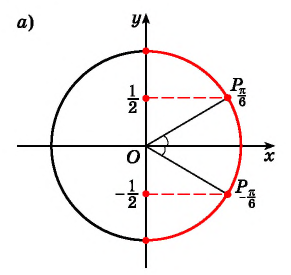
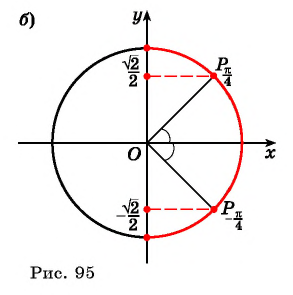
Например, найдем все значения аргумента, при которых значение функции
На единичной окружности найдем точки 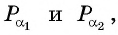
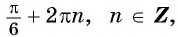
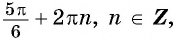
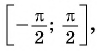
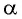
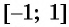
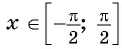
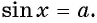
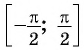
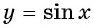
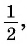
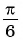
Определение Арксинуса
Определение:
Арксинусом числа 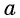
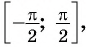
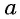
Этот угол обозначают 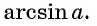
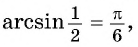
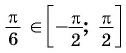
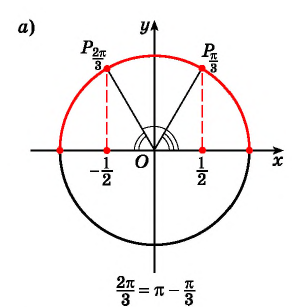
Пример №1
Вычислите:
Решение:
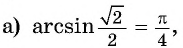
Пример №2
Найдите значение выражения:
Решение:
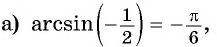
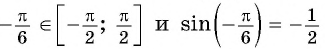
Заметим, что 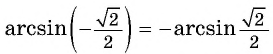
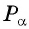
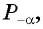
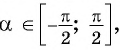
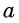
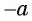
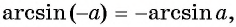
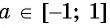
Пусть 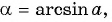
Так как точки
Поскольку 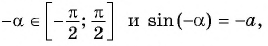
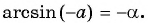
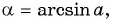
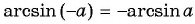
Воспользуемся полученным равенством и найдем значение выражения
Так как
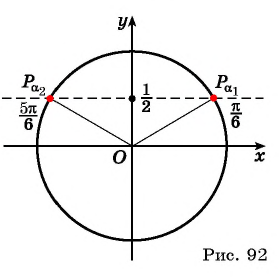
Отметим, что областью определения выражения 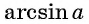
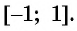
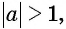
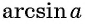
Например, выражения 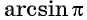
Выражение 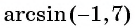
Из определения арксинуса числа следует, что 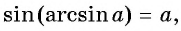
Например,
Рассмотрим промежуток 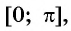
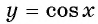
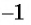
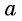
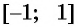
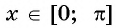
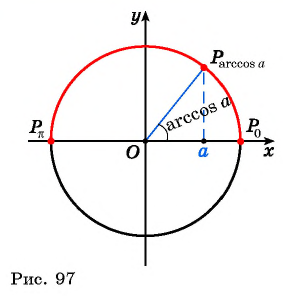
Определение Арккосинуса
Определение:
Арккосинусом числа 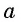
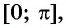
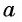
Этот угол обозначают
Например: 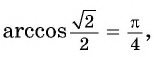
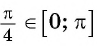
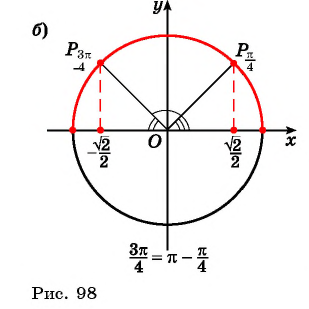
Пример №3
Вычислите:
Решение:
Пример №4
Найдите значение выражения:
Решение:
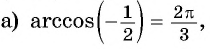
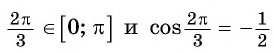
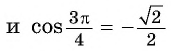
Заметим, что 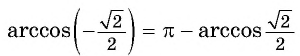
Пусть 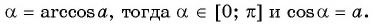
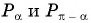
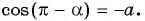
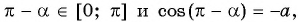
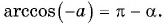
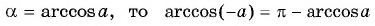
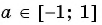
Воспользуемся полученным равенством и найдем значение выражения
Так как
Областью определения выражения 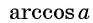
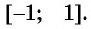
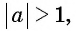
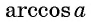
Так, выражения 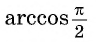
Выражение 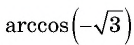
Из определения арккосинуса числа следует, что 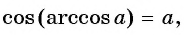
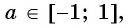
Например,
На промежутке монотонности 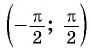
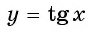
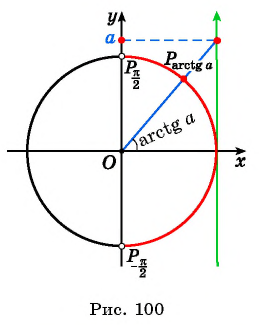
Определение Арктангенса
Определение:
Арктангенсом числа 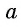
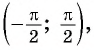
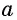
Этот угол обозначают 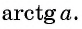
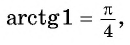
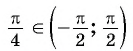
Пример №5
Вычислите:
Решение:
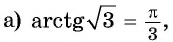
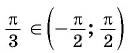
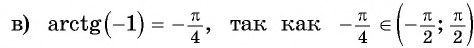
Для любого числа 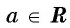
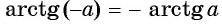
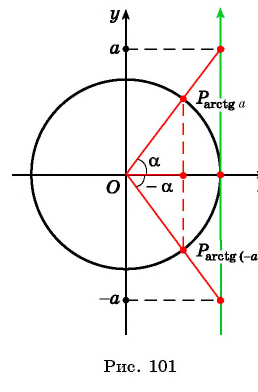
Пример №6
Найдите значение выражения
Решение:
Так как
Из определения арктангенса числа следует, что 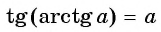
Например,
На промежутке монотонности 
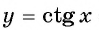
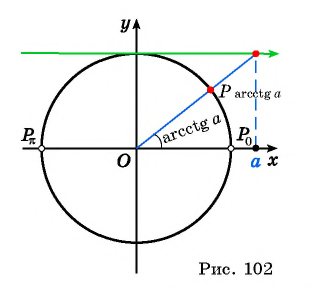
Определение Арккотангенса
Определение:
Арккотангенсом числа 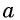
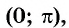
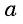
Этот угол обозначают 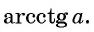
- Заказать решение задач по высшей математике
Пример №7
Вычислите:
Решение:
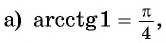
Для любого числа 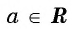
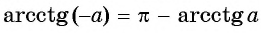
Пример №8
Найдите значение выражения
Решение:
Так как
Из определения арккотангенса числа следует, что 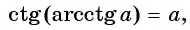
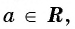
Например,
Примеры заданий и их решения
Пример №9
Верно ли, что:
Решение:
а) Верно, так как
б) верно, так как
в) неверно, так как
г) неверно, так как
Пример №10
Вычислите:
Решение:
Пример №11
Найдите значение выражения:
Решение:
Пример №12
Оцените значение выражения
Решение:
По определению арктангенса числа
Воспользуемся свойствами числовых неравенств и получим:
Пример №13
Найдите область определения выражения:
Решение:
а) По определению арксинуса числа 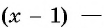
б) По определению арккосинуса числа 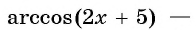
Пример №14
Найдите значение выражения:
Решение:
Пример №15
Вычислите
Решение:
Пример №16
Найдите значение выражения
Решение:
Воспользуемся формулой 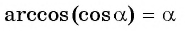
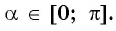
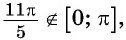
Так как
Пример №17
Найдите значение выражения
Решение:
Так как 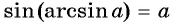
- Тригонометрические уравнения
- Тригонометрические неравенства
- Формулы приведения
- Синус, косинус, тангенс суммы и разности
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики