Поступила вот просьба сделать калькулятор для расчета цилиндрических шестерён — Техника,машиностроение.
Погружаясь в тему шестерён и их расчетов, встретил понятие инволюта, а потом — эвольвента. Показалось занятным и заслуживающим отдельных калькуляторов. Калькуляторы смотри ниже — первый рассчитывает инволюту, два следующих по заданной инволюте находят угол. Интересующимся — текст про инволюту после калькуляторов.
Инволюта угла
Точность вычисления
Знаков после запятой: 6
Нахождение угла по инволюте методом Ласкина
Точность вычисления
Знаков после запятой: 2
Нахождение угла по инволюте методом Ченга
Точность вычисления
Знаков после запятой: 2
Так вот, в дифференциальной геометрии кривых эвольвента — это кривая, нормаль в каждой точке которой является касательной к исходной кривой (см. Эвольвента в Википедии).
Поскольку сразу осознать сказанное выше сложно, перескажу своими словами более образное определение, данное в английской версии статьи (см. Involute on Wikipedia).
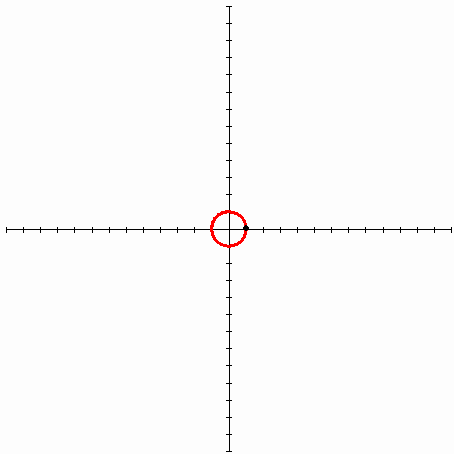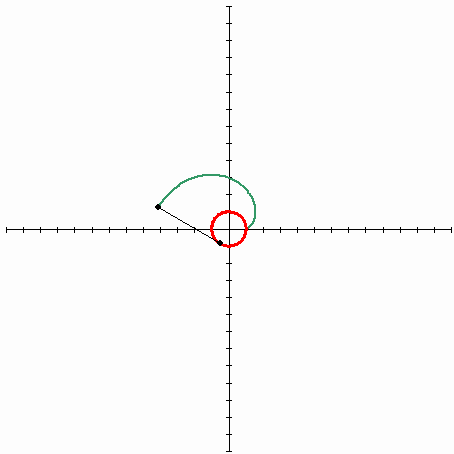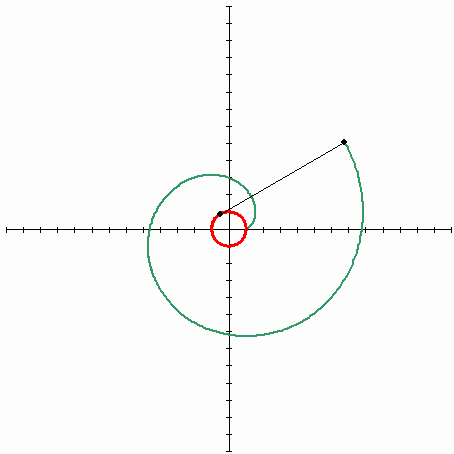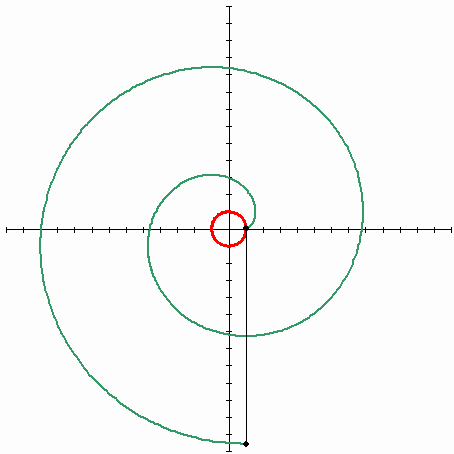
Итак, представим себе катушку ниток, где свободный край нити лежит на катушке. Если взять этот край и начать разматывать нить, все время держа ее натянутой, край нити опишет некую кривую, которая и будет эвольвентой, причем эвольвентой окружности (катушка суть исходная кривая, представляющая собой окружность).
Рисунок ниже изображает эвольвенту окружности (Источник — Википедия). Красная линия — исходная кривая (окружность), черная — натянутая нить, зеленая — траектория конца нити, кривая, называемая эвольвентой окружности.
Что касается инволюты — в англоязычных источниках, как я понял, термин инволюта (involute) применяется взаимозаменяемо с термином эвольвента (evolvent). То есть может обозначать как саму кривую, так и ее функцию. В русскоязычных источниках, которые я видел, эвольвента — это кривая, а инволюта — ее функция.
Думаю, что такое эвольвента, стало более менее ясно после картинки сверху. Теперь разберемся, что это за функция такая.
В этом нам поможет рисунок, который я нарисовал
На рисунке отрезок равен дуге
(потому что эта наша «нить»). Угол «фи», соответствующий дуге
называется углом развернутости эвольвенты, и состоит суммы угла «тета» (эвольвентного угла) и угла «альфа» (угла давления). Длина дуги
Поскольку — прямоугольный треугольник, то
Приравнивая эти две дуги друг к другу, получим , откуда
Вот эта-то функция — и называется инволютой, или эвольвентной функцией.
Уравнения эвольвентной кривой в полярных координатах выглядят так
По построению видно, что угол «альфа» может меняться от 0 до 90, не включая 90, так как в таком случае прямая KK будет параллельна MxN.
Зачем это все? Эвольвента окружности используется в эвольвентном зацеплении — зубчатом зацеплении, в котором профили зубьев очерчены по эвольвенте окружности. При эвольвентном зацеплении общая нормаль к соприкасающимся профилям зубьев всегда совпадает с общей касательной к основным окружностям. Эта касательная называется линией зацепления, так как по ней перемещается точка касания зубьев при движении колёс (картинка). Это наиболее распространенный вид зубчатого зацепления.
А инволюта используется в расчетах, связанных с эвольвентным зацеплением. Причем возникает задача как расчета самой инволюты (что просто), так и обратная задача — нахождение угла давления по его инволюте. Вот обратная задача является не такой простой, ибо уравнение является трансцендентным уравнением, и решить его можно только численными методами.
В завершение рассмотрим численные методы, использованные в калькуляторах выше — метод Ласкина и метод Ченга (подробнее — здесь)
Метод Ласкина (Laskin)
Основан на методе Ньютона, заключающемся в итерационной процедуре вычисления
Ноу-хау, как я понимаю, здесь в выборе начального значения, которое по методу Ласкина вычисляется как
, где I — заданное значение инволюты.
Для вычисления следующих приближений после раскрытия производной получается выражение
В калькуляторе используется пять итераций, но уже четыре должны давать точность до шести знаков после запятой. Метод работает для значений инволюты в диапазоне от 0 до 1, то есть можно находить углы от 0 до 64.87 градусов. На практике этого хватает. Для нахождения инволюты выпускаются таблицы, подобные таблицам тригонометрических функций, так вот там приводимый диапазон углов от 0 до 60.
Метод Ченга (Cheng)
Основан на нахождении приближенного значения с помощью асимптотических кривых. Ченг вывел следующую формулу:
Формула Ченга
Метод работает для значения инволюты строго меньших 1.8, то есть может находить углы примерно до 71.87 градуса. А дальше оно и не надо — при приближении к 90 тангенс стремится к бесконечности, со всеми вытекающими отсюда последствиями, и, в общем, ну не бывает зубчатых передач с такими большими углами.
Инволюта угла
Калькулятор вычисляет инволюту угла и находит угол по уже заданной инволюте.
Калькулятор даже больше не математический, а инженерный, даже машиностроительный больше.
Если кто знаком с машиностроением, то должен хотя бы слышать о инволюте и о эвольвенте.
Если не слышали, то можете прочитать о данной теме на данных страницах:
https://en.wikipedia.org/wiki/Involute
https://ru.wikipedia.org/wiki/evolvent
И так, перед вами 3 калькулятора: 1-й считает инволюту, 2-й и 3-й по заданной инволюте найдет угол.&
Таблица значений эвольвентной функции или таблица инвалют.
Таблица разбитая по градусам, секундам, порядкам. Необходима для расчета зубчатой передачи.
| Градус | Порядок | 0′ | 5′ | 10′ | 15′ | 20′ | 25′ | 30′ | 35′ | 40′ | 45′ | 50′ | 55′ | Порядок | Градус |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 1 | 0,000 | 00177 | 00225 | 00281 | 00346 | 00420 | 00504 | 00598 | 00704 | 00821 | 00950 | 01092 | 01248 | 0,000 | 1 |
| 2 | 0,000 | 01318 | 01603 | 01804 | 02020 | 02253 | 02503 | 02771 | 03058 | 03364 | 03689 | 04035 | 04402 | 0,000 | 2 |
| 3 | 0,000 | 04790 | 05201 | 05634 | 06091 | 06573 | 07078 | 07610 | 08167 | 08751 | 09362 | 10000 | 10668 | 0,000 | 3 |
| 4 | 0,000 | 11364 | 12090 | 12847 | 13634 | 14453 | 15305 | 16189 | 17107 | 18059 | 19045 | 20067 | 21125 | 0,000 | 4 |
| 5 | 0,000 | 22220 | 23352 | 24522 | 25731 | 26978 | 28266 | 29594 | 30963 | 32394 | 33827 | 35324 | 36864 | 0,000 | 5 |
| 6 | 0,00 | 03845 | 04008 | 04175 | 04347 | 04524 | 04706 | 04892 | 05083 | 05280 | 05481 | 05687 | 05898 | 0,00 | 6 |
| 7 | 0,00 | 06115 | 06337 | 06564 | 06797 | 07035 | 07279 | 07528 | 07783 | 08044 | 08310 | 08582 | 08861 | 0,00 | 7 |
| 8 | 0,00 | 09145 | 09435 | 09732 | 10034 | 10343 | 10659 | 10980 | 11308 | 11643 | 11984 | 12332 | 12687 | 0,00 | 8 |
| 9 | 0,00 | 13048 | 13416 | 13792 | 14174 | 14563 | 14960 | 15363 | 15774 | 16193 | 16618 | 17051 | 17492 | 0,00 | 9 |
| 10 | 0,00 | 17941 | 18397 | 18860 | 19332 | 19812 | 20299 | 20795 | 21299 | 21810 | 22330 | 22859 | 23396 | 0,00 | 10 |
| 11 | 0,00 | 23941 | 24495 | 25057 | 25628 | 26208 | 26797 | 27394 | 28001 | 28016 | 29241 | 29875 | 30518 | 0,00 | 11 |
| 12 | 0,00 | 31171 | 31832 | 32504 | 33185 | 33875 | 34555 | 35285 | 36005 | 36735 | 37474 | 38224 | 38984 | 0,00 | 12 |
| 13 | 0,00 | 39754 | 40534 | 41325 | 42126 | 42938 | 43760 | 44593 | 45437 | 46291 | 47157 | 48033 | 48921 | 0,00 | 13 |
| 14 | 0,00 | 49819 | 50729 | 51650 | 52582 | 53526 | 54482 | 55448 | 56427 | 57417 | 58420 | 59434 | 60460 | 0,00 | 14 |
| 15 | 0,00 | 61488 | 62548 | 63611 | 64686 | 65773 | 66873 | 67985 | 69110 | 70248 | 71398 | 72561 | 73738 | 0,00 | 15 |
| 16 | 0,0 | 07493 | 07613 | 07735 | 07857 | 07982 | 08107 | 08234 | 08362 | 08492 | 08623 | 08756 | 08889 | 0,0 | 16 |
| 17 | 0,0 | 09025 | 09161 | 09299 | 09439 | 09580 | 09722 | 09866 | 10012 | 10158 | 10307 | 10456 | 10608 | 0,0 | 17 |
| 18 | 0,0 | 10760 | 10915 | 11071 | 11228 | 11387 | 11547 | 11709 | 11873 | 12038 | 12205 | 12373 | 12543 | 0,0 | 18 |
| 19 | 0,0 | 12715 | 12888 | 13063 | 13240 | 13418 | 13598 | 13779 | 13963 | 14148 | 14334 | 14523 | 14713 | 0,0 | 19 |
| 20 | 0,0 | 14904 | 15098 | 15293 | 15490 | 15689 | 15890 | 16092 | 16296 | 16502 | 16710 | 16920 | 17132 | 0,0 | 20 |
| 21 | 0,0 | 17345 | 17560 | 17777 | 17996 | 18217 | 18440 | 18665 | 18891 | 19120 | 19350 | 19583 | 19817 | 0,0 | 21 |
| 22 | 0,0 | 20054 | 20292 | 20533 | 20775 | 21019 | 21266 | 21514 | 21765 | 22018 | 22272 | 22529 | 22788 | 0,0 | 22 |
| 23 | 0,0 | 23044 | 23312 | 23577 | 23845 | 24414 | 24386 | 24660 | 24936 | 25214 | 25495 | 25778 | 26062 | 0,0 | 23 |
| 24 | 0,0 | 26350 | 26639 | 26931 | 27225 | 27521 | 27820 | 28121 | 28424 | 28729 | 29037 | 29348 | 29660 | 0,0 | 24 |
| 25 | 0,0 | 29975 | 30293 | 30613 | 30935 | 31260 | 31587 | 31917 | 32249 | 32583 | 32920 | 33260 | 33602 | 0,0 | 25 |
| 26 | 0,0 | 33947 | 34294 | 34644 | 34997 | 35352 | 35709 | 36069 | 36432 | 36798 | 37166 | 37537 | 37910 | 0,0 | 26 |
| 27 | 0,0 | 38287 | 38666 | 39047 | 39432 | 39819 | 40209 | 40602 | 40997 | 41395 | 41797 | 42201 | 42607 | 0,0 | 27 |
| Градус | Порядок | 0′ | 5′ | 10′ | 15′ | 20′ | 25′ | 30′ | 35′ | 40′ | 45′ | 50′ | 55′ | Порядок | Градус |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 28 | 0,0 | 43017 | 43430 | 43845 | 44264 | 44685 | 45110 | 45537 | 45967 | 46400 | 46837 | 47276 | 47718 | 0,0 | 28 |
| 29 | 0,0 | 48164 | 48612 | 49064 | 49518 | 49976 | 50437 | 50901 | 51363 | 51838 | 52312 | 52788 | 53268 | 0,0 | 29 |
| 30 | 0,0 | 53751 | 54238 | 54728 | 55221 | 55711 | 56217 | 56720 | 57226 | 57736 | 58249 | 58765 | 59285 | 0,0 | 30 |
| 31 | 0,0 | 58809 | 60335 | 60856 | 61400 | 61937 | 62478 | 63022 | 63570 | 64122 | 64677 | 65236 | 65798 | 0,0 | 31 |
| 32 | 0,0 | 66364 | 66934 | 67507 | 68084 | 68665 | 69250 | 69838 | 70430 | 71026 | 71626 | 72230 | 72838 | 0,0 | 32 |
| 33 | 0,0 | 73449 | 74064 | 74684 | 75307 | 75934 | 76565 | 77200 | 77839 | 78483 | 79130 | 79781 | 80437 | 0,0 | 33 |
| 34 | 0,0 | 81097 | 81760 | 82422 | 83100 | 83777 | 84457 | 85142 | 85832 | 86525 | 87223 | 87925 | 88631 | 0,0 | 34 |
| 35 | 0,0 | 89342 | 90058 | 90777 | 91502 | 92230 | 92963 | 63701 | 94443 | 95190 | 95942 | 96698 | 97459 | 0,0 | 35 |
| 36 | 0 | 09822 | 09899 | 09977 | 10055 | 10133 | 10212 | 10292 | 10371 | 10452 | 10533 | 10614 | 10696 | 0 | 36 |
| 37 | 0 | 10778 | 10861 | 10944 | 11028 | 11113 | 11197 | 11283 | 11369 | 11455 | 11542 | 11630 | 11718 | 0 | 37 |
| 38 | 0 | 11806 | 11895 | 11985 | 12075 | 12165 | 12257 | 12348 | 12441 | 12534 | 12627 | 12721 | 12815 | 0 | 38 |
| 39 | 0 | 12911 | 13006 | 13102 | 13199 | 13297 | 13395 | 13493 | 13592 | 13692 | 13792 | 13893 | 13995 | 0 | 39 |
| 40 | 0 | 14097 | 14200 | 14303 | 14407 | 14511 | 14616 | 14722 | 14829 | 14936 | 15043 | 15152 | 15261 | 0 | 40 |
| 41 | 0 | 15370 | 15480 | 15591 | 15703 | 15815 | 15928 | 16041 | 16156 | 16270 | 16386 | 16502 | 16619 | 0 | 41 |
| 42 | 0 | 16737 | 16855 | 16974 | 17093 | 17214 | 17335 | 17457 | 17579 | 17702 | 17826 | 17951 | 18076 | 0 | 42 |
| 43 | 0 | 18202 | 18329 | 18457 | 18585 | 18714 | 18844 | 18975 | 19106 | 19238 | 19371 | 19505 | 19639 | 0 | 43 |
| 44 | 0 | 19774 | 19910 | 20047 | 20185 | 20323 | 20463 | 20603 | 20743 | 20885 | 21028 | 21171 | 21315 | 0 | 44 |
| 45 | 0 | 21460 | 21606 | 21753 | 21900 | 22049 | 22198 | 22348 | 22499 | 22651 | 22804 | 22958 | 23112 | 0 | 45 |
| 46 | 0 | 23268 | 23424 | 23582 | 23740 | 23899 | 24099 | 24220 | 24382 | 24545 | 24709 | 24874 | 25040 | 0 | 46 |
| 47 | 0 | 25206 | 25374 | 25543 | 25713 | 25883 | 26055 | 26228 | 26401 | 26576 | 26752 | 26929 | 27107 | 0 | 47 |
| 48 | 0 | 27285 | 27465 | 27646 | 27828 | 28012 | 28196 | 23381 | 28567 | 28755 | 28943 | 29133 | 29724 | 0 | 48 |
| 49 | 0 | 29516 | 29709 | 29983 | 30098 | 30295 | 30492 | 30691 | 30891 | 31092 | 31295 | 31498 | 31708 | 0 | 49 |
| 50 | 0 | 31909 | 32116 | 32324 | 32534 | 32745 | 32957 | 33171 | 33385 | 33681 | 33818 | 34037 | 34257 | 0 | 50 |
| 51 | 0 | 34478 | 34700 | 34924 | 35149 | 36376 | 35604 | 35833 | 36063 | 36295 | 36529 | 36763 | 36999 | 0 | 51 |
| 52 | 0 | 37237 | 37476 | 37716 | 37958 | 38202 | 38446 | 38693 | 38941 | 39190 | 39441 | 39693 | 39947 | 0 | 52 |
| 53 | 0 | 40202 | 40459 | 40717 | 40977 | 41239 | 41502 | 41767 | 42034 | 42302 | 42571 | 42843 | 43116 | 0 | 53 |
|
0 / 0 / 0 Регистрация: 31.12.2017 Сообщений: 4 |
|
|
1 |
|
Найти угол, зная его инволюту28.01.2019, 22:53. Показов 6268. Ответов 3
PTC Mathcad Prime 5.0.0.0 Требуется найти угол зная его инволюту
0 |
|
Модератор 5094 / 3909 / 1343 Регистрация: 30.07.2012 Сообщений: 11,689 |
|
|
29.01.2019, 11:43 |
2 |
|
troshka, с помощью Блока решений… Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 31.12.2017 Сообщений: 4 |
|
|
29.01.2019, 15:25 [ТС] |
3 |
|
У меня после нажатия на знак «=» автоматически пишет значение
0 |
|
Модератор 5094 / 3909 / 1343 Регистрация: 30.07.2012 Сообщений: 11,689 |
|
|
29.01.2019, 19:48 |
4 |
|
Решение
tan(a)-a=0.557408 Здесь надо нажимать CTRL+=
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
29.01.2019, 19:48 |
|
Помогаю со студенческими работами здесь Найти угол, зная косинус или синус Как найти координаты вектора, зная длину и угол? Как найти вектор направления тела, зная угол поворота? Найти стороны косоугольного треугольника, зная периметр и один угол Найти площадь прямоугольного треугольника, зная гипотенузу и прилежащий угол #include <iostream> Зная периметр и одну из диагоналей, найти площадь ромба и угол гамма Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 4 |
Одним
из основных достоинств зубчатого
зацепления механизмов является его
компактность при передаче большой
мощности. Для уменьшения геометрических
размеров зубчатых колес и механизма в
целом используют зубчатые колеса с
минимальным числом зубьев. Однако при
изготовлении зубчатых колес с числом
зубьев меньше 17 происходит подрез
эвольвентной части зуба в районе ножки.
Во избежание подрезания профиля зуба
режущий инструмент при изготовлении
зубчатых колес отодвигается от центра
заготовки (положительное смещение).
Изготовленные таким образом зубчатые
колеса со смещением имеют большую
прочность и устойчивость к износу, но
меньший коэффициент перекрытия εα,
показывающий сколько пар зубьев
одновременно находится в зацеплении.
Величина смещения
инструмента «а»
определяется из соотношения:
a
= xm,
где х—
коэффициент смещения,
m—
модуль зубчатого колеса.
Правильно выбранный
коэффициент смещения обеспечивает
получение необходимых свойств и
геометрических параметров зубчатой
передачи. В связи с этим при выборе
коэффициентов смещения необходимо
пользоваться рекомендациями по
проектированию зубчатых передач с
заданными свойствами.
Так, например, для
силовых передач общего назначения при
выборе коэффициентов смещения можно
пользоваться рекомендациями, приведенными
в таблице 2.
Таблица 2 Рекомендуемые
значения коэффициентов смещения
|
Числа зубьев |
x1 |
x2 |
|
z1,2≥30 |
0 |
0 |
|
z1=14-20 z2≥50 |
0,3 |
-0,3 |
|
z1=10÷30 z2≤30 |
0,5 |
0,5 |
|
z1= z2≥ |
0,5 |
0 |
|
z1=5…9 z2≤ |
Х1=0,03(30-z1) |
Х2=0,03(30-z2) |
В специальной
литературе имеются рекомендации по
выбору коэффициентов смещения при
проектировании зубчатых передач с
различными свойствами [2].
Выбор коэффициентов
смещения можно осуществить также по
так называемым блокирующим контурам.
После выбора
коэффициентов смещения х1
и х2
при заданных числах зубьев z1
и z2
и модуля зацепления m
определяем основные размеры зубчатых
колес и качественные характеристики
зацепления.
Суммарный коэффициент
смещения:
Х∑=х1+х2
Эвольвентная
функция (инвалюта) угла зацепления αw:
inv
αw=invα+2((x1+x2)/z1+z2)tgα,
где α — угол профиля
реечного инструмента (α=20º).
Угол αw
находят по таблицам эвольвентной
функции. При необходимости определения
инвалюты угла пользуются следующей
формулой:
invαi=
tgαi
— αi,
где αi
— угол в радианах.
Все геометрические
параметры зубчатой передачи определяются
в миллиметрах.
Диаметры делительных
окружностей:
d1=mz1
d2=mz2
Диаметры основных
окружностей:
dв1=d1cosα
dв2=d2cosα
Делительное
межосевое расстояние:
a=(m(z1+z2))/2
Межосевое расстояние
передачи со смещением:
aw=a(cosα)/
cosαw
Коэффициент
воспринимаемого смещения:
у=(аW—a)/m
Коэффициент
уравнительного смещения:
∆у=х∑-у
Радиусы начальных
окружностей:
rw1=r1(cosα)/
cosαw
rw2=r2(cosα)/
cosαw
Контрольная
проверка:
aw=rw1+rw2
Радиусы вершин
зубьев:
ra1=m((z1/2)+ha*+x1-∆y)
ra2=m((z2/2)+ha*+x2-∆y)
Радиусы окружностей
впадин зубьев:
rf1=m((z1/2)-ha*+x1-с*)
rf2=m((z2/2)-ha*+x2-с*)
Высота зуба:
h=ra1—rf1
Толщина зубьев по
делительной окружности:
S1=m((π/2)+2x1tgα)
S2=m((π/2)+2x2tgα)
Угол профиля в
точке на окружности вершин:
αa1=arccos(rв1/ra1)
αa2=arccos(rв2/ra2)
Толщина зубьев по
окружности вершин:
Sa1=m(cosα/cosαw)[(π/2)+2x1tgα—z1(invαa1—invα)]
Sa2=m(cosα/cosαw)[(π/2)+2x2tgα—z2(invαa2—invα)]
Толщина зубьев по
окружности вершин должна быть больше
или равна 0,4m,
коэффициенты высоты головки зуба
ha*
= 1, коэффициент
радиального зазора с*=0,25.
Коэффициент
торцового перекрытия:
εα=(z1/2π)(tgαa1—tgαw)+(z2/2π)(tgαa2—tgαw)
≥ [εα]
В зависимости от
точности изготовления зубчатых колес
минимальная величина коэффициента
перекрытия принимается от 1,05 до 1,35.
Например, если εα=
1,2, то в зацеплении находится в среднем
1,2 пар зубьев, а фактически в течение
20% времени работы передачи в зацеплении
находятся две пары зубьев, а в течение
80% — одна пара.
На основании
выполненных расчетов вычерчивается
зацепление 2х зубчатых колес с определением
активной линии зацепления и активной
части профилей зубьев.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #


 Сообщение было отмечено troshka как решение
Сообщение было отмечено troshka как решение
