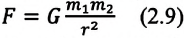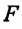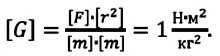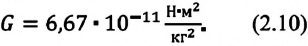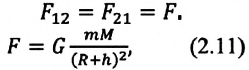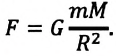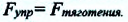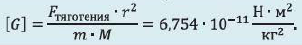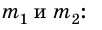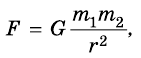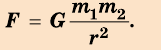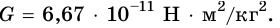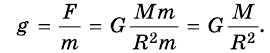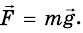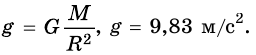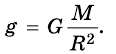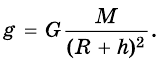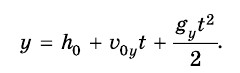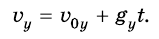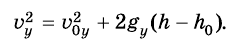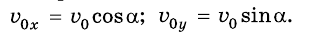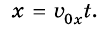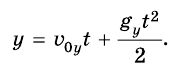На чтение 8 мин Просмотров 2.2к.
Наблюдая за перемещением небесных объектов, люди пытались найти объяснение происходящим на небе событиям. У древних людей преобладали версии мистического характера. Но в 17-м веке Исааком Ньютоном было предложено первое научное объяснение перемещению астрономических тел. Теория гравитации совершенствовалась еще несколько столетий, пока не приобрела современный вид.
Однако, несмотря на наблюдения и опыт, в современной астрофизике есть много пробелов и нестыковок, которые ученые затрудняются объяснить. Например, гравитационная константа, значение которой до сих пор не получается определить с достаточной степенью точности. А в последнее время появились предположения, что эта величина не совсем и константа. В этой статье мы и рассмотрим данный вопрос.
Содержание
- Что такое гравитационная постоянная
- Единица измерения гравитационной постоянной
- Как найти гравитационную постоянную, история открытия
- Работы Ньютона
- Экспериментальное определение гравитационной постоянной, эксперимент Кавендиша
- Измерение гравитационной постоянной
- Современная история изменений гравитационной постоянной
Что такое гравитационная постоянная
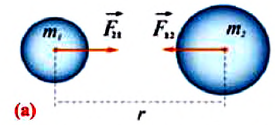
Гравитационной постоянной (постоянной Ньютона) называют коэффициент, входящий в формулу закона всемирного тяготения. Численное значение константы гравитации (G, GN или g) равно:
Постоянная Ньютона не зависит от характеристик взаимодействующих объектов и внешних критериев. Данный показатель активно используется практиками при вычислении орбит небесных объектов, в геолого-разведывательных процессах, в геодезии и геофизике.
Единица измерения гравитационной постоянной
Сила в физике сила измеряется в ньютонах:
Гравитационная постоянная численно равна силе, но при этом имеет другую размерность:
Данная единица измерения выводится при помощи несложных расчетов. Два тела весом по 1кг будут взаимно притягиваться с силой, обратно пропорциональной квадрату расстояния между ними:
Коэффициент, уравнивающий Н и единицу измерения гравитационной постоянной, вычисляется следующим образом:
Как найти гравитационную постоянную, история открытия
Открытию явления гравитации предшествовали труды многих исследователей. Еще в древней Греции были предложены гипотезы, которые пытались объяснить, почему материальные тела падают на землю, а не летят в произвольном направлении. История открытия гравитации представлена в таблице.
| Николай Коперник | Обосновал модель мира, в которой Солнце занимает центральное место, а остальные объекты вращаются вокруг него (гелиоцентрическая модель). |
| Уильям Гилберт | Высказал предположение, что наша планета и ее спутник являются магнитами друг для друга, при этом магнитная сила Земли больше из-за того, что больше ее масса. |
| Иоганн Кеплер | Сформулировал ряд законов, в том числе 3-й, который был использован при разработке теории гравитации: период обращения планет в квадрате соотносится как большие полуоси орбит в кубе. |
| Галилео Галилей | Обосновал, что если на тело не оказывать никаких воздействий, то оно будет оставаться в бездействии. Сформулировал закон, смысл которого заключался в том, что все тела, независимо от их тяжести, падают вниз с одинаковой скоростью, при этом пройденный путь пропорционален квадрату времени, за которое тело достигло поверхности Земли. |
| Роберт Гук | Сформулировал закон всемирного тяготения для некруговых орбит и предложил Ньютону обосновать его математически. Создал теорию об универсальной силе тяжести. |
| Эдмунд Галлей | Просчитал обратно пропорциональную зависимость силы тяжести и квадрата расстояния. |
| Исаак Ньютон | На основании работ предшественников вывел закон всемирного тяготения. |
| Генри Кавендиш | Собрал приспособление, с помощью которого можно определить величину константы гравитации. |
| Симеон Дени Пуассон | В его трудах впервые появляется понятие гравитационной константы. |
Ньютона интересовало выведение научных правил, а не чистота искомых значений. Экспериментаторы, которые применяли формулу Ньютона на практике, столкнулись с необходимостью введения поправочного коэффициента, который позже получил название ньютоновская константа. Возник вопрос, чему равна гравитационная постоянная. Последовавшие в данном направлении работы показали, что найти гравитационную постоянную можно только опытным путем.
Работы Ньютона
Научная почва для обоснования закона всемирного тяготения была основательно подготовлена предшественниками Ньютона. Большая часть расчетов базировалась на 3-м законе Кеплера. Сила, благодаря которой планеты удерживаются на орбитах, соизмерима с центростремительным ускорением, и должна быть обратно пропорциональна квадрату расстояния от центра планеты до центра Солнца. Сила, вызывающая падение предметов (пресловутого яблока) на землю, была сопоставлена ученым с силой, удерживающей Луну на ее орбите. Кроме того, физик установил центростремительное ускорение Луны относительно Земли.
Ранее опытным путем было установлено значение ускорения свободного падения объектов. Ученый применил удобные для вычислений цифры: дистанция от Луны до центра Земли в 60 раз больше, чем дистанция от объекта, находящегося на поверхности Земли. Если объект направить к центру Земли, то он за 1 секунду пролетит такой же путь, который пройдет Луна за 1 минуту. Эксперименты подтвердили точность теоретических выкладок с погрешностью около 1%. Это указывало на общность природы происхождения сил тяготения.
Из этого можно заключить, что сила обоюдного притяжения должна соответствовать каждой из масс. Также было подтверждено, что гравитация обратно пропорциональна квадрату расстояния между объектами. Исходя из вышесказанного, формула закона всемирного тяготения будет иметь следующий вид:
где F – сила гравитационного тяготения, g – гравитационная постоянная, m1 и m2 – массы объектов, R – расстояние между объектами.
Работы Ньютона внесли вклад в решение следующих вопросов:
- перемещения тел по космическим орбитам;
- ускорение свободного падения;
- приливы океанических вод;
- причины экваториальной выпуклости.
Эйнштейн использовал закон всемирного тяготения при разработке теории относительности. Постоянная гравитационная показывает соотношение между такими характеристиками уравнений поля, как геометрия пространства-времени и тензор энергии-импульса.
Вместо G Ньютон применял в расчетах «гравитационный параметр» µ. Практические наблюдения за космическими телами позволили определить для ряда небесных объектов значение µ с минимальной погрешностью. Рассчитывают µ по формуле:
µ=GM;
где G – константа гравитации, M – масса объекта
В трудах Кеплера также фигурирует гравитационный параметр. В физике с его помощью упрощают некоторые громоздкие формулы.
Экспериментальное определение гравитационной постоянной, эксперимент Кавендиша
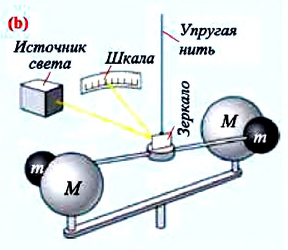
Британец Джон Мичелл увековечил свое имя как создатель крутильных весов, с помощью которых впервые смогли определить величину g. Экспериментальное определение гравитационной постоянной не входило в планы исследователя. Он хотел «взвесить» нашу планету. Однако воплотить свои планы Мичелл не успел, и сконструированное им устройство после его кончины досталось Генри Кавендишу.
Кавендиш доработал установку. Конструкция включала шестифутовый стержень, закрепленный на медном волокне длиной 1 м. К плечам коромысла ученый прикрепил два шара из свинца по 775 грамм каждый, соорудив таким образом гантельку. Затем рядом с маленькими шариками он разместил крупные шары по 49,5 кг, что привело к возникновению явления гравитации между объектами. Стержень конструкции отклонился от первоначального положения, что дало возможность найти величину угла поворота гантельки. Опыт Кавендиша оказался успешным: увязав упругие свойства волокна, массу шаров, размер установки и значение угла, он определил массу Земли и ее среднюю плотность. Сегодня эксперимент Кавендиша по-прежнему актуален, исследователями разрабатываются инновационные модификации прибора.
Измерение гравитационной постоянной
С измерением степени точности гравитационной постоянной g сложилась парадоксальная ситуация. Последние многочисленные эксперименты определяют отклонение с точностью 10-4. Это хуже на несколько порядков по сравнению с точностью определения прочих базисных величин. Сравнительно аккуратные результаты можно получить в условиях лаборатории, измеряя силу гравитации между двумя телами с известной массой (модификации эксперимента Кавендиша). Новые атомно-интерферометрические устройства оказались непригодными в измерении гравитационной постоянной в связи с гораздо большей величиной погрешности, чем при эксперименте на механических устройствах.
Современная история изменений гравитационной постоянной
Неординарность ситуации с нахождением точного значения гравитационной константы привела к возникновению догадки, что G не является постоянной в классическом понимании и может с течением времени изменяться. В уравнениях общей теории относительности Эйнштейн увязал гравитационную постоянную и космологическую константу – параметр, который влияет на устойчивость Вселенной.
Хаббл и Фридман обосновали опытным путем модель расширяющейся Вселенной, что противоречило теории стационарной Вселенной Эйнштейна. На долгое время ученые прекратили учитывать при вычислениях космологическую постоянную. В конце 1990-х годов было выявлено и подтверждено ускорение расширения Вселенной. Вновь открытые результаты не вписывались в теорию Хаббла-Фридмана, концепцию пришлось пересматривать, и космологическая постоянная вернулась в физику.
Современная Лямбда-CDM модель Вселенной учитывает космологическую постоянную. Данная концепция объясняет наличие антигравитации, «темной материи», реликтового излучения, и является стандартом в астрофизике с 1998-го года.
Интересно, что Лямбда-CDM модель хорошо коррелирует с космологией черной дыры. Все больше ученых склонны отказываться от Теории большого взрыва, поскольку накопившиеся научные данные противоречат общепринятому взгляду на образование Вселенной. В гипотезу, что видимое нами пространство-время (и мы вместе с ним) бесконечно «падает» в гигантскую черную дыру, отлично вписывается явление ускорения расширения Вселенной, «странности» реликтового излучения, наличие темной материи.
Современная история изменений гравитационной постоянной привела к попыткам астрономов переосмыслить данный физический параметр. Так, Филипп Мангейм считает, что константа g в зависимости от условий ее измерения может менять свое значение. В условиях нашей планеты постоянная g будет иметь известную ученым величину, а вот в космосе значение G будет гораздо меньше.
Космологическая постоянная, описывающая скорость расширения Вселенной, имеет расчетное значение в 10120 раз превосходящее наблюдаемое. Если бы значение g было верным, то галактики не успели бы образоваться. По мнению Мангейма, в расчеты следует ввести новую величину, которая будет пропорциональна произведению космологической и гравитационной констант.
Такой подход позволит устранить существующие противоречия, но у него есть и свои недостатки: подвергаются сомнению основы теории относительности, не объясняется существование реликтового излучения и двойных пульсаров. Преимуществом идеи Мангейма является возможность синтеза теории гравитации и физики элементарных частиц в одну универсальную доктрину.
По вашему мнению, ньютоновская константа – это объективный параметр, или мы просто не все знаем о физических феноменах?



Калькулятор расчётов по закону всемирного тяготения Ньютона
Условные обозначения формулы: F — сила гравитации, m1,m2 — масса двух тел, G — гравитационная константа, приблизительно 6.67384 (80) x10^-11, R — расстояние между телами.
Формула расчёта силы гравитации: F=G*m1*m2/R2. Гравитационная константа, умноженная на массы двух тел и разделённая на расстояние в квадрате.
Формула расчёта массы одного из тел: m1=(F*R2*10^11)/(G/m2). Силу гравитации, умножаем на расстояние, в квадрате, на 10 в 11 степени, и делим на гравитационную константу умноженную на массу другого тела.
Формула расчёта расстояния между телами: R=[квадратный корень][(G*m1*m2)/(F*10^11)]. Гравитационную константу умноженную на массы тел, делим на силу гравитации, умноженную на 10 в 11 степени и извлекаем квадратный корень.
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.

Максим *******
В соответствии с законом всемирного тяготения, вытекающим из третьего закона Ньютона —
сила взаимодействия между телами F = G*m1*m2/R^2,
где G = 6,67*10^-11 (Н*м^2/кг^2) — гравитационная постоянная.
Из приведенной формулы можно вычислить R — расстояние междку телами как квадратный корень
R = sqrt (G*m1*m2/F)
Вот и все. «Любые две материальные точки притягиваются с силами, прямо пропорциональными произведению их масс и обратнопропорциональными квадрату расстояния между ними»(направлены силы по центру материальных точек) .
Успехов в учебе !
Привет.
Я Настя из ИвГУ (это город Иваново).
«Сегодня от своего лица хочу поблагодарить этот сайт за помощь мне с учебой. Здесь я пользовалась не только материалами, но и нашла преподавателей которые решали мне задачи.
Если тебе нужно что-то сделать в универе, я сама рекомендую. А также пользуйся моей ссылкой и получай 300 руб. на счёт при регистрации.»
Пунктуация и орфография автора сохранены
Получить 300 руб. от Насти
Webmath — преподаватель со стажем более 5 лет выполнит учебную работу за вас
Договор
Строго соблюдаем условия договора от заказа до защиты
Наши авторы
10 000+ преподавателей и научных сотрудников
Гарантии
Точное соответствие ТЗ с бесплатными доработками
АкцияСкидка 25% на вашу работу + речь в подарок. Дарим вам 100₽ на первый заказ!
Содержание:
Закон всемирного тяготения:
В таблице представлены орбитальные скорости планет и карликовых планет Солнечной системы. Исследуя эту информацию, с легкостью можно определить, что небесные тела этой системы, близко расположенные к Солнцу, имеют более высокую орбитальную скорость.
Орбитальная скорость Луны вокруг Земли, по сравнению со скоростями из повседневной жизни, так же очень большая: -3682,8 км/час. Однако эта скорость во много раз меньше скорости Земли вокруг Солнца.
| Планеты и карликовые планеты | Орбитальная скорость | |
| км/с | км/с | |
| Меркурий | 47,87 | 172 332 |
| Венера | 35,02 | 126 072 |
| Земля | 29,78 | 107 208 |
| Марс | 24,13 | 86 868 |
| Церера | 17,88 | 64 368 |
| Юпитер | 13,07 | 47 052 |
| Сатурн | 9,69 | 34 884 |
| Уран | 6,81 | 24 516 |
| Нептун | 5,43 | 19 548 |
| Плутон | 4,67 | 16 812 |
| Хаумеа | 4,48 | 16 128 |
| Макемаке | 4,41 | 15 876 |
| Эрида | 3,44 | 12 384 |
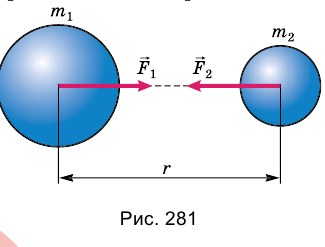
Вы знаете, что все тела во Вселенной, имеющие массу — звезды, галактики, Солнце и планеты, тела Земной системы, молекулы, атомы и другие, взаимно притягиваются друг к другу с силой, называемой силой тяготения (или гравитационной силой). Исследовав, от каких величин и как зависит эта сила, Исаак Ньютон сформулировал закон всемирного тяготения.
Закон всемирного тяготения
Между любыми двумя материальными точками действует сила взаимного притяжения, прямо пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними:
Где
Гравитационная постоянная
Единица гравитационной постоянной в СИ:
Гравитационная постоянная численно равна силе притяжения друг к другу двух материальных точек массами по 1 кг каждый, если расстояние между ними равно 1 м.
Численное значение гравитационной постоянной опытным путем определил английский ученый Генри Кавендиш (1731—1810) в 1798 году. Это значение одинаково для всех тел во Вселенной вне зависимости от их размеров и масс:
Как видно, численное значение гравитационной постоянной очень мало. Поэтому между телами с относительно малыми массами сила притяжения не чувствуется. Эта сила принимает ощутимые значения при взаимодействии тел с очень большой массой, например, между звездой и планетой, планетой и спутником и т.д.
Формула закона всемирного тяготения
Сила притяжения между двумя произвольными телами, не являющимися материальными точками при данных условиях, также определяется формулой закона всемирного тяготения. В этом случае эти тела рассматриваются как совокупность материальных точек, вычисляются силы притяжения между всеми материальными точками этих тел, результаты вычислений суммируются и определяются сила притяжения между этими телами. Такие вычисление представляет собой сложную математическую операцию. Однако формула Всемирного тяготения легко применяется для тел шарообразной формы. За расстояние между телами при этом принимается расстояние между их центрами (а). Поэтому для вычисления силы притяжения между произвольным телом и Землей можно применить формулу закона всемирного тяготения. В этом случае расстояние между ними берется до центра Земли: 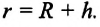
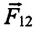
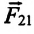
Согласно III закону Ньютона 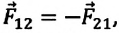
Где 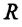
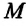
Измерение гравитационной постоянной
С этой целью Г. Кавендиш использовал крутильные весы. Схема весов показана на рисунке: на концах стержня длиной 2 м он установил два свинцовых шарика массой по 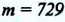
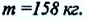
Зная угол поворота, можно определить силу упругости 
Таким образом, ученый, подставив известные величины в формулу закона всемирного тяготения, получил для гравитационной постоянной значение, очень близкое к его современному значению:
Что такое закон всемирного тяготения
Все тела во Вселенной, как небесные, так и находящиеся на Земле, взаимно притягиваются. Даже если мы не замечаем притягивания между обычными предметами, которые окружают нас в повседневной жизни (например, между книгами, тетрадями, мебелью и т. п.), то это потому, что оно в таких случаях очень слабое.
Взаимодействие, свойственное всем телам во Вселенной и проявляющееся взаимным притягиванием друг к другу, называют гравитационным, а само явление всемирного тяготения — гравитацией (лат. gravitas — «тяжесть»).
Гравитационное взаимодействие осуществляется с помощью особенного вида материи, который называют гравитационным полем. Такое поле существует вокруг любого тела — планеты, камня, человека или листа бумаги. При этом тело, создающее гравитационное поле, действует им на любое другое тело так, что у того появляется ускорение, всегда направленное к источнику поля. Появление такого ускорения и значит, что между телами возникает притяжение.
Гравитационное поле не следует путать с электромагнитными полями, существующими вокруг наэлектризованных тел, проводников с током и магнитов.
Интересной особенностью гравитационного поля, которую не имеют электромагнитные поля, является его всепроникающая способность. Если от электрических и магнитных полей можно защититься с помощью специальных металлических экранов, то от гравитационного поля защититься ничем нельзя: оно проникает сквозь любые материалы.
Выражение для силы притяжения Исаак Ныотон получил еще в 1666 г., когда ему было 24 года. Сначала ученый установил, как зависит от расстояния ускорение свободного падения. Он заметил, что вблизи поверхности Земли, то есть на расстоянии 6400 км от ее центра, это ускорение равно 9,8 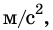
Окончательную формулу силы притяжения можно получить, если учесть, что эта сила должна быть пропорциональна массам тел
где G — гравитационная постоянная.
Так, Ньютон нашел выражение для силы гравитационного взаимодействия Земли с телами, которые притягивались ею. Но интуиция подсказывала ему, что по данной формуле можно рассчитывать и силу притяжения, действующую между любыми другими телами Вселенной, если только их размеры малы по сравнению с расстоянием г между ними. Поэтому он начал рассматривать полученное выражение как закон всемирного тяготения, который выполняется и для небесных тел, и для тел на Земле.
Сила гравитационного притяжения любых двух частиц прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними:
Закон всемирного тяготения сформулирован для частиц, размеры которых значительно меньше расстояния г между ними. Однако одна особенность закона дает возможность использовать его и в некоторых иных случаях. Такой особенностью является обратно пропорциональная зависимость силы притяжения именно от квадрата расстояния между частицами, а не от третьей или четвертой степени расстояния. Расчеты показывают, что благодаря этой особенности формулу 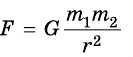
Формула 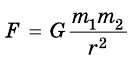
Когда Ньютон открыл закон всемирного тяготения, он не знал ни одного числового значения масс небесных тел, в том числе и Земли. Неизвестно ему было и значение постоянной.
Вместе с тем, гравитационная постоянная G имеет для всех тел Вселенной одно и то же значение и является одной из фундаментальных физических констант. Каким же образом можно определить ее значение? Из закона всемирного тяготения следует, что 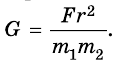
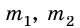
Первые измерения гравитационной постоянной были осуществлены в середине XVIII в. Оценить, правда очень грубо, значение G в то время удалось в результате рассмотрения притягивания маятника к горе, масса которой была определена с помощью геологических методов.
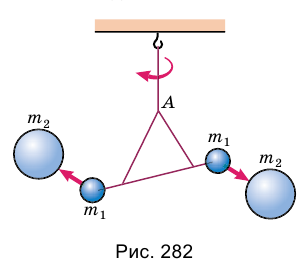
Точные измерения гравитационной постоянной впервые осуществил в 1798 г. Генри Кавендиш — английский физик, член Лондонского королевского общества. С помощью так называемых крутильных весов (рис. 282) ученый по углу закручивания нити А сумел измерить ничтожно малую силу притяжения между маленькими и большими металлическими шарами. Для этого ему пришлось использовать очень чувствительные приборы, потому что даже слабые воздушные потоки могли исказить измерение. Во избежание посторонних влияний, Кавендиш разместил свои приборы в ящике, который оставил в комнате, а сам проводил наблюдение за приборами с помощью телескопа из другого помещения.
Опыты показали, что
Физическое содержание гравитационной постоянной заключается в том, что она определяется силой, с которой притягиваются два тела массами 1 кг каждое, находящиеся на расстоянии 1 м друг от друга.
Если на тело действует только одна сила, направленная вниз (а все другие уравновешены), то оно осуществляет свободное падение. Ускорение свободного падения можно определить, применив второй закон Ньютона:
Отсюда следует, что ускорение свободного падения 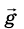
Теперь для силы притяжения можно записать выражение:
По существу говоря, формула 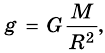
Приведенные значения показывают, что ускорение свободного падения в разных районах земного шара отличается очень мало от значения, вычисленного по формуле
Поэтому при грубых подсчетах пренебрегают неинерциальностые системы отсчета, связанной с поверхностью Земли, и отличием формы Земли от сферической. Ускорение свободного падения считают всюду одинаковым и вычисляют по формуле
В некоторых районах земного шара ускорение свободного падения отличается от приведенного выше значения еще по одной причине. Такие отклонения наблюдаются там, где в недрах Земли залегают породы, плотность которых больше или меньше средней плотности Земли. Там, где есть залежи пород, имеющих большую плотность, значение g больше. Это дает возможность геологам по измерениям значения g находить месторождения полезных ископаемых.
Следовательно, сила притяжения, а значит, и ускорение свободного падения изменяются с отдалением от поверхности Земли. Если тело находится на высоте h над поверхностью Земли, то выражение для модуля ускорения свободного падения g следует записывать следующим образом:
Так, на высоте 300 км ускорение свободного падения уменьшается на 1 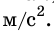
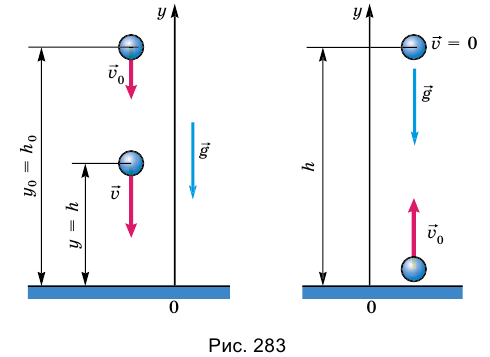
Движение тела под действием силы притяжения: тело движется по вертикали. Если предоставить телу начальную скорость д0, направленную вверх, то это не изменит ни направления, ни значения ускорения тела, потому что толчок вверх не может изменить силу притяжения. В обоих случаях траекторией тела является вертикальная прямая.
Решая задачи на такое движение, за тело отсчета удобно выбирать Землю с началом отсчета на ее поверхности или в любой точке выше или ниже от поверхности, а координатную ось направлять по вертикали вверх или вниз. Высоту тела над определенной поверхностью принято обозначать буквой h (рис. 283).
Тогда координата y тела — это просто его высота h над точкой начала отсчета. Проекция вектора перемещения тела соответствует изменению высоты и равна h — 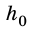
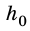
Формулы для вычисления координат (высот) и скоростей ничем не отличаются от формул для прямолинейного равноускоренного движения.
Координата тела (высота):
Скорость тела в любой момент времени:
Скорость тела в любой точке траектории:
Проекция 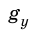
- Заказать решение задач по физике
Движение тела под действием силы притяжения: начальная скорость тела направлена под углом к горизонту. Часто приходится рассматривать движения тел, начальная скорость которых не параллельна силе притяжения, а направлена под определенным углом к ней (или к горизонту). Когда, например, спортсмен толкает ядро, бросает диск или копье, он придает этим предметам именно такую скорость. При артиллерийской стрельбе стволы пушек имеют определенный угол поднятия, так что снаряд в стволе также получает начальную скорость, направленную под углом к горизонту.
Будем считать, что силой сопротивления воздуха можно пренебречь. Как в этом случае движется тело?
На рисунке 284 показан стробоскопический снимок шарика, брошенного под углом 60° к горизонту. Соединив последовательно положения шарика плавной кривой, получим траекторию движения шарика — параболу.
Если пренебречь влиянием воздуха на движение тела, то на тело, брошенное под углом к горизонту, как и на свободно падающее тело, или на тело, которое получило начальную скорость, направленную вертикально, действует только сила притяжения. Как бы ни двигалось тело, сила притяжения может сообщить ему только ускорение 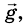
Предположим, что из некоторой точки О брошено тело с начальной скоростью 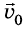
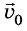
Поскольку на тело действует сила притяжения, то при движении тела будет меняться только проекция 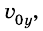
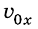
А координата у меняется так же, как при прямолинейном равноускоренном движении:
Чтобы найти траекторию движения тела, надо подставить в уравнение значения времени t, какие последовательно увеличиваются, и вычислить координаты х и у для каждого значения t, если известны значения модуля начальной скорости 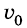
Что будет если тело брошено горизонтально
Тело можно бросить и так, что его начальная скорость 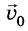
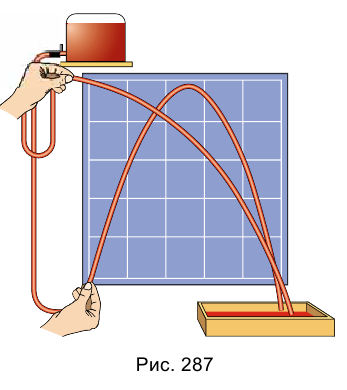
Траекторию движения тел, брошенных горизонтально или под углом к горизонту, можно показать на опыте. Сосуд, заполненный водой, размещают на определенной высоте над столом и соединяют его резиновой трубкой с наконечником, который имеет кран (рис. 287). Выпущенные струи воды непосредственно показывают траектории частиц воды. Таким образом можно наблюдать траекторию для разных значений угла а и скорости
Мы рассмотрели несколько примеров движения тел под действием силы притяжения. Во всех случаях тело движется с ускорением свободного падения, которое не зависит от того, имело ли тело еще и скорость в горизонтальном направлении или нет. Например, пуля, выпущенная стрелком из винтовки в горизонтальном направлении, упадет на землю одновременно с пулей, которую случайно уронил стрелок в момент выстрела. Но вторая пуля упадет у ног стрелка, а пуля, вылетевшая из ствола винтовки, — на определенном расстоянии.
История:
Попытки объяснить наблюдаемую картину мира, и прежде всего строение Солнечной системы, делали многие ученые. Что связывает планеты и Солнце в единую систему? Каким законам подчиняется их движение?
Во II в. н. э. древнегреческий ученый Клавдий Птолемей разработал геоцентрическую систему мира, согласно которой все наблюдаемые перемещения небесных светил объяснялись их движением вокруг неподвижной Земли.
В XVI в. польский астроном Миколай Коперник предложил гелиоцентрическую систему мира: в центре находится Солнце, а вокруг него движутся планеты и их спутники. Что же удерживает планеты, в частности Землю, когда они движутся вокруг Солнца?
Если придерживаться утверждений Аристотеля и связывать силу притяжения тел со скоростью их движения, а не с ускорением, то причиной движения планет является именно направление скорости.
Ньютон связал силу с ускорением. Именно силу притяжения Солнца естественно считать причиной вращения вокруг него Земли и планет.
Но не только планеты притягиваются к Солнцу. Солнце также притягивается планетами. Да и сами планеты взаимодействуют между собой. Одним из первых, кто это понял, был английский ученый Роберт Гук. В 1674 г. он писал: «Все небесные тела имеют притяжение, или силу тяготения к своему центру, вследствие чего они не только притягивают собственные части и препятствуют им разлетаться, как наблюдаем на Земле, но притягивают также все другие небесные тела, находящиеся в сфере их действия. Поэтому не только Солнце и Луна имеют влияние на движение Земли, но и Меркурий, и Венера, и Марс, и Юпитер, и Сатурн также своим притяжением имеют значительное влияние на ее движение. Подобным образом и Земля притяжением влияет на движение каждого из этих тел».
В своем труде «Математические начала натуральной философии» Ньютон сформулировал три фундаментальных закона (известны как законы Ньютона). В соответствии с данными законами, все тела Вселенной, как небесные, так и те, которые находятся на Земле, склонны к взаимному тяготению, причем силы, с которыми притягиваются все эти тела, имеют одинаковую природу и подчиняются одному и тому же закону.
Согласно легенде, мысль о всемирном тяготении озарила Ньютона в тот момент, когда он, отдыхая в своем саду, увидел яблоко, которое падает. Рассказывают даже, что знаменитой яблоне, плод которой сумел так «вовремя» упасть к ногам Ньютона, не дали исчезнуть бесследно и кусочки этого дерева якобы хранятся в Англии и в настоящее время.
Открытие закона всемирного тяготения дало возможность Ньютону создать теорию движения небесных тел, основанную на строгих математических доказательствах. Ничего подобного в науке до того времени не было.
Эта теория, бесспорно, поразила современников Ньютона, но у них возник вопрос: почему все тела притягиваются друг к другу? Ответа на него выдающийся физик не дал. «Причину же свойств силы тяготения я до сих пор не мог вывести из явлений, гипотез же я не выдумываю, — писал он в своих «Математических началах”. — Достаточно того, что притяжение в действительности существует, и действует согласно изложенному закону, и является полностью достаточным для объяснения всех движений небесных тел и моря».
Говоря о море, Ньютон имел в виду явление приливов, обусловленных притягиванием воды Луной и Солнцем. За две тысячи лет до Ньютона над причинами этого явления рассуждал Аристотель, который, однако, объяснить его не смог. Для философа это оказалось трагедией. «Наблюдая длительное время это явление со скалы Негро-понта, он, охваченный отчаянием, бросился в море и нашел там добровольную смерть», — утверждал Г. Галилей.
- Свободное падение тела
- Равнодействующая сила и движение тела под действием нескольких сил
- Сила давления в физике и единицы давления
- Механическое давление в физике
- Деформация в физике
- Плотность вещества в физике
- Сила трения в физике
- Вес тела в физике