Введите длину первой стороны треугольника в мм (миллиметрах) а =
Введите длину второй стороны треугольника в мм (миллиметрах) b =
Введите длину третьей стороны треугольника в мм (миллиметрах) с =
Введите толщину треугольника в мм (миллиметрах) h =
Как рассчитать объем треугольника по трем сторонам и толщине?
Если треугольник имеет толщину или высоту, то фактически это треугольная призма. Объем треугольной призмы в общем случае рассчитывается по формуле:
V = S х h
V — объем призмы. Объем треугольника имеющего толщину (высоту).
S — площадь треугольника
h — высота призмы. Толщина треугольника
Нахождение площади треугольника по трем сторонам
Можно воспользоваться формулой Герона:
S = √ (p (p-a) (p-b) (p-c))
p = (a+b+c) / 2
p — полупериметр треугольника;
S — площадь треугольника образованного сторонами a, b и c;
a — первая сторона треугольника;
b — первая сторона треугольника;
с — первая сторона треугольника.
Таким образом объем треугольника по сторонам и толщине равен:
V = √ (p (p-a) (p-b) (p-c)) х h
p = (a+b+c) / 2
формула для правильной треугольной и четырехугольной
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Геометрия Нахождение объема пирамиды: формула и задачи
В данной публикации мы рассмотрим, как можно найти объем пирамиды и разберем примеры решения задач для закрепления материала.
- Формула вычисления объема пирамиды
- 1. Общая формула
- 2. Объем правильной треугольной пирамиды
- 3. Объем правильной четырехугольной пирамиды
- 4. Объем правильной шестиугольной пирамиды
- Примеры задач
Формула вычисления объема пирамиды
1. Общая формула
Объем (V) пирамиды равняется одной третьей произведения ее высоты на площадь основания.
- ABCD – основание;
- E – вершина;
- h – высота, перпендикулярная основанию.
2. Объем правильной треугольной пирамиды
Основанием правильной треугольной пирамиды является равносторонний треугольник (ABC), площадь которого вычисляется так (а – сторона треугольника):
Подставляем данное выражение в формулу расчета объема фигуры и получаем:
3.
Объем правильной четырехугольной пирамиды
Основанием правильной четырехугольной пирамиды является квадрат, площадь которого считается так: S = a2, где а – длина его стороны.
Следовательно, формулу объема можно представить в виде:
4. Объем правильной шестиугольной пирамиды
Основанием правильной шестиугольной пирамиды является правильный шестиугольник, площадь которого вычисляется по формуле (а – сторона основания):
С учетом этого, объем фигуры считается так:
Примеры задач
Задание 1
Найдите объем правильной треугольной пирамиды, если известно, что ее высота составляет 16 см, а длина стороны ее основания – 8 см.
Решение:
Воспользуемся соответствующей формулой, подставив в нее известные значения:
Задание 2
Высота правильной четырехугольной пирамиды равна 12 см, а сторона ее основания – 3 см. Найдите объем фигуры.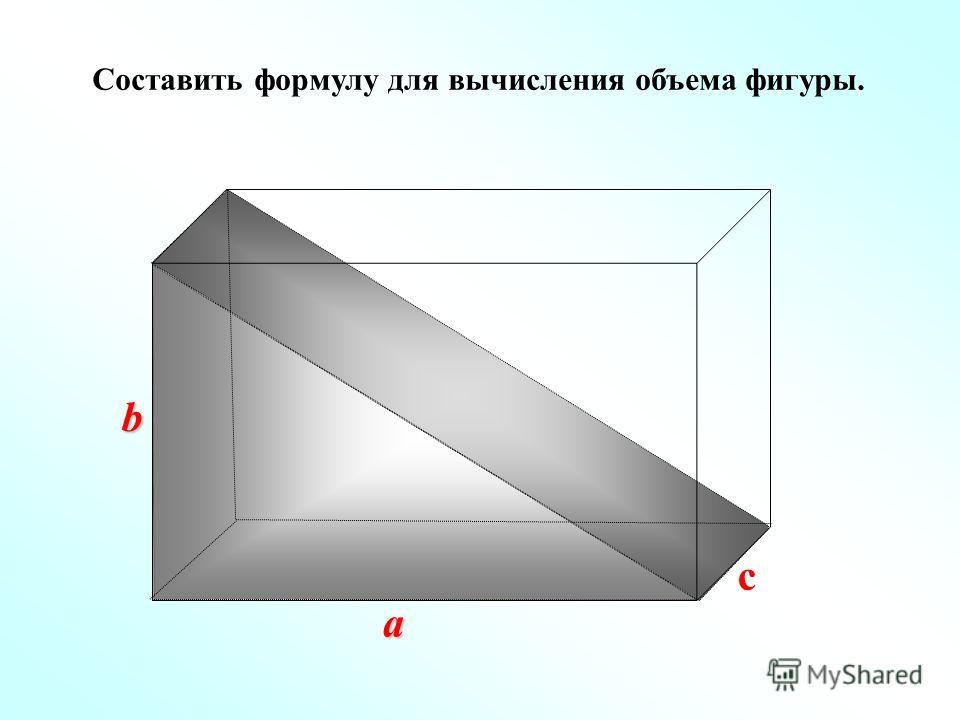
Решение:
Площадь квадрата, который является основанием пирамиды, равна 9 см2 (3 см ⋅ 3 см). Следовательно, объем равен:
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Объем треугольной призмы Калькулятор | Вычислить Объем треугольной призмы
|
✖Длина — это измерение или протяженность чего-либо от конца до конца. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
|
|
✖Высота — это расстояние между самой низкой и самой высокой точками человека/фигуры/объекта, стоящего прямо. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
|
|
✖Основание — это самая нижняя часть или край чего-либо, особенно та часть, на которой оно опирается или поддерживается. |
створаАнгстремарпанастрономическая единицаАттометрAU длиныЯчменное зерноМиллиардный светБор РадиусКабель (международный)Кабель (UK)Кабель (США)калибрсантиметрцепьCubit (греческий)Кубит (Длинный)Cubit (Великобритания)ДекаметрДециметрЗемля Расстояние от ЛуныЗемля Расстояние от СолнцаЭкваториальный радиус ЗемлиПолярный радиус ЗемлиРадиус электрона (классическая)флигельЭкзаметрFamnВникатьFemtometerФермиПалец (ткань)ширина пальцаФутFoot (служба США)ФарлонгГигаметрРукаЛадоньгектометрдюймкругозоркилометркилопарсеккилоярдлигаЛига (Статут)Световой годСсылкаМегаметрМегапарсекметрмикродюйммикрометрмикронмилмилиМиля (Роман)Миля (служба США)МиллиметрМиллион светлого годаNail (ткань)нанометрМорская лига (международная)Морская лига ВеликобританииМорская миля (Международный)Морская миля (Великобритания)парсекОкуньпетаметрцицеропикометраПланка ДлинаТочкаполюскварталРидРид (длинный)прутРоман Actusканатныйрусский АрчинSpan (ткань)Солнечный радиусТераметрТвипVara КастелланаVara ConuqueraVara De ФаареяДворЙоктометрЙоттаметрЗептометрЗеттаметр |
+10% -10% |
|
✖Объем — это количество пространства, которое занимает вещество или объект или которое заключено в контейнере. |
Акр-футАкр-фут (исследование США)Акко-дюймовыйБочка (масло)Бочка (UK)Ствол (США)Ванна (библейский)Совет для ногКабина (библейский)СантилитрКентум кубический футКор (библейский)шнурКубический Ангстремкубический сантиметркубический дециметркубический футкубический дюймКилометры CubicКубический метрКубический Mileкубический миллиметркубический ярдКубок (метрический)Кубок (Великобритания)Кубок (США)ДекалитрДецилитрДестистерДекастерДесертная ложка (Великобритания)Десертная ложка (США)драхмаКапляFemtoliterЖидкость Унция (Великобритания)Жидкость Унция (США)Галлон (Великобритания)Галлона (США)гигалитрГилл (Великобритания)Гилл (США)ГектолитрHin (библейский)хогсхедГомер (библейский)Сто кубический футкилолитрЛитрLog (библейский)мегалитрМикролитрМиллилитрMinim (Великобритания)Minim (США)нанолитрPetaliterпиколитрПинта (Великобритания)Пинта (США)Кварта (Великобритания)Quart (США)StereСтоловая ложка (метрическая)Столовая ложка (Великобритания)Столовая ложка (США)Таза (испанский)Чайная ложка (метрическая)Чайная ложка (Великобритания)Чайная ложка (США)тералитрTon РегистрацияТунОбъем Земли |
⎘ копия |
👎
Формула
сбросить
👍
Объем треугольной призмы Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Преобразование входов в базовый блок
Длина: 3 метр —> 3 метр Конверсия не требуется
Высота: 12 метр —> 12 метр Конверсия не требуется
Основание: 2 метр —> 2 метр Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
36 Кубический метр —> Конверсия не требуется
<
10+ объем Калькуляторы
<
5 Объем треугольной призмы Калькуляторы
Объем треугольной призмы формула
Объем = (Длина*Высота*Основание)/2
VT = (L*h*b)/2
Что такое треугольная призма?
Треугольная призма — это многогранник (трехмерная форма), состоящий из двух треугольных оснований и трех прямоугольных сторон. Как и другие призмы, здесь два основания параллельны и конгруэнтны друг другу. Всего у него 5 граней, 6 вершин и 9 ребер. Треугольная призма — это пентаэдр с девятью отдельными сетками.
Всего у него 5 граней, 6 вершин и 9 ребер. Треугольная призма — это пентаэдр с девятью отдельными сетками.
Share
Copied!
Калькулятор треугольной призмы
Создано Ханной Памула, докторантом и Жасмин Дж. Мах
Отредактировано Богной Шик, Джеком Боуотером и Аденой Бенн
Последнее обновление: 05 октября 2022 г.
Содержание:
- Формулы треугольной призмы
- Объем треугольной призмы
- Площадь поверхности треугольной призмы
- Как найти объем треугольной призмы с помощью этого инструмента?
- Часто задаваемые вопросы
Если вы когда-нибудь задавались вопросом, как найти объем треугольной призмы, этот калькулятор треугольной призмы — то, что вам нужно. Он не только может рассчитать объем, но также может быть полезен, если вам нужно определить площадь поверхности треугольной призмы. Выберите вариант, который соответствует вашим потребностям, и экспериментируйте с инструментом! Если вам интересны формулы треугольной призмы за калькулятором, прокрутите вниз, чтобы узнать больше.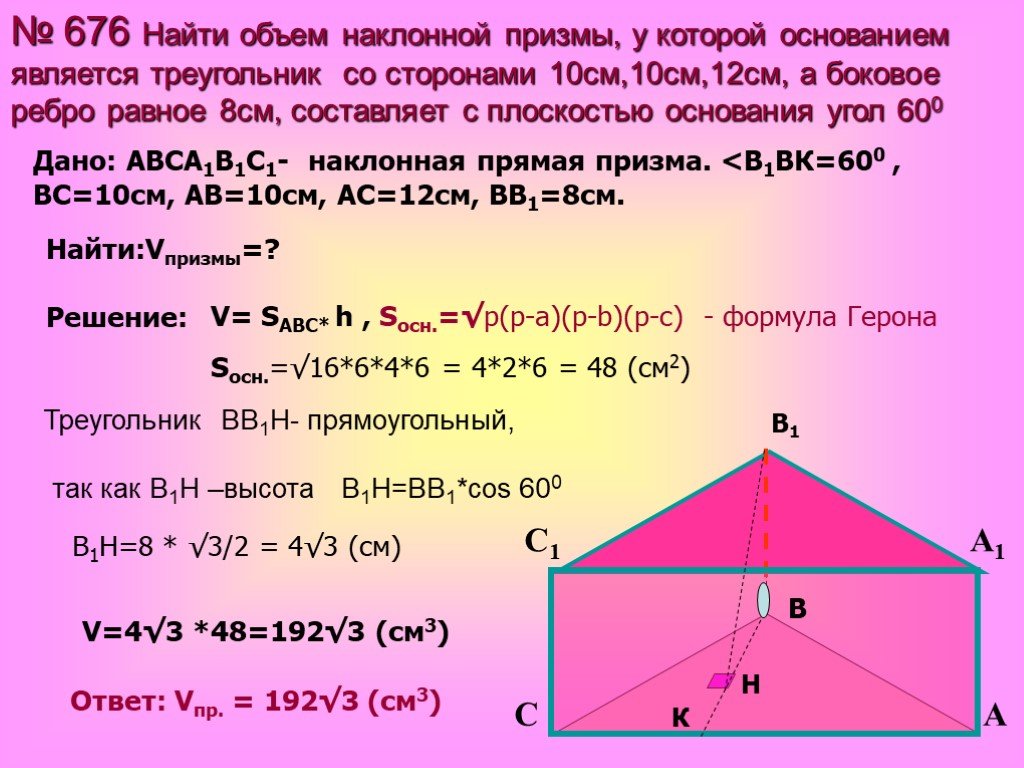
Что такое треугольная призма?
Треугольная призма представляет собой твердое тело, имеющее:
- два одинаковых треугольных основания
- три прямоугольные грани (прямая призма) или в форме параллелограмма (косая призма)
- одинаковое поперечное сечение по всей длине
Мы используем термин треугольная призма для описания правильной треугольной призмы, что является довольно распространенной практикой. Если вы ищете другой тип призмы, воспользуйтесь нашим калькулятором прямоугольных призм.
Формулы треугольной призмы
Обычно вам необходимо рассчитать объем треугольной призмы и площадь ее поверхности. Два самых основных уравнения:
-
объем = 0,5 * b * h * длина, гдеbдлина основания треугольника,hвысота треугольника,длинадлина призмы -
площадь = длина * (a + b + c) + (2 * base_area), гдеa, b, c— это стороны треугольника, аbase_area— это базовая площадь треугольника.

Но что, если у нас нет высоты и основания треугольника? А как найти площадь поверхности треугольной призмы без учета всех сторон треугольного основания? Ознакомьтесь с другими формулами треугольной призмы!
Объем треугольной призмы
В калькуляторе треугольной призмы вы можете легко узнать объем этого твердого тела. Общая формула: объем = длина * базовая_площадь ; единственный параметр, который вам всегда нужно указывать, — это длина призмы, и есть четыре способа рассчитать площадь основания — треугольника. Все они реализованы в нашем калькуляторе треугольной призмы. Разве это не потрясающе?
Конкретные формулы выглядят следующим образом:
-
Длина * Площадь основания треугольника Даны основание и высота треугольника
Это известная формула, упомянутая ранее:
объем = длина * 0,5 * ширина * высота -
Длина * Треугольная площадь основания с учетом трех сторон (SSS)
Если известны длины всех сторон, используйте
формулу Герона , чтобы найти площадь основания треугольника:объем = длина * 0,25 * √( (a + b + c) * (-a + b + c) * (a - b + c) * (a + b - c)) -
Длина * Площадь треугольного основания с учетом двух сторон и угла между ними (SAS)
Вы можете легко вычислить площадь треугольника с помощью тригонометрии:
объем = длина * 0,5 * a * b * sin(γ) -
Длина * Площадь основания треугольника с учетом двух углов и стороны между ними (ASA)
Вы можете вычислить это с помощью тригонометрии:
объем = = длина * a² * sin(β) * sin(γ) / (2 * sin(β + γ))
Площадь поверхности треугольной призмы
Если вы хотите рассчитать площадь поверхности твердого тела, наиболее известной формулой является формула для трех сторон треугольного основания:
-
площадь = длина * (a + b + c) + (2 * базовая_площадь) = длина * базовый_периметр + (2 * базовая_площадь)
Однако нам не всегда известны три стороны. Что тогда?
Что тогда?
-
Треугольное основание: по двум сторонам и углу между ними (SAS)
Используя закон косинусов, мы можем найти третью сторону треугольника:
площадь = длина * (a + b + √( b² + a² - (2 * b * a * cos(угол)))) + a * b * sin(угол) -
Треугольное основание: даны два угла и сторона между ними (ASA)
Используя закон синусов, мы можем найти две стороны треугольного основания:
площадь = (длина * (a + a * (sin(угол1) / sin(угол1+угол2)) + a * (sin(угол2) / sin(угол1+угол2)))) + a * ((a * грех(угол1)) / грех(угол1 + угол2)) * грех(угол2)
Единственный вариант, когда вы не можете вычислить объем треугольной призмы, это иметь заданное основание треугольника и его высоту (знаете почему? Задумайтесь об этом на минутку). Все остальные варианты можно рассчитать с помощью нашего калькулятора треугольной призмы.
Как найти объем треугольной призмы с помощью этого инструмента?
Проверим, каковы объем и площадь поверхности палатки в виде треугольной призмы:
- Выясним, какова длина треугольной призмы .
 Предположим, что оно равно 80 дюймам, введите это значение в первое поле калькулятора треугольной призмы.
Предположим, что оно равно 80 дюймам, введите это значение в первое поле калькулятора треугольной призмы. - Выберите вариант с указанными параметрами . Например, даны три стороны нашей базы.
- Введите стороны основания . Наша палатка имеет a = 60 дюймов, b = 50 дюймов и c = 50 дюймов.
- Площадь поверхности и объем треугольной призмы появляются мгновенно . Это 96 000 кубических дюймов (55,56 кубических футов) и 15 200 дюймов² (105,56 футов²).
FAQ
Как нарисовать треугольную призму?
Чтобы нарисовать треугольную призму:
- Нарисуйте основание призмы в виде треугольника.
- Нарисуйте верхнюю грань призмы в виде треугольника, параллельного основанию.
- Соедините соответствующие вершины обоих треугольников так, чтобы они не пересекались.
Сколько ребер у треугольной призмы?
Треугольная призма имеет 9 ребер, по три из которых образуют нижнюю и верхнюю грани.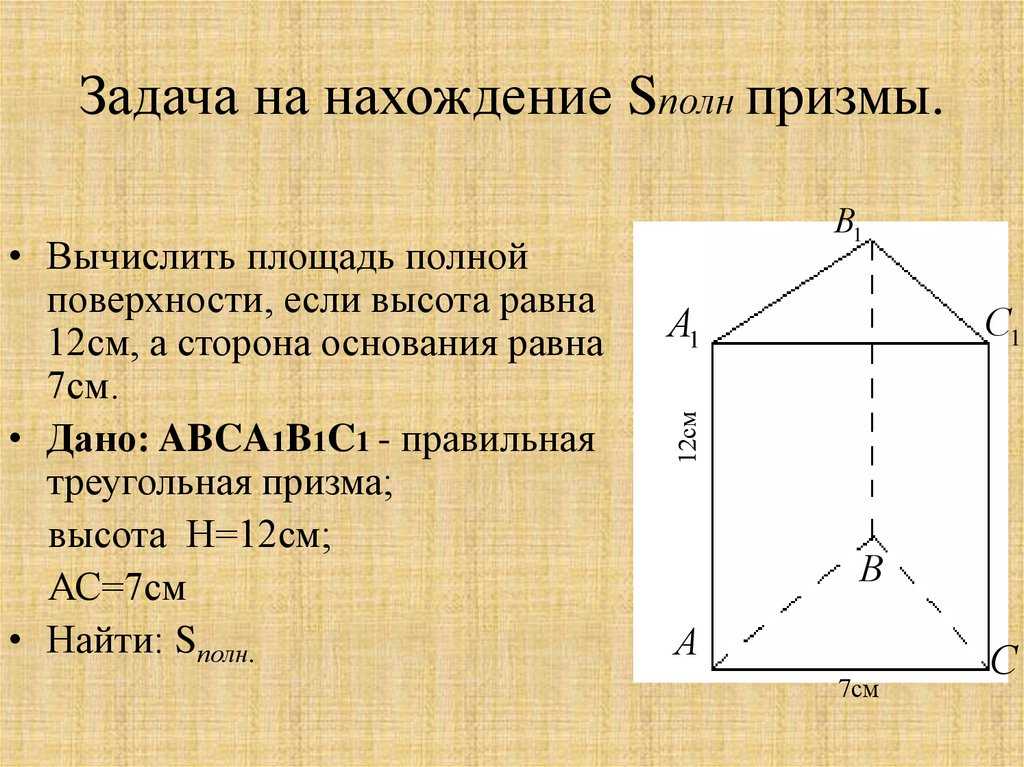 Остальные из них образуют боковые грани.
Остальные из них образуют боковые грани.
Сколько граней у треугольной призмы?
Треугольная призма имеет 5 граней, т. е. основание и верхнюю грань, а также 3 боковые грани.
Сколько вершин у треугольной призмы?
Треугольная призма имеет 6 вершин, т. е. по 3 на верхней и нижней треугольных гранях.
Ханна Памула, кандидат доктора философии и жасмин J MAH
Треугольный тип
Основание (B)
Высота (H)
Длина призмы (L)
Prism Том
Проверьте 21 Аналогичные геометрические раскаты 📦
. Площадь полушарияКубКуб Рассчитать: найти v, a, d… 18 больше
Объем треугольной призмы — Формула, определение, примеры
Объем треугольной призмы — это пространство, занимаемое ею со всех трех измерений. Призма представляет собой твердое тело, имеющее одинаковые основания, плоские прямоугольные боковые грани и одинаковое поперечное сечение по всей длине. Существуют различные типы призм, которые классифицируются и называются в соответствии с формой их основания.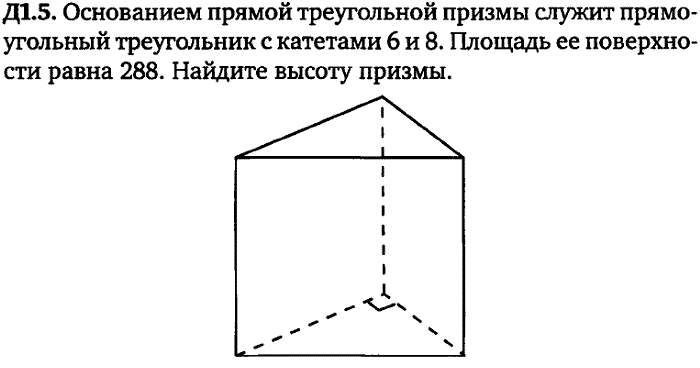 Треугольная призма имеет 2 одинаковых треугольных основания и 3 прямоугольные боковые грани.
Треугольная призма имеет 2 одинаковых треугольных основания и 3 прямоугольные боковые грани.
| 1. | Каков объем треугольной призмы? |
| 2. | Объем треугольной призмы Формула |
| 3. | Как найти объем треугольной призмы? |
| 4. | Часто задаваемые вопросы по объему треугольной призмы |
Каков объем треугольной призмы?
Объем треугольной призмы можно рассчитать, взяв произведение площади треугольного основания и высоты призмы, также известной как длина призмы. Для этого давайте сначала разберемся, как выглядит треугольная призма.
Определение треугольной призмы
Треугольная призма представляет собой многогранник, состоящий из двух треугольных оснований и трех прямоугольных сторон. Или его можно рассматривать как пятигранник (всего у него 5 граней), в котором ребра и вершины оснований соединены друг с другом тремя прямоугольными сторонами.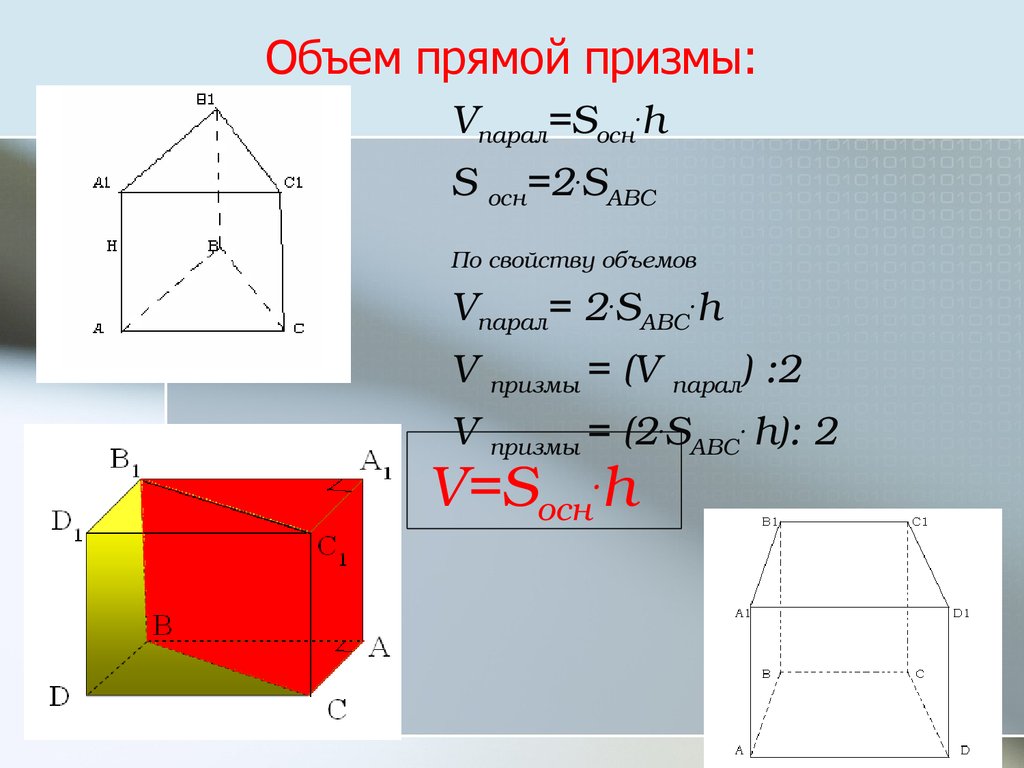 По определению, два треугольных основания параллельны и конгруэнтны друг другу. Он имеет:
По определению, два треугольных основания параллельны и конгруэнтны друг другу. Он имеет:
- 2 основания (равные треугольники)
- 3 боковые грани (конгруэнтные прямоугольники)
- Общее количество граней — 5
- 9 ребер
- 6 углов или вершин
Длина треугольной призмы – это перпендикулярное расстояние между центрами двух оснований. Он представлен буквой «l» на рисунке ниже.
Обратите внимание на треугольную призму, показанную выше, где «b» — основание каждой стороны двух конгруэнтных треугольников, «h» — высота треугольника в основании, а «l» — длина призмы.
Объем треугольной призмы Формула
Объем треугольной призмы – это пространство внутри нее или занимаемое ею пространство. Он измеряется в кубических единицах, таких как см 3 , м 3 , 3 и т. д. Мы увидим формулы для расчета объемов различных типов треугольных призм. Объем любой призмы получается путем умножения площади ее основания на длину.
Объем призмы = площадь основания × длина призмы
Мы также будем использовать эту формулу для вычисления объема треугольной призмы. Мы знаем, что основание треугольной призмы — треугольник. Применяя приведенную выше формулу к треугольной призме, мы получаем:
Объем треугольной призмы = площадь треугольника с основанием × длина призмы
Здесь мы можем найти площадь треугольника с основанием на основе его типа и доступных Информация. В следующем списке показаны формулы для нахождения площади треугольника с основанием.
- Если треугольник в основании является равносторонним треугольником (в этом случае призма называется равносторонней треугольной призмой) с каждой стороной ‘a’, то его площадь = √3a 2 /4
- Если известны основание треугольника b и высота h, то его площадь = (1/2) bh
- Если треугольник в основании представляет собой прямоугольный треугольник (в этом случае призма называется прямоугольной треугольной призмой) с двумя катетами ‘b’ и ‘h’, то его площадь = (1/2) bh
- Если треугольник с основанием равнобедренный, стороны которого равны ‘a’, ‘a’ и ‘b’, то его площадь равна (b/4) × √(4a 2 — б 2 )
- Если треугольник с основанием представляет собой разносторонний треугольник, в котором даны все три стороны ‘a’, ‘b’ и ‘c’, то его площадь вычисляется по формуле √[s(s-a)(s-b)(s-c)]; где s = (а + b + с)/2.
 Обратите внимание, что вы можете применить эту формулу (которую также называют формулой Герона) для равнобедренного треугольника (или) равностороннего треугольника.
Обратите внимание, что вы можете применить эту формулу (которую также называют формулой Герона) для равнобедренного треугольника (или) равностороннего треугольника. - Если известны две стороны базового треугольника ‘a’ и ‘b’ и угол между ними ‘θ’, то его площадь находится с помощью 1/2 ab sin θ
Как найти объем треугольной призмы?
Объем треугольной призмы можно рассчитать с помощью следующих шагов и приведенного ниже примера. Перед этим убедитесь, что все измерения в одних и тех же единицах.
- Шаг 1: Определите тип базового треугольника и найдите его площадь, используя подходящую формулу (как описано в предыдущем разделе).
- Шаг 2: Определите длину призмы (Обратите внимание, что эта длина призмы также известна как высота призмы, и ее не следует путать с высотой треугольника основания).
- Шаг 3: Умножьте площадь основания (из шага 1) и длину призмы, чтобы найти объем.
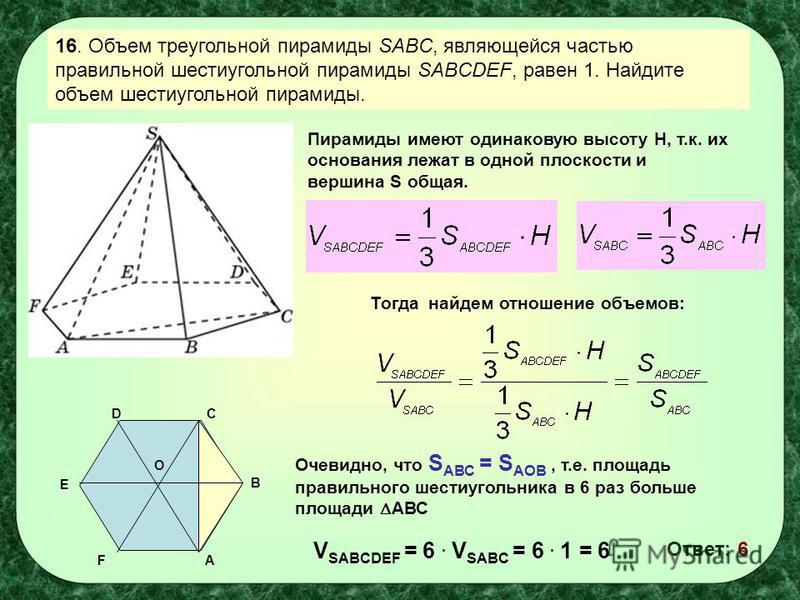
Пример: Вычислите объем треугольной призмы длиной 15 дюймов, основанием которой является равносторонний треугольник со стороной 6 дюймов.
Решение: Объем треугольной призмы можно рассчитать, выполнив следующие действия.
- Шаг 1: Треугольник с основанием является равносторонним треугольником со стороной a = 6. Таким образом, его площадь находится по формуле √3a 2 /4 = √3(6) 2 /4 = 9√3 квадратных дюйма.
- Шаг 2: Длина призмы 15 дюймов.
- Шаг 3: Объем заданной треугольной призмы = площадь основания × длина = 9√3 × 15 = 135√3 кубических дюйма.
Советы по объему треугольной призмы
- Длина треугольной призмы также известна как высота призмы.
- Эту высоту призмы не следует путать с высотой основания треугольника.
☛ Статьи по теме
- Объем 3D-фигур
- Объем куба
- Объем цилиндра
- Объем кубоида
- Объем сферы
- Объем прямоугольной призмы
Примеры объема треугольной призмы
-
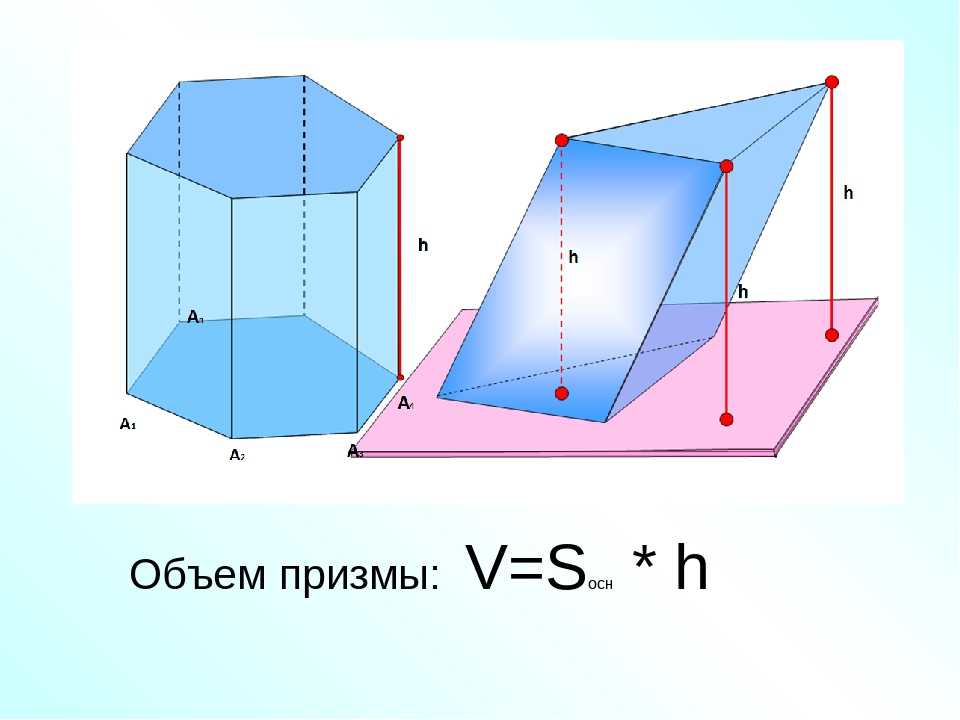
Пример 1: Определите объем треугольной призмы, в которой основание равно 7 дюймов, высота 5 дюймов, а длина призмы 10 дюймов.
Решение:
Основание треугольника (b) = 7 дюймов, высота основания треугольника (h) = 5 дюймов
Итак, площадь основания = (1/2)(bh) = (1/2) × (7 × 5) = 35/2 в 2 .
Длина призмы L = 10 дюймов.
Используя формулу объема треугольной призмы,
Объем данной треугольной призмы = площадь основания × длина призмы = (35/2) × (10) = 175 в 3 .
-
Пример 2: Найдите объем следующей прямоугольной призмы.
Решение:
Основание треугольника (b) = 14 футов, а его высота (h) = 8 футов.
Таким образом, площадь основания = (1/2) × (bh) = (1/2) × (14 ×
= 56 квадратных футов.
Длина призмы L = 10 футов.
Используя формулу объема треугольной призмы,
Объем данной треугольной призмы = площадь основания × длина призмы = 56 × 10 = 560 футов 3 .
-
Пример 3: Укажите истинное или ложное значение.

а.) Треугольная призма – это многогранник, состоящий из двух треугольных оснований и трех прямоугольных сторон.
b.) Объем треугольной призмы измеряется в квадратных единицах, таких как см 2 , м 2 , 2 и так далее.
Решение:
а.) Верно, что треугольная призма представляет собой многогранник, состоящий из двух треугольных оснований и трех прямоугольных сторон.
б.) Неверно, объем треугольной призмы измеряется в кубических единицах, таких как см 3 , м 3 , в 3 и так далее.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по объему треугольной призмы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по объему треугольной призмы
Каков объем треугольной призмы?
Объем треугольной призмы — это пространство внутри нее.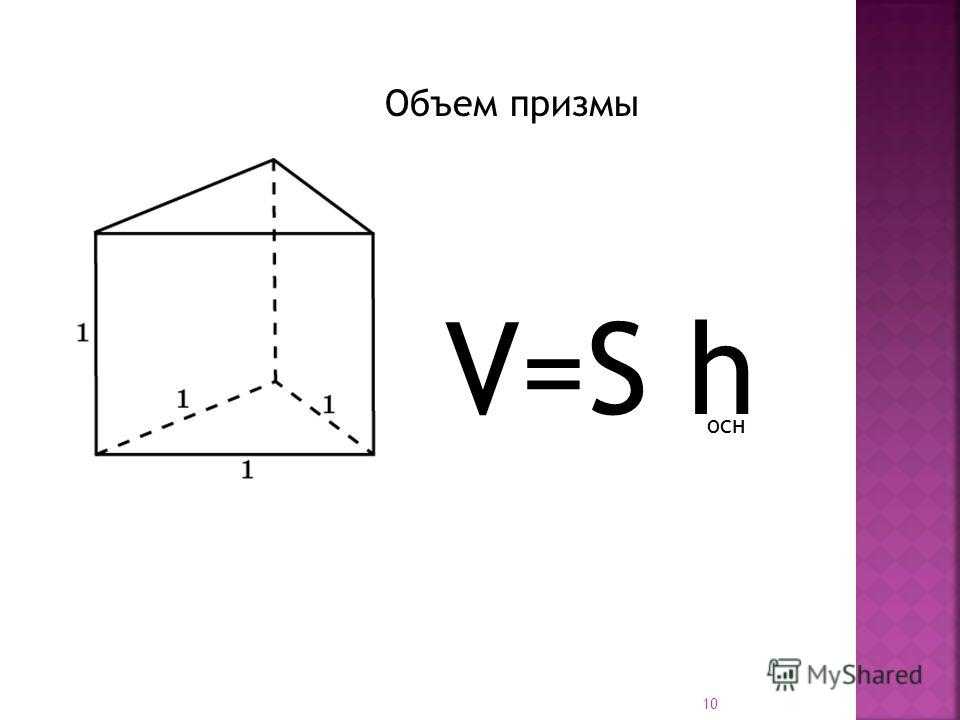 Он рассчитывается путем умножения площади треугольного основания на высоту призмы, также известную как длина призмы. Объем треугольной призмы выражается в кубических единицах, таких как см 3 , м 3 , 3 и т. д.
Он рассчитывается путем умножения площади треугольного основания на высоту призмы, также известную как длина призмы. Объем треугольной призмы выражается в кубических единицах, таких как см 3 , м 3 , 3 и т. д.
Какая формула для нахождения объема треугольной призмы?
Формула для нахождения объема треугольной призмы: Объем = площадь основания × длина, где
- Площадь основания = площадь основания (треугольника)
- Длина = длина треугольной призмы (также известная как высота призмы)
Как найти высоту треугольной призмы по объему?
Высота треугольной призмы также известна как длина призмы. Его можно вычислить, если известны площадь основания и объем призмы. Формула объема треугольной призмы = площадь основания × длина призмы. Отсюда высота треугольной призмы получается делением ее объема на площадь основания.
Как найти объем треугольной призмы с прямым углом?
Если основание треугольной призмы представляет собой прямоугольный треугольник с основанием «b» и высотой «h», а длина призмы равна «L», то площадь ее основания = (1/2) bh. Мы знаем что объем призмы = площадь основания × длина призмы, поэтому объем призмы в этом случае рассчитывается по той же формуле Объем треугольной призмы = (1/2) bh × L.
Мы знаем что объем призмы = площадь основания × длина призмы, поэтому объем призмы в этом случае рассчитывается по той же формуле Объем треугольной призмы = (1/2) bh × L.
По какой формуле вычислить объем равносторонней треугольной призмы?
Рассмотрим треугольную призму, длина которой равна «L», а основание — равносторонний треугольник со стороной «а». Тогда его базовая площадь равна √3a 2 /4. Мы знаем, что объем призмы = площадь основания × длина призмы, следовательно, объем призмы в данном случае находится по формуле (√3a 2 × L)/4
Как найти объем треугольной призмы с заданным углом?
Рассмотрим треугольную призму, длина которой равна «L», а «а» и «b» — это две стороны ее основания с прилежащим к ней углом θ. Тогда его базовая площадь равна (1/2) ab × sin θ. Мы знаем, что объем призмы равен площади основания × длине призмы, поэтому объем призмы в данном случае находится по формуле (1/2) ab sin θ × L.
Как площадь треугольника связана с объемом треугольной призмы?
Площадь треугольника используется для нахождения объема треугольной призмы, поскольку основание треугольной призмы представляет собой треугольник, а формула, используемая для нахождения объема треугольной призмы, такова: Объем = площадь основания × длина призма, где площадь основания равна площади треугольника.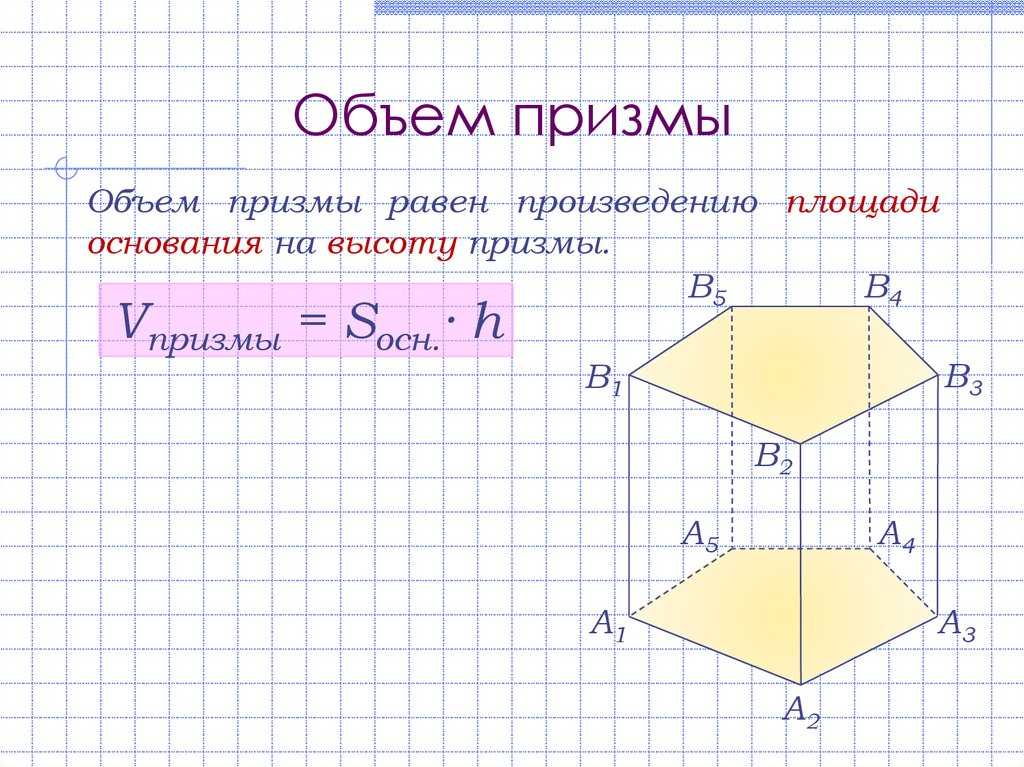
Как найти объем через площадь
Объем – мера вместимости, выраженная для геометрических фигур в виде формулы V=l*b*h. Где l – длина, b – ширина, h – высота объекта. При наличии только одной или двух характеристик вычислить объем в большинстве случаев нельзя. Однако при некоторых условиях представляется возможным сделать это через площадь.

Инструкция
Задача первая: вычислить объем, зная высоту и площадь. Это самая простая задача, т.к. площадь (S) — это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.Пример: Площадь одной из сторон параллелепипеда — 36 см², высота – 10 см. Найдите объем параллелепипеда.V = 36 см² * 10 см = 360 см³.Ответ: Объем параллелепипеда равен 360 см³.
Задача вторая: вычислить объем, зная только площадь. Это возможно, если вы вычисляете объем куба, зная площадь одной из его граней. Т.к. ребра куба равны, то извлекая из значения площади квадратный корень, вы получите длину одного ребра. Эта длина будет и высотой, и шириной.Пример: площадь одной грани куба — 36 см². Вычислите объем.Извлеките квадратный корень из 36 см². Вы получили длину – 6 см. Для куба формула будет иметь вид: V = a³, где а – ребро куба. Или V = S*a, где S – площадь одной стороны, а – ребро (высота) куба.V = 36 см² * 6 см = 216 см³. Или V = 6³см = 216 см³.Ответ: Объем куба равен 216 см³.
Задача третья: вычислить объем, если известна площадь и некоторые другие условия. Условия могут быть разные, помимо площади могут быть известны другие параметры. Длина или ширина могут быть равны высоте, больше или меньше высоты в несколько раз. Также могут даваться дополнительные сведения о фигурах, которые помогут в вычислениях объема.Пример 1: найдите объем призмы, если известно, что площадь одной стороны 60 см², длина 10 см, а высота равна ширине.S = l * b; l = S : b
l = 60 см² : 10 см = 6 см – ширина призмы. Т.к. ширина равна высоте, вычислите объем:
V=l*b*h
V = 10 см * 6 см *6 см = 360 см³Ответ:объем призмы 360 см³
Пример 2: найдите объем фигуры, если площадь 28 см², длина фигуры 7 см. Дополнительное условие: четыре стороны равны между собой, и соединены друг с другом по ширине.Для решения следует построить параллелепипед. l = S : b
l = 28 см² : 7 см = 4 см – ширинаКаждая сторона представляет собой прямоугольник, длина которого 7 см, а ширина 4 см. Если четыре таких прямоугольника соединить между собой по ширине, то получится параллелепипед. Длина и ширина в нем по 7 см, а высота 4 см. V = 7 см * 7 см * 4 см = 196 см³Ответ: Объем параллелепипеда = 196 см³.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Изучение объемных фигур начинается со школы. В это время происходит знакомство с цилиндром, параллелепипедом, шаром, конусом и другими геометрическими телами. Одна из главных задача, которая сопровождает учеников, это вычисление объема фигур. Оперируя формулами, удается произвести расчет и получить ответ в метрах кубических (м3).
Чтобы вычислить объем, применяйте следующее правило – длину, ширину и высоту нужно перемножить между собой. Объем для каждой фигуры рассчитывается по специальной формуле, о которых, мы расскажем ниже.
Подписывайтесь на наш Telegram — канал
Содержание:
- Как найти объем трехмерных объектов
- Как найти объем для фигур цилиндрической формы
- Как рассчитать объем треугольной пирамиды
- Как посчитать объем куба
- Как найти объем прямоугольного параллелепипеда
- Как найти объем цилиндра
- Как найти объем пирамиды
Как найти объем трехмерных объектов
Начнем с расчета для прямоугольных и квадратных фигур. Придерживайтесь инструкции и постарайтесь рассчитать самостоятельно, чтобы закрепить знания. Числа, указанные в описании, берутся в качестве примера. Вы можете производить другие расчеты.
- Измеряем длину предмета в сантиметрах – 9. Сантиметры приходят на помощь, когда невозможно получить целое число в метрах .
- Замеряем ширину в сантиметрах – 17.
- Умножаем между собой длину и ширину 9 * 17 = 152 см2 – получили площадь основания
- Производим замер высоты – 28 см.
- Умножаем площадь основания на высоту 152 см2 * 28 см = 4256.
Полученное число необходимо перевести в кубические метры. Для этого конечный результат делим на 1.000.000. Пример будет выглядеть следующим образом – 4256 м3/1000000 = 0,004256 м3
Как найти объем для фигур цилиндрической формы
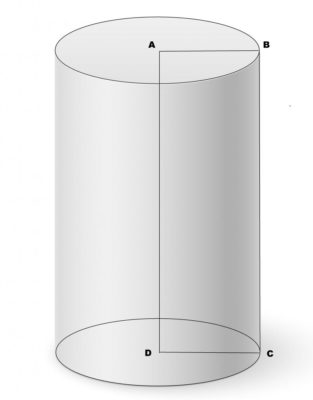
Цилиндр – это тело, ограниченное цилиндрической поверхностью с замкнутой направляющей и двумя параллельными плоскостями. Одним из видов цилиндра является призма.
Чтобы произвести вычисления нужно найти диаметр тела (ширина) одного круглого основания и полученное число поделить на 2. Допустим, диаметр основания равен 30 см.
- Производим расчеты: 30 см / 2 = 15 см. Половина диаметра круга ‒ радиус.
- Возводим полученный радиус в квадрат или умножаем самого на себя: 15 * 15 = 225 см2.
- Полученное число 225 см2 – это квадрат радиуса. Эту цифру умножаем на число ПИ — 3,14. Например: 225 см2 * 3,14 = 706,5 см2.
- Проводим новый замер, чтобы узнать расстояние между круглыми основаниями, допустим, оно равно 12 см.
- Это число умножаем на площадь круглого основания: 706,5 см2 * 12 см = 8 478 см3
- Полученное значение и будет искомым объемом. Для перевода в кубические метры необходимо конечное число поделить на один миллион. Как мы делали в предыдущем примере.
Как рассчитать объем треугольной пирамиды
Пирамида – это многогранник, где есть одна грань основания и боковые грани. Пирамиды бывают треугольные, четырехугольные и другие. Также есть правильная и усеченная пирамида. Объем для каждой фигуры рассчитывается по разным формулам.
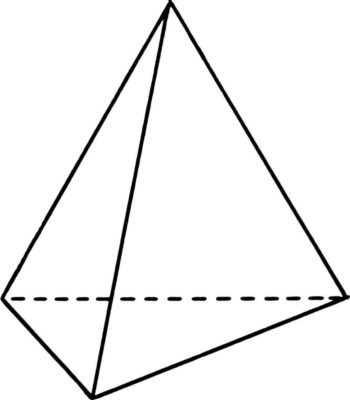
- Чтобы найти объём пирамиды замеряем длину стороны треугольника в основании пирамиды, предположим, что он равен 10 см.
- Затем повторим то же самое, но с высотой – 13 см.
- Длину высоты и стороны необходимо перемножить между собой и разделить на 2: 10 *13 = 130 см2 / 2 =65 см2.
- Замеряем высоту пирамиды – 33 см.
- Умножаем площадь треугольника у основания на высоту и делим на 3. Например: 65 см2 * 33 см =2 145 см2 / 3 = 715 см3.
- Для преобразования в кубические метры производим деление конечного числа на миллион.
Расчёт четырехгранной пирамиды производится тем же принципом. Потренируйтесь, используя разные задачи. Чтобы все замеры происходили правильно, не забудьте обзавестись хорошей линейкой, также на помощь придёт калькулятор, который поможет перемножать числа между собой.
В интернете представлено много онлайн-калькулятор, они дают подсказку и позволяют без лишних трудностей рассчитать объём куба, цилиндра и других фигур. Перед началом пользования таких подсказок, необходимо обладать базовыми знаниями, чтобы быстрее разобраться в полученном результате.
Как посчитать объем куба
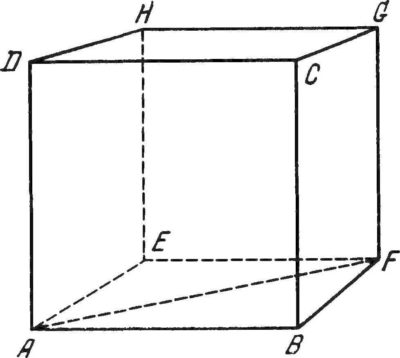
Параллелепипед складывается из шести граней, которые являются параллелограммом. Все противоположные грани попарно равны и параллельны. Фигура получилась 4 диагонали, и все они пересекаются в одной точке, разделяют эту точку пополам. Параллелепипед, грани которого являются квадратами, будет называться кубом.
Все рёбра куба всегда будут равны. Для проведения вычислений, воспользуйтесь следующей формулой V = H3, где H ‒ высота ребра куба. Например: высота куба равняется ‒ 3 см, получается, что объем равен 33 = 27 см3.
Как найти объем прямоугольного параллелепипеда
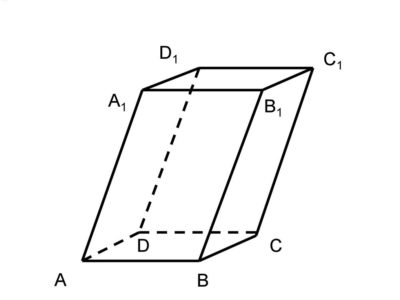
Прямоугольным параллелепипедом называется фигура, у которой все шесть граней прямоугольники. Для вычисления работает следующая формула:
V = SH = abc
Где H ‒ высота, S ‒ площадь основания, abc – ребра. Чтобы произвести расчеты и найти объём, необходимо узнать произведение площади основания на высоту. Например: 1 см * 2 см * 3 см = 6 см3
Советы по измерению:
- Измерить стороны.
- Каждая сторона параллелепипеда должна находиться в одинаковых единицах измерения.
- Вычисляем площадь основания.
- Умножаем площадь основания на высоту параллелепипеда.
Убедитесь, что перед вами параллелепипед, а не куб, так как в случае с кубом расчетная формула будет проще.
Как найти объем цилиндра
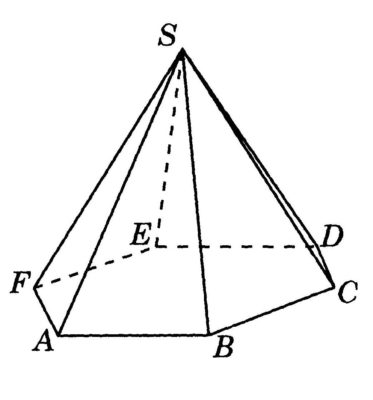
Цилиндр считать круглой фигурой, т.к. в его основании лежит круг. Чтобы произвести вычисления, необходимо узнать произведение площади основания на высоту. Для этого используется следующая формула:
V= π * r2 * h
Где r ‒ радиус цилиндра, h – высота цилиндра. Чисто π – является константой и равно 3,14. Оно всегда одинаковое и не требует никаких измерений. Рассмотрим на примере:
3,14 * 2 см2 * 5 см = 62.831853071796 = 63см3
Если вы не можете вычислить радиус, измерьте диаметр с помощью формулы преобразования.
Как найти объем пирамиды
фото 6 — посчитать объём
Чтобы произвести расчет объема, нам нужно найти произведение площади основания на высоту. Для вычисления используется следующая формула:
V = S*h
Где S (A*B*C*D*E) – площадь основания пирамиды, а h ‒ высота пирамиды. Рассмотрим на примере:
V = 3 * 2 = 2 см3 ‒ это и будет являться объемом искомой геометрической фигуры.
Не забывайте, что пирамиды бывают усеченные, правильные, трех- и четырехугольные. Для каждого тела действуют свои расчеты, но важно начинать с основного и не упускать базовые знания, в дальнейшем все примеры будут базироваться именно на них.
Если какая-то формула осталась непонятной, лучше вернуться к этому и поупражняться ещё раз, доведя знание до автоматизма. Так решение задач не будет вызывать сложности. Постоянная практика ‒ это основа успешного результата.
Вычислить объем пирамиды довольно просто, если вы знаете размеры. Используя формулу объема пирамиды (V), единственное, что вам нужно сделать, это выяснить ширину, длину и высоту пирамиды.
-
Никогда не забывайте использовать квадратные единицы (например, квадратные метры), когда вы ссылаетесь на объемные и кубические единицы.
Измерьте ширину и длину основания. Убедитесь, что вы используете общую единицу измерения, например, сантиметры (см).
Умножьте ширину на длину, чтобы вычислить базовую область, которую мы назовем «B.» Если, например, ширина и длина 6 и 7 см соответственно, то базовая площадь будет 42 см ^ 2.
Измерьте высоту пирамиды (ч). Высота — это перпендикулярное расстояние между вершиной пирамиды (кончиком) и основанием. Другими словами, это линия, которая образует прямой угол с основанием, соединяя при этом верх и низ.
Используйте теорему Пифагора, чтобы узнать высоту пирамиды, если вам не разрешено использовать линейку как часть упражнения. Теорема утверждает, что в любом треугольнике квадрат стороны, противоположной прямому углу, равен сумме квадратов двух оставшихся сторон. Например, если расстояние между осью высоты и стороной пирамиды составляет 3 см, а длина стороны — 5 см, то высота будет: 5 ^ 2 = 3 ^ 2 + h ^ 2 или h ^ 2 = 25-9 = 16, следовательно, h = 4 см.
Применим формулу V = Bh / 3. В нашем примере это будет V = (42×4) / 3 = 168/3 = 56 см ^ 3.

 ⓘ Длина [L]
ⓘ Длина [L]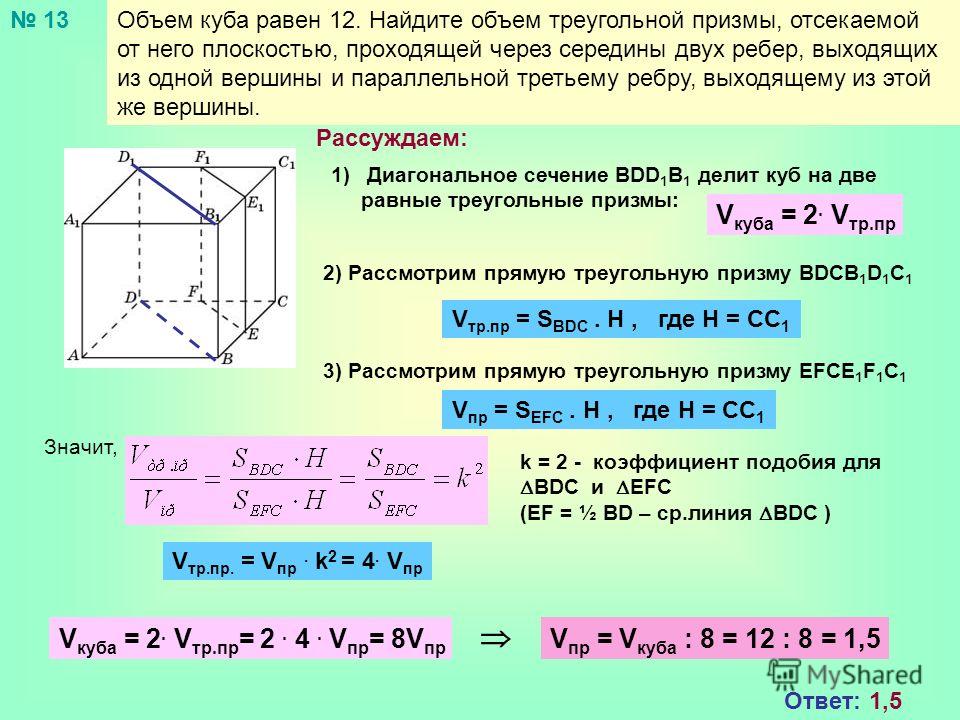 ⓘ Высота [h]
ⓘ Высота [h]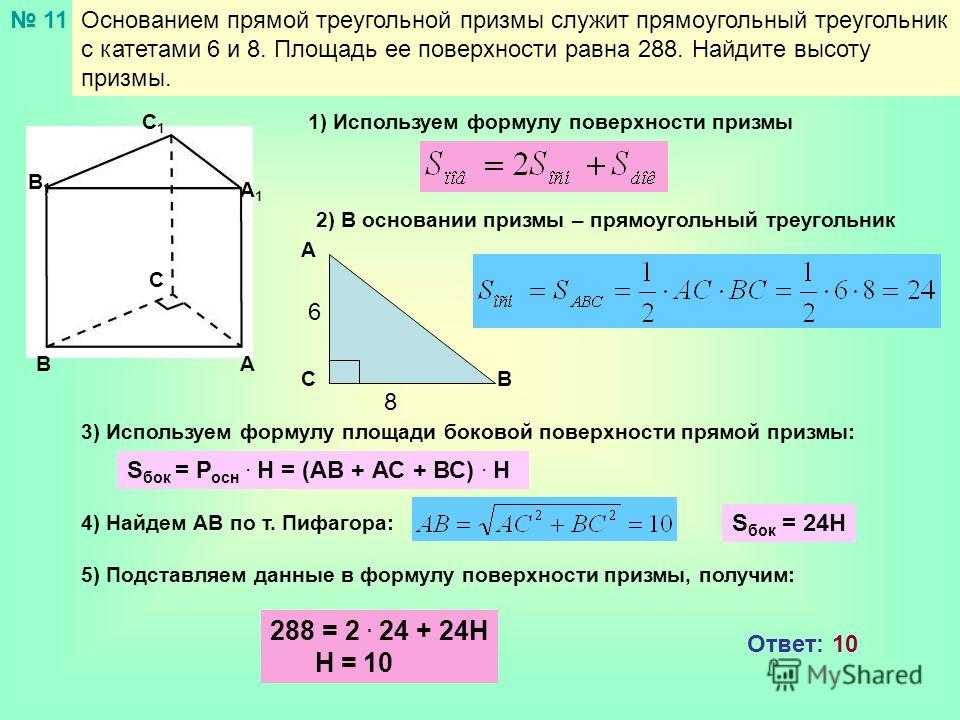 ⓘ Основание [b]
ⓘ Основание [b]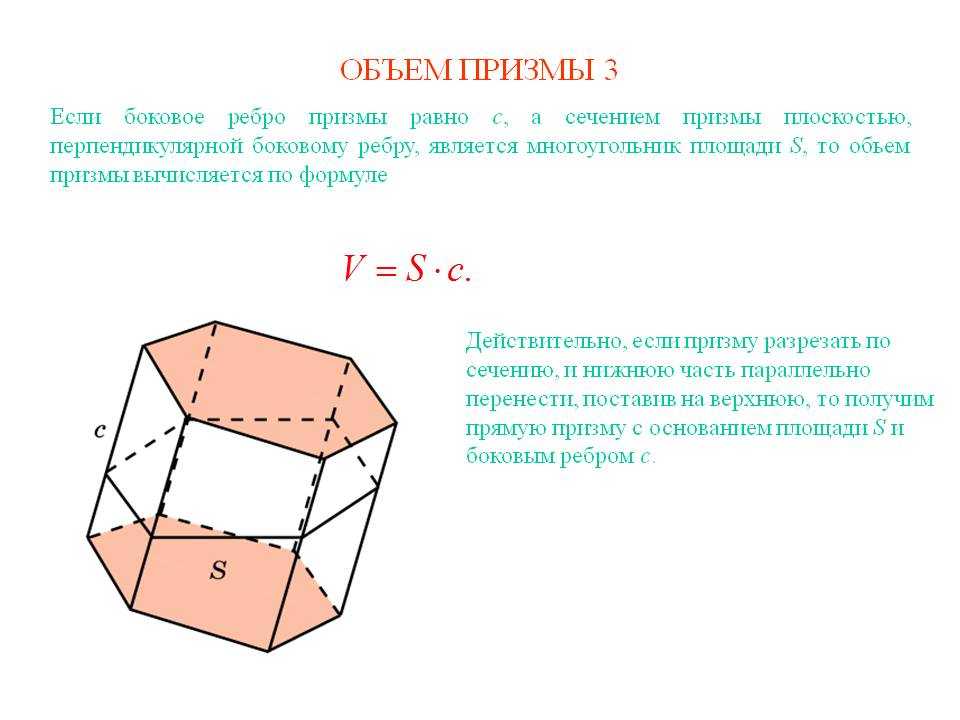 ⓘ Объем треугольной призмы [VT]
ⓘ Объем треугольной призмы [VT]
 = 56 квадратных футов.
= 56 квадратных футов.