Диагональ квадрата как найти пример


Загрузить PDF


Загрузить PDF

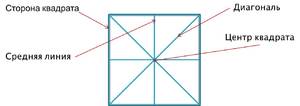
Диагональ квадрата — это отрезок, который соединяет противолежащие углы квадрата и проходит через его центр. Чтобы вычислить диагональ квадрата, воспользуйтесь формулой d=s{sqrt {2}}, где s — сторона квадрата. В задачах требуется найти диагональ квадрата по данному значению другой величины, например, периметра или площади. В этих случаях необходимо использовать другие формулы, чтобы сначала вычислить сторону квадрата, а потом – его диагональ.

  1. Изображение с названием Calculate a Diagonal of a Square Step 1

    1

    Найдите длину стороны квадрата. Скорее всего, значение длины стороны квадрата будет дано в условии задачи. Если же вы работаете с реальным предметом, измерьте его сторону при помощи линейки или рулетки. Так как у квадрата все стороны равны, измерьте или найдите длину любой стороны. Если длина стороны квадрата неизвестна, этим методом пользоваться нельзя.

    • Например, дан квадрат со стороной 5 см.

  2. Изображение с названием Calculate a Diagonal of a Square Step 2

    2

  3. Изображение с названием Calculate a Diagonal of a Square Step 3

    3

    Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо s.

    • Например, если сторона квадрата равна 5 см, формула запишется так:
      d=5{sqrt {2}}

  4. Изображение с названием Calculate a Diagonal of a Square Step 4

    4

    Умножьте сторону квадрата на {sqrt {2}}, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите {sqrt {2}} до 1,414.

    Реклама

  1. Изображение с названием Calculate a Diagonal of a Square Step 5

    1

  2. Изображение с названием Calculate a Diagonal of a Square Step 6

    2

    Подставьте в формулу значение периметра квадрата. То есть данное значение нужно подставить вместо P.

    • Например, периметр квадрата равен 20 см. Запишите формулу так:
      20=4s

  3. Изображение с названием Calculate a Diagonal of a Square Step 7

    3

    Найдите s. Для этого разделите каждую сторону уравнения на 4. В результате будет вычислена сторона квадрата.

  4. Изображение с названием Calculate a Diagonal of a Square Step 8

    4

  5. Изображение с названием Calculate a Diagonal of a Square Step 9

    5

    Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо s.

    • Например, если сторона квадрата равна 5 см, формула запишется так:
      d=5{sqrt {2}}

  6. Изображение с названием Calculate a Diagonal of a Square Step 10

    6

    Умножьте сторону квадрата на {sqrt {2}}, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите {sqrt {2}} до 1,414.

    Реклама

  1. Изображение с названием Calculate a Diagonal of a Square Step 11

    1

  2. Изображение с названием Calculate a Diagonal of a Square Step 12

    2

    В формулу подставьте значение площади квадрата. То есть данное значение нужно подставить вместо A.

    • Например, площадь квадрата равна 25 см2. Запишите формулу так:
      25=s^{{2}}.

  3. Изображение с названием Calculate a Diagonal of a Square Step 13

    3

    Найдите s. Для этого извлеките квадратный корень из значения площади квадрата. В результате будет вычислена сторона квадрата. Воспользуйтесь калькулятором, чтобы извлечь квадратный корень. Если квадратный корень нужно извлечь вручную, прочитайте эту статью.

  4. Изображение с названием Calculate a Diagonal of a Square Step 14

    4

  5. Изображение с названием Calculate a Diagonal of a Square Step 15

    5

    Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо s.

    • Например, если сторона квадрата равна 5 см, формула запишется так:
      d=5{sqrt {2}}

  6. Изображение с названием Calculate a Diagonal of a Square Step 16

    6

    Умножьте сторону квадрата на {sqrt {2}}, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите {sqrt {2}} до 1,414.

    Реклама

Что вам понадобится

  • Калькулятор

Об этой статье

Эту страницу просматривали 425 059 раз.

Была ли эта статья полезной?

Источник

Из школьного курса математики мы знаем, что квадрат — это четырёхугольник у которого все углы прямые, а все стороны равны.

Диагональ — отрезок, соединяющий две противоположные вершины квадрата. Задача нахождения диагонали квадрата может встретиться и после окончания школы. К примеру, при постройке дома у которого фундамент должен быть квадратным. Когда размечается фундамент, мало убедиться, что все 4 стороны равны. Ведь у ромба тоже все стороны равны. И получить ромбовидный фундамент вряд ли кто захочет.

В этом случае, чтобы убедиться в том, что фундамент действительно представляет собой квадрат, вычисляют диагональ квадрата и измеряют обе диагонали фундамента. Если все 4 стороны равны между собой и две диагонали также имеют одинаковую длину — фундамент точно будет квадратным. Для вычисления длины диагонали квадрата достаточно знать длину его стороны и простую формулу.

Как найти диагональ квадрата

d=a cdot sqrt{2}

d — диагональ квадрата

a — сторона квадрата

Достаточно подставить в формулу длину стороны квадрата вместо a.

А можно воспользоваться нашим калькулятором. Просто введите длину стороны и тут же получите длину диагонали квадрата. У нас также можно найти диагональ прямоугольника.

Диагональ квадрата онлайн

Примеры нахождения диагонали квадрата

Найдем диагональ квадрата со стороной 3 см.

Подставим в формулу вместо a число 3 и получим d=3 cdot sqrt{2} = sqrt{3^2 cdot 2} = sqrt{18} = 4,24264

Найдем диагональ квадрата со сторонами 2 на 2 см.

Подставим в формулу вместо a число 3 и получим d=2 cdot sqrt{2} = sqrt{2^2 cdot 2} = sqrt{8} = 2,828427

Ваша оценка

[Оценок: 287 Средняя: 2.9]

Диагональ квадрата формула и расчет Автор admin средний рейтинг 2.9/5 — 287 рейтинги пользователей

Источник

Квадрат – это четырёхугольник, у которого все стороны и углы раны. Он обладает следующими
свойствами:

  • все углы равны между собой и равняются 90;
  • смежные стороны перпендикулярны друг другу;
  • квадрат имеет только две равные диагонали;
  • диагонали в точке пересечения делятся пополам;
  • диагонали перпендикулярны друг другу и являются биссектрисами улов квадрата;
  • радиус описанной окружности равен половине диагонали квадрата;
  • диаметр вписанной окружности равен стороне квадрата.
  • Диагональ квадрата через длину стороны
  • Диагональ квадрата через площадь квадрата
  • Диагональ квадрата через периметр квадрата
  • Диагональ квадрата через радиус описанной окружности
  • Диагональ квадрата через диаметр описанной окружности
  • Диагональ квадрата через радиус вписанной окружности
  • Диагональ квадрата через диаметр вписанной окружности
  • Диагональ квадрата через линию, котороя выходит из угла на
    середину стороны квадрата

Через длину стороны

Чтобы найти диагональ квадрата через длину стороны, необходимо значение стороны а умножить на
квадратный корень из двух. Данная формула выводится из теоремы Пифагора для прямоугольных
треугольников, так как диагональ делит квадрат на два прямоугольных треугольника. Сама диагональ
является гипотенузой данных треугольников. Теорема записывается c² = a² + b², и в данном случае вместо c выступает диагональ d, а вместо
b выступает а, так как катеты равны. Преобразуем: d² = a² + a²; d² = a² * 2. Теперь необходимо извлечь квадратный корень:

D = √(a² * 2)

где D – диагональ квадрата, а – длина стороны.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата d, если сторона квадрата a = 10 см.
Необходимая формула: D = √(a² * 2). Вместо а подставляем значение
10: D = √(10² * 2). После того как находим квадратный корень из двух,
производится умножение и получившееся значение округляем до нужного знака после запятой: D ~ 14,14
см.

Через периметр квадрата

Диагональ квадрата равна отношению периметра P квадрата к произведению четырех на квадратный корень
из двух.

D = P / 4√2

где d – диагональ квадрата, S – периметр квадрата

Цифр после
запятой:

Результат в:

Пример.Необходимо найти диагональ квадрата d, если периметр P = 20 см. Необходимая
формула: D = P / 4√2. Вместо P подставляем значение 20: D = 20 / 4√2.  Получившееся значение округляем до нужного знака после
запятой: D ~ 3,54 см.

Через площадь квадрата

Чтобы найти диагональ квадрата через площадь S, нужно вычислить квадратный корень из произведения S ×
2 . Сама площадь S для прямоугольника имеет формулу S = a * b. Так как
квадрат — это прямоугольник с равными сторонами, формула для площади квадрата S = a². Если
выразить сторону через площадь, формула будет иметь вид: а = √S.

D = √(S * 2)

где D – диагональ квадрата, S – площадь квадрата.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата d, если площадь S = 10 см². Необходимая
формула: D = √(S * 2) Вместо S подставляем значение 10: D = √(10 * 2).  Получившееся значение округляем до нужного знака после
запятой: D ~ 4,47 см.

Через диаметр вписанной окружности

Диагональ квадрата равна произведению диаметра вписанной окружности D на квадратный корень из
двух.

D = d * √2

где D – диагональ квадрата, d – диаметр вписанной окружности.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата d, если диаметр вписанной окружности d =
10 см. Необходимая формула: D = d * √2. Вместо R подставляем значение 10:
d = 10 * √2. Диагональ равна 14,14 см.

Диагональ квадрата через диаметр описанной окружности

Диагональ квадрата равна диаметру d описанной окружности.

D = d

где D – диагональ квадрата, d – радиус описанной окружности.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата d, если диаметр описанной окружности d =
10 см. Необходимая формула: d = D. Вместо d подставляем значение
10. Диагональ равна 10 см.

Через радиус описанной окружности

Диагональ квадрата равна радиусу описанной окружности, умноженному на два.

D = 2R

где D – диагональ квадрата, R – радиус описанной окружности.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата D, если радиус описанной окружности R =
10 см. Необходимая формула: Вместо R подставляем значение 10: D = 2 * 10.
Получившееся значение округляем до нужного знака после запятой: D = 20 см.

Через радиус вписанной окружности

Диагональ квадрата равна произведению удвоенного радиуса вписанной окружности R на квадратный корень
из двух.

D = 2R√2

где D – диагональ квадрата, R– радиус вписанной окружности.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата D, если радиус описанной окружности D =
10 см. Необходимая формула: D = 2R√2. Вместо R подставляем значение 10:
d = 2 * 10 * √2. Диагональ равна 28,28 см.

Через линию, которая выходит из угла на середину стороны квадрата

Диагональ квадрата равна произведению квадратного корня из восьми пятых и линии C, выходящей из угла
на середину стороны квадрата.

D = √(8/5) * C

где D – диагональ квадрата, C – линия, выходящая из угла на середину квадрата.

Цифр после
запятой:

Результат в:

Пример. Необходимо найти диагональ квадрата D, если линия, которая проходит из угла
на середину стороны квадрата С = 10 см. Необходимая формула: D = √(8/5) * C. Вместо R подставляем значение 10: D = √(8/5) * 10. Диагональ
равна 12,64 см.

Источник


Download Article


Download Article

The diagonal of a square is the line stretching from one corner of the square to the opposite corner. To find the diagonal of a square, you can use the formula d=s{sqrt {2}}, where s equals one side length of the square. Sometimes, however, you might be asked to find the length of the diagonal given another value, such as the perimeter or area of the square. In these instances it is necessary to use different formulas first, so that you can determine the side length before using the diagonal formula.

  1. Image titled Calculate a Diagonal of a Square Step 1

    1

    Find the length of one side of the square. This will probably be given to you. If you are working with a square in the real world, use a ruler or piece of measuring tape to find the length. Since all four sides of the square are the same length, you can use any side of the square. If you do not know the length of one side of the square, you cannot use this method.

    • For example, you might want to find the length of the diagonal of a square that has sides 5 centimeters long.

  2. Image titled Calculate a Diagonal of a Square Step 2

    2

    Advertisement

  3. Image titled Calculate a Diagonal of a Square Step 3

    3

    Plug the side length of the square into the formula. Make sure you are substituting for the variable s.

    • For example, if the square has a side length of 5 centimeters, set up the formula like this:
      d=5{sqrt {2}}

  4. Image titled Calculate a Diagonal of a Square Step 4

    4

    Multiply the length of the side by {sqrt {2}}. This will give you the length of the diagonal. It’s best to perform the calculation on a calculator, so that you can get a more precise result. If you don’t have a calculator, you can round {sqrt {2}} to 1.414.

    5. Advertisement

  1. Image titled Calculate a Diagonal of a Square Step 5

    1

  2. Image titled Calculate a Diagonal of a Square Step 6

    2

    Plug the length of the perimeter into the formula. Make sure you are substituting for the variable P.

    • For example, if the perimeter of the square is 20 centimeters, your formula will look like this:
      20=4s

  3. Image titled Calculate a Diagonal of a Square Step 7

    3

    Solve for s. To do this, divide each side of the equation by 4. This will give you the length of one side of the square.

  4. Image titled Calculate a Diagonal of a Square Step 8

    4

  5. Image titled Calculate a Diagonal of a Square Step 9

    5

    Plug the side length of the square into the formula. Make sure you are substituting for the variable s.

    • For example, if the square has a side length of 5 centimeters, set up the formula like this:
      d=5{sqrt {2}}

  6. Image titled Calculate a Diagonal of a Square Step 10

    6

    Multiply the length of the side by {sqrt {2}}. This will give you the length of the diagonal. It’s best to perform the calculation on a calculator, so that you can get a more precise result. If you don’t have a calculator, you can round {sqrt {2}} to 1.414.

    7. Advertisement

  1. Image titled Calculate a Diagonal of a Square Step 11

    1

  2. Image titled Calculate a Diagonal of a Square Step 12

    2

    Plug the area measurement into the formula. Make sure you are substituting for the variable A.

    • For example, if the area of the square is 25 square centimeters, your formula will look like this:
      25=s^{{2}}

  3. Image titled Calculate a Diagonal of a Square Step 13

    3

    Solve for s. To do this, find the square root of the area. This will give you the length of one side of the square. To find the square root, use a calculator. If you need help calculating the square root by hand, read Calculate a Square Root by Hand.

  4. Image titled Calculate a Diagonal of a Square Step 14

    4

  5. Image titled Calculate a Diagonal of a Square Step 15

    5

    Plug the side length of the square into the formula. Make sure you are substituting for the variable s.

    • For example, if the square has a side length of 5 centimeters, set up the formula like this:
      d=5{sqrt {2}}

  6. Image titled Calculate a Diagonal of a Square Step 16

    6

    Multiply the length of the side by {sqrt {2}}. This will give you the length of the diagonal. *It’s best to perform the calculation on a calculator, so that you can get a more precise result. If you don’t have a calculator, you can round {sqrt {2}} to 1.414.

    7. Advertisement

Calculator, Practice Problems, and Answers

Add New Question

  • Question

    How do I calculate the sides of a square if the diagonal is given?

    Donagan

    First square the diagonal’s length. Divide that by two. Then find the square root of that last number. That’s the side of the square.

  • Question

    How do you find the diagonal of a 24 x 24 foot square?

    Community Answer

    Since you know the length of one side (24) you can use method 1:
    d = s x sqrt*2
    d = 24 x 1.414
    d = 33.936

  • Question

    How do I identify a right angle?

    Community Answer

    You’ll know if an angle is right angle if it is 90 degrees.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

Advertisement

Things You’ll Need

  • Calculator

About This Article

Article SummaryX

To calculate a diagonal of a square, multiply the length of one of the square’s sides by the square root of 2. If you don’t know the length of one side, you can find it by plugging the square’s perimeter into the formula: perimeter = 4s, where s is the length of one side. If you don’t know the perimeter, you can still find the length of one side by plugging the square’s area into the formula: area = s^2, where s is the length of one side. For help solving these formulas, keep reading!

Did this summary help you?

Thanks to all authors for creating a page that has been read 759,150 times.

Did this article help you?

Источник

При решении задач по школьной математике часто требуется определить, чему равняется диагональ заданного квадрата. При кажущейся некоторой сложности, эта задача является весьма простой и имеет несколько несложных способов решения. Рассмотрим их, для начала введём некоторые понятия и определения.

Содержание:

  • Определения и соглашения
  • Вычисление диагонали квадрата по известной стороне
  • Вычисление диагонали квадрата по известной площади
  • Вычисление диагонали по известному периметру
  • Вычисление по радиусу описанной и вписанной окружности
  • Заключение
  • Видео

Определения и соглашения

  1. Квадрат — это четырёхугольник с равными сторонами, все углы которого являются прямыми, то есть равны 90 градусов. Данная фигура одновременно и ромб, и прямоугольник, поэтому сохраняет все их свойства.
  2. Диагональ многоугольника — это отрезок, соединяющий две его противоположные вершины. В статье её будем обозначать буквой d.
  3. Противоположными называются вершины, не лежащие на одной стороне.
  4. Корень квадратный из числа, это такое число, которое при умножении само на себя даст исходное. В геометрии используются только положительные значения квадратного корня. В статье его будем обозначать сокращением rad (от латинского radical — корень).
  5. Сторону квадрата будем обозначать буквой a.

Как понятно из вышеизложенного, у квадрата только две диагонали. Поскольку квадрат является прямоугольником и сохраняет его свойства, то они равны между собой. Рассмотрим различные методы нахождения её длины.

Вычисление диагонали квадрата по известной стороне

Самым простым способом является вычисление диагонали, если известна сторона квадрата. Здесь действует широко известная теорема Пифагора для прямоугольных треугольников. Запишем эту формулу: c^2 = a^2+b^2.

Отметим, что в нашем случае диагональ квадрата есть гипотенуза треугольника с равными катетами. Перепишем формулу исходя из наших условий: d^2 = a^2+a^2. Преобразуем, получим: d^2 = 2*a^2. Следующим шагом извлечём квадратный корень, получится: d = rad2*a. Это и есть наша конечная формула.

Рассмотрим вычисление на примере. Пусть a = 64. Подставим наше значение в формулу. Получим d = 64*rad2. Это и есть ответ.

Диагональ квадрата

Вычисление диагонали квадрата по известной площади

Пусть нам дана площадь квадрата, её обозначают латинской буквой S, найдём его диагональ.

Используем свойства прямоугольника и запишем формулу его площади.

S = a*b. Перепишем для b = a. Получим: s = a^2. Отсюда найдём сторону: a = radS. Итак, нам удалось выразить сторону через площадь. Подставим полученное выражение в конечную формулу из предыдущей части. Формула примет вид: d = rad2*a = rad2*radS.

Пример: допустим, площадь равна 32 квадратных метра. Подставим это число. Получим rad2*rad32 = rad2*4*rad2 = 4*2 = 8 метров.

Вычисление диагонали по известному периметру

Пусть нам известен периметр. В дальнейшем его будем записывать латинской буквой P, найдём его d. Воспользуемся свойствами прямоугольника и запишем формулу его периметра.

P = два*(a + b). Перепишем для b = a. У нас получится: P = два*(a + a) = 2*2a = 4*a. Выразим из последней формулы сторону. Имеем: a = P/4. Воспользуемся тем, что: d = rad2*a. Выразим сторону через периметр. Наша формула примет видd = rad2*P/4.

Примере: пусть периметр равен 128 метров. Проведём несложный расчёт. Имеем, rad =d2*128/4 = 32*rad2 метров.

Как найти диагональ

Вычисление по радиусу описанной и вписанной окружности

Ещё один способ, который на само деле очень простой. Радиус описанной окружности будем обозначать латинской буквой R, радиус вписанной окружности будем обозначать латинской буквой r.

Сначала разберёмся с описанной окружностью. В данной ситуации её радиус составляет ровно половину диагонали (это нетрудно убедиться с использованием построения), таким образом: R = 1/2*d. отсюда имеем: d = два*R. Снова поясним наши рассуждения на примере. Пусть R = 45 километров. Получим, d = два*45 = 90 километров.

И, наконец, рассмотрим метод, связанный с радиусом вписанной окружности. Опять-таки из построения чётко видно, что диаметр вписанной окружности равняется стороне квадрата. Таким образом, её радиус вдвое меньше стороны. Запишем это в виде формулы: r = 1/2*a. Отсюда следует, a = 2*r. Снова воспользуемся формулой из первого метода, подставим вместо стороны её выражение через радиус вписанной окружности. Выражение примет вид: d = rad2*a = rad2*2*r.

Ещё раз воспользуемся помощью примера. Пусть r = 98 метров. Тогда имеем, d = rad2*2*98 = 196*rad2.

Заключение

Таким образом, мы рассмотрели в статье пять принципиально различных методов вычисления диагонали квадрата. Если, на первый взгляд, задача казалась сложной, то после проведённых нами рассуждений стало очевидно, что особых проблем здесь нет. Сведём все полученные нами формулы в одну таблицу.

  1. d = rad2*a;
  2. d = rad2*radS;
  3. d = rad2*P/4;
  4. d = 2*R;
  5. d = rad2*2*r.

Хочется ещё отметить, что с помощью первой из наших формул очень легко построить отрезок, равный корню квадратному из двух. Для этого строим квадрат со стороной единица, его диагональ и будет равняться искомому отрезку.

Если на полученной диагонали мы построим прямоугольник, используя её как длину, а ширину возьмём равной единице, то получим отрезок равный ещё одному иррациональному числу корень квадратный из трёх.

Как найти диагональ квадрата

Продолжая нашу цепочку и далее, мы научимся строить отрезки равные любому иррациональному числу.

Видео

Из видео вы узнаете, как найти диагональ квадрата, если известна его площадь.

Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Как составить презентацию сказки
  • Как найти медицинский центр по адресу
  • Как найти альфу на клавиатуре
  • Как исправить приложение опера
  • Как найти координаты центрально симметричной точки

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии