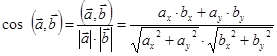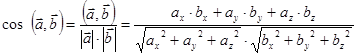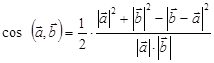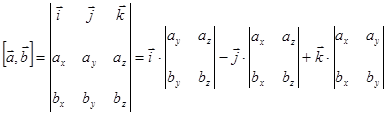Арифметический вектор как найти

Множество
всех одно-, двух- и трехмерных арифметических
векторов обозначают R,
R²
, R³
соответственно, а сами векторы, так же,
как и их геометрические образы: ,
,…
Подчеркнем, что векторы одинаковой
размерности различаются между собой
не только значениями координат, но и
порядком их следования, что совершенно
естественно, имея ввиду геометрический
смысл координат. Например, векторы на
плоскости с координатами (1,2) и (2,1) – это
разные векторы.

Записывают
арифметические векторы либо в виде
строки:

либо в виде столбца:

Форма
записи определяется условиями задачи.
Поскольку построчная запись более
удобна, вектор столбец можно записать
строкой, указав символом «T»
его истинный вид (формула 2.4). Замена
столбца строкой или строки столбцом
называется операцией транспонирования,
отсюда и символ ^«T»
.

Во
множествах арифметических векторов
определены все основные понятия и все
операции, что и во множествах геометрических
векторов.

1.Нуль
вектор.
.

2.Равенство
векторов.
Пусть ,
—
два вектора одинаковой размерности 3 .

3.Норма
вектора.

Норма
вектора — аналог длины геометрического
вектора.
Норма арифметического вектора может
быть определена по-разному. Мы будем
пользоваться нормой, определяемой
следующей формулой:

где
—
координаты .

Если
одно- двух- или трехмерному вектору
соответствует
геометрический вектор
,
то по теореме
Пифагора его длина также определяется
формулой (2.6).

4.
Умножение вектора на число:

5.
Коллинеарность, сонаправленность и
противонаправленность векторов.

Ненулевые
векторы
и

коллинеарны, если существует число 
такое, что

При этом:

Из
(2.8) следует, что два вектора с
ненулевыми
координатами
коллинеарны
тогда и только тогда, когда их координаты
пропорциональны. Пусть
=

,
=,
тогда:

Если
же одна или две координаты вектора
равны
нулю, то одноименные им координаты
коллинеарного вектора также
равны нулю.

6.Нормированный
вектор

или

().

Как
и в случае геометрических векторов,
—
это вектор, норма которого равна 1 , и
который при этом сонаправлен
:

Чтобы
нормировать
вектор,
надо разделить все его координаты на
норму.

7.
Сложение
и вычитание векторов:

9.
Скалярное
произведение арифметических векторов.

Рассмотрим
скалярное произведение арифметических
векторов, опираясь на их геометрические
аналоги.

Пусть
имеем два трехмерных геометрических
вектора:
=
и =,
и два арифметических вектора:
=(),
=.

Пользуясь
свойствами скалярного произведения
(см. стр.), можем записать:

=()()=

=.

По определению
скалярного произведения геометрических
векторов:

.
Аналогично: =1,
=1.

Поскольку
базисные векторы
взаимно перпендикулярны, имеем:

.
Аналогично: .

Используя эти
равенства, получаем:

Скалярное
произведение арифметических векторов
естественно определить в соответствии
с формулой (2.13):

Скалярное
произведение арифметических векторов
или произведение строки на столбец есть
сумма произведений соответствующих
координат векторов.

10.
Векторное
произведение арифметических векторов.

Векторное
произведение арифметических векторов,
как и скалярное, определяют, опираясь
на взаимосвязь геометрических и
арифметических векторов.

Пользуясь
свойствами векторного произведения
геометрических векторов (см. стр.), можем
записать:

=()
()=

=

.

По определению
векторного произведения геометрических
векторов:

.
Аналогично: =,
=.

По
определению векторного произведения
(стр. ) и поскольку ,—
правые тройки векторов (см. рис.1.20 а),
имеем: ,
,
,
а в силу антикоммутативности векторного
произведения: ,
,
.

С учетом этих
равенств получаем:

==

=+.

Векторное
произведение трехмерных арифметических
векторов естественно определить в
соответствии с формулой (2.15):

Если
векторы-отрезки лежат в координатной
плоскости xOy,
то соответствующие им арифметические
векторы имеют вид:
=(),
=,
и их векторное произведение имеет
координаты:

=(,,)
(2.14’’)

Такой
вектор коллинеарен базисному вектору
.

11.Смешанное
произведение арифметических векторов.

Определение
скалярного и векторного произведений
арифметических векторов, позволяет
естественным образом определить их
смешанное произведение. Пусть ,

=(),
=.

=

=—+

Приведенные
в этом разделе формулы широко используются
при решении геометрических задач на
вычисление углов, проекций, площадей,
объемов и т.п. Развитие геометрической
составляющей понятия арифметического
вектора является предметом аналитической
геометрии.
С другой стороны, понятие одно-, двух-
и трехмерных арифметических векторов
допускает естественное обобщение на
векторы произвольной размерности,
которые составляют предмет изучения
линейной
алгебры. Как
видно из схемы изучения курса (см. стр.
), геометрическая и алгебраическая линии
идут параллельно, поэтому изучать их
можно в произвольном порядке. Однако
следует учесть, что исходным пунктом
обеих линий является данный раздел.

Соседние файлы в папке Математика

• #
• #
• #
• #
• #
• #
• #
• #
• #

Арифметическим вектором называется упорядоченная совокупность n чисел.

Обозначается x = (x₁, x₂, …, x_n);

числа x₁, x₂, …, x_n называются компонентами арифметического вектора.

Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число:

для любых x = (x₁, x₂, …, x_n), y = (y₁, y₂, …, y_n) и любого числа α справедливо:

x + y = (x₁+ y₁, x₂ +y₂, …, x_n+ y_n); αx = (αx₁, αx₂, …, αx_n).

Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn.

Вектор θ = (0, 0, …, 0) называется нулевым вектором Rn,

а вектор −x = (−x₁, −x₂, …, −x_n) — противоположным вектором для вектора x в Rn.

Рекомендуемые материалы

Для любых векторов x, y и z из Rn и любых чисел α и β справедливо:

1. x + y = x + y, сложение коммутативно;

2. x + (y + z) = (x + y)+ z, сложение ассоциативно;

3. x + θ = x;

4. x + (−x) = θ;

5. α(x + y) = αx + αy, умножение на число дистрибутивно относительно сложения векторов;

6. α(βx) = (αβ)x, умножение на число ассоциативно;

7. (α + β)x = αx + βx , умножение вектора на число дистрибутивно относительно сложения чисел.

8. 1·x = x.

Пространство Rn − n-мерное векторное пространство, dimRn = n.

Если в пространстве Rn определен естественный базис e₁, e₂, … e_n ,

e₁= (1, 0, 0,…, 0, 0), e₂= (0, 1, 0,…, 0, 0), …, e_n-1= (0, 0, 0,…, 1, 0), e_n= (0, 0, 0,…, 0, 1),

то компоненты вектора x = (x₁, x₂, …, x_n) из Rn являются координатами вектора x в естественном базисе e₁, e₂, … e_n:

x = (x₁, x₂, …, x_n) = x₁e₁+ x₂e₂+ …+ x_ne_n.

Всякое конечномерное n-мерное линейное пространство изоморфно пространству арифметических векторов Rn.

Пример

L − множество 6-мерных арифметических векторов, у которых чётные коомпоненты равны нулю, {x =(x₁, 0, x₂, 0, x₅, 0 )} − трёхмерное линейное пространство, изоморфное пространству арифметических векторов R₃.

Действительно.

2. Заметка — лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

Как видно из приведенных выше соотношений, множество L − трёхмерное линейное пространство (три вектора e₁, e₂и e₃ образуют базис), изоморфное пространству трёхмерных арифметических векторов R₃.

Содержание:

1. Арифметические n-мерные векторные пространства. Векторы и действия над ними. Понятие векторного пространства
2. Скалярное произведение векторов и его свойства
3. Понятие линейной зависимости и независимости векторов

Арифметические n-мерные векторные пространства. Векторы и действия над ними. Понятие векторного пространства

Из школьного курса математики известно понятие вектора — направленного отрезка. Если на плоскости ввести прямоугольную систему координат, то каждому вектору соответствует пара чисел — координат этого вектора. Этот факт записывают так . Аналогично в трехмерном пространстве имеем .

Определение 1. Любая последовательность из действительных чисел называется арифметическим —мерным вектором.

Векторы обозначают: , . Числа задающие вектор , называют координатами вектора. Заметим, что — любое натуральное число, т.е. .

Непосредственный геометрический смысл имеют только одномерные, двухмерные и трехмерные векторы. Первые изображаются направленными отрезками на числовой прямой, вторые — на координатной плоскости, третьи — в координатном пространстве.

Определение 2. Два вектора и с одинаковым числом координат считаются равными, если имеет место покоординатное равенство: = .

Определение 3. Суммой векторов и называется вектор

Определение 4. Произведением вектора на число называется вектор .

Для векторов выполняются следующие свойства:

1. ;

2. ;

3. , где 0 = (0, 0, . . . ,0) — нулевой вектор;

4. , где — = () называется противоположным вектору ;

5. ;

6. ;

7. 1 • = .

Определение 5. Множество всех -мерных арифметических векторов, в котором введены операции сложения векторов и умножения вектора на число, называется арифметическим —мерным векторным пространством и обозначается . Число называется размерностью пространства.

Естественно, что реальный геометрический смысл имеют лишь пространства , , . Пространство при > 3 — абстрактный математический объект. Этот объект удобен для описания реальных процессов, в том числе экономических.

Скалярное произведение векторов и его свойства

Из школьного курса известно, что скалярное произведение векторов обозначается или , и рассчитывается как произведение длин векторов на косинус угла между ними:

. (1)

Введем скалярное произведение векторов из пространства .

Определение 6. Скалярным произведением векторов и называется число .

Перечислим основные свойства скалярного произведения:

1. ;

2. ;

3. ;

4. (, ) > 0, если , и (, ) = 0, если .

С помощью (1) можно ввести в пространстве понятие длины (модуля) вектора :

, (2)

а также понятие косинуса угла между двумя ненулевыми векторами и :

(3)

Пример №1

Даны векторы = (-2,2,0,1) и =(-1,1,1,-1). Найти: 1) ; 2) ; 3) (, ); 4) косинус угла между векторами и .

Решение:

Последовательно вычисляя, имеем:

1) = (4,-4,0,-2) + (-1,1,1,-1) = (3,-3,1,-3);

2) ;

3) (, ) = -2 • (-1) + 2 • 1 + 0 • 1 + 1 • (-1) = 3 ;

4) , .

Пример №2

Предприятие выполняет заказ, для выполнения которого требуются продукты пяти видов (см. табл. 1):

Табл. 1. Данные примера 2

Определить общие затраты на приобретение продуктов.

Решение:

Введем два пятимерных вектора: вектор потребностей = (3,2,5,3,1) и вектор стоимостей = (10,6,2,5,11). Тогда общие затраты — это скалярное произведение векторов и : (, ) = 3 • 10 + 2 • 6 + 5 • 2 + 3 • 5 + 1 • 11 = 78 (тыс. грн.).

Понятие линейной зависимости и независимости векторов

Операции сложения векторов и умножения вектора на число лежат в основе раздела высшей математики, называемого линейной алгеброй. Условимся называть произвольный набор векторов системой векторов и будем ее обозначать .

Определение 7. Пусть даны векторы . Любой вектор вида

(4)

называется линейной комбинацией векторов , а числа коэффициентами этой линейной комбинации.

При наличии равенства (4) говорят, что вектор линейно выражается через векторы или что разлагается по векторам .

Пример №3

Даны векторы =(2, 2, 3), = (0, -4,5), = (3,13, -8). Рассмотрим выражение:

= (6,6,9) -(0,-20,25) -(6,26,-16) = (0,0,0).

Следовательно, вектор (0,0,0) является линейной комбинацией векторов .

Определение 8. Система векторов называется линейно зависимой, если существуют такие числа , не равные одновременно нулю, что выполняется равенство

. (5)

В частности, система из примера 3.1 линейно зависима.

Определение 9. Если система векторов такова, что равенство (5) возможно только при , то эта система называется линейно независимой.

Перечислим некоторые свойства линейной зависимости:

1. Система из одного вектора линейно зависима ;

2. Система, содержащая более одного вектора, линейно зависима в том и только в том случае, когда среди данных векторов имеется такой, который линейно выражается через остальные;

3. Если часть системы линейно зависима, то и вся система линейно зависима (из этого свойства следует, что система, содержащая вектор , линейно зависима);

4. Если система линейно независима, но при добавлении к ней еще одного вектора становится линейно зависимой, то вектор линейно выражается через .

Рассмотрим систему векторов , число которых не превосходит число координат в каждом векторе (т.е. ) Пусть эта система имеет следующим вид:

(6)

Эти векторы имеют координаты , где ( ) означает номер вектора в системе, а означает номер координаты. Причем числа отличны от нуля. Системы вида (6) называют лестничными.

5. Любая лестничная система векторов линейно независима.

Теорема 1. В пространстве любая система из векторов, где >, линейно зависима.

Из теоремы 1 следует, что взяв любые три (или больше) вектора, лежащие в одной плоскости (т.е. принадлежащие пространству ), получим линейно зависимую систему векторов в .

Эта лекция взята из раздела о предмете высшая математика, там вы найдёте другие лекци по всем темам высшей математики:

Другие темы которые вам помогут понять высшую математику:

Математические или физические величины могут быть представлены как скалярными величинами (численным значением), так и векторными величинами (величиной и направлением в пространстве).

Вектор представляет собой направленный отрезок прямой, для которого указано, какая из его граничных точек является началом, а какая — концом. Таким образом, в векторе присутствует две составляющих – это его длина и направление.

Рис.1. Изображение вектора на чертеже.

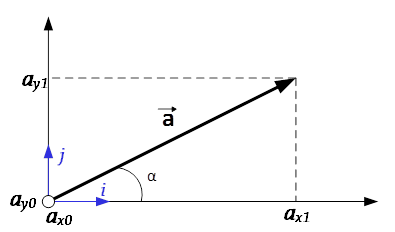
При работе с векторами часто вводят некоторую декартову систему координат в которой определяют координаты вектора, раскладывая его по базисным векторам:

— для вектора, расположенного в пространстве координат (x,y) и выходящего из начала координат 

— для вектора, расположенного в пространстве координат (x,y,z) и выходящего из начала координат 

Расстояние между началом и концом вектора называется его длиной, а для обозначения длины вектора (его абсолютной величины) пользуются символом модуля.

Векторы расположенные либо на одной прямой, либо на параллельных прямых называются коллинеарными. Нулевой вектор считается коллинеарным любому вектору. Среди коллинеарных векторов различают одинаково направленные (сонаправленные) и противоположно направленные векторы. Векторы называются компланарными, если они лежат либо на одной плоскости, либо на прямых, параллельных одной и той же плоскости. 

1. Длина вектора (модуль вектора)

Длина вектора определяет его скалярное значение и зависит от его координат, но не зависит от его направления. Длина вектора (или модуль вектора) вычисляется через арифметический квадратный корень из суммы квадратов координат (компонент) вектора (используется правило вычисления гипотенузы в прямоугольном треугольнике, где сам вектор становится гипотенузой).

Через координаты модуль вектора вычисляется следующим образом:

— для вектора, расположенного в пространстве координат (x,y) и выходящего из начала координат 

— для вектора, расположенного в пространстве координат (x,y,z) и выходящего из начала координат,  формула будет аналогична формуле диагонали прямоугольного параллелепипеда, так как вектор в пространстве принимает такое же положение относительно осей координат. 

2. Угол между векторами

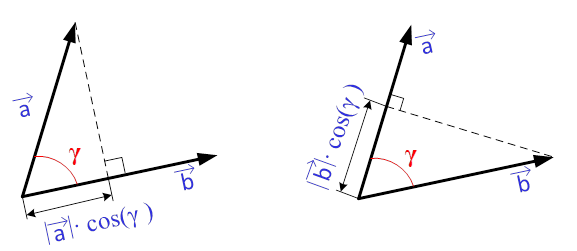
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения второго вектора. Угол между векторами определяется с использованием выражения для определения скалярного произведения векторов

Таким образом, косинус угла между векторами равен отношению скалярного произведения к произведению длин или модулей векторов. Данной формулой можно пользоваться в случае, если известны длины векторов и их скалярное произведение, либо векторы заданы координатами в прямоугольной системе координат на плоскости или в пространстве в виде:  и .

Если векторы A и B заданы в трехмерном пространстве и координаты каждого из них заданы в виде:  и , то угол между векторами определяется по следующему выражению:

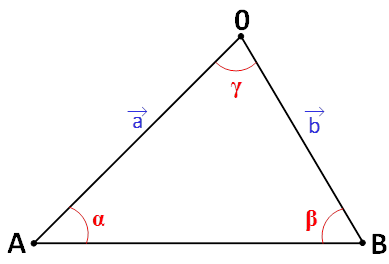
Следует отметить, что угол между векторами  и  можно также определить применяя теорему косинусов для треугольника: квадрат любой стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

где AB, OA, OB – соответствующая сторона треугольника.

Рис.2. Теорема косинусов для треугольника

Применительно к векторным исчислением данная формула перепишется следующим образом:

Таким образом, угол между векторами  и  определяется по следующему выражению:

где  и  — модуль (длина) вектора, а  — модуль (длина) вектора, который определяется из разности двух векторов. Неизвестные входящие в уравнение определяются по координатам векторов  и .

3. Сложение векторов

Сложение двух векторов  и  (сумма двух векторов) — это операция вычисления вектора , все элементы которого равны попарной сумме соответствующих элементов векторов  и . В случае если вектора заданы в прямоугольной системе координат сумму векторов  и  можно найти по следующей формуле:

В графическом виде, сложение двух свободных векторов можно осуществлять как по правилу треугольника, так и по правилу параллелограмма.

Рис.3. Сложение двух векторов

Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало.

Правило треугольника.

Для сложения двух векторов  и  по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Модуль (длину) вектора суммы определяют по теореме косинусов:

где  — угол между векторами, когда начало одного совпадает с концом другого.

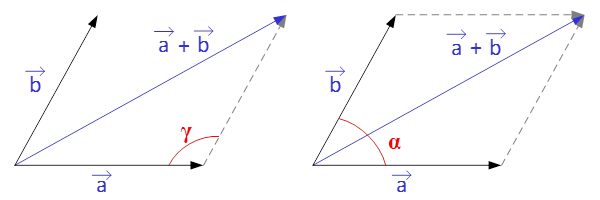
Правило параллелограмма.

Для сложения двух векторов  и  по правилу параллелограмма оба эти вектора переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.

Модуль (длину) вектора суммы определяют по теореме косинусов:

где  — угол между векторами выходящими из одной точки.

Примечание:

Как видно, в зависимости от того какой угол выбирается, изменяется знак перед косинусом угла в формуле для определения модуля (длины) вектора суммы.

4. Разность векторов

Разность векторов  и  (вычитание векторов) — это операция вычисления вектора , все элементы которого равны попарной разности соответствующих элементов векторов  и . В случае если вектора заданы в прямоугольной системе координат разность векторов  и  можно найти по следующей формуле:

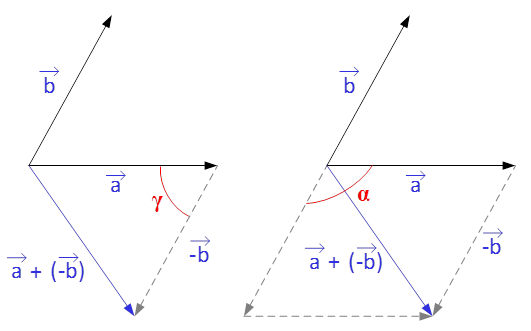
В графическом виде, разностью векторов  и  называется сумма вектора  и вектора противоположного вектору , т.е. 

Рис.4. Разность двух свободных векторов

Разность двух свободных векторов в графическом виде может быть определена как по правилу треугольника, так и по правилу параллелограмма. Модуль (длина) вектора разности определяется по теореме косинусов. В зависимости от используемого угла в формуле изменяется знак перед косинусом (рассматривалось ранее).

5. Скалярное произведение векторов

Скалярным произведением двух векторов называется действительное число, равное произведению длин умножаемых векторов на косинус угла между ними. Скалярное произведение векторов  и  обозначается одним из следующих обозначений  или  или  и определяется по формуле:

где— длины векторов   и  соответственно, а  — косинус угла между векторами.

Рис.5. Скалярное произведение двух векторов

Скалярное произведение также можно вычислить через координаты векторов в прямоугольной системе координат на плоскости или в пространстве.

Скалярным произведением двух векторов на плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов  и .

Таким образом, для векторов  и  на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет следующий вид:

Для трехмерного пространства формула для вычисления скалярного произведения векторов  и  имеет следующий вид:

Свойства скалярного произведения.

1. Свойство коммутативности скалярного произведения

2. Свойство дистрибутивности скалярного произведения

3. Сочетательное свойство скалярного произведения (ассоциативность)

где  — произвольное действительное число.

Следует отметить, что в случае:

если скалярное произведение положительно, следовательно, угол между векторами – острый (менее 90 градусов);

если скалярное произведение отрицательно, следовательно,  угол между векторами  – тупой (больше 90 градусов);

если скалярное произведение равно 0, следовательно, вектора являются ортогональными (которые лежат перпендикулярно друг к другу);

если скалярное произведение равно произведению длин векторов, следовательно, данные векторы коллинеарные между собой (параллельные).

6. Векторное произведение векторов

Векторным произведением двух векторов  и называется вектор  для которого выполняются следующие условия:

1. вектор  ортогонален (перпендикулярен) плоскости векторов  и ;

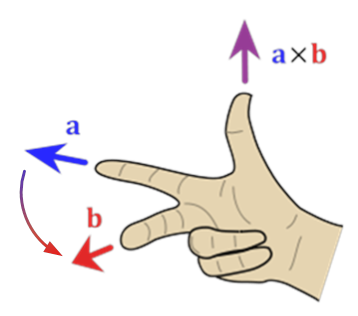
2. направление вектора  определяется по правилу правой руки (вектор  направлен так, что из конца вектора  кратчайший поворот от вектора  к вектору  виден происходящим против часовой стрелки);

Рис.6. Нахождение направления векторного произведения с помощью правила правой руки.

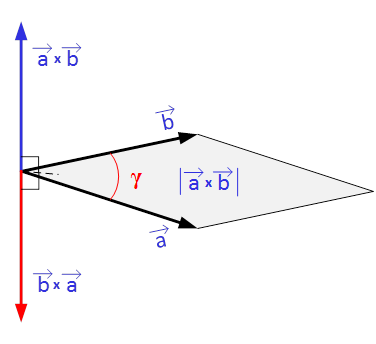
3. длина вектора   равняется площади параллелограмма, образованного векторами, и может быть определена из выражения, равного произведению длин умножаемых векторов на синус угла между ними.

Векторное произведение векторов  и  обозначается следующим образом  (или ), а  длина (модуль) векторного произведения определяется по формуле:

где— длины векторов   и  соответственно, а  — синус угла между векторами.

Векторное произведение векторов отличается от скалярного произведения тем, что оно представляет собой не просто число, а вектор, имеющий свое собственное направление (направление обуславливает трехмерность системы). Таким образом, векторное произведение векторов по определению возможно только в трехмерном пространстве, где у каждого вектора указаны три координаты (i,j,k). Векторное произведение не обладает свойствами коммутативности в отличие от скалярного произведения векторов.

Рис.7. Векторное произведение двух векторов

Векторное произведение также можно вычислить через координаты векторов в прямоугольной системе координат в пространстве.

Свойства векторного произведения.

1. Свойство антикоммутативности векторного произведения

2. Свойство дистрибутивности векторного произведения

3. Сочетательное свойство векторного произведения (ассоциативность)

где  — произвольное действительное число.

Следует отметить, что в случае:

если векторное произведение равно 0, следовательно, вектора являются коллинеарными (вектора параллельны друг другу);

если векторное произведение равно произведению длин векторов, следовательно, вектора являются ортогональными (которые лежат перпендикулярно друг к другу).